2. 渤海造船厂集团有限公司,辽宁 葫芦岛 125005;
3. 大连理工大学船舶工程学院,辽宁 大连 116024
2. Bohai Shipyard Group CO., Ltd., Huludao 125005, China;
3. School of Naval Architecture and Ocean Engineering, Dalian University of Technology, Dalian 116024, China
浮筏隔振系统是将多台设备置于一个中间平台上,此隔振平台能大幅减小动力机械振动和噪声,并能提高设备工作的稳定性。浮筏隔振系统已在舰船上大量的使用并取得了非常理想的减振降噪效果[1],但是也面临过多占用总体重量和空间的矛盾。因此,为了进一步提高浮筏隔振系统的使用性能,同时降低浮筏隔振装置重量和空间尺寸,对浮筏隔振系统进行优化设计和隔振特性研究具有极其重要的意义和相当大的工程应用价值[2]。
针对浮筏隔振系统,筏体的结构及其质量的不同对其隔振性能有较大的影响,浮筏隔振系统的筏体结构通常是板架或框架结构,很多学者将筏体结构的板厚或者尺寸作为优化设计的变量,从而进行结构优化研究[3 – 6]。一些研究人员对影响浮筏隔振系统隔振效果的因素进行了大量的探讨,具有极其重要的参考价值[7 – 10]。一些学者研究了浮筏隔振系统的动力学模型和功率流传递特点,对浮筏隔振性能的优劣评定做出了重要贡献[11–12]。Xiong等[13]将等效导纳矩阵的概念应用于多输入多输出的复杂耦合系统,对其振动功率流传递特性进行研究。伍先俊等[14]阐述了将有限元计算应用于功率流研究的可能性。
本文将基于Optistruct优化软件进行浮筏隔振系统筏体结构形式的拓扑优化研究,旨在通过对筏体结构的优化设计,使其在保证隔振效果的情况下,重量可以大大减轻。并对优化后的结构进行功率流分析,研究浮筏隔振系统的振动特性。
1 筏体结构拓扑优化设计结构拓扑优化技术是目前结构优化中比较突出的技术,其可以在给定的设计空间内,在给定的外载荷和边界条件下找到最佳的结构材料分布,实现结构性能的最优设计。
变密度法是应用最广泛的拓扑优化方法之一,其中心思想是引入一种假定的密度可变的材料。将材料密度作为优化设计变量,结构的拓扑优化问题就被转变成了材料的最优分布问题,从而建立数学模型如下:
| $ \left\{ \begin{array}{l} {\rm{Find}}\;\;\;\;x = {({x_1},{x_2}\text{,} \cdots ,{x_n})^{\rm T}}\text{,}\\ {\rm Min}\;\;\;\;C\left( x \right) = {F^{\rm T}}U\text{,}\\ {\rm s.t.}\;\left\{ \begin{array}{l} V \leqslant f{V_0}\text{,}\\ F = KU\text{,}\\ 0 < {x_{\min }} \leqslant {x_i}\leqslant 1\text{,}(i = 1,2, \cdots ,n)\text{。} \end{array} \right. \end{array} \right. $ | (1) |
式中:
固体各向同性材料惩罚模型(SIMP)是变密度法常用的插值模型,它为了使结构在拓扑优化过程中不会出现中间密度单元,引入惩罚因子,方便结构在实际工程中的加工制造,其数学模型如下:
| ${E_i} = x_i^p{E_0}\text{,}\;\;\;\;\;\left( {i = 1,2, \cdots ,n} \right)\text{。}$ | (2) |
式中:Ei为单元i的弹性模量,E0为实体部分材料单元(即xi=1)的弹性模量;p为惩罚因子;xi为单元相对密度。
本文采用的算法为优化准则法,其具有物理概念简单,易于程序化,求解问题效率高等优点,是拓扑优化技术中应用较广泛的算法之一。基于SIMP插值模型的最小柔度拓扑优化问题的模型如下:
| $ \left\{ \begin{array}{l} F{\rm{ind}}\;\;\;\;x = {({x_1},{x_2}, \cdots ,{x_n})^{\rm T}}\text{,}\\ Min\;\;\;\;C\left( x \right) = {F^T}U = {U^{\rm T}}KU =\\ \begin{array}{*{20}{c}} {}&{} \end{array}\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{} \end{array}}&{} \end{array}\displaystyle\sum\limits_{i = 1}^n {x_i^p{u_i}^T{k_0}{u_i}} \text{,}\\ {\rm{s.t.}}\;\left\{ \begin{array}{l} V = \displaystyle\sum\limits_{i = 1}^n {{x_i}{v_i}} \leqslant f{V_0}\text{,}\\ F = KU\text{,}\\ 0 < {x_{\min }} \leqslant {x_i} \leqslant 1\text{,}({{i}} = 1,2, \cdots ,{{n}})\text{。} \end{array} \right. \end{array} \right. $ | (3) |
分析SIMP插值函数模型,利用结构刚度矩阵的对称性,可得到下式:
将
| $ \frac{{p{{\left( {{x_i}} \right)}^{\left( {p - 1} \right)}}u_i^{\rm T}{k_0}{u_i}}}{{{\lambda _1}{v_i}}} = 1\text{,} $ | (4) |
令
考虑优化准则法中设计变量的上下限,可得到相应的迭代公式如下:
| $ x_i^{k + 1} = \left\{ \begin{array}{l} {\left( {C_i^k} \right)^\xi }x_i^k\;\;if \text{,}\;\;\;{x_{\min }} < {\left( {C_i^k} \right)^\xi }x_i^k < 1\text{,}\\ {x_{\min }}\text{,}\;\;\;\;\;\;\;\;\;{\rm if}\;\;\;{\left( {C_i^k} \right)^\xi }x_i^k < {x_{\min }}\text{,}\\ 1\text{,}\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm if}\;\;\;\;{\left( {C_i^k} \right)^\xi }x_i^k \geqslant 1\text{。} \end{array} \right. $ | (5) |
式中:
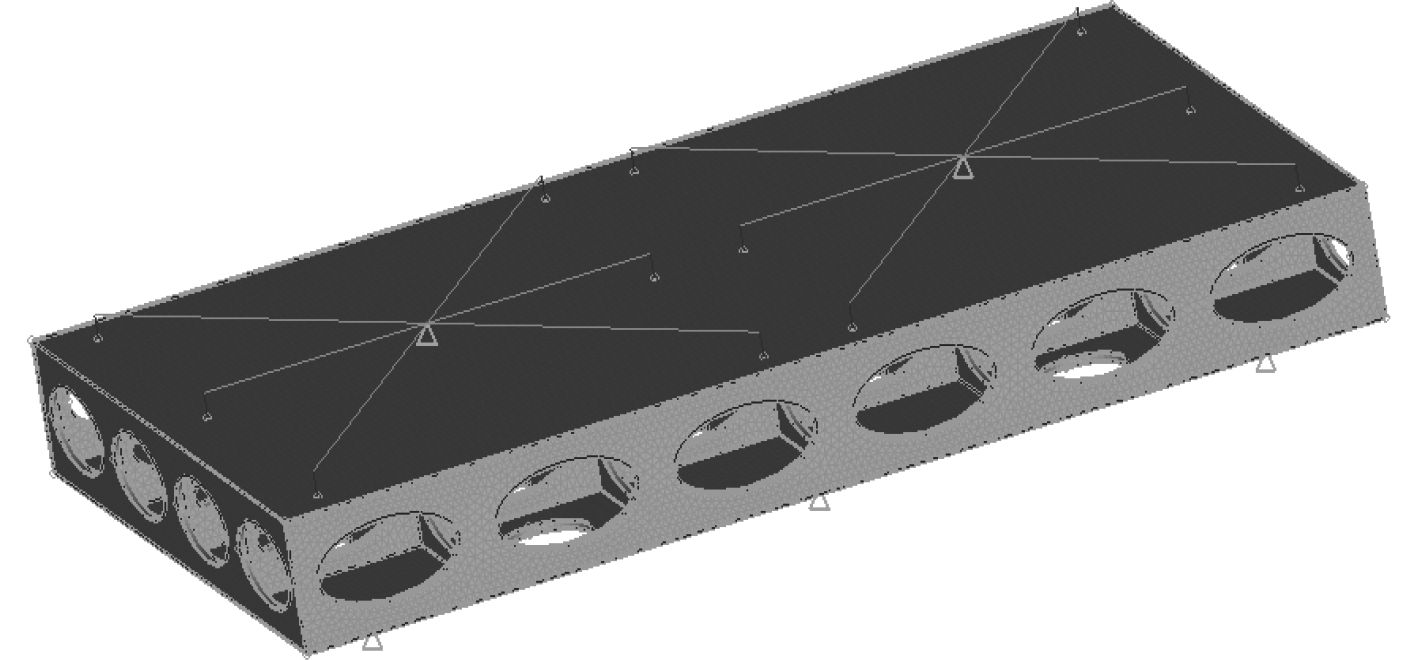
本文采用变密度法对浮筏隔振系统进行拓扑优化分析,使筏体在满足隔振特性的前提条件下,质量最小。优化对象为某舰艇空气压缩机浮筏隔振装置的中间筏体,该浮筏上对称布置2台空气压缩机组,单台设备质量500 kg,筏体材料为Q235钢,筏体的上下表面设置垫板作为隔振器安装点。上层减振器为12个BE120型橡胶减振器,额定载荷为120 kg,额定载荷固有频率约10 Hz,动刚度为480 N/mm,静刚度为300 N/mm,阻尼比为0.07~0.11;下层减振器为6个BE400型橡胶减振器,额定载荷为400 kg,额定载荷固有频率约10 Hz,动刚度为1 610 N/mm,静刚度为1 000 N/mm,阻尼比为0.07~0.11。在初始筏体的表面设置硬点来连接隔振器,并用PSOLID单元来离散优化空间,从而建立筏体结构的有限元模型如图1所示。本文采用CONM2单元来模拟机械设备的质量,共2台,其大小均为1 000 kg。隔振器采用CELAS1单元来进行模拟,可设置刚度和阻尼值。CONM2单元与上层隔振器的上端进行多点约束(RBE2单元),以此来确保机械设备和隔振器上端的运动保持一致。
|
图 1 Optistruct中的有限元模型 Fig. 1 The raft’s finite element model by Optistruct |
在建立筏体的拓扑优化有限元模型之后,针对优化模型进行相关的优化设置:
1)优化变量:离散结构的优化空间之后,每个离散单元的材料相对密度(其值在0~1之间)。
2)优化响应:上层隔振器与筏体连接点处的静力位移(共12个);下层隔振器与筏体连接点处的静力位移(共6个);筏体的质量。
3)优化约束:筏体上部承载有较大重量的机械设备,除了需要考虑整个浮筏隔振系统的隔振性能,还需要保证筏体结构上的响应较小,即具有一定程度的强度,以此来保证整个系统的承载。因此,优化模型中以下端隔振器与筏体连接的6个节点的位移以及上端隔振器与筏体连接的12个节点的位移为约束条件。
4)优化目标:筏体在满足一定隔振特性和刚度的前提条件下,质量最小。
2 筏体结构拓扑优化结果分析通过拓扑优化迭代计算,计算收敛,从而得到拓扑优化结果,即设计空间的材料密度分布云图,如图2所示。

|
图 2 优化后密度分布云图 Fig. 2 The density nephogram of optimized raft |
从上面密度分布云图中可以看出,在上层隔振器和下层隔振器与筏体连接点处密度比较集中,筏体中心处以及靠近筏体边缘的位置,材料分布较少。因此在进行筏体结构设计时,可以对面板和肋板进行减重设计。
拓扑优化迭代计算得到的仅仅是满足结构优化设置的材料密度分布情况,在优化结果的基础上考虑工程实际应用中的筏体结构,根据OSSmooth的尺寸数据,经过规则化处理,在上下面板材料分布较少的位置增设减轻孔,并将受力不大的肋板变薄,最终优化筏体结构如图3所示。

|
图 3 优化筏体结构图 Fig. 3 Optimized raft’s structure drawing |
为了跟拓扑优化中的模型保持一致,将下层隔振器的下端施加全约束,并将浮筏的基础视为刚体。使用Ansys中的shell63单元来离散浮筏筏体结构,使用COMBIN14单元来模拟弹簧隔振器,进行有限元建模仿真。
1)优化筏体的模态和振型
在Ansys中进行优化筏体的建模,并对其进行有限元分析,计算得到优化筏体的前四阶固有频率和振型,如图4所示。

|
图 4 优化筏体前四阶固有振型 Fig. 4 The previous four natural modes of optimized raft |
优化后筏体质量减少了约20%,但由表1可以看出优化筏体前四阶固有频率高于初始筏体,说明优化筏体在质量大大减轻的情况下,仍具有较好的刚度。
|
|
表 1 优化前后筏体前四阶固有频率(Hz) Tab.1 The previous four natural frequencies of before and after optimization raft |
2)初始筏体和优化筏体的应力分布
在Ansys中建立初始筏体与优化筏体的有限元模型,除中间筏体结构形式外,其余参数(包括设备重量、隔振器参数等)设置相同。对其进行静力分析,得到应力分布结果如图5所示。

|
图 5 优化前后筏体结构应力对比图 Fig. 5 The stress diagram of before and after optimization raft |
由图5和表2中数据可以看出,优化后筏体最大应力与初始筏体相差不大,并且远远小于材料的屈服应力。
|
|
表 2 优化前后筏体最大应力值 Tab.2 The maximum stress of before and after optimization raft |
本文采用功率流的分析手段来探讨浮筏隔振系统中振动能量传递的特性。功率流方法既考虑到了传到结构上的力,也考虑到了传到结构上的速度,具有更佳的评定价值,同时功率流方法能给出了振动传输的一种绝对度量。
可将力和位移分别写成下式:
| $ F\left( t \right) = \operatorname{Re} \left\{ {\tilde F \cdot {e^{i\omega t}}} \right\}\text{,} $ | (6) |
| $X\left( t \right) = \operatorname{Re} \left\{ {\tilde X \cdot {e^{i\omega t}}} \right\}\text{,}$ | (7) |
| $ \begin{array}{l} P = \dfrac{1}{T}\displaystyle\int_0^T {F\left( t \right)} \cdot V\left( t \right) \cdot {\rm d}t= \\ \ \ \ \mathop {}\limits^{} \dfrac{1}{T}\displaystyle\int_0^T {{\mathop{\rm Re}\nolimits} \left\{ {\tilde F \cdot {e^{i\omega t}}} \right\}} \cdot {\mathop{\rm Re}\nolimits} \left\{ {i\omega \tilde X \cdot {e^{i\omega t}}} \right\} \cdot {\rm d}t\text{。} \end{array} $ | (8) |
式中
令
| $ \begin{split} P =& \dfrac{1}{T}\displaystyle\int_0^T {\left[ {F'\cos \omega t - F''\sin \omega t} \right]}\times \\ &\left( { - \omega } \right)\left[ {X'\sin \omega t + X''\cos \omega t} \right] \cdot {\rm d}t= \\ &\left( { - \omega } \right) \times \left( {\dfrac{1}{2}F'X'' - \dfrac{1}{2}X'F''} \right) ={\text{π}}f\left( {X'F'' - F'X''} \right)\text{。}\!\!\!\! \end{split} $ | (9) |
浮筏隔振系统的有限元模型如图6所示,对于代表机械设备的质量点施加垂直方向的简谐集中力,对于下层隔振器的下端施加全约束。对整个浮筏隔振系统进行谐响应分析,获取其在简谐激励下的动态响应数据。为了获得某点处的功率流,选取该处隔振器与筏体连接的节点的位移响应和广义内力,代入式(10)即可。但按此方法求出的仅仅是各个节点处的功率流,为了提高计算的可靠性和精确度,将响应节点的功率流进行叠加,然后再进行对比分析。

|
图 6 优化前后浮筏隔振系统有限元模型 Fig. 6 The finite element model of before and after optimization floating raft |
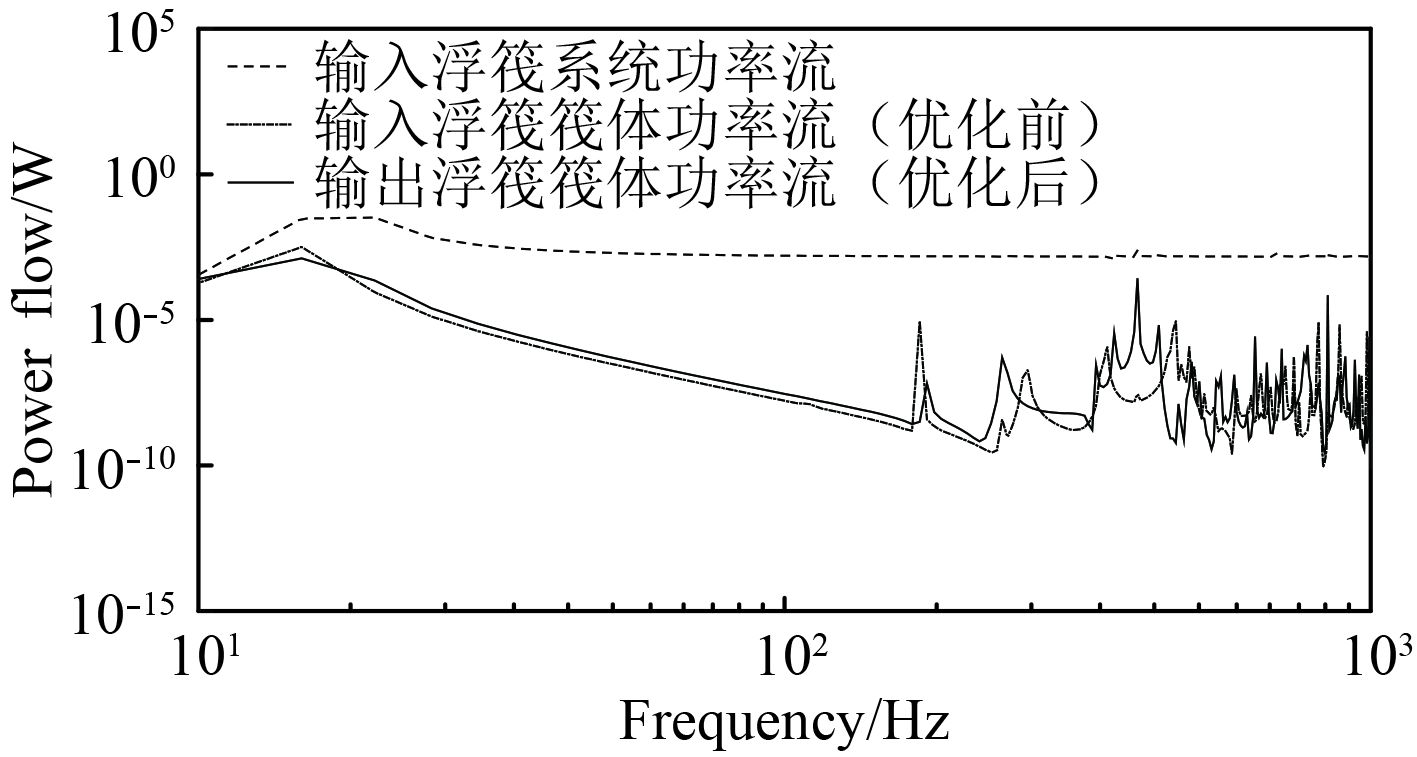
实际工程应用中,垂直方向的能量是浮筏系统中传递的主要振动能量形式。通过有限元仿真分析,得到优化前后垂直方向上的输入浮筏系统、输出浮筏筏体的功率流对比图,如图7所示。
|
图 7 优化前后浮筏隔振系统功率流传递曲线 Fig. 7 The powerflow's transfer curve of before and after optimization floating raft |
优化后筏体质量减少了约20%,但由图7可以看出,其依旧有较好的隔振性能。说明在优化前后筏体的隔振效果差异不大,但是筏体重量却大大减小,本文较好地改造了筏体的结构。由图7可以进一步看出,浮筏隔振平台中高频区域的振动衰减效果相对于低频区域要更好。
5 结 语本文借助于有限元技术和优化算法,建立浮筏隔振系统的拓扑优化模型,并对其进行了优化。经过规则化处理,得到满足优化约束条件的浮筏隔振系统。使用有限元分析软件建立了浮筏隔振系统的有限元仿真模型并进行了谐响应分析,绘制出了功率流传递曲线图。通过有限元分析证明优化后的筏体结构在重量减轻的情况下,仍具有较好的隔振性能。本文将拓扑优化用于浮筏隔振系统结构设计的方法能很好地满足工程需要,具有重要的应用价值。
| [1] |
马永涛, 周炎. 舰船浮筏隔振技术综述[J]. 舰船科学技术, 2008, 30(4): 22-26. DOI:10.3404/j.issn.1672-7649.2008.04.002 |
| [2] |
张乐. 浮筏系统隔振优化设计[J]. 中国水运, 2014, 14(2): 150-151. |
| [3] |
杨德庆, 郭凤骏. 振级落差约束下齿轮箱基座拓扑构型设计[J]. 振动与冲击, 2008, 27(6): 173-177. DOI:10.3969/j.issn.1000-3835.2008.06.040 |
| [4] |
汪玉, 陈国钧, 华宏星, 等. 船舶动力装置双层隔振系统的优化设计[J]. 中国造船, 2001, 42(1): 45-49. DOI:10.3969/j.issn.1000-4882.2001.01.008 |
| [5] |
刘克龙, 姚卫星, 穆雪峰. 基于Kriging代理模型的结构形状优化方法研究[J]. 计算力学学报, 2006, 23(3): 344-347. DOI:10.3969/j.issn.1007-4708.2006.03.017 |
| [6] |
赵晓明, 黄浩. 基于ANSYS的舰艇浮筏隔振系统特性[J]. 机电设备, 2017, 34(3): 1-4. |
| [7] |
严济宽, 沈密群, 尚国清. 浮筏结构动力参数的选定[J]. 噪声与振动控制, 1995(1): 2-9. |
| [8] |
华宏星, 林莉. 浮筏系统频率响应灵敏度分析[J]. 中国造船, 1999(3): 92-97. |
| [9] |
张华良, 傅志方. 浮筏隔振系统各主要参数对系统隔振性能的影响[J]. 振动与冲击, 2000, 19(2): 5-8. DOI:10.3969/j.issn.1000-3835.2000.02.002 |
| [10] |
郑学贵. 舰船浮筏减振特性研究[J]. 舰船科学技术, 2018(2): 7-9. |
| [11] |
SCIULLIA, D. D. J. Inmanb. Isolation design for a flexible system[J]. Journal of Sound and Vibration, 1998, 246(N0. 2): 251-267. |
| [12] |
LI, W. L., M. DANIELSW. ZHOU. Vibrational power transmission from a machine to its supporting cylindrical shell[J]. Journal of Sound and Vibration, 2002, 257(2): 283-299. DOI:10.1006/jsvi.2001.3835 |
| [13] |
XIONG, Y P, J T XINGW G. Price. Power flow analysis of complex coupled systems by progressive approaches[J]. Journal Of Sound And Vibration, 2001, 239(2): 275-295. DOI:10.1006/jsvi.2000.3159 |
| [14] |
伍先俊, 朱石坚. 基于有限元分析的功率流计算技术及隔振系统优化设计[J]. 船舶力学, 2005, 9(4): 138-145. DOI:10.3969/j.issn.1007-7294.2005.04.019 |
 2019, Vol. 41
2019, Vol. 41
