人字齿轮凭借其承载力大、轴向力相互抵消以及传动平稳等特点,在船舶传动系统中得到了广泛的应用,而其动态特性是衡量设计优劣的重要指标之一[1]。在实际传动过程中,人字齿轮很难达到理想啮合条件而会造成啮合冲击的出现,影响因素有制造和安装误差、轮齿承载间隙以及热变形等[4]。其中,由于制造和安装误差以及齿轮轴颈涡动导致的啮合中心距的改变,也会影响齿侧间隙的改变,进而产生啮合冲击[5]。因而开展人字齿轮啮合响应的分析研究,对降低齿轮噪声、提高系统疲劳寿命有着积极的意义。已有的研究虽然对造成齿轮啮合冲击的因素进行了较为深入的探讨,但有关考虑中心距变化对啮合冲击造成影响的研究相对较少。为此,本文主要研究齿轮啮合中心距变化的影响,在不考虑啮合误差和弹流润滑的情况下,建立齿轮系统的动力学模型,并通过动力学仿真软件ADAMS得到中心距变化对齿轮副动力学特性的影响,为合理选择轴承配合公差,进一步改善舰船用齿轮传动系统动态特性提供参考。
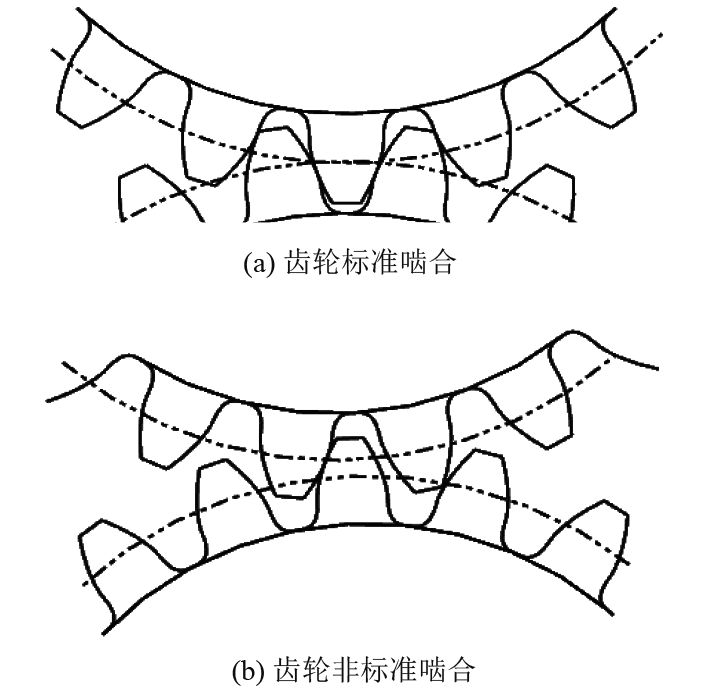
1 齿轮啮合动力学模型在不考虑轮齿承载变形以及加工误差的条件下,轮齿啮合过程中,由于齿轮副的中心距改变,使轮齿啮合产生基节误差,如图1所示,图1(a)中齿轮处于标准啮合状态,中心距等于两齿轮分度圆半径之和,齿轮能够平稳传动。图1(b)中,实际中心距大于标准中心距,当轮齿进入啮合时,实际啮合起始点偏离理论啮合起始点,引起啮入冲击,同理在啮出时也会产生啮出冲击。齿轮啮合产生的冲击激励是齿轮传动系统的内部激励源之一[8]。
|
图 1 齿轮啮合状态示意图 Fig. 1 Schematic diagram of gear meshing |
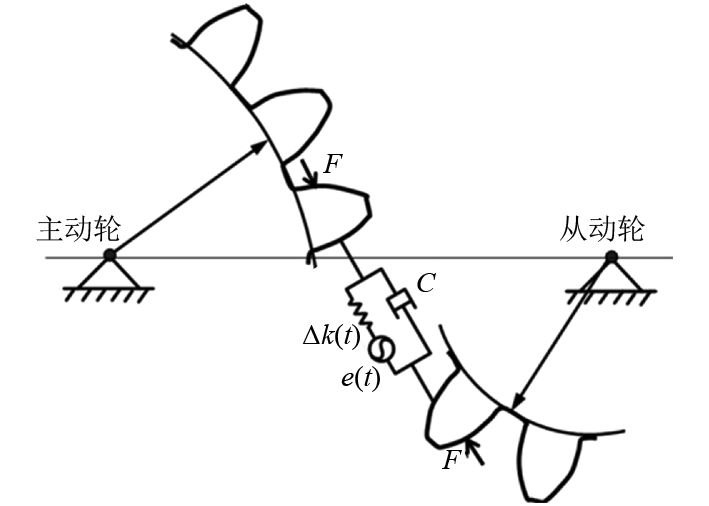
分析齿轮啮合冲击时,可以把啮合齿轮对简化为一振动模型,如图2所示。这种模型不考虑齿轮的横向振动,只考虑齿轮副的扭转振动。该模型中,
|
图 2 齿轮啮合振动模型 Fig. 2 Gear meshing vibration model |
| $ m\ddot x + c\dot x + k(t)[{{x}} + {{{x}}_s} + {{e}}({{t}})] = {{F}}(t){\text{,}} $ | (1) |
改写方程,同时忽略相对位移后有:
| $ m\ddot x + c\dot x + \bar kx = - \Delta k(t){{e}}({{t}}) + s(t) + {{F}}(t), $ | (2) |
| $ s(t) = - \Delta k(t)x - \bar k {{e}}({{t}}){\text{。}} $ | (3) |
式中:
为方便问题的讨论,在分析时引入一些假设:认为齿轮是刚体;无弹流润滑作用;齿轮制造没有误差。虽然假设会对分析结果带来一定的局限性,但其能对理论分析和仿真进行简化,使得系统动力特性的阐述简单明了。
2.1 人字齿轮啮合刚度激励由于在齿轮传动过程中,同时参与啮合的轮齿对数随着时间而周期变化,因而引起了轮齿啮合刚度的周期变化,从而引起啮合力的周期变化[9]。与此同时,当啮合齿轮副的中心距发生变化时,也会导致啮合刚度的变化。由啮合刚度变化而引起的动态激励称之为刚度激励[3]。
本文主要研究中心距对啮合刚度的影响,因此先忽略齿轮传动中由于啮合齿轮对不同造成的啮合刚度的变化,此时理论单齿刚度计算公式为[10]:
| $ \begin{split} {k^{'}} =& 1/(0.047\;23 + \dfrac{{0.155\;1}}{{{z_1}}} + \frac{{0.257\;91}}{{{z_2}}}- \\ & 0.006\;35{{{{X}}}_1} - 0.001\;93{{{{X}}}_2}- 0.116\;54\dfrac{{{X_1}}}{{{z_1}}}- \\ &0.241\;88\frac{{{X_2}}}{{{z_2}}} + 0.005\;29{X_1}^2 + 0.001\;82{{{{X}}}_2}^2)\text{。} \end{split} $ | (4) |
式中:
当重合度
| $ {k_{\rm{G}}}^{'}{\rm{ = }}{{\rm{C}}_R}{b_y}(0.75\varepsilon + 0.25){k^{'}} \times {10^6}\text{。} $ | (5) |
式中:
斜齿轮的重合度由2部分组成:
| $ {\varepsilon ^{'}} = {\varepsilon _\alpha } + {\varepsilon _\beta }\text{,} $ | (6) |
式中
| $ {\varepsilon _\alpha } = [{z_1}(\tan {\alpha _{at1}} - \tan {\alpha _t}^{'}) + {z_2}(\tan {\alpha _{at2}} - \tan {\alpha _t}^{'})]/2{\text{π}}, $ | (7) |
| $ {\varepsilon _\beta } = {b_y}\sin \beta /({\text{π}} {{{m}}_n})\text{。} $ | (8) |
式中:
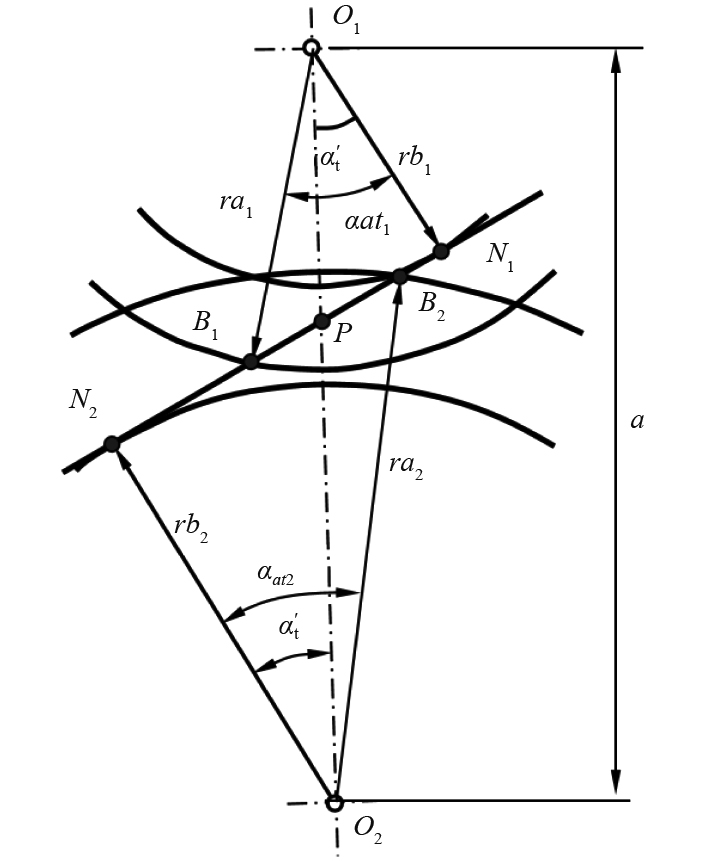
图3为齿轮啮合传动示意图,图中
|
图 3 斜齿轮端面啮合几何模型 Fig. 3 Geometric model of helical gear end face meshing |
| $ \tan {\alpha _t}^{'} = \frac{{\sqrt {{a^2} - {{({{{r}}_{b1}} + {{{r}}_{b2}})}^2}} }}{{{{{r}}_{b1}} + {{{r}}_{b2}}}}\text{。} $ | (9) |
结合式(4)、式(5)可整理得到斜齿轮啮合刚度与啮合中心距的关系为:
| $ \begin{split} {k_{\rm{G}}}^{'}{\rm{ = }}&{{\rm{C}}_R}{b_y}\Biggr(0.75\Biggr(\Biggr[{z_1}\Biggr(\tan {\alpha _{at1}} - \frac{{\sqrt {{a^2} - {{({{\rm{r}}_{b1}} + {{\rm{r}}_{b2}})}^2}} }}{{{{\rm{r}}_{b1}} + {{\rm{r}}_{b2}}}}\Biggr)+ \\ & {z_2}\Biggr(\tan {\alpha _{at2}} - \frac{{\sqrt {{a^2} - {{({{\rm{r}}_{b1}} + {{\rm{r}}_{b2}})}^2}} }}{{{{\rm{r}}_{b1}} + {{\rm{r}}_{b2}}}}\Biggr)\Biggr]/2{\text{π}}+ \\ & b\sin \beta /({\text{π}} {{\rm{m}}_n})) + 0.25\Biggr){k^{'}} \times {10^6}\text{。} \end{split} $ | (10) |
人字齿轮由1组螺旋角旋向相反其他参数相同的斜齿轮组合而成,因而人字齿轮与相对应的斜齿轮的啮合刚度、重合度的关系为:
| $ \left\{ \begin{array}{l} {k_{\rm{G}}}{\rm{ = 2}}{k_{\rm{G}}}^{'},\\ \varepsilon = 2{\varepsilon ^{'}}\text{。} \end{array} \right. $ | (11) |
其中:
由于加工误差、齿轮轴颈涡动等原因,齿轮副的实际中心距会变化。受制于齿轮的设计参数,标准斜齿轮中心距的最小值等于标准啮合值
| $ {a_s} = {m_n}({{\rm{z}}_1} + {{\rm{z}}_2})/2 \cos(\beta ), $ | (12) |
同时要保证齿轮对啮合的连续性,一般取重合度
| $ [{z_1}(\tan {\alpha _{at1}} - \tan {\alpha _t}^{'}) + {z_2}(\tan {\alpha _{at2}} - \tan {\alpha _t}^{'})]/2{\text{π}} \geqslant 1.2, $ | (13) |
结合式(9)可得:
| $ a \!\leqslant\! \frac{{{{\rm{r}}_{b1}} + {{\rm{r}}_{b2}}}}{{{z_1} + {z_2}}}\sqrt {[{{({z_1}\tan {\alpha _{at1}} + {z_2}\tan {\alpha _{at2}} - 2.4{\text{π}})}^2} + {{({z_1} + {z_2})}^2}]} \text{。} $ | (14) |
表1为某型船用齿轮箱人字齿轮副参数。将表中的数据代入式(14)可得:
|
|
表 1 某型船用齿轮箱啮合齿轮副参数 Tab.1 A certain type of marine gearbox meshing gear pair parameters |
由上述计算可知,为保证齿轮能够连续啮合,齿轮的中心距范围是
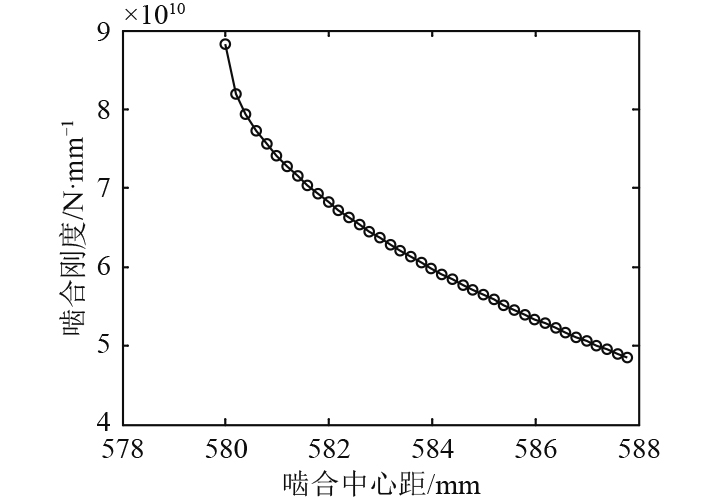
|
图 4 人字齿轮啮合刚度与中心距的关系 Fig. 4 Relationship between meshing stiffness of herringbone gear and center distance |
|
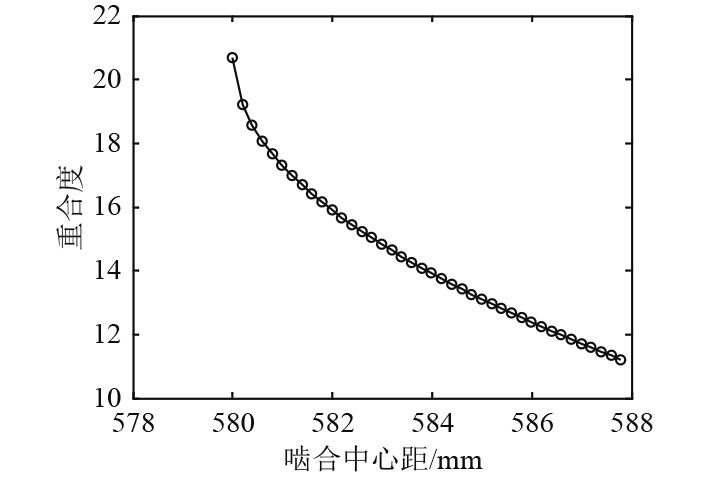
图 5 人字齿轮重合度与中心距的关系 Fig. 5 The relationship between the coincidence degree of herringbone gear and the center distance |
由图中曲线可以看出,随着中心距的增加,齿轮的重合度和啮合刚度都在减小,特别是中心距从580 mm减小到580.6 mm时刚度和重合度减小的速度较快,因此在齿轮啮合传动时,实际中心距在标准中心距的基础上有微小的变化就会造成啮合刚度的迅速变化,进而产生较大的啮合冲击。
3 啮合冲击动力学仿真计算根据表1中的参数利用SolidWorks构建人字齿轮的三维仿真模型,文中对齿轮进行了适当简化,建模时没有建立齿轮轴。将齿轮模型导入多体动力学分析软件ADAMS中,进行人字齿轮的啮合动力学仿真。齿轮动力学仿真模型如图6所示,其中小齿轮为主动齿轮,大齿轮为从动齿轮。

|
图 6 人字齿轮副动力学仿真模型 Fig. 6 Herringbone gear pair dynamics simulation model |
在利用ADAMS软件进行仿真之前需要对模型进行约束定义,确定齿轮间的相对运动关系。图中的人字齿轮副主要约束设置如下:
1)两人字齿轮与地面间设置为旋转副;
2)两齿轮间采用实体-实体接触约束,模拟齿轮传动过程中的接触碰撞;
3)小齿轮作为主动轮,在其旋转副上添加转速激励;
4)大齿轮作为从动轮,在其旋转副上添加负载力矩。
设定小齿轮的输入转速为150 r/min,负载转矩
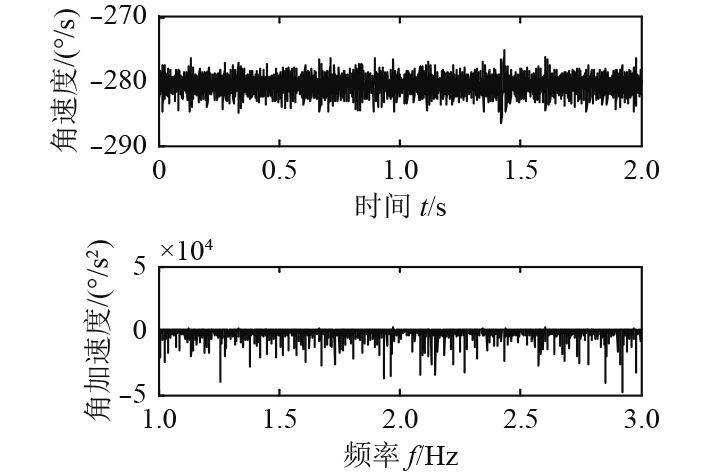
1)图7为从动轮(大齿轮)的角速度和角加速度曲线,由曲线可以看出去除初始冲击,大齿轮角速度和角加速度波动比较平稳。仿真得到的平均角速度为280.54 °/s,传动比为0.311 7,理论设计的传动比为0.311 6,误差为0.032%,满足传动比要求,证明了模型的正确性。
|
图 7 大齿轮角速度及角加速度(d=580 mm) Fig. 7 Large gear angular velocity and angular acceleration(d=580 mm) |
2)分别设置仿真模型中齿轮的中心距参数为580 mm,580.2 mm,580.4 mm,580.6 mm,580.8 mm和581 mm,得到齿轮接触力的时域和频域曲线,如图8(a)~8(f)所示。图8(a)是在标准啮合状态下得到的啮合力曲线,由时域曲线可以看出啮合力波动较为平稳,从频域曲线分析,啮合具有一定的周期变化,周期是单个轮齿啮合所需的时间,但周期性此时并不明显。随着啮合中心距的不断增加,由图8(b)~8(f)中的时域曲线可以看出啮合冲击波动逐渐加剧,通过第1节和第2节的分析可知,齿轮的啮合刚度、啮合重合度随着中心距的增加而减小,会造成啮合冲击波动的增加。

|
图 8 齿轮接触力时域及频域曲线 Fig. 8 Gear contact force time domain and frequency domain curve |
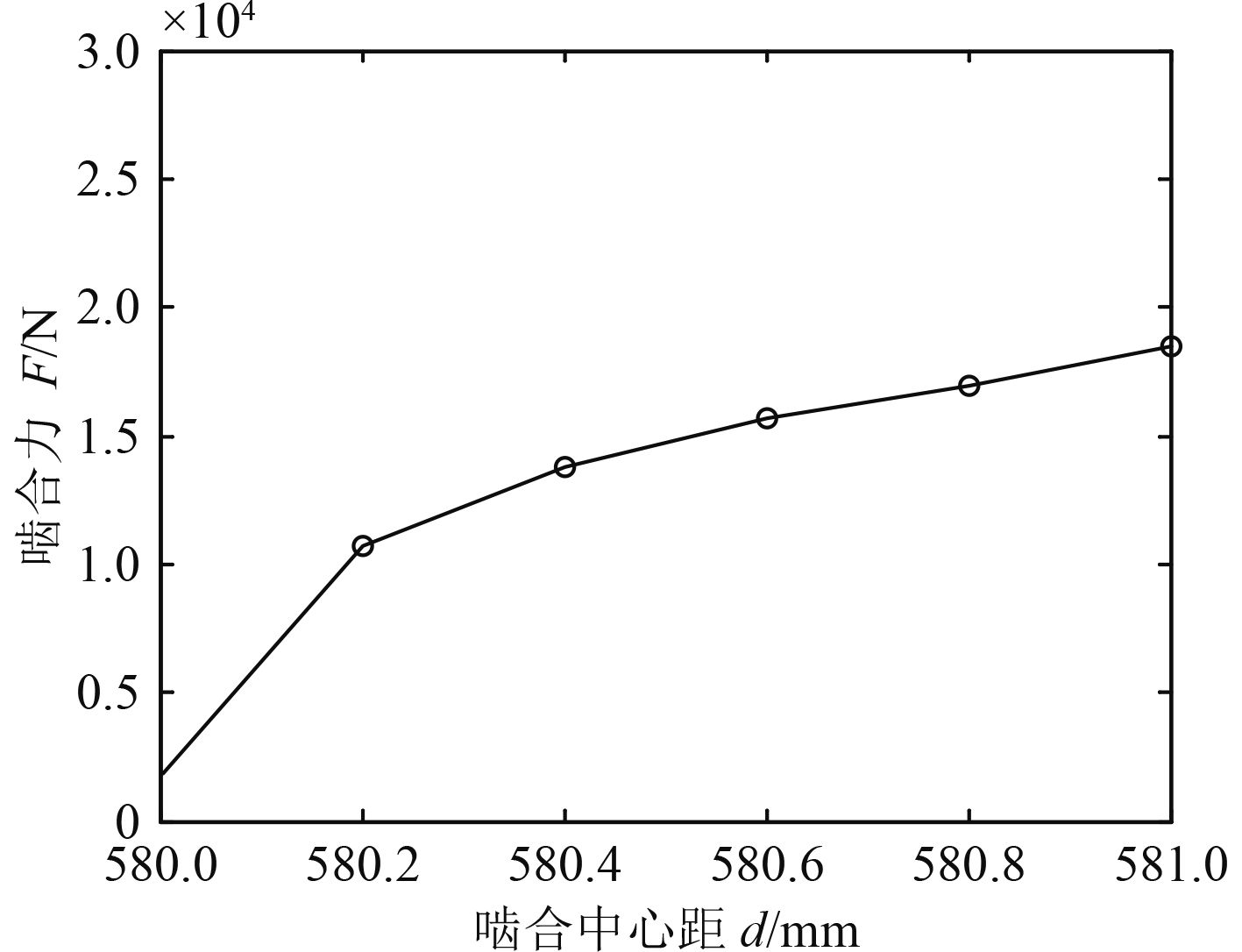
3)图9为齿轮副一阶啮合频率对应的啮合力与中心距的关系。由曲线可以看出,中心距由580 mm增加到580.2 mm时,啮合力从1 886 N迅速增加到了10 700 N,随后啮合力随中心距增加而增加的趋势逐渐放缓,仿真结果与2.2节中对刚度与中心距关系的分析结论基本一致,验证了仿真结果的有效性。
|
图 9 一阶啮合频率啮合力与中心距的关系 Fig. 9 The relationship between the first-order meshing frequency meshing force and the center distance |
本文在齿轮啮合振动模型的基础上,理论分析了人字齿轮啮合刚度、重合度与啮合中心距的关系,并利用仿真软件ADAMS进行了齿轮啮合动力学仿真,得到了齿轮副在不同中心距时的啮合力时域与频域曲线。通过对比分析,在不考虑啮合刚度和弹流润滑的情况下,可以得到以下结论:
1)啮合刚度和啮合重合度会受到啮合中心距的影响,随着中心距的增加而减小,且中心距在标准值附近的微小变化会造成啮合刚度和重合度的较大波动;
2)齿轮啮合力随着中心距的增加而增加,从频域的角度来看,中心距的增加会导致啮合频率谐波分量的增加,这会增加系统发生共振的风险,在设计时需要引起注意。
3)中心距在标准值处发生微小变化时,齿轮的1阶啮合频率啮合力会发生较大变化,这与啮合刚度、重合度的变化规律相一致。因此根据本文的分析结果,应从齿轮的设计、加工、安装等多个方面保证中心距的精度。
4)本文所建立的模型是对真实齿轮副的部分简化,所建立的模型为刚体,没有考虑齿轮的弹流润滑特性以及齿轮的加工误差,以齿轮副的中心距为影响振动特性的唯一变量进行仿真分析,所得结果与理论分析相一致且符合实际经验,因此具有一定的参考意义。
| [1] |
常乐浩, 刘更, 周建星. 功率双分支齿轮系统动力学特性研究[J]. 船舶力学, 2013, 17(10): 1176-1184. CHANG Le-hao, LIU Geng, ZHOU Jian-xing. Research on dynamic characteristics of dual-branching gear system[J]. Journal of Ship Mechanics, 2013, 17(10): 1176-1184. DOI:10.3969/j.issn.1007-7294.2013.10.011 |
| [2] |
王峰. 人字齿轮传动系统振动特性分析与试验研究[D]. 西安: 西北工业大学, 2014.
|
| [3] |
周建星, 刘更, 马尚君. 内激励作用下齿轮箱动态响应与振动噪声分析[J]. 振动与冲击, 2011, 30(6): 234-238. DOI:10.3969/j.issn.1000-3835.2011.06.047 |
| [4] |
ZHANG J J, ESAT I I, SHI Y H. Load analysis with varying mesh stiffness[J]. Computers & Structures, 1999, 70(3): 273-280. |
| [5] |
胡晓禾, 刘邱祖, 常宗旭, 等. 考虑可变刚度的CST齿轮传动系统刚柔耦合动力学研究[J]. 舰船科学技术, 2017, 39(7): 94-97. DOI:10.3404/j.issn.1672-7649.2017.07.019 |
| [6] |
常乐浩, 贺朝霞, 李岚, 等. 一种确定斜齿轮传递误差和啮合刚度的快速有效方法[J]. 振动与冲击, 2017, 36(10): 235-240. CHANG Le-hao, HE zhao-xia, LIU han, et al. Express method for determining the transmission error and mesh stiffness of helical gears[J]. Journal of Vibration and Shock, 2017, 36(10): 235-240. |
| [7] |
VAN K N, CAU T M, DIEN N P. Modelling parametric vibration of gear-pair systems as a tool for aiding gear fault diagnosis[J]. Technical Mechanic, 2004, 24(3-4): 198-205. |
| [8] |
郭会珍, 谭长均, 陈俊峰. 基于ADAMS的行星轮系动力学仿真[J]. 机械传动, 2013, 37(5): 86-89. |
| [9] |
李杰, 张磊, 赵旗, 等. 斜齿轮三维弯曲有限元模型及应力分析[J]. 沈阳工业大学学报, 2011, 33(3): 265–269. LI Jie, ZHANG Lei, ZHAO Qi, et al. Three- dimensional bending finite element model and stress analysis of helical gear[J]. Journal of Shenyang University of Technology, 2011, 33(3): 265–269. |
| [10] |
ISO. ISO 6336-1-1996. Calculation of load capacity of spur and helical gears-Part 1: basic principles, introduction and general influence factors[S]. Geneva: ISO. 1996.
|
 2019, Vol. 41
2019, Vol. 41
