2. 中国船舶重工集团有限公司,北京 100097;
3. 哈尔滨工业大学(威海)船舶与海洋工程学院,山东 威海 264209
2. China Shipbuilding Industry Corporation Co., Ltd., Beijing 100097, China;
3. Harbin Institute of Technology (Weihai), School of Naval Architecture and Ocean Engineering, Weihai 264209, China
深潜器对海洋开发十分重要,其中深潜器的耐压壳作为保证潜水器设备和人员安全的关键部件,它的结构设计直接关系到深潜器总体性能和重量指标[1]。对于大深度潜水器耐压壳,为了尽量减小耐压壳的重量排水量比,为潜水器提供较大的有效载荷,同时产生较小的应力水平,球壳是最为理想的承压结构[2],比强度、比刚度较高的钛合金是较为理想的结构材料。
鉴于耐压球壳结构极限强度研究在深海开发技术装备及其他领域的潜在应用价值,国内外众多学者先后研究了理想球壳和非理想球壳的失效模式,探讨了影响球壳极限强度的核心要素,发展了球壳极限强度的计算方法。例如:在理想球壳方面,R. Zoelly[3 – 4]在1915年用小变形假设导出受外压薄球壳弹性失稳的最早理论公式,Haghi和Anand[5]分析了各向同性的应变加强粘塑性材料加工而成的厚壳在承受外压时的强度问题;非理想球壳方面,Krenzke和Kiernan[6]通过对200多个耐压球壳试验模型的极限强度测试,形成了美国海军耐压球壳设计公式,与理想球壳计算结果相比,该公式计算结果只有70%。崔维成及其团队对载人潜水器载人球备选钛合金断裂韧性进行了试验,重点考察了相同韧带尺寸下试件厚度的效应[7],并针对钛合金耐压球壳的极限强度进行了一系列的研究[8 – 10],利用有限元Anasys分析结果提出了钛合金耐压球壳的设计公式[11],并开展了相关试验研究[12]对所提出的实际公式进行了验证,指出壳体焊接工艺参数对结构极限强度有不可忽视的影响,但对其影响机理与规律并未做进一步深入的研究。
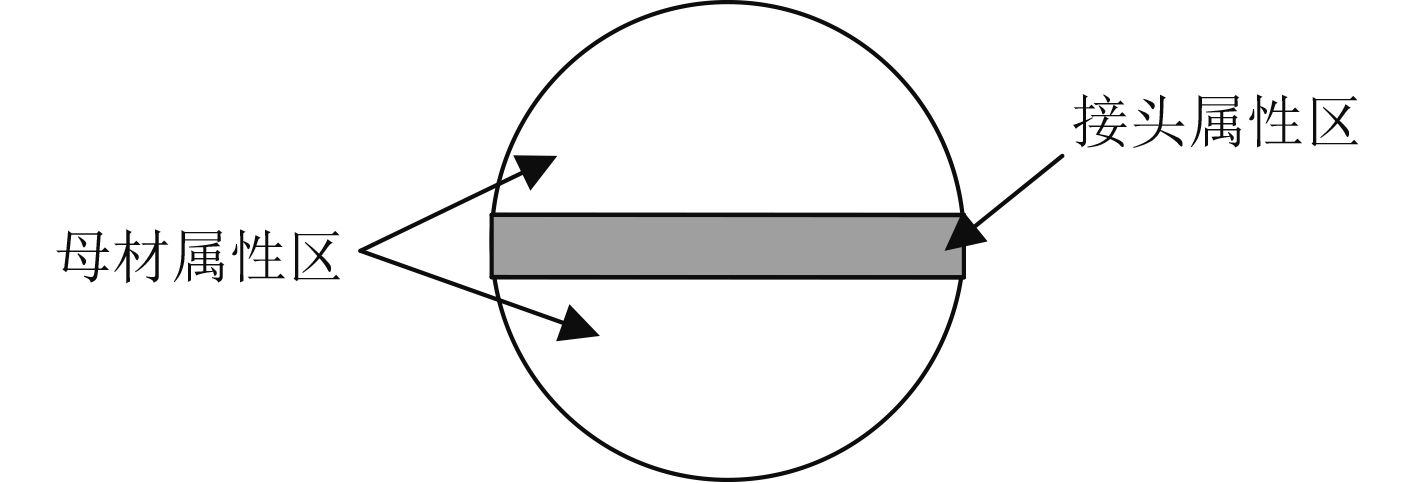
基于现有研究成果,本文提出一种考虑加工工艺对材料属性变化的球壳极限强度研究方法,通过将耐压球壳划分为接头属性区和母材属性区两部分(见图1),母材属性区材料性能仍沿用母材材料属性,而接头属性区则使用等效材料属性,并将焊接所致的焊接变形和残余应力加载到理想结构模型中,计算结构的极限强度。
|
图 1 耐压球壳材料属性区划分 Fig. 1 Material properties distinction scheme of pressure spherical shell |
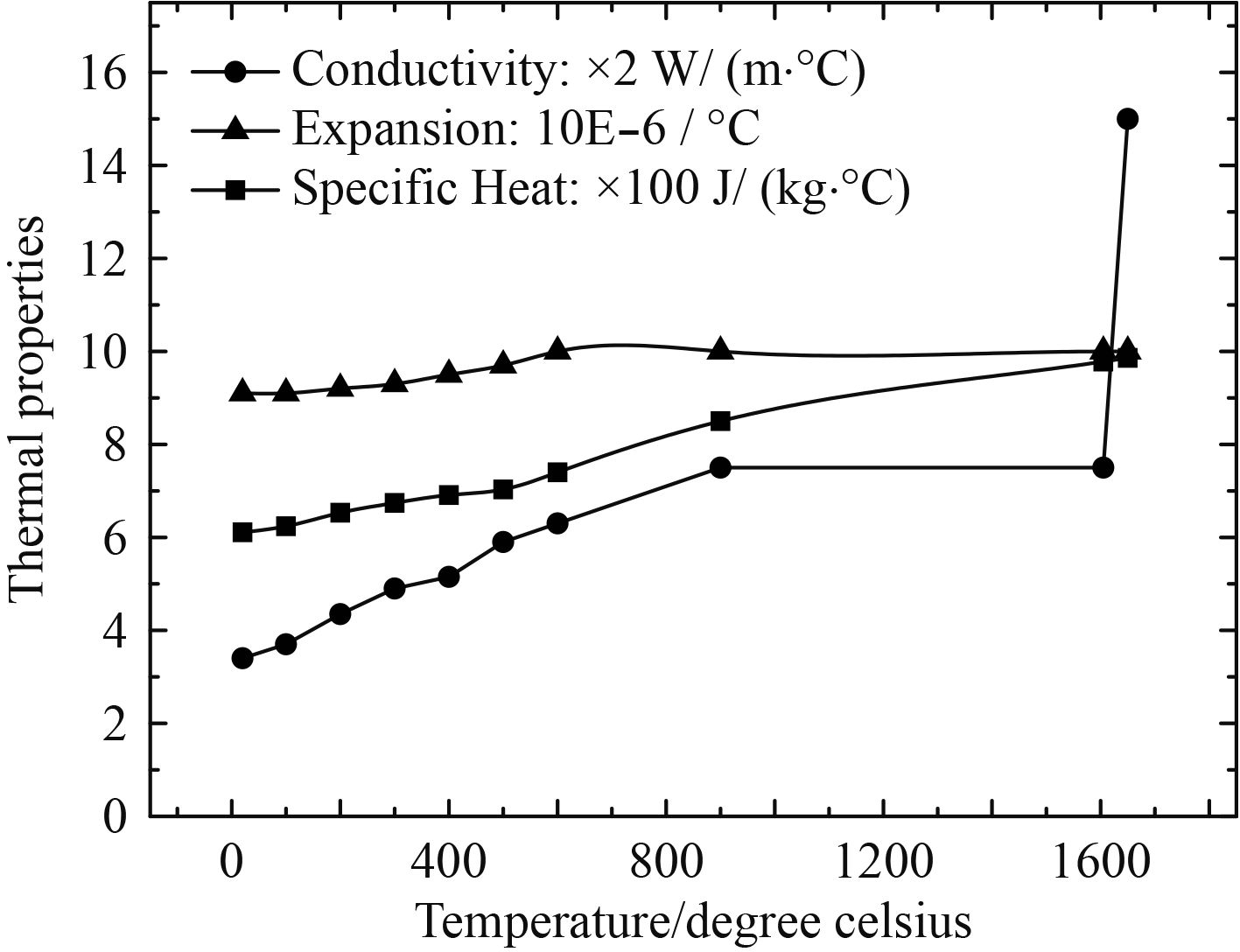
采用有限元商业软件Abaqus的直接热-力耦合模块对钛合金耐压球壳的焊接过程和极限强度估算进行数值模拟,球壳建模采用将圆弧线旋转360°,球壳半径为r=500 mm。钛合金由于其良好的强度重量比和耐腐蚀性,被广泛应用于深潜器耐压结构中,本研究采用TC4钛合金属性对材料进行赋值,具体材料力学属性如表1所示。材料随温度改变的热动力学属性如图2所示。
|
|
表 1 钛合金材料的力学属性 Tab.1 Mechanical properties of TC4 |
|
图 2 随温度变化的材料热动力属性 Fig. 2 The Change of material thermodynamic properties with temperature |
网格计算单元采用8节点的热耦合单元(C3D8T)。为了平衡计算时间和精度,设置网格尺寸为30 mm,同时焊接区域的网格加密,尺寸为厚度的一半,网格划分方案如图3所示。

|
图 3 网格划分方案 Fig. 3 Scheme of meshing |
加工过程中所导致的初始缺陷对结构的极限强度具有重要的影响,在评估结构极限承载能力时必须考虑其影响。本文采用弹性屈曲计算模块用来模拟结构初始缺陷,初始缺陷的最大幅值依据下式进行计算。
| $ {w_i} = \frac{{0.01 \cdot t}}{{{2^{i - 1}}}}\text{。} $ | (1) |
式中:i为模态阶数;t为球壳厚度。
边界条件设定为约束到球体外端的一位移固定点上,以确保计算收敛。在焊接模拟步骤之后设置足够的时间(7 200 s)允许焊接熔池温度恢复到室温(20 ℃)。
2 钛合金球壳焊接数值模拟焊接热源模型是实现焊接过程数值模拟的基本条件,其局部集中和瞬时移动的特点易形成在时间和空间域内梯度都很大的不均匀温度场,导致焊接过程中出现较大的焊接应力和变形,因此选择合适的热原模型对焊接模拟的研究至关重要。本文采用椭球状热源模型模拟焊接热源,很好的模拟了体热源的能量分布,椭球状热源分布函数如下式[13]:
| $\begin{split} {{q}_{r}}= &\frac{6\sqrt{3}Q}{{}^{{{{\text{π}} }^{3}}}\!\!\diagup\!\!{}_{2abc}\;}\exp \left(-3\left( {{\left( \frac{x}{a} \right)}^{2}}+ \right.\right. \\ & \left.\left. {{\left( \frac{y}{b} \right)}^{2}}+{{\left( \frac{z}{c} \right)}^{2}} \right) \right) {\text{。}} \end{split} $ | (2) |
式中:Q=ηUI;η为热源效率;U为焊接电压,V;I为焊接电流,A;a,b,c为椭球形状参数。焊接热源模型由Fortune子程序建立,通过子程序Dflux接口输入到Abaqus程序。
钛合金在施焊过程中,温度在300 ℃以上能够快速吸氢,410 ℃以上时能快速吸氧,600 ℃以上时能快速吸氮。而当熔池中侵入这些有害气体后,焊接接头的塑性和韧性都会发生明显的变化,特别是在820 ℃以上,接头晶粒严重粗大化,冷却时形成马氏体组织,使接头强度、硬度、塑性和韧性下降,过热倾向严重,接头严重脆化。根据表2中原始β晶体尺寸与钛合金性能匹配关系,随着焊接温度的升高,β晶粒不断增大[14],同时随着β晶粒的增大,钛合金的材料属性发生变化,因此,将820 ℃设置为焊接热影响区域边界温度。
|
|
表 2 钛合金晶粒大小与温度关系[14] Tab.2 The relationship between titanium alloy grain size and temperature |
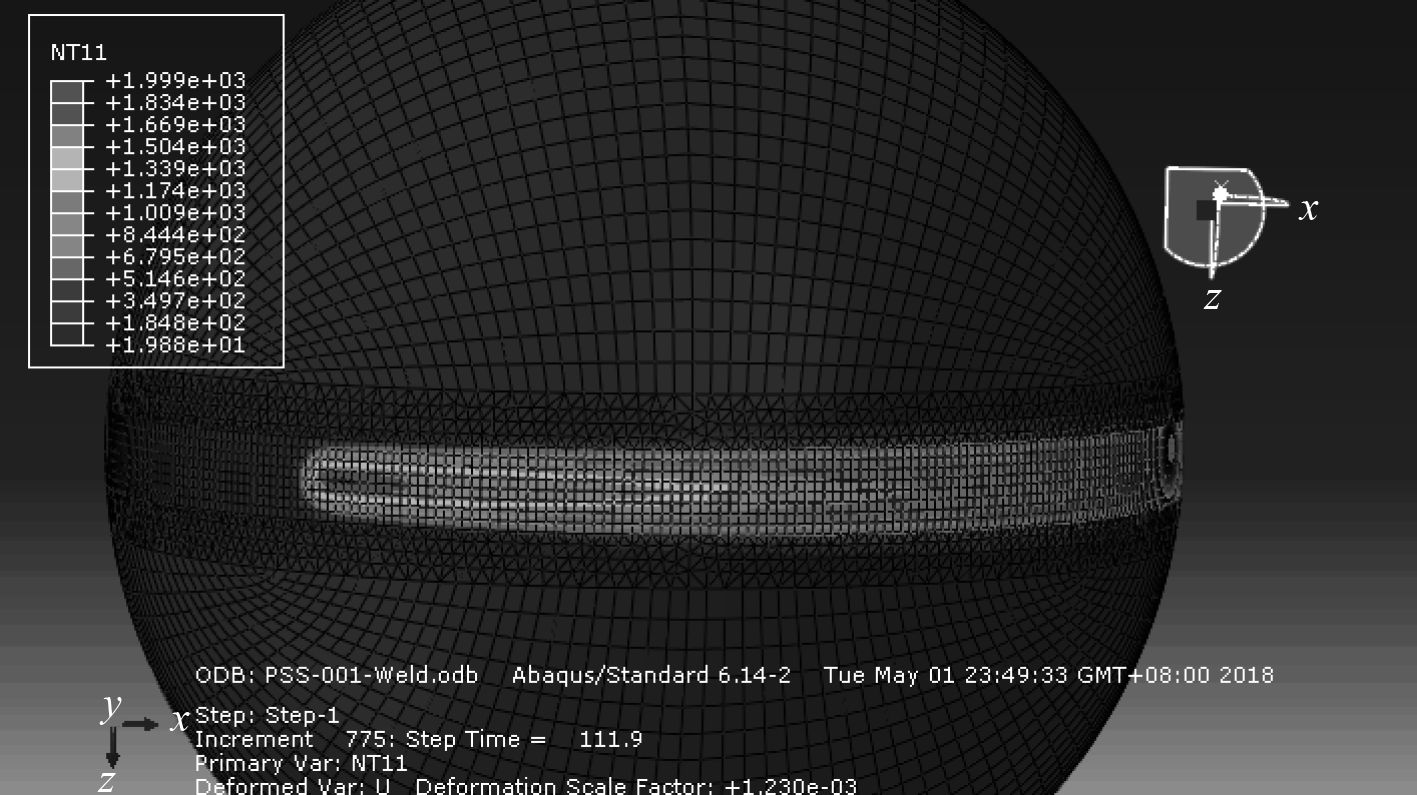
以球壳厚度t=10 mm时为例,焊接初始阶段结果如图4所示,随着焊接热源能量向外辐射,应力分布也由中心焊点的高应力区向外逐渐减小变化。焊接数值模拟过程结果如图5所示,随着焊点的移动,焊接路径中温度场发生变化,如图6所示,焊接完成区域的应力值有所降低,但仍处于较高的应力范围内。

|
图 4 焊接初始阶段模拟结果 Fig. 4 Numerical result for welding inital stage |

|
图 5 焊接模拟过程结果 Fig. 5 Numerical result for welding process |
|
图 6 过程温度场 Fig. 6 Teperature distribution for welding process |
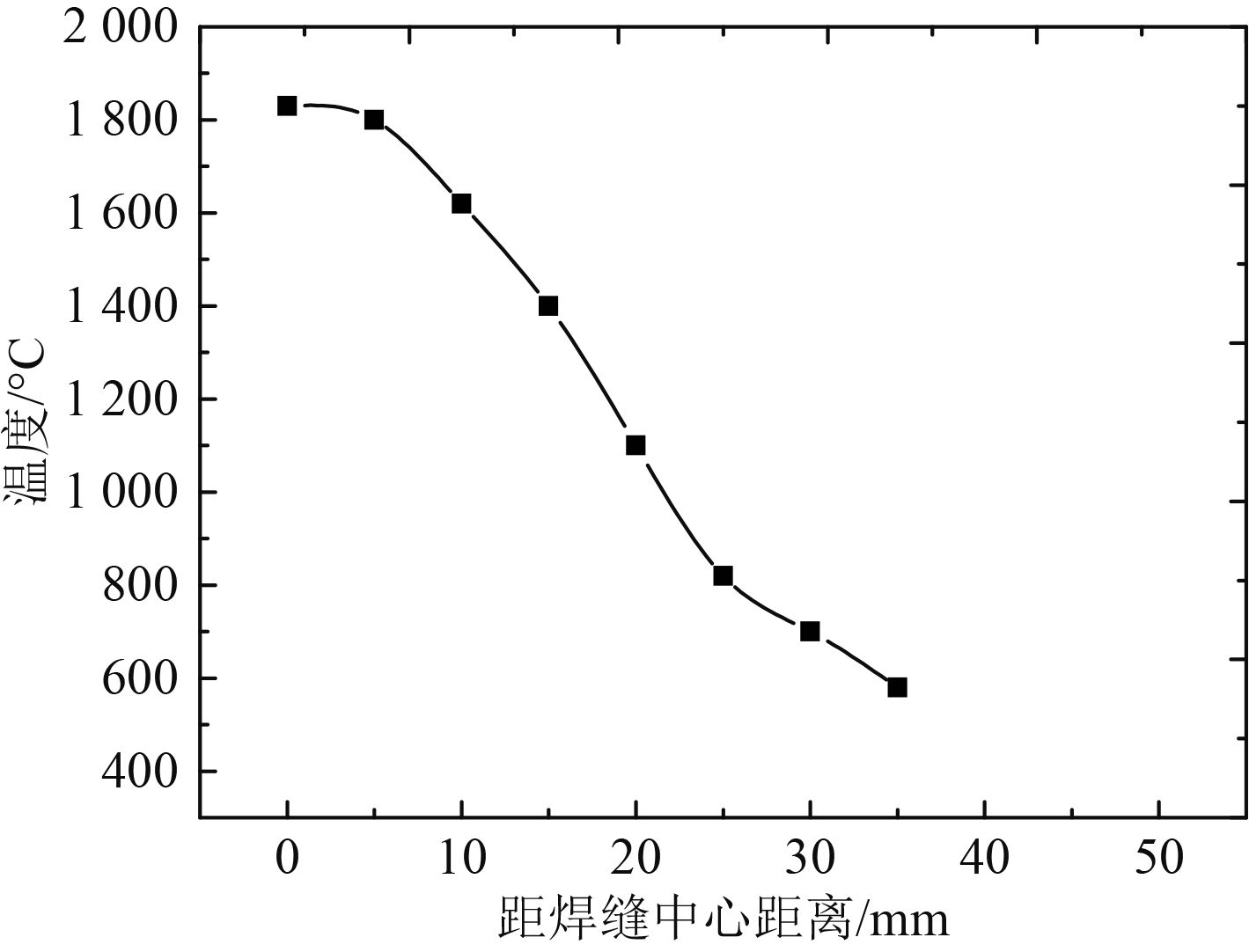
为了确定焊接热影响区域的范围,在焊接数值模拟过程中沿焊缝垂直方向设置观测点,绘制焊缝周边温度变化情况,结果如图7所示。寻找温度为820 ℃所对应的距离焊缝中心线宽度约为21 mm,由于焊接能量关于焊缝中心线对称,因此确定焊接热影响区域为42 mm。
|
图 7 焊缝垂线位置温度变化曲线 Fig. 7 Temperature variation of position vertical welding track |
由焊接数值模拟确定热影响区域,热影响区域内的,采用.等效材料属性赋值,热影响区域之外材料采用母材属性。钛合金焊接试件拉伸试验测得,钛合金焊接后屈服强度与杨氏模量按4.5%减少,以此来确定焊接热影响区内的材料属性。
弧长法用来计算结构极限承载能力,最大外部均匀压强设置为100 MPa保证结构达到失效,最大和最小弧长增量分别设置为2×10–2和1×10–5。
典型的压力承载能力随弧长变化曲线如图8所示,曲线峰值点即为结构的极限承载能力。通过图8中是否残余应力的加载过程的2条曲线的对比可以发现,残余应力对钛合金耐压球壳结构极限承载能力有小幅的削减影响,但影响程度较小,甚至可以忽略,主要原因为加工工艺所致的残余应力在结构局部存在,但对于结构整体,残余应力是平衡分布。
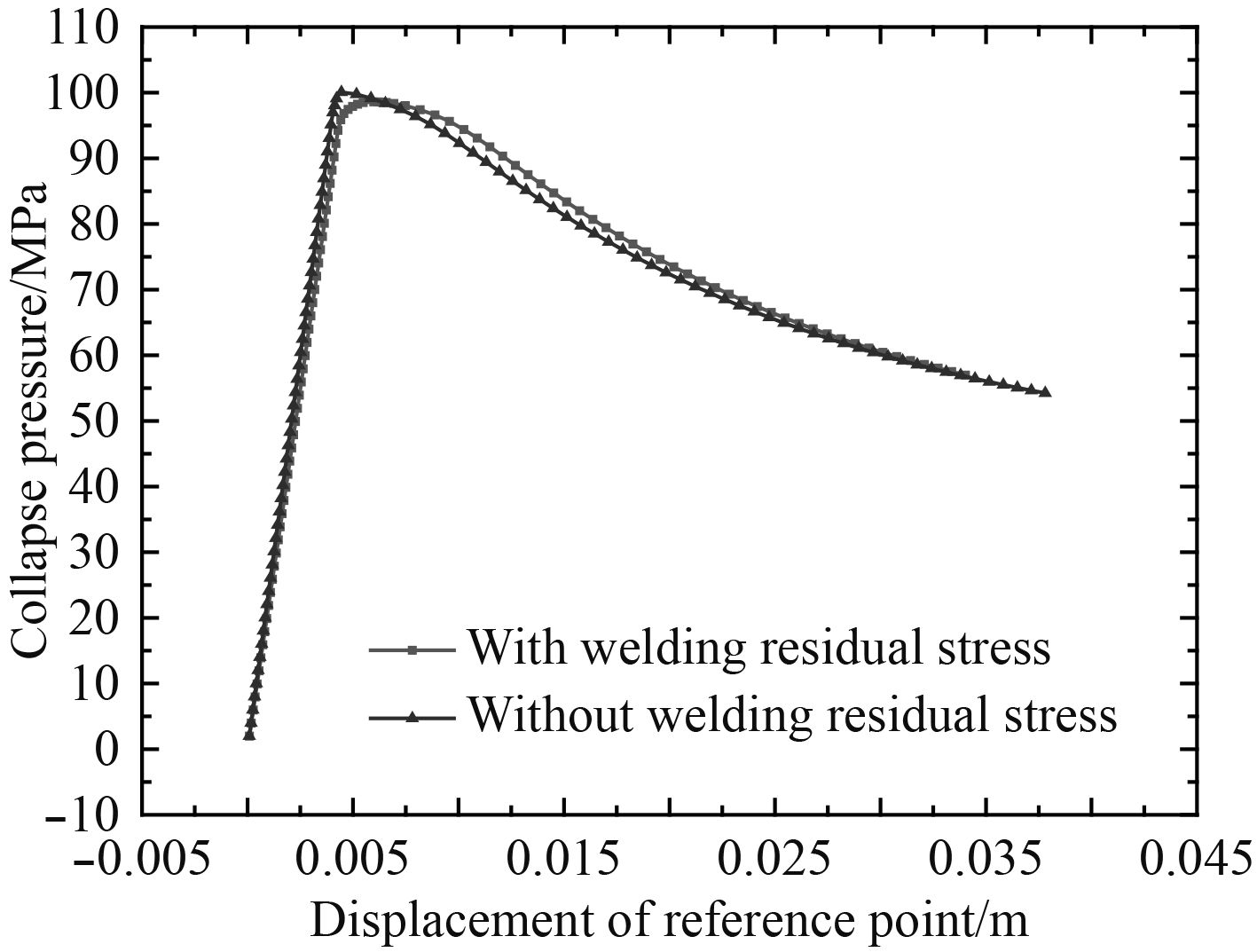
|
图 8 耐压球壳加载过程变化曲线 Fig. 8 Loading process of pressure spherical shell |
随着载荷的不断增大,高应力区范围遍布整个球壳,在两端中心处开始被击溃。当钛合金耐压球壳结构达到极限强度时的应力分布如图9所示,耐压球壳完全被击溃时的失效模式如图10所示。
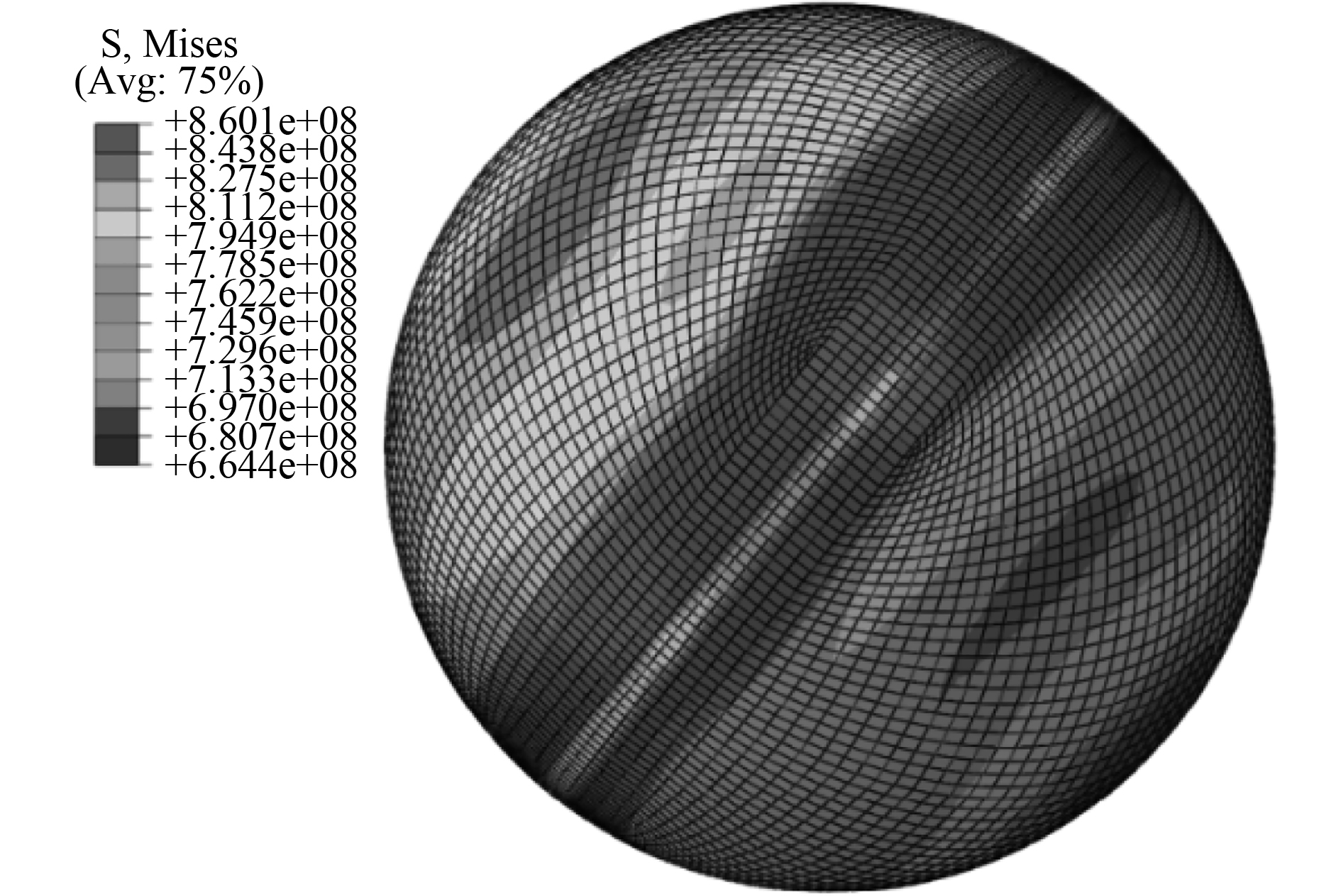
|
图 9 耐压球壳极限强度时应力分布 Fig. 9 Stress distribution of pressure spherical shell inlimite state |

|
图 10 耐压球壳击溃时失效模式图 Fig. 10 Failure mode of collapse pressure spherical shell |
耐压球壳厚度半径比
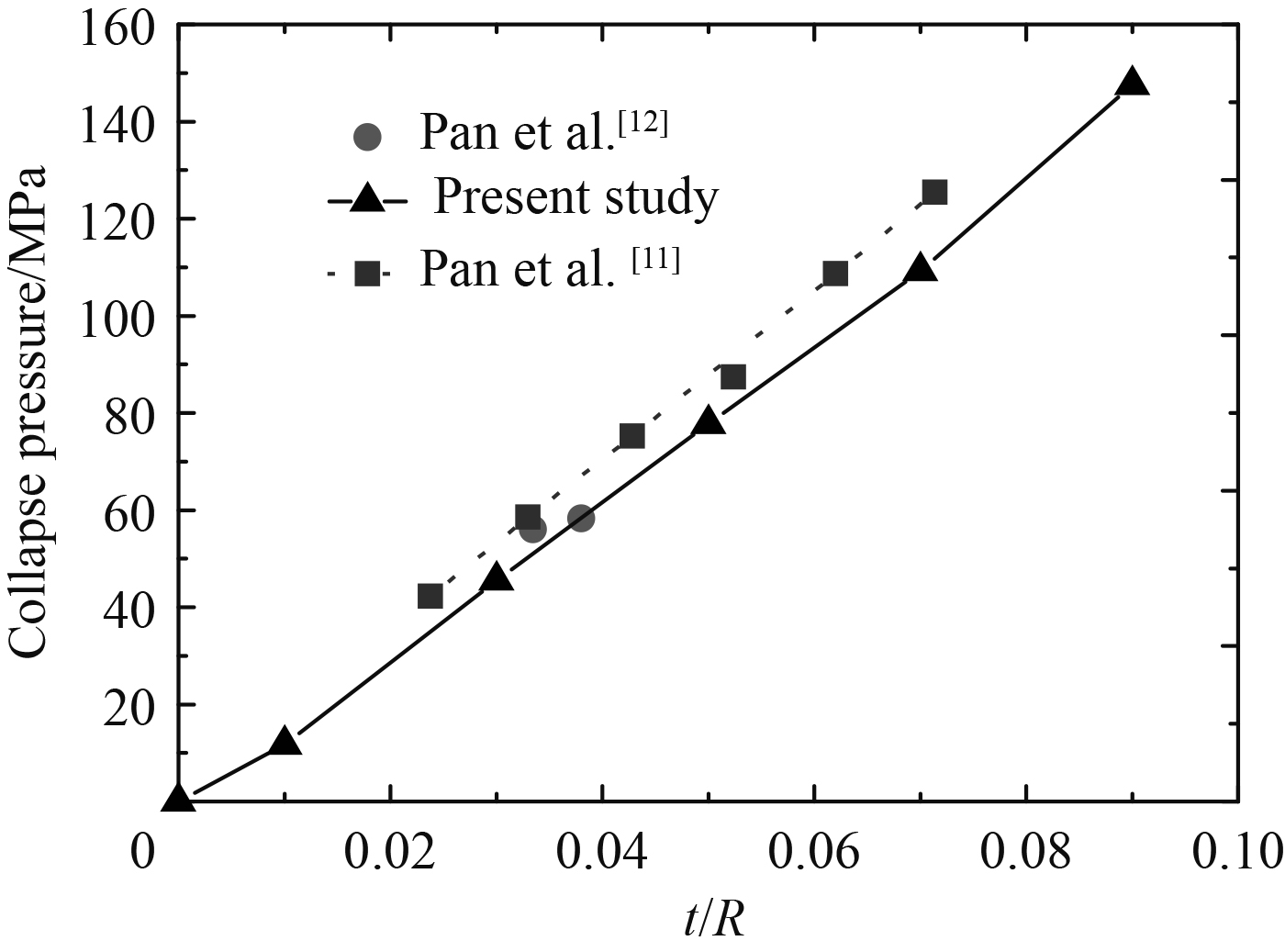
|
图 11 评估结果对比 Fig. 11 Comparison of assessment results with references |
为了便于实际工程设计应用,采用递归算法对钛合金耐压球的极限强度进行了经验公式拟合。利用Matlab曲线拟合工具,选择多项式表达形式,通过对比拟合误差,最终确定多项式的指数为3次,拟合出的经验公式如下:
| $ \begin{split} {{P}_{U}}= &-1.408\times {{10}^{5}}\times {{\left( {t}/{R}\; \right)}^{3}}+1.822\times {{10}^{4}}\times \\ & {{\left( {t}/{R}\; \right)}^{2}}+1.065\times {{10}^{3}}\times \left( {t}/{R}\; \right)-0.714\ 7 \text{。} \end{split} $ | (3) |
Matlab中和方差(SSE)与确定系数(R-square)可以很好地反应数据拟合的效果,其中SSE越接近0,R-square越接近1,说明拟合效果越好。式(3)拟合的SSE值足够小,仅为4.949,而R-Square值为0.999 8,足够接近1,证明式(3)充分反映了原始数据之间的关系。
4 结 语本文针对焊接球体加工工艺的特点,提出了基于等效材料属性计算耐压球壳极限强度的数值方法。经过数值模拟计算与以往试验以及数值模拟结果的对比,得出如下结论:
该方法充分考虑了耐压球壳在焊接过程中焊道附近材料属性的变化、残余应力与焊接变形。数值模拟计算结果同试验结果误差很小,且计算结果偏于保守,因为在以往的耐压球壳极限强度数值模拟中,并未全面考虑焊接工艺所造成的影响,表明该方法能考虑到工程安全性,有较强的工程应用价值。本文采用的递归算法所拟合的经验公式,具有足够的精度,可供钛合金耐压球壳初步设计阶段参考。
| [1] |
陆蓓, 刘涛, 崔维成. 深海载人潜水器耐压球壳极限强度研究[J]. 船舶力学, 2004, 8(1): 51-58. DOI:10.3969/j.issn.1007-7294.2004.01.007 |
| [2] |
俞铭华, 王自力, 李良碧, 等. 大深度载人潜水器耐压壳体结构研究进展[J]. 华东船舶工业学院学报(自然科学版), 2004, 18(4): 1-6. DOI:10.3969/j.issn.1673-4807.2004.04.001 |
| [3] |
陈铁云, 沈惠申. 结构的屈曲[M]. 上海: 上海科学技术文献出版社, 1993
|
| [4] |
施德培, 李长春. 潜水器结构强度[M]. 上海: 上海交通大学出版社, 1991.
|
| [5] |
HAGHI M, ANAND L. Analysis of strain-hardening viscoplastic thick-walled sphere and cylinder under external pressure[J]. International Journal of Plasticity, 1991, 7(3): 123-140. DOI:10.1016/0749-6419(91)90027-V |
| [6] |
KRENZKE MA, KIERNAN TJ. Test of stiffened and unstiffened machined spherical shells under external hydrostatic pressure[S]. David Taylor Model Basin, report 1741, S-R0110101; 1963.
|
| [7] |
WANG F, CUI WC, SHEN YS, et al. Analysis on fracture toughness test results of candidate Titanium alloys used in deep manned submersible[J]. Journal of Ship Mechanics, 2012, 16(9): 1056-1063. |
| [8] |
刘涛. 深海载人潜水器耐压球壳设计特性分析[J]. 船舶力学, 2007, 11(2): 214-220. DOI:10.3969/j.issn.1007-7294.2007.02.008 |
| [9] |
刘涛. 大深度潜水器结构分析与设计研究[D]. 武汉: 中国船舶科学研究中心. 2001.
|
| [10] |
PAN BB, CUI WC. An overview of buckling and ultimate strength of spherical pressure hull under external pressure[J]. Marine Structures, 2010, 23: 227-240. DOI:10.1016/j.marstruc.2010.07.005 |
| [11] |
PAN BB, CUI WC, SHEN YS, et al. Further study on the ultimate strength analysis of spherical pressure hulls[J]. Marine Structures, 2010, 23: 444-461. DOI:10.1016/j.marstruc.2010.11.001 |
| [12] |
PAN BB, CUI WC, SHEN YS. Experimental verification of the new ultimate strength equation of spherical pressure hulls[J]. Marine Structures, 2012, 29: 169-176. DOI:10.1016/j.marstruc.2012.05.007 |
| [13] |
方洪渊. 焊接结构学[M]. 北京: 机械工业出版社, 2008
|
| [14] |
BUFFA G, DUCATO A, FRATINI L. FEM based prediction of phase transformations during friction stir welding of Ti6Al4V titanium alloy[J]. Materials Science and Engineering A, 2013, 581: 56-65. DOI:10.1016/j.msea.2013.06.009 |
 2019, Vol. 41
2019, Vol. 41
