2. 武汉理工大学 交通学院,湖北 武汉 430063
2. School of Transportation, Wuhan University of Technology, Wuhan 430063, China
国内外学者对船体梁极限强度的研究已经有好多年的历史,从2006年起,船体梁的极限强度评估已经写入了国际船级社协会(IACS)所发布的共同规范里,作为大型海船所必须的强度校核之一,发展到现在,求解船体极限强度的方法已经很成熟,例如直接法、逐步崩溃法、非线性有限元计算法、理想结构单元法等,很多方法都能够较好地进行极限承载能力校核。不过大多数的研究目的都是为了得到极限总纵弯矩的值,且普遍认为船体梁的破坏是一次性行为,然而事实上船体梁的破坏常常并不是一次性加载的结果。船舶在实际海洋波浪环境中受到的是交变载荷,在多次外力的作用下,船体梁的构件将反复受到不同载荷的作用,当有局部外力超过构件承载能力时,船体梁结构中部分构件必然会发生一定程度的屈曲甚至屈服,而一旦进入塑性阶段,一定会产生塑性应变,这些应变并不会随着外载荷的卸载而消失,其造成的结果是,船体梁断面的极限承载能力降低,这种塑性应变积累越多,总纵弯曲强度的降低越明显,称这种结构失效行为为船舶梁结构的递增塑性破坏。日本船舶“尾道丸”号的沉没就是由于这样的多次塑性累积,导致极限承载能力下降而引起的灾难性事故。
2014年4月,国际船级社协会颁布的协调版共同规范中,除了极限强度校核的要求之外,还增加了剩余强度校核,指出船舶在遭受高于极限强度的载荷后,仍然具有一定程度的承载能力,即所谓的后剩余承载能力。目前已有不少关于单板、加筋板、箱形梁等结构的研究成果发表。如Paik[1]采用半解析法预测船体板格在受外力屈曲后的剩余极限强度。Yao[2]运用有限元方法分析了矩形板在轴向面内压力作用下的后极限强度承载能力以及变形行为。Fujikubo[3]等运用水弹塑性分析方法研究箱型梁的剩余承载能力。目前比较有效的方法有试验法、非线性有限元法、逐步崩溃法等,这些方法都能够得到完整的应力-变形曲线,由此来分析结构承载能力的变化。
而在经历超过构件极限强度的过载后,相关构件必然会产生塑性应变,使得构件承载能力下降,从而引起该断面承载能力降低,但此时该断面往往依然能承受一定的的外载荷作用。那么究竟构件受到的外载荷会引起多大塑性应变,而塑性应变的不断累积对船体梁的极限强度以及后剩余承载能力有多大影响,就需要结构的应力-变形曲线进行分析。
所以,船体梁的极限强度的分析是值得深入研究的,施加循环交变载荷比一次性加载的校核能更准确的反映船舶的实际失效过程,更准确地计算出船体梁的剩余承载能力。本文以逐步崩溃法为基础,引入递增塑性分析,用Fortran编写了计算程序,得到了在循环外力作用下的后极限强度阶段的应力-变形曲线。并使用了通用有限元计算软件Abaqus进行了加筋板,箱形梁,实船的总纵极限强度非线性有限元分析,作为自编程序的验证。
1 循环载荷下加筋板的后极限承载能力分析要分析船体梁在外载荷下的力学行为,最关键的要研究加筋板的平均应力-应变关系。一般来说,非线性有限元的计算结果已经得到广大学者认可,计算方法也比较成熟,往往被用来作为其他解析方法的参考标准。对于加筋板的一次性加载的研究,已经有许多学者做了大量研究,其中有一些方法可以模拟其在后极限强度阶段的非线性变化,如Yao[4]采用半解析法来模拟加筋板后极限强度的平均应力-应变关系,Nikolov[5]运用参数法获得加筋板平均应力-应变关系曲线等。这些方法有的偏于理论,有的偏于实验;有的侧重于效率,有的侧重于精度。对于一次性加载来说,除了非线性有限元法,其他能够较好的模拟加筋板后极限强度阶段行为的方法普遍较为复杂,例如Ueda[6]的理想结构单元法(ISUM)等,这些方法虽然精度较高,计算加筋板优势很大,但用于计算船体梁结构时过于复杂,需要花费大量时间来做计算的准备工作,比起有限元法无明显优点。而如果要考虑循环载荷,需要在指定载荷步下改变载荷大小以及方向,如果过程控制过于复杂,在进行船体梁计算时很难实现,所以选择一种显式的应力-应变关系式才能提高简化算法的可行性。
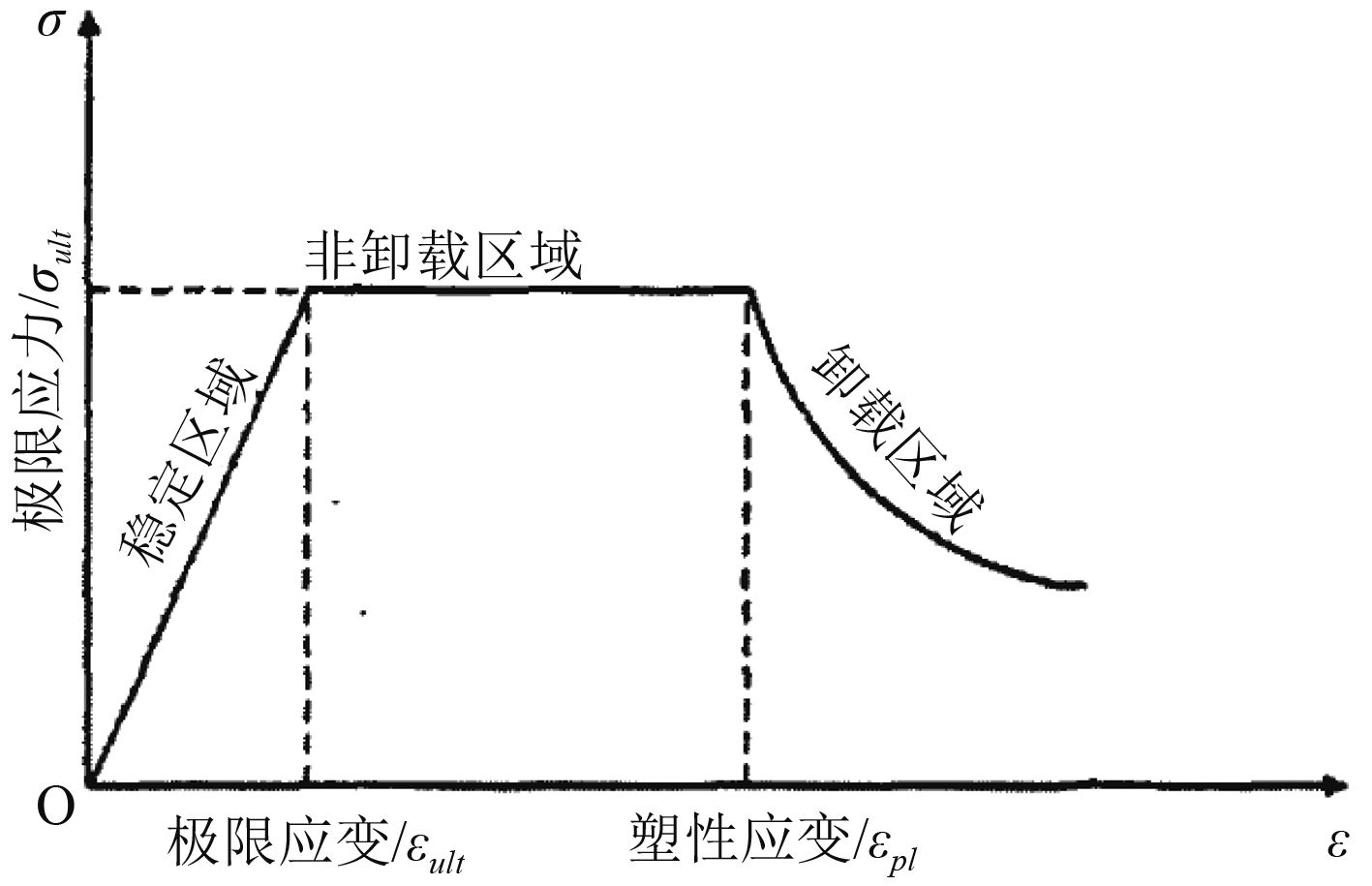
Rahman[7]运用梁理论,将船体梁离散成若干加筋板单元,并运用逐步崩溃法来进行极限强度分析。在他的计算单元中,采用的是分段函数来表达平均应力应变关系,认为单元受压时,会经历稳定阶段,非卸载阶段和卸载3个阶段,如图1所示。
|
图 1 Rahman梁理论的应力应变关系 Fig. 1 Stress-strain relationship in Rahman beam theory |
详细公式请见Rahman[7]的论文。
而考虑到交变载荷作用下,还需分析受拉及卸载阶段,在受拉阶段,因为不会发生面外变形,所以平均应力-应变关系比较简单,如下式:
| $\sigma = \left\{ {\begin{array}{*{20}{c}} {E{\varepsilon _x}\text{,} \quad \quad {\rm if}\;0 < {\varepsilon _x} \leqslant {\varepsilon _y}}\text{,} \\ {{\sigma _y}\text{,}\quad \quad \;\quad {\rm if}\;{\varepsilon _y} < {\varepsilon _x}} \text{。} \end{array}} \right.$ | (1) |
而卸载时,在任一阶段均认为应力应变关系为弹性,实际上也是如此,即
| $\sigma = E\varepsilon \text{。}$ | (2) |
于是,在循环载荷下的各个阶段的应力应变关系都能通过显式表达式来计算得到,此时采用递增塑性法来分析全过程,如图2所示。将上一载荷步的残余塑性变形代入下一载荷步,作为下一步的初始条件,以此来实现塑性累积,考虑交变载荷的影响。

|
图 2 递增塑性法流程图 Fig. 2 Flow chart of incremental plastic method |
对于船体梁结构的极限总纵弯矩的计算,目前国内外已经有很多种方法,其中一些已经很成熟,而其中涉及到后极限承载能力的分析,主要还是采用非线性有限元法,因为有限元法适用性强,且计算精度较高,同时也可以通过施加交变载荷来分析循环弯矩所造成的影响。本文将采用通用有限元计算软件进行循环弯矩作用下的船体梁后极限承载能力分析,并得到相关计算曲线。此外,还希望能够得到一种较为简单快速的方法,来得到循环弯曲载荷下的船体梁的后极限强度行为,使其在船舶设计阶段就能够提供较高的参考价值。
目前研究极限强度问题主要有以下几种方法:直接法、非线性有限元法、逐步崩溃法和理想结构单元法等。其中,直接法只能计算出极限强度值,无法分析极限强度前后的过程。非线性有限元方法精度高,但该方法计算的准备工作依然繁琐,特别是对于大型海船,仅仅是有限元模型的建立就需要大量的工时,并且计算时间过长,即使采用多核计算服务器并行计算,光计算时间往往都需要数十小时;而且循环加载的过程中,往往因为载荷突然反向而无法收敛,需要经过多次尝试,就目前来看还无法应用于船舶设计阶段。理想结构单元法在船体梁的单次加载分析中有着非常高的精度,且需要的计算时间比有限元法短得多,但是该方法需要提前开发适用于循环分析的单元函数,其单元的变形函数推导将会变得极其复杂,可行性不高。
经过比较及分析,逐步崩溃法作为一种简单有效的计算方法,精度也被广泛认可,目前已经应用于船舶设计中,被各大船级社所认可。该方法的关键主要是要得到加筋板单元平均应力-应变关系,同时不同的应力-应变关系将决定该方法的计算精度,可以较方便的进行修正及扩展。为了能考虑循环载荷,采用了递增累积塑性[8]的概念,若有单元在循环的过程中进入塑性阶段,可以把上一步卸载后的残余应变作为下一步的初始条件施加到计算中,以此来模拟构件的塑性积累。该方法准备工作少,计算速度快,可以迅速得到结果,只要精度合格,将能够应用于船舶设计工作中。本文选用逐步崩溃法,采用计算效率较高的Fortran语言来编写计算程序,得到了多个船体梁在循环弯矩作用下的弯矩-曲率曲线,分析了其后极限承载能力,并与通用有限元软件Abaqus的计算结构进行对比。
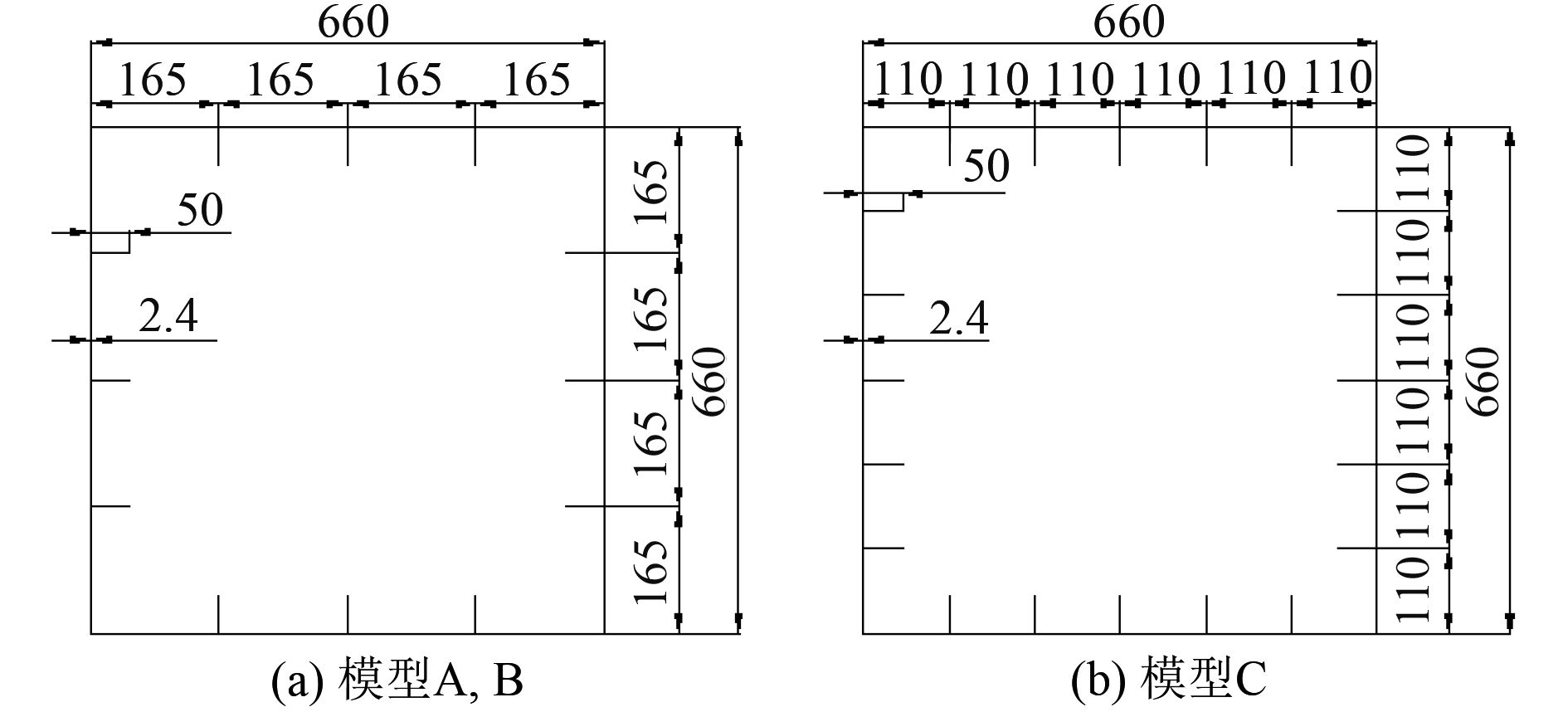
2.1 箱型梁模型计算及讨论 2.1.1 单向循环载荷目前有关船体梁在循环外力作用下行为的研究并不多,原华中理工大学的黄震球曾经用箱型梁做过循环试验,研究箱型梁的破坏行为[9]。由于原试验只做了单向循环加载,可对比数据有限,所以此处只是采用了他的模型,分别使用非线性有限元和自编的计算程序进行分析。计算模型是具有纵向加强筋的箱型薄壁梁结构,分为模型A,B和C进行计算。模型的横截面和构件尺寸如图3所示,纵向加强筋的为50×2.94 mm的扁钢,模型的力学性能如表1所示。模型全长495 mm。
|
图 3 箱型梁结构试验模型 Fig. 3 Test model of box girder structure |
|
|
表 1 力学性能数据 Tab.1 Mechanical properties data |
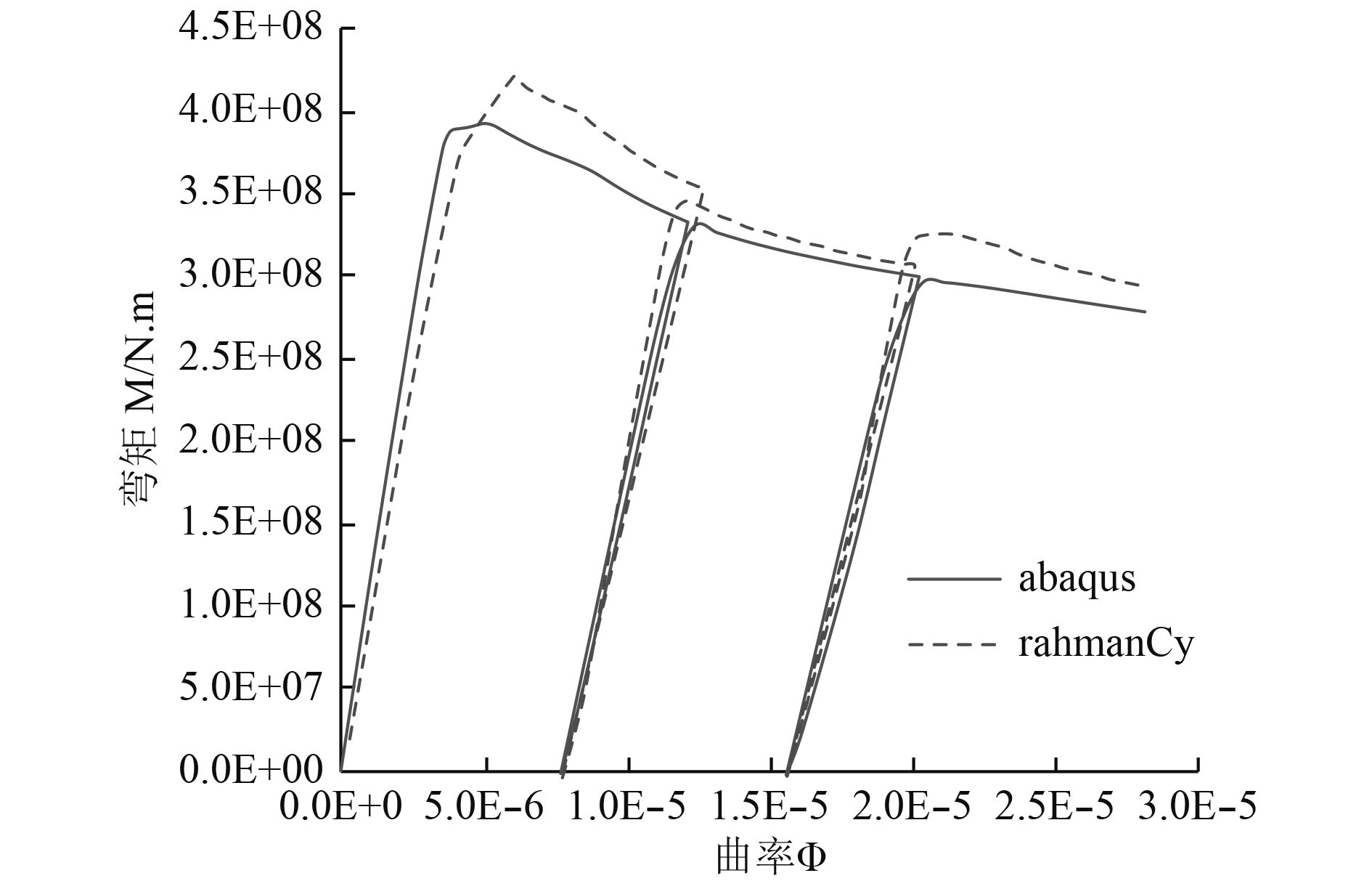
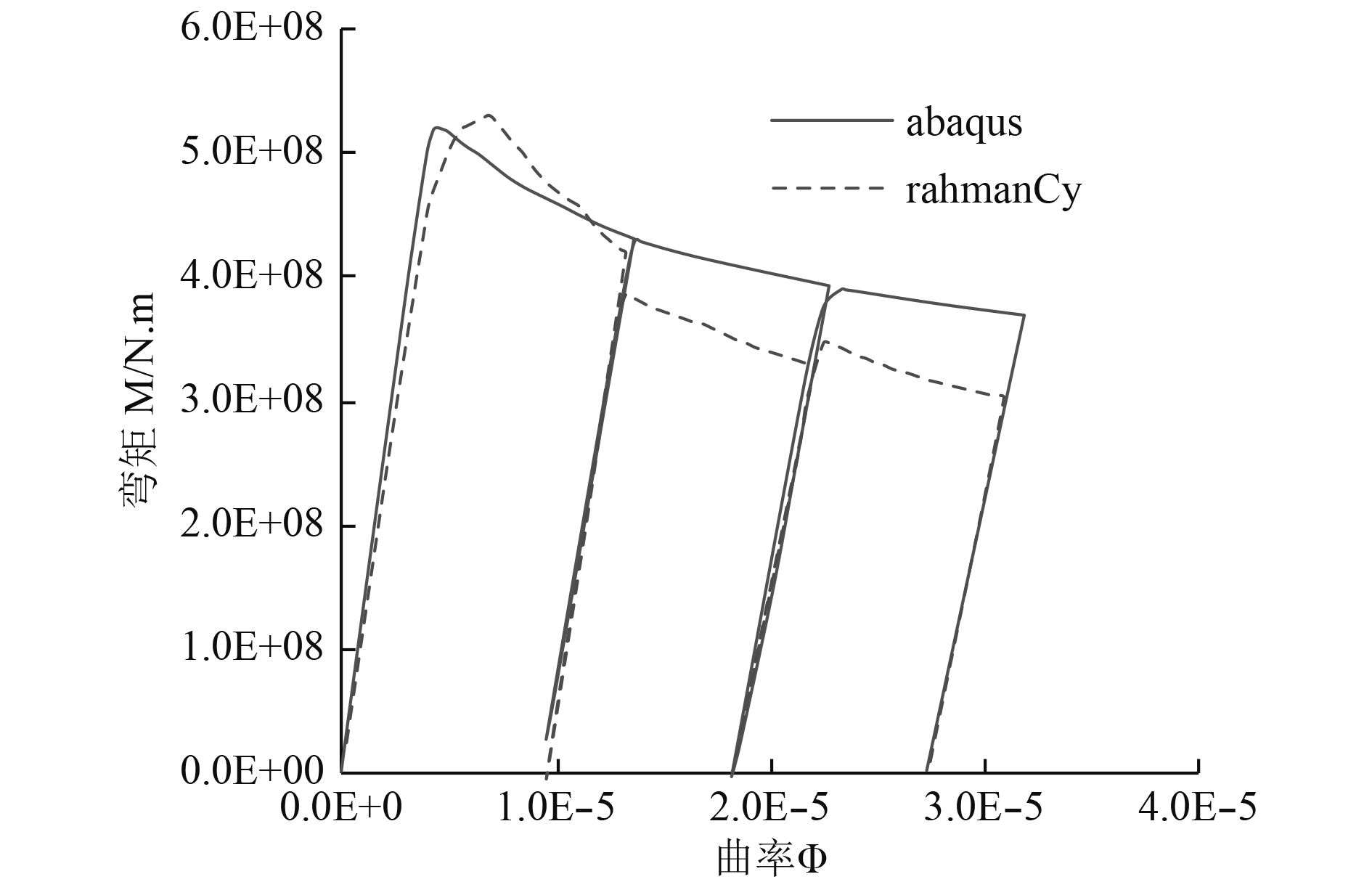
本文分别使用了通用非线性有限元软件Abaqus和自编的程序rahmanCy进行计算。首先进行中垂方向的加载,使用2种方法达到相同的曲率后进行卸载,当弯矩为0后再次进行加载,即加载-卸载-加载-卸载-加载,这种控制方法和黄震球的实验思路一致。得到的弯矩-曲率曲线如图2和图3所示。
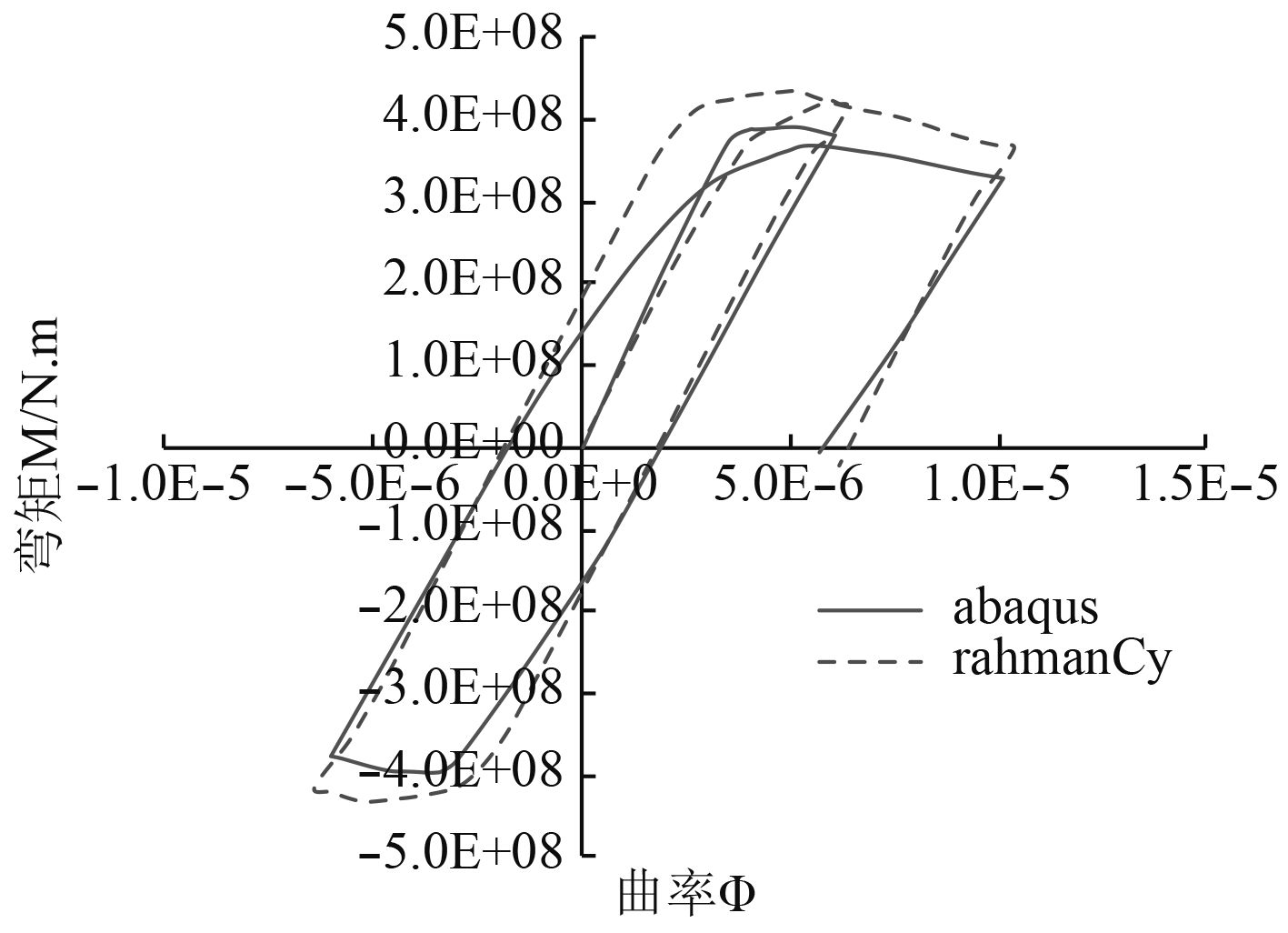
2.1.2 双向循环载荷双向循环计算选择中垂-中拱-中垂-卸载的计算过程。其计算结果如图4和图5所示。通过计算可以发现,2种方法都能够得到循环加载下的弯矩曲率曲线,且崩溃趋势基本吻合,精度有待提高。
|
图 6 模型A双向循环加载 Fig. 6 Two-way cyclic loading of model A |

|
图 7 模型C双向循环加载 Fig. 7 Two-way cyclic loading of model C |
|
图 4 黄震球模型A单向循环加载 Fig. 4 One-way cyclic loading of huang’s model A |
|
图 5 黄震球模型C单向循环加载 Fig. 5 One-way cyclic loading of huang’s model C |
所选择的实船计算对象是1艘长108 m的内河集散货船,图8是其中剖面结构图。
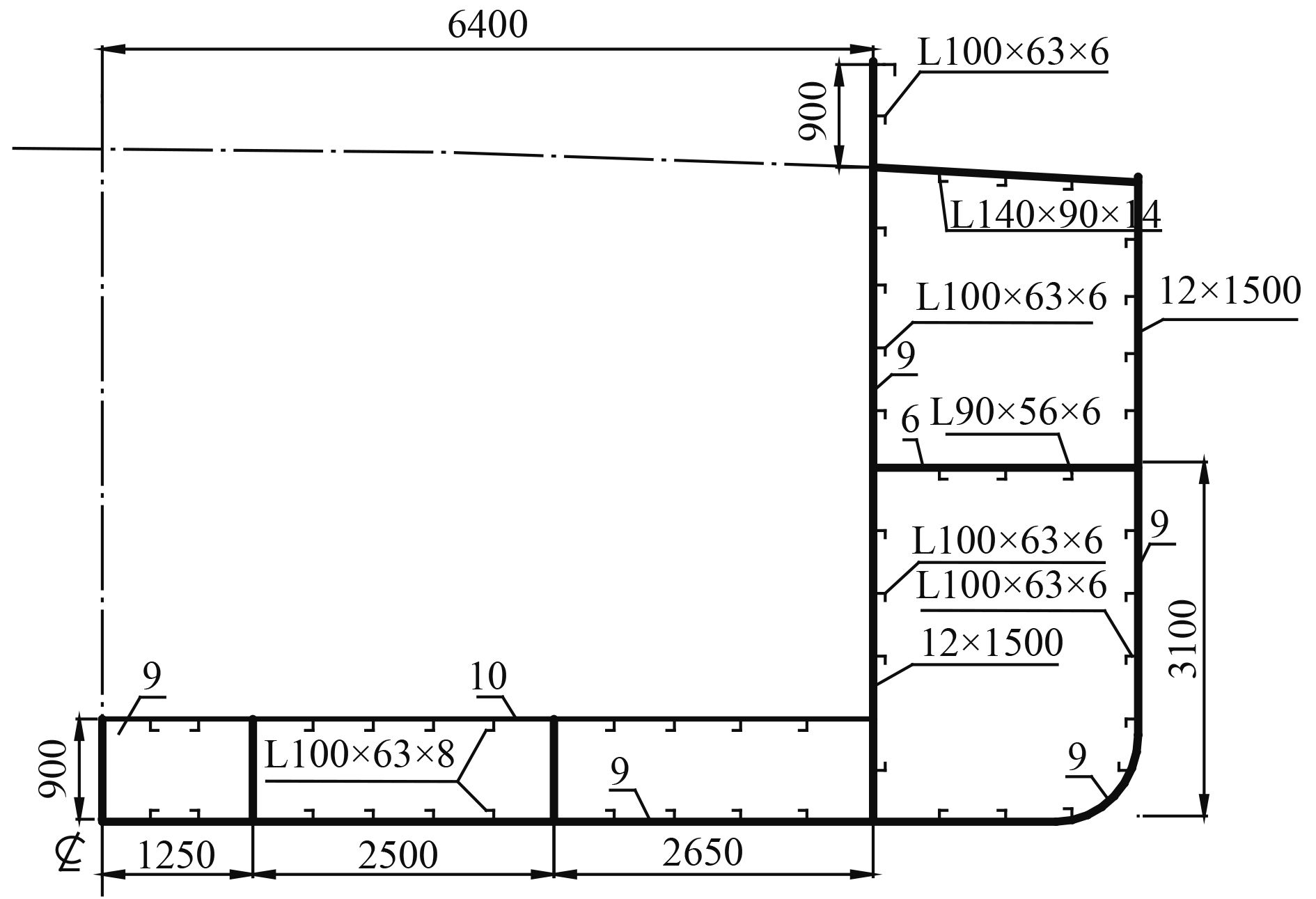
|
图 8 108 m集散货船横剖面结构图 Fig. 8 Cross section of 108 m distributed cargo ship |
该船强框架间距为1 500 m,屈服极限为235 MPa,弹性模量取205 800 MPa。具体构件尺寸参见文献[10]。
计算步骤与箱型梁相同,分别进行单向和双向计算,计算结果如图9和图10所示。

|
图 9 某内河船单向循环加载 Fig. 9 One-way cyclic loading of river ship |

|
图 10 某内河船双向循环加载 Fig. 10 Two-way cyclic loading of river ship |
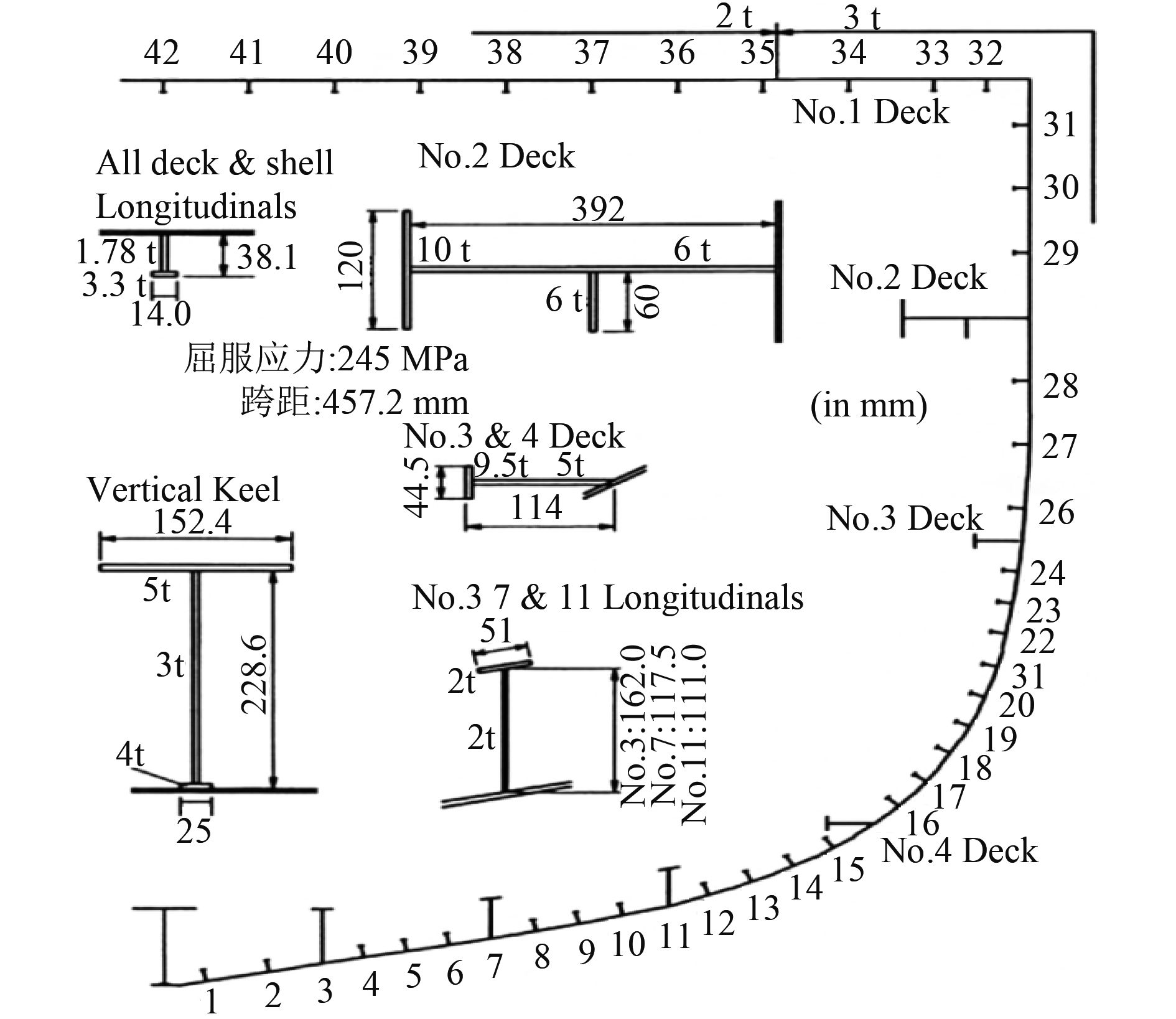
这是1艘驱逐舰模型,曾作为验证极限强度评估的验证实验,但只是一次性加载直至崩溃破坏,未进行循环分析。船体中剖面结构如图11所示,具体构件尺寸参见文献[10]。计算结果如图12和图13所示。
|
图 11 中剖面结构图 Fig. 11 Cross section of 108 m dow’s 1/3 test hull |
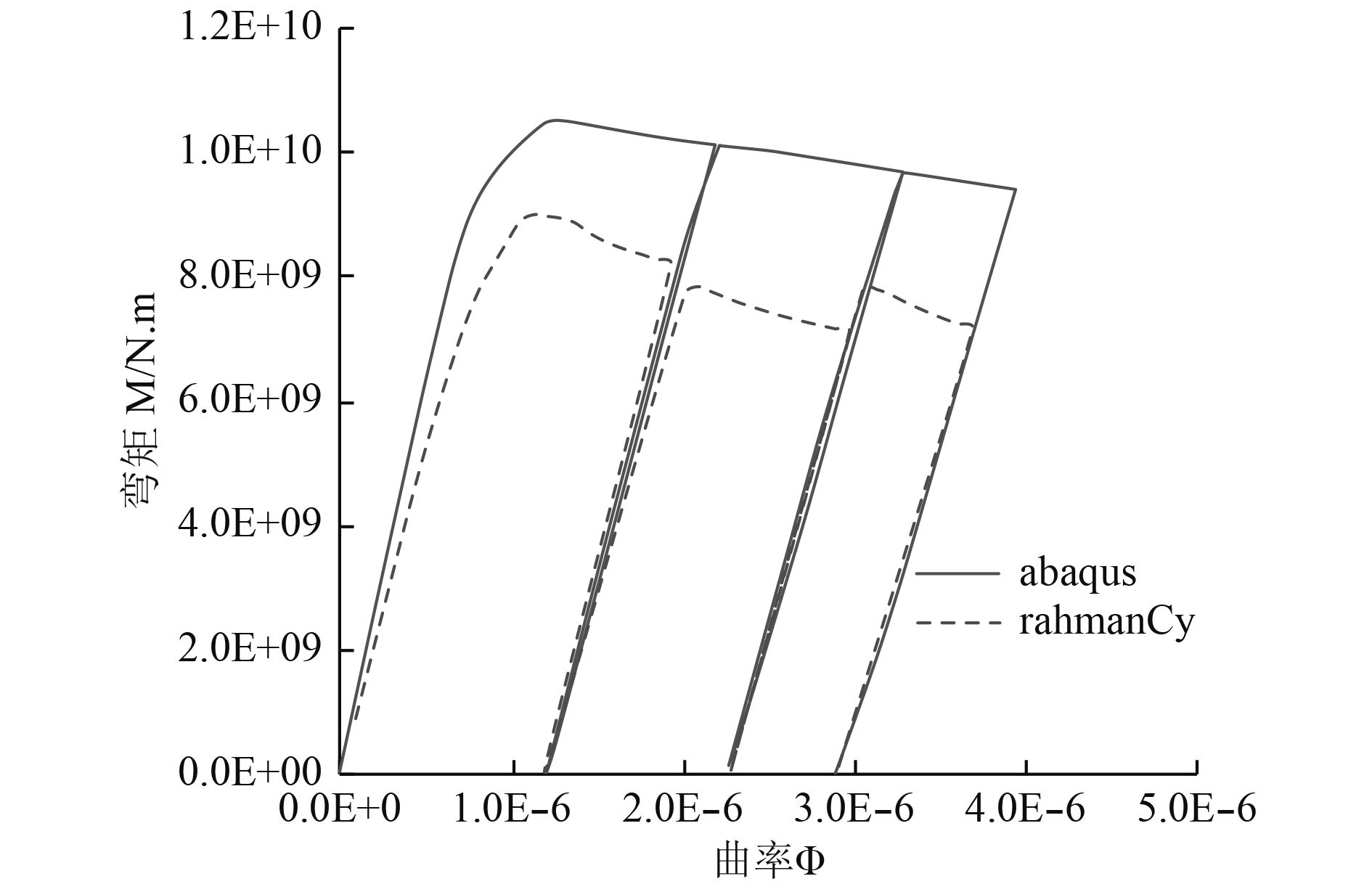
|
图 12 Dow's 1/3 Test Hull单向循环加载 Fig. 12 One-way cyclic loading of dow’s 1/3 test hull |

|
图 13 Dow's 1/3 Test Hull双向循环加载 Fig. 13 Two-way cyclic loading of dow’s 1/3 test hull |
从以上计算结果可以看到,非线性有限元法和本文自编程序都能进行循环载荷下的后极限强度分析,且由于产生的塑性变形不断积累,使得承载能力下降,这说明在经历极限载荷之后,结构仍然具有剩余强度,但由于部分构件已经进入塑性,承载能力降低,使得整船极限强度明显下降,所以评估循环载荷下的后极限强度行为,对船舶在极端海况下的自存能力有重要意义。
而从计算精度上来看,本文自编程序与有限元法有差距,原因之一是逐步崩溃法无法考虑单元之间的影响,牺牲了一定精度,其次就是本文使用的单元应力应变关系较为简单,将来如果开发出更加合适的计算单元,将能提高精度。同时有限元法虽然从理论上可以较好模拟实际情况,但往往与试验值也有出入,特别是循环载荷这样复杂的情况下,也只能作为一种参考。相对来说,开发出更适合循环加载的计算单元也许会更符合实际情况。
如果从计算效率方面来比较,使用非线性有限元法,对这样一个简单的箱形梁来说,需要建模,加属性,加初始缺陷,设置载况等,至少花费30 min,而在服务器级别的工作站上计算也要将近花费40 min,而用本文程序从准备到计算完毕,花费不过5 min。如果计算实际船舶,根据其结构复杂程度,有限元法的计算刚度矩阵会更加庞大,计算时间会成指数增加,同时,以Abaqus非线性有限元程序为例,由于非线性分析的收敛性问题,时常发生不收敛的情况,需要反复试算,特别是载荷从加载到卸载,往往需要分多次调整参数。顺利的时候一个加载步骤也需要数小时,不顺利的时候甚至要花费数天时间来反复调整。而该简化方法由于采用简化公式,受结构复杂程度的影响不大,该方法的效率优势将更加明显。
本文计算的意义为,目前对于循环载荷下的船体梁极限强度的研究还在初级阶段,特别有效地模拟船体梁循环载荷下的力学行为的方法不多,本文提出了一种简单的计算方法来得到循环载荷下的力学曲线,并采用了非线性有限元进行对比,虽还有许多问题,但也希望能抛砖引玉,使其更加完善。
3 结 语本文采用了非线性有限元法分析了船体梁在单向,双向循环载荷下的后极限承载能力,并得到其弯矩-曲率曲线。并基于逐步崩溃法,以塑性递增的思路得出一套计算循环载荷下船体承载力的简化方法,并编写计算程序,与通用非线性有限元方法进行对比。
总体来看,2种方法都能够模拟循环载荷下的后极限强度行为。与有限元法相比,计算程序计算效率高,有较好的工程应用价值,但精度有待提高,进一步完善后有望成为分析该类问题的一种实用的评估方法与手段。
| [1] |
PAIK J K, PEDERSEN P T. A simplified method for predicting ultimate compression strength of ship panels[J]. Int. Shipbuild. Progr., 1996, 43(434): 139-157. |
| [2] |
YAO T, et al. Post-ultimate strength behavior of long rectangular plate subjected to uni-axial thrust[R]. Stavanger, Norway:International Society of offshore and Polar Engineers, 2001.
|
| [3] |
XU W, IIJIMA K, FUJIKUBO M. Parametric dependencies of post-ultimate strength behavior of a ship’s hull girder in waves[J]. Journal of Marine Science and Technology, 2012, 17(2): 203-215. DOI:10.1007/s00773-012-0158-1 |
| [4] |
YAO T, NIKOLOV P I. Buckling/Plastic Collapse of Plates under Cyclic Loading[J]. Journal of The Society of Naval Architects of Japan, 1990, 168: 449-462. |
| [5] |
PLAMEN Ivanov Nikolov, Progressive collapse analysis of a ship’s hull under longitudinal bending[D]. 1992(6).
|
| [6] |
UEDA Y. Advances in the application of ISUM to marine structures[J]. Advances in Marine Structure, 1991, 628-649P. |
| [7] |
RAHMAN M K, CHOWDHURY M. Estimation of ultimate longitudinal bending moment of ships and box girders[J]. Journal of Ship Research, 1996, 40(3): 244-257. |
| [8] |
李辉程. 基于递增塑性法的船体极限强度研究[D]. 哈尔滨: 哈尔滨工程大学, 2009.
|
| [9] |
黄震球, 陈齐树, 骆子夜. 循环弯曲载荷下船体梁的极限总强度[J]. 中国造船, 1996(3): 87-95. |
| [10] |
喻霁. 循环弯曲作用下船体梁逐步崩溃行为的研究[D]. 武汉: 武汉理工大学, 2013.
|
 2019, Vol. 41
2019, Vol. 41
