2. 水动力学重点实验室,江苏 无锡 214082
2. National Key Laboratory of Hydrodynamics, Wuxi 214082, China
风机是一种量大面广的通用机械设备,几乎所有行业均有使用,其中离心风机更是占风机市场总量的50%左右[1]。离心风机的风速一般与转速和叶片出口角有关[2],在使用时一般需要安装管道,风管的压力损失有沿程压力损失和局部压力损失,可以用工程方法估算[2],根据损失就可以选择风机与电机,以满足风速要求。随着数值模拟技术的发展,管道中的风速可以通过数值计算得到。
在数值计算方面,除了网格质量之外,边界条件对计算准确性有较大影响。对于不可压缩流体,入口或出口边界条件一般可以设置速度入口或速度出口边界,压力入口或压力出口边界,进风口或通风口边界条件,其中比较常见的是速度入口、自由出口,如在车载高效离心风机内部流动的数值模拟[3]、离心风机整机三维数值仿真方法[4]中使用了这种边界条件,另外在与风机类似的离心泵激励力模拟时[5]也使用了这种边界条件。对于压力入口、压力出口,在轴流风机流场模拟[6]中,采用了这种边界条件,但无试验结果验证。在离心风机流场数值模拟研究[7],在验证时是用计算出来的全压与风机性能试验测得的结果进入验证,没有进行速度验证。
如果风机安装的管道比较复杂,用工程方法难以估算准确风速,管中速度低则无法满足要求,速度高又须减少转速或增加挡风装置,从而增加能源消耗。在风机实际运行中,只有一个转速参量,还有自由出入口,由这些条件采用数值计算理应得到精确的出口速度。本文采用一种专业的前处理软件ICEM CFD对离心风机全域绘制了质量较高的结构化网格离心风机,采用Fluent进行计算,并与测量结果进行了比较。
1 计算对象与网格划分计算对象为一离心式通风机,如图1所示。风机重约117 kg,高约1.25 m。风机型号为4-72-5A,电机为三相异步电机,电压380 V,功率2.2 kW,电流3.43 A。

|
图 1 离心式风机 Fig. 1 The centrifugal fan |
首先测量风机的几何尺寸,对于叶片采用便携式节能推进装置三维激光扫描仪,最终在UG软件中生成叶片,叶片最大直径为503 mm,如图2所示。
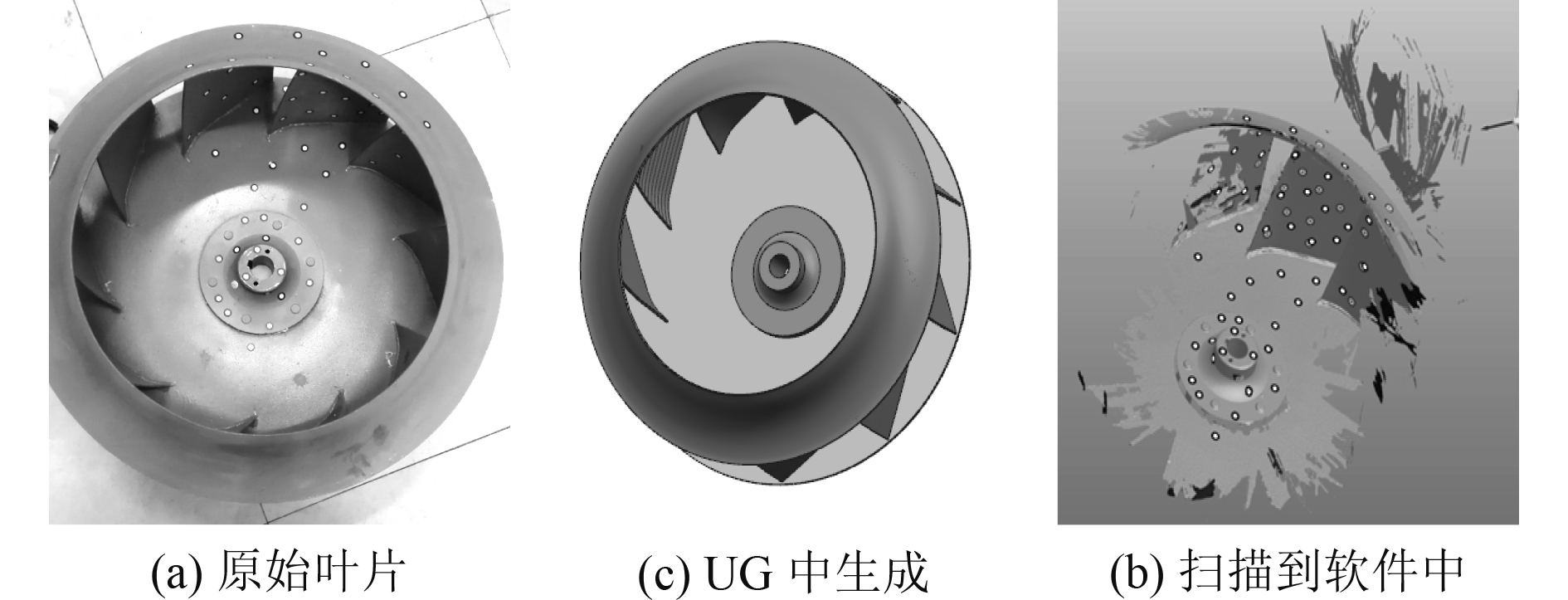
|
图 2 叶片绘制过程 Fig. 2 The process of fan drawing |
对于蜗壳等其他部分采用钢尺、游标卡尺等进行测量,最终包含管道的整个模型如图3所示。进口长约12.3 m,出口长约11.6 m,出口管道直径为267 mm,进口管道开始部分为267 mm,经扩张段后为300 mm。

|
图 3 整体模型示意图 Fig. 3 Sketch of the whole model |
数值计算中采用多参考系模型(multiple reference frame model,MRF)模拟风机叶片旋转运动,具体实施方法:风机叶片所在区域划分出一个小圆柱体区域,如图4所示,交界面有阶梯。小圆柱体内包含叶片,此区域作为转动部分,其他区域作为外域,为静止部分,静止部分和转动部分设置交界面(interface)进行数据交换,以此来保证各物理量守恒。
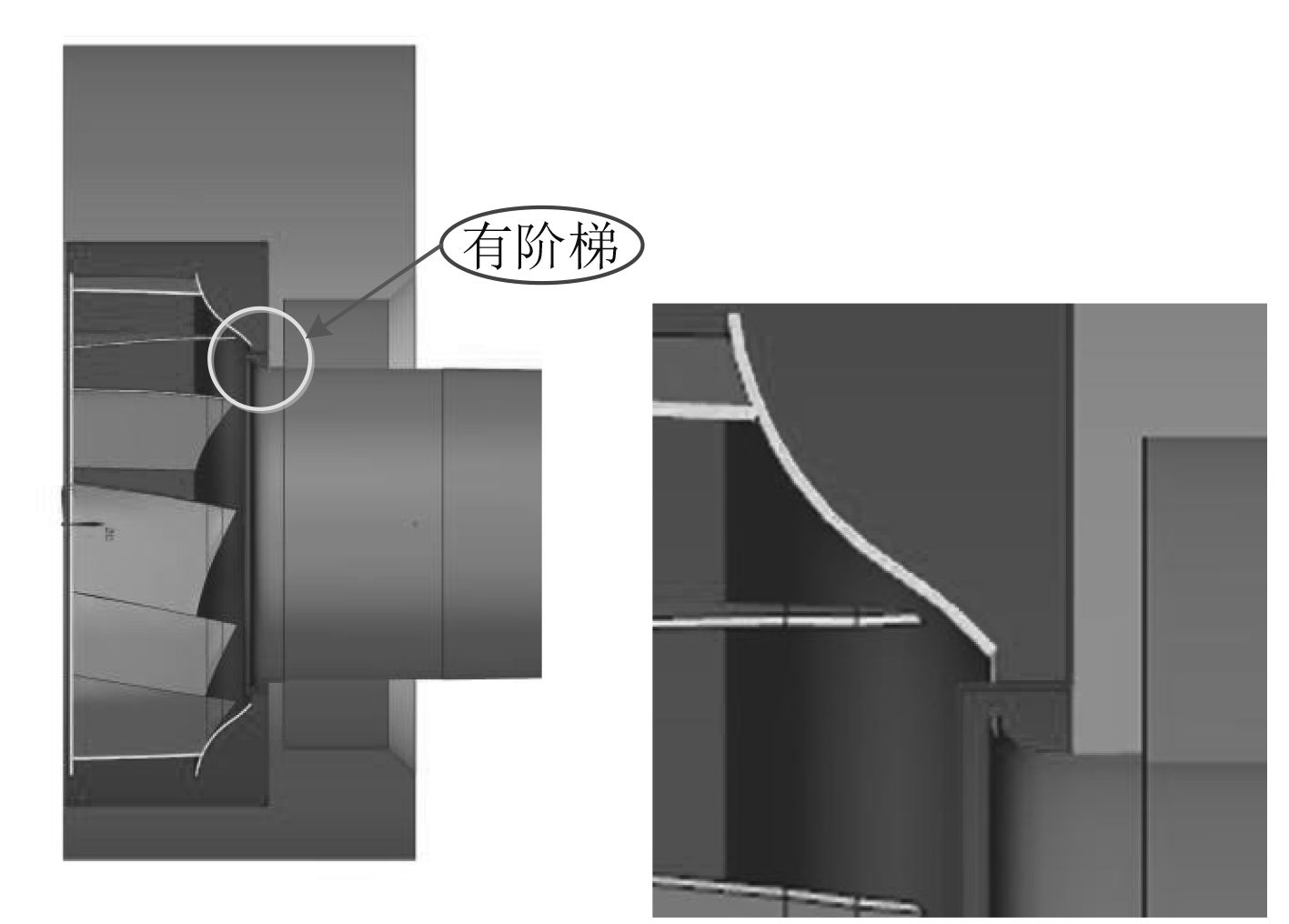
|
图 4 交界面划分示意图(右侧为局部放大图) Fig. 4 The sketch of interface splitting (the right part is enlarged view) |
由于风机内部流场复杂(气体由叶片甩出、进风管与出风管垂直),而且体积较大,因此对网格质量要求较高,另外网格数量应尽可能少一些,因此所有网格均采用结构化网格绘制,均在ICEM中划分完成。叶片是10叶,在划分时,先在UG中剖分行1/10部分,然后再划分网格,由于叶片和前盘是扭曲的,在绘制时需要添加辅助线,进行线的关联,最终旋转生成总体的网格,划分过程如图5所示。
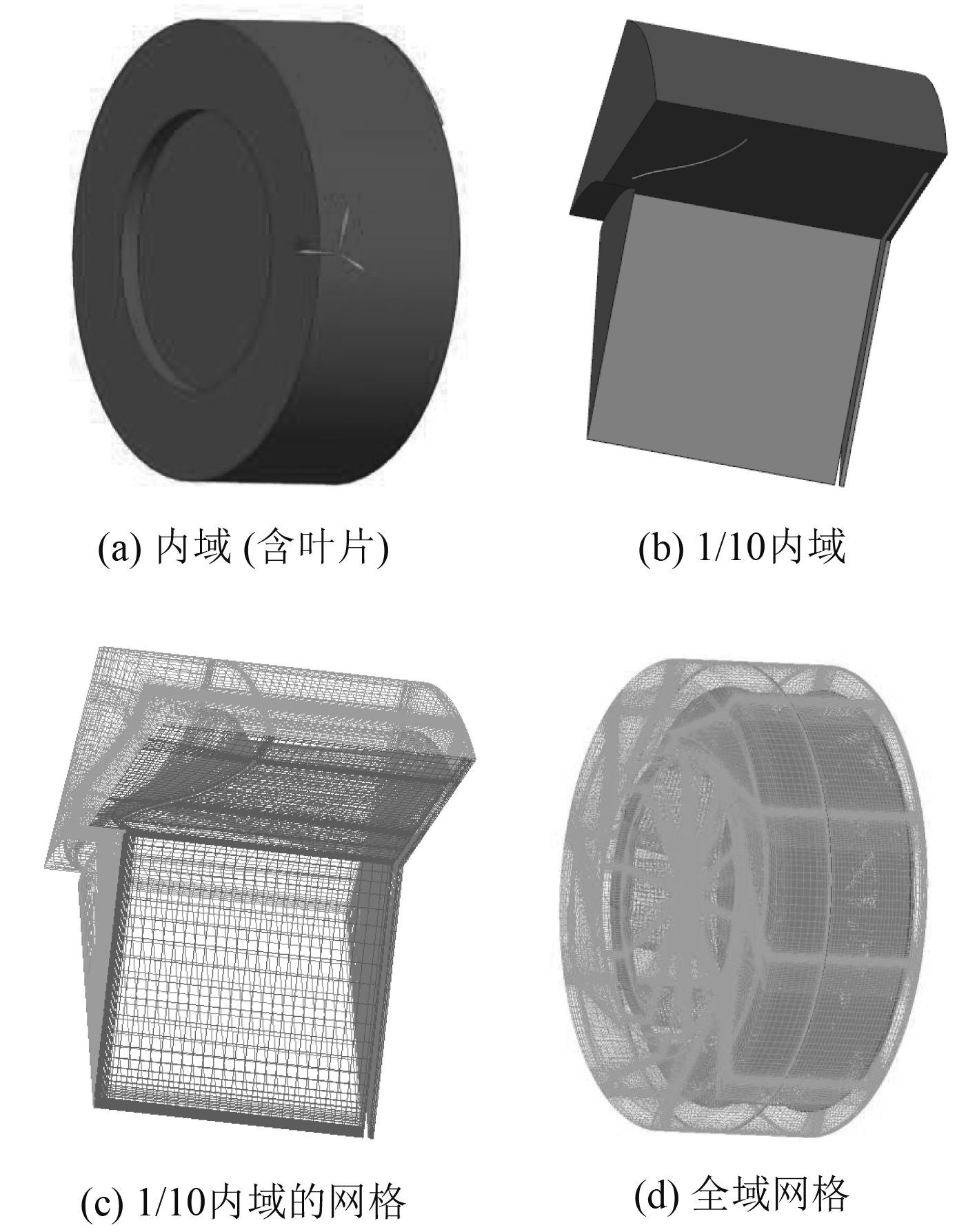
|
图 5 风机网格的划分 Fig. 5 The generation of the fan's grid |
由于风机出口部分是圆段,而之前是方段,这样静止区域的网格由蜗壳部分和出口部分2部分组成。其中蜗壳部分需要有如图6所示的拓扑结构(箭头表示线的关联),才能得到高质量的网格。图7和图8分别为蜗壳网格和出口段网格。
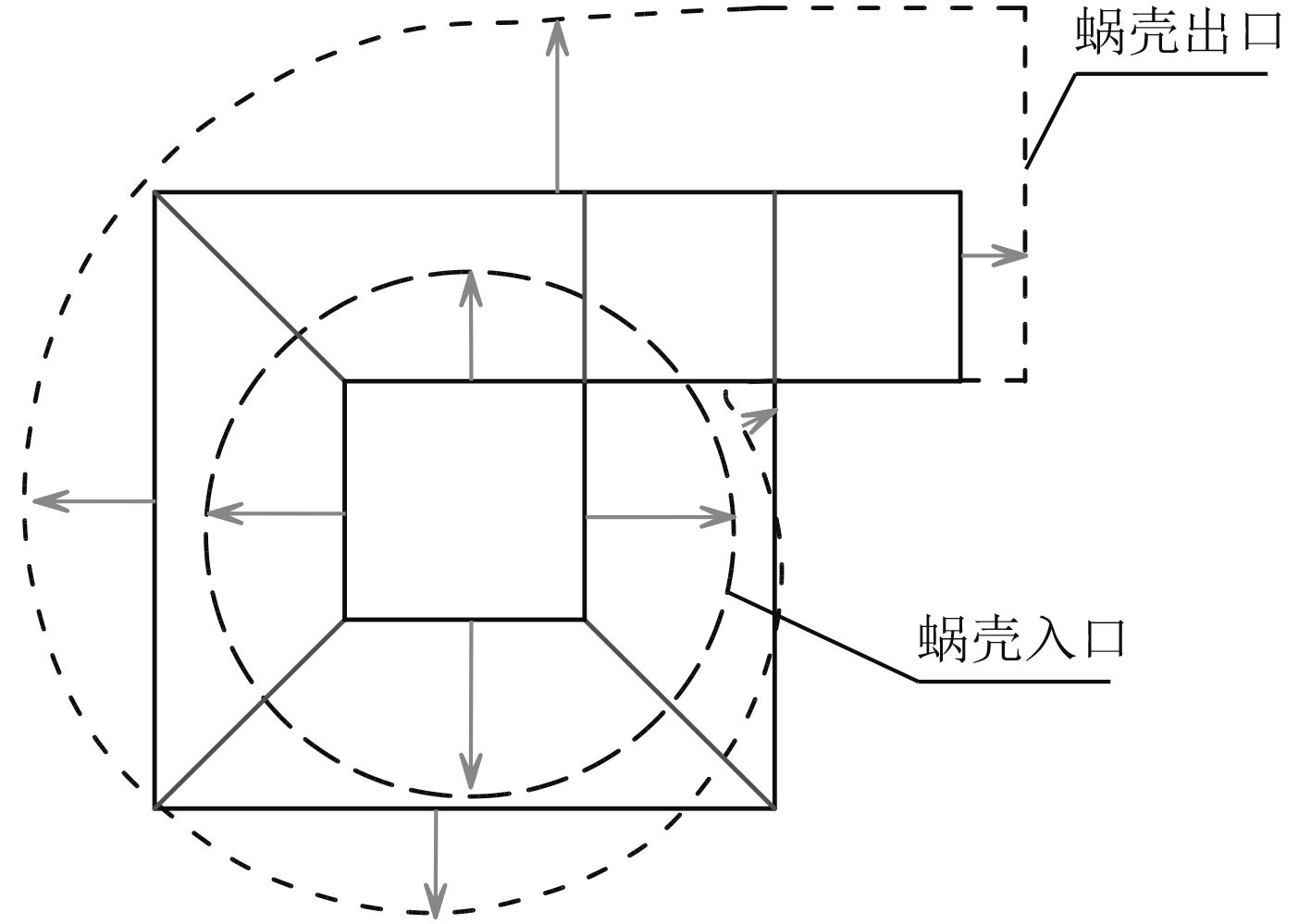
|
图 6 蜗壳部分的拓扑结构 Fig. 6 The topology structure of volute |

|
图 7 蜗壳部分(含入口与部分出口)网格 Fig. 7 The grid of the volute (including the inlet and part of the vent) |

|
图 8 风机出口段网格 Fig. 8 The grid of the vent |
网格的蜗壳部分第1层网格设置为0.6 mm,叶片为0.3 mm,出口段也为0.3 mm。在运算稳定后,无因次壁面法向高度
由于风机管中速度不高,可当做不可压缩气体处理。求解时采用RNG k-ε模型,是由Yakhot及Orzag提出的[8]。在此模型中,方程和系数是来自解析解,ε方程改善了模拟高应变流动的能力,其他增加选项用来预测涡流和低雷诺数流动;修正后的粘度项体现小尺度的影响,而使这些小尺度运动有系统地从控制方程中去除。它可以更好地处理高应变率及流线弯曲程序较大的流动,相应的方程为[9]
| $\frac{{\partial (\rho k)}}{{\partial t}} + \frac{{\partial (\rho k{u_i})}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}\left[ {{a_k}{\mu _{eff}}\frac{{\partial k}}{{\partial {x_j}}}} \right] + {G_k} + \rho \varepsilon \text{,}$ | (1) |
| $\frac{{\partial (\rho \varepsilon )}}{{\partial t}} + \frac{{\partial (\rho \varepsilon {u_i})}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}\left[ {{a_\varepsilon }{\mu _{eff}}\frac{{\partial \varepsilon }}{{\partial {x_j}}}} \right] + \frac{{C_{1\varepsilon }^*\varepsilon }}{k}{G_k} - {C_{2\varepsilon }}\rho \frac{{{\varepsilon ^2}}}{k}{\text{。}}$ | (2) |
其中:
| $ \left\{ \begin{array}{l} {\mu _{eff}} = \mu + {\mu _t}\text{,}\\ {\mu _t} = \rho {C_\mu }\displaystyle\frac{{{k^2}}}{\varepsilon }\text{,}\\ {C_\mu } = 0.0845,{a_k} = {a_\varepsilon } = 1.39\text{,}\\ C_{1\varepsilon }^* = {C_{1\varepsilon }} -\displaystyle\frac{{\eta (1 - \eta /{\eta _0})}}{{1 + \beta {\eta ^3}}}\text{,}\\ {C_{1\varepsilon }} = 1.42{\rm{ }}{C_{2\varepsilon }} = 1.68\text{,}\\ \eta = {(2{E_{ij}} \cdot {E_{ij}})^{1/2}}\frac{k}{\varepsilon }\text{,}\\ {E_{ij}} = \displaystyle\frac{1}{2}\left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \displaystyle\frac{{\partial {u_j}}}{{\partial {x_i}}}} \right)\text{,}\\ {\eta _0} = 4.377,\beta = 0.012\text{。} \end{array} \right. $ | (3) |
模型仍是针对充分发展的湍流有效的,而对近壁区内的流动及Re数较低的流动,需用壁面函数法来模拟,本次壁面函数采用的是标准壁面函数。
叶片转速通过蜗壳表面脉动压力的频谱分析后得到,为1 470 r/min。整个区域设置为运动参考系(Frame Motion)。自由入口的湍流强度设为2%,湍流粘性比设为2,而出口处由于湍流已经充分发展,所以出口的湍流强度设为5%,湍流粘性比设为5。除了交界面外,其他边界条件均设为壁面条件,即无滑移边界条件。由于网格分为3部分,因此需设置2个交界面,1个是蜗壳与叶片,另外1个是蜗壳与出口段。
在求解时采用求解压力耦合方程的半隐方法,梯度采用基于单元的最小二乘法、动量方程差分采用二阶迎风格式,湍动能、耗散率的差分等均采用一阶迎风格式。
2.2 网格收敛性分析数值计算软件采用Fluent。由于网格数量对数值计算的结果有影响,首先进行网格无关性检查,共使用了5套网格,其中第1套的网格量最大,从表1可以看出,网格数量从低到高变化时计算结果已趋于稳定。在后继的数值计算中采用的是第1套网格。
|
|
表 1 不同数量网格计算结果 Tab.1 The result calculated by different nets |
Fluent中计算6 000步后,计算结果就已经收敛。与测量位置相对应在出口管距出口处6.1 m处,垂直于气流方向,做一个平面,在这个平面上可以得到速度矢量图,如图9所示。

|
图 9 风机出风管截面处速度矢量图 Fig. 9 The velocity vector at section of the fan outlet pipe |
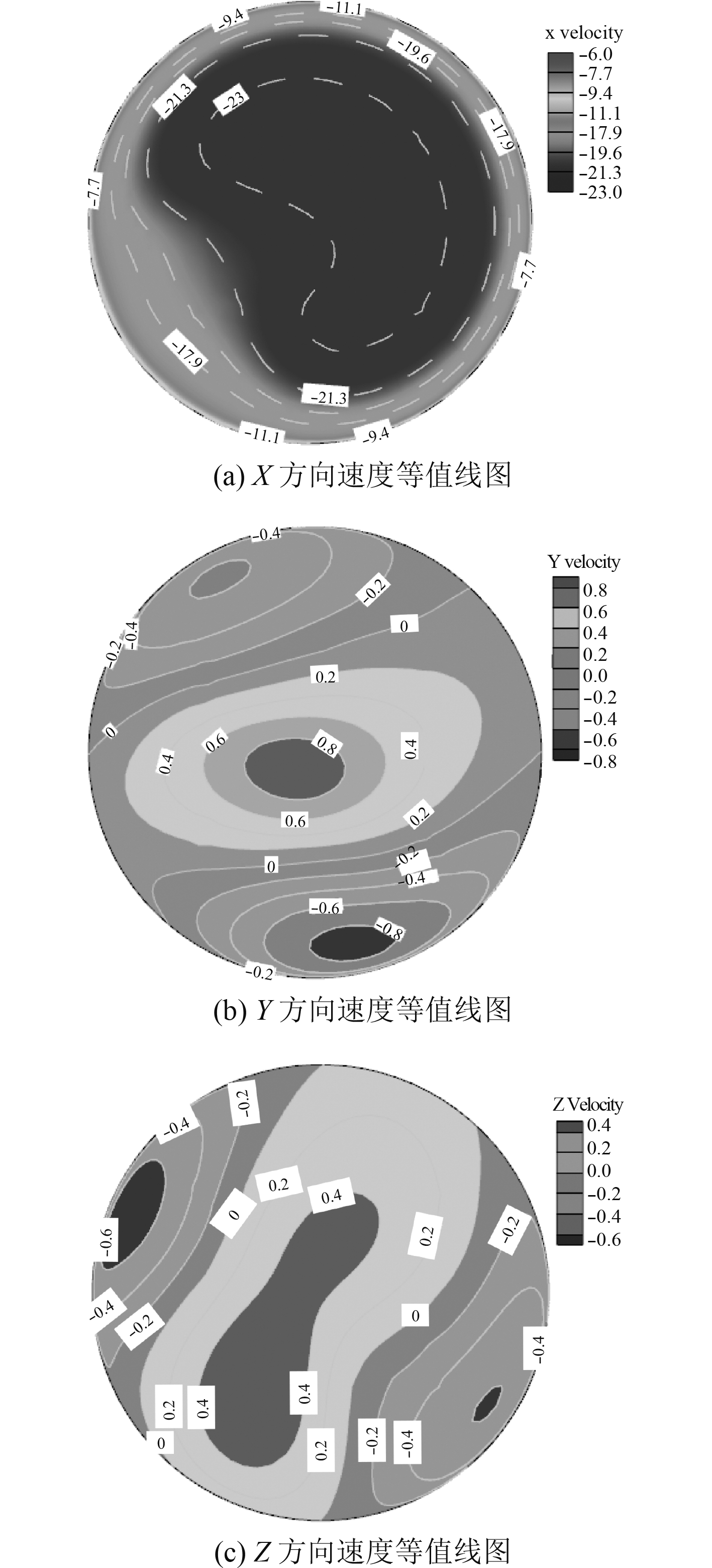
管中速度在X,Y,Z三个方向的分量分别使用Tecplot软件(美国Tecplot公司的数据分析和可视化处理软件)绘出,如图10所示,可以看出X方向的速度在管中心区域达到了22 m/s,远大于Y方向与Z方向的结果,同时在图10(a)中的左下方,速度稍小,等值线有些向中心凹陷,而图10(c)中同样位置的速度较大,结合图9中同样位置的矢量图,可以看出这里的气体速度矢量并不是垂直平面的,气体是扭转喷出的。通过在Fluent中提取管道中心的速度,可以得出在这点处的值为22.9 m/s。
|
图 10 风机出风管截面处速度等值线图 Fig. 10 The contour map at section of the fan vent pipe |
试验现场如图11所示,风机的管道较长,部分延伸到墙壁外面。

|
图 11 试验中的风机 Fig. 11 The fan in the experiment |
风管中风速测量采用的是手持式风级计,测量时在壁面钻一小孔,探头位置在风管中间,测量中采用短时求平均值的功能,结果为21.9 m/s。数值模拟得到的计算结果(22.9 m/s)与实际结果非常接近,差别的原因有可能是实际风管由多段连接而成,在接口处无法对齐,流道并不如数值模拟中的光顺。
从图中可以看出离心风机风管很长,其中有267~300 mm的扩展段、出口方管、方变圆段,管道类型多。而经过几何建模与网格绘制和数值求解后,可以得到非常接近的流速结果,这说明数值模拟是十分精确的。
4 结 语本文对一离心通风机进行流场的数值模拟和实际管中速度测量后,可以得出以下结论:
1)通过激光设备扫描后进行逆向建模可以得到风机叶轮模型。根据叶轮与蜗壳几何特征,可以绘制高质量的结构化网格。
2)由于叶轮旋转,用有台阶的小圆柱体内包含叶片,并作为旋转区域,数据通过圆柱体外表面与蜗壳相应部分进行数据传递。风机边界条件采用入口自由、进口自由,采用RNG k-ε模型可以进行流场模拟。出口管中心速度比实验结果仅高出4.6%。
3)风机管道形状多样、尺寸多变,且整体有90°的转向,说明采用结构化网格后数值模拟的结果是十分可靠的。数值模拟结果可以给风管设计、风机选型、电动机配置提供重要参考依据。
| [1] |
中国风机技术网. 中国风机行业发展分析报告[EB/OL]. http://www.cftn.cn/news/cftn_1/81/2009060411263815_1964.html. 2016-09-10.
|
| [2] |
张世芳. 泵与风机[M]. 北京: 机械工业出版社. 1998年.
|
| [3] |
范玉亭. 车载高效离心风机内部流动的数值模拟[D]. 东营: 中国石油大学, 2011年.
|
| [4] |
李照军. 离心风机流场数值模拟研究[J]. 中州煤炭, 2012(9): 17-19. LI Zhaojun. Simulation of the inside field for the centrifugal fan[J]. Zhong Zhou Coal, 2012(9): 17-19. DOI:10.3969/j.issn.1003-0506.2012.09.006 |
| [5] |
蒋爱华, 章艺, 靳思宇, 等. 离心泵流体激励力的研究: 蜗壳部分[J]. 振动与冲击, 2012, 31(4): 60-66. JIANG Ai-hua, ZHANG Yi, JIN Si-yu. et al.. Fluid exciting forces on centrifugual pump partⅠ: force on volute[J]. Journal of Vibration and Shock, 2012, 31(4): 60-66. DOI:10.3969/j.issn.1000-3835.2012.04.012 |
| [6] |
方开翔, 李豪杰, 高慧. 基于Fluent 6.0的风机流场模拟与噪声预估[J]. 江苏科技大学学报: 自然科学版, 2008, 22(4): 42-47. FANG Kaixiang, LI Haojie, GAO Hui. Simulation of inside flow field and noise forecast for a fan based on Fluent 6.0[J]. Journal of Jiangsu University of Science and Technology, 2008, 22(4): 42-47. |
| [7] |
李晓丽, 楚武利, 袁森. 离心风机整机三维数值仿真方法及分析[J]. 计算机仿真, 2010, 27(10): 335-340. LI Xiaoli, CHU Wuli, YUAN Sen. Three dimensional numerical emulation method and analysis of a whole centrifugal fan[J]. Computer Simulation, 2010, 27(10): 335-340. DOI:10.3969/j.issn.1006-9348.2010.10.083 |
| [8] |
YAKHOT V, ORZAGS S A. Renormalization group analysis of turbu1ence: basic theory[J]. Scient Comput. 1: 3–11, 1986.
|
| [9] |
王福军. 计算流体动力学分析-CFD软件原理与应用[M]. 北京: 清华大学出版社. 2004年.
|
 2019, Vol. 41
2019, Vol. 41
