0 引　言

在当今海洋石油开发中，浮式生产储油船（FPSO）已成为海上平台开采的油气处理、加工、存储和转运的重要装备之一。由于FPSO长期系泊于特定海域，海洋环境十分恶劣。因此，必须在设计阶段对其可能遭受的极限载荷进行计算，使船体具有足够的强度储备，以保证FPSO全寿命期内正常安全的运营。波浪载荷是评估船体结构安全性的关键性载荷，在海洋平台结构设计中，正确地预报其波浪设计载荷对平台的安全运营至关重要。

对于海洋平台结构的波浪设计载荷与强度分析，根据其结构类型不同与考虑计算工作量等因素，方法上有所变化和选择，大体上可分为确定性的设计波法、随机性设计波法以及长期预报设计波法，长期预报设计波法由于考虑了多种因素的变化，成为船级社船体结构强度校核应用较多的波浪载荷直接计算方法，本文采用长期预报设计波方法针对某型FPSO的波浪载荷进行计算，为同类型船舶的波浪载荷计算提供参考，并作为船体结构强度有限元分析的设计输入，进行船体结构强度校核以及后续的结构优化设计工作。

1 设计波参数确定方法 1.1 载荷控制参数

由于不同波浪环境下船体结构出现高应力的部位不同，一般选取多个设计波来校核全船的结构应力水平。一般采用主要控制参数来确定对船体不同结构部位的最不利波浪，针对所有主要控制参数对应的每个设计波进行船体结构强度校核，最终确定船体结构设计是否满足船级社结构规范的强度要求。不同船级社对于设计波的载荷控制参数的选取不同，根据船型不同，设计波控制参数的选取也不同。结合目标船的功能特点和结构特点，参考《海上浮式装置入级规范（2014版）》^[1]的相关要求，选取目标船的船中波浪弯矩以及最大剖面垂向剪力作为主要控制载荷进行设计波计算。

1.2 波浪载荷传递函数（RAO）计算

波浪载荷传递函数指的是船舶在单位波幅规则波中的各控制载荷参数的响应（如加速度，水动压力，剖面载荷等）对应波浪频率的传递函数^[2]，可用三维波浪载荷计算程序得到。

在计算中，浪向角的范围一般选取0～330°以30°为步长递增，波浪频率选取0.1～2.0 rad/s以0.1 rad/s为间隔。

1.3 长期预报

为了估算极值波浪载荷，先计算该载荷振幅的长期分布，然后按照超越概率确定其极值^[3]。

对一般的海洋结构物的响应振幅，其长期分布的超越概率P（X>x），可表示为：

$ P({{X}} > {{x}}) = \frac{{\mathop \Sigma \limits_i \mathop \Sigma \limits_j \mathop \Sigma \limits_k \mathop \Sigma \limits_l {N_ * }{p_i}{p_j}{p_k}{p_l}{P_ * }({{X}} > {{x}})}}{{\mathop \Sigma \limits_i \mathop \Sigma \limits_j \mathop \Sigma \limits_k \mathop \Sigma \limits_l {N_ * }{p_i}{p_j}{p_k}{p_l}}}\text{。} $

式中： ${P_ * }({{X}} > x{\rm{)}}$ 为短期响应振幅的超越概率； ${N_ * }$ 为在每秒钟内短期响应振幅的平均出现次数，例如可取 ${N_ * } = \frac{1}{{2{\text π} }}\sqrt {\frac{{{{({{{m}}_2})}_ * }}}{{{{({{{m}}_0})}_ * }}}} $ ； ${({{{m}}_0})_ * }$ 为短期响应谱的零阶矩； ${({{{m}}_2})_ * }$ 为短期响应谱的二阶矩； ${p_i}$ 为各种海情（有效波高）的加权因子； ${p_j}$ 为在给定有效波高下，选用的海浪谱变化时的加权因子，如采用双参数海浪谱，则可令 ${p_i}{p_j} = {p_{ij}}$ ， ${p_{ij}}$ 为有效波高 ${H_i}$ 与周期 ${T_j}$ 的联合出现率； ${p_k}$ 为工程系统遭遇波向角变化时的加权因子； ${p_l}$ 为在上述各因素给定下，工程系统的其他因素（航速、吃水）变化时的加权因子。

在响应谱是窄谱情况下，响应振幅的短期分布是雷利分布^[4]，其超越概率

$ {P_ * }({{X}} > x) = {\rm{exp}}\left\{ - \frac{{{x^2}}}{{2{{({{{m}}_0})}_*}}}\right\} \text{。} $

在工程系统的设计重现期T小时中，上述响应振幅的总出现次数为：

$N = \left\{ \mathop \Sigma \limits_i \mathop \Sigma \limits_j \mathop \Sigma \limits_k \mathop \Sigma \limits_l {N_ * }{p_i}{p_j}{p_k}{p_l}\right\} \times T \times 3\ 600/\left\{ \mathop \Sigma \limits_i \mathop \Sigma \limits_j \mathop \Sigma \limits_k \mathop \Sigma \limits_l {p_i}{p_j}{p_k}{p_l}\right\}\text{，} $

于是设计载荷极值 $\mathop x\limits^ \wedge (N)$ 可按下式确定：

$ \frac{1}{{P(X > \mathop x\limits^ \wedge (N)}} = N\text{。} $

1.4 设计波参数确定

分析控制参数的幅频响应计算结果，并在浪向和频率范围内进行搜索，获得幅频响应最大时对应的浪向、频率及初相位，便为由该控制载荷参数出发得到的设计波参数^[5]（浪向、频率及初相位）。

通过波浪载荷计算程序得到对应于一定超越概率的控制载荷参数长期值R_L，通过搜索可获得幅频响应传递函数最大值R_M，于是对应的设计波的波幅为 $\zeta = \displaystyle\frac{{{R_L}}}{{{R_M}}}$ 。

2 计算结果与分析 2.1 目标船体与计算条件

针对工作海域为渤海海域的某FPSO进行波浪载荷分析，设计海况选取为工作海域百年一遇下的自存工况，目标船的主要参数如表 1所示。

应用COMPASS-WALCS软件计算目标船船体运动响应和波浪载荷，目标船的水动力模型如图1所示。

2.2 计算结果 2.2.1 载荷响应RAO

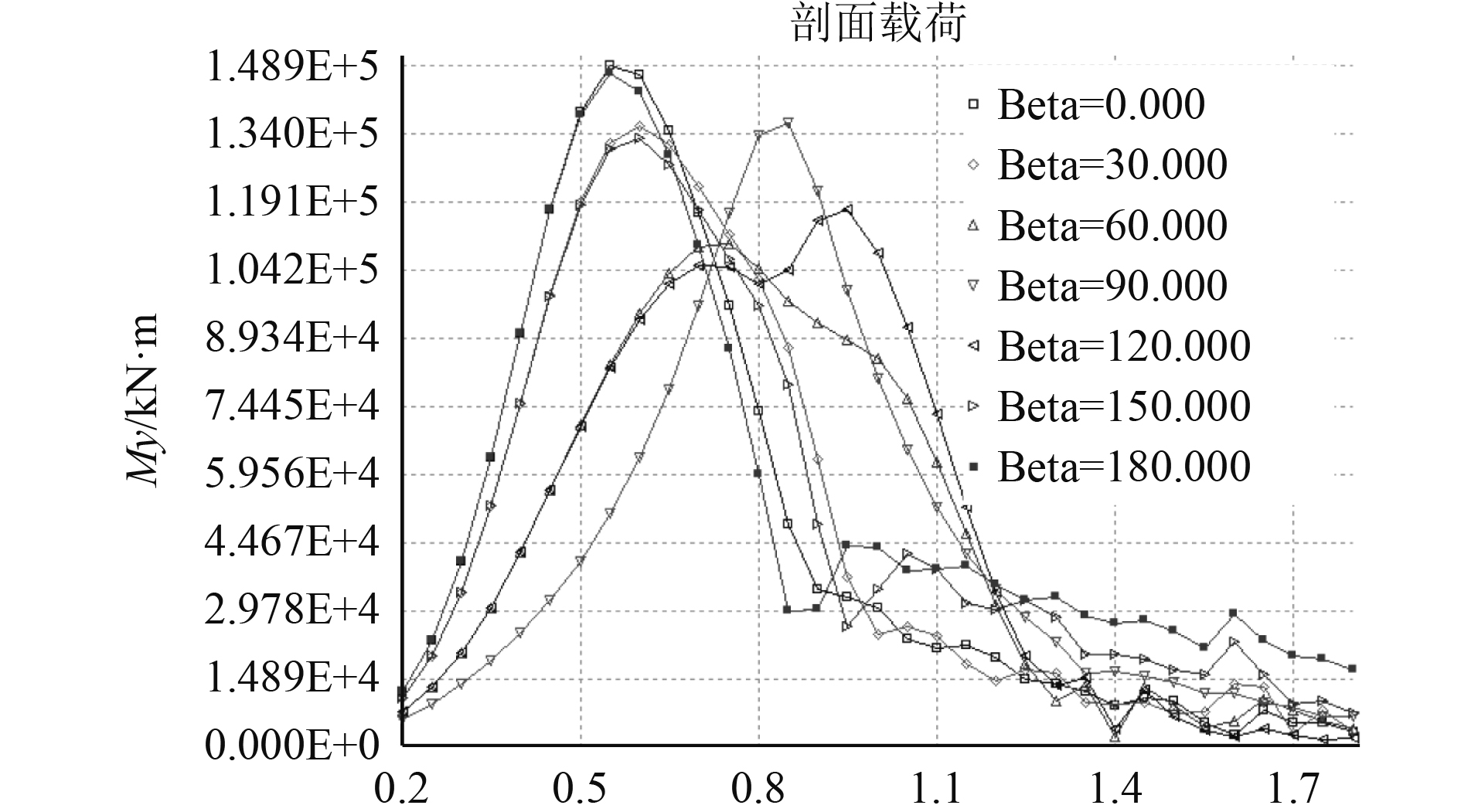
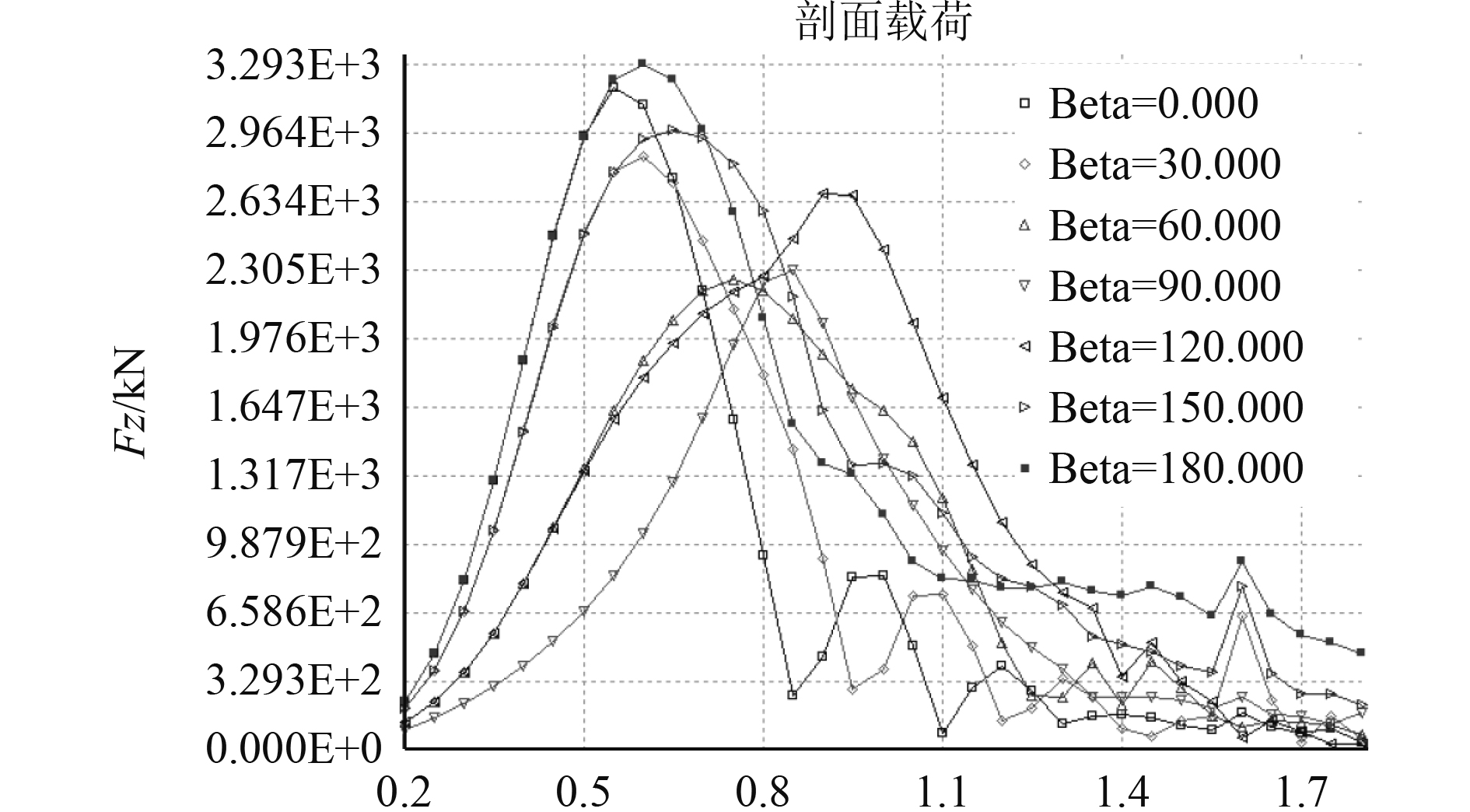
为了节省计算时间，考虑到船舶运动的对称性，计算中，选取浪向角为0°，30°，60°，90°，120°，150°和180°下的船中垂向波浪弯矩和最大剖面垂向剪力响应RAO进行分析，计算结果分别如图2和图3所示。

2.2.2 长期预报结果

在计算中，波浪载荷长期预报的计算统计参数选取分别如下：

1）波浪谱选取为Jonswap谱；

2）波浪形式考虑短峰波的影响；

3）扩散函数为 $\displaystyle\frac{2}{{\text{π}}}{\cos ^2}\theta $ ；

4）海浪散布图为渤海海域波浪散布图；

5）超越概率为重现期百年一遇海况下的超越概率。

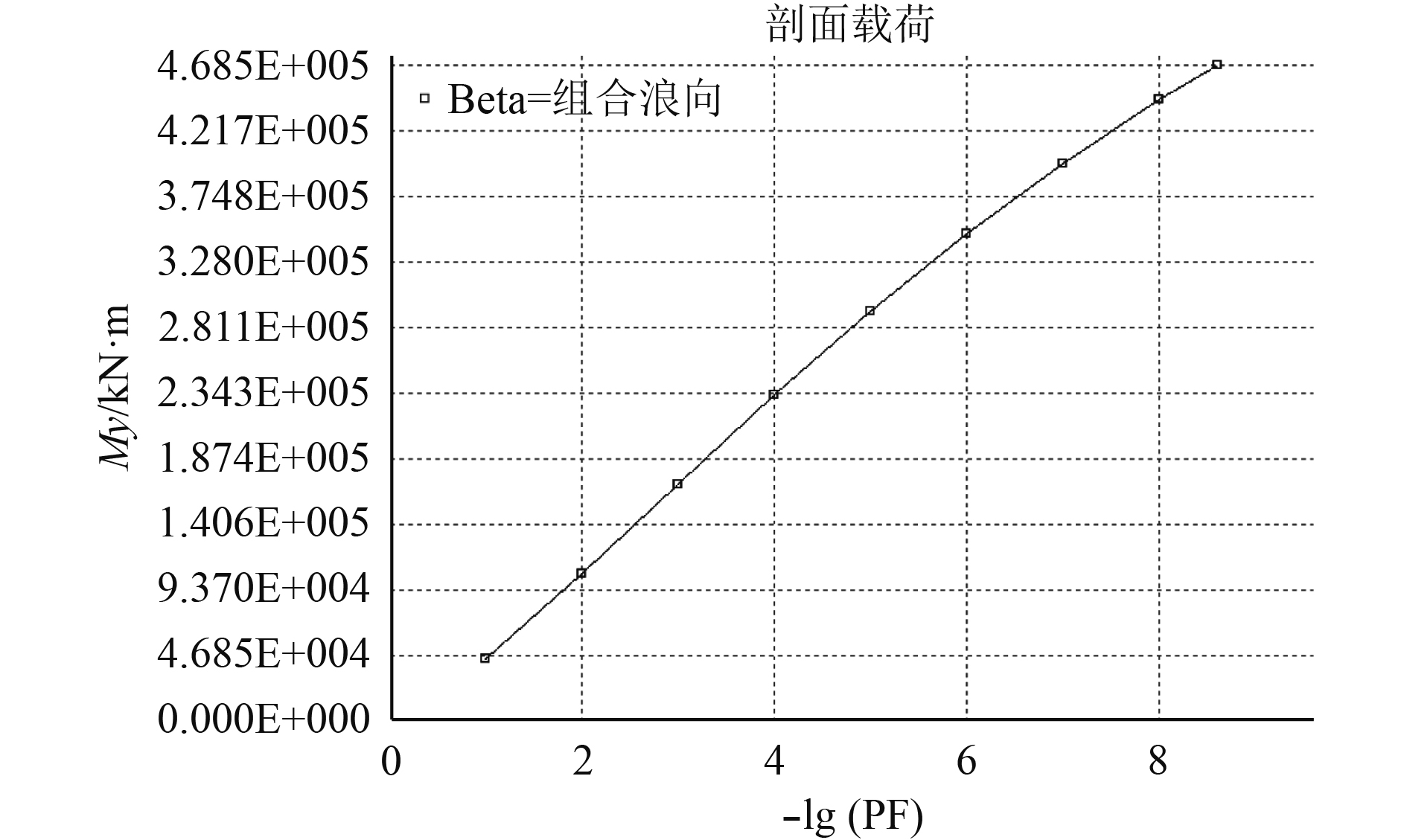
计算得到的船中垂向波浪弯矩长期预报极值如图4所示，最大剖面垂向剪力长期预报极值如图5所示。

2.2.3 设计波结果

通过目标船的波浪载荷RAO及载荷极值计算得到的设计波波浪参数如表 2所示。

确定了各控制参数的设计波波浪参数后，就可采用波浪载荷计算程序得到设计波载荷（包括船体湿表面静压力、波动压力、运动瞬时加速度等），进而进行船体结构强度评估。

2.2.4 规范计算结果

根据《钢质海船入级规范（2015版）》的公式对目标船的船中垂向波浪弯矩和最大剖面垂向剪力进行计算，计算结果如表3所示。

2.3 波浪载荷计算结果分析

中国船级社（CCS）在《钢质海船入级规范（2015版）》当中规定了使用设计波进行波浪载荷的直接计算方法，并且规定通过线性波浪理论得到的波浪弯矩和波浪剪力应按相关要求进行非线性修正，其中波浪弯矩非线性修正系数如下：

$ {f_{nl - h}} = \frac{{190{C_b}}}{{95{C_b} + 55({C_b} + 0.7)}}\text{，} $

$ {f_{nl - s}} = \frac{{110({C_b} + 0.7)}}{{95{C_b} + 55({C_b} + 0.7)}}\text{。} $

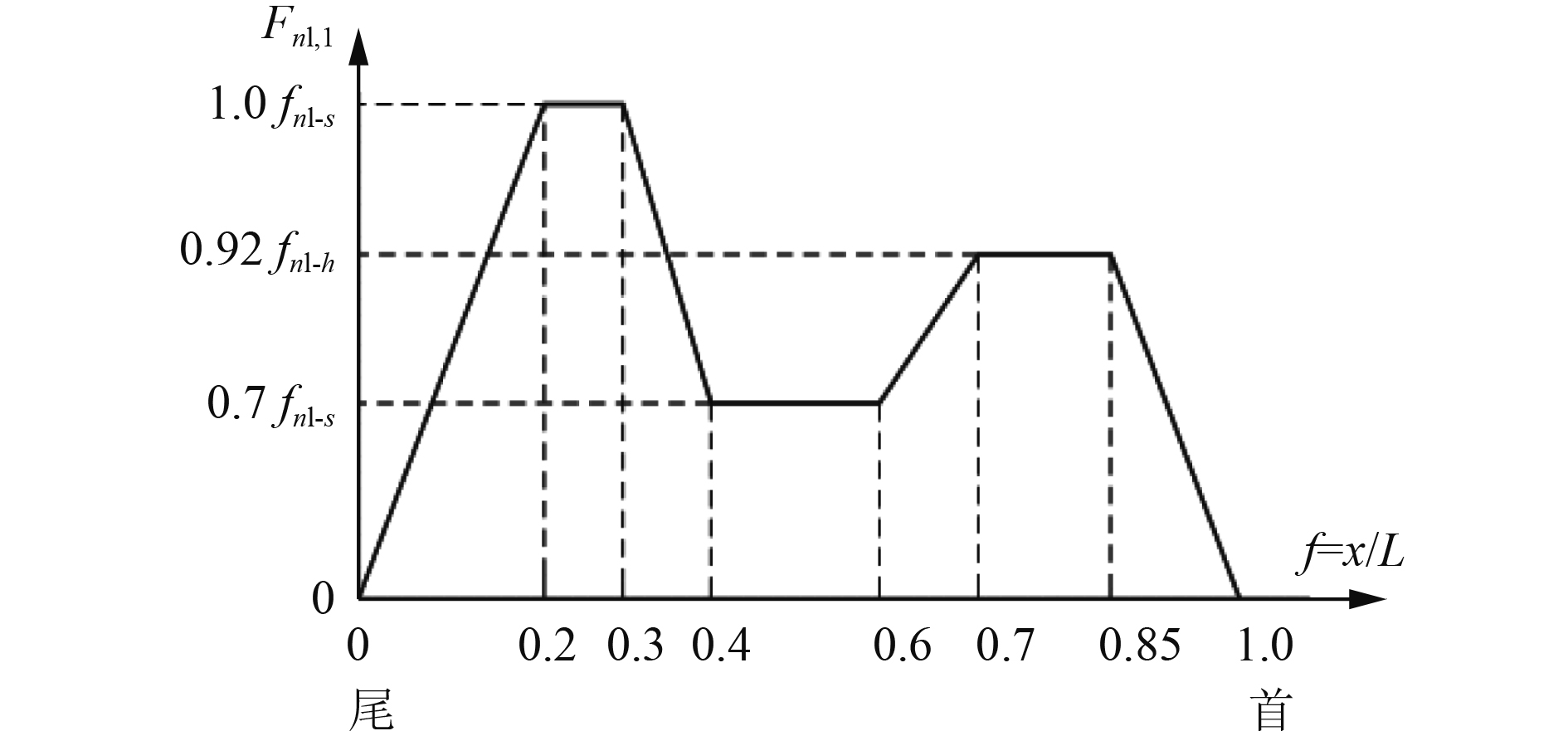
考虑非线性修正后剪力沿船长的分布系数分别按MERGEFORMAT 图6和图7进行计算。

图中， ${f_{nl - h}}$ ， ${f_{nl - s}}$ 分别为中拱波浪弯矩和中垂波浪弯矩的非线性修正系数； ${f_{nh - 1}}$ ， ${f_{nl - 2}}$ 分别为中拱波浪剪力和中垂波浪剪力考虑非线性修正后沿船长的分布系数。

长期预报设计波法计算的船中垂向波浪弯矩、最大剖面垂向剪力与CCS规范计算的波浪弯矩、波浪剪力计算结果对比见表3。

3 船体结构强度评估 3.1 模型建立

使用MSC.Patran软件建立了FPSO全船有限元模型如图8所示。模型采用右手坐标系，坐标原点位于FR0尾垂线与基线交点处，X轴指向船首为正，Y轴指向左舷为正，Z轴向上为正。模型中使用了板单元和梁单元，网格按照纵骨间距和肋距进行划分。

3.2 计算载荷施加

船体结构强度评估的设计载荷包括静载荷与动载荷。其中静载荷包括重力载荷（船舶自重）、舷外静水压力及液舱静压力，动载荷包括舷外水动压力、液舱动压力及全船惯性载荷。通过编写PCL程序将设计波下的舷外水压力（包括静水压力与波浪动压力，如图9和图10所示）及液舱压力（包括液舱静压力与液舱动压力）计算结果以压力场的形式施加在patran模型中，重力载荷与全船惯性载荷则以加速度场的形式施加于模型上。

3.3 边界条件

根据CCS《海上浮式装置入级规范（2014版）》的相关要求，采用惯性释放的方法实现全船的准静态强度的分析。惯性释放的原理即相当于在整船的重心位置处施加一个“虚支座”，用来平衡整个系统的不平衡力，该方法的应用前提是惯性释放之前整个系统应达到近似的平衡状态，其整体不平衡力应满足：在迎浪状态下，不超过对应排水量的1%；横浪及斜浪状态，不超过对应排水量的2%。

3.4 评估结果

通过有限元软件MSC.Nastran的计算，经过后处理得到设计波载荷作用下的极限工况（各设计波载荷工况的包络）整船应力云图如图11所示。

排除应力集中及网格形状不佳的单元应力，提取主要构件局部最大相当应力结果如表4所示。

4 结　语

本文使用线性设计波法，对某FPSO进行波浪载荷计算，得到其等效设计波波浪参数。同时，根据其设计波载荷进行了该FPSO的船体结构强度分析。分析结果表明：

1）用线性设计波法计算的波浪载荷比规范计算法得到的波浪载荷稍大，这是因为规范中波浪载荷的计算公式适用于L<500 m，L/B>5，B/D<2.5， ${C_b} \geqslant 0.6$ 的常规船型，而目标船L/B=3.78超出了规范计算公式的使用要求，需要采用直接计算法计算其波浪载荷，采用线性设计波法计算的目标船波浪载荷更为保守。

2）CCS《钢质海船入级规范（2015）》中给定了对于线性设计波法直接计算波浪载荷的非线性修正公式，波浪载荷非线性修正结果与线性设计波直接计算结果相差不大，用线性设计波法能较好的预报目标船这类方形系数较大、非线性效应不显著的船型。

3）由船体结构强度评估结果可以看出，在不考虑应力集中的情况下，极限工况下的船体主要构件的应力水平满足规范对总纵强度的要求。