螺旋桨空泡性能是评价螺旋桨性能的重要指标之一。片空泡作为一种主要的空泡形式,其生成、脱落、溃灭等现象对螺旋桨水动力、振动、噪声等有重要影响。近年来随着计算流体力学的快速发展,通过数值模拟方法研究螺旋桨空泡现象得到广泛使用,并在工程应用中得到认可。
Salvatore[1]基于RANS和DES比较了均匀流和非均匀流下,有空泡和无空泡时螺旋桨的水动力性能,以及空泡面积。Morgut[2]分别用CFD中3种空泡模型Zwart模型、全空泡模型(FCM)、Kunz模型对螺旋桨空泡形态进行预报,结果显示,在不考虑网格划分等其他因素下,3种预报结果接近,空泡面积都比试验结果要大一些。国内应用 CFD 预报螺旋桨空泡技术也不断开展。刘登成[3]采用 CFD 对螺旋桨进行空泡预报,所采用空泡模型为全空泡模型,预报出的片空泡形态与文献结果及公开发表的试验结果相一致。温亮军等[4]分析了螺旋桨侧斜、纵倾分布以及叶剖面等设计参数对空泡性能的影响,为空泡螺旋桨的优化设计提供了基础。刘亚非等[5]以典型槽道式侧推调距螺旋桨及其附体为对象,采用数值模拟的方法对其空泡形态和槽道脉动压力进行研究,分别计算了不同来流速度、不同推力大小及不同推力方向下桨叶附近的空泡形态和槽道内壁的脉动压力。蒲汲君等[6]采用LES湍流模型对E799A螺旋桨在全湿和一定空泡数下的水动力系数,以及不同工况下的空泡生成情况进行数值模拟研究,研究了来流速度和模型尺度的变化对螺旋桨片空泡产生的影响。
在商用软件Fluent中,螺旋桨空化数值研究可以采取非结构网格和结构网格2种。结构网格可以更加精细模拟梢涡空化的产生,然而,其质量对计算结果影响较大。作者在实际工作中发现在对某些大侧斜大螺距螺旋桨进行结构网格划分时,由于桨叶形状复杂、曲率变化大,网格质量并不高。鉴于此,本文将以E799A螺旋桨为研究对象,对结构网格、非结构网格在空化模拟中的表现进行对比研究,以期为今后的空化研究奠定基础。
1 数学模型 1.1 控制方程目前,对于N-S方程的统计平均方法以及补充反映湍流特性的其他方程,如湍动能方程和湍流耗散率方程,是目前的基本方法。
连续性方程是质量守恒定律在流体运动中的具体表现形式,流体连续性方程为:
| $ \frac{{\partial \rho }}{{\partial t}} + \frac{\partial }{{\partial {x_i}}}(\rho {u_i}) = 0{\text{,}} $ |
雷诺平均N-S方程为:
| $ \begin{array}{l} \dfrac{\partial }{{\partial t}}(\rho {u_i}) + \dfrac{\partial }{{\partial {x_j}}}(\rho {u_i}{u_j}) = - \dfrac{{\partial p}}{{\partial x{}_i}} + \\ \dfrac{\partial }{{\partial {x_j}}}\left[ \begin{array}{l} {\mu _0}\left(\dfrac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}\right) - \\ \dfrac{2}{3}{\mu _0}\dfrac{{\partial {u_l}}}{{\partial {x_l}}}{\delta _{ij}} \end{array} \right] + \dfrac{\partial }{{\partial {x_j}}}( - \rho \overline {{{u'}_i}{{u'}_j}} ) + \rho {f_i}{\text{。}} \end{array} $ |
式中的变量都是时历平均值。其中:
为了求解N-S方程中增加的雷诺应力,需要额外增加方程,以使雷诺应力中的脉动值与时均值联系起来,使方程组封闭,即湍流模型。本文采用的湍流模型为Standard
通过假设系统内所有气泡具有相同的尺寸,Zwart等提出使用气泡密度(n)来计算整个单位体积内汽液相间质量传输率(R),单个气泡的质量传输率为:
| $ {{R = n}} \times \left( {4{\text{π}} {{R}}_{{B}}^{\rm{2}}{\rho _{{v}}}\frac{{{{D}}{{{R}}_{{B}}}}}{{{{Dt}}}}} \right){\text{,}} $ |
代入n的值,可以得到净质量传输的表达式:
| $ {{R = }}\frac{{{\rm{3}}\alpha {\rho _{{v}}}}}{{{{{R}}_{{B}}}}}\sqrt {\frac{{\rm{2}}}{{\rm{3}}}\frac{{{{{P}}_{{B}}}{{ - P}}}}{{{\rho _{\rm{l}}}}}} {\text{。}} $ |
由上式可见,单位体积内的质量传输率仅仅与气相密度(
当
当
式中:气核半径
本文选用4叶侧斜螺旋桨E779A为研究对象。国外已经对该桨模做了大量相关的实验研究和数值模拟,其实验数据真实可靠,具有较好的参考价值。E799A螺旋桨模型直径为227.27 mm,螺距比为1.1,详细参数见文献[7]。
选用MRF方法[8]进行螺旋桨空泡性能计算。计算域入口距桨盘面2D,出口距桨盘面5D,外域直径为3D,如图1所示。计算外域选用结构网格进行划分,计算内域分别采用结构网格和非结构网格2种方法进行划分,其中结构网格1套和非结构网格2套,共3套网格。网格基本参数如表1所示,桨叶网格如图2所示。

|
图 1 螺旋桨敞水计算域 Fig. 1 Computational field of the propeller |

|
图 2 螺旋桨表面网格划分 Fig. 2 Grid on the propeller blade |
|
|
表 1 网格基本参数 Tab.1 Parameters of mesh |
在计算中,螺旋桨转速
本文首先对3种网格在J=0.71时全湿模态和空泡数为1.515两种状态下的推力系数进行计算比较,如表2所示。结果显示,在全湿模态下,3种网格的计算误差都在3%以内,说明了网格的可靠性和计算设置的准确性。在空泡数为1.515时,3种网格的计算误差都有明显增大,说明空泡的产生对于计算精度产生了较大影响。
|
|
表 2 敞水因子对比 Tab.2 Comparison of open water factor |
采用3种网格对
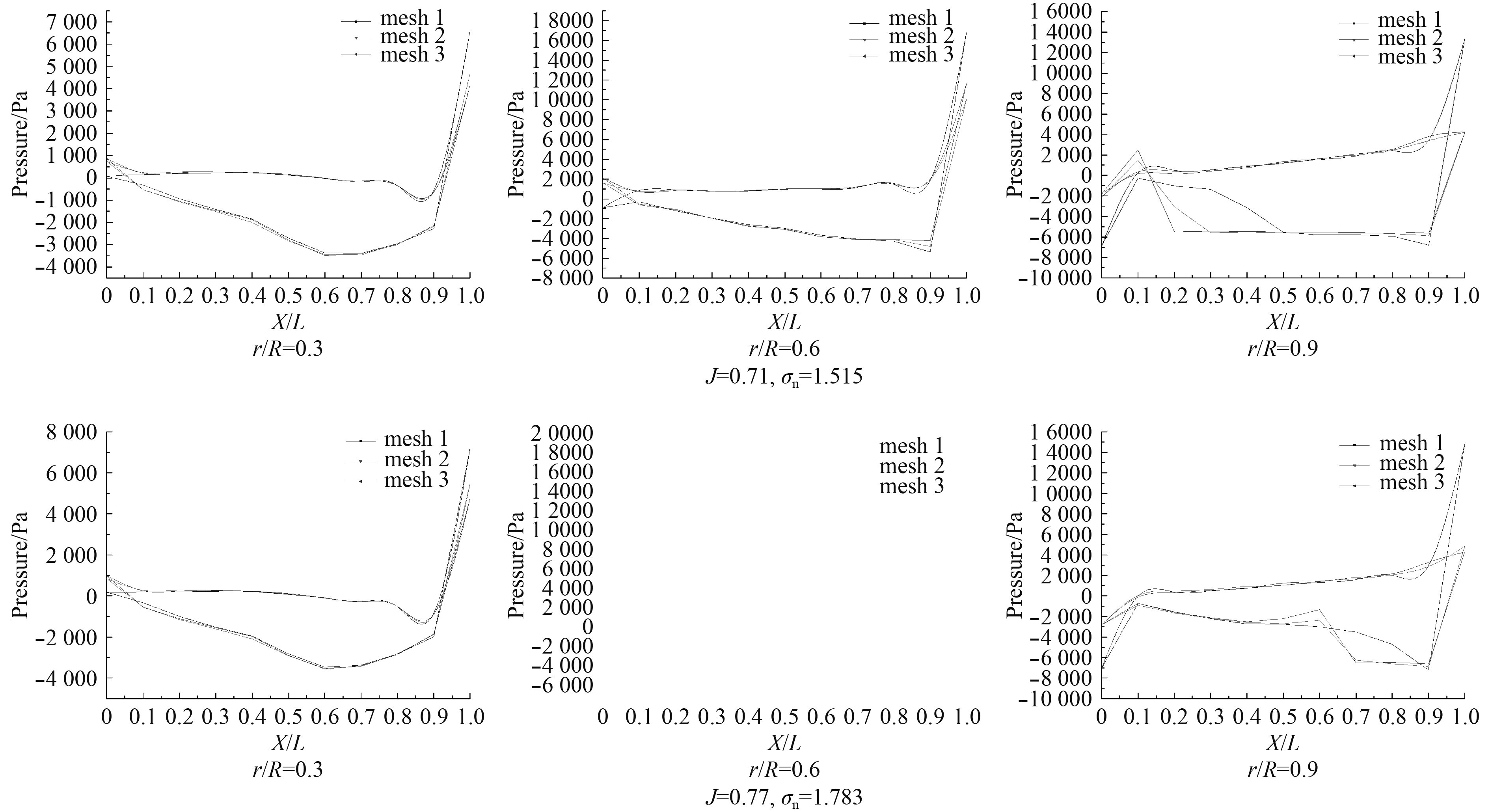
|
图 3 不同半径处桨叶表面压力对比图 Fig. 3 Comparison of surface pressure at different ritches |
图4显示了计算得到的气体体积分数分布图与试验所得空泡分布图的对比,该分布图与上述桨叶表面最低压力的分布基本一致。通过对比可以看出,结构网格所得空泡体积相比于试验结果偏小,2种非结构网格所得空泡体积基本一致,与试验结果符合较好。图5为桨盘面处水流速度轴向变化图,在桨盘面处,3种网格计算结果基本一致。从X/D=0.044开始时,结构网格对于叶梢处水流速度的捕捉好于非结构网格,从侧面可以体现出结构网格对于梢涡空泡的捕捉好于非结构网格。
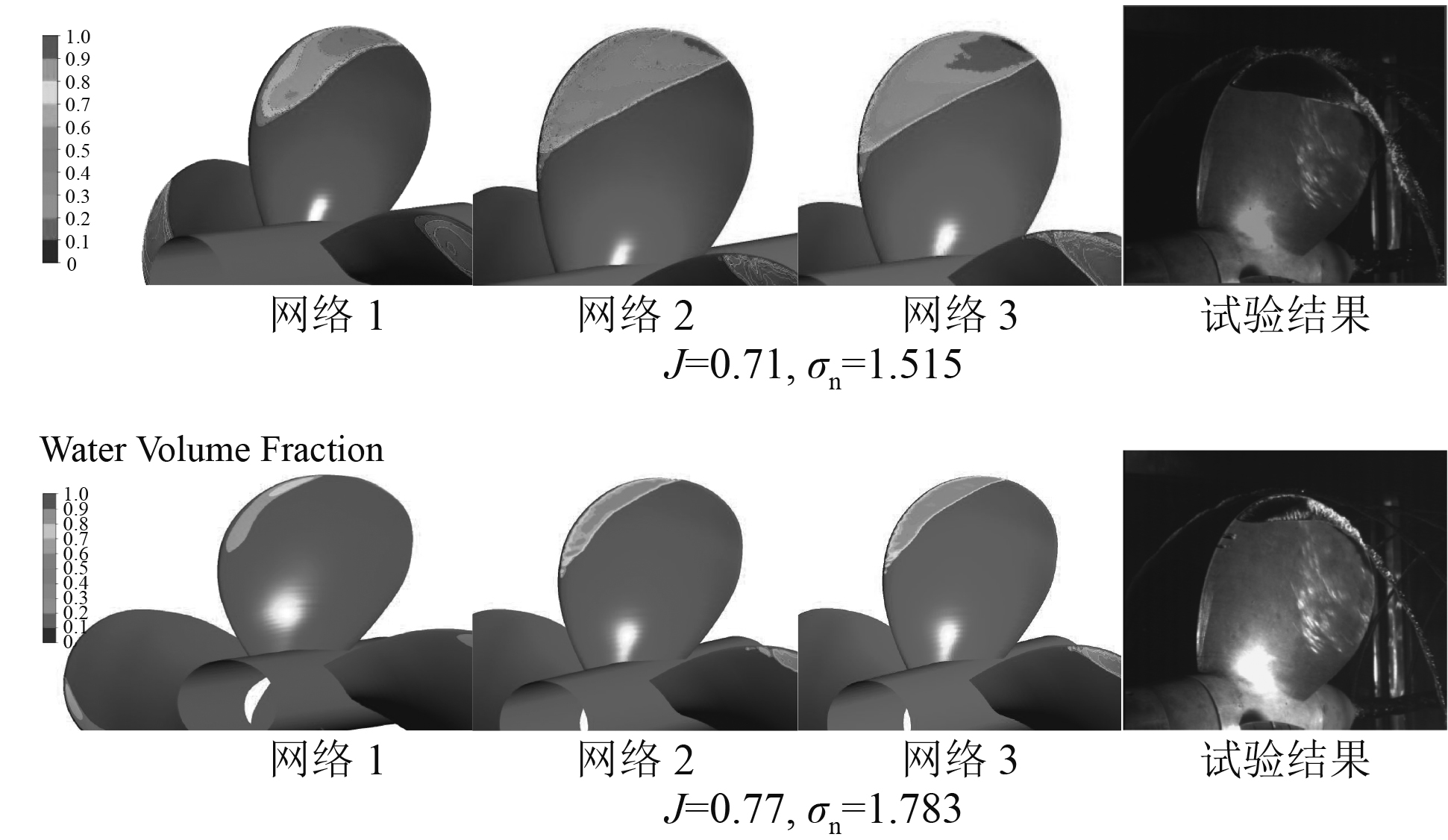
|
图 4 空泡形态对比 Fig. 4 Comparison of cavitation |

|
图 5 桨盘面水流速度轴向变化图 Fig. 5 Axial transformation of water velocity at propeller plane |
本文以E799A为研究对象,分别采用结构网格和非结构网格计算了其空泡性能。首先对J=0.71时空泡和无空泡状态下的推力系数与试验值进行对比,验证了计算的准确性和网格的可靠性。然后提取了桨叶表面压力,所示规律与空泡发生位置符合良好。空泡面积的对比显示,非结构网格对于片空泡的模拟结果与试验结果更加吻合,而桨盘面水流速度轴向变化图显示结构网格对于叶梢处伴流场的捕捉更好,从侧面可以体现出结构网格对于梢涡空泡的捕捉好于非结构网格。因此,在进行螺旋桨片空泡研究时,尤其是某些大曲率螺旋桨的片空泡研究时,非结构网格是可靠的选择,而在进行梢涡空泡研究或者某些需要考虑桨后流场的研究时,采用结构网格是更好的选择。
本文对E799A的空泡性能计算进行了初步探讨,对今后的研究工作有一定的借鉴意义。
| [1] |
FRANCESCO Salvatore. Propeller cavitation modelling by CFD -results from the VIRTUE 2008Rome workshop//[C] First International Symposium on Marine Propulsors smp’09, Trondheim,Norway, June 2009.
|
| [2] |
MITJA Morgut, ENRICO Nobile. Influence of the mass transfer model on the numerical predictionof the cavitating flow around a marine propeller[C]//Second International Symposium onMarine Propulsors smp’11, Hamburg, Germany, June 2011.
|
| [3] |
LIU Deng-cheng. The CFD analysis of propeller sheet cavitation[C]//Nantes France : Proceedingsof the 8th International Conference on Hydrodynamics, 2008: 171–176.
|
| [4] |
温亮军. 船舶螺旋桨空泡数值预报及参数影响分析[D]. 武汉: 中国舰船研究院, 2016.
|
| [5] |
刘亚非. 典型侧推调距螺旋桨空泡形态及激振力研究[C]//第十四届全国水动力学术会议暨第二十八届全国水动力学研讨会文集.
|
| [6] |
蒲汲君, 熊鹰. 螺旋桨片空泡尺度效应研究[J]. 武汉理工大学学报(交通科学与工程版), 2016, 40(4): 705-708. DOI:10.3963/j.issn.2095-3844.2016.04.027 |
| [7] |
FRANCESCO Salvatore , CLAUDIO Testa , LUCA Greco. A viscous/inviscid coupled formulation for unteady sheet cavitation modelling of ma2rine profellers[C]∥Fifth International Symposium on Cavitation (CAV2003). Osaka: [s.n.] ,2003: 1–16.
|
| [8] |
王超, 黄胜, 解学参. 基于CFD方法的螺旋桨水动力性能预报[J]. 海军工程大学学报, 2008, 20(4): 107-112. |
 2019, Vol. 41
2019, Vol. 41
