2. 海军工程大学,湖北 武汉 430033
2. Naval University of Engineering, Wuhan 430033, China
潜艇水下操纵性能研究,与潜艇的安全航行密切相关,是其进行战术机动的重要保证,同时有着直接的作战应用背景。实际航行中的潜艇是一种复杂运动的组合体。一方面,其高速、大攻角及强机动的运动特征,使其呈现出非定常性与强非线性;另一方面,潜艇作有攻角机动时,即使攻角保持不变,由于边界层分离产生漩涡,流动仍然会呈现出非定常特征。这就给理论和试验研究带来了很大的困难,采用数值模拟是切实可行的研究方法[1 – 3]。
本文以DARPA2潜艇模型为研究对象,采用基于非结构化网格的有限体积法,数值求解非定常、不可压缩的RANS方程,湍流模型采用SA模式,在SA模式中
采用CFD软件数值求解DARPA2潜艇模型粘性流场和水动力,采用基于非结构化网格的有限体积法,数值求解非定常、不可压缩的RANS方程。
| $\frac{{\partial {u_i}}}{{\partial {x_i}}} = 0\text{,}$ | (1) |
| $ \begin{split} & \frac{{\partial \rho {u_i}}}{{\partial t}} + \frac{{\partial \rho {u_i}{u_j}}}{{\partial {x_j}}} = - \frac{{\partial p}}{{\partial {x_i}}} +\\ & \frac{\partial }{{\partial {x_j}}}\left[ {\mu \left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right) + \frac{{\partial \left( { - \rho \overline {{u'_i}{u'_j}} } \right)}}{{\partial {x_j}}}} \right]\text{。} \end{split} $ | (2) |
湍流模型采用SA模式,在SA模式中,生成项所采用的形式为:
| $ {G_\upsilon } = \rho {C_{b1}}{\tilde S}\tilde \nu ,\ \ {\tilde S} = \Omega + {C_\upsilon }{\rm min}(0,\ {S} - \Omega ),\ \ {\text{取}}{C_\upsilon } = 30\text{。} $ | (3) |
速度-压力耦合采用SIMPLE方法处理,对流项采用2阶迎风格式,非定常项采用2阶精度离散,隐式迭代求解方程组。计算雷诺数Re=5.52×106,初值收敛准则为所有求解变量的无量纲残差下降4个量级,非稳态迭代时间步长
计算对象为DARPA2潜艇模型(见图1),模型主要参数如表1所示,包括艇主体、指挥台围壳、尾附体。数值计算在惯性坐标系中进行,采用直角坐标系,原点取在模型头部顶端,x轴与艇体的对称轴重合,方向与无攻角时来流方向一致,z轴竖直向上,y轴水平,计算时直角坐标系保持为模型处于零攻角时的位置,当模型作操纵运动时,坐标不变,而模型与坐标系产生相对运动;在所定义的坐标系下,规定来流的z方向速度分量正时为正攻角,初始攻角为0°。

|
图 1 全附体DARPA2模型 Fig. 1 DARPA2 submarine model with sail and stern appendages mounted |
|
|
表 1 DARPA2潜艇模型主要参数 Tab.1 DARPA2 model scale |
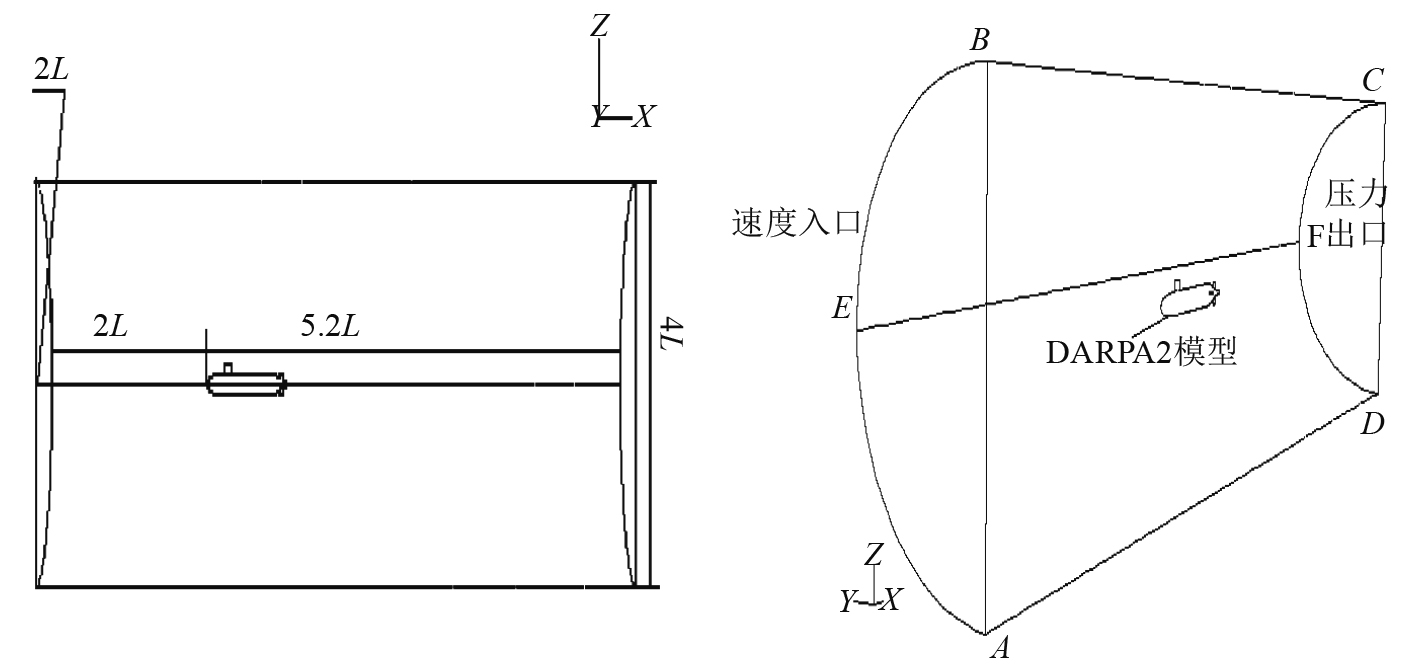
考虑到模型本身的对称性,同时操纵运动仅为xz面内的非定常回转运动,在不影响数值计算的准确性前提下,仅对半艇体流动进行数值计算,以减少计算量;计算域为半圆柱体区域,范围:–2.0≤x/L≤5.2,–2≤z/L≤2,0≤y/L≤2,其中L为艇体长度,L=2.236 m,计算域如图2所示。
|
图 2 模型的边界条件设置 Fig. 2 Boundary setting of the computational domain |
边界条件设置可分为初始流场状态和非稳态运动状态2个阶段。
初始边界条件(见图2):半圆柱体的左半圆面AEB(x/L=–2.0处)定义为速度入口,给定速度大小和方向;半圆柱体的右半圆面DFC(x/L=5.2处)定义为压力出口;半圆柱面的上、下两部分(EBCF/AEFD),及主体、指挥台围壳、尾附体,定义为无滑移壁面,速度分量和湍动能为0,以加速收敛,获得较好的初值;对称面上,法向速度分量为0,平行于对称面的速度分量的法向导数和所有标量的法向导数为0;初始攻角为0。
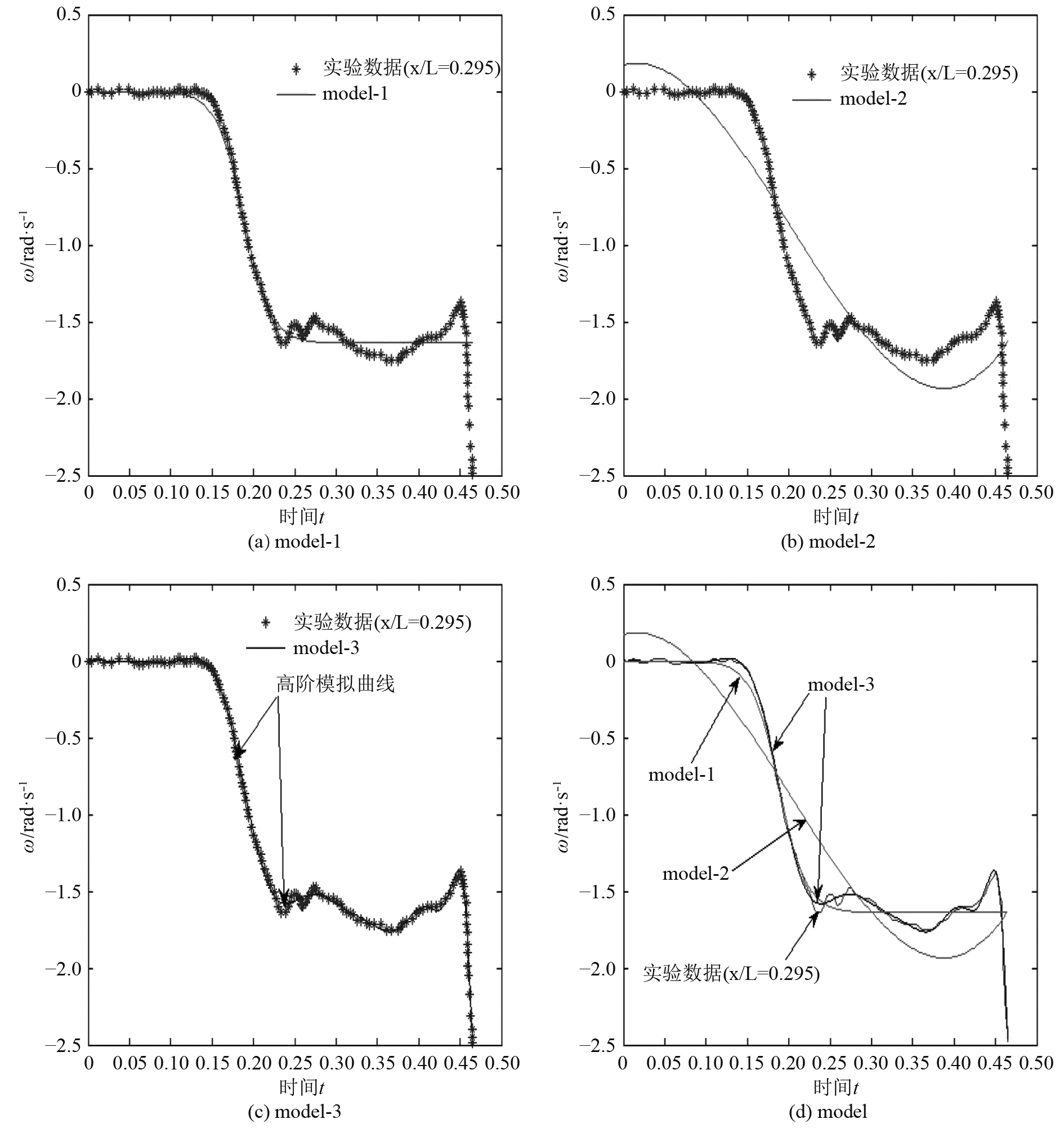
非稳态时模型作操纵运动,攻角发生改变,变化范围由0°~–25°,须调整边界条件,以适应运动状态的变化,此时定义半圆柱面的上半部分EBCF(z>0)为速度入口;半圆柱面的下半部分AEFD(z≤0)为压力出口,考虑到在迭代过程中,有可能存在数值上的反向流动,设置出口回流方向的方式为垂直于出口面;由于采用惯性坐标系,体网格是运动的,定义体网格和物面旋转中心(0.659 62,0,0)和旋转轴y轴,角速度由UDF定义。角速度曲线,具体描述如如图3及表2所示(实验数据来自文献[1])。
|
图 3 角速度ω随时间变化曲线 Fig. 3 ω vs. time |
|
|
表 2 不同模型的角速度函数 Tab.2 The function of ω for different model |
体网格采用基于四面体的非结构化网格形式,边界层网格进行加密处理,网格密度由模型表面至远场由密到疏分布。
网格主要参数见表3,
|
|
表 3 网格主要参数 Tab.3 The grids for simulation |
|
图 4
攻角–25°物面
|
|
图 5
攻角–25°物面
|
考虑到对模型进行非稳态运动模拟时,网格动态变化,网格需要均匀衔接,以避免网格的奇异变化导致迭代不收敛。
2 动态边界处理本文中应用动网格技术处理含有动态边界问题的非稳态运动状态,边界运动由UDF定义。
2.1 UDF编写用户自定义函数UDF(User-Defined Function)是CFD软件提供的一个用户接口,使用者可以通过它与CFD软件的内部数据进行交流,方便用户解决一些标准的CFD软件模块不能解决的问题[4 – 6]。
本文考虑到非稳态问题的复杂性,以及计算机本身的运行环境(已安装Visual Studio C++ 开发软件),采用编译的UDF定义其运动(非稳态场的角速度函数),以提高执行速度[7]。
2.2 网格更新动网格模型,即在每一个时间歩迭代之前,根据边界或物体的运动和变形来更新和重新构建计算域网格,从而达到求解非定常问题的目的[8 – 10]。而边界的形变和运动由UDF加以定义。计算中的网格更新情况如图6所示。
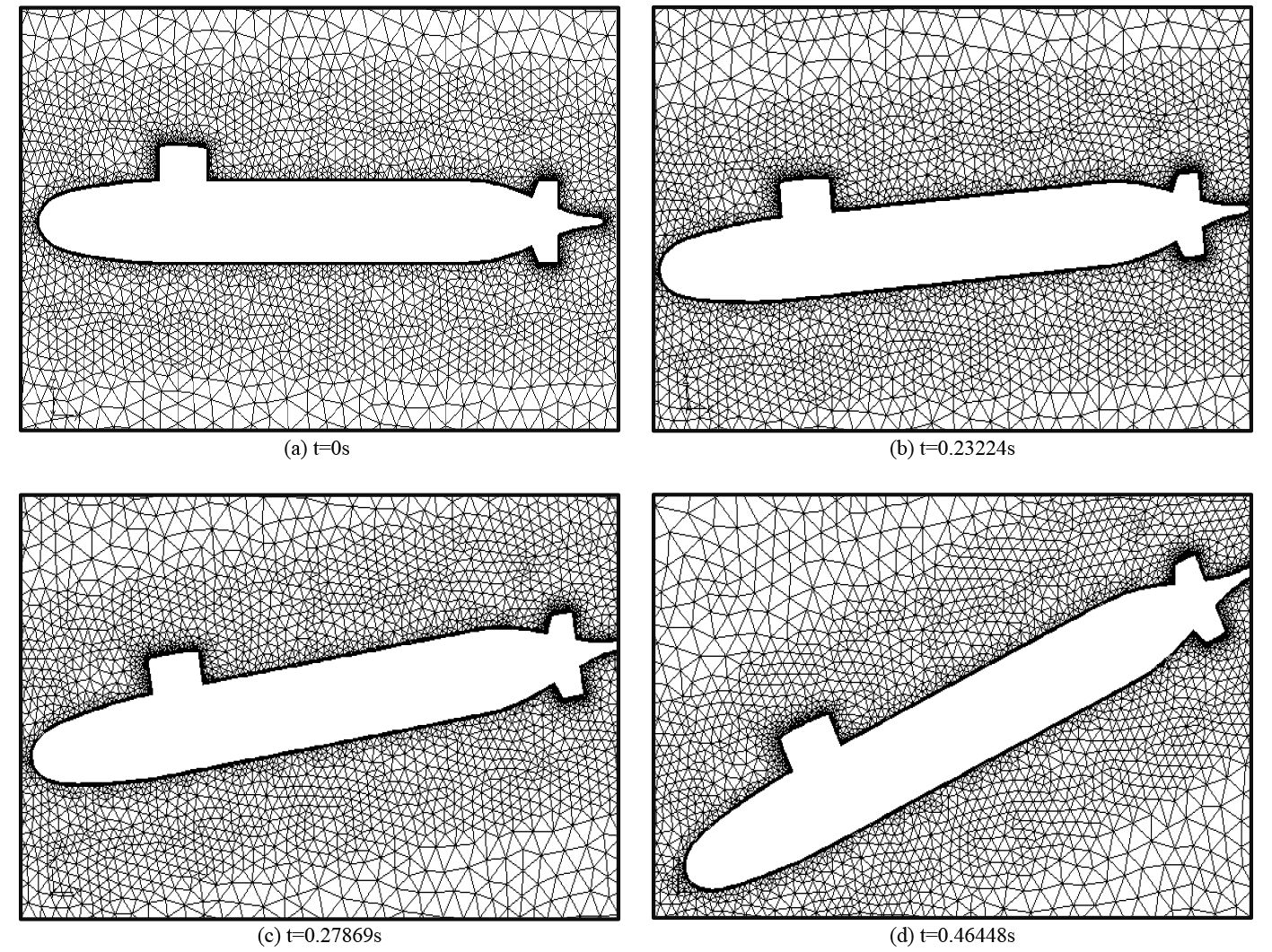
|
图 6 网格更新示意图(model-1) Fig. 6 The view of mesh motion (model-1) |
由图6可知,艇体和附体的物面边界层都参与了网格的重构过程,网格质量没有受到影响,网格更新过程中没有负体积和大长宽比网格出现,从而保证了数值迭代的延续。
3 初始流场计算为了得到较好的非定常结果,需要对初始流场进行讨论。本文中非定常因素,一方面,大攻角时,分离流动导致伴随涡的出现;另一方面,给定的模型运动状态,即角速度的定义本身就是随时间变化的函数。图7给出不同计算参数和边界条件下的初始流场变量收敛曲线。最初,分析初始时刻时,没有过多地考虑零攻角的流场特征,将边界条件半圆柱面的上、下两部分(EBCF/AEFD)分别定义为压力出口和速度出口,在迭代过程中流场变量波动起伏,近似周期性变化,但收敛精度未达到要求,如图7(a)所示;分析上述收敛精度持续不下的情况,可能是松弛因子过大的原因,将部分松弛因子降低30%,流场变量的波动情况消失,但收敛精度未出现改观,如图7(b)所示;观察到速度分量残差未发生变化,追溯根源,可能是边界条件有待优化,在图7(a)所定义的边界条件的基础上,将半圆柱面的上、下两部分(EBCF/AEFD)分别定义为无滑移壁面,速度分量残差迅速收敛,如图7(c)所示;图7(d)再次调整部分松弛因子,流场变量在925次迭代后达到收敛精度。
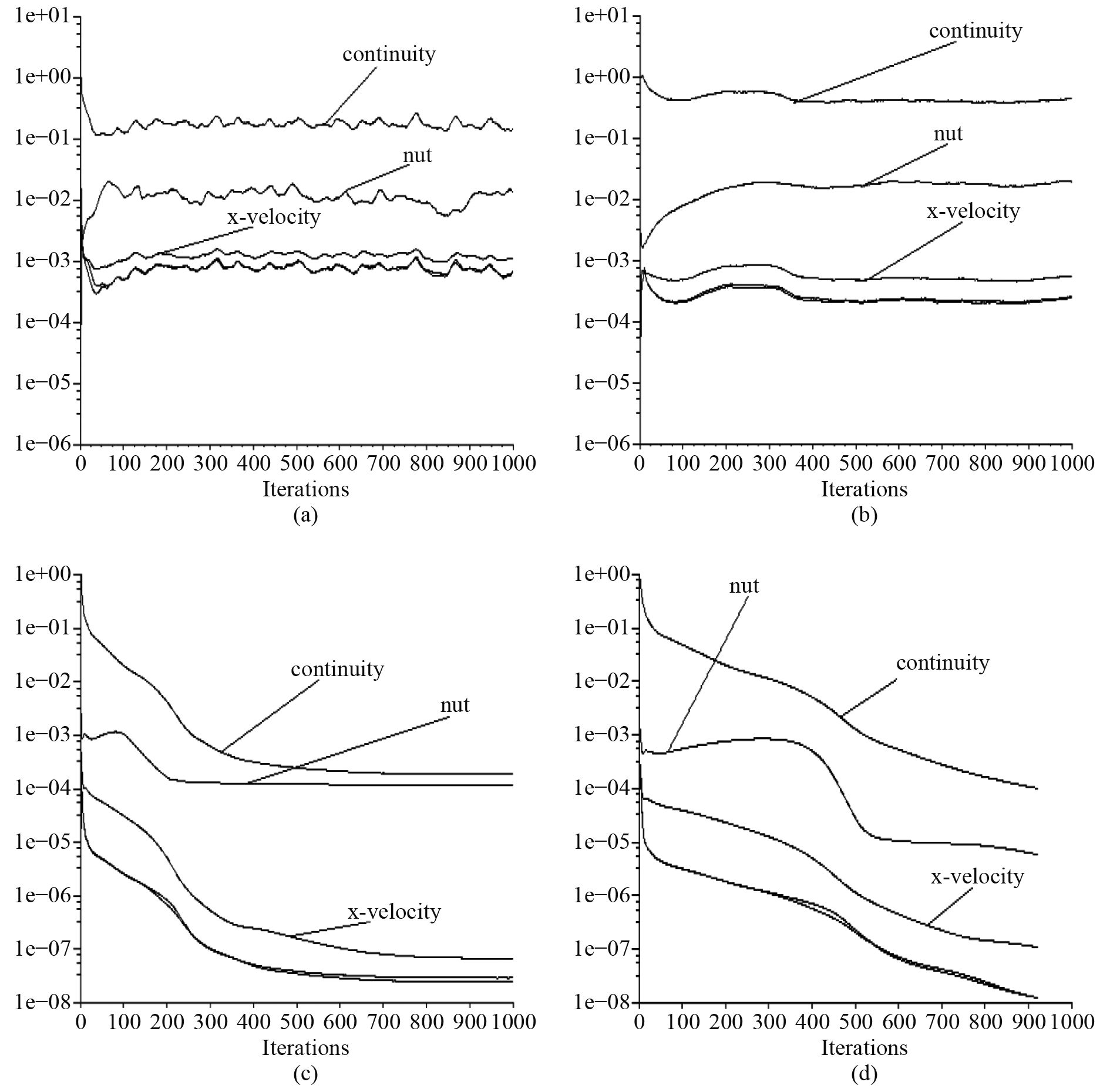
|
图 7 初始流场变量收敛历史 Fig. 7 Convergence history of flowfied variables |
初始流场由零攻角定常结果给出,进行非定常计算时需给定时间步长。依据文献[1]中的模型实验,给定角速度随无量纲时间t'的变化关系如图8所示,无量纲时间定义为

|
图 8 角速度ω(rad/s)随无量纲时间变化曲线 Fig. 8 ω(rad/s) vs. non-dimensional time |
本例中选取时间步长
应用表2中的3种模型曲线,对模型运动进行定义。初始化流场后,进行非定常数值模拟。
为追求曲线拟合的精确性,采用最小二乘法高阶多项式拟合实验数据,如图3(model-3)所示,当n=18时,除波动较复杂的拐点处略有差别外,整条曲线基本重合;但进行非定常数值计算时,角速度给定值持续增加,在不到100歩的迭代过程中,迭代时间不到半数,残差竟迅速增至102数量级,超出预定值近100倍,最后导致计算结果发散。分析原因,认为是时间精度不够的原因,将时间步长下降一个量级后,结果仍旧如前所述。尝试时间步长的一味降低,势必导致计算量的增大。
重新分析计算结果发散的原因,非稳态问题本身需要进行空间和时间的离散,变量之间的耦合关系将导致非线性增强,同时高阶曲线拟合容易造成较大的截断误差,综合上述原因,应用model-2,降低多项式阶次拟合实验数据,以验证是否是截断误差过大导致结果发散;非定常结果稳定,且角速度按给定值正常迭代。
但model-2对实验数据拟合效果不够理想,需要寻找其他函数,进行数值计算。本例采用model-1对实验数据进行拟合,同时略去角速度变化较大的尾端,拟合效果较好,数值计算结果稳定。
5.1 水动力分析图9给出了模型进行非定常数值计算时,升力系数CL随时间的变化情况。图中曲线unsteady,Quais-Steady+Time Lag和Quais-Steady为文献[1]中的实验结果,曲线unsteady为某一次非定常试验结果,Quais-Steady+Time Lag为20次非定常试验结果的平均值,Quais-Steady为准定常状态下的试验结果。
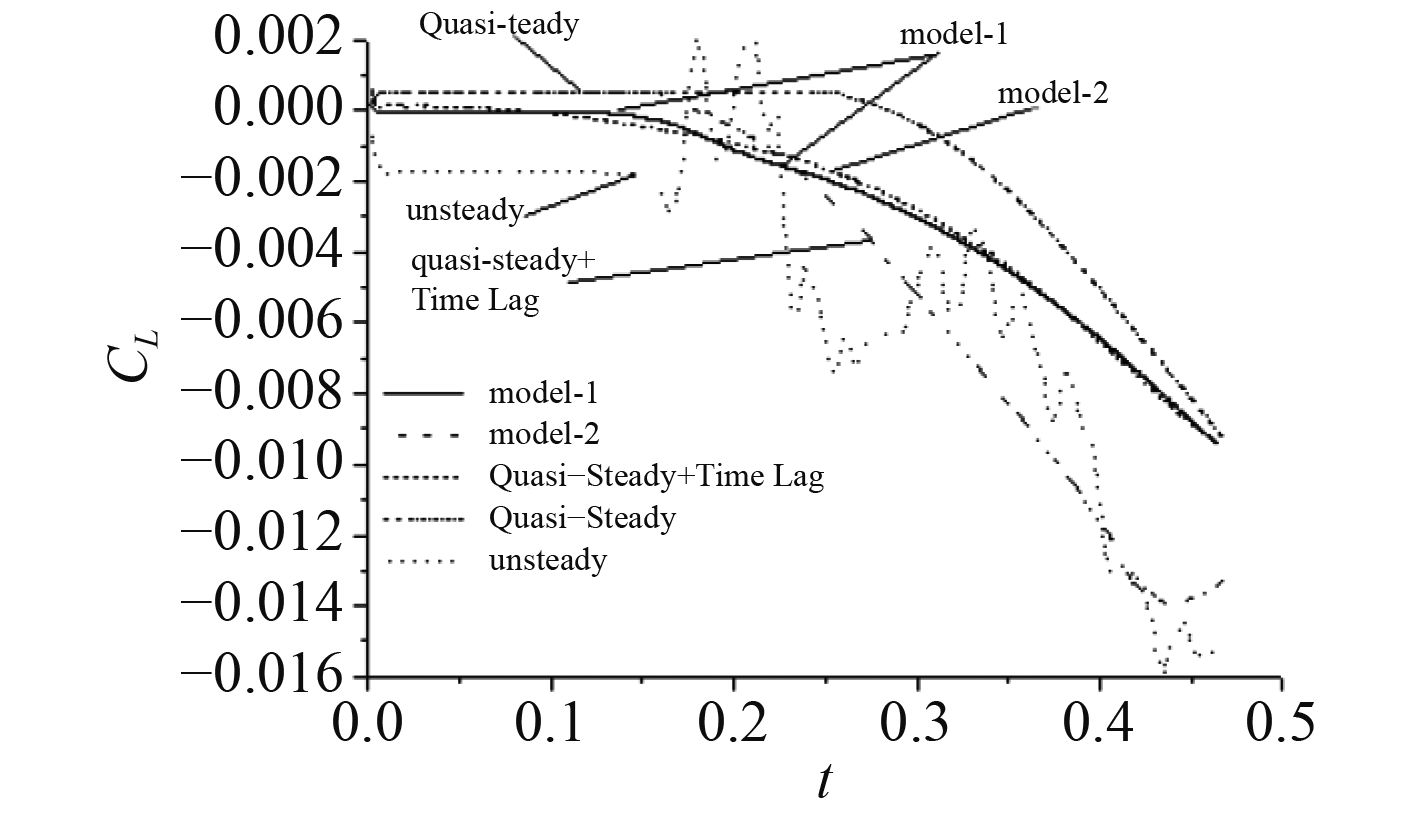
|
图 9 升力系数与时间的关系 Fig. 9 Normal force development against time |
从图中可以看到,定义相同的运动状态,unsteady的升力系数却表现出较强的不确定性,Quais-Steady+Time Lag曲线在描述unsteady曲线时符合程度也存在较大的偏差。分析上述问题产生的原因(参考图3),本文在对实验所定义的运动曲线的模拟上也存在局限性;同时,不得不指出非定常试验本身所具有的不确定性因素,如风洞中温度、风速的变化、及气流对操纵运动装置的影响(易使模型发生振动)等,随着时间的变化,流场中物理量的变化容易受到这些不确定因素的影响。
比较2种模型的数值计算结果,升力系数随时间变化平稳,在前0.25 s与实验值符合较好;模型model-1对升力系数的计算值在中间段(0.15~0.25 s)有较明显的减小过程(参考图3),这与model-1所定义的角速度曲线在中间段有一个负向加速过程相对应;模型model-2在初始阶段,升力系数由正转负,是与其所定义的角速度值在初始阶段大于0相一致的;要取得与实验一致的模拟效果,由实验中的不确定因素产生的误差需要加以考虑。
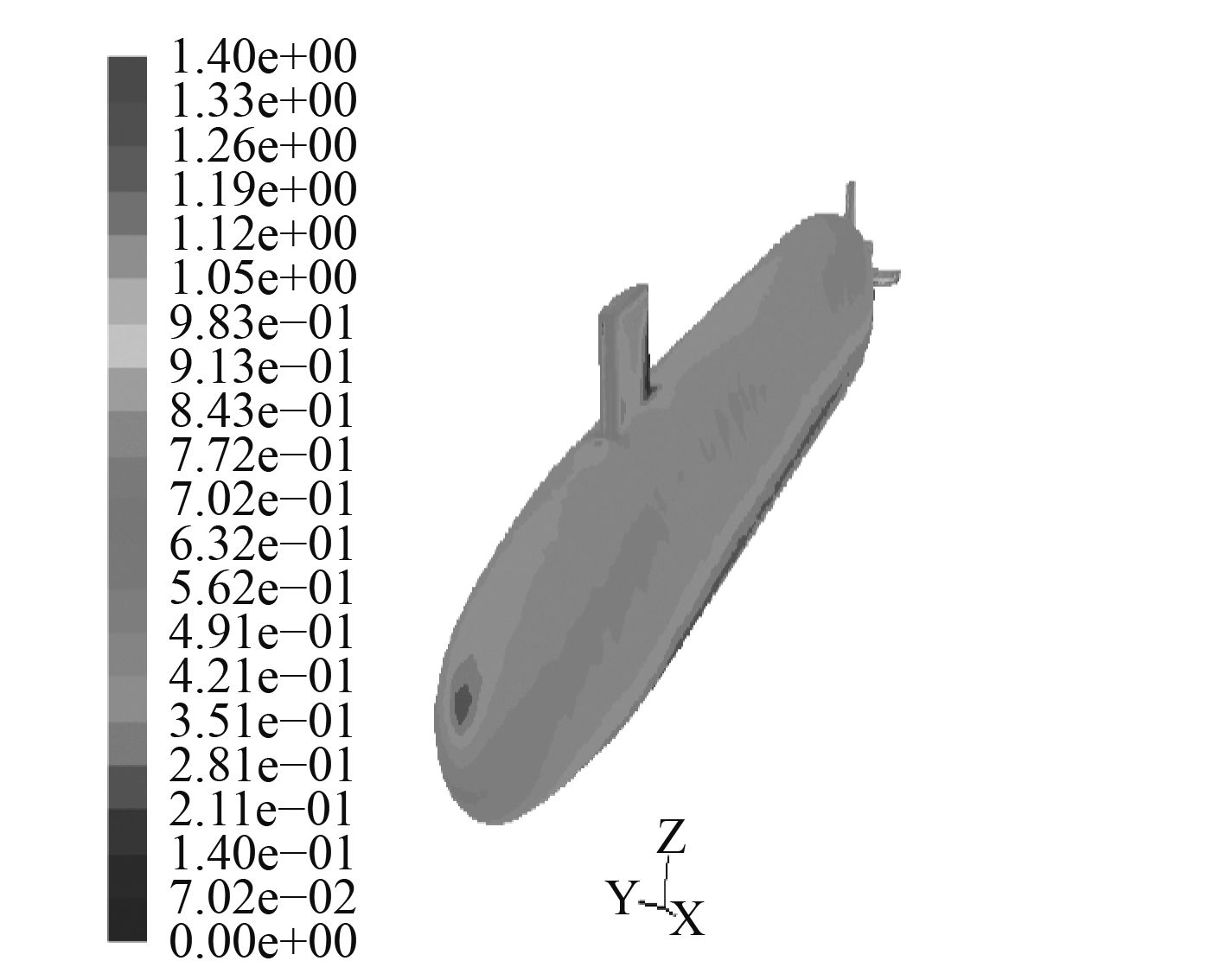
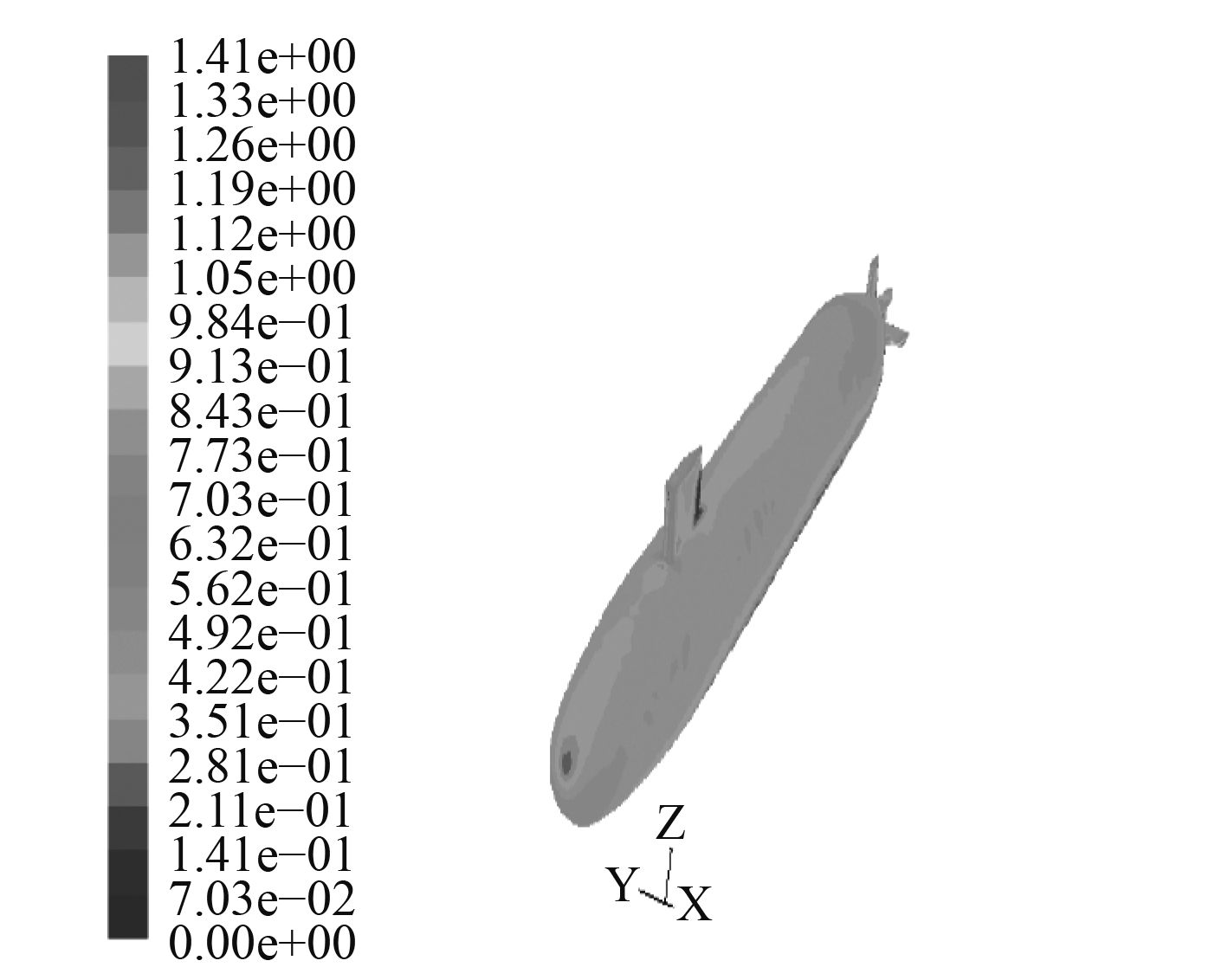
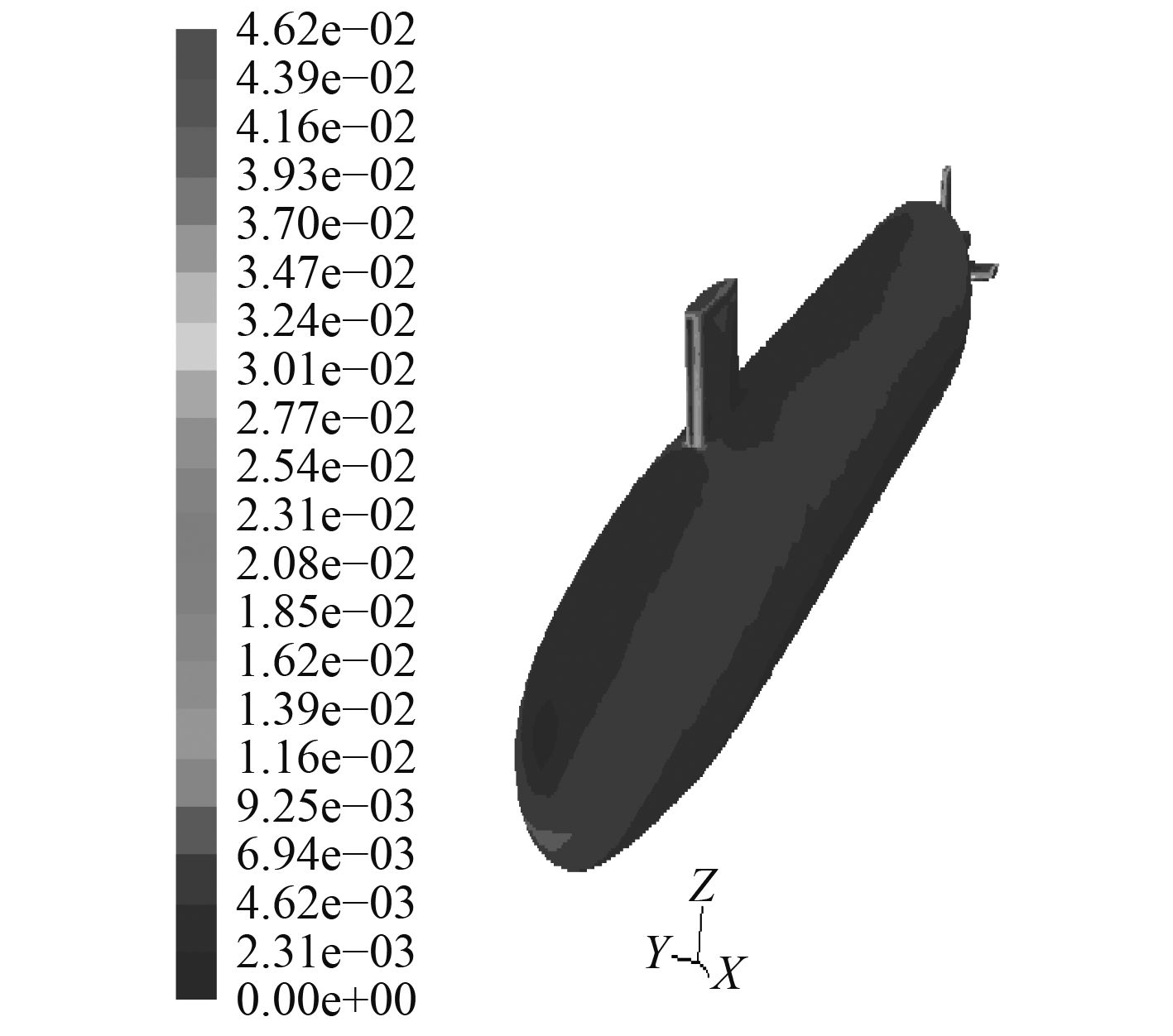
5.2 粘性流场分析图10~图13给出了分别采用2种模型得到攻角–25°时物面压强系数和物面切应力系数的数值计算结果,两者在物面上的连贯性和均匀性均较好,在迎风处出现极值,这与理论上此处对应速度的最小值是相符合的。与定常攻角–25°(见图14和图15)时的结果相比,在变化趋势和数值分布上一致。

|
图 10 攻角–25°物面压强系数(mode-l) Fig. 10 Surface pressure cofficient at –25° (mode-2) |
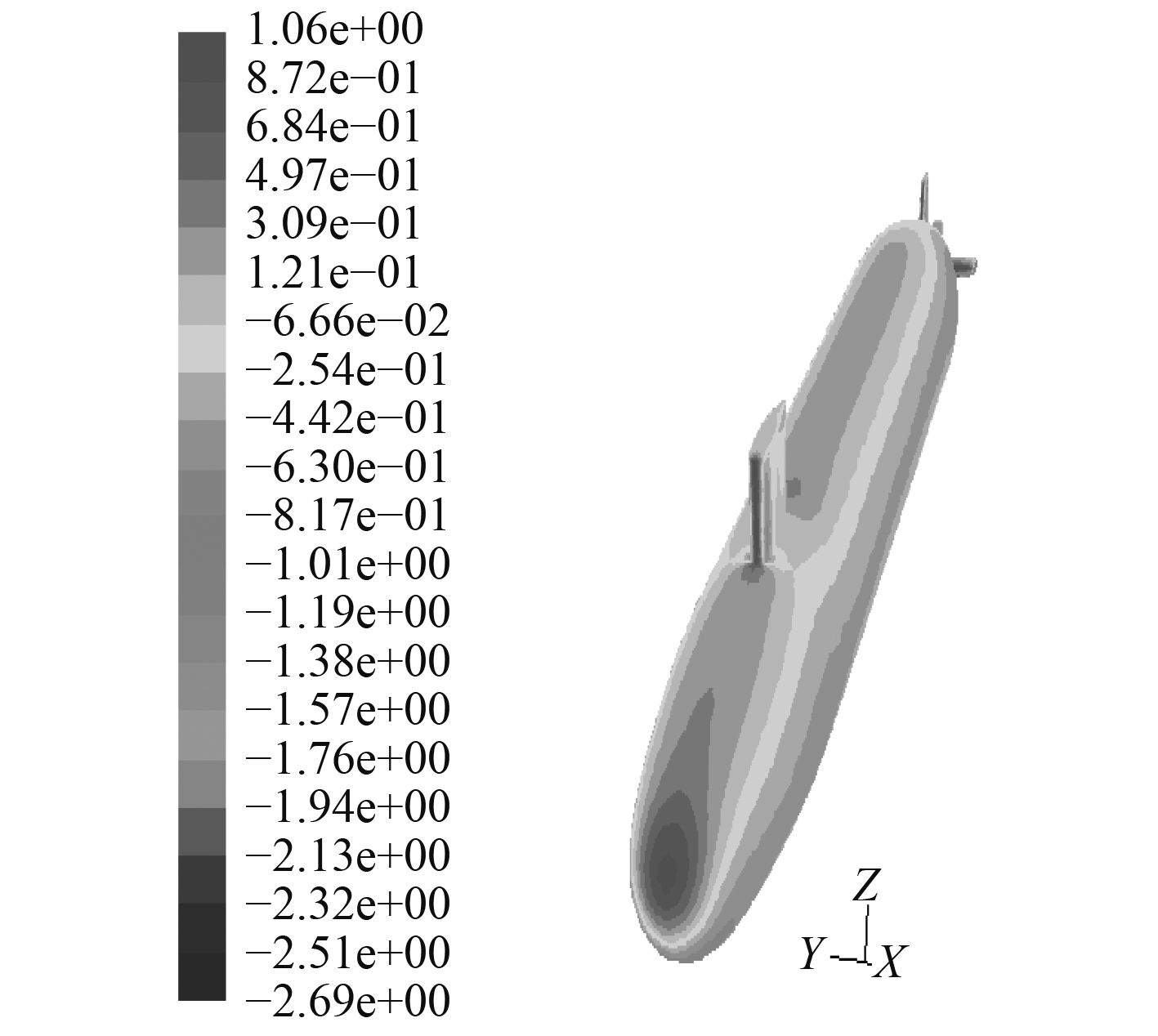
|
图 11 攻角–25°物面压强系数(mode-2) Fig. 11 Surface pressure cofficient at –25° (mode-1) |
|
图 12 攻角–25°物面剪切力系数(mode-l) Fig. 12 Surface friction cofficient at –25° (mode-l) |
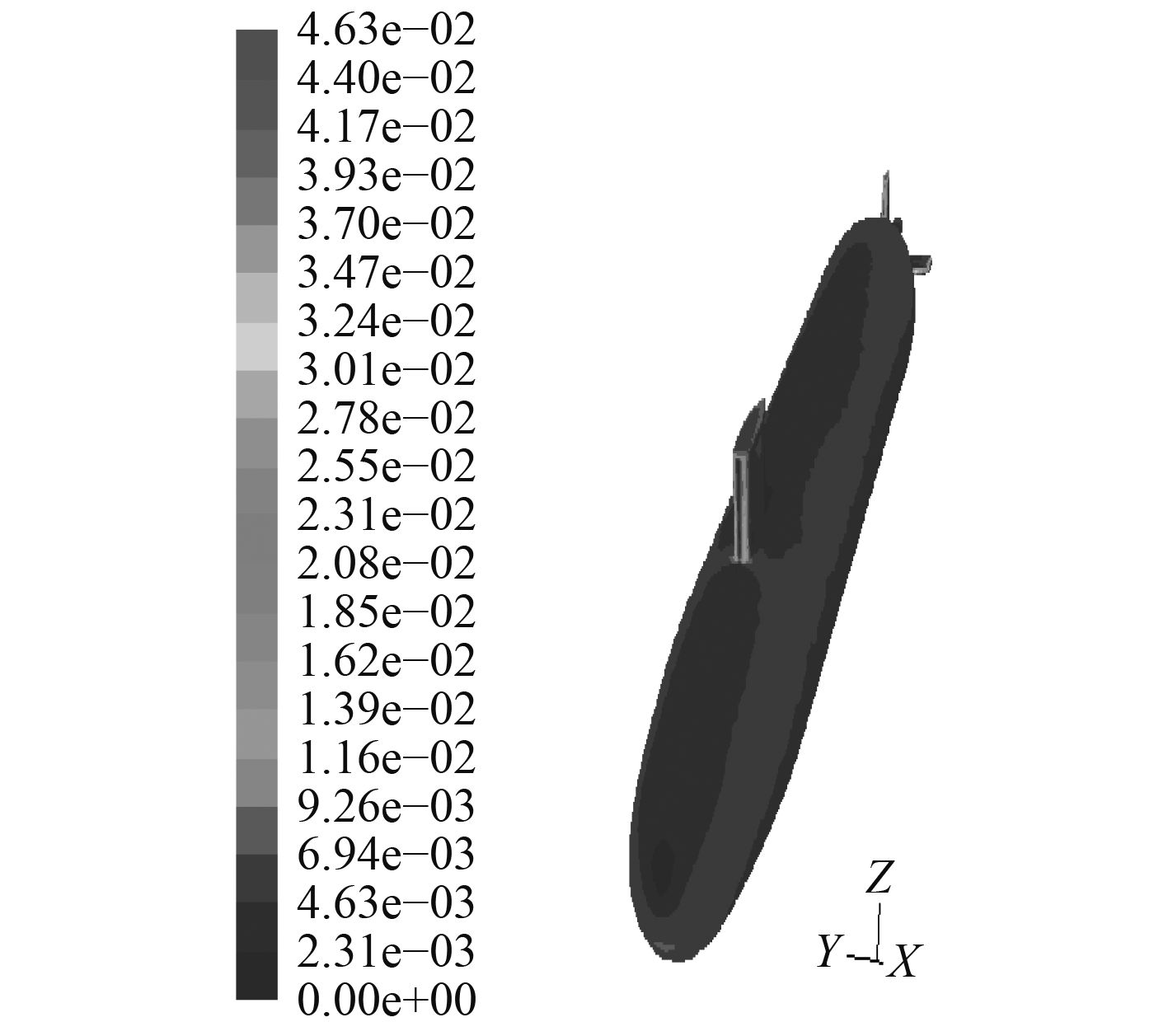
|
图 13 攻角–25°物面剪切力系数(mode-2) Fig. 13 Surface friction cofficient at –25° (mode-2) |

|
图 14 攻角–25°物面压强系数 Fig. 14 Surface pressure cofficient at –25° |
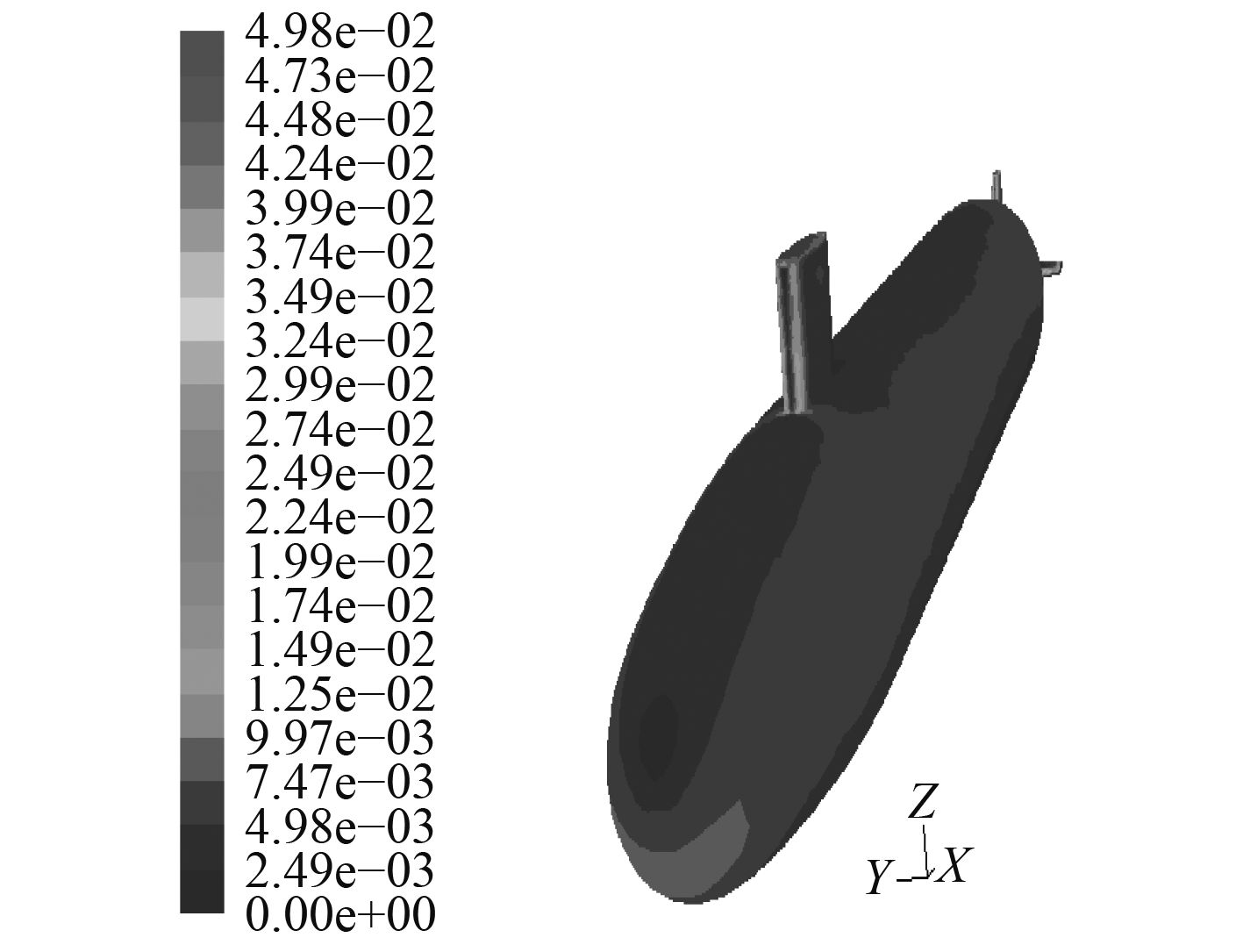
|
图 15 攻角–25°物面切应力系数 Fig. 15 Surface friction cofficient at –25° |
图16给出了攻角–25°时x/L=0.863截面速度向量图(model-1),在背风面可以清晰地看到有分离涡出现,反映了流场的粘性分离特性。

|
图 16 攻角–25°时x/L=0.863截面速度向量图 Fig. 16 Velocity vector diagram at x/L=0.863 section and –25° angle of attack against time |
采用CFD软件数值求解非定常的DARPA2潜艇模型粘性流场和水动力,采用基于非结构化网格的有限体积法,数值求解非定常、不可压缩的RANS方程,湍流模型采用SA模式,在SA模式中
为了得到较好的非定常结果,需要对初始流场进行讨论。通过调整边界条件和部分松弛因子,初始流场变量在925次迭代后达到收敛精度。
在初始流场稳定的基础上,应用表2中的3种模型曲线,分别定义运动状态,进行非定常数值模拟。过分追求曲线拟合的精确性,采用高阶多项式拟合实验数据导致将计算结果发散;降低多项式阶次,得到稳定的非定常结果;采用model-1对实验数据进行拟合,拟合效果较好,数值计算结果稳定。
要取得与实验一致的模拟效果,由实验中的不确定因素产生的误差需要加以考虑。攻角–25°时物面压强系数和物面切应力系数的数值计算结果,在壁面上的连贯性和均匀性均较好,与定常攻角–25°时的结果在变化趋势和数值分布上一致。
| [1] |
WHITFIELD C C. Steady and unsteady force and moment data on a DARPA2 submarine[D]. Virginia: Faculty of the Virginia Polytechnic Institute and State University, 1999.
|
| [2] |
林兆伟, 孟生, 殷洪, 等. 潜器操纵性水动力系数的数值预报方法[J]. 中国造船, 2016, 57(1): 59-68. DOI:10.3969/j.issn.1000-4882.2016.01.007 |
| [3] |
曹留帅, 朱军, 黄昆仑, 等. 全附体潜艇模型回转运动流场数值模拟[J]. 海军工程大学学报, 2015, 27(04): 17-20. |
| [4] |
PAN Y C, ZHOU Q D, ZHANG H X. Numerical simulation of rotating arm test for prediction of submarine rotary derivatives[J]. Journal of Hydrodynamics, 2015, 27(1): 68-75. DOI:10.1016/S1001-6058(15)60457-7 |
| [5] |
周广礼, 欧勇鹏, 高霄鹏. 潜艇上浮出水运动及粘性流场直接数值模拟方法[J]. 海军工程大学学报, 2017, 29(4): 86-92. |
| [6] |
温正, 石良辰, 等. Fluent流体计算应用教程[M]. 北京: 清华大学出版社, 2009: 26–38.
|
| [7] |
孙铭泽, 王永生, 杨琼方. 潜艇操纵性数值模拟中雷诺数的影响分析[J]. 哈尔滨工程大学学报, 2012, 33(11): 1334-1340. |
| [8] |
周广礼, 董文才, 欧勇鹏. 潜艇应急上浮六自由度运动及黏性流场数值模拟[J]. 国防科技大学学报, 2017, 39(2): 199-206. |
| [9] |
叶金铭, 张凯奇, 于安斌. 基于STAR-CCM+的全附体潜艇尾流场数值分析[J]. 海军工程大学学报, 2017, 29(4): 53-58. |
| [10] |
戴天奇, 姚世卫, 魏志国. 基于动网格技术的潜艇热尾流浮升规律研究[J]. 舰船科学技术, 2015, 37(5): 86-89. DOI:10.3404/j.issn.1672-7649.2015.05.018 |
 2019, Vol. 41
2019, Vol. 41
