2. 大连海洋大学,辽宁 大连 116023
2. Dalian Ocean Universit, Dalian 116023, China
水声测距是水下测量中的一个必要组成部分。测距精度对测量结果有重要影响。现有设备多采用时间同步触发方式,检测时间差计算距离。在无时间同步前提下不能很精确的测量发射声源距离。本文采用线性调频信号通过分数阶傅里叶变换(FrFt)[1 – 3]处理信号,利用可获取的辅助信息实现测距,并进一步研究了使用此种方法测距时的主要影响因素。
1 分数阶傅里叶变换理论时间x(t)的分数阶傅里叶变换和逆变换定义为[1]:
| $ {X_p}(u) = \{ {F^p}[x(t)]\} (u) = \int_{ - \infty }^\infty x(t){K_p}(t,u){{\rm {d}}t} \text{,} $ | (1) |
| $x(t) = \{ {F^{ - p}}[x(u)]\} (t) = \int_{ - \infty }^\infty {{X_p}(u){K_{ - p}}(t,u){\rm d}u}\text{。} $ | (2) |
式中:p为FrFt的阶数,可为任意实数;Fp为FrFt的算子符号;
| ${K_p}\left( {t,u} \right) = \left\{ {\begin{array}{*{20}{l}} {\sqrt {\frac{{1 - i\cot \alpha }}{{2\pi }}} {e^{\left( {i\frac{{{t^2} + {u^2}}}{2}\left( {\cot \alpha - itu\csc \alpha } \right)} \right)}},}&{\alpha \ne n\pi }\text{;}\\ {\delta \left( {t - u} \right),}&{\alpha = 2n\pi }\text{;}\\ {\delta \left( {t - u} \right),}&{\alpha = \left( {2n + 1} \right)\pi } \text{。} \end{array}}\right.$ | (3) |
其中:
当x(t)中处理的主要信号为LFM信号
此时“最佳”FrFt阶数p0为
| $p_0 = \frac{2}{\pi }\arctan (\kappa ) - 1\text{,}$ | (4) |
其中
FrFt可以认为是一种广义的傅里叶变换。傅里叶变换是线性变换,是FrFt的一个特例。即若将FrFt的变换算子逆时针旋转时间轴到u轴的任意角度
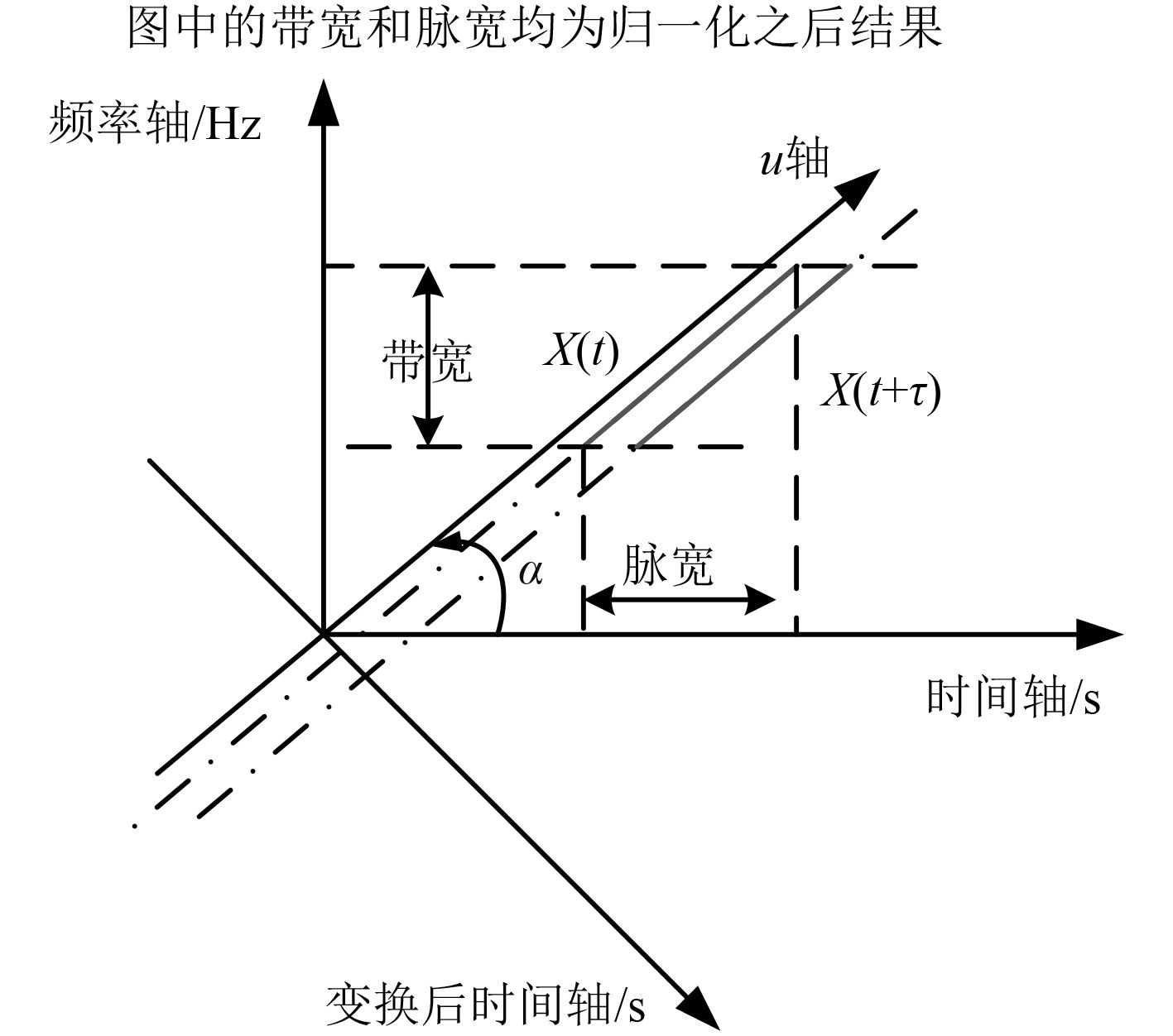
|
图 1 FrFt变换原理示意图 Fig. 1 Schematic diagram of the principle of FrFt transformation |
在距离为较近时,声线在水中传播时弯曲不大,可以认为声线直线传播[4]。利用射线声学理论,建立浅海近程声传播模型如图2所示。
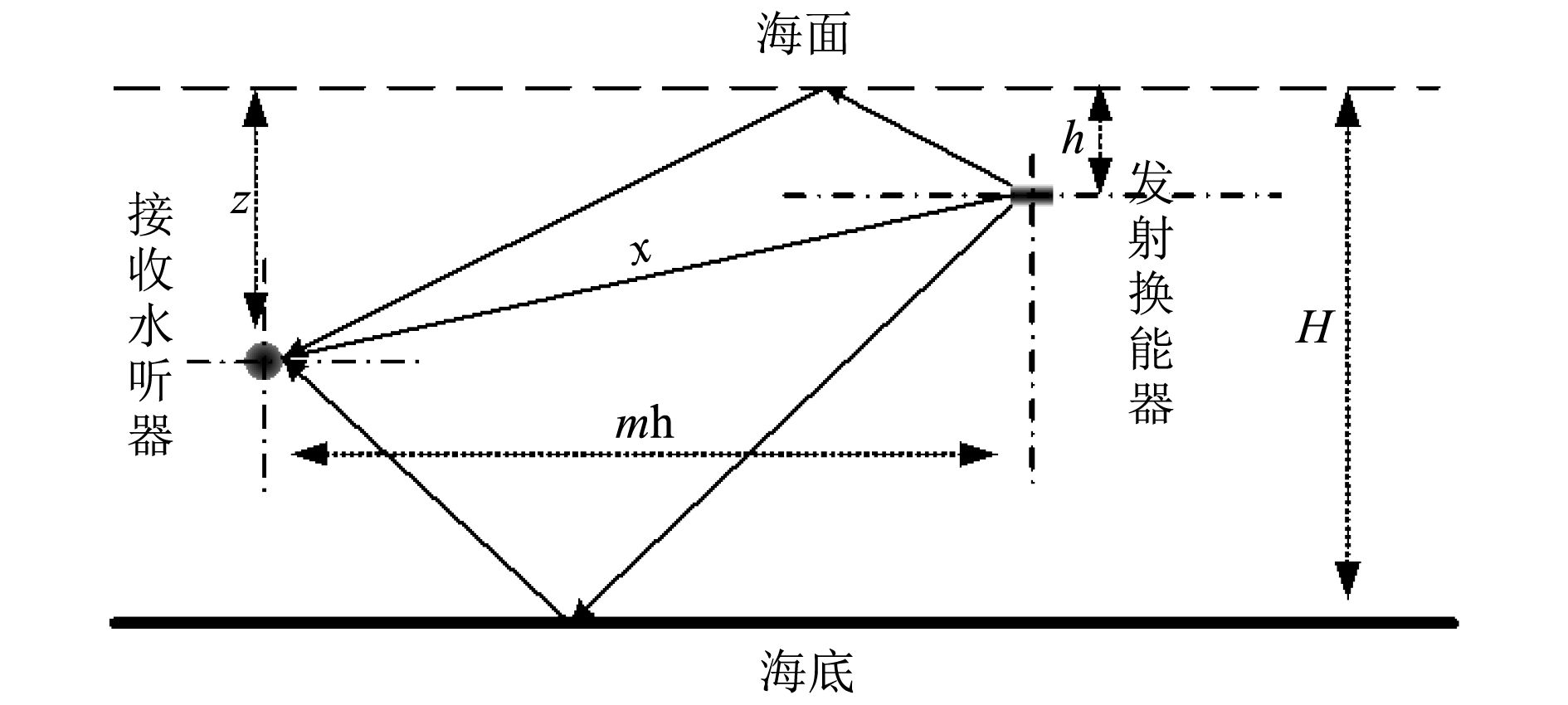
|
图 2 海洋近程声线传播图 Fig. 2 2 Marine short-range ray travel map |
在所获得信号距离分辨率较高的前提下,试验中可将海面、海底的反射信号区分开来。若经过海底、海面信号与直达声信号的声程差为s,在已知接收水听器与海面距离z,发射换能器与海面距离h和海深H的前提下,设声速c已知(一般取c=1 500 m/s)可通过式(5)或式(6)得到发射换能器与接收水听器的距离x,及未经过反射直接到达声线的声程。式(5)是当s为声线经过海面反射与直达声的声程差时,获得直达声距离的反演式。式(6)是当s为声线经过海底反射与直达声的声程差时,获得直达声距离的反演公式
| $x = \frac{{4zh - {s^2}}}{{2 s}}\text{,}$ | (5) |
| $x = \frac{{4(H - z)(H - h) - {s^2}}}{{2 s}}\text{。}$ | (6) |
在式(5)和式(6)的所有变量中,s为通过信号处理后获得的量,s=c*t;c为声速,t为最早到达的信号时刻与第2个或第3个到达时刻的时间差。这里使用第2个还是第3个取决于实际情况,即是使用海面反射还是使用海底反射来反演直达声程。这里采用线性调频信号(LFM)并使用分数阶傅里叶变换来对信号进行处理。
通过FrFt处理可以提高距离分辨率ds=c/B,其中c为声速,B为LFM信号带宽;当c=1 500 m/s时,B=20 000 Hz时,LFM信号为20 000~40 000 Hz线性调频信号,脉宽为0.01 s,则ds=0.075 m。
通过仿真可以得到,使用FrFt可以提高距离分辨率,其距离分辨率与信号带宽有关如表1所示。
|
|
表 1 FrFt中带宽与距离分辨率关系表 Tab.1 FrFt bandwidth and range resolution table |
当时间差为0.000 05 s时,距离为0.075 m,当时间差为0.000 5 s时,距离为0.75 m。所以当ds=0.075 m及B=20 000 Hz时,可以分开距离大于0.01 m的反射信号,如图3~图6所示。

|
图 3 时间差值为0.000 05 s时的混跌信号 Fig. 3 Mixed drop signal with a time difference of 0.000 05 s |
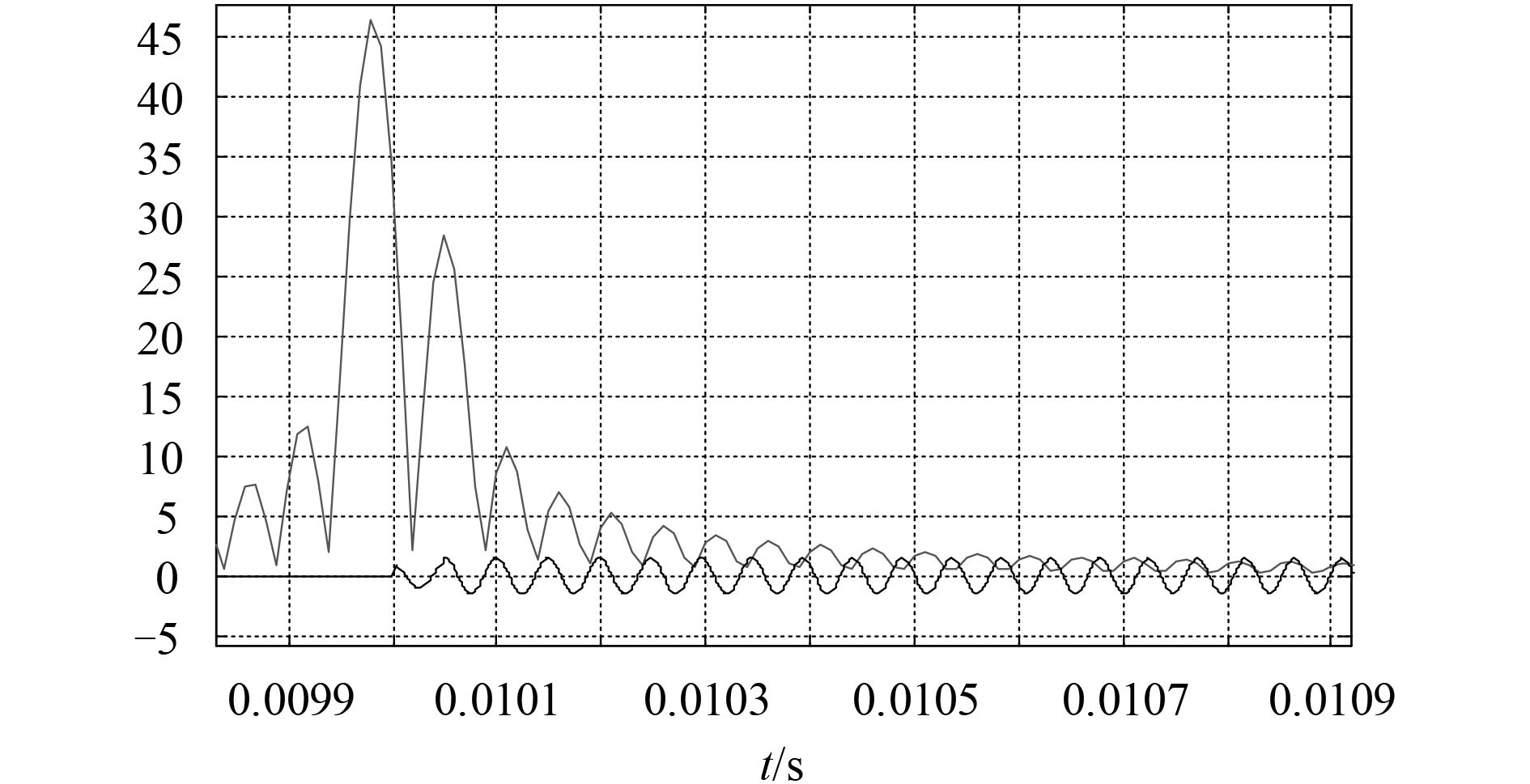
|
图 4 时间差值为0.000 05 s时分数阶傅里叶变换后的信号 Fig. 4 The signal after fractional Fourier transform when the time difference is 0.000 05s. |
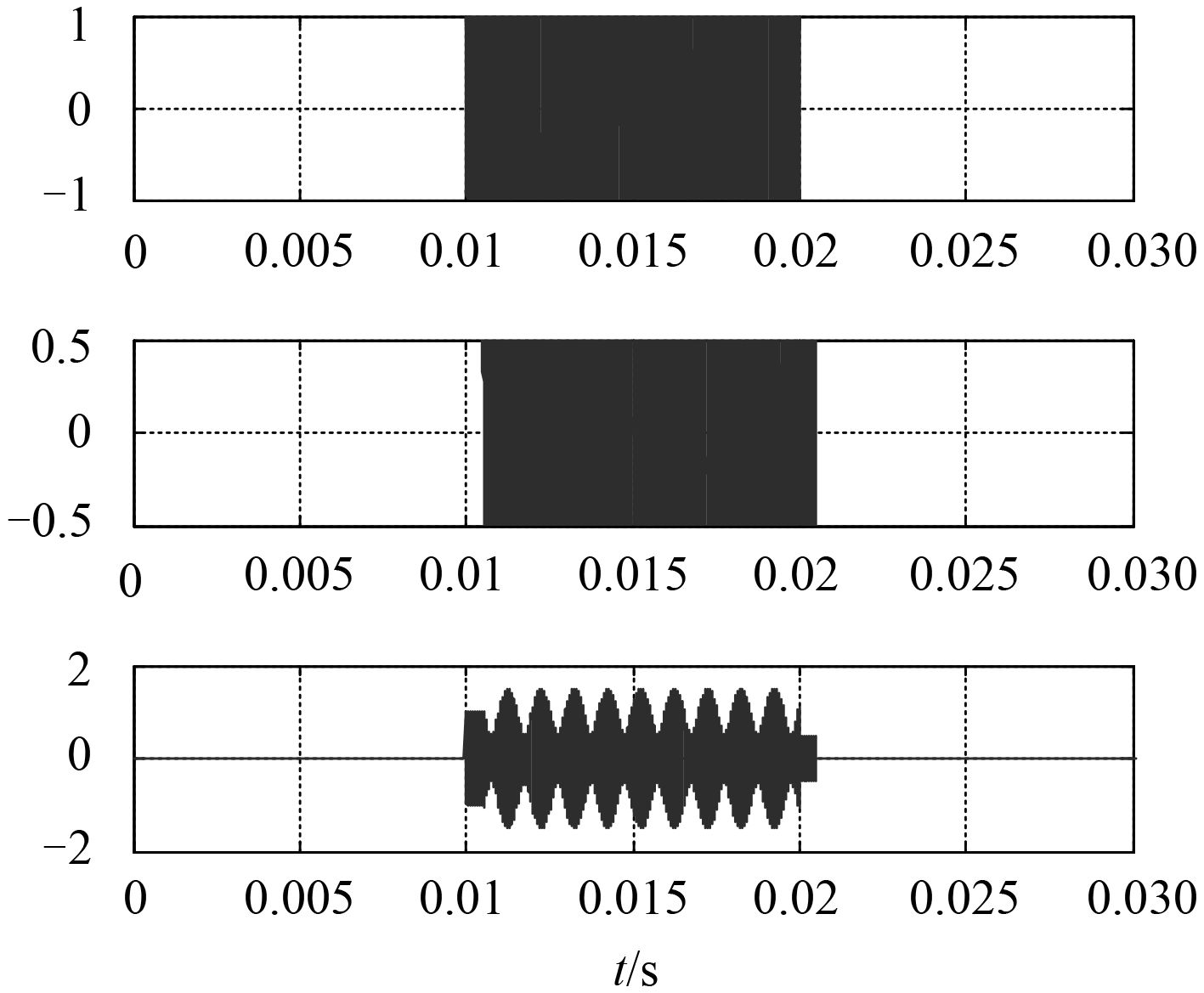
|
图 5 时间差值为0.000 5 s时的混跌信号 Fig. 5 Mixed drop signal with a time difference of 0.00 05 s |
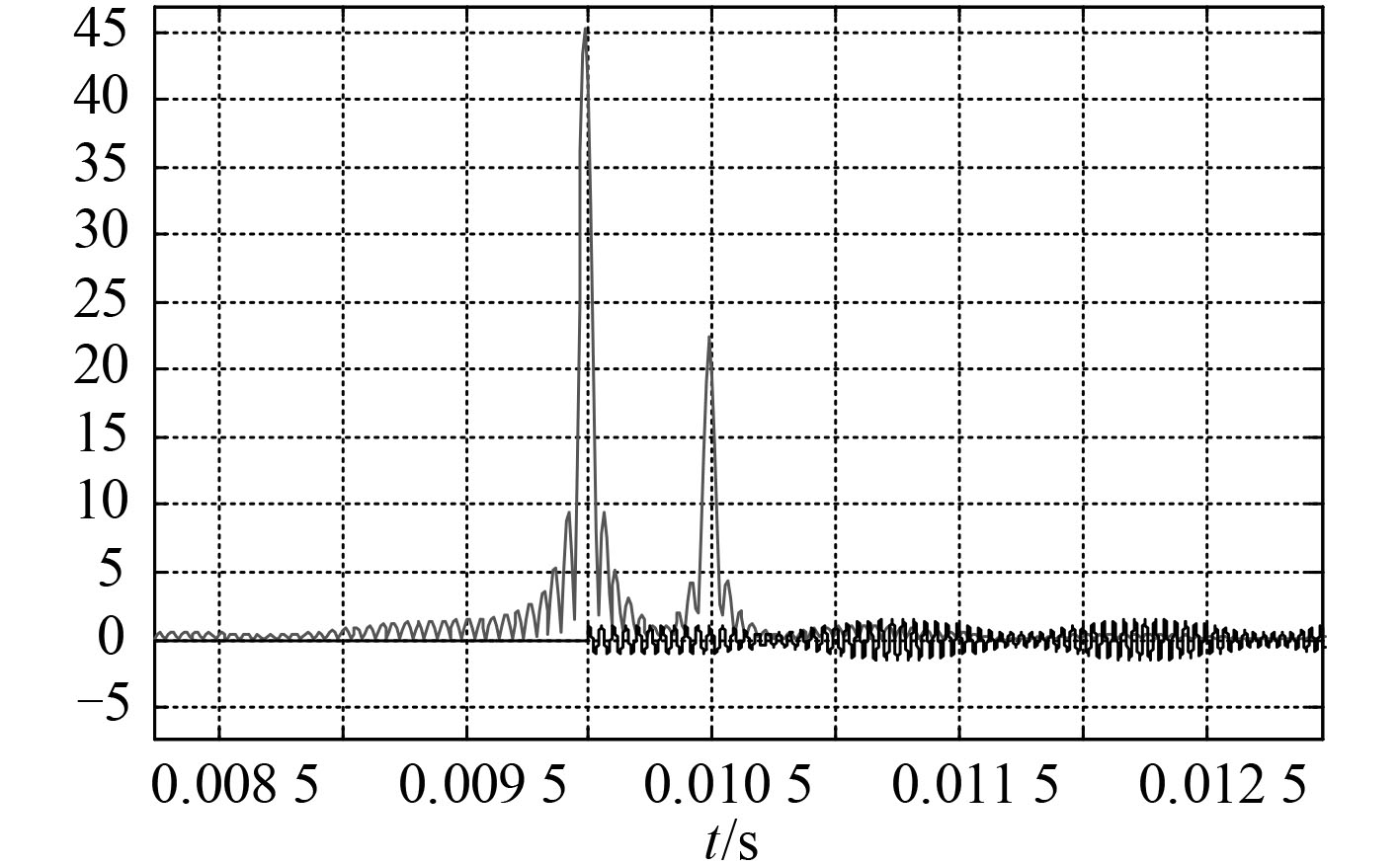
|
图 6 时间差值为0.000 5 s时分数阶傅里叶变换后的信号 Fig. 6 The signal after fractional Fourier transform when the time difference is 0.0005 s |
综上所述,若需要下一个脉冲不受前一个脉冲的影响,这里应去发射间隔大于0.15 s。
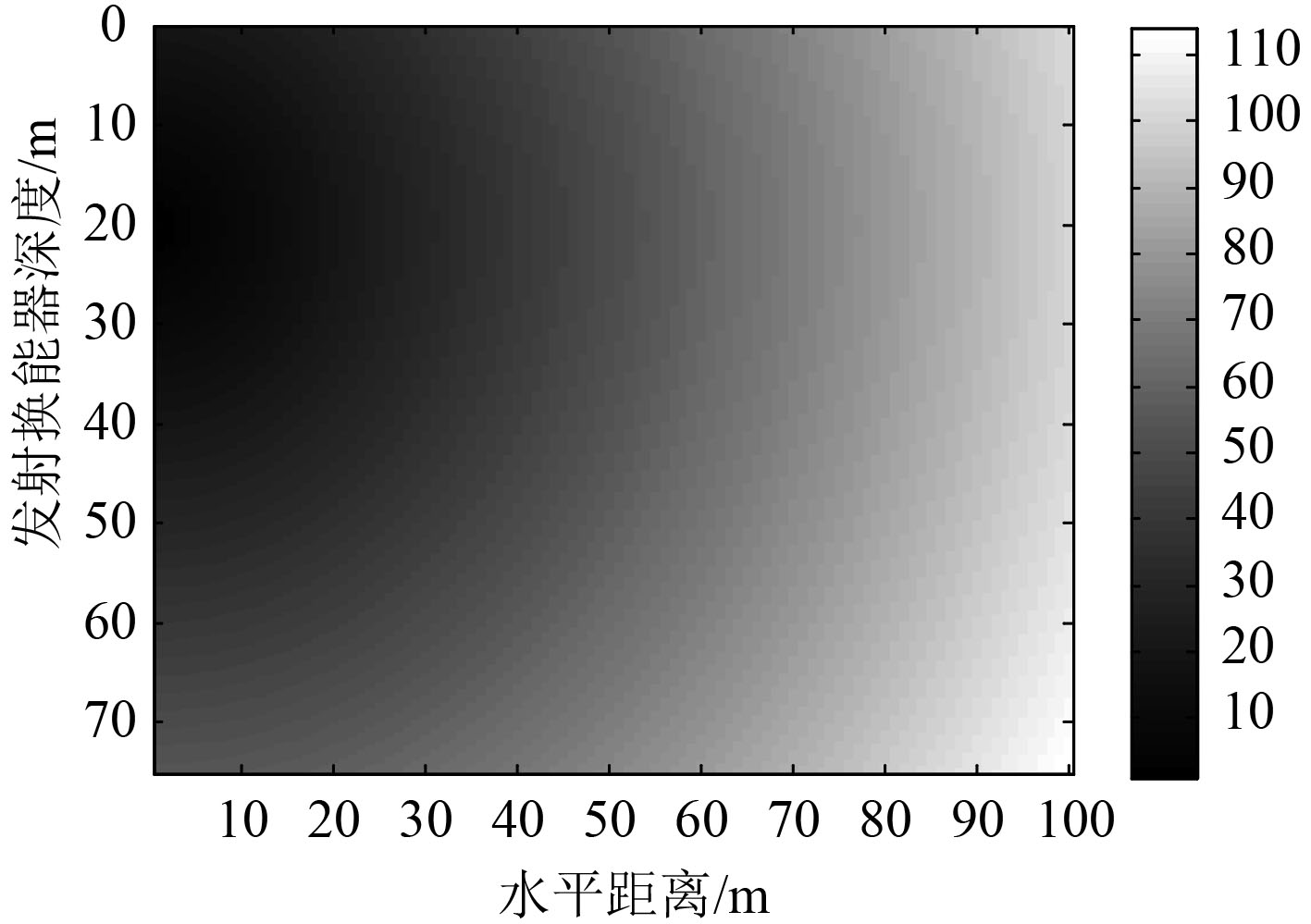
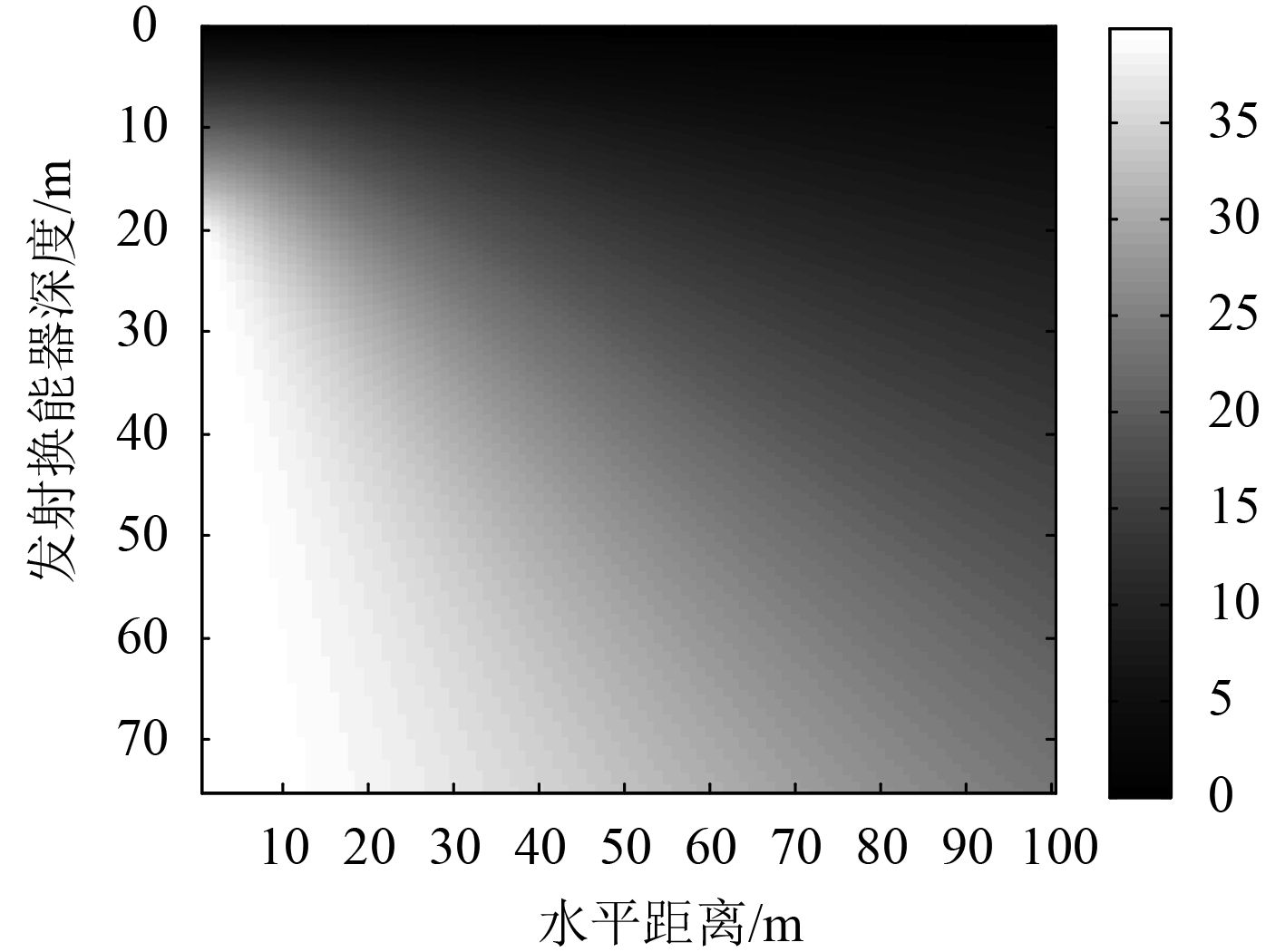
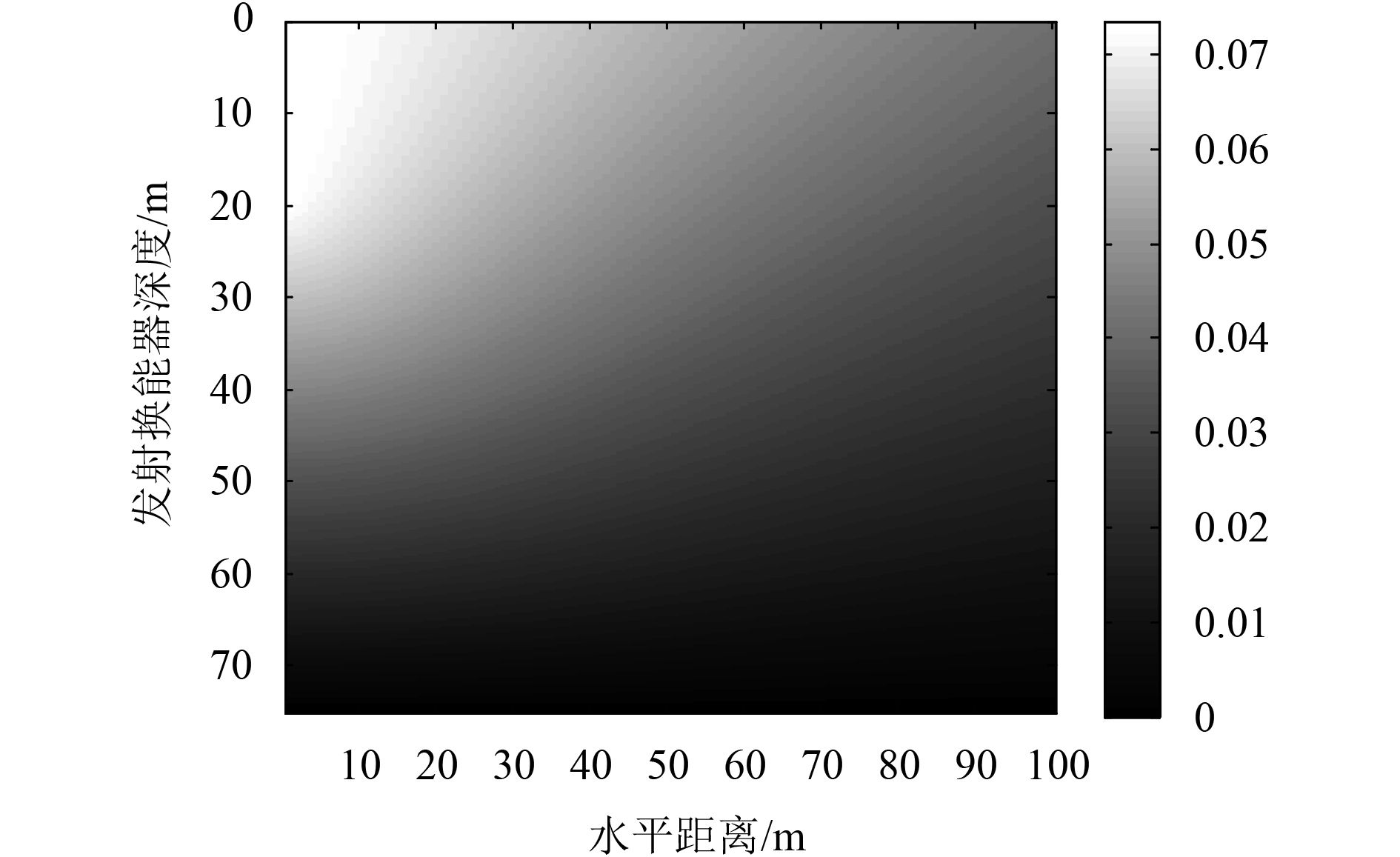
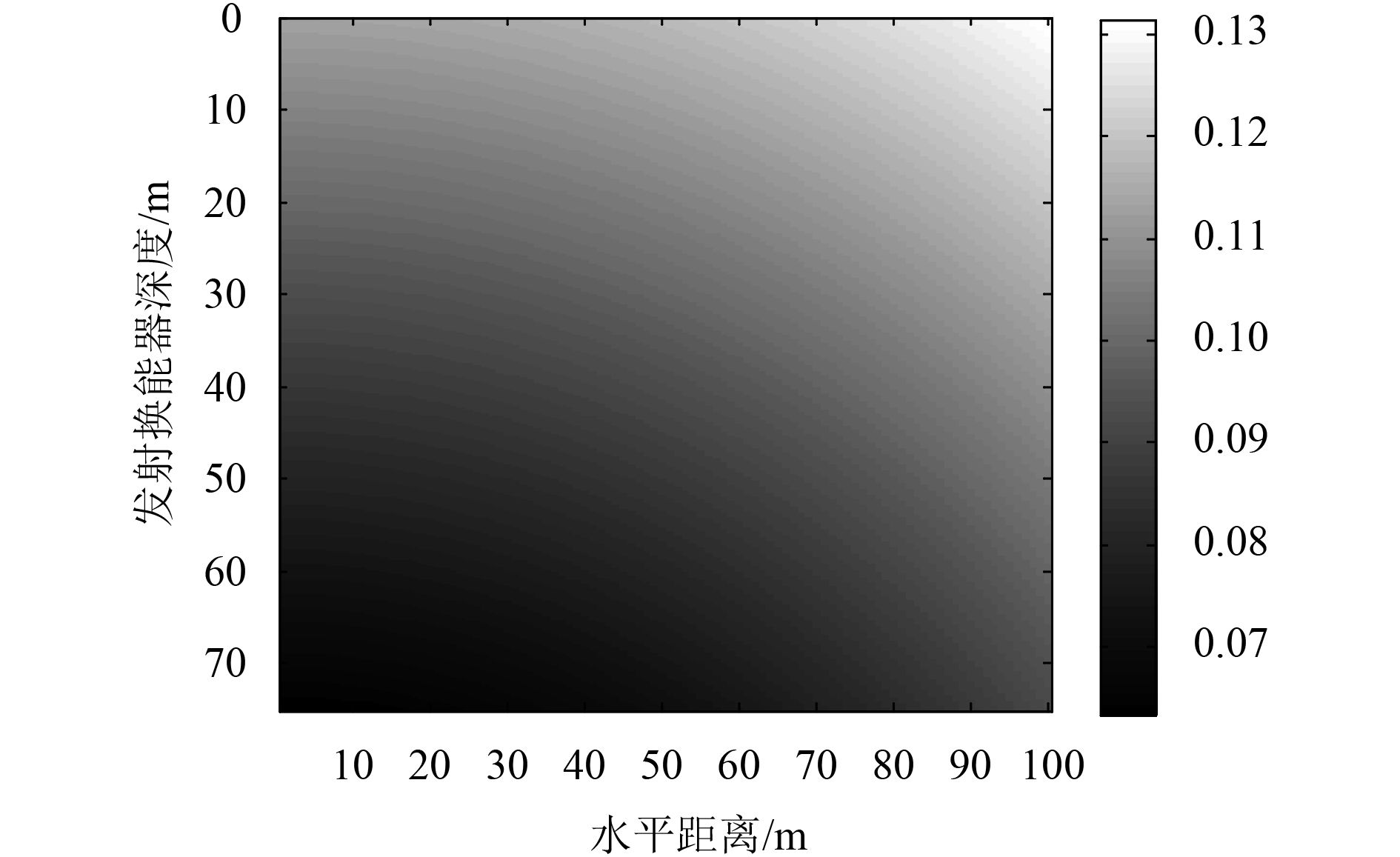
当接收深度为20 m时,直达声声程和经海面反射距离差随水平距离和深度变化见图7和图8。经海底、海面反射距离/时间差随水平距离和深度变化见图9~图11。经海面海底反射的时间差随水平距离和发射深度的变化规律见图12。
|
图 7 直达声程随水平距离和发射深度变化规律图 Fig. 7 The change rule of direct distance of sound with horizontal distance and emission depth |
|
图 8 经海面反射的距离差随水平距离和发射深度变化规律图 Fig. 8 Variation rule of distance difference with horizontal distance and emission depth reflected by sea surface |

|
图 9 经海底反射的距离差随水平距离和发射深度变化规律图 Fig. 9 Variation rule of distance difference with horizontal distance and launching depth reflected by sea bottom |

|
图 10 经海面反射的时间差随水平距离和发射深度变化规律图 Fig. 10 The time difference of horizontal reflection and the depth of horizontal transmission |
|
图 11 经海底反射的时间差随水平距离和发射深度变化规律图 Fig. 11 The time difference of seafloor reflection with horizontal distance and emission depth |
|
图 12 经海面海底反射的时间差随水平距离和发射深度变化规律 Fig. 12 The time difference of sea bottom reflection with horizontal distance and emission depth |
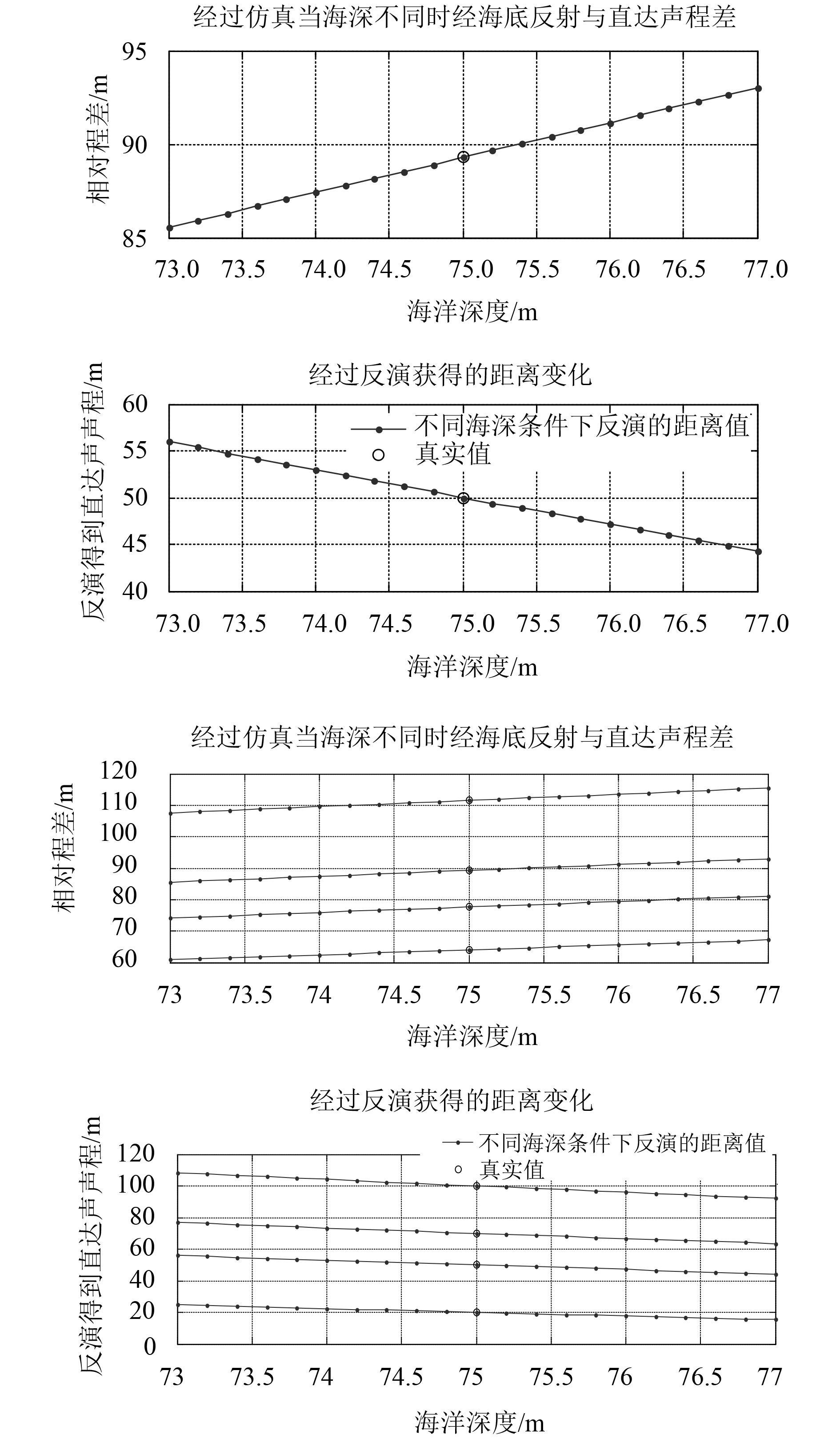
海深变化对反演结果的影响见图13,海底所使用深度影响到所反演的直达声程。在其他均为理想值的条件下,当海底不确定度为1 m时,使用公式反演的直达声程不确定度为3 m。所以若想达到3 m的不确定度,海深的精度不能超过0.5 m。
|
图 13 海深变化对反演结果的影响 Fig. 13 Changes of deep impact on the inversion results of the sea |
由式(6)可知,式中的H,h,z,s等变量没有相互依存的关系。其通过海底反射与直达到达间距离差反演的误差分析考虑各个分量误差的累加如式(7)~式(21)所示。通过海面反射与直达到达间距离差反演的误差分析如式(11)、式(12)所示。
| $\Delta = \sqrt {{{\left( {\frac{{\partial x}}{{\partial H}}} \right)}^2} + {{\left( {\frac{{\partial x}}{{\partial h}}} \right)}^2} + {{\left( {\frac{{\partial x}}{{\partial z}}} \right)}^2} + {{\left( {\frac{{\partial x}}{{\partial s}}} \right)}^2}} \text{,}$ | (7) |
其中:
| $s = \sqrt {m{h^2} + {{(2 H - h - z)}^2}} - \sqrt {m{h^2} + {{(h - z)}^2}} \text{,}$ | (8) |
| $\frac{{\partial x}}{{\partial H}} = \frac{{4 H - 2(z + h)}}{s}{\rm{ d}}H\text{,}$ | (9) |
| $\frac{{\partial x}}{{\partial z}} = \frac{{2(h - H)}}{s}{\rm d}z\text{,}$ | (10) |
| $\frac{{\partial x}}{{\partial h}} = \frac{{2(z - H)}}{s}{\rm d}h\text{,}$ | (11) |
| $\frac{{\partial x}}{{\partial s}} = (\frac{{ - 4(H - z)(H - h)}}{{{s^2}}} - 0.5){\rm d}s\text{。}$ | (12) |
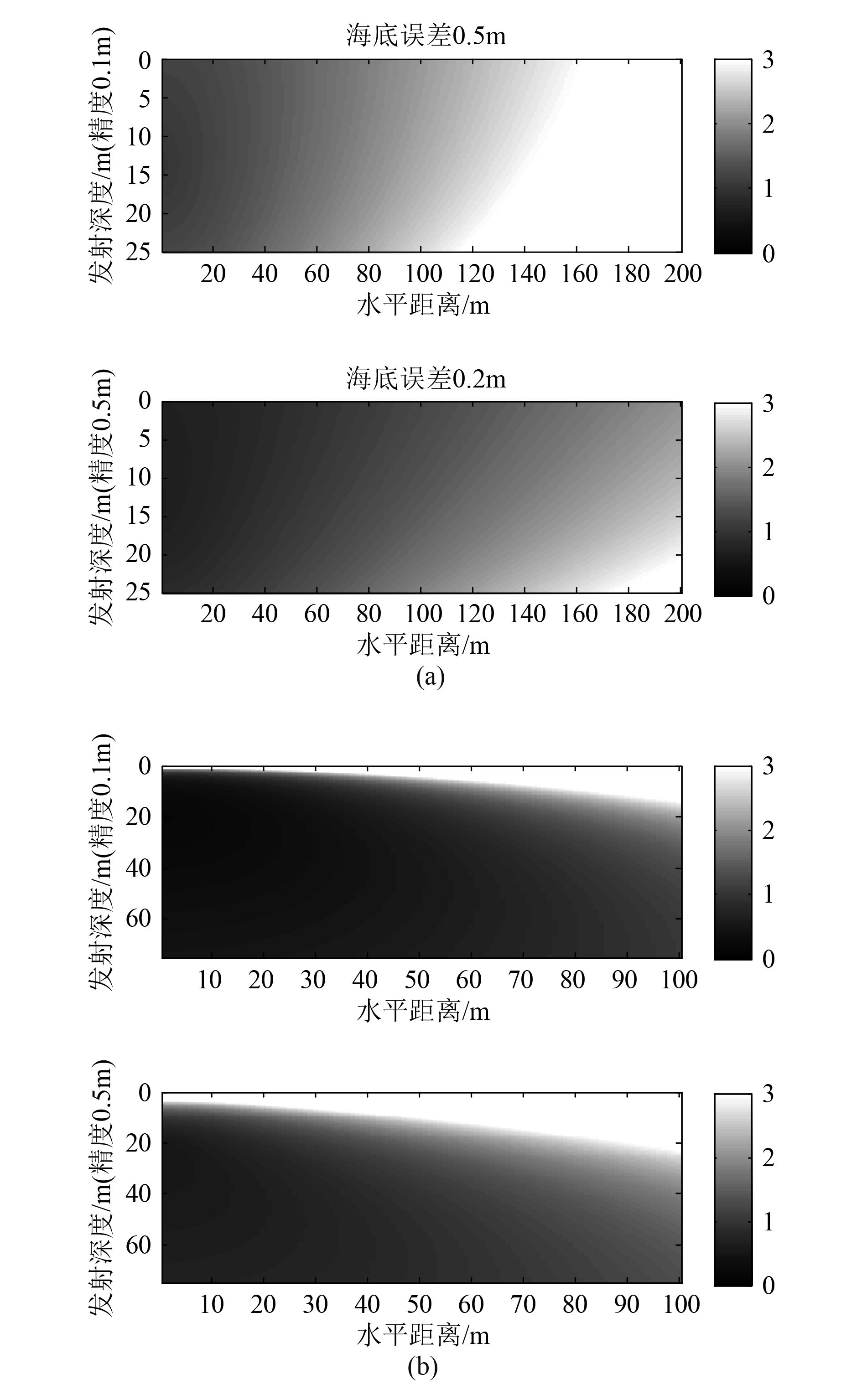
假设声速c=1 500 m/s;发射深度:h=1 m ~75 m,dh=0.1 m;接收深度z=20 m,dz=0.1 m;水平距离:mh=1 ~100 m;带宽:B=5 000 Hz;距离分辨率:ds=c/B=0.3 m;海深H=75 m,dH=0.2 m(或0.5 m);通过Matlab软件仿真可以得到当参数不同时的距离反演误差,如图14所示。
|
图 14 通过海底海面反演误差随发射深度和水平距离变化图 Fig. 14 The variation of error with depth of emission and horizontal distance is retrieved from the bottom and sea surface |
当使用海面反演时
| $s = \sqrt {{{(z + h)}^2} + m{h^2}} - \sqrt {{{(z - h)}^2} + m{h^2}}\text{,} $ | (13) |
| $\Delta = \sqrt {{{(\frac{{2h}}{s}dz)}^2} + {{(\frac{{2z}}{s}dh)}^2} + {{( - \frac{{2zh}}{{{s^2}}}ds)}^2} + {{( - \frac{{ds}}{2})}^2}} \text{。}$ | (14) |
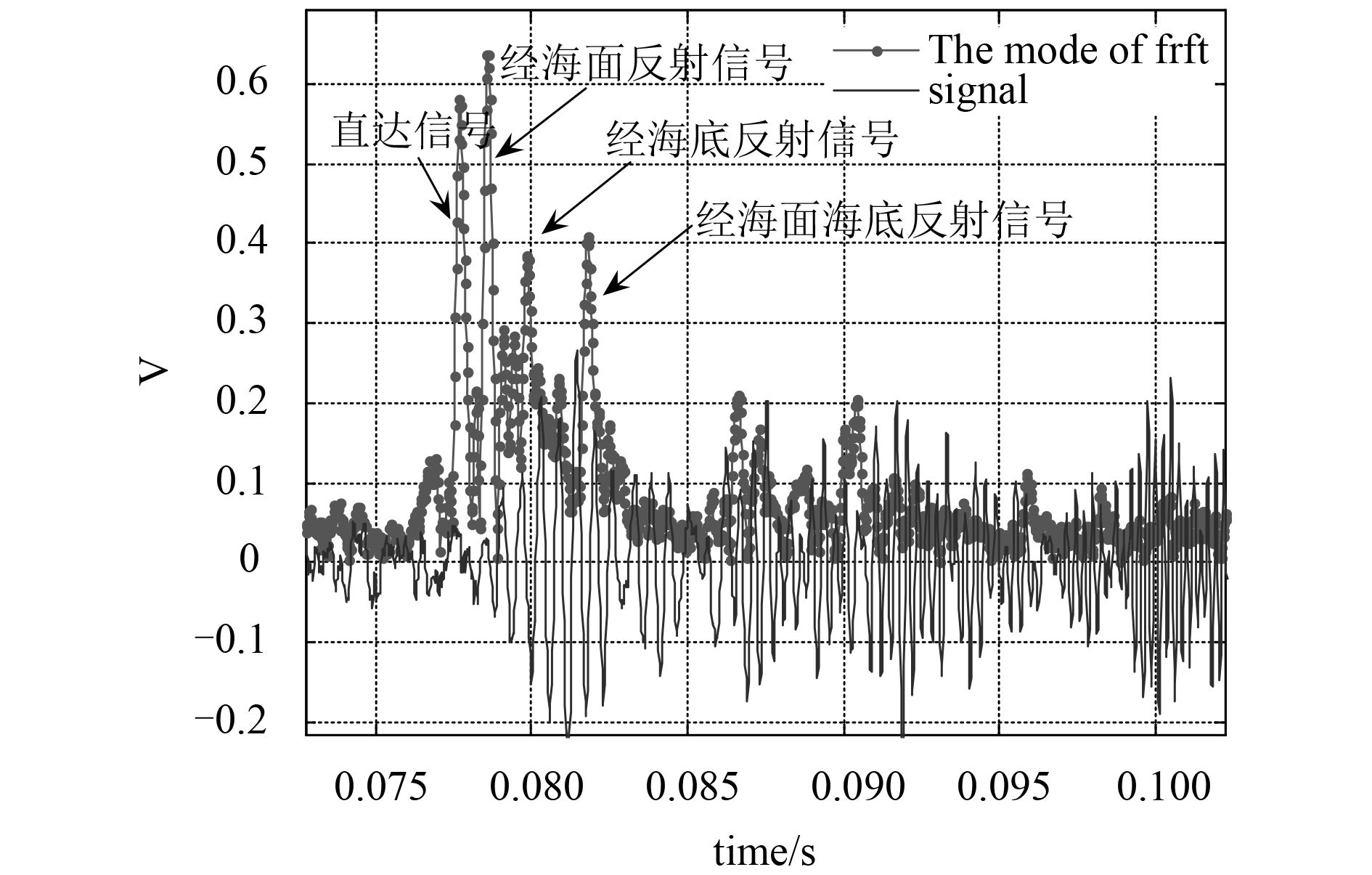
在2014年12月,在大连锚地做了一次验证性试验。试验设计:一船抛锚,一船随海流漂泊,漂泊船只每间隔1 min发射间隔为1 s的10个LFM信号。发射信号形式为1.5 ~5 kHz,脉宽30 ms的LFM信号。抛锚船只接收信号。接收深度10 ~12 m,通过反演可以拟合得到接收为10.65 m发射深度25 m,海深H
|
图 15 海上实验实际获得信号的时域图和经FrFt变换图 Fig. 15 Real time signal obtained from marine experiment and FrFt transformation map |

|
图 16 反演时所用海深简图(精度0.1 m) Fig. 16 Sea depth map used for inversion (precision 0.1m) |
计算公式为:
| $x = \frac{{4zh - {{(ct)}^2}}}{{2ct}}$ | (15) |
其中:x为反射与接收间距离,m;c为声速,m/s;t为时间差,s;z为接收水听器距离海面深度,m;h为发射换能器距离海面深度,m。
通过图17和图18可以得到由于现有数据的距离分辨率较低ds=1/5 000*1 500=0.3 m,距离大于200 m,使得测距精度较低,所以这里的实际数据的处理只是对该方法进行可行性验证。当获得更精确的反演条件,增大LFM信号带宽及距离分辨率提高后,可使得定位精度获得提高。

|
图 17 通过海底发射反演值与真实值对比及误差 Fig. 17 Comparison and error between inversion value and real value of submarine launching |
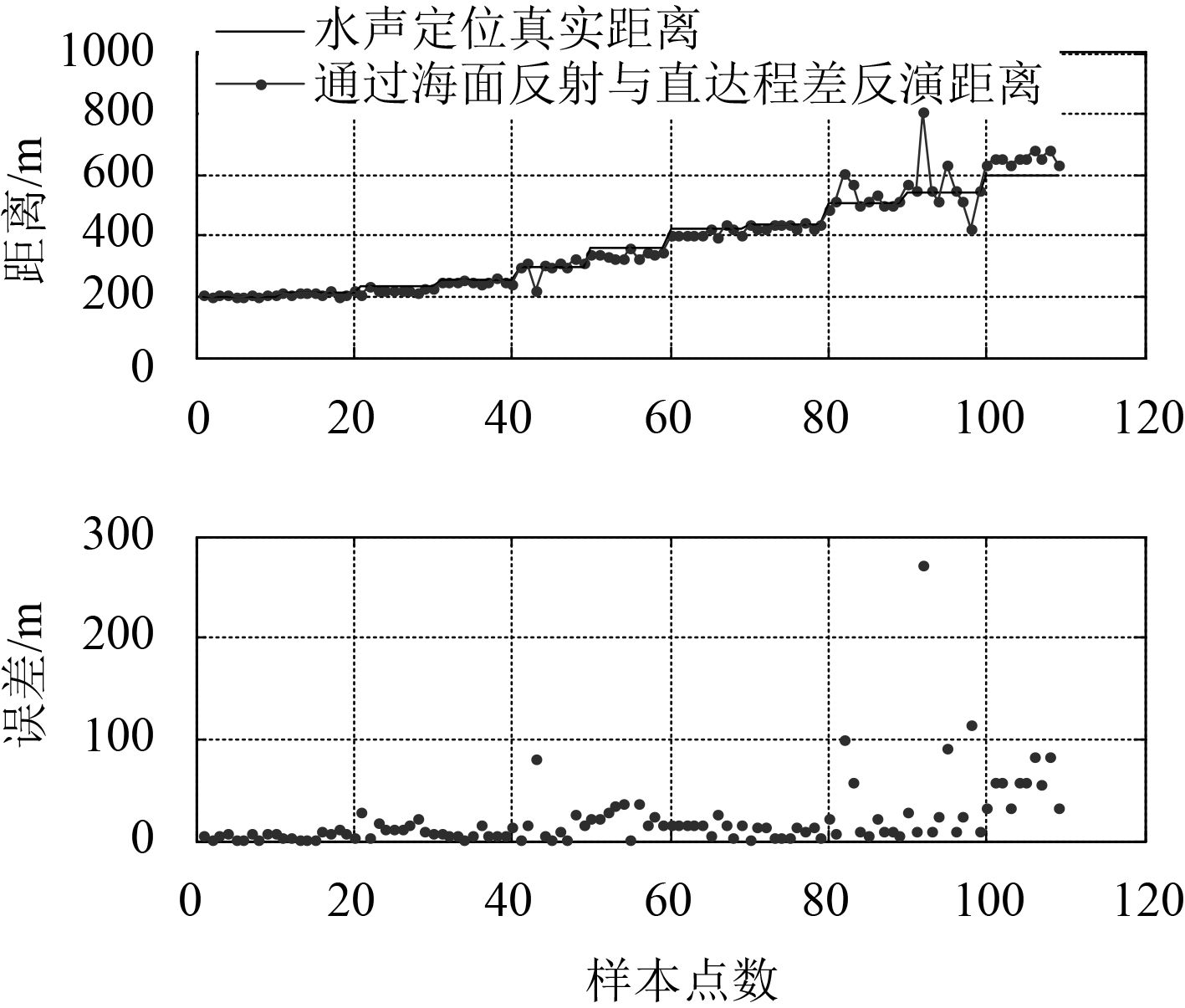
|
图 18 通过海面发射反演值与真实值对比及误差 Fig. 18 Comparison and error between the inversion value and the real value of the sea surface launch |
使用LFM信号,通过分数阶傅里叶变换可有效提高测距精度。在已知海深的前提下可精确测量发射源位置。测量精度与已知海深精度和发射信号频率带宽积有关。
1)使用海底反射信号与直达声信号差值反演直达距离时,受到海深的影响较大,当获得海深的精度较高时,其定位精度较高。且随发射深度增加,误差变大,距离变远,误差增大。
2)使用海面反射信号与直达声信号差值反演直达距离时,随发射深度减小,误差变大;距离变远,误差增大。由于海面起伏较大,所以其发射距离海面深度变化大,只有当海面较平稳时使用此种定位较好。
| [1] |
ALMEIDA LB. The fractional Fourier transform and time-frequency representation[J]. IEEE Trans. On signal processing, 1994, 42(11): 3084-3091. DOI:10.1109/78.330368 |
| [2] |
邓兵, 陶然, 齐林, 等. 基于分数阶傅里叶变换的混响抑制方法研究[J]. 兵工学报, 2005, 26(6): 761-765. DOI:10.3321/j.issn:1000-1093.2005.06.010 |
| [3] |
邓兵, 齐林, 王越. 分数阶Fourier变换原理与应用[M]. 北京: 清华大学出版社, 2004: 31–35.
|
| [4] |
何进. 大范围超声波测距技术在海上船舶定位系统的应用研究[J]. 舰船科学技术, 2017(18): 50-52
|
| [5] |
丁智慧, 王彪. 基于分数阶傅里叶变换的声呐探测信号鉴别[J]. 舰船科学技术, 2017(17): 146-151
|
| [6] |
刘伯胜, 雷家煜, 水声学原理[M].哈尔滨: 哈尔滨工程大学出版社, 2010.
|
| [7] |
Alan V. Oppenheim, Signals and Systems, 202–205.
|
| [8] |
R. J. 尤立克, 水声原理, 96–97.
|
 2019, Vol. 41
2019, Vol. 41
