2. 陆军军官学院,安徽 合肥 230031;
3. 海军工程大学 导航工程系,湖北 武汉 430031;
4. 海军海洋测绘研究所,天津 300061
2. Army Officer Academy, Hefei 230031, China;
3. Department of Navigation Engineering, Naval University of Engineering, Wuhan 430033, China;
4. Naval Institute of Hydrographic Surveying and Charting, Tianjin 300061, China
船舶轴频电磁场是因船舶主轴转动而调制流经螺旋桨-主轴-船体的腐蚀相关电流产生的一种极低频电磁场[1]。轴频电磁场分为轴频磁场和轴频电场,其基频即为主轴转动频率,约为1~7 Hz。由于频率极低,在海水中衰减很慢,传播距离很远,相比于其他物理场有着独特的优势,可以用于鱼水雷武器的探测引信和海战场的实时监测。而轴频磁场也能够在空气中以相同规律传播,可以用于航空磁探的信号源,能够极大地提高搜索效率。
国外对轴频电场研究较早,各军事强国在20世纪60年代起就对船舶轴频电磁场开展了相关理论和应用研究。Zolotarevskii Y等研究了船舶轴频电磁场的产生机理并介绍了俄罗斯的电磁场测量设备[2]。Bostick F等对运动商船的极低频电磁场进行了建模、测量和分析[3]。Hoitham P等对船舶的电磁场的静态场和交变场进行分析,并提出了减弱船舶交变电场的方法[4]。国内对轴频电磁场研究较晚,且大多集中在船舶轴频电场理论研究方面。卢新城等对船舶的轴频电场进行了水池实验测量和分析,并建立了电偶极子在海水中电磁场的模型,得到了解析解[5 – 6]。毛伟等分别对深海和浅海条件下运动的水平和垂直的电偶极子的电磁场进行建模和计算[7 – 8]。贾一卓等对船舶轴频电场的测量和信号处理做了进一步研究[9 – 10]。公开的文献对轴频磁场单独报道极少,吴志强等利用海底晃动平台测量了船舶在海水中的轴频磁场[11],尚没有对空气中的轴频磁场测量和分析的公开文献。本文以垂直时谐电偶极子为船舶轴频电流的等效源,建立浅海条件下电偶极子磁场模型并推导其在空气中的表达式,通过仿真计算和水池试验分析该磁场在空气中的传播特性。
1 船舶轴频磁场产生机理船舶通常由不同电位的金属材料制造并要浸入海水中,船体不同材料之间的电化学腐蚀以及船舶防腐系统工作都会产生电流,这些电流统称为腐蚀相关电流。船舶在海洋环境中航行时,主轴旋转过程中轴系与船体的接触电阻会周期性波动,因此流经螺旋桨-轴承-船体回路的腐蚀相关电流会受到周期性调制,调制的基频即为主轴旋转的频率,其基本原理如图1所示。

|
图 1 轴转动调制腐蚀相关电流 Fig. 1 Corrosion related current modulated by shaft rotating |
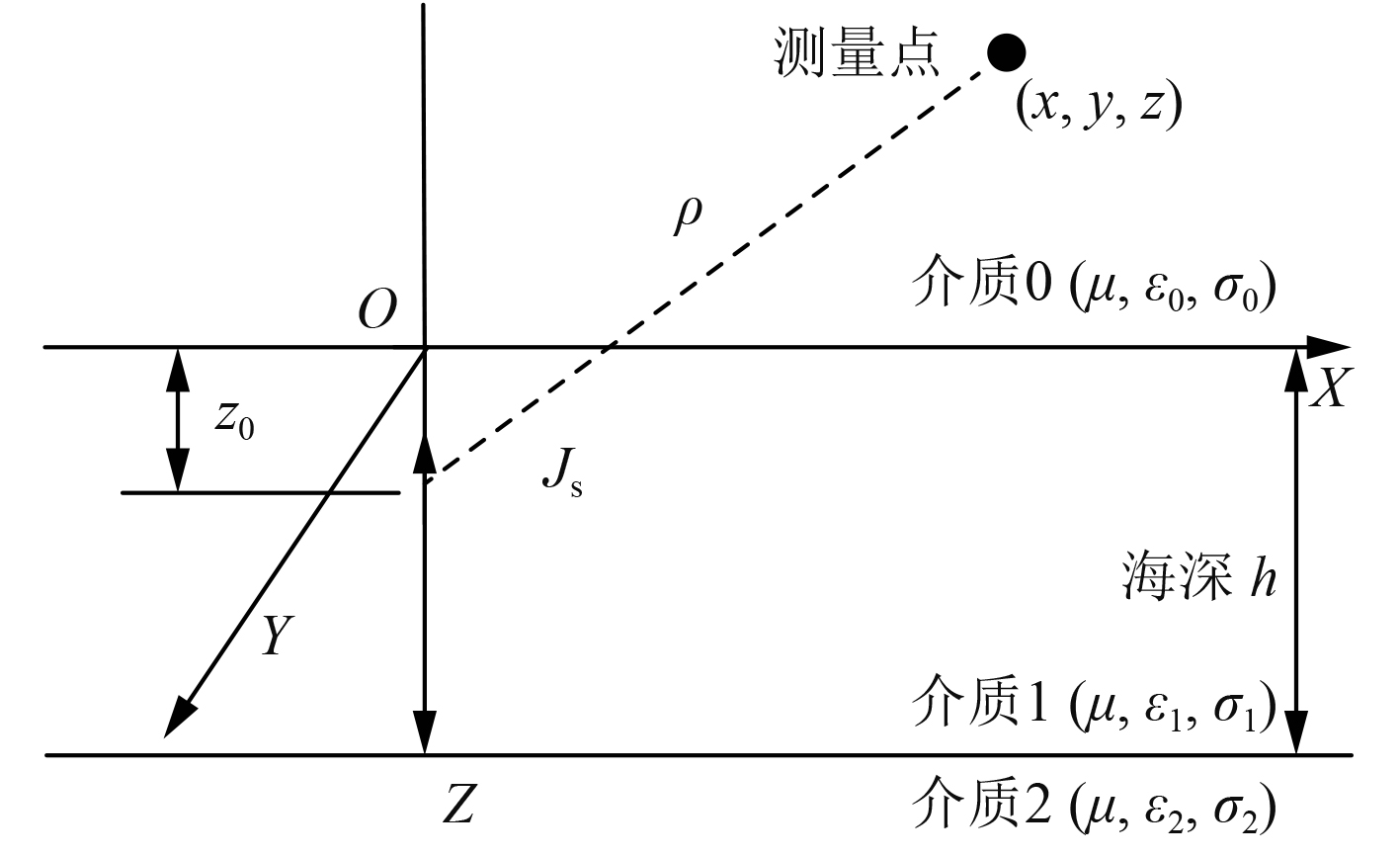
以垂直时谐电偶极子为船舶轴频电流等效源,其在浅海条件下示意图如图2所示。x轴正方向对应船舶的船首方向,y轴正方向指右舷方向,z轴垂直向下。
|
图 2 3层介质模型下垂直时谐电偶极子示意图 Fig. 2 Diagram of the vertically-directed time-harmonic dipole in three-layer medium |
垂直时谐电偶极子位于介质0、介质1和介质2组成的3层模型中,介质为各向同性线性均匀介质,初始坐标位置
| $ \left\{ \begin{array}{l} \nabla \times {{{H}}_i} = {{{J}}_s} + ({\sigma _i} + {{j}}\omega {\varepsilon _i}){{{E}}_i}{\text{,}}\\ \nabla \times {{{E}}_i} = - {{j}}\omega {{{B}}_i} = - {{j}}\omega {\mu _i}{{{H}}_i}{\text{,}}\\ \nabla \cdot {{{B}}_i} = {\mu _i}\nabla \cdot {{{H}}_i} = 0{\text{,}}\\ \nabla \cdot {{{D}}_i} = \rho {\text{。}} \end{array} \right. $ | (1) |
其中:
引入磁矢量势
| $ \left\{ \begin{array}{l} {{B}} = \nabla \times {{A}} {\text{,}}\\ {{E}} = - \nabla \phi - {{j}}\omega {{A}} {\text{,}}\\ \nabla \cdot {{A}} - {k^2}\phi /{{j}}\omega = 0 {\text{。}} \end{array} \right. $ | (2) |
可推得矢量磁位的亥姆霍兹方程:
| $\left\{ \begin{array}{l} {\nabla ^2}{{{A}}_0} + {k^2}{{{A}}_0} = 0 {\text{,}}\\ {\nabla ^2}{{{A}}_1} + {k^2}{{{A}}_1} = - \mu {{{J}}_{\rm{S}}} {\text{,}}\\ {\nabla ^2}{{{A}}_2} + {k^2}{{{A}}_2} = 0 {\text{。}} \end{array} \right. $ | (3) |
式中,
与水平电偶极子不同,垂直电偶极子产生的矢量磁位仅有z方向分量[12]。图2中,海水层中的矢量磁位是由一次源和二次源产生的,可表示为
对于介质1,矢量磁位可表示为:
| $ {{{A}}_{1p}} = \frac{{{\mu _1}Il}}{{4{\text{π}} }}\int_0^{ + \infty } {\frac{\lambda }{{{\upsilon _1}}}{e^{ - {\upsilon _0}\left| {z - {z_0}} \right|}}{J_0}(\lambda r)} {\rm d}\lambda \cdot {{{e}}_{{z}}}{\text{,}} $ | (4) |
而
| $ \left\{ \begin{aligned} &{{{A}}_0}(\rho ,\phi ,z) = \displaystyle\sum\limits_{m = - \infty }^\infty {{e^{jm\phi }}\int_0^\infty {{J_m}(\rho \xi )[{b_0}(\xi ,m){e^{z{\upsilon _0}}} + }} \\ & \qquad\qquad\quad {d_0}(\xi ,m){e^{ - z{\upsilon _0}}}]{\rm d}\xi \cdot {{{e}}_z} {\text{,}} \\ & {{{A}}_1}(\rho ,\phi ,z) = {{{A}}_{1p}} + {{{A}}_{1s}} = \\ & \qquad\qquad \dfrac{{{\mu _1}Il}}{{4{\text{π}} }}\int_0^{ + \infty } {\dfrac{\lambda }{{{\upsilon _1}}}{e^{ - {\upsilon _0}\left| {z - {z_0}} \right|}}{J_0}(\lambda r)} {\rm d}\lambda \cdot {{{e}}_{{z}}} + \\ & \qquad\qquad \displaystyle\sum\limits_{m = - \infty }^\infty {{e^{jm\phi }}\int_0^\infty {{J_m}(\rho \xi )[{b_1}(\xi ,m){e^{z{\upsilon _1}}} +} } \\ & \qquad\qquad{d_1}(\xi ,m){e^{ - z{\upsilon _1}}}]{\rm d}\xi \cdot {{{e}}_z}{\text{,}}\\ & {{{A}}_2}(\rho ,\phi ,z) =\\ & \qquad\qquad \displaystyle\sum\limits_{m = - \infty }^\infty {{e^{jm\phi }}\int_0^\infty {{J_m}(\rho \xi )[{b_2}(\xi ,m){e^{z{\upsilon _2}}} + } } \\ & \qquad\qquad {d_2}(\xi ,m){e^{ - z{\upsilon _2}}}]{\rm d}\xi \cdot {{{e}}_z}{\text{。}} \end{aligned} \right. $ | (5) |
其中:
矢量磁位仅有z方向分量,因此电磁场边界条件可以只写出2项。其中空气-海水边界条件为:
| $ \left\{ \begin{array}{l} {[\dfrac{{\nabla \cdot {{{A}}_1}}}{{k_1^2}} - \dfrac{{\nabla \cdot {{{A}}_0}}}{{k_0^2}}]_{z = 0}} = 0{\text{,}}\\ {[\dfrac{{{{{A}}_{1z}}}}{{{\mu _1}}} - \dfrac{{{{{A}}_{0z}}}}{{{\mu _0}}}]_{z = 0}} = 0{\text{。}} \end{array} \right. $ | (6) |
海水-海床边界条件为:
| $ \left\{ \begin{array}{l} {[\dfrac{{\nabla \cdot {{{A}}_2}}}{{k_2^2}} - \dfrac{{\nabla \cdot {{{A}}_1}}}{{k_1^2}}]_{z = d}} = 0{\text{,}}\\ {[\dfrac{{{{{A}}_{2z}}}}{{{\mu _2}}} - \dfrac{{{{{A}}_{1z}}}}{{{\mu _1}}}]_{z = d}} = 0 {\text{。}} \end{array} \right. $ | (7) |
当
由于空气、海水和海底的磁导率相同,均为真空磁导率,即
| $ \left\{ \!\!\!\!\! \begin{array}{l} {{{A}}_0}(\rho ,\phi ,z) = \displaystyle\int_0^\infty {{J_0}(\rho \xi )[{b_0}(\xi ,0){e^{z{\upsilon _0}}}]{\rm d}\xi } \cdot {{{e}}_z}{\text{,}}\\ {{{A}}_1}(\rho ,\phi ,z) = \dfrac{{{\mu _1}Il}}{{4{\text{π}} }}\displaystyle\int_0^{ + \infty } {\dfrac{\lambda }{{{\upsilon _1}}}{e^{ - {\upsilon _0}\left| {z - {z_0}} \right|}}{J_0}(\lambda r)} {\rm d}\lambda \cdot {{{e}}_{{z}}} + \\ \begin{array}{*{20}{c}} {}&{} \end{array}\!\!\displaystyle\int_0^\infty \!\!{{J_0}(\rho \xi )[{b_1}(\xi ,0){e^{z{\upsilon _1}}} + {d_1}(\xi ,0){e^{ - z{\upsilon _1}}}]{\rm d}\xi } \cdot {{{e}}_z}{\text{,}}\\ {{{A}}_2}(\rho ,\phi ,z) = \int_0^\infty {{J_0}(\rho \xi )[{d_2}(\xi ,0){e^{ - z{\upsilon _2}}}]{\rm d}\xi } \cdot {{{e}}_z}{\text{。}} \end{array} \right. $ | (8) |
由式(6)~式(8)可以解得
| $ {{\rm{A}}_0}(\rho ,\phi ,z) = \dfrac{{\mu Il}}{{2{\text{π}} }}\int_0^\infty {\xi {G_0}K{e^{z{\upsilon _0}}}{J_0}(\rho \xi ){\rm d}\xi } \cdot {{\rm{e}}_z}{\text{。}} $ | (9) |
其中:
| $ \begin{split} & K \!=\!\! \dfrac{{({G_1}{\upsilon _2} \!+\! {\upsilon _1}){e^{{\upsilon _1}(d \!-\! {z_0})}} \!-\! ({G_1}{\upsilon _2} \!-\! {\upsilon _1}){e^{ - {\upsilon _1}(d - {z_0})}}}}{{({G_0}{\upsilon _1} \!+\! {\upsilon _0})({G_1}{\upsilon _2} \!+\! {\upsilon _1}){e^{d{\upsilon _1}}} \!+\! ({G_0}{\upsilon _1} \!-\! {\upsilon _0})({G_1}{\upsilon _2} \!-\! {\upsilon _1}){e^{ - d{\upsilon _1}}}}}{\text{,}}\\ & {G_0} = {\raise0.7ex\hbox{${k_0^2}$} / \!\lower0.7ex\hbox{${k_1^2}$}},{G_1} = {\raise0.7ex\hbox{${k_1^2}$} \!/ \!\lower0.7ex\hbox{${k_2^2}$}}{\text{。}} \end{split} $ |
由式(2)中的
| $ \left\{ \begin{array}{l} {B_{0x}} = - \dfrac{{\partial \rho }}{{\partial y}}\dfrac{{\mu Il}}{{2{\text{π}} }}\int_0^\infty {{\xi ^2}{G_0}K{e^{z{\upsilon _0}}}{J_1}(\rho \xi ){\rm d}\xi }{\text{,}} \\ {B_{0y}} = \dfrac{{\partial \rho }}{{\partial x}}\dfrac{{\mu Il}}{{2{\text{π}} }}\int_0^\infty {{\xi ^2}{G_0}K{e^{z{\upsilon _0}}}{J_1}(\rho \xi ){\rm d}\xi } {\text{,}}\\ {B_{0z}} = 0 {\text{。}} \end{array} \right. $ | (10) |
假定浅海模型中的垂直时谐电偶极子满足正弦变化,频率为5 Hz,峰值大小为10 A·m。取空气的3个电磁参数为
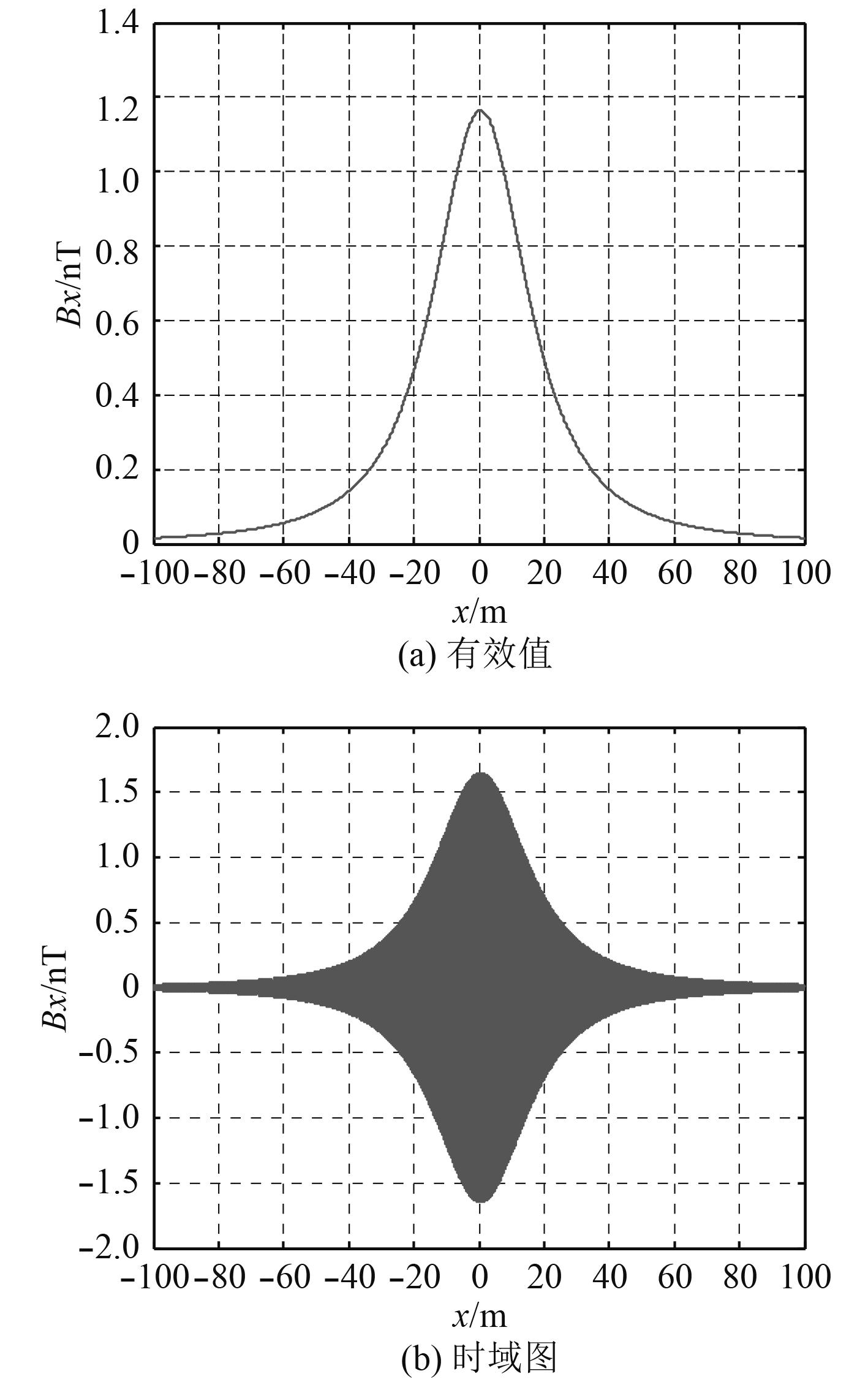
|
图 3 空气层磁场的x分量 Fig. 3 The x component of magnetic field in air |
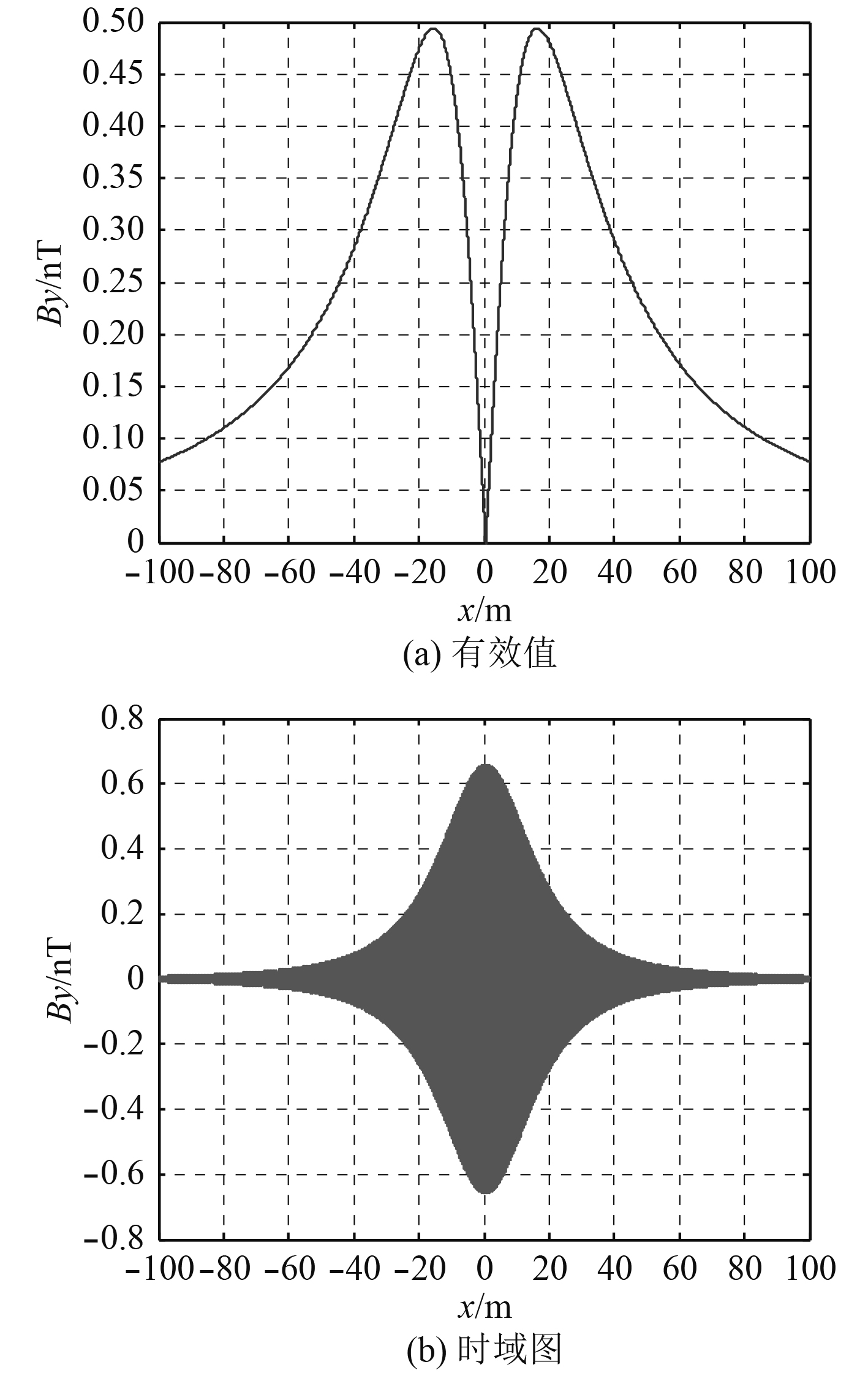
|
图 4 空气层磁场的y分量 Fig. 4 The y component of magnetic field in air |
由于磁场的z分量为0,只对x和y分量计算作图。从计算结果来看,时谐水平电偶极子在空气中产生的磁场随着距离增大逐步衰减,距离越远,衰减越慢。
试验采用一对碳棒电极模拟垂直时谐电偶极子进行了水池试验。实验条件包括无磁性实验水池、一对碳棒电极和磁场测量系统。无磁性水池的尺寸为8 m×5 m×1.5 m,水池水深为1 m。用工业盐调制出电导率约为4 S/m,近似于海水。磁场测量系统中,磁感应棒输出的信号经过滤波后,通过NI采集上传到上位机。电偶极子的电极间距10 cm,通以频率5 Hz、峰值为500 mA的正弦交流电。将碳棒用支架固定于水池中,使2个端头成垂直位置,支架可以水平移动。选择合适的坐标系,测量点固定在(0,90 cm,100 cm)。碳棒沿x轴由(–220 cm,0,30 cm)移动到(220 cm,0,30 cm),速度5 cm/s。测量结果如图5所示。
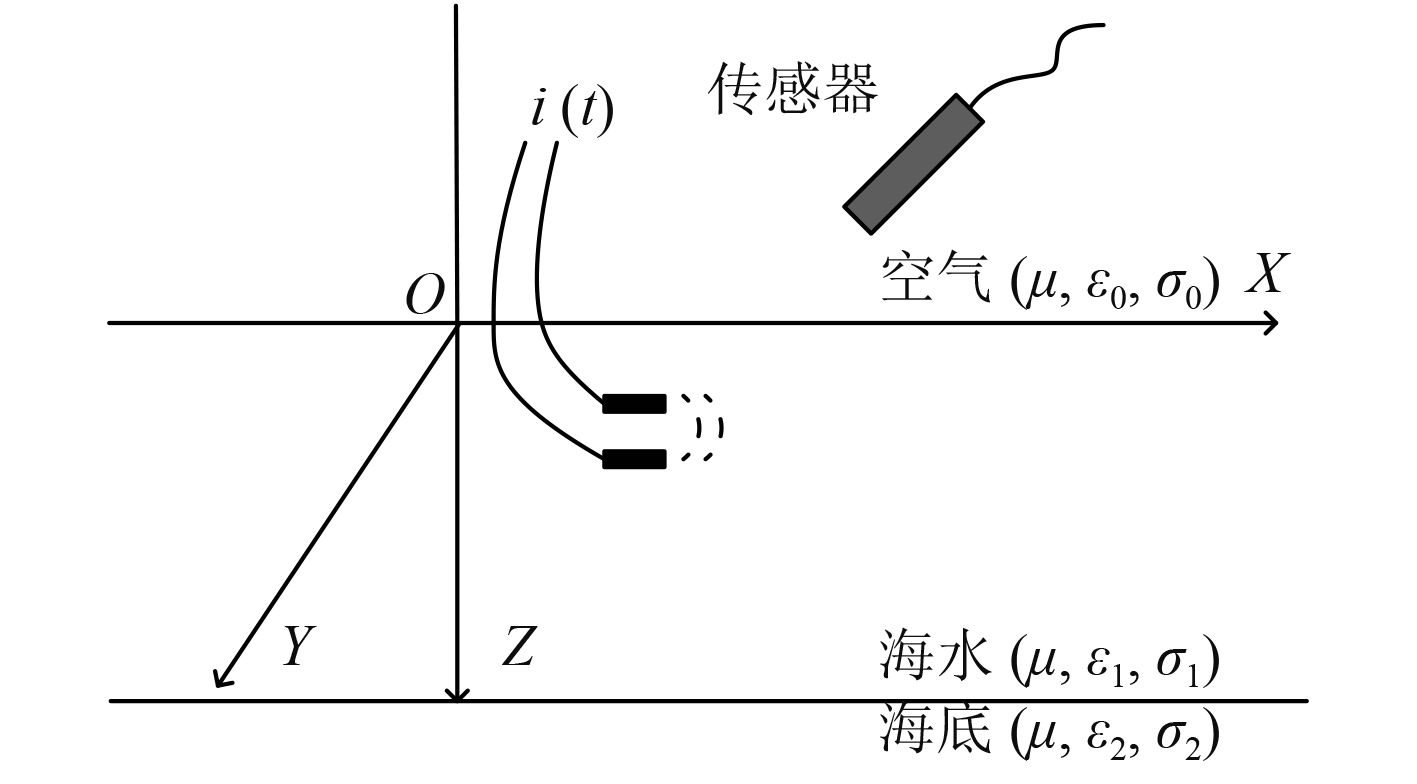
|
图 5 碳棒电极试验示意图 Fig. 5 Diagram of carbon electrodes experiment |
垂直时谐电偶极子的磁场仿真计算中没有z分量值,但是在文中的碳棒电极实验时,存在幅值微弱的z分量,文中未列出。原因为碳棒电极的布放方式使得水中电流不能严格满足以z轴轴对称分布。从测量结果来看,磁场x分量和y分量周期性能够辨识,与仿真计算的包络比较一致,但幅值均比较小。在测量中更易受到环境磁场和实验设备磁场干扰,从图中可以看出噪声比较大。此时就不适合用时域信息分析磁场。图6(b)和图7(b)分别对磁场x分量和y分量做时频分析,可以看出频谱中5 Hz的线谱成分明显,因此利用磁场线谱特征进行在空气中对水中目标进行探测将更为有效。
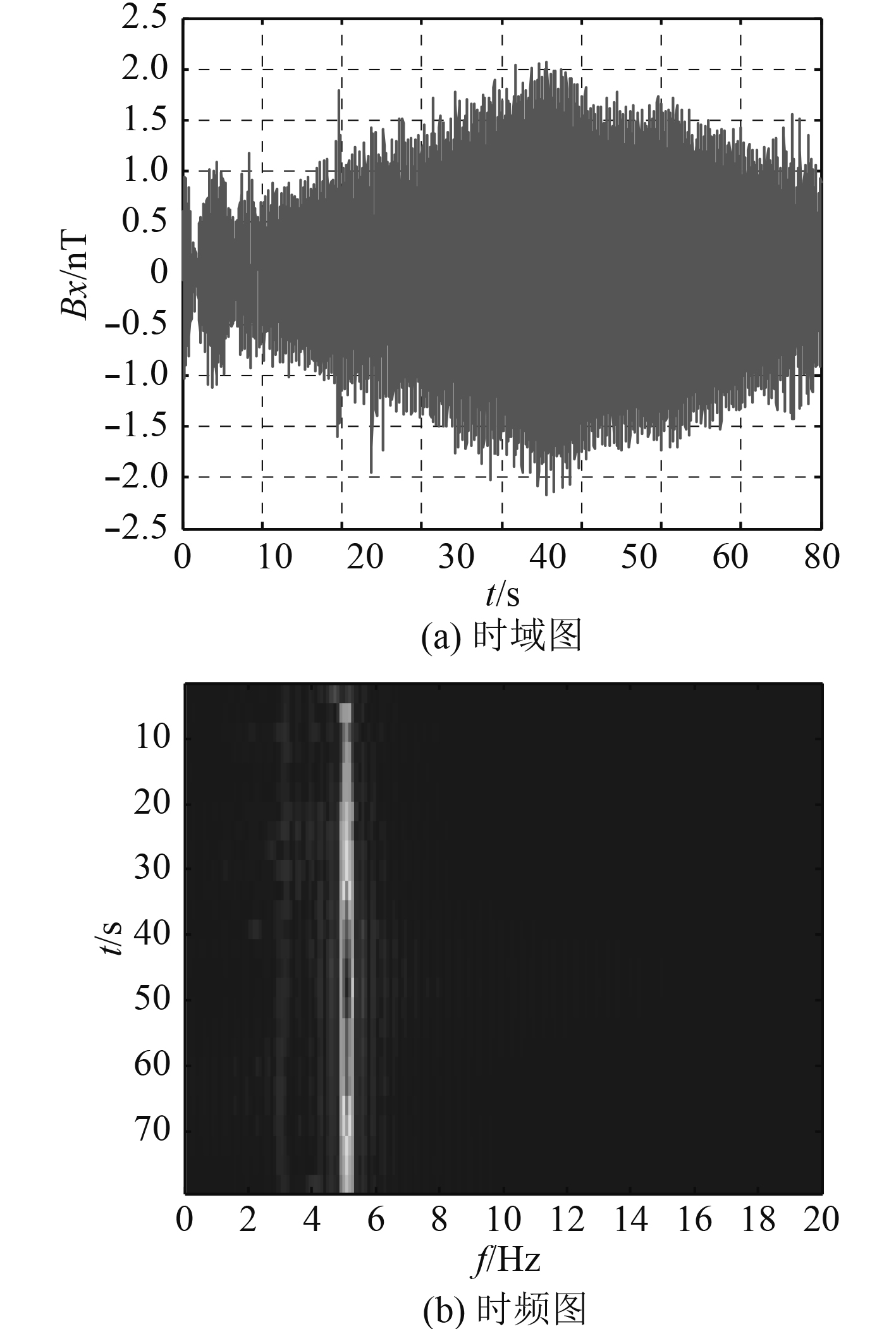
|
图 6 碳棒电极产生的磁场x分量 Fig. 6 The x component of ELF magnetic field generated by the carbon electrodes |
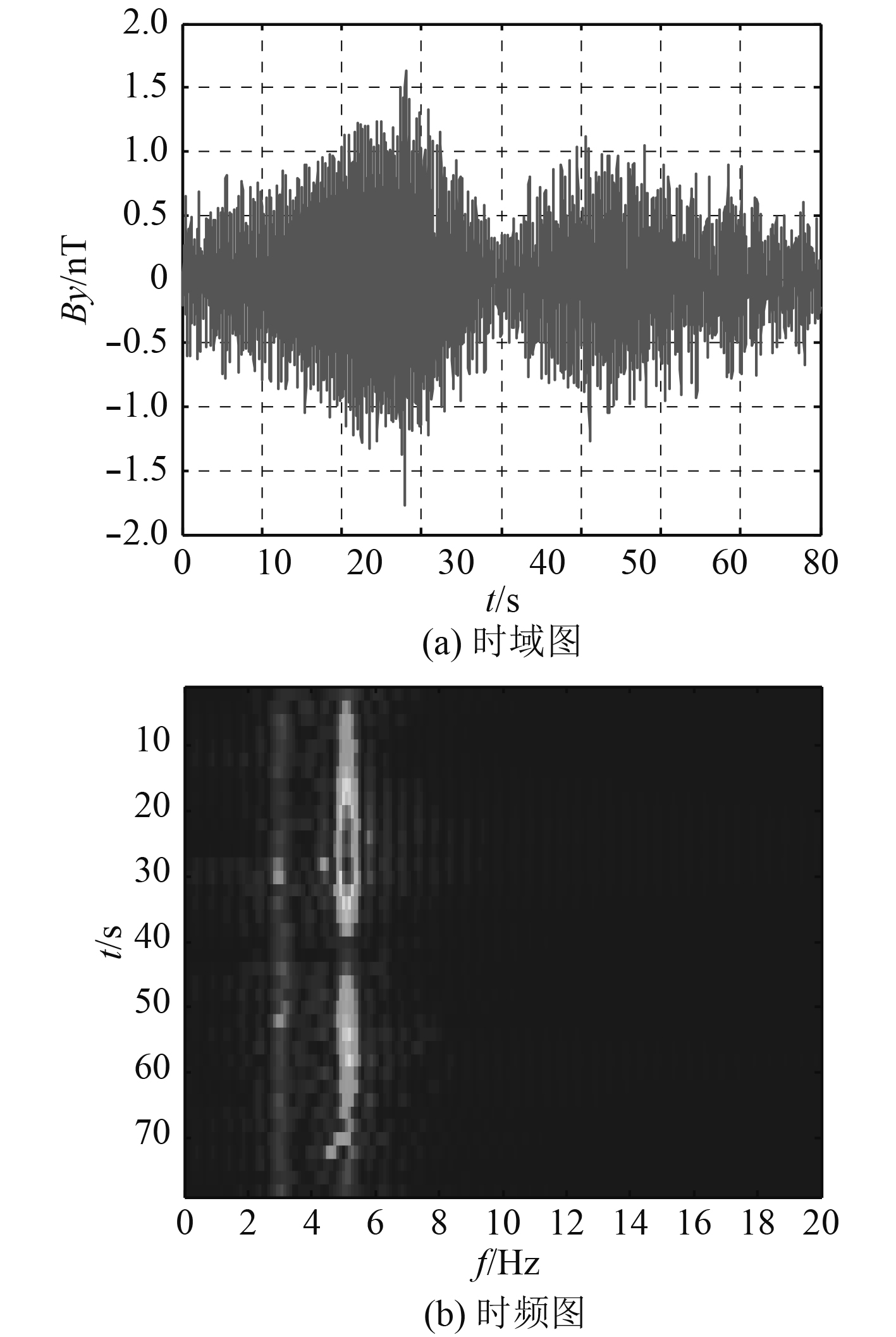
|
图 7 碳棒电极产生的磁场y分量 Fig. 7 The y component of ELF magnetic field generated by the carbon electrodes |
本文分析船舶轴频磁场产生机理,建立浅海条件下垂直时谐电偶极子在空气层产生的极低频磁场模型,并采用快速汉克尔变换进行数值运算。碳棒电极在海水水池中的试验结果验证了模型有效性。磁传感器技术的发展使得其分辨率已达到pT级,能够检测到远距离目标的磁场信号。从文中的分析可知利用信号的频谱信息能够更好地实现检测,在此基础上,谱线增强技术和测量平台的磁补偿技术需要进一步研究。
| [1] |
林春生, 龚沈光. 舰船物理场[M]. 北京: 兵器工业出版社, 2007: 237–240.
|
| [2] |
ZOLOTAREVSKII Y, BULYGIN F, PONOMAREV A, et al. Methods of measuring the low-frequency electric and magnetic fields of ships[J]. Measurement Techniques, 2005, 48(11): 1140-1144. DOI:10.1007/s11018-006-0035-6 |
| [3] |
BOSTICK F, SMITH H, BOEHL J. The detection of ULF- ELF emissions from moving ships[R]. New York: State Academic Educational Institutions, 1977.
|
| [4] |
HOITHAM P, JEFFERY I, BROOKING B, et al. Electromagnetic signature modeling and reduction[C]//Conference Proceeding UDT Europe, 1999.
|
| [5] |
卢新城, 龚沈光, 周骏, 等. 海水中极低频水平电偶极子电磁场的解析解[J]. 电波科学学报, 2004, 19(03): 290-295. DOI:10.3969/j.issn.1005-0388.2004.03.008 |
| [6] |
卢新城, 龚沈光, 孙明, 等. 轴转动调制腐蚀电流产生的极低频电场的测定[J]. 兵工学报, 2004, 25(5): 544-546. DOI:10.3321/j.issn:1000-1093.2004.05.009 |
| [7] |
毛伟, 林春生. 两层介质中运动水平时谐偶极子产生的电磁场[J]. 兵工学报, 2009, 30(5): 555-560. DOI:10.3321/j.issn:1000-1093.2009.05.009 |
| [8] |
毛伟, 周萌, 周耀忠. 浅海中运动时谐垂直电偶极子产生的电磁场[J]. 哈尔滨工程大学学报, 2010, 31(12): 1580-1586. DOI:10.3969/j.issn.1006-7043.2010.12.004 |
| [9] |
贾亦卓, 姜润翔, 龚沈光. 基于小波模极大值的船舶轴频电场检测算法研究[J]. 兵工学报, 2013, 34(5): 579-584. |
| [10] |
程锐, 姜润翔, 龚沈光, 等. 基于EMD和4阶累积量的船舶轴频电场线谱提取[J]. 舰船科学技术, 2016(1): 94-98. DOI:10.3404/j.issn.1672-7649.2016.1.020 |
| [11] |
WU Zhi-qiang, ZHU Xin-hua, LI Bin. Modeling and measurements of alternating magnetic signatures of ships[J]. Sensor & Transducers, 2015, 186(3): 161-167. |
| [12] |
雷银照. 时谐电磁场解析方法[M]. 北京: 科学出版社, 2000: 112–118, 147–150.
|
| [13] |
胡俊, 聂在平. 索末菲尔德积分新方法-快速汉克尔变换[J]. 电子学报, 1998, 26(3): 126-128. DOI:10.3321/j.issn:0372-2112.1998.03.030 |
 2019, Vol. 41
2019, Vol. 41
