电磁发射技术是机械能发射、化学能发射之后的一次发射方式的革命,利用电磁力(能)推进物体到高速或超高速的发射技术[1 – 2]。电磁轨道发射武器电枢以超高速运动,身管所受载荷随电枢运动高速变化,已经超出静力学研究的范畴。而且从本质上讲,力学中静力学问题实际上都是动力学问题的近似[3],与静力学相比,动力学分析需要考虑系统惯性和阻尼作用。电磁轨道发射身管的动态响应影响系统性能,导轨振动影响电枢与导轨接触状态,当电枢与导轨失去有效接触时,就会发生转捩[4 – 5]。此外,身管的振动势必影响电枢与弹丸内弹道和出口姿态,进而对射击精度也有影响。
电磁轨道发射原理模型如图1所示,电流从平行导轨一端流入,经过电枢从导轨另一端流出,导轨周围产生的电磁场推动有电流通过的电枢向前运动。由于电磁场的存在,平行导轨之间会受到电磁斥力;由于枢轨之间的过盈配合,电枢对导轨也会有过盈力。Tzeng首次提出将复合型电磁轨道发射身管简化为弹性基础上的单层梁模型,利用应变能方法计算弹性基础的刚度系数[6 – 7] 。Lewis和Nechitailo将内径与壁厚比在1.6左右的复合型电磁轨道发射身管简化为弹性基础上的Timoshenko梁[8]。Stonkus和Rackauskas等将一种螺栓预紧型电磁轨道发射身管简化为弹性基础上的单层梁模型[4]。Johnson和Moon为了解释电磁发射过程中的转捩现象,同样采用弹性基础上的单层梁模型计算轨道受电磁压力下的应力波传播特性以及轨道变形,但是模型并不符合实际工况[5]。何威将电磁轨道发射身管简化为弹性基础上的双层梁模型,但是并未引入阻尼[9]。
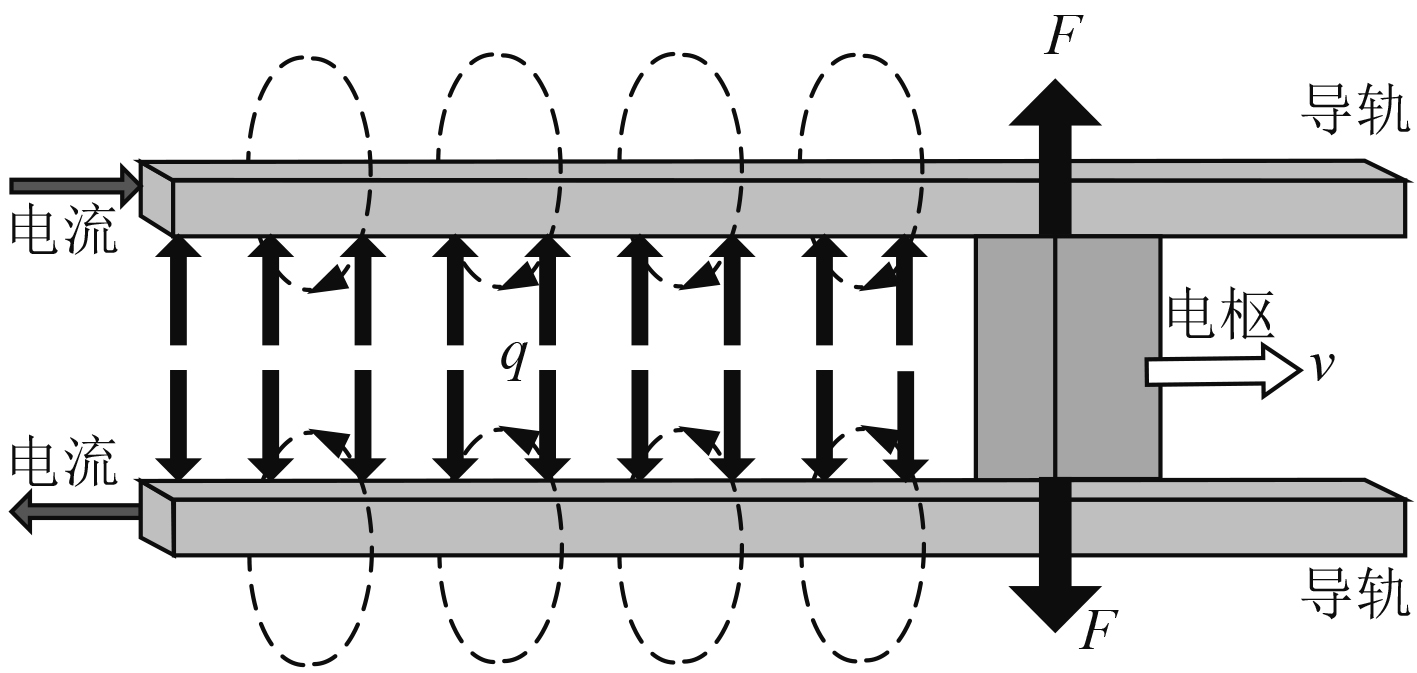
|
图 1 发射装置模型图 Fig. 1 Electromagnetic launcher model |
本文将一种螺栓预紧型电磁轨道发射身管简化为Winkler弹性基础上的双层Euler-Bernoulli梁,考虑阻尼,建立双层梁的振动微分方程,推导出齐次方程通解并得到在电磁轨道发射工况下导轨振动位移的解析解。建立模型在有限元软件中仿真计算并分析电磁轨道发射身管动力学特性。
1 身管动力学双层梁模型的建立 1.1 身管动力学模型简化本文建模分析的螺栓预紧型电磁轨道发射模型为上下对称结构,截面如图2所示。上下导轨之间和上下导轨与外封装板之间由绝缘压板分开,外封装板由螺栓预紧。将电磁轨道发射身管简化为弹性基础上双层简支梁模型,导轨简化为第1层梁,外封装板为第2层梁,导轨与外封装板之间绝缘压板简化为第1层弹性支撑,螺栓起到第2层弹性支撑的作用。身管动力学分析模型如图3所示。
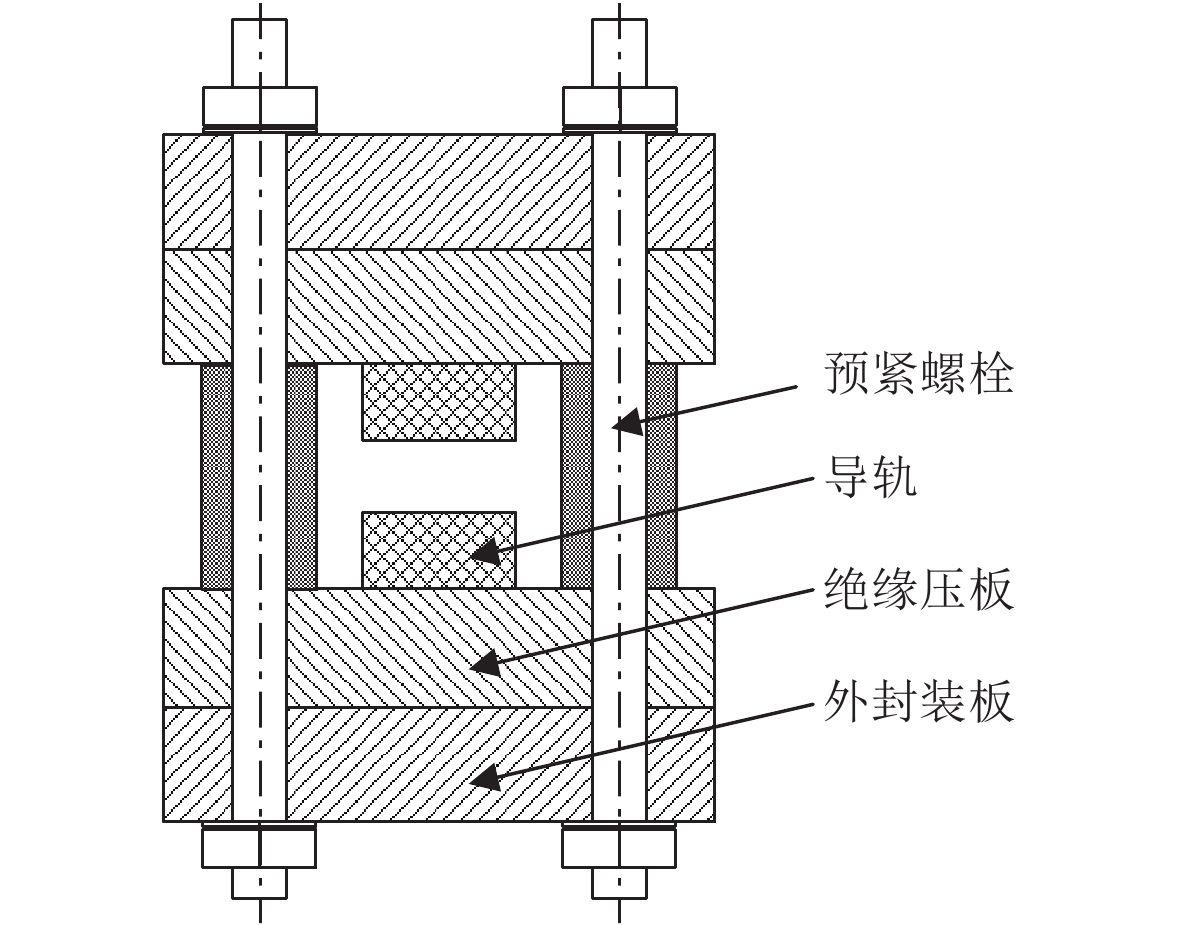
|
图 2 身管截面 Fig. 2 Cross section of electromagnetic launcher tube |
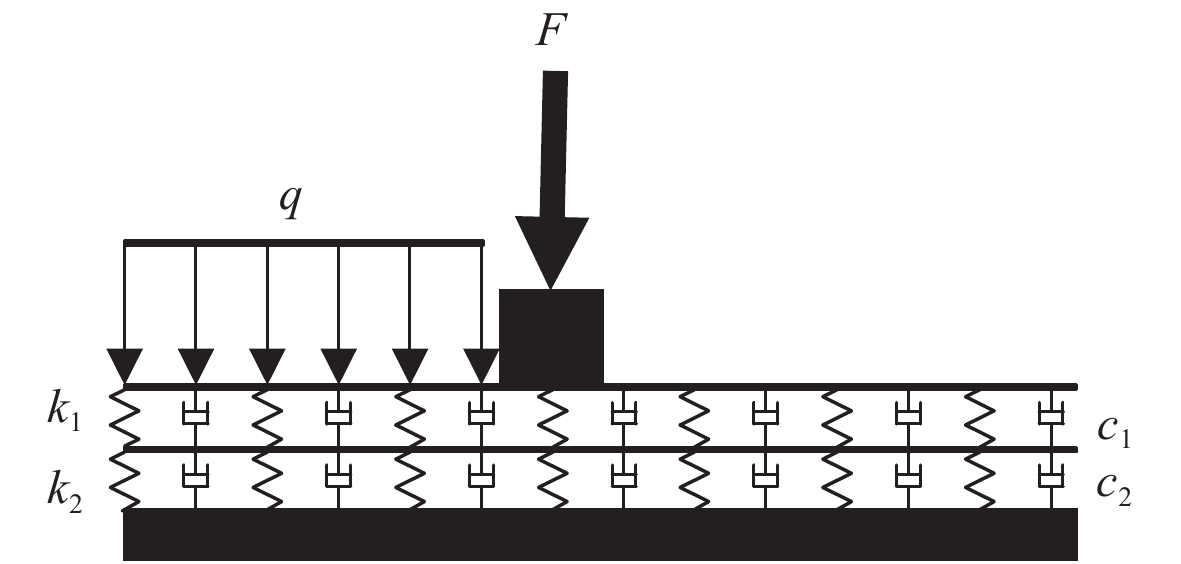
|
图 3 身管动力学分析模型 Fig. 3 Structural analysis model of electromagnetic launcher tube |
在外加载荷
| $Mx'' + Cx' + Kx = F(t)\text{。}$ | (1-1) |
其中:
弹性基础上双层Euler-Bernoulli梁的动力学微分方程为:
| $\begin{split} & {E_1}{I_1}\frac{{{\partial ^4}{w_1}}}{{\partial {x^4}}} + {m_1}\frac{{{\partial ^2}{w_1}}}{{\partial {t^2}}} + {k_1}\left( {{w_1} - {w_2}} \right) + \\ & {c_1}\left( {\frac{{\partial {w_1}}}{{\partial t}} - \frac{{\partial {w_2}}}{{\partial t}}} \right) = f\left( {x,t} \right)\text{,} \end{split} $ | (1-2) |
| $\begin{split} \!\!{E_2}{I_2}\frac{{{\partial ^4}{w_2}}}{{\partial {x^4}}} + {m_2}\frac{{{\partial ^2}{w_2}}}{{\partial {t^2}}} \!+\! {k_2}{w_2}\! +\! {c_2}\frac{{\partial {w_2}}}{{\partial t}} = \!-\! {k_1}\left( {{w_2} \!-\! {w_1}} \right) \text{。} \end{split} $ | (1-3) |
其中:
| $f\left( {x,t} \right) = - qH\left( {{L_a} - x} \right) - F\delta \left( {x - {L_a}} \right)\text{,}\;\;\left( {0 < t < t'} \right)\text{。}$ | (1-4) |
其中:
根据刚度定义,第1层Winkler弹性基础的弹性常数为:
| ${k_1} = \frac{{{E_3}L{b_3}}}{{{h_3}}}\text{,}$ | (1-5) |
其中:
| ${k_2} = \frac{{{n_1}{E_4}\text{π} {r^2}}}{l}\text{。}$ | (1-6) |
其中:
身管不受外加载荷情况下,式(2)和式(3)齐次方程形式为:
| $\begin{split} & {E_1}{I_1}\frac{{{\partial ^4}{w_1}}}{{\partial {x^4}}} + {m_1}\frac{{{\partial ^2}{w_1}}}{{\partial {t^2}}} + {k_1}\left( {{w_1} - {w_2}} \right) +\\ & \quad {c_1}\left( {\frac{{\partial {w_1}}}{{\partial t}} - \frac{{\partial {w_2}}}{{\partial t}}} \right) = 0 \text{,} \end{split} $ | (2-1) |
| $\begin{split} {E_2}{I_2}\frac{{{\partial ^4}{w_2}}}{{\partial {x^4}}} \! + {m_2}\frac{{{\partial ^2}{w_2}}}{{\partial {t^2}}} \!+ \! {k_2}{w_2} \!+ {c_2}\frac{{\partial {w_2}}}{{\partial t}} \!= \!- \! {k_1}\left( {{w_2} \!- \!{w_1}} \right) \text{,} \end{split} $ | (2-2) |
联立式(7)和式(8)得到:
| $ {w_1} = \frac{{{E_2}{I_2}}}{{{k_1}}}\frac{{{\partial ^4}{w_2}}}{{\partial {x^4}}} + \frac{{{m_2}}}{{{k_1}}}\frac{{{\partial ^2}{w_2}}}{{\partial {t^2}}} + \frac{{{c_2}}}{{{k_1}}}\frac{{\partial {w_2}}}{{\partial t}} + \frac{{{k_1} + {k_2}}}{{{k_1}}}{w_2}\text{,} $ | (2-3) |
| $\begin{split} & \frac{{{E_1}{I_1}{E_2}{I_2}}}{{{k_1}}}\frac{{{\partial ^8}{w_2}}}{{\partial {x^8}}} + \frac{{{m_1}{E_2}{I_2} + {E_1}{I_1}{m_2}}}{{{k_1}}}\frac{{{\partial ^6}{w_2}}}{{\partial {x^4}\partial {t^2}}} + \\ & \frac{{{E_1}{I_1}{c_2} + {c_1}{E_2}{I_2}}}{{{k_1}}}\frac{{{\partial ^5}{w_2}}}{{\partial t\partial {x^4}}} + \\ & \left( {\frac{{{k_1} + {k_2}}}{{{k_1}}}{E_1}{I_1} + {E_2}{I_2}} \right)\frac{{{\partial ^4}{w_2}}}{{\partial {x^4}}} + \\ & \frac{{{m_1}{m_2}}}{{{k_1}}}\frac{{{\partial ^4}{w_2}}}{{\partial {t^4}}} + \frac{{{m_1}{c_2} + {c_1}{m_2}}}{{{k_1}}}\frac{{{\partial ^3}{w_2}}}{{\partial {t^3}}} + \\ & \left( {\frac{{{k_1} + {k_2}}}{{{k_1}}}{m_1} + {m_2} + \frac{{{c_1}{c_2}}}{{{k_1}}}} \right)\frac{{{\partial ^2}{w_2}}}{{\partial {t^2}}} + \\ & \frac{{{c_1}{k_2} + {c_2}{k_1}}}{{{k_1}}}\frac{{\partial {w_2}}}{{\partial t}} + {k_2}{w_2} = 0 \text{。} \end{split} $ | (2-4) |
根据振动理论[9 – 10],
| $ {w_2} = \sum\limits_{i = 1}^\infty {{X_i}\left( {{A_i}\sin {\omega _i}t + {B_i}\cos {\omega _i}t} \right)} = \sum\limits_{i = 1}^\infty {{X_i}{T_i}} \text{,} $ | (2-5) |
其中,
| $\left\{ {\begin{split} & {{w_{1,2}}\left( 0 \right) = 0} \text{,}\\ & {{w_{1,2}}\left( L \right) = 0} \text{,}\\ & {{{\left. {\frac{{{\partial ^2}{w_{1,2}}}}{{\partial {x^2}}}} \right|}_{x = 0}} = 0} \text{,}\\ & {{{\left. {\frac{{{\partial ^2}{w_{1,2}}}}{{\partial {x^2}}}} \right|}_{x = L}} = 0} \text{。} \end{split}}\right.$ | (2-6) |
另外,考虑振型函数正交性,身管不受外加载荷条件下双层梁振动微分方程的解为:
| $\begin{split} {w_1} = & \sum\limits_{i = 1}^\infty [ \frac{{{E_2}{I_2}}}{{{k_1}}}{X_i}^{\left( 4 \right)}{T_i} + \\ & \left( {\frac{{{k_1} + {k_2}}}{{{k_1}}} - \frac{{{m_2}}}{{{k_1}}}\omega _i^2} \right){X_i}{T_i} + \frac{{{c_2}}}{{{k_1}}}{X_i}{{T'}_i}] = \\ & \sum\limits_{i = 1}^\infty {\left[ {{P_i} + {Q_i} + {R_i}} \right]} \text{,}\end{split} $ | (2-7) |
| ${w_2} = \sum\limits_{i = 1}^\infty {\sqrt {\frac{2}{{{m_t}}}} } \sin {\beta _i}x{T_i}\text{。}$ | (2-8) |
其中,
| ${\beta _i} = \frac{i}{l}\text{π} \;\;\;(i = 1,2,3 \cdots )\text{,}$ | (2-9) |
| $ {P_i} = \frac{{{E_2}{I_2}}}{{{k_1}}}\sqrt {\frac{2}{{{m_t}}}} \beta _i^4\sin {\beta _i}x \times \left( {{A_i}\sin {\omega _i}t + {B_i}\cos {\omega _i}t} \right) \text{,} $ | (2-10) |
| $\begin{split} {Q_i} =& \left( {\frac{{{k_1} + {k_2}}}{{{k_1}}} - \frac{{{m_2}}}{{{k_1}}}\omega _i^2} \right)\sqrt {\frac{2}{{{m_t}}}} \times \\ & \sin {\beta _i}x\left( {{A_i}\sin {\omega _i}t + {B_i}\cos {\omega _i}t} \right) \text{,} \end{split} $ | (2-11) |
| $\begin{split} {R_i} = \frac{{{c_2}}}{{{k_1}}}\sqrt {\frac{2}{{{m_t}}}} \sin {\beta _i}x \times \left( {{A_i}{\omega _i}\cos {\omega _i}t - {B_i}{\omega _i}\sin {\omega _i}t} \right)\text{。} \end{split} $ | (2-12) |
实际发射工况下,身管动态响应,即双层梁模型受外加载荷情况下,联立式(2)、式(13)、式(15)~式(18),对式(2)等号左右两边同时乘以
| ${\int_0^L {\left( {\sin {\beta _i}x} \right)} ^2}{\rm d}x = \frac{L}{2}\text{,}$ | (2-13) |
| $\int_0^L {\sin {\beta _i}x\cos {\beta _i}x} {\rm d}x = 0\text{,}$ | (2-14) |
得到:
| $\mu \frac{{\partial {T_i}}}{{\partial t}} + \eta {T_i} = {F_i}\left( {x,t} \right)\text{。}$ | (2-15) |
其中:
| $\begin{split} \mu = & \frac{{{c_1}{E_2}{I_2} + {c_2}{E_1}{I_1}}}{{{k_1}}}\sqrt {\frac{2}{{{m_t}}}} \beta _i^4\frac{L}{2} - \\ & \frac{{{m_1}{c_2} + {c_1}{m_2}}}{{{k_1}}}\sqrt {\frac{2}{{{m_t}}}} \omega _i^2\frac{L}{2} + \frac{{{c_1}{k_2} + {k_1}{c_2}}}{{{k_1}}}\sqrt {\frac{2}{{{m_t}}}} \frac{L}{2}\text{,} \end{split} $ | (2-16) |
| $\begin{split} \eta = & \frac{{{E_1}{I_1}{E_2}{I_2}}}{{{k_1}}}\sqrt {\frac{2}{{{m_t}}}} \beta _i^8\frac{L}{2} + {k_2}\sqrt {\frac{2}{{{m_t}}}} \frac{L}{2}+ \\ & \frac{{\left( {{k_1} + {k_2}} \right){E_1}{I_1} + {k_1}{E_2}{I_2}}}{{{k_1}}} \times \sqrt {\frac{2}{{{m_t}}}} \beta _i^4\frac{L}{2} - \\ & \frac{{{m_2}{E_1}{I_1} + {m_1}{E_2}{I_2}}}{{{k_1}}}\omega _i^2\sqrt {\frac{2}{{{m_t}}}} \beta _i^4\frac{L}{2} - \\ & {m_1}\left( {\frac{{{k_1} + {k_2}}}{{{k_1}}} - \frac{{{m_2}}}{{{k_1}}}\omega _i^2 - \frac{{{c_1}{c_2}}}{{{k_1}}} - {m_2}} \right) \times \sqrt {\frac{2}{{{m_t}}}} \omega _i^2\frac{L}{2} \text{,} \end{split} $ | (2-17) |
| ${F_i}\left( {x,t} \right) = \int_0^L {f\left( {x,t} \right)\sin {\beta _i}x{\rm d}x}\text{,} $ | (2-18) |
对于式(21),其解为:
| ${T_i} = {e^{ - \frac{\eta }{\mu }t}}\int {\frac{{{F_i}}}{\mu }{e^{\frac{\eta }{\mu }t}}{\rm d}t}\text{。} $ | (2-19) |
于是,双层梁模型振动方程的解,即导轨和外封装板振动解析解为:
| $\begin{split} {w_1} = & \sum\limits_{i = 1}^\infty {\bigg[\bigg(\frac{{{E_2}{I_2}}}{{{k_1}}}\beta _i^4 + \frac{{{k_1} + {k_2}}}{{{k_1}}} - \frac{{{m_2}}}{{{k_1}}}\omega _i^2} - \\ & \frac{{{c_2}\eta }}{{{k_1}\mu }}\bigg) \times {e^{ - \frac{\eta }{\mu }t}}\int {\frac{{{F_i}}}{\mu }{e^{\frac{\eta }{\mu }t}}{\rm d}t} + \frac{{{c_2}{F_i}}}{{{k_1}\mu }}\bigg]{X_i} \text{,} \end{split} $ | (2-20) |
| ${w_2} = \sum\limits_{i = 1}^\infty {\sqrt {\frac{2}{{{m_t}}}} } {e^{ - \frac{\eta }{\mu }t}}\int {\frac{{{F_i}}}{\mu }{e^{\frac{\eta }{\mu }t}}{\rm d}t} \sin {\beta _i}x\text{。}$ | (2-21) |
从身管振动角度来讲,身管结构设计和材料选取主要考虑以下方面:1)导轨振动尽量小;2)导轨与外封装板之间的相对位移要小。
由第2节可知电磁轨道发射时身管振动与身管各部分几何尺寸以及材料性能都有关系。为了更加直观地研究电磁轨道发射身管动力学特性,本文应用有限元分析软件建立电磁轨道发射身管Winkler弹性基础上的双层Euler-Bernoulli梁模型,并进行动力学仿真分析。模型参数使用导轨尺寸为长3m,宽30 mm,高15 mm,材料为铜合金,密度8 900 kg/m3,弹性模量120 GPa;上封装板长3 m,宽160 mm,高40 mm,材料为合金钢,密度7850kg/m3,弹性模量210 GPa;绝缘压板长3 m,宽160 mm,高40 mm,材料为GRP,弹性模量18 GPa[4];预紧螺栓数量为80个,有效作用长度0.205 m,半径9 mm,材料为合金钢,弹性模量210 GPa。发射初始位置

|
图 4 导轨和外封装板挠度随位置和时间的变化 Fig. 4 Deflection of the rail and containment with time and location |

|
图 5 发射过程中身管挠度最大值 Fig. 5 The maximum deflection of railgun during the launching process |
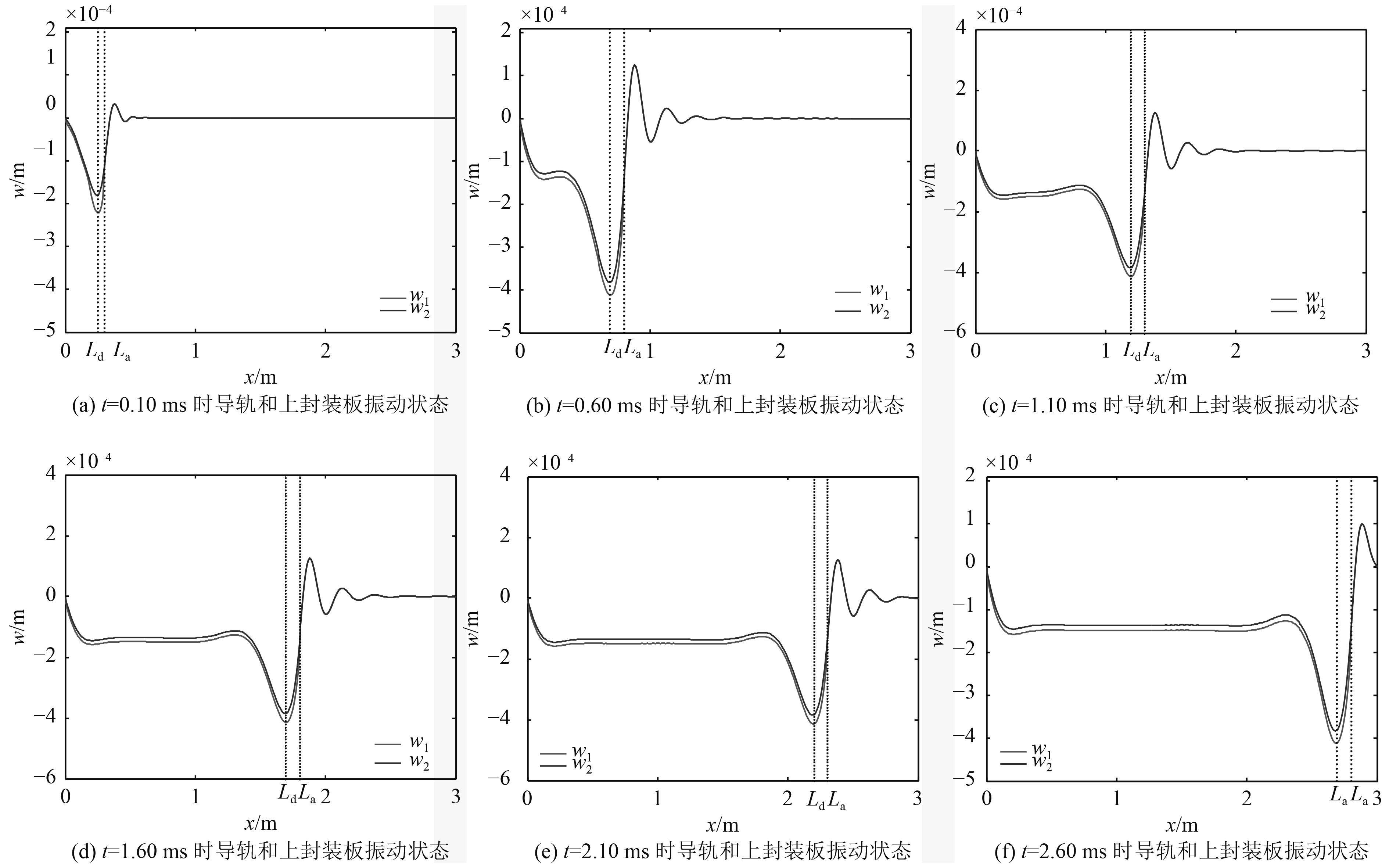
|
图 6 发射时间历程中身管振动状态 Fig. 6 Vibration of railgun during the launching process |
从图4可以看出,导轨和外封装板的挠度变形在整个时空分布情况基本一致,导轨和外封装板主要向外侧变形,向内弯曲无论是从幅度还是时间分布都相对较小,因此预紧螺栓必须有足够的强度足以支撑和约束身管的外向变形。
从图5(a)可以看出,随着电枢的前进,导轨和外封装板挠度变化趋势基本一致,在初始阶段挠度大小成直线增大趋势,达到一定值后在接下来大部分时间挠度大小基本保持稳定,在发射后期挠度稍有波动并在最后时刻达到最大值。从图5(b)可以看出,沿着导轨长度方向,导轨和外封装板挠度大小先增大然后保持基本不变,最后在出口段挠度最大。在电磁轨道发射初始时刻,身管振动变形在短时间内迅速加大,在达到一定值后导轨和外封装板挠度大小虽然保持基本不变,但是最大变形位置在随着电枢位置的变化也在不断变化;从时间上看,在发射出膛前导轨和外封装板挠度存在一个不稳定状态,挠度大小出现波动,并在出膛时刻达到最大值;从空间位置上看,在出口段导轨和外封装板挠度存在不稳定状态,挠度大小出现波动,在出口段挠度达到最大值。初步判断身管振动不稳定状态和最大挠度时间和空间的对应。
图6为从发射开始后0.10~2.60 ms间隔0.50 ms分别截取此时导轨和外封装板振动状态。可以看出,发射初始阶段,电枢运动距离较短,导轨间受电磁斥力作用区域较短身管的振动还不大。随着电枢前进,挠度最大点也在向前推进,证实前文中对身管振动不稳定状态和最大挠度的对应关系,即在发射出膛前一段时间在出口段挠度不稳定,在出膛时刻出口位置处挠度达到最大值。并且还可以知道,在整个发射过程任何时刻,导轨与外封装板间隙的最大值位置发生在导轨和身管处于最大挠度处。图6中电枢到达位置和该时刻导轨挠度最大位置如表1所示。
|
|
表 1 发射过程中电枢位置和最大挠度位置 Tab.1 Location of armature and maximum deflection during the launching process |
可以看出,最大挠度位置落后于电枢位置,这是身管受到集中载荷和分布载荷共同作用的结果。最大挠度位置落后电枢位置的距离随着发射的进行慢慢拉大,这是由于在初始阶段均布载荷作用区域较小,集中载荷对身管变形的作用较大,随着发射的进行,均布载荷作用区域增加,集中载荷的影响相对减小。
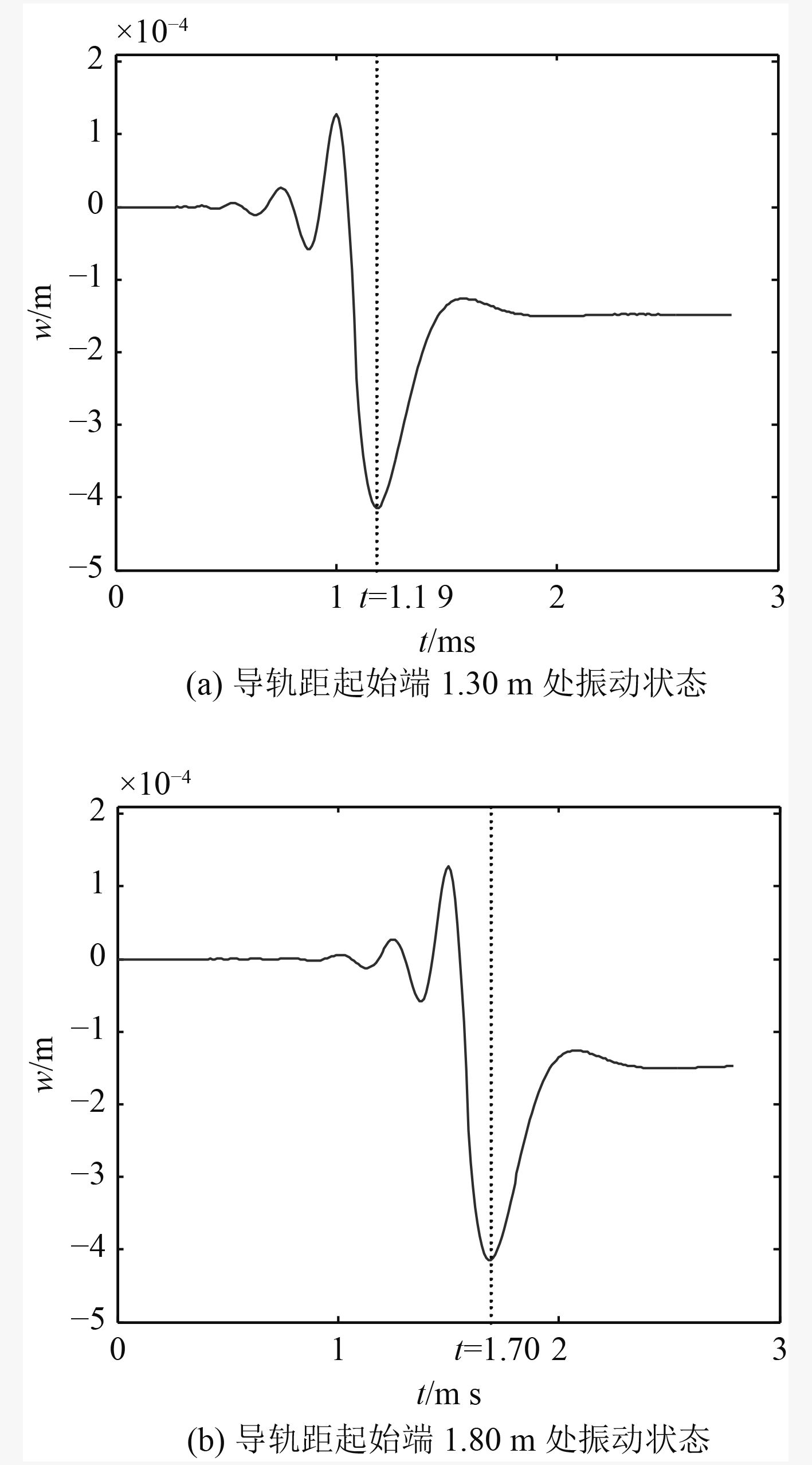
图7分别截取1.30 m和1.80 m导轨在整个发射过程中振动状态,结合图6分析可知电磁轨道发射过程中,受应力波的作用,在电枢还未行进到导轨距起始端
|
图 7 导轨距起始端1.30 m和1.80 m处振动状态 Fig. 7 Vibration of the rail at 1.30 m and 1.80 m location |
|
图 8 导轨变形过程 Fig. 8 The deformation process of rail |
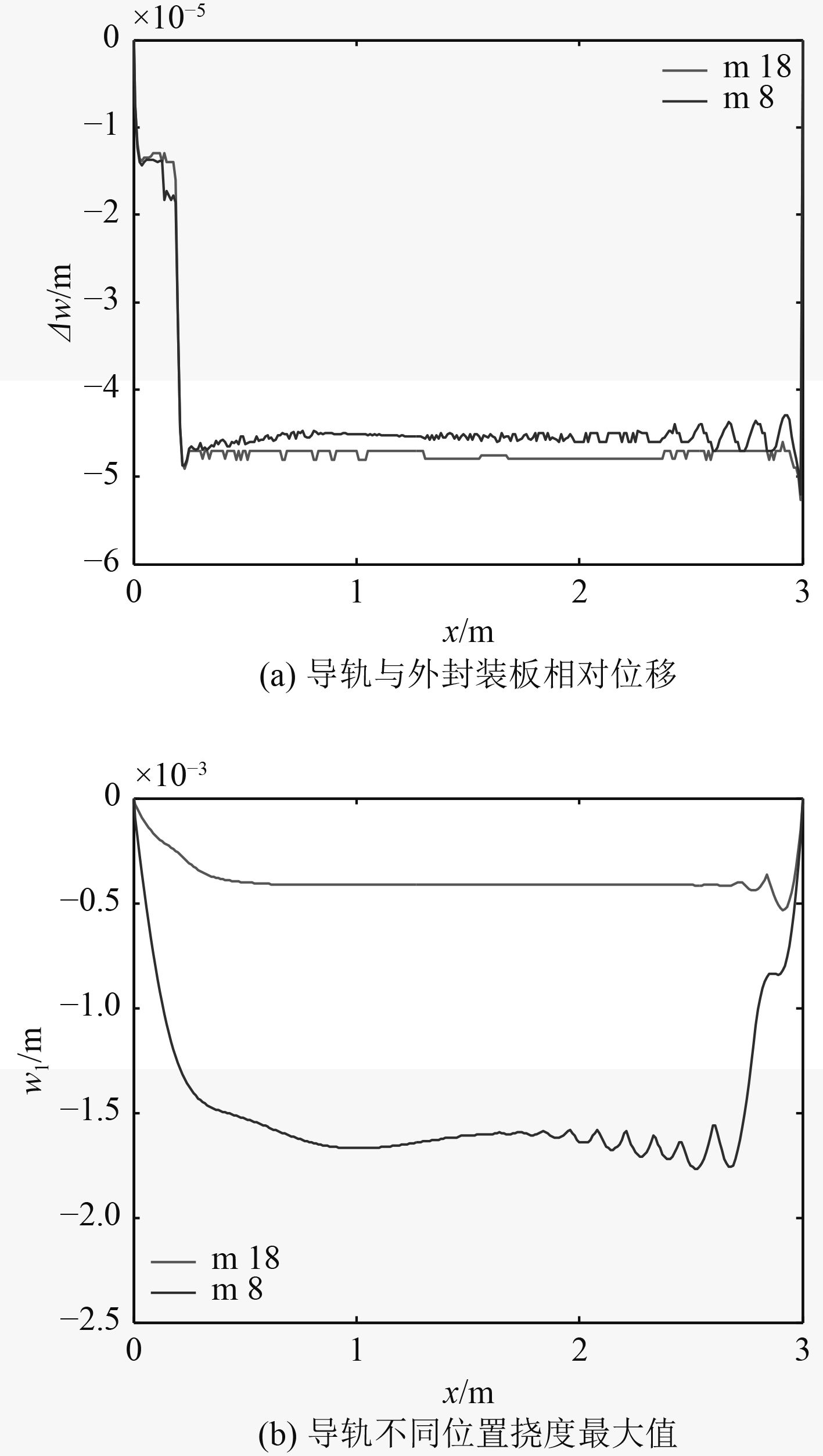
为了考察预紧螺栓对身管动力学特性的影响,改变螺栓半径为4 mm,对比分析导轨与外封装板间隙和导轨不同位置挠度最大值变化情况,结果如图9所示。
|
图 9 预紧螺栓对身管振动的影响 Fig. 9 The influence of the bolt on the vibration of railgun |
可以看出,导轨与外封装板间隙受预紧螺栓半径影响较小,但是减小螺栓半径,导轨挠度随之增大。结合第1节和第2节内容分析可知:螺栓半径的改变主要影响第2层弹性层等效刚度,螺栓半径的减小等效刚度随之减小。因此可以推论:增大第2层弹性层等效刚度,如增加预紧螺栓半径和数量可以有效减小身管振动。
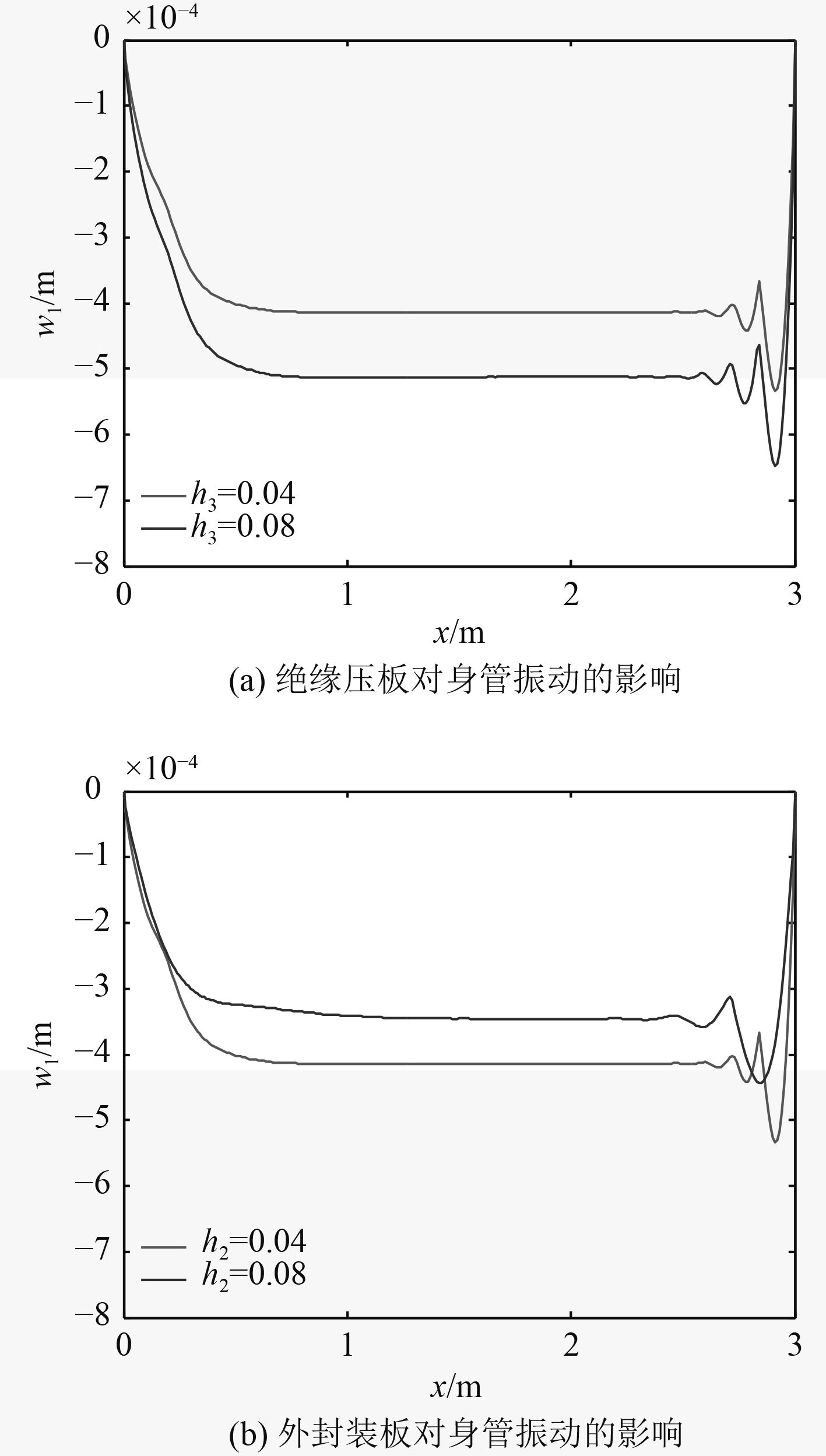
为了考察绝缘压板和外封装板对身管动力学特性的影响,分别改变绝缘压板厚度为80 mm,外封装板厚度为8 mm,对比分析导轨不同位置挠度最大值变化情况,结果如图10所示。
|
图 10 绝缘压板和外封装板对身管振动的影响 Fig. 10 The influence of the insulation clamping and containment on the vibration of railgun |
可以看出,增加绝缘压板厚度导轨挠度会随之增大,而增加外封装板厚度导轨挠度则随之减小。结合第1节和第2节内容分析可知:绝缘压板的改变主要影响第1层弹性基础等效刚度,绝缘压板厚度增加,第1层弹性层等效刚度减小,导轨挠度增大。外封装板对身管振动的影响主要是靠影响下梁的惯性矩进而影响下梁抗弯刚度作用的,下梁抗弯刚度越大,身管振动越小,但是外封装板厚度的增加会使得身管尺寸增加,预紧螺栓有效作用长度增加,进而减小第2层弹性基础刚度。因此,在一定范围内,综合增加第1层弹性层等效刚度,提高外封装板的抗弯刚度,如减小绝缘压板厚度并选用高模量材料做绝缘压板,增加外封装板厚度并选用高模量材料做外封装板能减小身管振动。
4 结 语对螺栓预紧型电磁轨道发射身管建立了基于Winkler弹性基础上的双层Euler-Bernoulli梁模型,考虑实际工况,推导身管振动微分方程解析解。建立身管动力学有限元模型,仿真分析了发射过程中电磁轨道发射身管不同位置处变形随时间的变化情况,并改变参数对比分析了不同电磁轨道发射身管结构参数和材料性能对身管动力学特性的影响。得到结论如下:
1)发射过程中导轨和外封装板的挠度变形在整个时空分布情况基本一致,导轨和外封装板主要向外侧变形;
2)发射初始阶段,电枢运动距离较短,身管振动随着电枢前进迅速增大。随着电枢前进,外加载荷作用区域增大,挠度最大点也在向前推进,最大变形值基本不变,在出口阶段出现波动。任何一个时刻,导轨与外封装板间隙的最大值位置发生在导轨处于最大挠度处;
3)集中载荷和分布载荷共同作用和应力波传播的影响,对于导轨上任何位置处,在电枢行进到该位置处之前,导轨该位置处已经开始振动,振幅逐渐增大,并在电枢驶过该位置一段时间后,该位置振动才达到最大值,之后振动不断衰减;
4)综合增加第1层和第2层弹性层等效刚度,提高外封装板的抗弯刚度,如减小绝缘压板厚度并选用高模量材料做绝缘压板,增加预紧螺栓半径和数量,增加外封装板厚度并选用高模量材料做外封装板都可以有效减小电磁轨道发射身管振动。
| [1] |
FAIR H D. Progress in electromagnetic launch science and technology[J]. IEEE Transactions on Magnetics, 2007, 43(1): 93-98. DOI:10.1109/TMAG.2006.887596 |
| [2] |
MCNAB I R. Large-scale pulsed power opportunities and challenges[J]. IEEE Transactions on Plasma Science, 2014, 42(5): 1118-1127. DOI:10.1109/TPS.2014.2303884 |
| [3] |
李永池. 波动力学[M]. 合肥: 中国科学技术大学出版社, 2015.
|
| [4] |
STONKUS R, RACKAUSKAS J, SCHNEIDER M, et al. Structural mechanics of railguns with open barrels and elastic supports: The influence of multishot operation[J]. IEEE Transactions on Plasma Science, 2015, 43(5): 1510-1515. DOI:10.1109/TPS.2014.2387791 |
| [5] |
JOHNSON A J, MOON F C. Elastic waves and solid armature contact pressure in electromagnetic launchers[J]. IEEE Transactions on Magnetics, 2006, 42(3): 422-429. DOI:10.1109/TMAG.2005.862105 |
| [6] |
TZENG J T. Dynamic response of electromagnetic railgun due to projectile movement[J]. IEEE Transactions on Magnetics, 2003, 39(1): 472-475. DOI:10.1109/TMAG.2002.806384 |
| [7] |
TZENG J T. Structural mechanics for electromagnetic railguns[J]. IEEE Transactions on Magnetics, 2005, 41(1): 246-250. DOI:10.1109/TMAG.2004.839828 |
| [8] |
LEWIS K B, NECHITAILO N V. Transient resonance in hypervelocity launchers at critical velocities[J]. IEEE Transactions on Magnetics, 2007, 43(1): 157-162. DOI:10.1109/TMAG.2006.887648 |
| [9] |
何威, 白象忠. 方口径电磁轨道发射装置导轨及壁板的动力响应[J]. 振动与冲击, 2013, 32(15): 144-148. HE Wei, BAI Xiang-zhong. Dynamic responses of rails and panels of rectangular electromagnetic rail launcher[J]. Journal of Vibration and Shock, 2013, 32(15): 144-148. DOI:10.3969/j.issn.1000-3835.2013.15.026 |
| [10] |
WILLIAM T T, MARIE D D, DA Li, et al. Theory of vibration with application (Fifth Edition)[M]. Beijing: Tsinghua University Press, 2005, 258–289.
|
 2019, Vol. 41
2019, Vol. 41
