水下自主航行器(AUV)广泛应用于水下监测、侦察等工程作业,目前以军用为主,但小型、民用的AUV产品需求已逐渐在市场上升温。水下通信、路径规划、水动力性能分析等成为小型AUV产品设计实现亟需解决的难题。相对于大型深海作业的AUV,小型民用AUV体积质量小、航行速度慢、作业水深小、水环境多变,对水动力性能试验和动力定位控制的设计要求较高。
小型AUV的动力定位系统要求能够实时地根据当前的位置、姿态反馈信息发出控制信号,推进器执行信号产生抵抗风、浪等外界干扰力的作用力并推动AUV运行,从而在不施加外力控制的条件下,沿预先规划的路径轨迹实现AUV的定位航行。
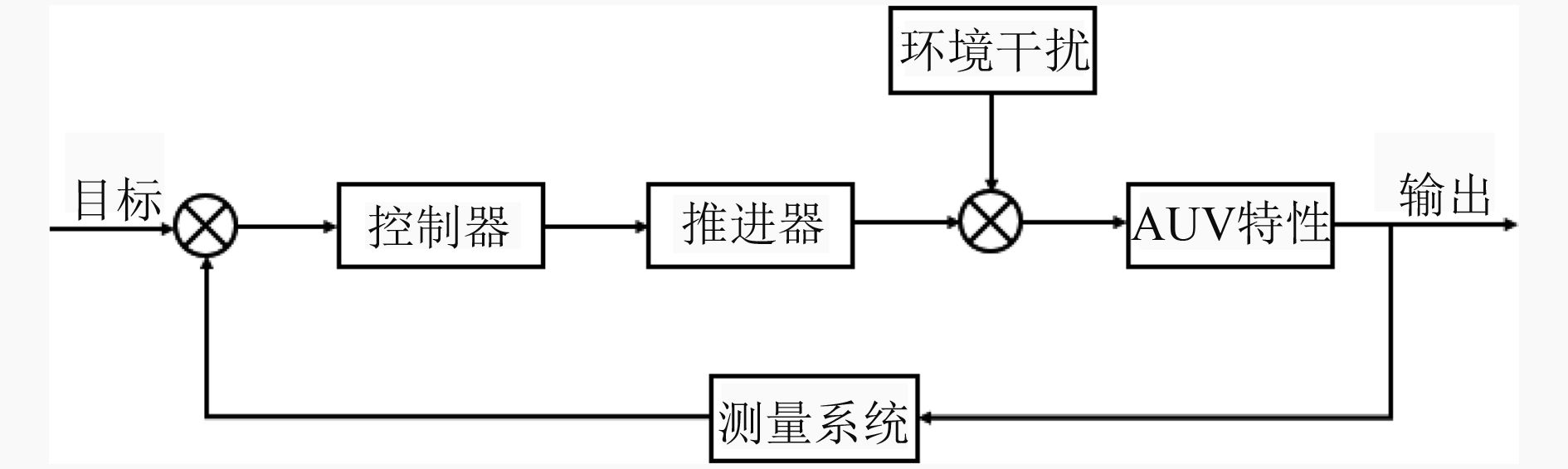
AUV动力定位系统框图如图1所示。
|
图 1 AUV动力定位系统框图 Fig. 1 The diagram of AUV dynamic positioning system |
对于AUV动力定位控制系统而言,首要工作是建立水环境、AUV自身以及推进系统的数学模型。
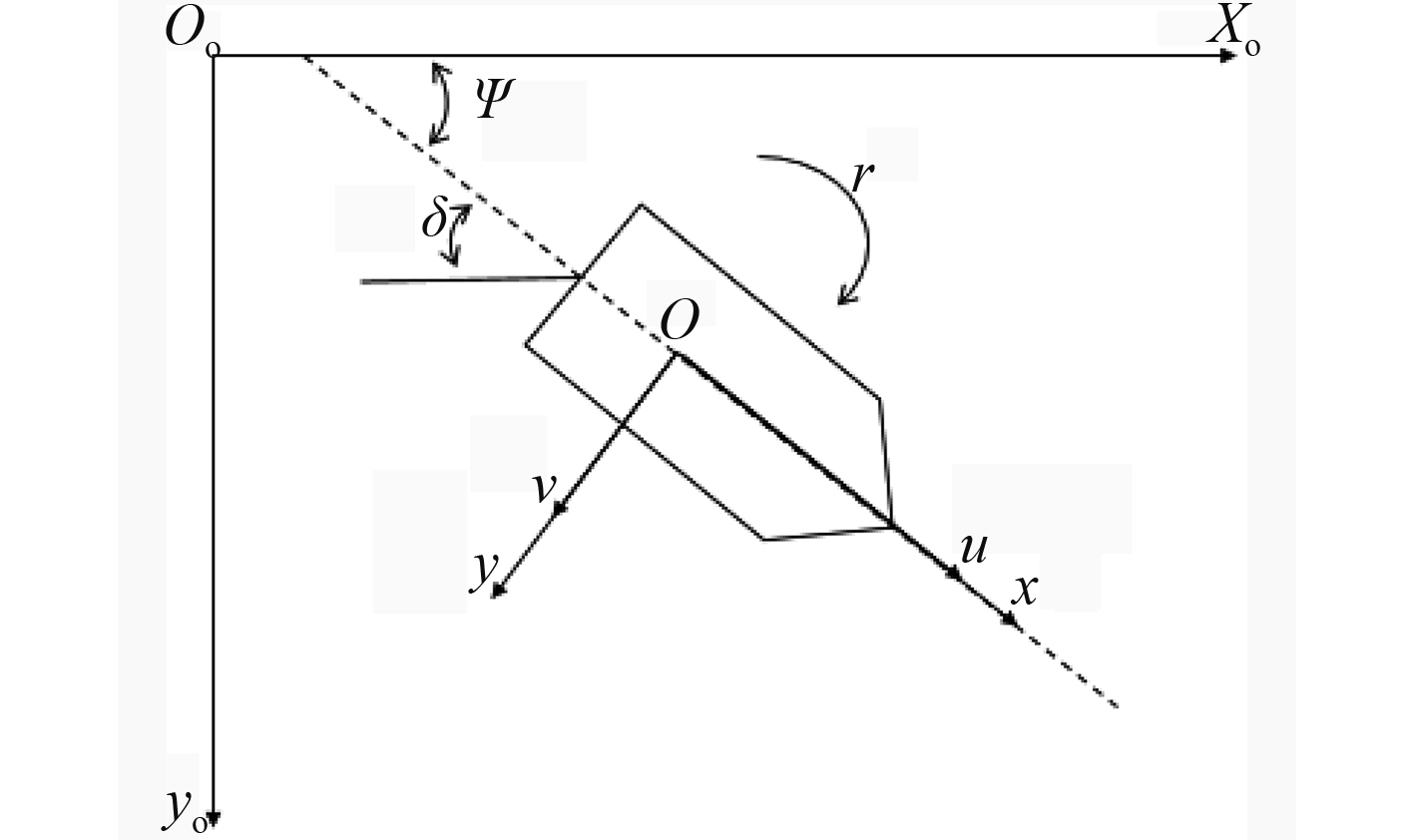
为了描述AUV的运动,采用如图2所示的固定坐标系
|
图 2 AUV固定坐标系和运动坐标系 Fig. 2 Fixed coordinate and moving coordinate of AUV |
由于小型民用AUV的作业水深小,姿态保持相对稳定,横倾和纵倾幅度很小,因此仅考虑三自由度(纵荡、横荡、首摇)的运动情况。以位置向量
AUV在水下面临的作业环境属于不规则波浪环境,研究上经常把仅存在于主风方向且有无穷长波线、单向波峰彼此保持平行的二次不规则波称为不规则长峰波[2]。
不规则波可以看成是各种频率规则波的线性叠加,对于长峰波,海面上任一点的波高可表示为:
| $ \begin{split} \zeta (t) = & \sum\limits_{i = 1}^n {{\zeta _{ai}}\cos ({\omega _i}t + {\varepsilon _i})} = \\ & \sum\limits_{i = 1}^n {\sqrt {2{S_{\zeta \zeta }}({\omega _i})\Delta {\omega _i}} \cos ({\omega _i}t + {\varepsilon _i})} \text{。} \end{split} $ | (1) |
式中:
常用的波谱密度函数有P-M谱、纽曼(Newman)谱、JONSWAP谱、ITTC双参数谱等。其中,ITTC双参数谱以有义波高
| $ {S_{\zeta \zeta }}(\omega ) = \frac{{173h_{1/3}^2}}{{T_1^4{\omega ^5}}}\exp \left( - \frac{{691}}{{T_1^4{\omega ^4}}}\right)\text{。} $ | (2) |
波浪力包括2部分:1)1阶波浪力引起的高频往复运动;2)2阶波浪力引起的慢漂运动,使AUV缓慢地漂离原来的位置。高频运动位置变化频繁,动力定位系统很难也没有必要对其进行控制,因为这样会大大加速推进系统的磨损和能量损耗。
规则波的2阶波浪力一般采用Daidola公式进行计算[3]:
| $ \left\{ \begin{aligned} & F_x^D = \frac{1}{2}\rho L\zeta _a^2\cos \chi C_x^D\text{,}\\ & F_y^D = \frac{1}{2}\rho L\zeta _a^2\sin \chi C_y^D\text{,}\\ & M_n^D = \frac{1}{2}\rho {L^2}\zeta _a^2\sin \chi C_n^D\text{。} \end{aligned} \right. $ | (3) |
式中:ρ为水密度;L为船长;χ为波向角,即航行方向与波浪方向的夹角;
波浪力系数的计算公式如下:
| $ \left\{ \begin{aligned} & C_x^D(\lambda ) = 0.05 - 0.2\left(\frac{\lambda }{L}\right) + 0.75{(\frac{\lambda }{L})^2} - 0.51{\left(\frac{\lambda }{L}\right)^3}\text{,}\\ & C_y^D(\lambda ) = 0.46 + 6.83\left(\frac{\lambda }{L}\right) - 15.65{\left(\frac{\lambda }{L}\right)^2} + 8.44{\left(\frac{\lambda }{L}\right)^3}\text{,}\\ & C_n^D(\lambda ) = - 0.11 + 0.68\left(\frac{\lambda }{L}\right) - 0.79{\left(\frac{\lambda }{L}\right)^2} + 0.21{\left(\frac{\lambda }{L}\right)^3}\text{,} \end{aligned} \right. $ | (4) |
| $ \left\{ \begin{array}{l} \lambda = 2{\text{π}}/k\text{,}\\ k = {\omega ^2}/g\text{。} \end{array} \right. $ | (5) |
式中:λ为波长;k为波数。
整理得到不规则2阶随机波浪力的计算公式:
| $ \left\{ \begin{aligned} & F_x^D = \rho L\cos \chi \sum\limits_{i = 1}^n {C_x^D(2{\text{π}} g/\omega _i^2){S_{\zeta \zeta }}({\omega _i})\Delta \omega }\text{,} \\ & F_y^D = \rho L\sin \chi \sum\limits_{i = 1}^n {C_y^D(2{\text{π}} g/\omega _i^2){S_{\zeta \zeta }}({\omega _i})\Delta \omega } \text{,}\\ & M_n^D = \rho {L^2}\sin \chi \sum\limits_{i = 1}^n {C_n^D(2{\text{π}} g/\omega _i^2){S_{\zeta \zeta }}({\omega _i})\Delta \omega }\text{。} \end{aligned} \right. $ | (6) |
在图2所示的坐标系下,AUV三自由度低频运动学方程可表示为如下矩阵形式[4]:
| $ { M}\dot { v} + { Dv} = { \tau _t}\text{。} $ | (7) |
式中:
20世纪70年代,Fossen提出非线性PID控制方法,实现了船舶自航控制。至今,PID控制以其算法成熟、结构简单、控制效果好等优点仍然成为工程项目控制系统的主要选择。
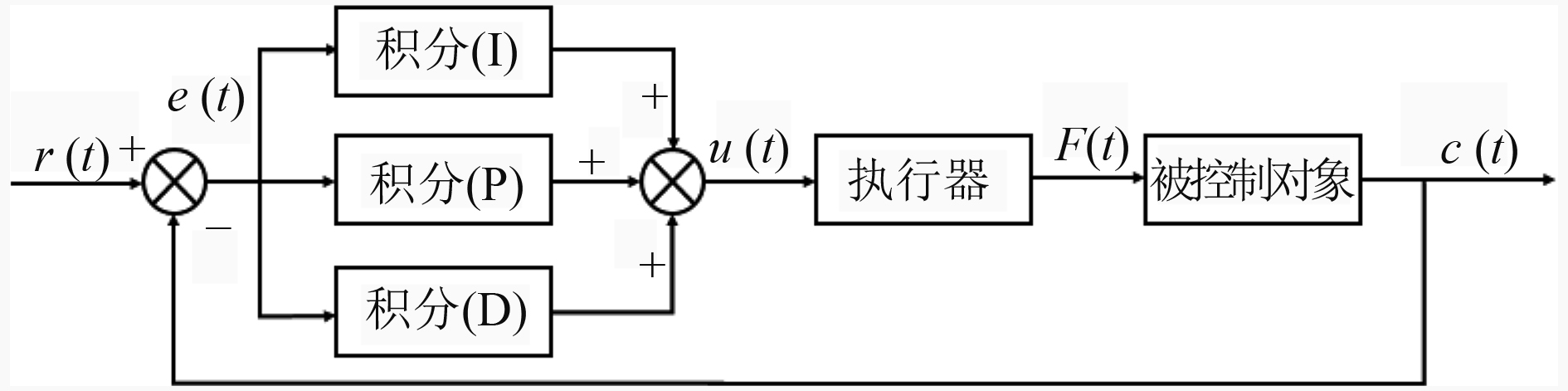
PID控制器以目标设定值与实际测量值的偏差作为输入量,将偏差值的比例(P)、积分(I)和微分(D)分量通过线性组合构成控制量,传递给执行机构,继而作用于控制对象。PID系统原理如图3所示。
|
图 3 PID系统原理图 Fig. 3 Schematic diagram of PID control system |
AUV动力定位系统的PID控制算法如下:
| $ \left\{ \begin{aligned} & u(t) = {K_p}[\varepsilon (t) + \frac{1}{{{T_i}}}\int_0^t {\varepsilon (t){\rm d}t + {T_d}\frac{{{\rm d}\varepsilon (t)}}{{{\rm d}t}}]} \text{,}\\ & \varepsilon (t) = {x_0} - x(t)\text{,}\\ & \dot \varepsilon (t) = - \dot x(t)\text{。} \end{aligned} \right. $ | (8) |
其中:
PID参数的整定与优化是PID控制器设计实现的核心,随着智能控制理论的发展,出现了粒子群算法、遗传算法、神经网络算法等PID参数优化方法。
粒子群算法(PSO)是从鸟群觅食行为特性中获得启发并研究发明的一种数值优化算法。在PSO中,每个优化问题的潜在解都可以看成是搜索空间区域上的一个点,称之为粒子,每个粒子都有一个被目标函数所决定的适应值,依据全局和个体适应值的最优值,修正更新每个粒子的飞行速度和飞行方向,直至搜寻到空间区域内以目标函数为导向的最优解。
d维空间上的第i个粒子的位置信息记为
每次迭代过程中,依据粒子本身的位置速度信息和2个极值的大小对粒子的搜索速度和位置进行修正,具体更新公式如下:
| $ \left\{ \begin{aligned} & V_i^{n + 1} = wV_i^n + {c_1} \cdot rand() \cdot (P_{ibest}^n - X_i^n) + \\ & {\rm{ }}{c_2} \cdot rand() \cdot (g_{best}^n - X_i^n)\text{,}\\ & X_i^{n + 1} = X_i^n + rV_i^{n + 1}\text{。} \end{aligned} \right. $ | (9) |
其中:w为惯性权重;c1为粒子跟踪自己最优值的权重系数,称之为“认知”,通常设置为2;w2为粒子跟踪全局最优值的权重系数,称之为“社会”,通常设置为2;
选用PSO算法对PID参数进行优化,用三维空间中的粒子表示PID的3个参数
| $ J = \int_0^{ + \infty } {t\left| {e(t)} \right|{\rm d}t} \text{。} $ | (10) |
在三维空间域内搜寻使得ITAE函数获得最小值的粒子参数值,作为优化后的PID参数,并与常规PID控制方法进行仿真比对。
2 仿真结果与分析以小型民用AUV产品为研究对象,主要参数如表1所示。基于ITTC双参数波浪谱和Daidola漂移力公式,在Matlab/Simulink中模拟AUV水环境,探究不施加作用力时,AUV的漂移运动情况。具体水况分布如表2所示。
|
|
表 1 AUV主参数 Tab.1 Principal parameters of AUV |
|
|
表 2 水况分布 Tab.2 Water condition for calculation |
AUV初始位置向量为

|
图 4 随机波浪波高时变曲线 Fig. 4 Wave height time-varying curve of random waves |
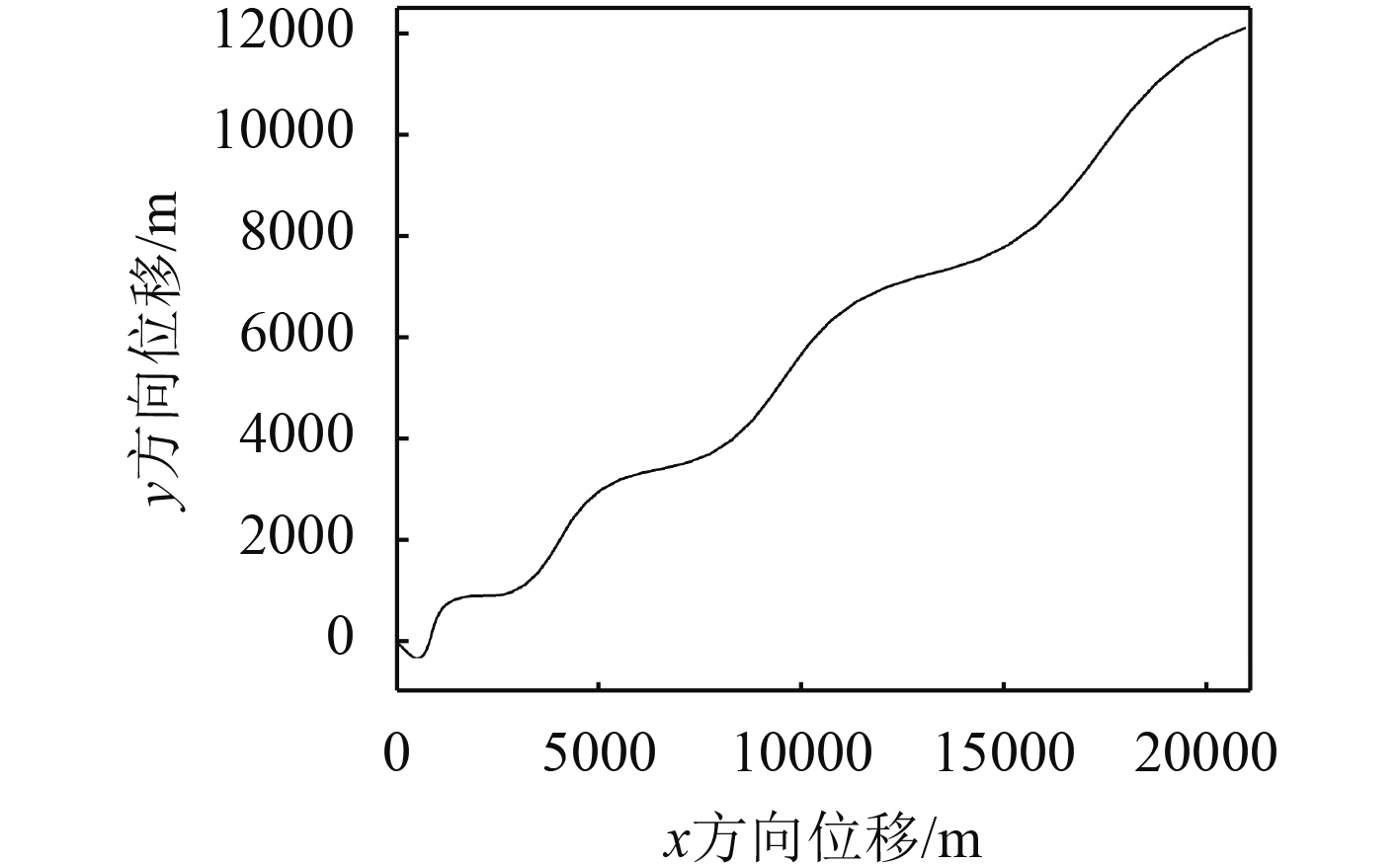
|
图 5 模拟波浪作用下的X–Y运动轨迹图 Fig. 5 X–Y moving trace with the effect of simulated wave |
在Simulink中搭建PSO优化模型,设置粒子规模为100,最大迭代步数为1 000,惯性权重从1.0随步数增长逐渐递减至0.1。优化后的PID参数如下:KP=
在Simulink中搭建基于PID控制器的动力定位控制系统,依据经验选取一组常规PID控制参数:KP=
|
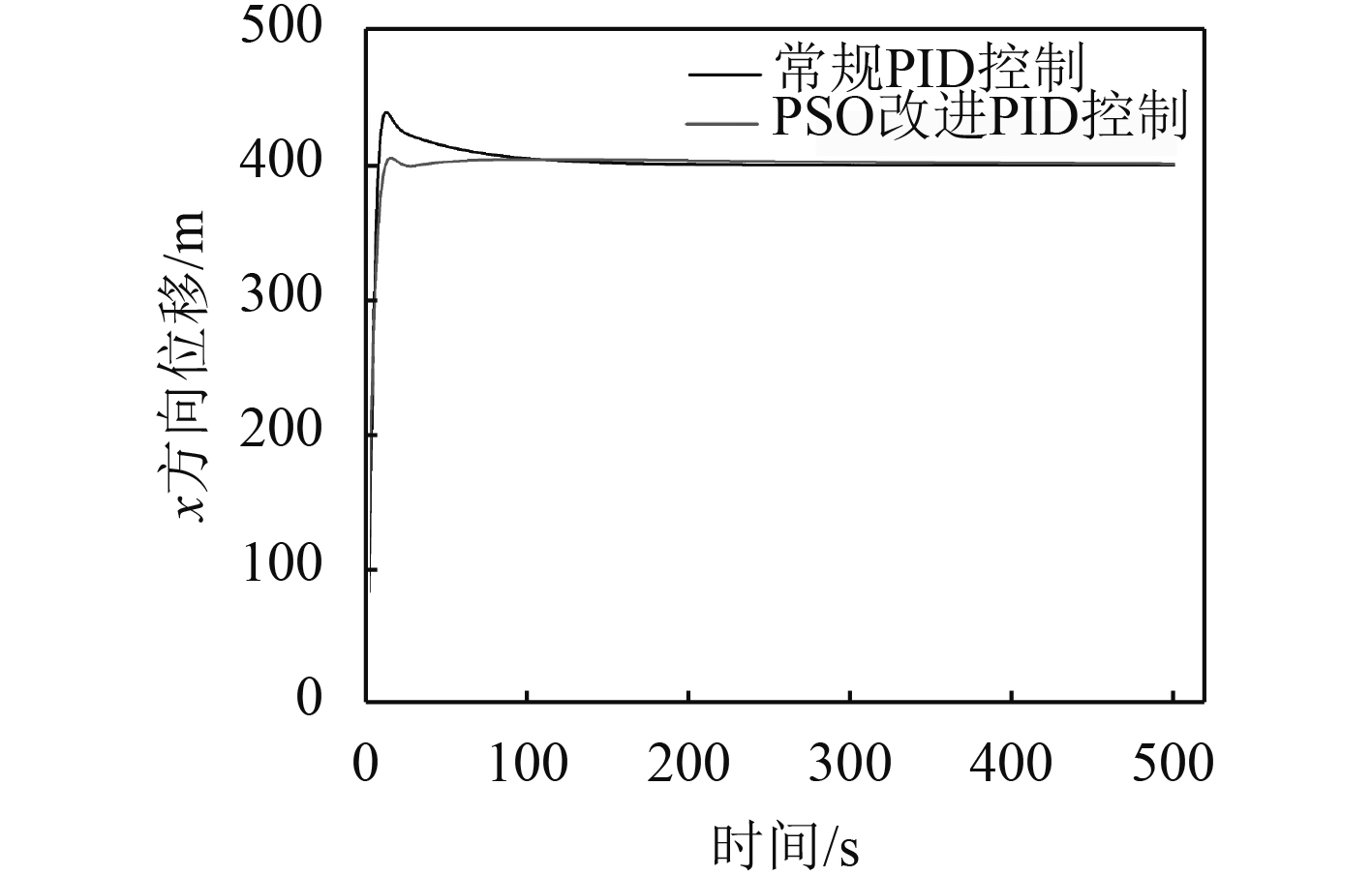
图 6 PID控制下的横向位移–时间变化曲线 Fig. 6 Horizontal displacement curve with PID controller |

|
图 7 PID控制下的纵向位移–时间变化曲线 Fig. 7 Vertical displacement curve with PID controller |
|
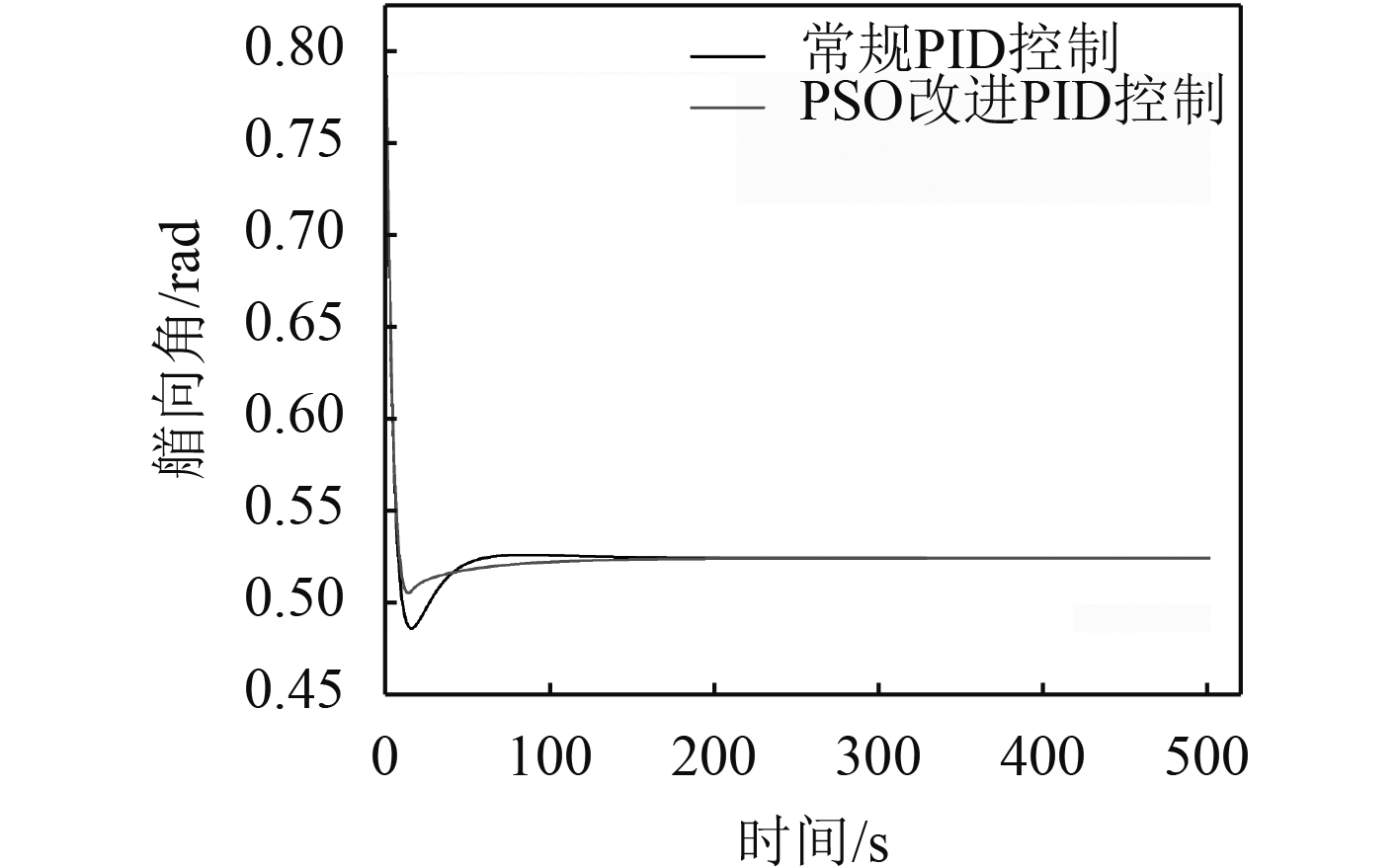
图 8 PID控制下的首向角–时间变化曲线 Fig. 8 Heading angle curve with PID controller |
|
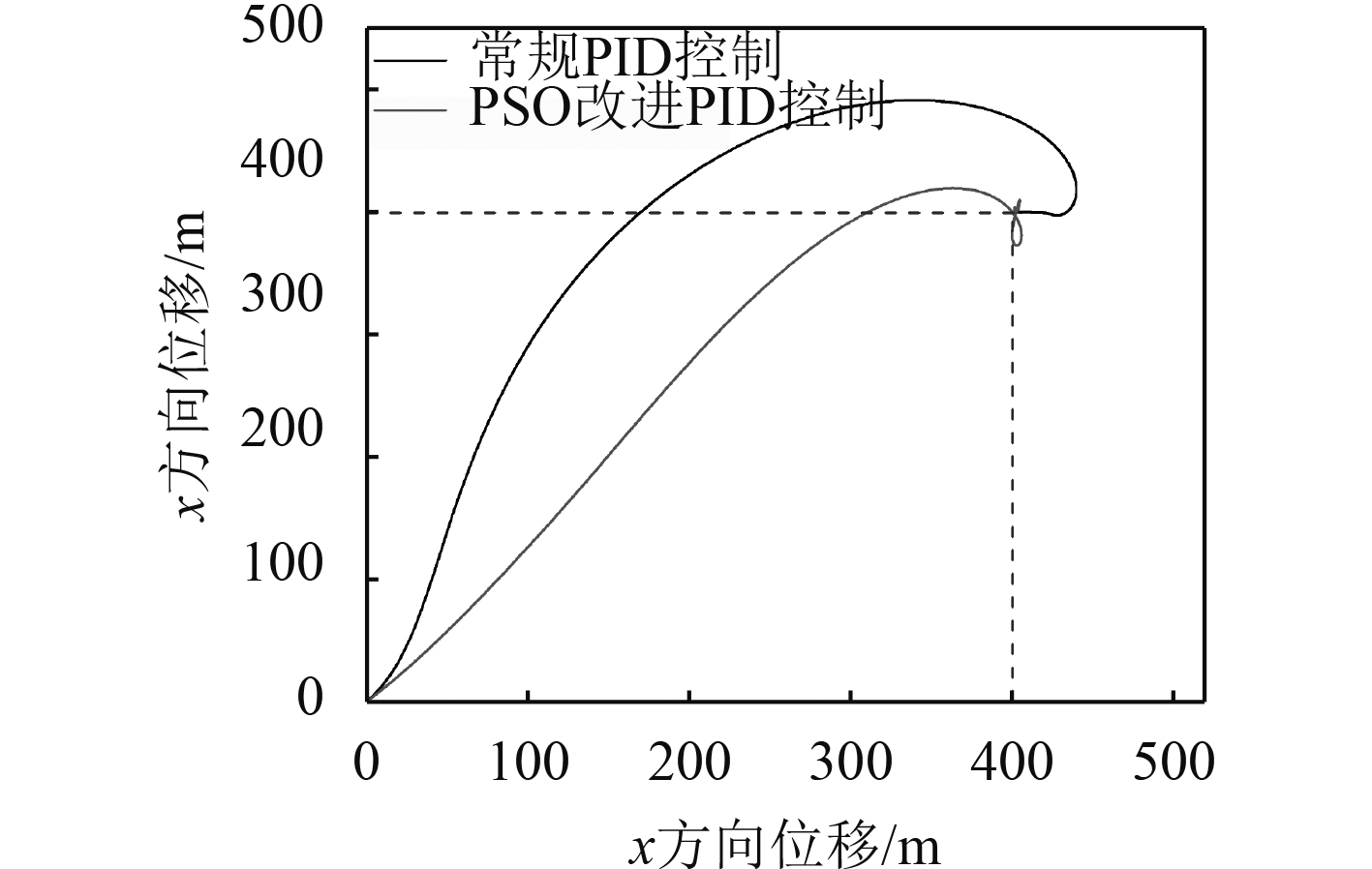
图 9 PID控制下的X–Y 运动轨迹图 Fig. 9 X–Y moving trace with PID controller |
2组PID控制下,AUV均由定位原点抵达目标位置。常规PID控制下,系统经历约100 s的调整达到稳定,同时超调量达到约20%,控制效果较差;经PSO优化后的PID控制器,系统约40 s后快速达到目标位置状态附近进行微调,整体超调量约5%,控制性能较常规PID控制得到大幅优化。
3 结 语AUV在军用项目的成功推动了将其向小型民用产品方向推广的设想,用以实现例如湖底景色拍摄、水产养殖巡视、内陆河水文信息采集等诸多功能。小型AUV产品设计的核心问题有水动力性能分析、路径规划、水下通信等。本文基于不规则随机长峰波浪理论,模拟小型AUV作业的水环境,获取AUV的慢漂运动规律,并基于PID控制器搭建动力定位控制仿真系统,利用粒子群算法(PSO)优化PID参数,实现AUV的定位控制,获取了较好的控制性能。为AUV水动力性能试验及动力定位系统的软硬件设计创造了条件,为小型AUV产品的设计实现奠定基础。
| [1] |
徐海祥, 冯辉. 船舶动力定位系统原理[M]. 北京:国防工业出版社, 2016:15–17.
|
| [2] |
钱小斌, 尹勇, 张秀凤, 等. 海上不规则波浪扰动对船舶运动的影响[J]. 交通运输工程学报, 2016, 16(3): 116-124. DOI:10.3969/j.issn.1671-1637.2016.03.014 |
| [3] |
魏泽, 赵战华, 刘家瑞. 二阶波浪力数值计算与试验方法研究[J]. 船舶力学, 2017(z1): 251-257. DOI:10.3969/j.issn.1007-7294.2017.z1.032 |
| [4] |
梁海军, 闫超. 环境干扰力作用下船舶操纵运动仿真数学模型研究[J]. 舰船科学技术, 2015, 37(7): 153-156. DOI:10.3404/j.issn.1672-7649.2015.07.035 |
 2019, Vol. 41
2019, Vol. 41
