2. 河南省水下智能装备重点实验室,河南 郑州 450015;
3. 江苏科技大学 能源与动力工程学院,江苏 镇江 212003
2. The Underwater Intelligent Equipment Laboratory of Henan Province, Zhengzhou 450015, China;
3. School of Energy and Power Engineering, Jiangsu University of Science and Technology, Zhenjiang 212003, China
大型回转负载可用于舰艇、航天、陆上等各领域的载体发射试验,并从军用领域向民用领域逐渐延伸。在各领域的发射装置和动力系统投入使用前,均需要经过多次的陆上弹射试验来模拟发射过程,以便对其各项性能指标进行验证。大型回转载体作为陆上弹射试验中的发射主体,为验证发射装置主要关键技术和总体方案的可行性,考核主要性能指标提供了必备条件。本文根据舰艇负载的陆上弹射试验为参考,对其发射后的受力情况进行分析,研究其可供重复使用的性能。
回转负载发射出筒后,飞行一段距离,然后跌落至预定区域。与水下发射工况相比较,回转负载陆上发射后跌落的落地区由液态水变为固态的地面,所受的冲击力会大幅提高,因此其结构强度也将受到极大的考验。影响到回转负载跌落强度的主要因素,除结构本身的材质外,还与其结构方式、落地区材质、发射角度等相关。因此,为了研究大型回转负载能否适应陆上发射的极端工况,找到最优的结构方案,在设计时需要建立仿真模型,对回转负载的跌落情况进行分析计算。
本文利用MSC.Dytran软件,通过对大型回转负载进行流固耦合数值仿真计算的方法,研究负载结构和发射姿态等对其跌落时的关键部位强度、整体应力和应变等的影响。取得保证回转负载主体结构不发生损坏、主体可重复使用的最优化结构,进而降低试验和制造成本、缩短研制工期。
1 跌落工况及结构简介在发射试验中,回转负载以一定的角度和速度发射出筒后,在空中飞行一段距离,然后落入落地区。由于回转负载没有姿态调整功能,并且其速度快,质量大,发射出筒后空气对其姿态影响可忽略不计,因此跌落瞬间的角度与发射时基本相同,而后负载将整体倾倒至着陆区。
回转负载的结构简图如图1所示。

|
图 1 回转负载结构简图 Fig. 1 Schematic diagram of rotating load structure |
如图,回转负载主体段内部分布了若干周向及轴向加强筋以增加负载强度,头段与主体段、主体段与头段之间均使用螺栓+法兰连接。回转负载主体段空腔内进行注水配重,以使其整体质量达到规定值。
为了对回转负载跌落时进行缓冲,减小负载损伤,落地区可选用具有一定缓冲作用的材质,例如橡胶或松散的沙土。由于回转负载跌落时的巨大冲击力,会导致落地区地面出现极大损坏,橡胶材质的地面修复耗时过长,且成本较大,因此落地区的材料选用松散的沙土。
2 有限元基本理论 2.1 土力学基本理论根据土力学有关理论,并考虑软件所提供的模型,本文使用可压垮泡沫材料模型计算。回转负载跌落冲击,要考虑土壤的弹性性能、体积压缩性能以及其特殊的屈服特性[1]。土壤材料的体积模量、屈服参数A2对最大加速度和冲击脉宽影响较大;土壤屈服参数A0,A1对最大加速度、冲击脉宽的影响较小,各参数的交互效应不明显[2]。
通过强夯法可以计算出返回舱着陆冲击过程中对土壤的影响深度:
| $ {{D}} = {{a}}\sqrt {{{MH}}} \text{。} $ | (1) |
式中:D为影响深度;a为与土质有关的系数,一般在0.42~0.8之间;M为落体的质量;H为落体自由下落的高度。
通过计算,土壤模型厚度D为2 m。
可压垮泡沫模型中的相关参数可以利用Drucker-Prager模型进行求解,其表达式为:
| $ \sqrt {{{{J}}_2}} + {{a}}{{{I}}_1} - {{k}} = 0\text{,} $ | (2) |
| $ {{{I}}_1} = - 3{{p}}\text{,} $ | (3) |
| $ {{a}} = \frac{{\sin {\rm{\varphi }}}}{{\sqrt 3 \sqrt {3 + {\rm{si}}{{\rm{n}}^2}{\rm{\varphi }}} }}\text{,} $ | (4) |
| ${{k}} = \frac{{\sqrt 3 \cdot {{c}} \cdot \sin {\rm{\varphi }}}}{{\sqrt {3 + {\rm{si}}{{\rm{n}}^2}{\rm{\varphi }}} }}\text{。} $ | (5) |
其中:J2为应力偏量的第二不变量;p为静水压力;
而土壤屈服函数为:
| $ \emptyset = {{{J}}_2} - \left( {{{{a}}_0} + {{{a}}_1}{{p}} + {{{a}}_2}{{{p}}^2}} \right)\text{,} $ | (6) |
因此,在屈服面上,土壤满足下述关系:
| $ {{{J}}_2} = {{{a}}_0} + {{{a}}_1}{{p}} + {{{a}}_2}{{{p}}^2}\text{。} $ | (7) |
由式(2)、式(3)及式(7)可得土壤的3个屈服参数:
| ${{{a}}_0} = {{{k}}^2},\ {{{a}}_1} = 6{{ak}},\ {{{a}}_2} = 9{{{a}}^2} \text{。} $ | (8) |
结构固体域动力学微分方程主要求解固体结构的受力情况,如应力、应变、位移、固有频率等相关参数,根据相关结构固体动力学微分方程[3]:
| $ {{Ma}} + {{Cv}} + {{Ku}} = {{F}}\text{,} $ | (9) |
其中:对流体域和固体域的运动方程进行离散。M为结构的质量矩阵;C为结构的阻尼矩阵;K为结构的刚度矩阵;F为外载荷;a,v,u分别为加速度、速度、位移。
根据式(9)并通过推导得到本结构系统完整的流体–结构耦合离散方程[4 – 5]:
| $ \left( \!\!{\begin{array}{*{20}{l}} \!\!{{{{M}}_{{x}}}}&0\!\!\\ \!\!{{{{M}}^{{{fx}}}}}&{{{{M}}_{{f}}}} \!\!\end{array}} \!\!\!\right)\left(\! \!\!{\begin{array}{*{20}{l}} \!\!{{{\ddot U}}}\!\!\\ \!\!{{{\ddot P}}}\!\! \end{array}}\!\!\! \right) \!\!+\!\! \left(\!\!\! {\begin{array}{*{20}{l}} {{{{C}}_{{x}}}}\!\!&0\!\!\\ \!\!0\!\!&\!\!{{{{C}}_{{f}}}} \!\!\end{array}} \!\!\right)\left( \!\!{\begin{array}{*{20}{l}} \!\!{{{\dot U}}}\!\!\\ \!\!{{{\dot P}}}\!\! \end{array}}\!\!\right) \!\!+\! \!\left(\!\! {\begin{array}{*{20}{l}} \!\!\!{{{{K}}_{{x}}}}\!\!\!&\!\!\!{{{{K}}^{{{fx}}}}}\!\!\\ \!0\!\!&{{K}}\!\!\! \end{array}} \!\!\!\right) \!\!=\!\! \left(\!\!\! {\begin{array}{*{20}{l}} \!\!{{{{F}}_{{x}}}}\!\!\\ \!\!0\!\! \end{array}} \right)\text{。} $ | (10) |
其中:Mfx=ρ0RT;Kfx=–R,R是一个耦合矩阵,该矩阵代表与流体、结构交界面上的节点相联系的有效表面面积以及交界面上的法线节点力的矢量。
由式(10)可知,流体域运动方程和固体域运动方程相互耦合,在进行求解时,可将流体对结构的影响近似以集中质量的形式代替,即附连水质量。在分析整个系统的受力情况时,可先将两者分别求解,将其中一个领域的结果以载荷的形式施加在另一个领域,利用中心差分法往复循环求出整个系统参数[6],以提高结果精度。
3 应力分布仿真计算为了找到合适的加强筋分布方法,首先需要对负载跌落时的应力沿负载壁的分布情况进行摸索。
由于此计算过程主要用于摸索跌落冲击时的应力分布状况,仅为后续的结构优化和分析计算做参考,因此为了减小计算量,先不考虑负载内的注水以及各段间的连接方式。同时由于结构庞大,三维模型计算量太大,因此在应力分布的分析计算过程中采用轴对称建模,只对一个剖面的运动及受力进行分析[7],以减少计算量,节省计算时间,计算模型如图2所示。
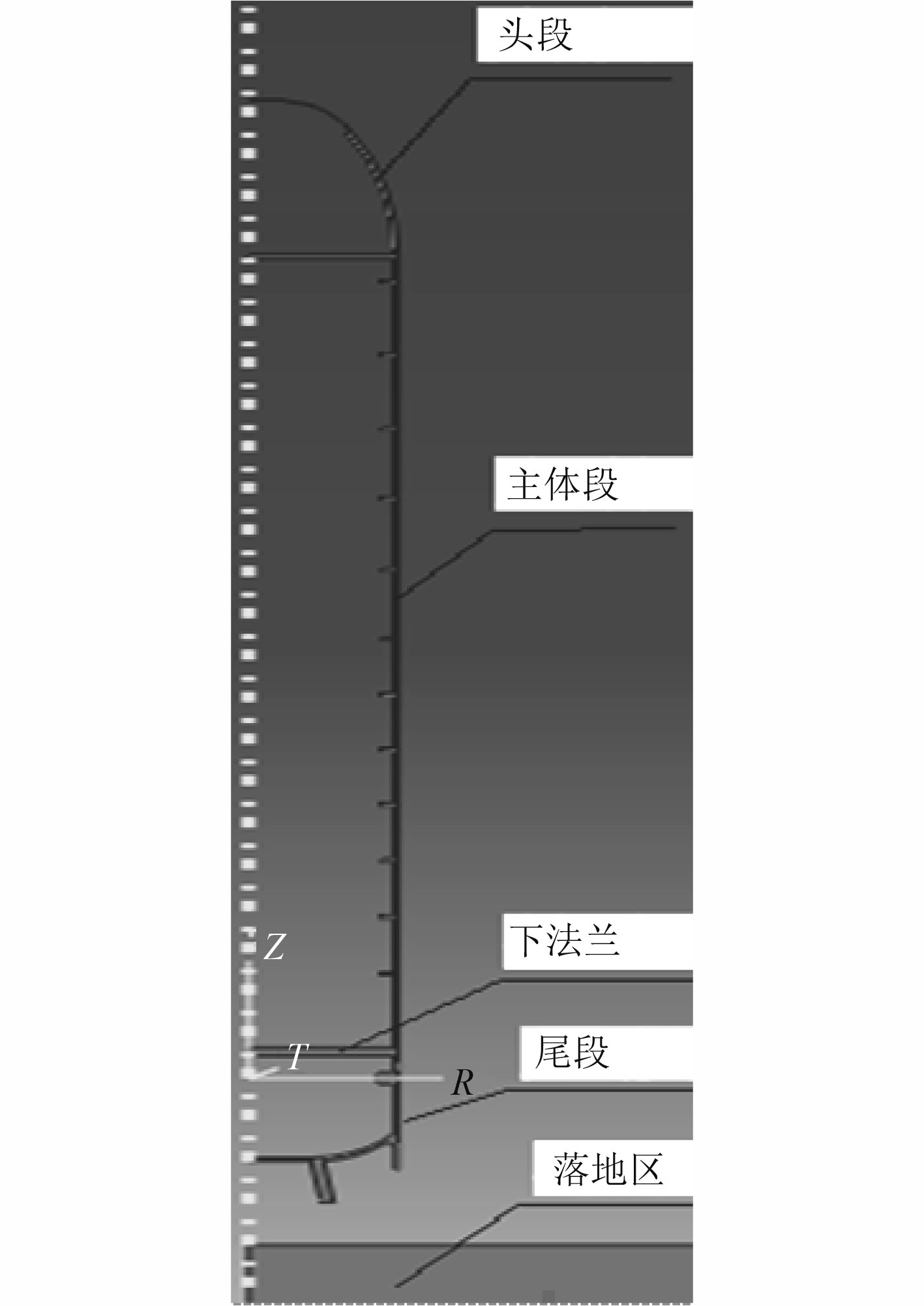
|
图 2 应力分布计算模型 Fig. 2 Stress distribution |
尾段和主体段跌落后的应力分布分别如图3和图4所示。可以看出,跌落后最大应力点出现在尾段,而后沿着负载壁向上,逐渐减小。

|
图 3 尾段应力分布 Fig. 3 Stress distribution at the end |
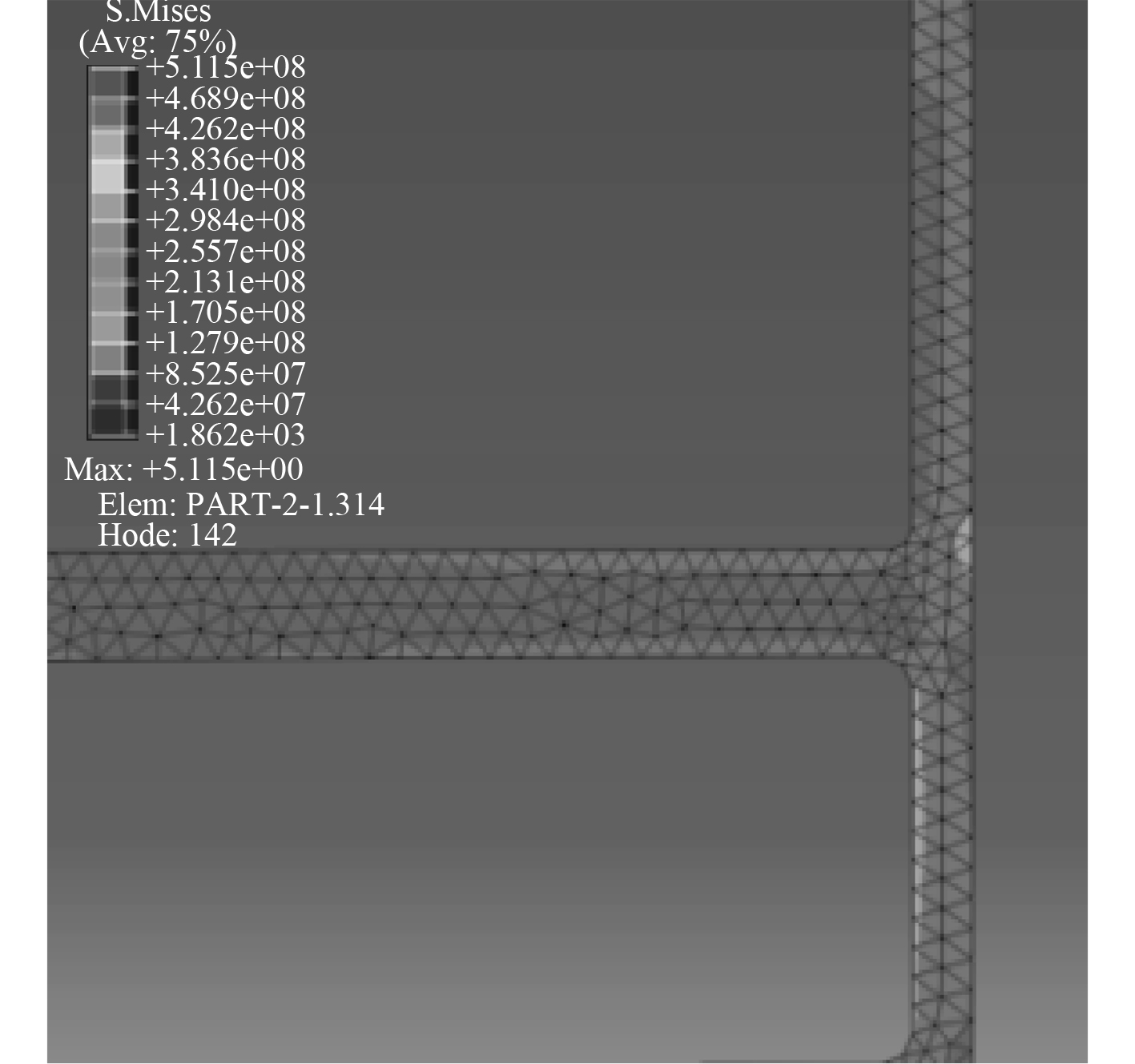
|
图 4 主体段应力分布 Fig. 4 Stress distribution calculation model in the main section |
根据上节的分析结果可知,回转负载跌落后最大应力出现在尾段,而后沿着负载壁向上逐渐减小。
由于回转负载尾段本身的功能要求,无法进行额外加强,并且回转负载需要具备重复使用性能的主要是主体段,因此主要针对保护主体段结构强度进行优化设计。
4.1 结构加强优化设计根据上节所述,回转负载的应力分布沿负载壁自下而上呈逐渐减小的趋势,因此在进行结构加强时,主体段负载壁内的加强筋分布密度也按照自下而上逐渐减小的趋势布置。
但由于主体段最下端负载壁的开孔需求,环筋在该位置的间隔不能太小,因此此处以增加纵筋数量来提高整体加强筋密度,整体加强筋分布趋势如图5所示。
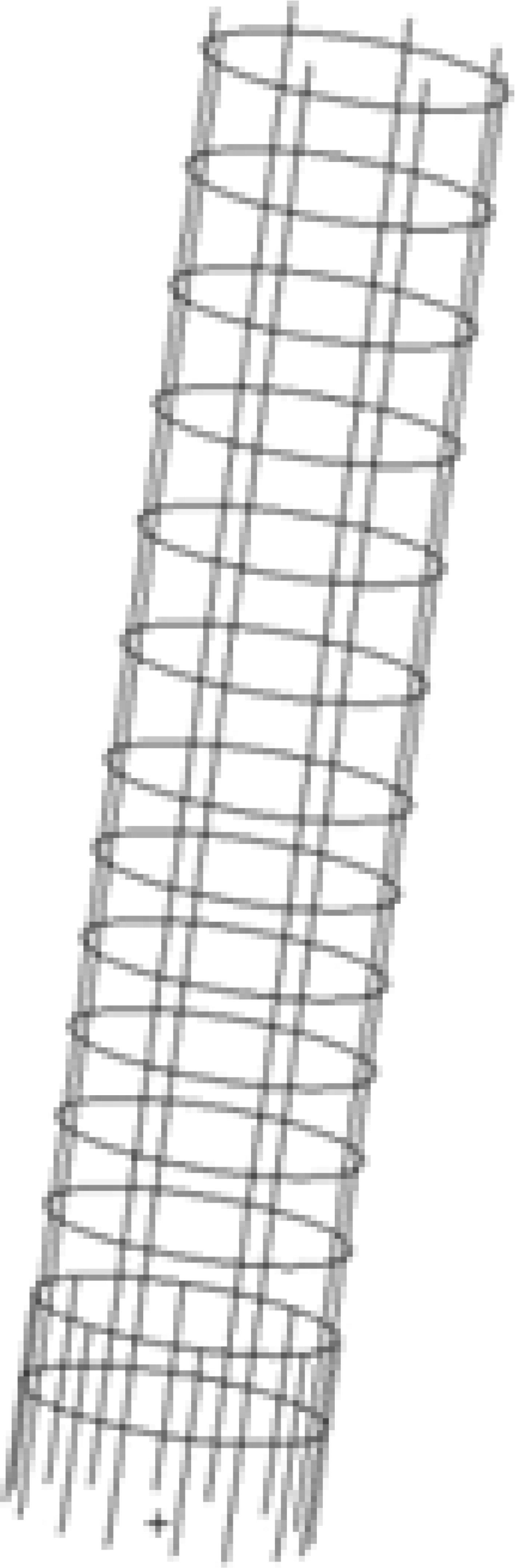
|
图 5 加强筋模型 Fig. 5 Stiffener model |
在靠近主体段的下端,纵筋密度较大,环筋密度较小;而后沿负载壁向上,纵筋密度较之下端减小,环筋密度增大;再次沿负载壁向上,纵筋密度与中间部分相同,但环筋密度减小。整体的加强筋分布密度按照沿负载壁自下而上逐渐减小的趋势布置。
4.2 结构保护优化设计根据回转负载应力分布结果可知,尾段跌落时的应力最大,且无法进行额外加强,因此在结构优化过程中,基于保护主体段的原则,将尾段作为缓冲保护结构,即牺牲尾段,保护主体段。
根据实际发射过程,回转负载将以一定角度以尾部先着地的方式跌落至落地区,而后整个负载倾倒落地。在此过程中,回转负载跌落所受的瞬间冲击力由尾段传递至尾段与主体段连接处,而后传递给主体段。基于牺牲尾段保护主体段的原则,在尾段和主体段的连接方法上,可借助弱连接的方式,即在主体段和尾段的连接螺栓的选择上,可选用满足负载吊装强度,但在受到较大剪切应力时会发生断裂的螺栓。
在上述的弱连接情况下,当回转负载以一定角度跌落至落地区,尾段受到瞬间的剧烈冲击,该力传递至尾段与主体段的连接处时,由于角度的影响,将对连接螺栓产生较大的剪切力,从而使螺栓产生断裂,主体段瞬间倾倒。因此在主体段的整个过程中,因大型回转负载飞行高度而产生的巨大冲击力被大幅消弱,其受力主要为落地后倾倒时与地面的较小冲击力。
5 跌落过程仿真分析 5.1 参数定义1)落地区模型定义
在回转负载的跌落冲击仿真中,建立合理的土壤模型是计算有效的基础。根据前文所述的土力学基本理论,可得负载跌落对土壤的影响深度可达27m,但随着深度的增加土壤变硬,其深度影响可忽略不计,因此计算中取土壤的厚度为5m,上面2m为松软的沙土,下面3m为较硬的土壤。
通过调整不同的参数组合,分析各参数的影响趋势,并与试验数据进行比较,可得土壤模型参数的初始值,如表1所示。
|
|
表 1 土壤模型参数初始值 Tab.1 Initial value of soil model parameter |
2)回转负载模型定义
整个仿真模型主要有模拟负载头部、主段、底座、上法兰、对接法兰上部、对接法兰下部、加强筋、螺栓、水、沙土、滑轨、沙土挡板等部分组成。有限元模型如图6~图8所示。

|
图 6 回转负载有限元模型 Fig. 6 Rotary load finite element model |

|
图 7 法兰及连接螺栓有限元模型 Fig. 7 Finite element model of flange and connecting bolt |

|
图 8 整体有限元模型 Fig. 8 Integral finite element model |
负载外壳、底座和对接法兰下部采用弹塑性壳材料定义,加强筋和螺栓采用弹塑性梁单元定义,材料应力-应变曲线如图9所示。空气选用欧拉实体材料单元,采用理想气体本构模型Ideal Gas。水选用欧拉实体材料单元,采用理想流体本构模型LinFluid。

|
图 9 钢材在模型中的应力-应变曲线 Fig. 9 Stress-strain curve of steel in the model |
在计算中,设置自适应主从接触面,主要包含回转负载–沙土;回转负载–滑轨;对接法兰下部–对接法兰上部。
模拟负载内部的流体与外壳之间应采用ALE耦合。流体采用欧拉网格定义,与耦合面之间网格要求完全一致。流体未充满模拟负载内部,液面距离上部法兰约1 m的距离。
5.2 仿真结果由于弹射角度会对负载的跌落冲击产生一定的影响,因此在仿真计算过程中,分别以不同的角度进行计算,进而获得角度的影响趋势[8]。
1)9°弹射角仿真计算结果
取9°弹射角度,从开始发射直至跌落至落地区时长取10s,当回转负载落地后,其所受冲击的仿真结果如图10和图11所示。

|
图 10 9°弹射角主体段最大应力-时间曲线 Fig. 10 Stress-strain curve of main section of 9° ejection angle |

|
图 11 9°发射角回转负载跌落阶段应力云图 Fig. 11 Stress cloud map of the falling phase of rotary load of 9° ejection angle |
计算结果显示,回转负载跌落瞬间,受力急剧增大。跌落后,结构的损伤变形主要集中在底座和对接法兰下部区域,底座部分区域出现破裂,螺栓断裂,主体段与尾段分离。在整个碰撞冲击过程中,主体段最大应力为193 MPa,最大等效应变为0.004 85,未达到单元失效准则中的应变,即未发生结构破损。
2)6°弹射角仿真计算结果
取6°弹射角度,计算时长与9°时相同,当回转负载落地后,其所受冲击的仿真结果如图12和图13所示。
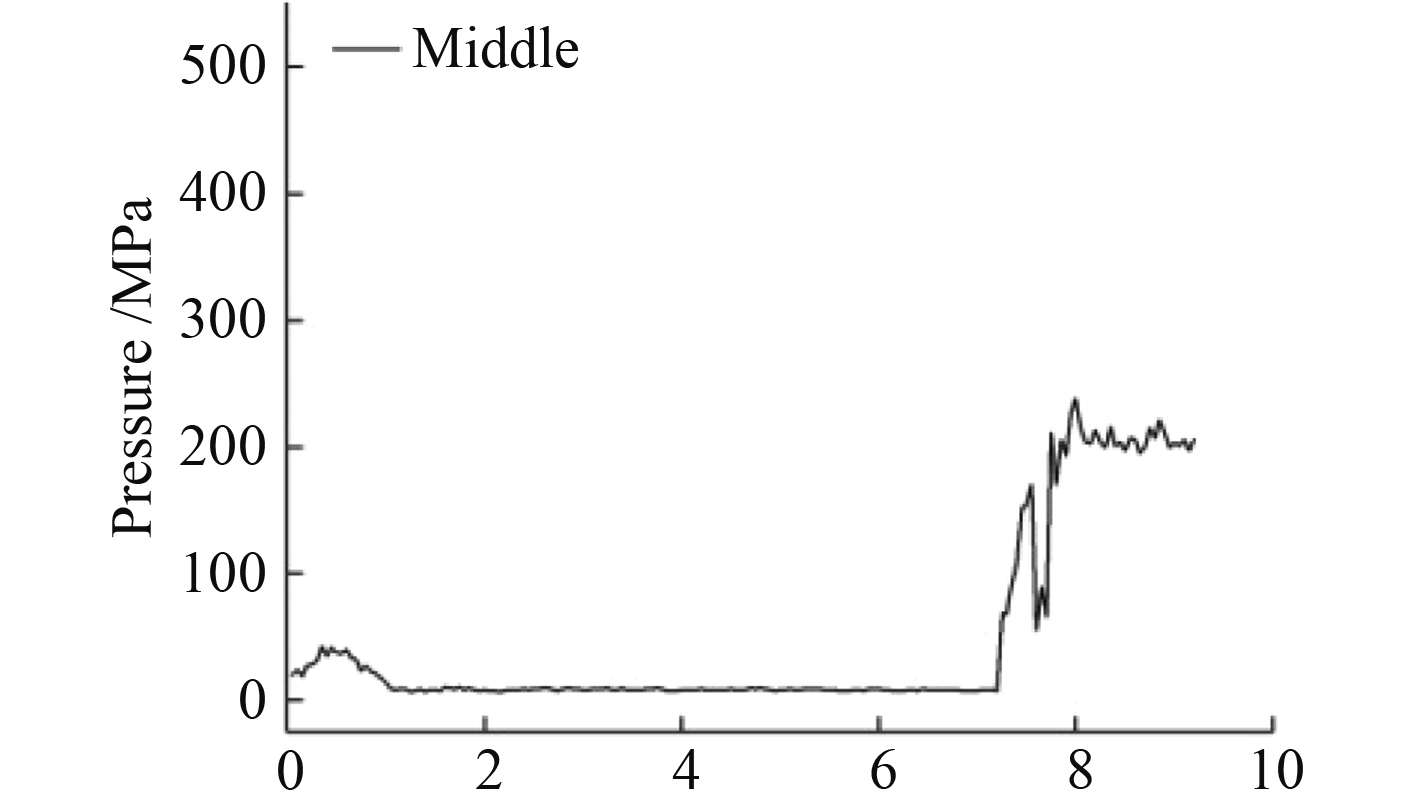
|
图 12 6°弹射角主体段最大应力-时间曲线 Fig. 12 Stress-strain curve of main section of 6° ejection angle |

|
图 13 6°弹射角回转负载跌落阶段应力云图 Fig. 13 Stress cloud map of the falling phase of rotary load of 6° ejection angle |
计算结果显示,回转负载依然是在跌落瞬间受力急剧增大,回转负载跌落后,结构的损伤变形也依然集中在底座和对接法兰下部区域,底座部分区域出现破裂,螺栓断裂,主体段与尾段分离。在整个碰撞冲击过程中,主体段最大应力为227 MPa,最大等效应变为0.009 78,未达到单元失效准则中的应变,即未发生结构破损。
将上述2种弹射工况的计算结果进行对比可以看到,弹射角越小,跌落时所受到的冲击力越大。
2种计算结果均显示,经过结构优化后,在2种工况下,回转负载跌落后均是尾段受力损坏,螺栓断裂,继而主体段分离倾倒,但主体段整体强度在其许用范围内,并未发生结构损坏,与预期的计算结果相符。
6 结 语1)通过初步应力跌落应力分布的估算,对回转负载的结构进行优化设计。
2)通过MSC.Dytran软件建立回转负载接触性模型、高速非线性动力模型和瞬态流固耦合模型。
3)模型的建立和优化设计为陆上弹射试验中,回转负载的可重复使用提供一定指导性作用。
4)经过真实的陆上弹射试验验证,仿真计算分析结果与实际状态相符。
5)通过对仿真分析研究表明:
① 按照应力分布状态,整体加强筋分布密度沿负载壁自下而上逐渐减小的趋势布置,该措施在负载跌落时可有效加强主体段结构强度;
② 借助弱连接的方式,可在回转负载跌落时使主体段整体分离,进而在极大程度上减小主体段的受力;
③ 弹射角度对负载跌落时所受到的冲击力具有一定的影响,发射角越大,受力越小。
| [1] |
王晓姝, 赵会光. 应用土壤修正模型的返回器着陆冲击响应预示[J]. 航天器工程, 2015, 24(3): 45-50. DOI:10.3969/j.issn.1673-8748.2015.03.008 |
| [2] |
张大鹏, 雷永军, 段静波, 等. 土壤参数对返回舱着陆冲击特性的影响分析[J]. 振动与冲击, 2014, 33(7): 120-125. |
| [3] |
张相庭. 结构振动学[M]. 上海: 同济大学出版社, 2005
|
| [4] |
汪玉, 周璞, 刘东岳. 考虑流固耦合作用的舰船抗冲击仿真计算[J]. 振动与冲击, 2005, 24(1): 73-76. DOI:10.3969/j.issn.1000-3835.2005.01.020 |
| [5] |
何涛. 流固耦合数值方法研究概述与浅析[J]. 振动与冲击, 2018, 40(5): 132-136. |
| [6] |
吴绍亮, 金咸定. 流固耦合计算方法在船舶局部结构中的应用[J]. 振动与冲击, 2003, 22(4): 26-28. DOI:10.3969/j.issn.1000-3835.2003.04.008 |
| [7] |
赵腾伦. ABAQUS6. 6在机械工程中的应用[M]. 北京: 中国水利水电出版社, 2007.
|
| [8] |
陈飞宇, 余文辉, 赵世平. 筒口气体射流下航形体出筒流场特性研究[J]. 舰船科学技术, 2018, 40(5): 132-136. DOI:10.3404/j.issn.1672-7649.2018.05.025 |
 2019, Vol. 41
2019, Vol. 41
