潜艇运动为六自由度空间运动,表现出大惯性、强非线性、各运动平面强耦合的复杂特点,通常难以获得精确的数学模型,且用于潜艇控制设计的方程系数会由于环境、水深及潜艇状态等的变化而变化,使系统工作点偏离设计状态,影响控制效果,使控制器的设计难度大大增加。
国内外众多学者基于经典控制理论和现代控制理论设计了潜艇控制器。基于伯德图和根轨迹法设计的控制器设计从频域角度入手,结构简单,容易实现,但对参数摄动和扰动鲁棒性较差,尤其是难以处理复杂非线性问题[1]。针对非线性系统的控制问题,多名学者进行了深入研究[2 – 3],但控制器结构复杂,难以实现。而通过模糊方法设计非线性鲁棒补偿器,一定程度上可以简化控制器的复杂度[4]。近年来,滑模控制(SMC,sliding mode control)对满足匹配条件的任意摄动和外界干扰具有较强鲁棒性,且其算法简单、响应快速、易于工程实现,受到广泛关注[5 – 10]。传统的滑模控制方法采用极点配置法、最优控制等方法设计线性切换函数,利用基于边界层方法的准滑模控制降低抖振,设计潜艇垂直面准滑模控制器。潜艇垂直面操纵运动为双输入双输出过程,深度控制通道与纵倾控制通道相互耦合,且耦合程度由潜艇的艇型与升降舵的配置密切相关,因此针对此类双入双出的多变量系统,一般可相对增益分析法分析其各回路的耦合程度[11],再进行解耦处理[12],在弱耦合和确保鲁棒性的情况下可忽略耦合[13 – 14]。不同机动情况下,潜艇水动力差异巨大,对控制模型的设计和控制器的鲁棒性提出较高要求。文献[15]采用线性化模型研究了潜艇大攻角下的滑模控制,起到了较好的控制效果。同时在不增加模型复杂度的情况下也可结合模糊控制等方法设计滑模控制器以降低抖振[16 – 17]。
基于以上考虑,为了使控制器模型简便且确保控制系统的鲁棒性,本文采用潜艇垂直面线性设计模型,基于双幂次趋近律设计了一个滑模控制器。为了估计系统不可测量的状态,引入了Luenberger状态观测器。将该控制器与经典PID控制器进行仿真对比,并应用于有部分参数摄动及有外界干扰情况下的垂直面控制。
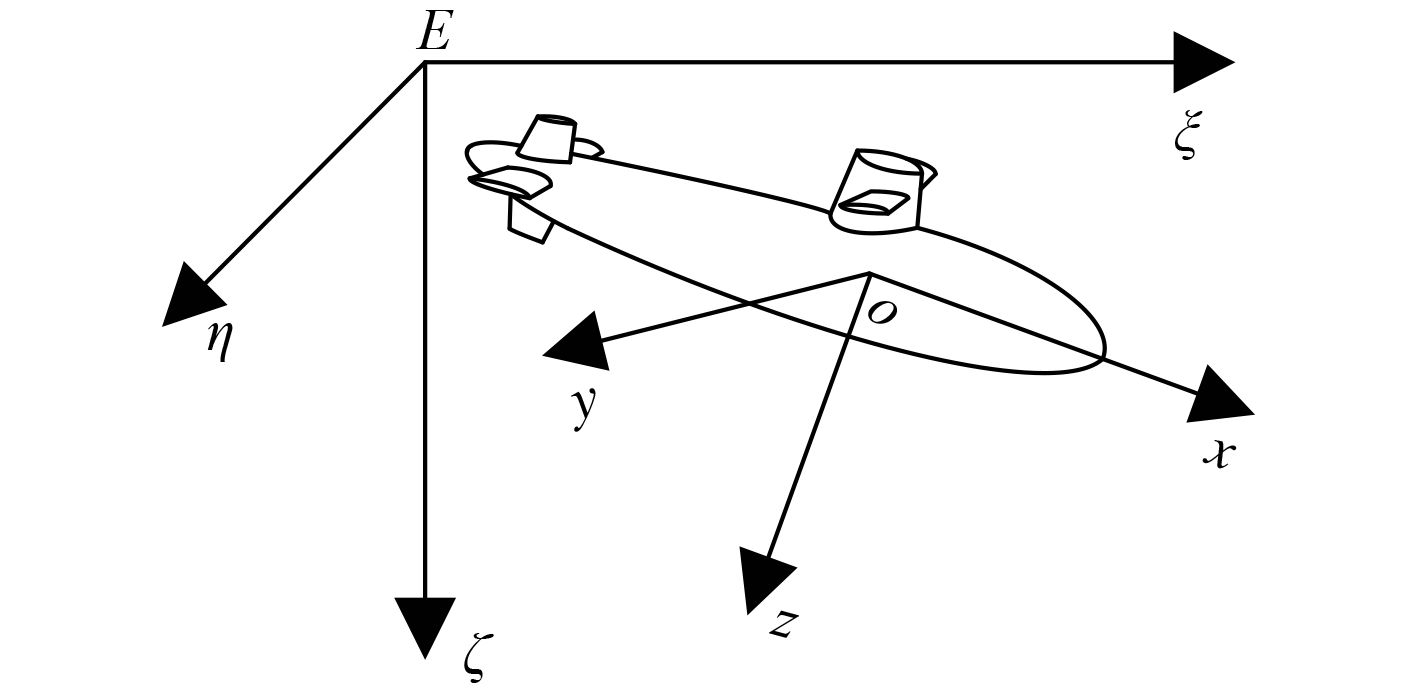
1 潜艇垂直面运动模型坐标系、名词术语、符号规则均采用ITTC和SNAME术语公报的体系[18 – 19]。固定坐标系(定系)E-ξηζ和运动坐标系(动系)O-xyz如图1所示。
|
图 1 固定坐标系和运动坐标系 Fig. 1 Fixed coordinate system and the motion coordinate system |
潜艇垂直面非线性操纵运动模型由潜艇标准运动方程简化得到[20]:
1)纵向方程
| $ \begin{split} &m\left( {\dot u - vr + wq} \right) = \\ &\frac{1}{2}\rho {L^4}\left( {X_{qq}'{q^2} + X_{rr}'{r^2} + X_{rp}'rp} \right) + \\ & \frac{1}{2}\rho {L^3}\left( {X_{\dot u}'\dot u + X_{vr}'vr + X_{wq}'wq} \right) + \\ &\frac{1}{2}\rho {L^2}\left( {X_{uu}'{u^2} + X_{vv}'{v^2} + X_{ww}'{w^2}} \right) + \\ &\frac{1}{2}\rho {L^2}{u^2}\left( {X_{{\delta _r}{\delta _r}}'\delta _r^2 + X_{{\delta _b}{\delta _b}}'\delta _b^2 + X_{{\delta _s}{\delta _s}}'\delta _s^2} \right) + \\ &\frac{1}{2}\rho {L^2}\left( {{a_T}{u^2} + {b_T}u{u_c} + {c_T}u_c^2} \right){\text{。}} \end{split} $ | (1) |
2)垂向方程
| $ \begin{split} &m\left( {\dot w - uq + vp} \right) = \\ &\frac{1}{2}\rho {L^4}\left( {Z_{\dot q}'\dot q + Z_{rr}'{r^2} + Z_{rp}'rp} \right) + \\ &\frac{1}{2}\rho {L^3}\left[ {Z_{\dot w}'\dot w + Z_{vr}'vr + Z_{vp}'vp + Z_{\left| q \right|{\delta _s}}'u\left| q \right|{\delta _s}} \right] + \\ &\frac{1}{2}\rho {L^3}\left[ {Z_q'uq + Z_{w\left| q \right|}'\frac{w}{{\left| w \right|}}\left| {{{\left( {{v^2} + {w^2}} \right)}^{{1 / 2}}}} \right|\left| q \right|} \right] + \\ &\frac{1}{2}\rho {L^2}\left[ {Z_0'{u^2} + Z_w'uw + Z_{vv}'{v^2} + Z_{w\left| w \right|}'w\left| {{{\left( {{v^2} + {w^2}} \right)}^{{1 / 2}}}} \right|} \right] + \\ & \frac{1}{2}\rho {L^2}\left( {Z_{{\delta _b}}'{u^2}{\delta _b} + Z_{{\delta _s}}'{u^2}{\delta _s}} \right){\text{。}} \end{split} $ | (2) |
3)纵倾方程
| $ \begin{split} & {I_y}\dot q + \left( {{I_x} - {I_z}} \right)rp = \\ & \frac{1}{2}\rho {L^5}\left( {M_{\dot q}'\dot q + M_{rr}'{r^2} + M_{rp}'rp} \right) + \\ & \frac{1}{2}\rho {L^4}\left[ {M_q'uq + M_{\left| w \right|q}'\left| {{{\left( {{v^2} + {w^2}} \right)}^{{1 / 2}}}} \right|q} \right] + \\ & \frac{1}{2}\rho {L^4}\left[ {M_{\dot w}'\dot w + M_{vr}'vr + M_{vp}'vp + M_{\left| q \right|{\delta _s}}'u\left| q \right|{\delta _s}} \right] + \\ & \frac{1}{2}\rho {L^3}\left[ {M_0'{u^2} + M_w'uw + M_{w\left| w \right|}'w\left| {{{\left( {{v^2} + {w^2}} \right)}^{{1 / 2}}}} \right| + M_{vv}'{v^2}} \right] + \\ & \frac{1}{2}\rho {L^3}\left( {M_{{\delta _b}}'{u^2}{\delta _b} + M_{{\delta _s}}'{u^2}{\delta _s}} \right) - mgh\sin \theta {\text{,}}\quad \qquad \qquad \;\;\;(3) \end{split} $ |
式中,h为潜艇稳心高。
4)运动方程
| $\left\{ \begin{array}{l} \dot \zeta = w\cos \theta - u\sin \theta {\text{,}}\\ \dot \theta = q{\text{。}} \end{array} \right.$ | (4) |
由于非线性方程不便于控制系统分析,本文作如下假设:1)纵向速度恒定;2)忽略所有非线性项;3)纵倾、横摇很小,
| $\left\{ \begin{array}{l} \dot w = {f_w} + {b_{wb}}{\delta _b} + {b_{ws}}{\delta _s}{\text{,}}\\ \dot q = {f_q} + {b_{qb}}{\delta _b} + {b_{qs}}{\delta _s}{\text{,}}\\ \dot \zeta = - u\theta + w{\text{,}}\\ \dot \theta = q{\text{。}} \end{array} \right.$ | (5) |
式中:
式(9)可进一步写为:
| $\left\{ \begin{gathered} \ddot \zeta = {f_\zeta } + {b_{wb}}{\delta _b} + {b_{ws}}{\delta _s} \hfill {\text{,}}\\ \ddot \theta = {f_\theta } + {b_{qb}}{\delta _b} + {b_{qs}}{\delta _s} \hfill{\text{。}} \\ \end{gathered} \right.$ |
2)舵机模型
首尾舵舵机模型均采用如下模型[13]:
| ${T_E}\dot \delta = {K_E}\left( {{\delta _E} - \delta } \right){\text{。}}$ | (6) |
式中:
首舵
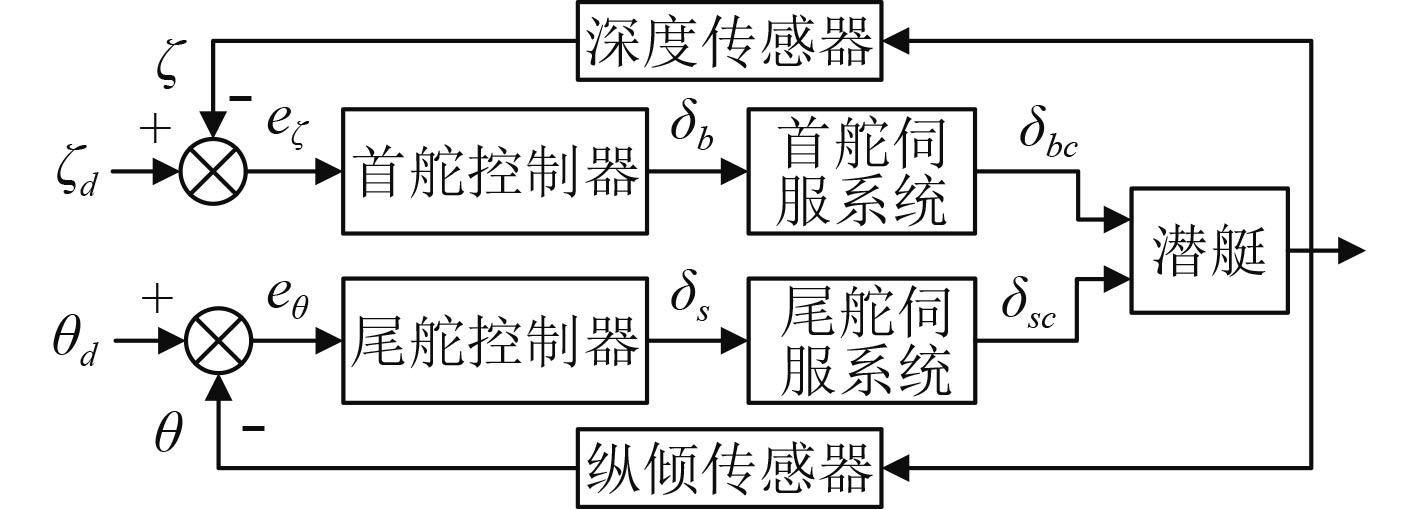
一般潜艇深度自动控制有如下几种模式:1)尾舵自动深度模式,即尾舵单独控制深度和纵倾,指令舵角的解算与深度的偏差和纵倾的偏差均有关,在给定深度变化的同时,纵倾角偏差反馈给尾舵,产生相应舵角以控制纵倾角不超过规定范围;2)首、尾舵联合自动深度模式,即深度和纵倾分别由首舵和尾舵控制。本文综合考虑首舵和尾舵和控制效果,选取第2种模式设计控制器。针对首舵和尾舵控制的耦合,采取策略为:首舵主要控制深度,视尾舵为干扰;尾舵主要控制纵倾,视首舵为干扰。
潜艇垂直面运动分变深机动和定深机动。其中变深步骤为:1)给定纵倾指令
|
图 2 首尾舵联合自动深度控制 Fig. 2 Combined automatic depth control of bow and stern rudder |
深度控制系统,定义深度误差
滑模控制控制由等效控制部分
| $\dot \sigma = \ddot e + k\dot e = 0{\text{,}}$ | (7) |
由式(5)和式(7)可得等效控制:
| $\left\{ \begin{array}{l} {\delta _b} = \displaystyle\frac{1}{{{b_{wb}}}}\left( {{{\ddot \zeta }_d} - {k_\zeta }{{\dot e}_\zeta } - {f_\zeta } - {b_{ws}}{\delta _s}} \right){\text{,}}\\ {\delta _s} = \displaystyle\frac{1}{{{b_{qs}}}}\left( {{{\ddot \theta }_d} - {k_\theta }{{\dot e}_\theta } - {f_\theta } - {b_{qb}}{\delta _b}} \right){\text{。}} \end{array} \right.$ | (8) |
切换控制部分采用准滑模控制[10]:
| ${u_{vss}} = K\operatorname{sgn} \left( \sigma \right){\text{,}}$ | (9) |
式中,
| $\tanh \left( {\mu \sigma } \right) = {{\left( {{e^{\mu \sigma }} - {e^{ - \mu \sigma }}} \right)} / {\left( {{e^{\mu \sigma }} + {e^{ - \mu \sigma }}} \right)}}{\text{,}}$ |
其中μ>0为待定调节系数,其值大小决定了双曲正切函数拐点的变化快慢。总的滑模控制律为:
| $\begin{aligned} & {\delta _b} = \frac{1}{{{b_{wb}}}}\left[ {{{\ddot \zeta }_d} - {k_\zeta }{{\dot e}_\zeta } - {f_\zeta } - {b_{ws}}{\delta _s}} \right] + {K_\zeta }\tanh \left( {{\mu _\zeta }{\sigma _\zeta }} \right){\text{,}}\\ & {\delta _s} = \frac{1}{{{b_{qs}}}}\left[ {{{\ddot \theta }_d} - {k_\theta }{{\dot e}_\theta } - {f_\theta } - {b_{qb}}{\delta _b}} \right] + {K_\theta }\tanh \left( {{\mu _\theta }{\sigma _\theta }} \right){\text{。}} \end{aligned}$ | (10) |
考虑首舵、尾舵动态响应并忽略相互间耦合影响,首、尾舵控制律
| $\left\{ \begin{array}{l} {\delta _{bc}} = {{{T_{E1}}} / {{K_{E1}}{{\dot \delta }_b}}} + {\delta _b}{\text{,}}\\ {\delta _{sc}} = {{{T_{E2}}} / {{K_{E2}}{{\dot \delta }_s}}} + {\delta _s}{\text{。}} \end{array} \right.$ |
滑模运动的稳定性完全取决于滑模参数的选取,滑模的存在性问题转化为式(9)系统的原点镇定问题,选取Lyapunov函数为:
| $ \begin{align} & {V_\zeta } = \frac{1}{2}\sigma _\zeta ^2,\;\;{\sigma _\zeta } \ne 0;\;\;{V_\theta } = \frac{1}{2}\sigma _\theta ^2,\;\;{\sigma _\theta } \ne 0{\text{;}}\\ & {\sigma _\zeta }{{\dot \sigma }_\zeta } = {\sigma _\zeta }\left( {{f_\zeta } + {b_{wb}}{\delta _b} + {b_{ws}}{\delta _s} - {{\ddot \zeta }_d} + {k_\zeta }{{\dot e}_\zeta }} \right){\rm{ = }}\\ & {K_\zeta }{\sigma _\zeta }\tanh \left( {{\mu _\zeta }{\sigma _\zeta }} \right){\text{;}}\\ &{\sigma _\theta }{{\dot \sigma }_\theta } = {\sigma _\theta }\left( {{f_\theta } + {b_{qb}}{\delta _b} + {b_{qs}}{\delta _s} - {{\ddot \theta }_d} + {k_\theta }{{\dot e}_\theta }} \right){\rm{ = }}\\ & {K_\theta }{\sigma _\theta }\tanh \left( {{\mu _\theta }{\sigma _\theta }} \right){\text{。}} \end{align} $ |
只要使滑模参数
为进一步降低抖振,采用双幂次趋近律[22]:
| $\dot \sigma = - \varepsilon {\left| \sigma \right|^\gamma }\tanh \left( {\mu \sigma } \right) - \lambda {\left| \sigma \right|^\chi }\tanh \left( {\mu \sigma } \right){\text{,}}$ | (11) |
式中,
根据滑模可达性,由式(11)可得:
| $\begin{array}{l} \sigma \dot \sigma = \sigma \left[ { - \varepsilon {{\left| \sigma \right|}^\gamma }\tanh \left( {\mu \sigma } \right) - \lambda {{\left| \sigma \right|}^\chi }\tanh \left( {\mu \sigma } \right)} \right]{\rm{ = }}\\ - \varepsilon {\left| \sigma \right|^{1 + \gamma }} - \lambda {\left| \sigma \right|^{1 + \chi }} < 0{\text{。}} \end{array}$ |
滑动态可在有限时间内趋于平衡零点。适当增大参数
当系统存在不确定性有界干扰时,状态
结合式(5)、式(7)和式(9)可得控制律:
| $ \!\!\!\!\!\begin{aligned} & {\delta _b} \!=\! \displaystyle\frac{1}{{{b_{wb}}}}\left[\!\!\!\!\! \begin{array}{l} {{\ddot \zeta }_d} - {k_\zeta }{{\dot e}_\zeta } \!-\! {f_\zeta } \!-\! {b_{ws}}{\delta _s} \!-\! \\ {\varepsilon _\zeta }{\left| {{\sigma _\zeta }} \right|^{{\gamma _{_\zeta }}}}\!\tanh \left( {{\mu _\zeta }{\sigma _\zeta }} \right) \!-\! {\lambda _\zeta }{\left| {{\sigma _\zeta }} \right|^{{\chi _{_\zeta }}}}\!\tanh \left( {{\mu _\zeta }{\sigma _\zeta }} \right) \end{array} \!\!\!\!\!\right]{\text{,}}\\ & {\delta _s} \!=\! \displaystyle\frac{1}{{{b_{qs}}}}\left[\!\!\!\!\! \begin{array}{l} {{\ddot \theta }_d} - {k_\theta }{{\dot e}_\theta } \!-\! {f_\theta } - {b_{qb}}{\delta _b} \!-\! \\ {\varepsilon _\theta }{\left| {{\sigma _\theta }} \right|^{{\gamma _{_\theta }}}}\!\tanh \left( {{\mu _\theta }{\sigma _\theta }} \right) \!-\! {\lambda _\theta }{\left| {{\sigma _\theta }} \right|^{{\chi _{_\theta }}}}\tanh \left( {{\mu _\theta }{\sigma _\theta }} \right) \end{array}\!\!\!\!\!\right]{\text{。}} \end{aligned} $ | (12) |
选取Lyapunov函数为:
| $ \begin{aligned} & {V_\zeta } = \frac{1}{2}\sigma _\zeta ^2,\;\;{\sigma _\zeta } \ne 0;\;\;{V_\theta } = \frac{1}{2}\sigma _\theta ^2,\;\;{\sigma _\theta } \ne 0{\text{;}}\\ & {\sigma _\zeta }{{\dot \sigma }_\zeta } = {\sigma _\zeta }\left( {{f_\zeta } + {b_{wb}}{\delta _b} + {b_{ws}}{\delta _s} - {{\ddot \zeta }_d} + {k_\zeta }{{\dot e}_\zeta }} \right){\rm{ = }}\\ & {\sigma _\zeta }\left[ { - {\varepsilon _\zeta }{{\left| {{\sigma _\zeta }} \right|}^{{\gamma _{_\zeta }}}}\tanh \left( {{\mu _\zeta }{\sigma _\zeta }} \right) - {\lambda _\zeta }{{\left| {{\sigma _\zeta }} \right|}^{{\chi _{_\zeta }}}}\tanh \left( {{\mu _\zeta }{\sigma _\zeta }} \right)} \right] < 0{\text{;}}\\ & {\sigma _\theta }{{\dot \sigma }_\theta } = \left( {{f_\theta } + {b_{qb}}{\delta _b} + {b_{qs}}{\delta _s} - {{\ddot \theta }_d} + {k_\theta }{{\dot e}_\theta }} \right){\rm{ = }}\\ & {\sigma _\theta }\left[ { - {\varepsilon _\theta }{{\left| {{\sigma _\theta }} \right|}^{{\gamma _{_\theta }}}}\tanh \left( {{\mu _\theta }{\sigma _\theta }} \right) - {\lambda _\theta }{{\left| {{\sigma _\theta }} \right|}^{{\chi _{_\theta }}}}\tanh \left( {{\mu _\zeta }{\sigma _\zeta }} \right)} \right] < 0{\text{。}} \end{aligned} $ |
该控制律满足全局渐近稳定性条件。
3 Luenberger状态观测器设计| $\left\{ \begin{array}{l} \dot X = AX + BU + DF{\text{,}}\\ Y = CX{\text{。}} \end{array} \right.$ | (13) |
式中:
| $ \hat X = \left( {A - LC} \right)\hat X + BU + LY{\text{,}}$ | (14) |
式中,
引入状态观测器后,滑模控制为:
| $ \begin{align} & {\delta _b} = \displaystyle\frac{1}{{{b_{wb}}}}\left[ \begin{array}{l} {{\ddot \zeta }_d} - {k_\zeta }{{\dot {\hat e}}_\zeta } - {{\hat f}_\zeta } - {b_{ws}}{\delta _s} - \\ {\varepsilon _\zeta }{\left| {{{\hat \sigma }_\zeta }} \right|^{{\gamma _{_\zeta }}}}\tanh \left( {{\mu _\zeta }{{\hat \sigma }_\zeta }} \right) - {\lambda _\zeta }{\left| {{{\hat \sigma }_\zeta }} \right|^{{\chi _{_\zeta }}}}\tanh \left( {{\mu _\zeta }{{\hat \sigma }_\zeta }} \right) \end{array} \right]{\text{,}}\\ & {\delta _s} = \displaystyle\frac{1}{{{b_{qs}}}}\left[ \begin{array}{l} {{\ddot \theta }_d} - {k_\theta }{{\dot {\hat e}}_\theta } - {{\hat f}_\theta } - {b_{qb}}{\delta _b} - \\ {\varepsilon _\theta }{\left| {{{\hat \sigma }_\theta }} \right|^{{\gamma _{_\theta }}}}\tanh \left( {{\mu _\theta }{{\hat \sigma }_\theta }} \right) - {\lambda _\theta }{\left| {{{\hat \sigma }_\theta }} \right|^{{\chi _{_\theta }}}}\tanh \left( {{\mu _\theta }{{\hat \sigma }_\theta }} \right) \end{array} \right]{\text{。}} \end{align} $ | (15) |
选取Lyapunov函数为:
| $ \begin{array}{l} {V_\zeta } = \frac{1}{2}\hat \sigma _\zeta ^2,\;\;{{\hat \sigma }_\zeta } \ne 0;\;\;{V_\theta } = \frac{1}{2}\hat \sigma _\theta ^2,\;\;{{\hat \sigma }_\theta } \ne 0 {\text{;}}\\ {{\hat \sigma }_\zeta }{{\dot {\hat \sigma} }_\zeta } = {{\hat \sigma }_\zeta }\left[ - {\varepsilon _\zeta }{{\left| {{{\hat \sigma }_\zeta }} \right|}^{{\gamma _{_\zeta }}}}\tanh \left( {{\mu _\zeta }{{\hat \sigma }_\zeta }} \right)\right.- \\ \quad \left. {\lambda _\zeta }{{\left| {{{\hat \sigma }_\zeta }} \right|}^{{\chi _{_\zeta }}}}\tanh \left( {{\mu _\zeta }{{\hat \sigma }_\zeta }} \right) \right] < 0 {\text{;}}\\ {{\hat \sigma }_\theta }{{\dot {\hat \sigma} }_\theta } = {{\hat \sigma }_\theta }\left[ - {\varepsilon _\theta }{{\left| {{{\hat \sigma }_\theta }} \right|}^{{\gamma _{_\theta }}}}\tanh \left( {{\mu _\theta }{{\hat \sigma }_\theta }} \right) \right. -\\ \quad \left. {\lambda _\theta }{{\left| {{{\hat \sigma }_\theta }} \right|}^{{\chi _{_\theta }}}}\tanh \left( {{\mu _\theta }{{\hat \sigma }_\theta }} \right) \right] < 0{\text{。}} \end{array} $ |
该控制律满足全局渐近稳定性条件。
4 仿真为验证控制器的正确性,针对潜艇定深和变深运动控制进行仿真和分析。潜艇仿真方程为完整的非线性运动方程。采用文献[1]的潜艇参数。控制器设计参数为:
潜艇初始航速
分3种情况将SMC的控制效果和经典PID控制器的控制效果对比仿真。
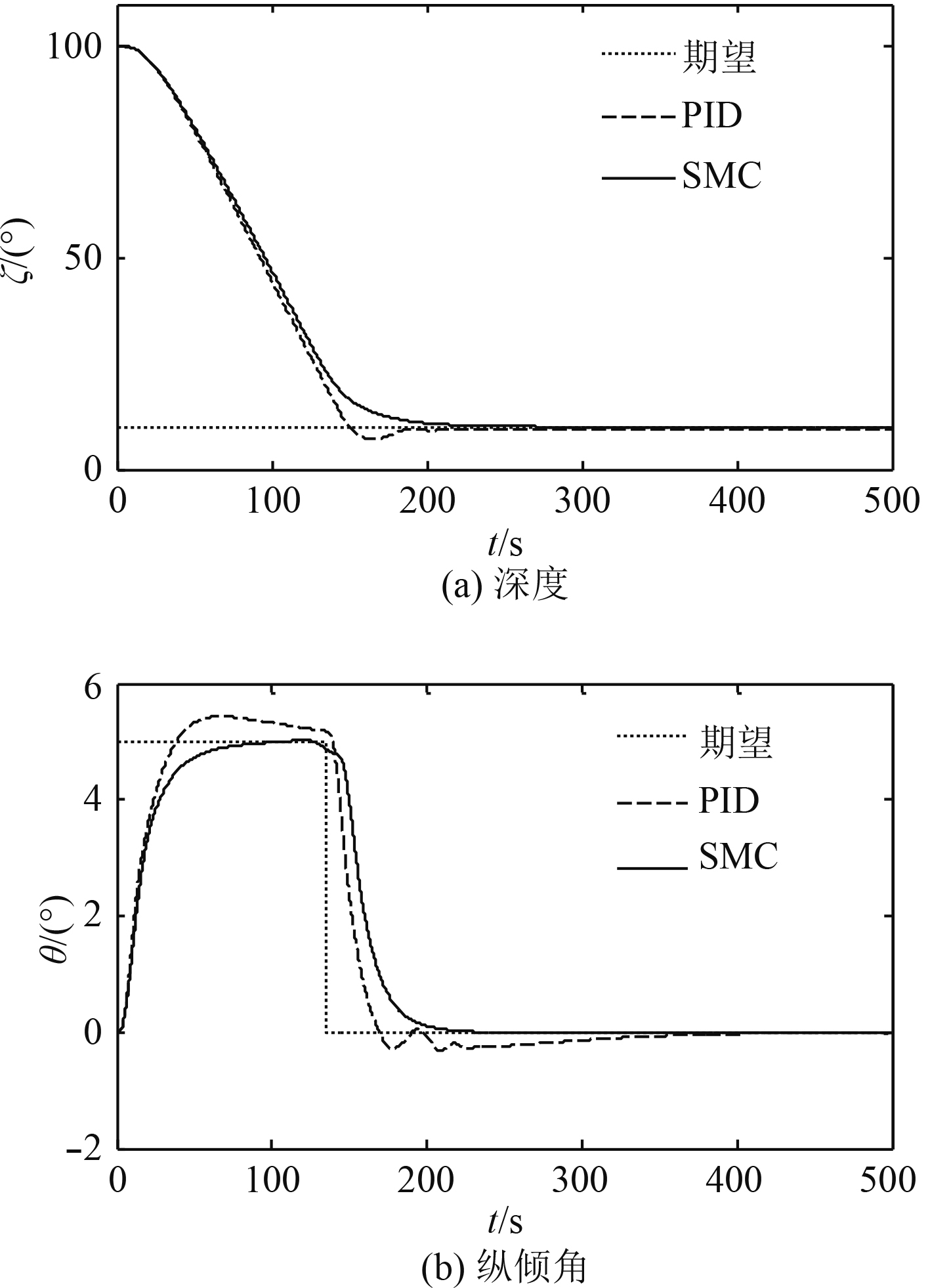
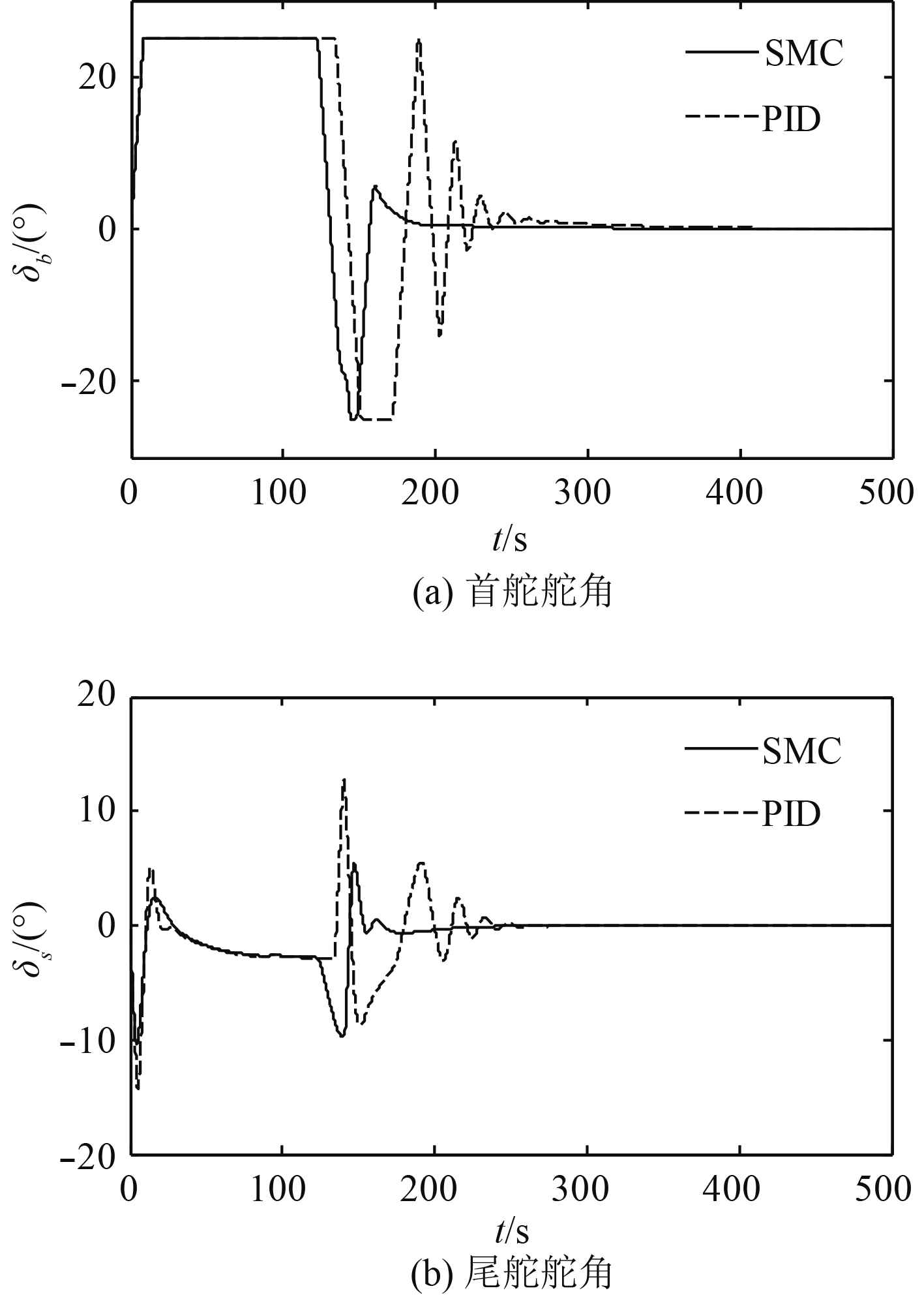
1)当潜艇参数无摄动和无外界扰动时,图3和图4分别给出了深度、纵倾响应曲线与舵角曲线。由图可见,SMC比PID控制使深度能更快速无超调趋近指令深度,达到指令深度后沿期望深度稳定航行,纵倾符合限制条件。滑模控制首、尾舵打舵比PID控制更为平滑。
|
图 3 潜艇参数无摄动时的深度和纵倾响应 Fig. 3 Depth and pitch response without parameterperturbations of submarine |
|
图 4 潜艇参数无摄动时的舵角 Fig. 4 Rudder angle without parameter perturbations of submarine |
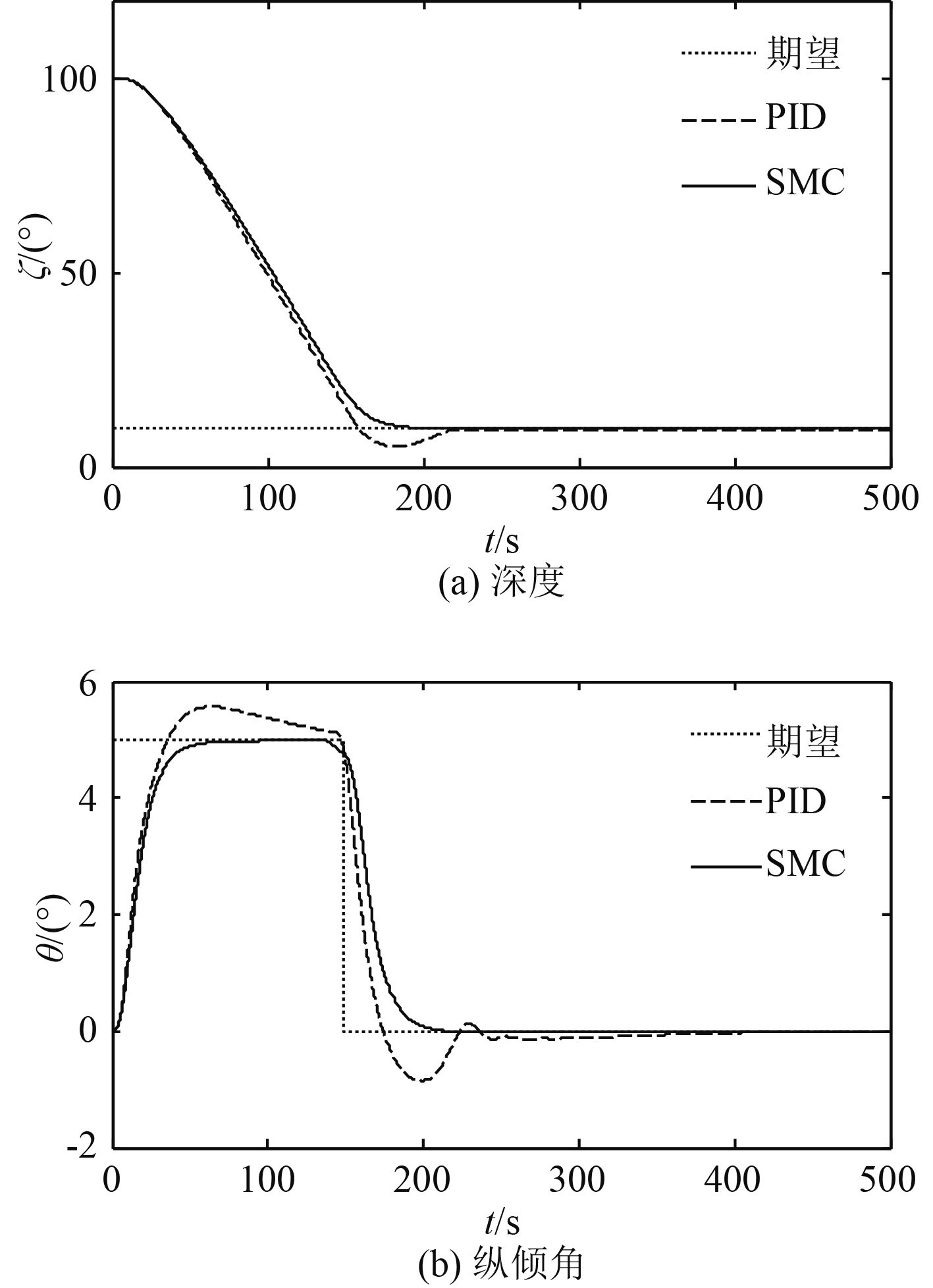
2)系统部分参数摄动但无外界扰动。由于控制性能主要受垂向方程和纵倾方程有关参数影响,由式(9)知,
|
图 5 潜艇参数摄动时的深度和纵倾响应 Fig. 5 Depth and pitch response with parameterperturbations of submarine |
|
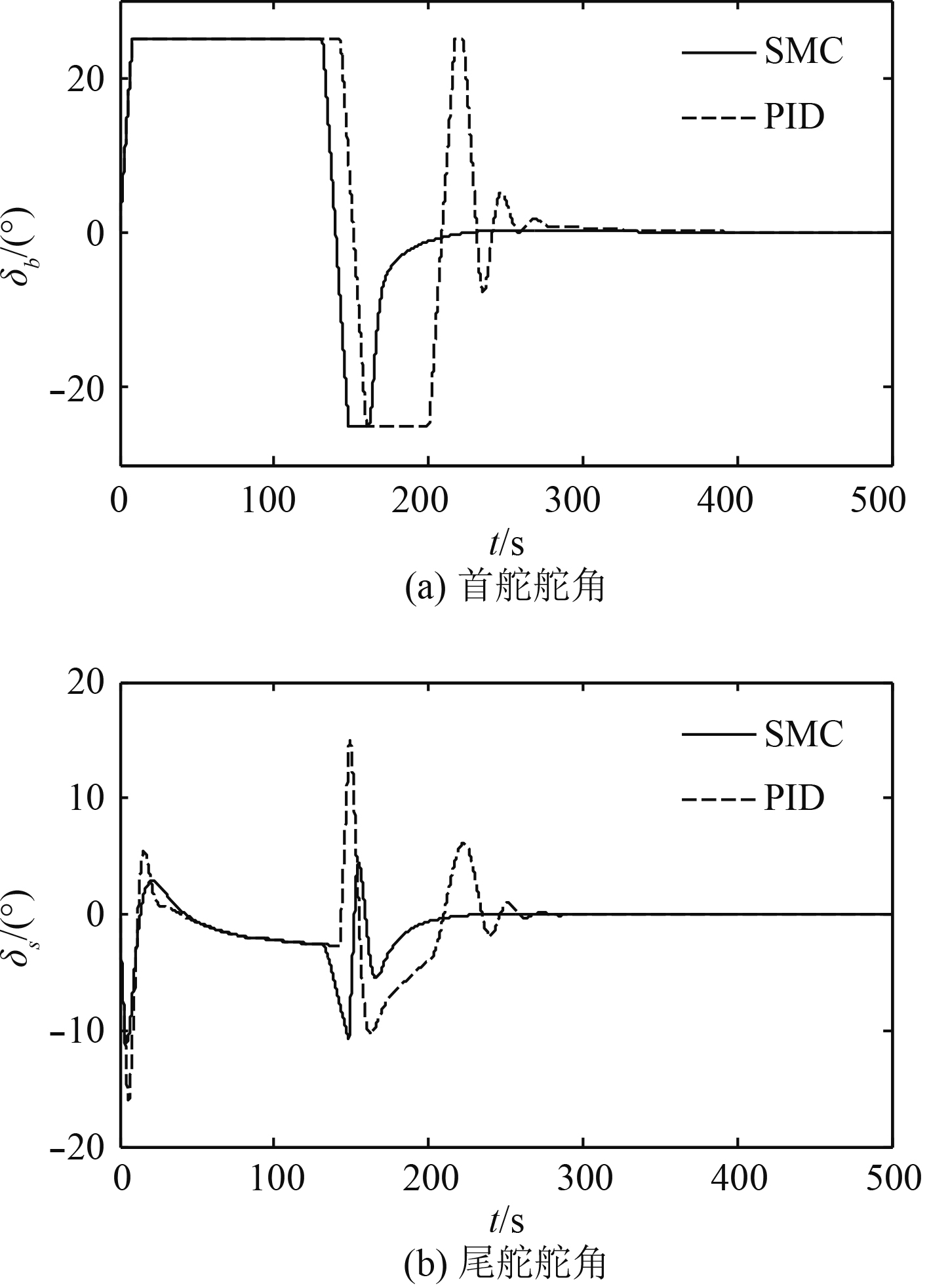
图 6 潜艇参数摄动时的舵角 Fig. 6 Rudder angle with parameter perturbations of submarine |
3)当无摄动但有外界扰动时,为便于分析,任意选取正弦扰动信号:
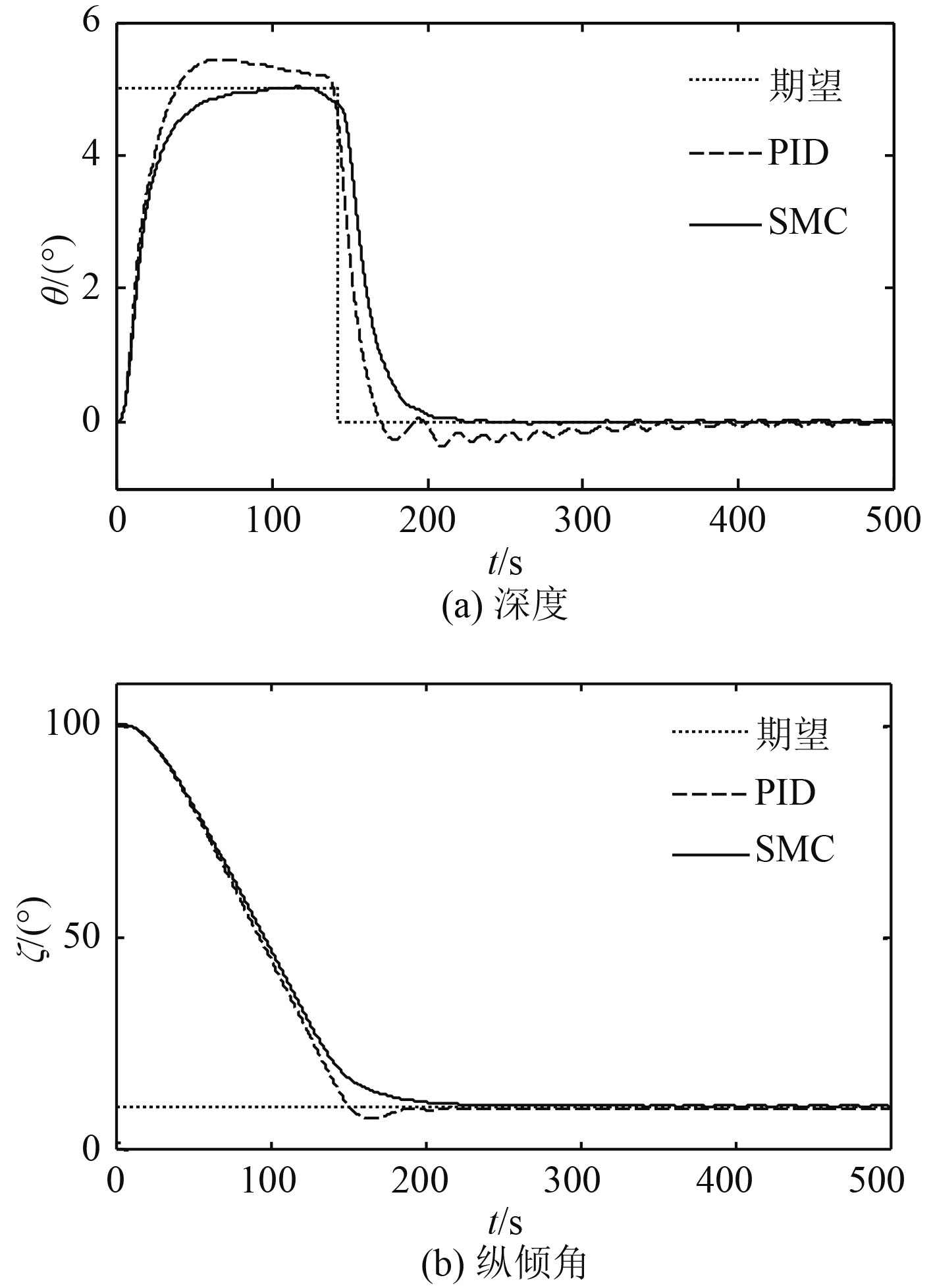
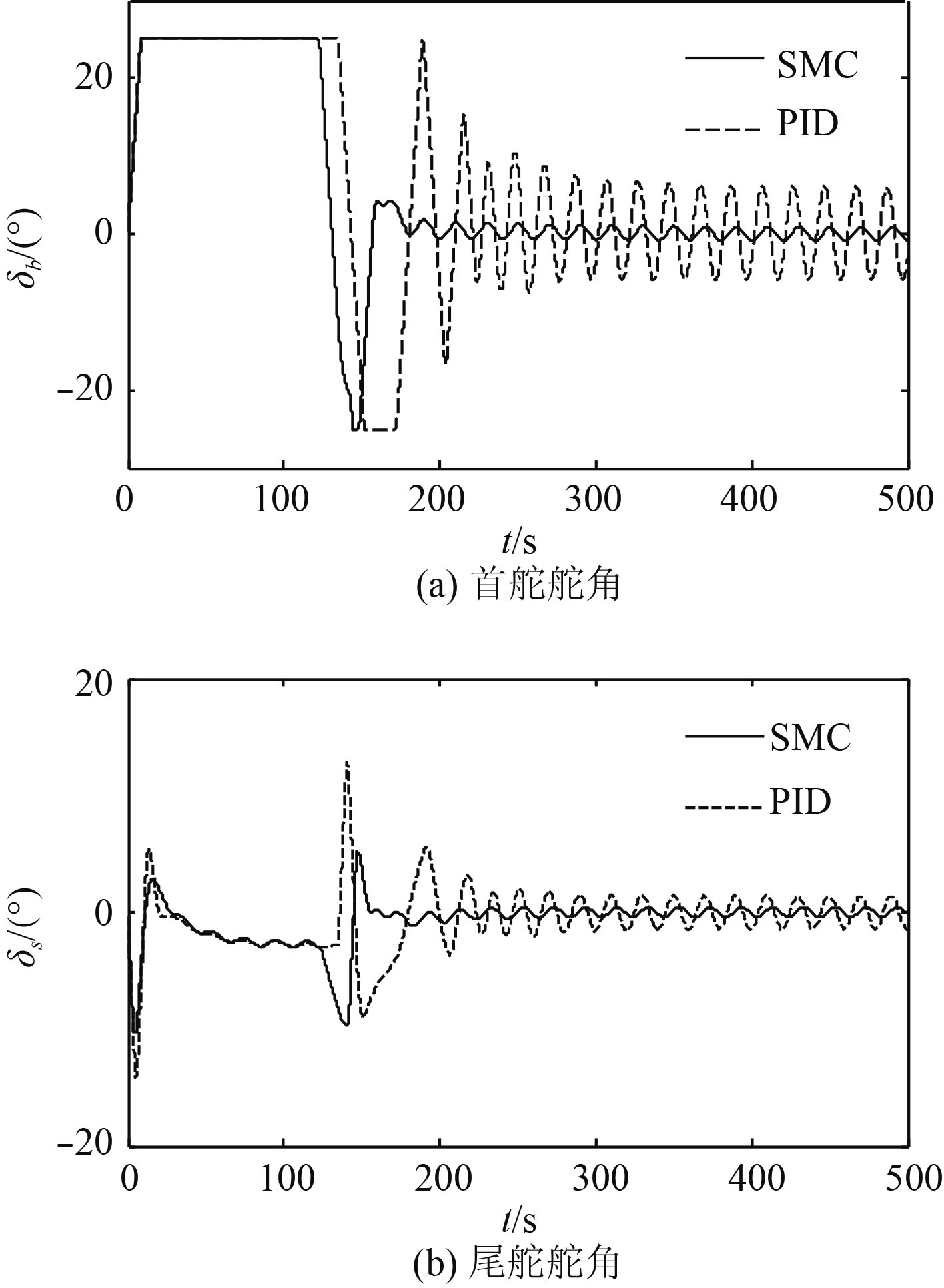
控制参数及初始条件不变。图7和图8分别给出了深度、纵倾响应曲线与舵角曲线。由图可见,SMC比PID控制使深度能更快速无超调趋近指令深度。滑模控制打舵次数与幅度明显小于PID控制,且收敛更快速。经测试,当外界扰动力量级小于
|
图 7 正弦干扰下的深度和纵倾响应 Fig. 7 Depth and pitch response of sinusoidal interference |
|
图 8 正弦干扰下的的舵角 Fig. 8 Rudder angle under sinusoidal interference |
表1分别给出了3种情况下,在SMC和PID控制下的潜艇深度和纵倾的超调量、稳态误差,SMC的控制效果均优于传统的PID控制效果。
|
|
表 1 SMC与PID控制效果对比 Tab.1 Comparison of control effect between SMC and PID |
本文基于潜艇垂直面线性模型,忽略首尾舵之间的耦合,采用首舵控制深度,尾舵控制纵倾的策略,采用新型趋近律设计滑模控制器。仿真结果表明,在参数无摄动和有摄动及有无外界干扰情况下滑模控制器控制效果均优于PID控制器,且无明显抖振,为了确保系统的稳定性,对控制器参数的整定优化应做进一步研究,因此可采用垂直面线性模型设计垂直面滑模控制器,从而既降低了控制器复杂度,又提高了控制器的鲁棒性,对工程应用及研究具有重要意义。
| [1] |
BABAOGLU, ORHAN K. Design an automatic control system for a submarine[R]. AD A-203925, 1988.
|
| [2] |
HWANG, C. Design of robust controllers for manipulators[J]. J. National Cheng-Kung University, Sci. Eng. and Med. Section, 1991, 26: 213-234. |
| [3] |
HEALEY A. Multivariable sliding mode control for autonomous diving and steering of unmanned underwater vehicles[J]. IEEE J. Oceanic Engin., 1993, 18(3): 327-339. DOI:10.1109/JOE.1993.236372 |
| [4] |
HWANG Cheng-neng, YANG Joe- ming. Design of fuzzy nonlinear robust compensator and its application on submarines[J]. Journal of Marine Science and Technology, 2003, 11(2): 83-95. |
| [5] |
SONG F, SMITH S M. A comparison of sliding mode fuzzy controller and fuzzy sliding mode controller[C]// Fuzzy Information Processing Society, 2000. N A FIP S. 19th International Conference of the North American. 2000: 480–484.
|
| [6] |
NAI O L, CHRISTOPHER E, SARAHK S. On output tracking using dynamic output feedback discrete-time sliding-mode controllers[J]. IEEE Transactions on Automatic Control, 2007, 52(10): 1975-1981. DOI:10.1109/TAC.2007.904256 |
| [7] |
CORRADINI M L, LEO T, ORLANDO G. Experinental testing of a discrete-time sliding mode controller for trajectory tracking of a wheeled mobile robot in the presence of skidding effects[J]. Journal of Robotic Systems, 2002, 19(4): 177-189. DOI:10.1002/(ISSN)1097-4563 |
| [8] |
KEUM W. Noncertainty-equ-ivalenmulti-variable adaptive control of submersibles using filtered signals[J]. Ocean Engineering, 2012, 53(7): 98-110. |
| [9] |
NAI O L, CHRISTOPHER E, SARAHK S. On output tracking using dynamic output feedback discrete-time sliding-mode controllers[J]. IEEE Transactions on Automatic Control, 2007, 52(10): 1975-1981. DOI:10.1109/TAC.2007.904256 |
| [10] |
牟军, 许汉珍. 潜艇操纵运动的变结构控制[J]. 华中理工大学学报, 1997, 25(6): 33-37. |
| [11] |
BRISTOL E H. On a new measure of interactions for multivariable process control[J]. IEEE Trans on Automatica Control, 1966, 11(1): 133-134. DOI:10.1109/TAC.1966.1098266 |
| [12] |
罗凯, 李俊, 许汉珍. 潜艇近水面运动的解耦控制[J]. 海洋工程, 1999, 17(3): 27-32. DOI:10.3969/j.issn.1005-9865.1999.03.004 |
| [13] |
夏极, 胡大斌. 潜艇深度终端滑模控制技术[J]. 舰船科学技术, 2012, 34(2): 55-62. DOI:10.3404/j.issn.1672-7649.2012.02.011 |
| [14] |
徐超, 刘刚, 徐国华, 等. 基于泵控液压舵机的潜艇深度及纵倾控制[J]. 中国舰船研究, 2017, 12(2): 116-123. DOI:10.3969/j.issn.1673-3185.2017.02.015 |
| [15] |
潘慧, 佘莹莹, 唐正茂. 大攻角时的潜艇操纵控制技术[J]. 华中科技大学学报, 2012, 40(5): 46-49. |
| [16] |
KIM H. Expanded adaptive fuzzy sliding mode controller using expert knowledge and fuzzy basis function expansion for UFV depth control[J]. Ocean Engineering, 2007, 34(8-9): 1080-1088. DOI:10.1016/j.oceaneng.2006.08.008 |
| [17] |
戴余良, 林俊兴, 苗海, 等. 潜艇空间机动的多变量滑模模糊控制[J]. 武汉理工大学学报(交通科学与工程版), 2009, 33(6): 1040-1043. DOI:10.3963/j.issn.1006-2823.2009.06.005 |
| [18] |
中国造船编辑部. 船舶动力学词典[M]. 上海: 中国造船编辑部, 1981.
|
| [19] |
Nomeneclature for Treating the Motion of a submerged Body Through a Fluid[R]. SNAME Technical and Research Bulletin 1–5, 1952.
|
| [20] |
GERTERLER M, HAGEN R. Standard Equations of Motion for Submarine Simulation[R]. AD 653861, SNAME, 1967.
|
| [21] |
苏磊, 姚宏, 杜军, 等. 飞行器自适应反推Terminal滑模轨迹跟踪控制[J]. 系统工程与电子技术, 2014, 36(11): 2249-2254. DOI:10.3969/j.issn.1001-506X.2014.11.22 |
| [22] |
张合新, 范金锁, 孟飞, 等. 一种新型滑模控制双幂次趋近律[J]. 控制与决策, 2013, 28(2): 289-293. |
 2019, Vol. 41
2019, Vol. 41
