0 引　言

螺旋桨能够将70%左右的机械动力转化为推进力，成为当前各类船舶上应用最为广泛的推进器形式。对于民船螺旋桨，特别是散货船、油船和集装箱船等三大主流船型，推进效率是这类船舶螺旋桨设计时最优先考虑的指标。在螺旋桨主参数确定后，螺旋桨的效率主要由其径向环量分布决定。开展螺旋桨最佳径向环量的研究可以从机理上给出提高推进器效率的方向。因此以效率为目标的螺旋桨最佳环量计算一直是螺旋桨设计研究的一个重要内容。

螺旋桨最佳环量的计算方法是伴随着升力线理论的发展而提出的。早期，Betz发展螺旋桨升力线理论时，根据在效率较高处增加环量，在效率较低处减小环量的思想，Betz得出了敞水条件下最佳环量分布条件。Lerbs^[1]首次提出了求解最佳环量分布的变分法，建立了优化方程式，限于当时的计算条件，未能在计算机上实现。但Lerbs提出的求解最佳环量分布的变分法思想，逐渐成为求解敞开螺旋桨、导管桨、对转桨等各类组合推进桨叶最佳环量的主流方法，一直沿用至今。近年来，国外关于螺旋桨最佳环量计算方面的研究工作，主要集中在麻省理工学院Kerwin教授及其学生身上^{[2 – 4]}。国内苏玉民^[5]、曹庆明^[6]、孙文愈^[7]等也采用变分法开展了船用推进器最佳环量计算的研究工作。

采用传统变分法进行最佳环量分布数值求解时，需要对升力线模型进行离散，将连续的环量分布离散为在涡格内均布的常量，连续的自由涡片离散为从涡格边界泄出的集中涡。根据Kerwin^[8]的研究成果，在使用离散化升力线模型时，在叶梢和叶根2个自由端存在1/2阶的奇性，因此需要对2个端部的网格划分和控制点布置进行特殊处理。本文给出一种求解螺旋桨最佳环量的改良方法，将径向环量分布用正弦级数表达出来，通过求解正弦级数模式函数的各项系数，从而得到螺旋桨最佳环量分布形式。

1 基本理论 1.1 正弦级数模式函数表达螺旋桨径向环量分布

设叶根环量为 ${G_0}$ ，叶梢环量为 ${G_M}$ ，可通过正弦级数把沿径向的环量分布表达成如下形式：

$ \begin{aligned} & \left\{ \begin{array}{*{20}{c}} {G(\varphi ) = \left( {1 - \displaystyle\frac{\varphi }{{\text{π}} }} \right){G_0} + \displaystyle\sum\limits_{m = 1}^{M - 1} {{G_m}\sin (m\varphi )} + \frac{\varphi }{{\text{π}}}{G_M}}{\text{，}}\\ {\bar r = \displaystyle\frac{1}{2}(1 + {{\bar r}_H}) - \displaystyle\frac{1}{2}(1 - {{\bar r}_H})\cos \varphi{\text{，}} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;} \end{array}\right.\\ & \quad\quad({{\bar r}_H} \text{≤} \bar r \text{≤} 1.0,0 \text{≤} \varphi \text{≤} \text{π} ){\text{。}} \end{aligned} $

(1)

其中： $\bar r$ 为无量纲半径； ${\bar r_H}$ 为叶根无量纲半径； $\varphi = 0$ 对应叶根，此时 $\bar r = {\bar r_H}$ ， $G(\varphi )$ 恒等于 ${G_0}$ ； $\varphi = {\text{π}} $ 对应叶叶梢，此时 $\bar r = 1.0$ ， $G(\varphi )$ 恒等于 ${G_M}$ ； ${G_0},{G_1},{G_2} \ldots {G_M}$ 为模式函数待求系数。采用本方法表达螺旋桨径向环量分布时，既可以指定叶梢和叶根的环量值（如敞开螺旋桨，叶梢和叶根环量为0，可令 ${G_0} = 0,{G_M} = 0$ ），也可以将 ${G_0}$ 和 ${G_M}$ 作为未知量求解（如考虑桨毂影响的情况或者导管桨等）。

1.2 螺旋桨诱导速度的计算

诱导因子仍按Lerbs的定义不变，则诱导速度的计算式如下：

$\frac{{{u_{a,t}}(\varphi )}}{{{v_s}}} = \frac{1}{{1 - {{\bar r}_H}}}\int_0^{\text{π}} {\frac{{{\rm d}G}}{{{\rm d}{\varphi _0}}}} \frac{{{i_{a,t}}(\varphi ,{\varphi _0})}}{{\cos {\varphi _0} - \cos \varphi }}{\rm d}{\varphi _0}{\text{。}}$

(2)

由式（1）可得：

$ \begin{split} \frac{{{\rm d}G}}{{{\rm d}{\varphi _0}}} =& \frac{{\rm d}}{{{\rm d}{\varphi _0}}}\left[ {\left( {1 - \frac{{{\varphi _0}}}{{\text{π}} }} \right){G_0} + \sum\limits_{m = 1}^{M - 1} {{G_m}\sin (m{\varphi _0}) + \frac{{{\varphi _0}}}{\text{π} }{G_M}} } \right] =\!\!\! \\ & - \frac{{{G_0}}}{{\text{π}} } + \sum\limits_{m = 1}^{M - 1} {m{G_m}\cos (m{\varphi _0})} + \frac{{{G_M}}}{\text{π}}{\text{，}} \end{split} $

(3)

$ \begin{split} \frac{{{u_{a,t}}(\varphi )}}{{{v_s}}} =& \frac{1}{{1 - {{\bar r}_H}}}\int_0^\text{π} {\left( - \frac{{{G_0}}}{\text{π}} + \sum\limits_{m = 1}^{M - 1} {m{G_m}\cos (m{\varphi _0})} + \frac{{{G_M}}}{\text{π} }\right)}\times\\ & \frac{{{i_{a,t}}(\varphi ,{\varphi _0})}}{{\cos {\varphi _0} - \cos \varphi }}{\rm d}{\varphi _0}{\text{。}} \end{split} $

(4)

式中： ${i_{a,t}}(\varphi ,{\varphi _0})$ 为诱导因子，下标 $a$ 和 $t$ 分别表示轴向和切向速度诱导因子； ${u_{a,t}}(\varphi ,{\varphi _0})$ 为诱导速度，下标 $a$ 和 $t$ 分别表示轴向和切向诱导速度； ${v_s}$ 为来流速度。

可以将式（4）写成如下形式：

$\frac{{{u_{a,t}}(\varphi )}}{{{v_s}}} = \sum\limits_{m = 0}^M {{G_m}} H_m^{a,t}(\varphi ){\text{。}}$

(5)

其中：

$ H_m^{a,t}(\varphi ) \!=\! \left\{ {\begin{split} & {\frac{1}{{1 \!-\! {{\bar r}_H}}}\!\int_0^{\text{π}} {\frac{{ - {i_{a,t}}(\varphi ,{\varphi _0})}}{{(\cos {\varphi _0} - \cos \varphi ){\text{π}} }}{\rm d}{\varphi _0}} ,\; m \!=\! 0}{\text{；}}\\ & \frac{1}{{1 \!-\! {{\bar r}_H}}}\int_0^{\text{π}} {\frac{{m{i_{a,t}}(\varphi ,{\varphi _0})\cos (m{\varphi _0})}}{{\cos {\varphi _0} - \cos \varphi }}} {\rm d}{\varphi _0},\\ & \; m \!=\! 1,2, \cdots ,M \!-\! 1{\text{；}}\\ & {\frac{1}{{1 - {{\bar r}_H}}}\int_0^{\text{π}} {\frac{{{i_{a,t}}(\varphi ,{\varphi _0})}}{{(\cos {\varphi _0} - \cos \varphi ){\text{π}} }}{\rm d}{\varphi _0}} ,\; m \!=\! M \!+\! 1}{\text{。}}\!\!\!\!\! \end{split}} \right. $

(6)

1.3 功率系数和推力系数的计算

将式（1）中的环量分布改写成如下形式：

$G(\varphi ) = \sum\limits_{m = 0}^M {{G_m}{P_m}(\varphi )}{\text{，}} $

(7)

功率系数

$\begin{split} {C_P} \!=\!& \frac{{4Z}}{{{\lambda _s}}}\int_{{{\bar r}_H}}^1 {G(\bar r)\bar r\left[ {1 - {w_x}(\bar r) \!+\! \displaystyle\frac{{{u_a}(\bar r)}}{{{v_s}}}} \right]} {\rm d}\bar r=\\ & \frac{{2Z\left( {1 \!-\! {{\bar r}_H}} \right)}}{{{\lambda _s}}}\int_0^{\text{π}} {G(\varphi )\bar r(\varphi )\left[ {1 - {w_x}(\varphi ) + \frac{{{u_a}(\varphi )}}{{{v_s}}}} \right]} \sin (\varphi ){\rm d}\varphi =\\ & \frac{{2Z\left( {1 - {{\bar r}_H}} \right)}}{{{\lambda _s}}}\int_0^{\text{π}} \left( {\sum\limits_{m = 0}^M {{G_m}{P_m}(\varphi )} } \right)\times\\ & \left[ {1 - {w_x}(\varphi ) + \sum\limits_{m = 0}^M {{G_m}} H_m^a(\varphi )} \right] \bar r(\varphi )\sin (\varphi ){\rm d}\varphi {\text{。}}\quad\quad\quad\;\;(8) \end{split}$

令

${A_m} = \frac{{2Z\left( {1 - {{\bar r}_H}} \right)}}{{{\lambda _s}}}\int_0^{\text{π}} {\bar r(\varphi ){P_m}(\varphi )\left[ {1 - {w_x}(\varphi )} \right]\sin (\varphi ){\rm d}\varphi } {\text{，}}$

(9)

改写

$\left( {\sum\limits_{m = 0}^M {{G_m}{P_m}(\varphi )} } \right)\left[ {\sum\limits_{m = 0}^M {{G_m}} H_m^a(\varphi )} \right] = \sum\limits_{m = 0}^M {\sum\limits_{n = 0}^M {{P_m}(\varphi )} } H_n^a(\varphi ){G_m}{G_n}{\text{，}}$

(10)

又令

${B_{mn}} = \frac{{2Z\left( {1 - {{\bar r}_H}} \right)}}{{{\lambda _s}}}\int_0^{\text{π}} {\bar r(\varphi ){P_m}(\varphi )H_n^a(\varphi )\sin (\varphi ){\rm d}\varphi }{\text{，}} $

(11)

则功率系数计算式可与成以下形式：

${C_P} = \sum\limits_{m = 0}^M {{A_m}{G_m} + } \sum\limits_{m = 0}^M {\sum\limits_{n = 0}^M {{B_{mn}}} } {G_m}{G_n}{\text{。}}$

(12)

同理，推力系数可以写成如下形式：

$\begin{split} {C_T} =& 4Z\int_{{{\bar r}_H}}^{1.0} {G(\bar r)\left[ {\frac{{\bar r}}{{{\lambda _s}}} + {w_t}(\bar r) - \frac{{{u_t}(\bar r)}}{{{v_s}}}} \right]} {\rm d}\bar r=\\ & 2Z(1 - {{\bar r}_H})\int_0^{\text{π}} {G(\varphi )\left[ {\frac{{\bar r(\varphi )}}{{{\lambda _s}}} + {w_t}(\varphi ) - \frac{{{u_t}(\varphi )}}{{{v_s}}}} \right]} \sin \varphi {\rm d}\varphi =\\ & \sum\limits_{m = 0}^M {{C_m}} {G_m} + \sum\limits_{m = 0}^M {\sum\limits_{n = 0}^M {{D_{mn}}} } {G_m}{G_n}{\text{。}}\;\;\;\quad\quad\quad\quad\quad\quad(13) \end{split}$

其中：

${C_m} = 2Z(1 - {\bar r_H})\int_0^{\text{π}} {{P_m}(\varphi )\left[ {\frac{{\bar r(\varphi )}}{{{\lambda _s}}} + {w_t}(\varphi )} \right]} \sin \varphi {\rm d}\varphi {\text{，}}$

(14)

${D_{mn}} = 2Z(1 - {\bar r_H})\int_0^{\text{π}} {{P_m}(\varphi )} H_n^t(\varphi )\sin \varphi {\rm d}\varphi {\text{。}}$

(15)

1.4 变分法求解最佳环量

求解最佳环量分布的条件是：推力系数须滿足指定值而功率系数为最小，或功率系数满足指定值而推力系数最大，这一问题可转化为多元函数求条件极值的问题。以指定推力系数 ${C_{Trequired}}$ 求 ${C_P}$ 的极小值为例，引入Lagrange乘子 $\lambda $ ，并构建辅助函数 $H = {C_Q} + $ $\lambda ({C_T} - {C_{Trequired}})$ ，则求极值条件的方程式为：

$\left\{ {\begin{split} & {\frac{{\partial H}}{{\partial {G_q}}} = \lambda \frac{{\partial {C_T}}}{{\partial {G_q}}} + \frac{{\partial {C_Q}}}{{\partial {G_q}}} = 0}\\ & {\frac{{\partial H}}{{\partial \lambda }} = {C_T} - {C_{Trequired}} = 0} \end{split}} \right.\quad(q = 0,1,2, \cdots ,M){\text{，}}$

(16)

其中：

$ \begin{split} \frac{{\partial {C_T}}}{{\partial {G_q}}} =& \frac{\partial }{{\partial {G_q}}}\left(\sum\limits_{m = 0}^M {{C_m}} {G_m} + \sum\limits_{m = 0}^M {\sum\limits_{n = 0}^M {{D_{mn}}} } {G_m}{G_n}\right)=\\ & {C_q} + \sum\limits_{m = 0}^M {({D_{qm}} + } {D_{mq}}){G_m}{\text{，}} \end{split} $

(17)

$ \begin{split} \frac{{\partial {C_Q}}}{{\partial {G_q}}} =& \frac{\partial }{{\partial {G_q}}}\left(\sum\limits_{m = 0}^M {A{}_m} {G_m} + \sum\limits_{m = 0}^M {\sum\limits_{n = 0}^M {{B_{mn}}} } {G_m}{G_n}\right) =\\ & {A_q} + \sum\limits_{m = 0}^M {({B_{qm}} + } B{}_{mq}){G_m}{\text{。}} \end{split} $

(18)

联立式（16）~式（18）可得：

$ \begin{split} \frac{{\partial H}}{{\partial {G_q}}} =& \lambda \left( {{C_q} + \sum\limits_{m = 0}^M {({D_{qm}} + } {D_{mq}}){G_m}} \right) +\\ & \left( {{A_q} + \sum\limits_{m = 0}^M {({B_{qm}} + } B{}_{mq}){G_m}} \right) = 0{\text{，}} \end{split} $

(19)

整理后可写成：

$ \begin{split} & \sum\limits_{m = 0}^M {\left[ {\lambda ({D_{qm}} + {D_{mq}}) + ({B_{qm}} + B{}_{mq})} \right]} {G_m}= \\ & - (\lambda {C_q} + {A_q}), \;\; (q = 0,1,2, \cdots ,M){\text{。}} \end{split} $

(20)

式（20）为 $M + 1$ 个线性方程构成的方程组，需要求解 $M + 2$ 个未知数（ $M + 1$ 个 ${G_m}$ 及1个 $\lambda $ ）。求解方法是先假定N个 $\lambda $ 值，对每一个 $\lambda $ 值求解得出一组 ${G_m}$ 的解。然后把每一组 ${G_m}$ 值代入式（13），计算出对应的 ${C_T}$ 值。然后通过插值求得指定的 ${C_{Trequired}}$ 值时对应的 $\lambda $ 值，然再代入到方程组（20）重新求出 ${G_m}$ 的解。把这组 ${G_m}$ 解再代入式（13）验算 ${C_T}$ 是否符合要求，否则还需再作修正迭代。

但是，这一轮的过程是建立在某一给定的水动力螺距角分布的基础上的，故需有迭代过程。在第一轮求解时可以先用进角分布代替水动力螺距角作为初值。在求出表达环量分布的正弦级数各项系数 ${G_m}$ 后，重新计算诱导速度和水动力螺距角分布，用新的水动力螺距角分布再重新计算得出新的最佳环量分布，一直迭代到 ${G_m}$ 和诱导速度收敛。至此方求出表达最佳环量的正弦级数各项系数 ${G_m}$ 的最终值后，代入式（1）最佳环量分布得解。

2 算例验证

编制求解螺旋桨最佳环量程序，选取Coney^[6]在1989年博士论文中给出的2个案例进行计算和对比。

考核案例1：均匀来流条件下螺旋桨最佳环量分布计算比较。

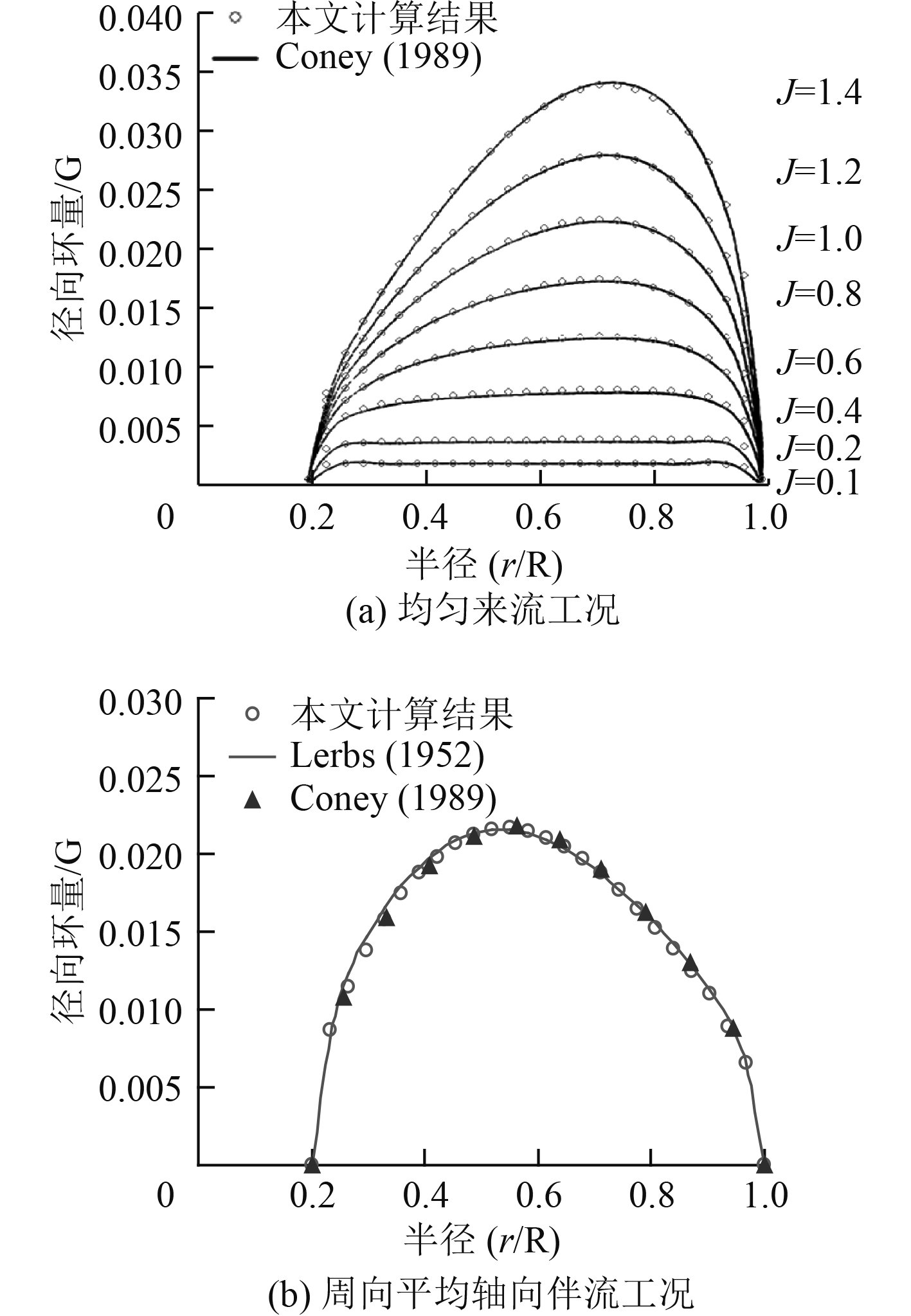
5叶螺旋桨，毂径比0.2，不考虑桨毂和粘性影响，不考虑尾涡变形和收缩，敞水工况，Ct=0.512，计算J=0.1，0.2，0.4，0.6，0.8，1.0，1.2和1.4时的最佳环量分布。计算对比结果见图1（a）。

考核案例2：周向平均的轴向伴流分布条件下螺旋桨最佳环量分布计算比较。

5叶螺旋桨，毂径比0.2，不考虑桨毂和粘性影响，不考虑尾涡变形和收缩，Ct=0.307，J=1.377，计算周向平均的轴向伴流下螺旋桨最佳环量分布。计算对比结果见图1（b）。关于本案例中具体的伴流分布可参见文献[9]。

从图2可以看出，敞水和伴流条件下的最佳环量计算结果均和Coney的计算吻合良好，表明本文基于正弦级数和变分法的螺旋桨最佳环量分布计算方法是可行和正确的。

为对本文所述方法的数值稳定性进行考核，针对案例2，在升力线模型离散时采用不同网格数量和网格划分方式进行最佳环量的计算，对比结果如图2所示。可以看出，计算结果并未因网格数量和划分方式的不同而发生较大跳动，该方法的数值稳定性良好。

3 结　语

本文介绍一种基于正弦级数模式函数和变分法的螺旋桨最佳环量计算改良方法，并编写相应的计算程序。算例验证表明，计算结果并未因为网格数量和划分方式的不同而发生较大跳动，该方法的数值稳定性良好，计算结果正确。本文的最佳环量改良计算方法有效和可行，可用于螺旋桨的效率优化及工程设计。