2. 上海交通大学高新船舶与深海开发装备协同创新中心,上海 200240
2. Shanghai Jiaotong University, Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration, Shanghai 200240, China
随着人类对海洋开发的逐步深入,出现了深拖母船、钻井船等在船中有月池结构的船舶。月池结构一般贯穿主船体,用于释放或回收设备,其内部与海水直接连通,形成自由液面。在船体和海水的作用下,月池内海水的运动会对船舶的航行产生一定影响。针对其流场特性,国内外学者做了大量的研究,但对于船舶操纵性的讨论却鲜有提及。作为船舶重要的水动力性能之一,船舶操纵性与船舶的安全航行密切相关,也越来越引起人们的重视[1]。目前预报操纵性主流的方法是建立船舶运动的数学模型,进而利用计算机模拟船舶操纵实验,得到船舶的运动轨迹及参数[2 – 3]。作为船舶运动方程中关键的参数之一,水动力导数对于预报船舶操纵性起着关键作用。传统计算水动力导数的方法主要有:拘束船模实验法、经验公式估算法和系统辨识法。近年来,计算机计算能力的提高和计算流体力学的发展为计算水动力导数提供了新途径,许多学者开始采用粘性流场模拟船舶操纵运动特性,如Ohmori[4]采用有限体积法计算了船舶操纵条件下的粘性流场;Simonsen[5]等利用CFD和EFD测得的水动力导数模拟了Z型实验和全回转实验;张赫等[6 – 9]利用CFD软件模拟平面运动机构实验(PMM)测定水动力导数。本文分别模拟了船舶月池在封闭和打开时的拘束模型试验,并计算出相应的水动力导数。在月池封闭时,通过与势流理论计算结果对比,验证了该方法的有效性。最后,通过比较月池打开和闭合时的水动力导数,发现大部分水动力导数都因为月池的存在而有所增加,这为研究其操纵性提供了参考。
1 基本理论 1.1 控制方程在各态遍历的假设下,湍流运动可以看成时间平均流动和瞬间脉动流动。船体周围的不可压粘性流场满足质量守恒和动量守恒定律,其连续性方程成和雷诺平均方程(RANS)如下:
| $ \left\{ \!\!\!\!\begin{array}{l} \dfrac{{\partial \overline {{u_i}} }}{{\partial {x_i}}} = 0\text{,}\\ \dfrac{{\partial \overline {{u_i}} }}{{\partial t}} + \overline {{u_j}} \dfrac{{\partial \overline {{u_i}} }}{{\partial {x_j}}} = - \dfrac{1}{\rho }\dfrac{{\partial \overline {{P_i}} }}{{\partial {x_i}}} + \dfrac{1}{\rho }\dfrac{\partial }{{\partial {x_j}}}\left(\mu \dfrac{{\partial \overline {{u_i}} }}{{\partial {x_j}}} - \rho \overline {{{u'}_i}{{u'}_j}} \right)\text{。} \end{array} \right. $ | (1) |
其中:
本文采用在工程上应用最广泛、结果较稳定的k-ε模型对RANS方程进行补充。
| $ \left\{ \!\!\!\!\begin{array}{l} \rho \dfrac{{dk}}{{dt}} = \dfrac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + \dfrac{{{\mu _t}}}{{{\sigma _k}}}} \right)\dfrac{{\partial k}}{{\partial {x_j}}}} \right] + {G_k} + {G_b} - \rho \varepsilon - {Y_M}\text{,}\\ \rho \dfrac{{d\varepsilon }}{{dt}} \!=\! \dfrac{\partial }{{\partial {x_i}}}\left[ {\left( {\mu \!+\! \dfrac{{{\mu _t}}}{{{\sigma _\varepsilon }}}} \right)\dfrac{{\partial \varepsilon }}{{\partial {x_i}}}} \right]{\rm{ + }}\rho {C_1}S\varepsilon \!-\! \rho {C_2}\dfrac{{{\varepsilon ^2}}}{{k \!+\! \sqrt {v\varepsilon } }} +\\ {C_{1\varepsilon }}\dfrac{\varepsilon }{k}{C_{3\varepsilon }}{G_b}\text{。} \end{array} \right. $ | (2) |
其中:
重叠网格又称Overset。该方法在建域时,采用大域与小域嵌套的形式,船体位于小域内,如图3所示。计算时,首先标记洞单元、活动单元、边界单元、贡献单元,然后,挖去洞单元,去除多余重叠单元,通过重叠网格单元,大域与小域之间的实现线性插值,完成数据的交换,从而完成整个流场的求解。对于船舶操纵性能预报问题,要涉及到船舶的纯橫荡、纯首摇运动,船体周围的网格容易破裂,因此,普通的网格不太适用。然而,重叠网格技术允许大域与小域之间的产生无约束的相对位移,在网格运动时,能够保证网格不发生变形、破裂,从而,保证网格的质量,提高求解的精度。因此,重叠网格技术对动态问题具有极强的处理能力。

|
图 3 网格划分 Fig. 3 The meshing method |
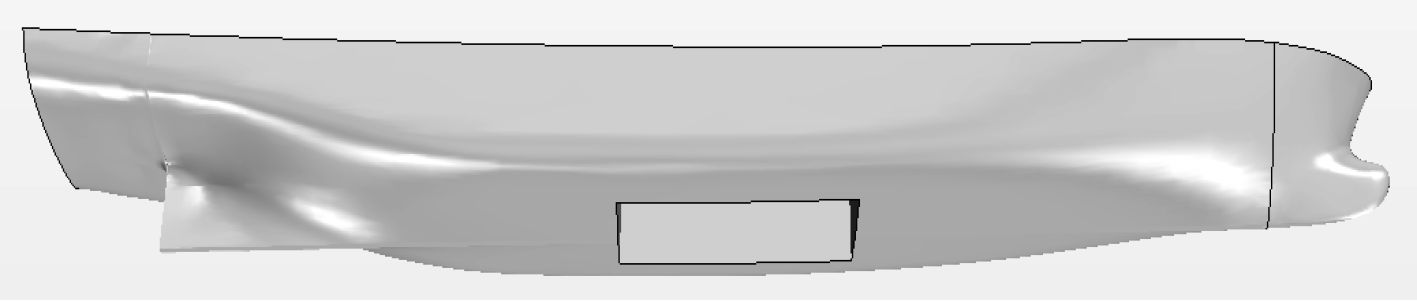
本文的研究对象为某深拖母船,船长39.6 m,船中的月池为6 m×3 m×3.2 m的矩形开口,月池可以打开和闭合,船模缩尺比为1:15。月池打开时几何模型如图1所示。
|
图 1 船体模型 Fig. 1 Hull model |
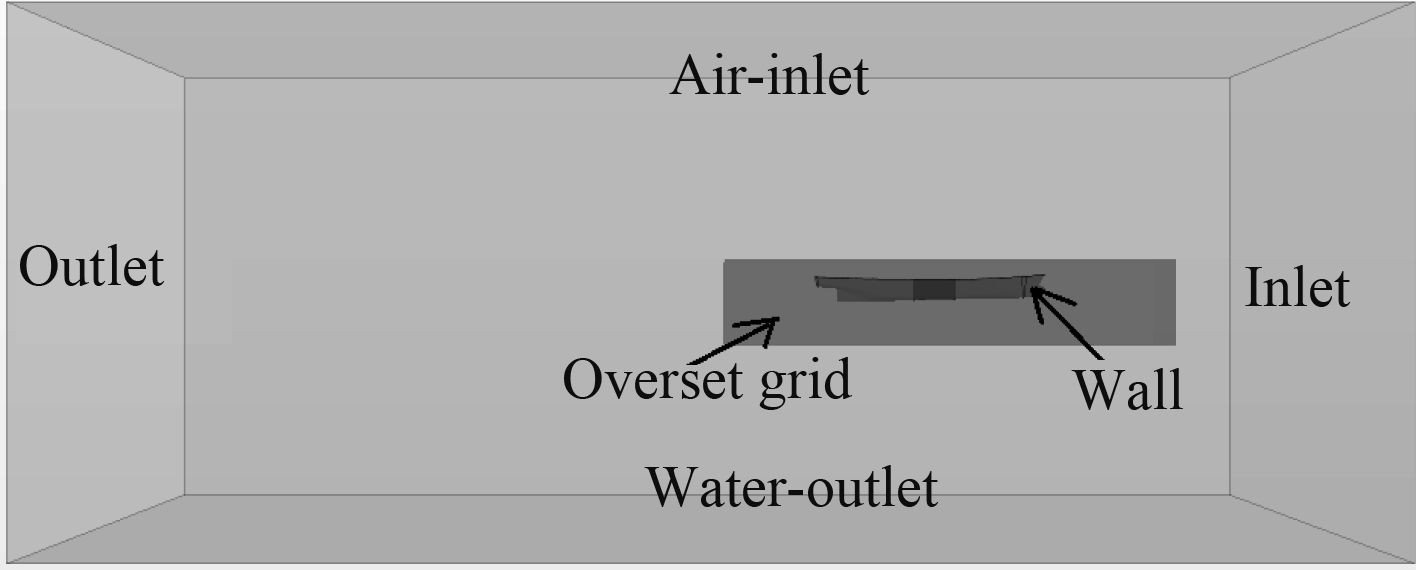
在计算域内,流体以特定速度流经船体,同时给船体以规定的运动,测量相应物理量。边界条件设置如图2所示。入流边界:距离船首1倍船长,设置为速度入口(velocity inlet);出流边界:距离船尾3倍船长,设置为压力出口(pressure outlet);其余边界:侧面距离纵向对称面1倍船长,上下对称面距离水线面1.5倍船长,设置为速度入口(velocity inlet);船体表面:无滑移壁面(wall)。
|
图 2 计算域与边界条件 Fig. 2 Computational domain and boundary conditions |
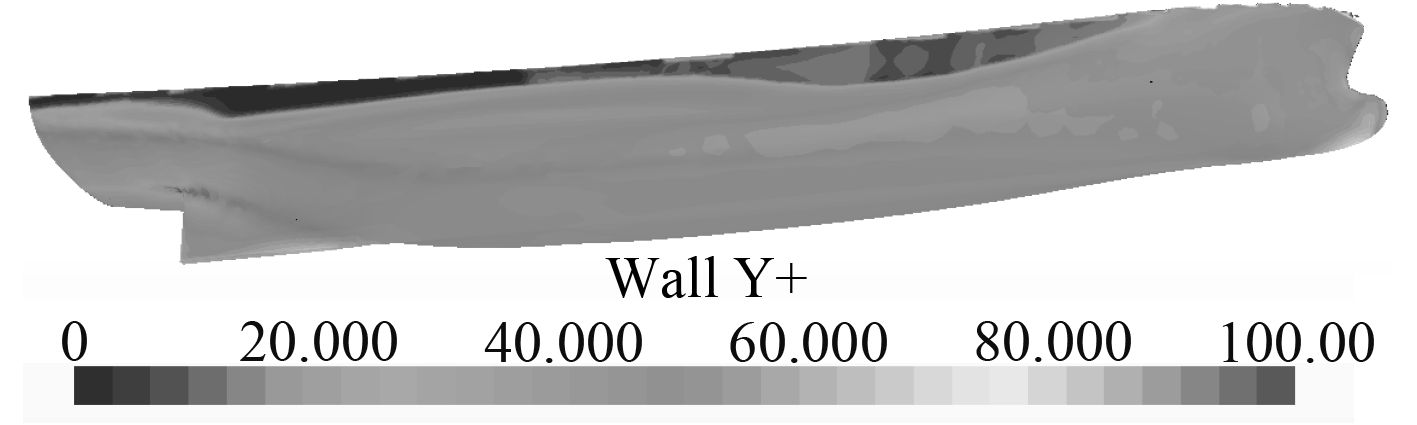
本文所选网格为切割体网格,对船体表面、船首、船尾、水线面进行了网格加密。通常利用无量纲数y+表征船体表面第1层网格与壁面的距离。为保证第1层网格位于湍流充分发展区y+的值应当满足30≤y+≤200[10]。对于非结构化网格,棱柱层网格数建议在10~20层[11]。网格划分如图3所示,计算后的y+值如图4所示,可以发现,船模水下部分y+大都为60左右,符合计算要求。
|
图 4 y+值 Fig. 4 The value of y+ |
为了减少计算量和保证计算的准确性,对船模速度为0.81 m/s的工况下,进行网格收敛性验证,如表1所示。这里采用5套不同的网格,网格数量近似按照
|
|
表 1 网格收敛性验证 Tab.1 Verification of grid convergence |
船舶纵中剖面与水池中心线成一夹角β,在入口处施加速度为V的来流,系统的改变漂角β,测得船模所受拘束横向力X、纵向力Y、力矩N,进而求得船模的位置水动力导数。计算数据进行了无因次化处理,具体无因次方法参照文献[12]。
3.2.2 纯横荡运动船模在纵向匀速运动的同时,叠加横向低频振荡运动,在运动时船模r=ψ=0。其运动规律可用下式表示:
| $ \left\{ \begin{array}{l} y = a\sin \omega t\text{,}\\ v = \dot y = a\omega \cos \omega t\text{。} \end{array} \right. $ | (3) |
设数值模拟测得的拘束横向力
| $ \left\{ \begin{array}{l} \overline Y {\rm{ = (}}m - {Y_{\dot v}})\dot v - {y_v}v\text{,}\\ \overline N = (m{x_G} - {N_{\dot v}})\dot v - {N_v}v\text{。} \end{array} \right. $ | (4) |
船模以速度
| $\left\{ \begin{array}{l} \psi \approx \dfrac{{{u_R}}}{{{u_c}}} = \dfrac{{a\omega }}{{{u_c}}}\cos \omega t = {\psi _0}\cos \omega t\text{,}\\ r = \dot \psi = - \dfrac{{a{\omega ^2}}}{{{u_c}}}\sin \omega t = {r_0}\sin \omega t\text{,} \end{array} \right. $ | (5) |
| $ \left\{ \begin{array}{l} \overline Y {\rm{ = (}}m{x_G} - {Y_{\dot r}}){{\dot r}} - (m{u_G} - {Y_r}){{r}}\text{,}\\ \overline N = ({{\rm{I}}_z} - {N_{\dot r}}){{\dot r}} - (m{x_G}{u_G} - {N_r}){{r}}\text{。} \end{array} \right. $ | (6) |
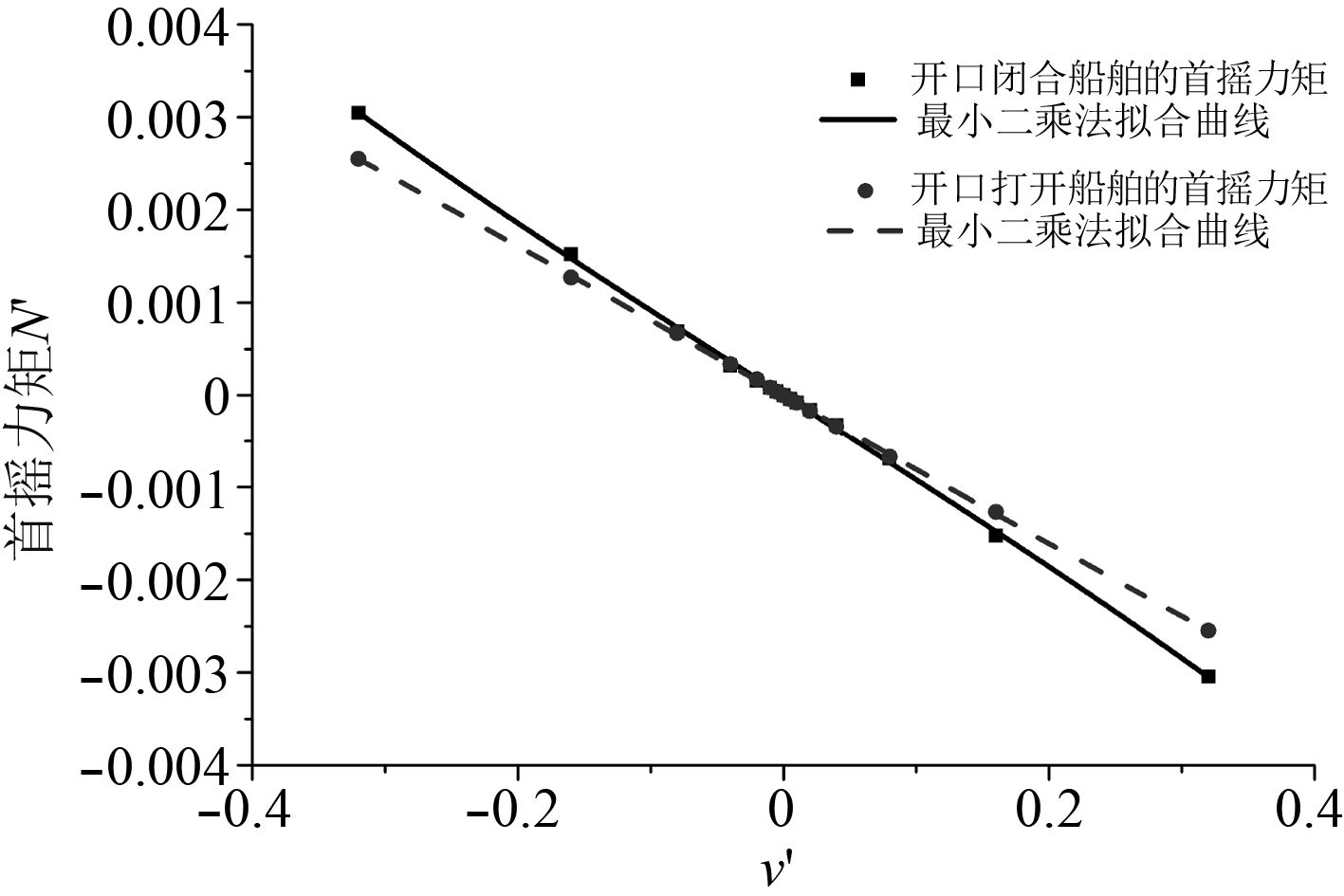
船模在做斜航运动时,漂角β的范围是–0.32~0.32 rad,数值模拟得到的不同漂角下的阻力、侧向力以及首摇力矩,用曲线拟合后如图5~图7所示。

|
图 5 不同漂角下的阻力曲线 Fig. 5 Resistance curves at different drift angles |

|
图 6 不同漂角下的侧向力曲线 Fig. 6 Lateral force curve at different drift angles |
|
图 7 不同漂角下的首摇力矩曲线 Fig. 7 Yaw moment curve at different drift angles |
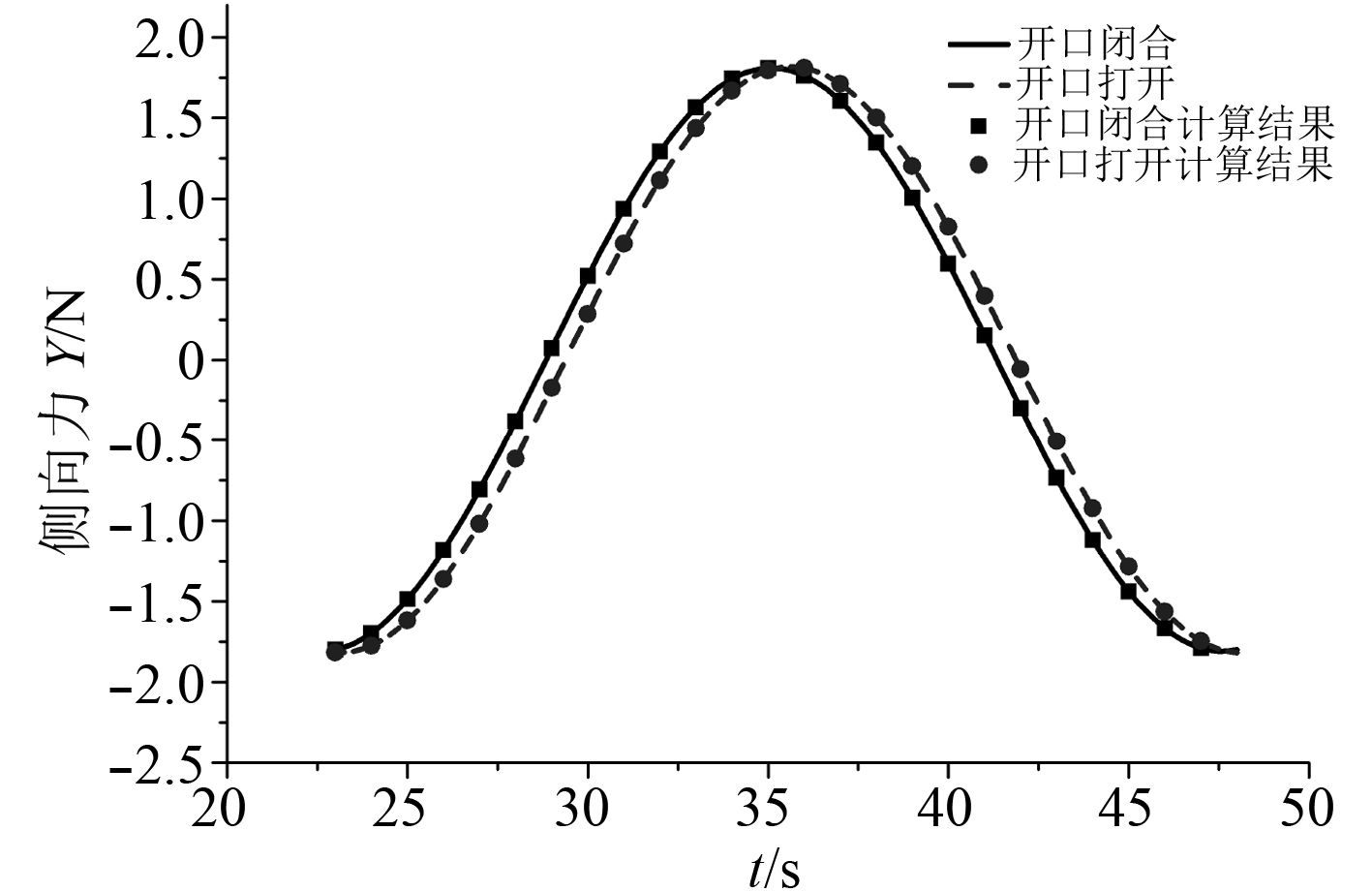
船模在做纯橫荡和纯首摇实验时,横向运动的幅值a为0.1 m,运动圆频率ω分别取0.125 rad/s、0.250 rad/s、0.50 rad/s,计算得到侧向力和首摇力矩随时间变化的曲线,ω=0.250 rad/s时,侧向力和首力矩的变化如图8~图11所示,月池闭合时纯横荡运动计算得到的水动力导数随频率变化如图12所示。
|
图 8 纯横荡运动船舶受到的侧向力 Fig. 8 Lateral force curve when in pure sway motion |
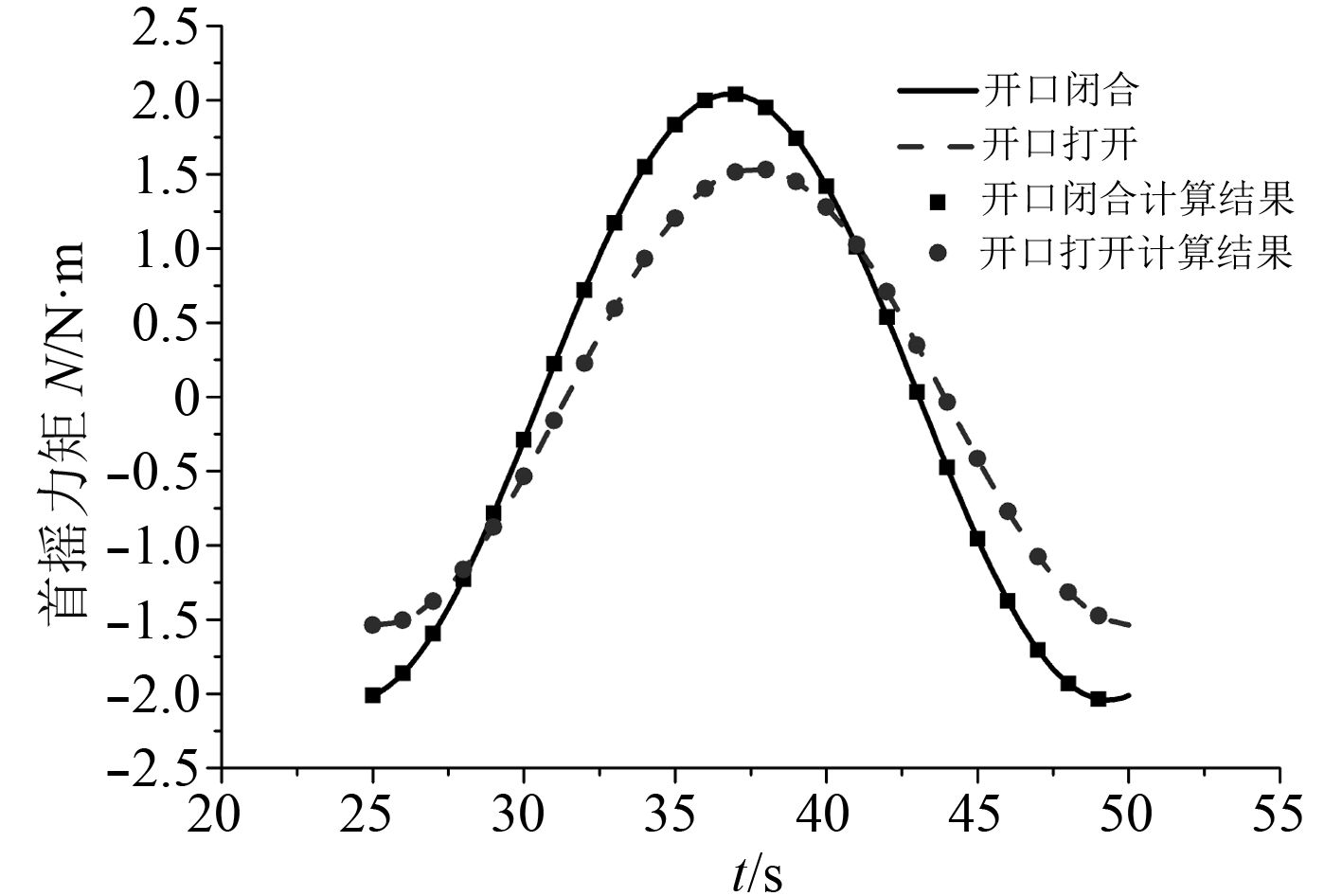
|
图 9 纯横荡运动船舶受到的首摇力矩 Fig. 9 Yaw moment curve when in pure sway motion |

|
图 10 纯首摇运动船舶受到的侧向力 Fig. 10 Lateral force curve when in pure yaw motion |
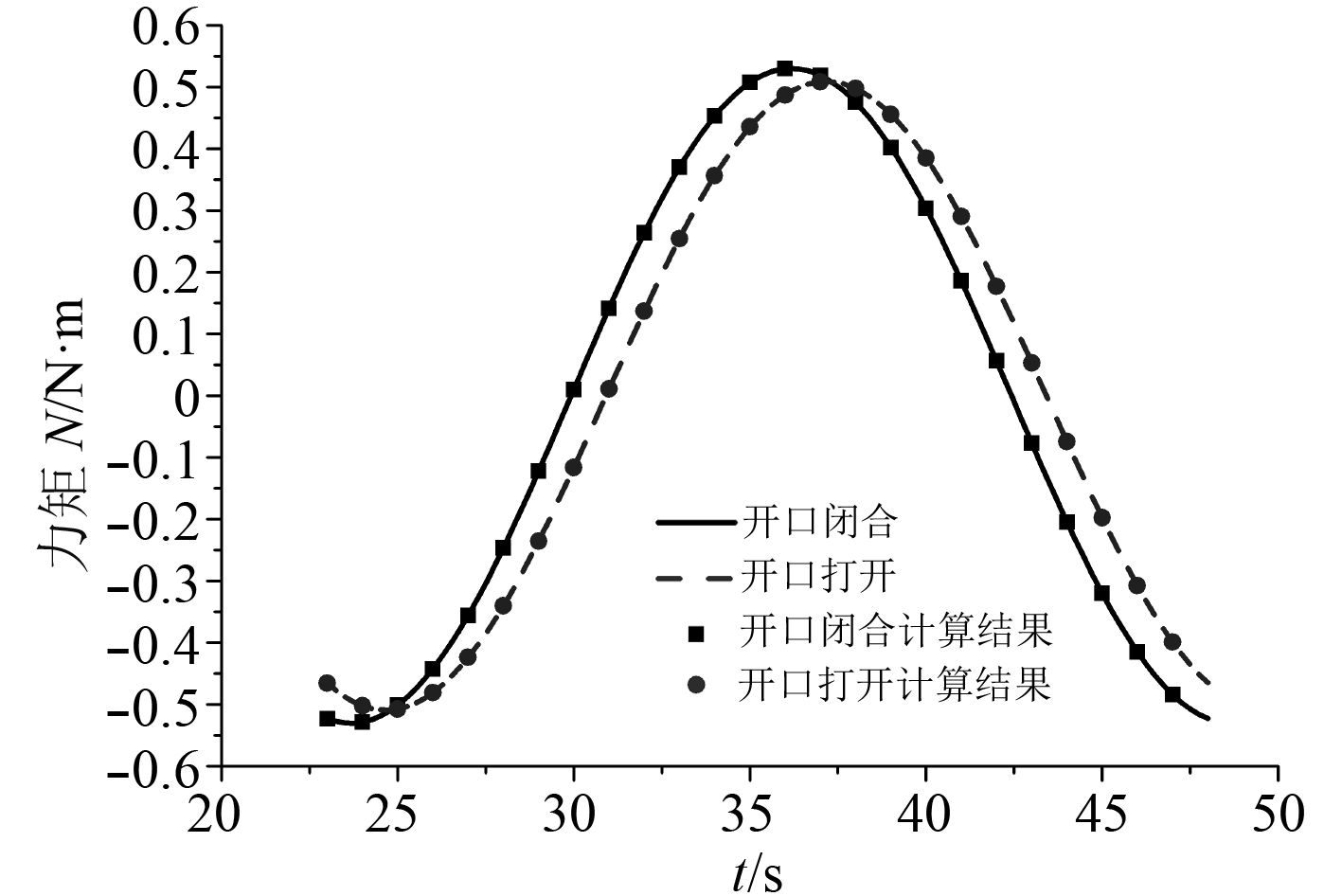
|
图 11 纯首摇运动船舶受到的首摇力矩 Fig. 11 Yaw moment curve when in pure yaw motion |
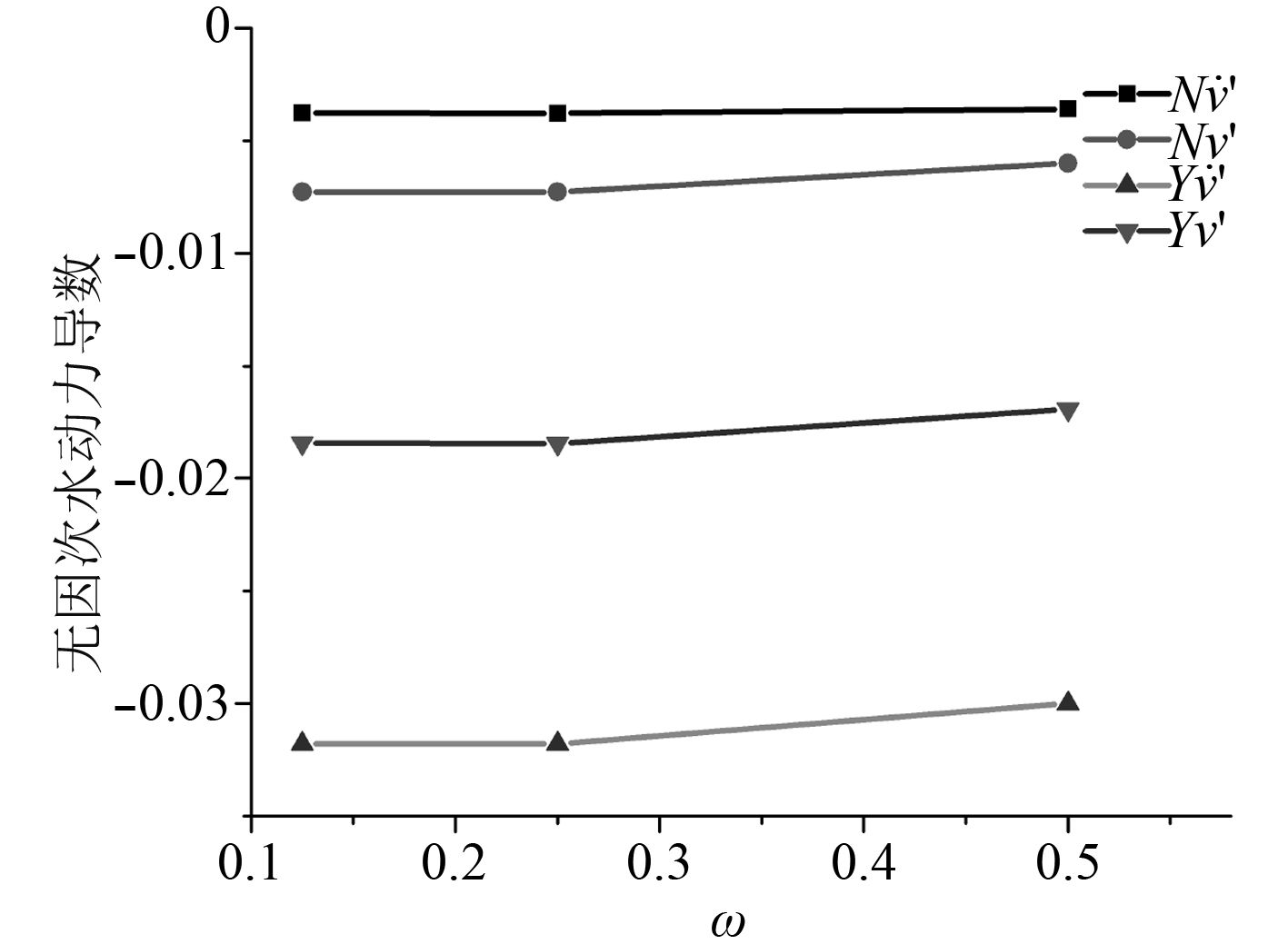
|
图 12 水动力导数随频率变化曲线 Fig. 12 The change of hydrodynamic derivatives along with frequency |
月池闭合时数值模拟计算的水动力导数与理论计算值相比较:1)当ω小于0.25 rad/s时,水动力导数几乎为一常数,因而所算得的水动力导数符合要求(见图12);2)斜航实验和纯横荡实验分别测定的位置导数与细长体理论计算值比较后发现,大部分水动力导数的对比值小于20%,对于水动力导数的计算来说精度较高,可以满足工程计算要求(见表2);3)利用周昭明回归表达式计算出船模的附加质量λ22=163.83 kg、λ66=55.17 kg·m2,这与算得的惯性类水动力导数
|
|
表 2 月池闭合时数值模拟值与势流理论计算值比较 Tab.2 Comparison of calculated values of numerical simulation and potential flow theory when the moon pool is closed |
|
|
表 3 月池打开时水动力导数的增量 Tab.3 The increment of hydrodynamic derivatives when moon pool is open |
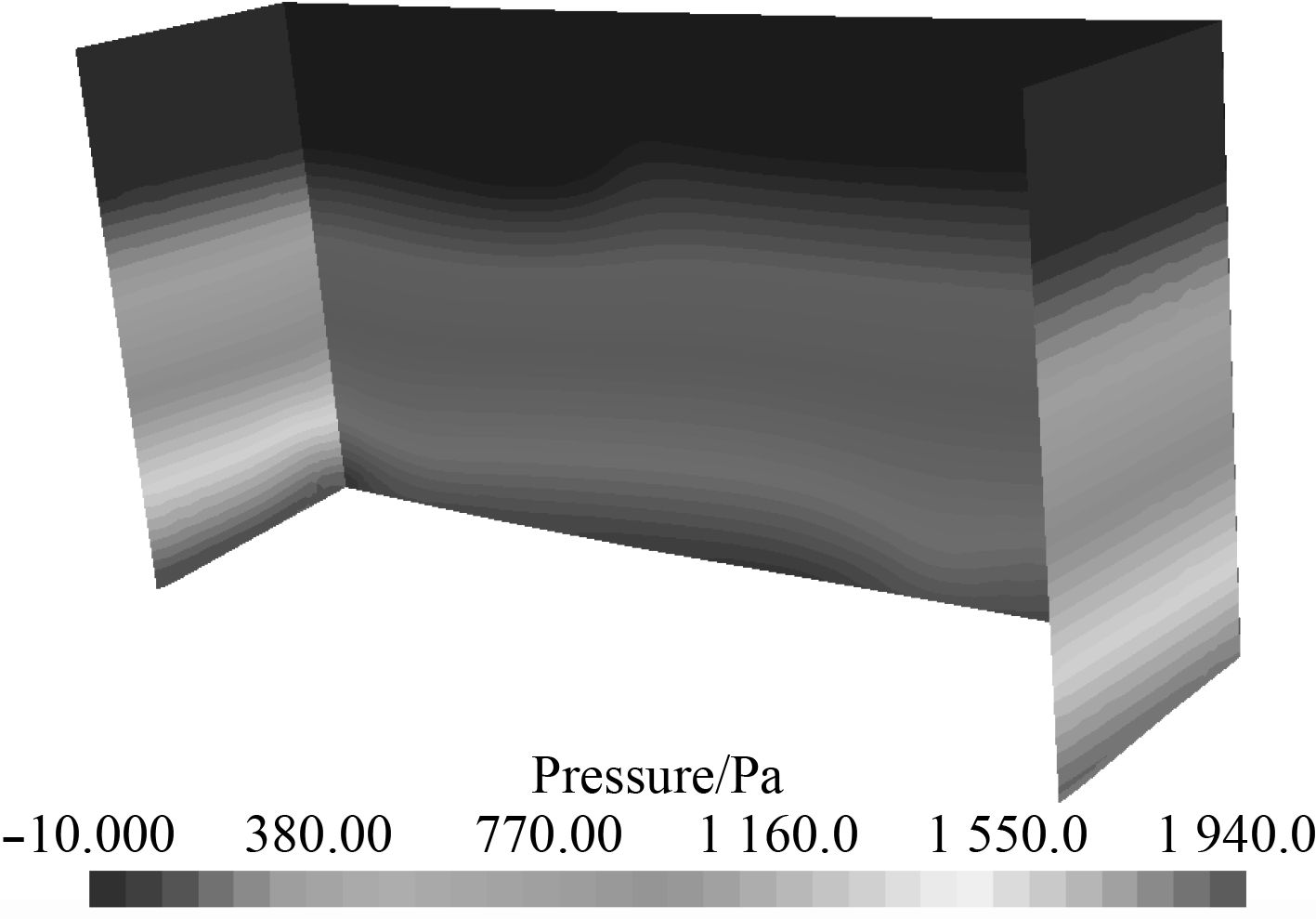
由图5可知,在做斜航实验时,月池打开时船舶阻力会明显大于月池闭合时的船舶阻力。分析船体周围流场发现,由于月池的存在诱导流体形成了如图13所示漩涡,漩涡的维持必须有持续不断的能量输入,由此改变了船体表面的压力分布,增加了船体受力。如图14所示,分析月池附近压力分布图发现,月池后壁和侧壁的压力具有增加,这会使得船模受到的阻力和侧向力增大,从而影响了水动力导数的大小。

|
图 13 开口内部流场 Fig. 13 Flow field inside the moon pool |
|
图 14 开口表面压力分布 Fig. 14 Pressure distribution of the surface of moon pool |
月池打开时水动力导数与月池封闭时的计算值相比较:1)由表3可以看出
本文基于重叠网格技术数值模拟了深拖母船在月池封闭和打开时的拘束航模实验,并求得了相应水动力导数。在船模月池闭合时,将数值模拟计算结果与势流理论计算值相比较,发现两者总体偏差不大,数值模拟算得的水动力导数有较高的精度。这表明基于重叠网格技术可以很好地模拟船模拘束实验,得到准确的数值预报值。在此基础上,对月池处于闭合与打开时算得的数值模拟结果相比较,发现:1)月池的存在诱导了旋涡的生成以及壁面的压力分布,从而引起船模的阻力的增加以及侧向力首摇力矩的变化,月池的存在也使得船体受力在时间上有所滞后;2)月池的存在使得大部分水动力导数有所增加,从而影响船舶的操纵性;3)旋转类水动力导数与理论计算值相差较大,这与计算时旋转中心点的选取有关,在实验时应予以注意。
| [1] |
ITTC. Proceedings of 25th ITTC[J], 2008, Volume Ⅰ: 143–203.
|
| [2] |
KIM Y G, KIM S Y, KIM H T, et al. Prediction of the maneuverability of a large container ship with twin propellers and twin rudders[J]. Journal of Marine Science & Technology, 2007, 12(3): 130-138. |
| [3] |
蔡创, 蔡新永, 赵传波, 等. 船舶浅水操纵性能的数值仿真[J]. 重庆大学学报, 2012(8): 116-121. |
| [4] |
OHMORI T. Finite-volume simulation of flows about a ship in maneuvering motion[J]. Journal of Marine Science & Technology, 1998, 3(2): 82-93. |
| [5] |
SIMONSEN C D, OTZEN J F, KLIMT C, et al. Maneuvering predictions in the early design phase using CFD generated PMM data[J].
|
| [6] |
张赫, 庞永杰, 李晔. 基于FLUENT软件模拟平面运动机构试验[J]. 系统仿真学报, 2010(3): 566-569. |
| [7] |
TURNOCK S R, PHILLIPS A B, FURLONG M. Urans simulations of static drift and dynamic manoeuvres of the KVLCC2 tanker[C]//SIMMAN 2008: workshop on verification and validation of ship manoeuvring Simulation Methods, 2008.
|
| [8] | |
| [9] |
杨勇. 非定常操纵运动船体水动力数值计算[D]. 上海: 上海交通大学, 2011.
|
| [10] |
邓锐, 黄德波, 于雷, 等. 影响双体船阻力计算的流场CFD因素探讨[J]. 哈尔滨工程大学学报, 2011(2): 141-147. DOI:10.3969/j.issn.1006-7043.2011.02.002 |
| [11] |
沈海龙, 苏玉民. 肥大型船伴流场数值模拟的网格划分方法研究[J]. 哈尔滨工程大学学报, 2008(11): 1190-1198. DOI:10.3969/j.issn.1006-7043.2008.11.010 |
| [12] |
邢磊. 三体船水动力导数及操纵性能预报研究[D]. 哈尔滨: 哈尔滨工程大学, 2012.
|
 2019, Vol. 41
2019, Vol. 41
