0 引　言

近年来，美国海军主导的新概念武器——舰载电磁轨道炮项目吸引了全世界的目光。2017年3月，美国海军公布了BAE公司研制的32MJ炮口动能舰载电磁轨道炮发射装置陆上发射试验视频。美国海军电磁轨道炮32MJ的炮口动能超过了美国现役127 mm舰炮和155 mm舰炮，炮口初速是常规舰炮的3倍左右，达到2 km/s以上。伴随着炮口初速、炮口动能的提高，在有限加速长度下，推动电磁炮弹加速的洛伦磁力将会达到数兆牛。直观分析，依据牛顿定律，电磁炮弹发射过程中的反作用力同样会达到数兆牛。也有文献从馈电部分分析，推理得到电磁反作用力^[1]，其数量级基本相同。为减小电磁发射过程中反作用力对炮架刚强度的不利影响，提高适装性，确保实现连发功能，电磁轨道炮同样需要设置反后坐装置。

通过设计反后坐装置的后坐阻力，将使电磁轨道炮后坐部分的能量得到合理消耗与利用，使得炮架在发射过程中受到的冲击力大幅减小，有利于减轻炮架的质量；同时通过反后坐装置的设计，将使电磁轨道炮后坐部分能够按照预定的阻力规律和后坐运动规律后坐，保证后坐部分在电磁炮弹在身管膛内运动期间的稳定性；并按照设计要求吸收和贮存复进能量，用于后坐结束后确保后坐部分按照设计的复进规律稳定复进到初始待发位置，并能按要求为相关机构储能；反后坐装置能够在高低射角范围内，随时抵抗后坐部分重力分力，使后坐部分稳定可靠地运动到规定的后坐位置、复进到规定的初始待发位置，为连续发射创造条件^[2]。

电磁轨道炮后坐部分的主体是电磁身管，其物理特性对反后坐装置的设计影响甚大。据悉，美军海上系统司令部正在为电磁轨道炮开发一种新型“集成炮架”，炮架的总重量将超过130 t，其中电磁身管自身重量约为18 t^[3]。电磁身管的这一特性，决定了电磁轨道炮反后坐装置与传统火炮反后坐装置在驻退、复进规律，以及后坐能量耗散与利用方面有着一定差别。

1 电磁轨道炮自由后坐时期及自由后坐运动诸元的计算

文献[4]给出了一种电磁轨道炮发射时的电流波形，该波形是一种典型的脉冲电流波形。文献[5]将电磁轨道炮的后坐运动分为3个时期:电枢膛内运动时期、电枢出膛后残余电能释放时期与惯性后坐时期。

本文将电磁轨道炮发射时的后坐过程简化为电磁炮弹沿膛内运动时期和后坐部分惯性运动时期2个阶段。本文认为电枢出炮口后，尽管有残余电能释放，但上下导轨物理上是断开的，不能构成导电回路，因此不能产生前向的洛伦磁力。该瞬时即便考虑空气被电离而使上下导轨构成了通路，但由于被电离的气体质量很小，使得后坐部分的动量很小。即便存在电枢出膛后残余电能释放时期，其对电磁轨道炮后坐过程的影响可以忽略不计。

在电磁炮弹沿膛内运动时期，设 $v$ 为弹丸相对于炮膛的运动速度， $V$ 为炮身相对于地面的后坐速度，则电磁炮弹弹丸相对于地面的绝对运动速度为（ $v - V$ ）。忽略后坐部分的外力，系统动量守恒，则有：

$m(v - V) = MV{\text{，}}$

(1)

由此可得：

$V = \frac{m}{{m + M}}v{\text{。}}$

(2)

式中： $m$ 为电磁炮弹的质量； $M$ 为后坐部分的质量。

对式（2）进行积分，可得：

$L = \frac{m}{{m + M}}x{\text{。}}$

(3)

式中： $L$ 为后坐部分相对于大地的后坐行程； $x$ 为电磁炮弹膛内运动的行程。

当电磁炮弹、后坐部分的质量确定后，通过测量电磁炮弹在膛内的速度、行程，即可求出任意瞬时后坐部分的自由后坐速度 $V$ 和自由后坐行程 $L$ 。

2 电磁轨道炮制动后坐诸元的计算

电磁轨道炮发射时，后坐部分在电磁反作用力及反后坐装置提供的后坐阻力的共同作用下后坐。电磁反作用力使后坐部分加速向后运动，由于反后坐装置提供的后坐阻力作用，速度逐渐减小，直到后坐终止。反后坐装置提供的后坐阻力 $R$ 主要由制退机力 ${F_Z}$ 、复进机力 ${F_f}$ 、各种摩擦力 $F$ （包括密封装置摩擦力及摇架导轨上的摩擦力）和后坐部分重力 ${M_g}$ 的分力所构成，其表达式为：

$R = {F_Z} + {F_f} + F - Mg\sin \varphi {\text{，}}$

(4)

式中， $\varphi $ 为电磁轨道炮的高低射角。

以后坐部分后坐方向为正，按照牛顿第二定律，后坐部分的运动微分方程为：

$M\frac{{{{\rm d}^2}x}}{{{\rm d}{t^2}}} = M\frac{{{\rm d}v}}{{{\rm d}t}} = {F_{dc}} - R{\text{。}}$

(5)

式中： $x$ 为后坐行程； $v$ 为后坐速度； ${F_{dc}}$ 为电磁反作用力。

按照式（5）就可以推导出制动后坐运动诸元。同时，可以看出，电磁反作用力 ${F_{dc}}$ 是使后坐部分后坐的主动力，后坐阻力 $R$ 是阻碍后坐部分运动的力。不同炮口动能对应的内弹道参数确定后，电磁反作用力 ${F_{dc}}$ 就可以确定。后坐阻力 $R$ 则需要根据电磁轨道炮具体的技术指标进行设计，其变化范围有着一定要求。后坐阻力R的变化不宜急剧，也不宜过于平缓，需要综合权衡。

3 电磁轨道炮自由后坐运动诸元分析

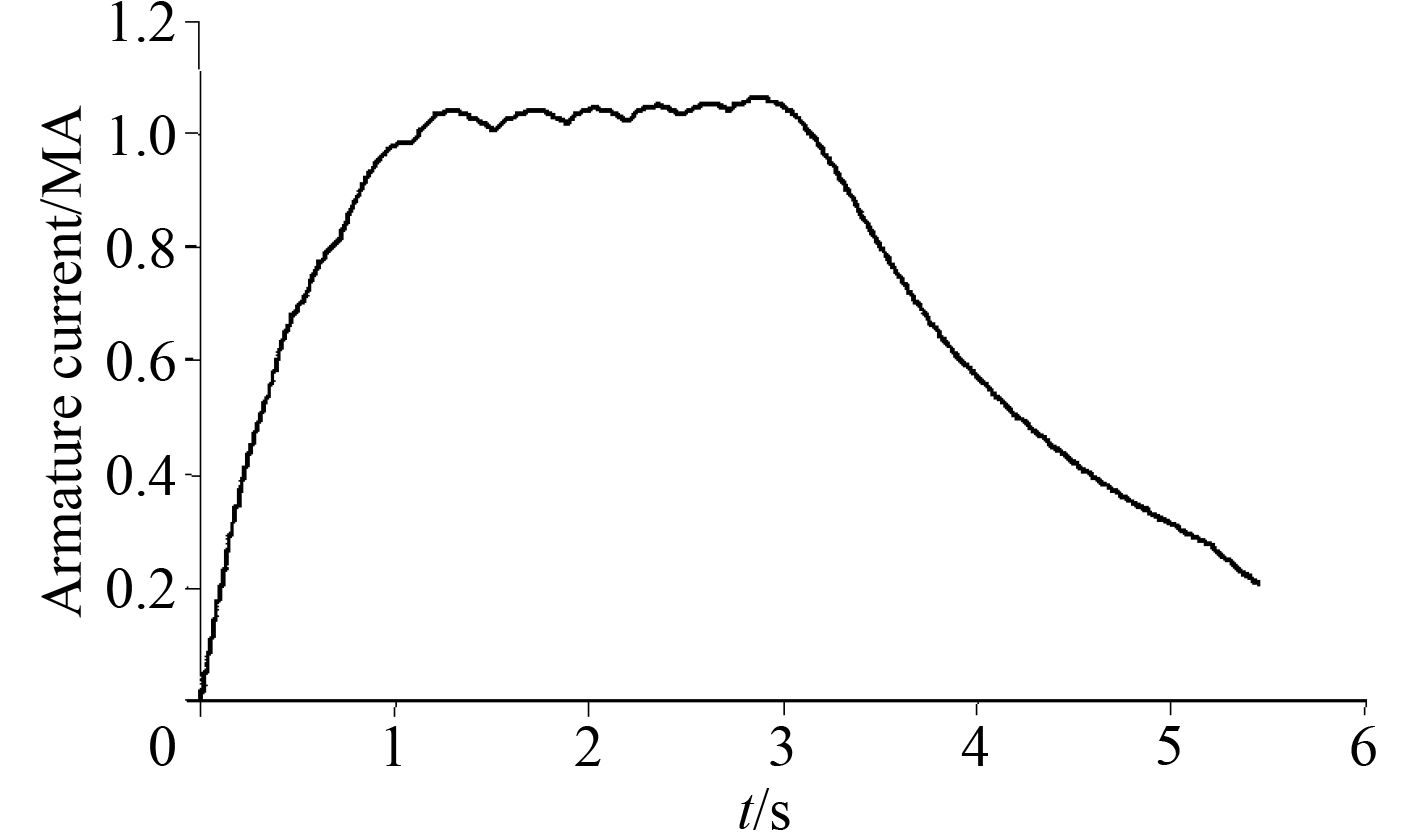
以美国公布的32MJ炮口动能、2 km/s炮口初速、加速长度10 m、身管质量18 t作为后坐部分质量作为假定计算条件，在图1给定的脉冲电流波形基础上放大到4MA量级进行分析。

由式（2）、式（3）可以推得电磁炮弹出炮口瞬时，后坐部分的最大自由后坐速度为1.776 m/s，后坐部分的最大自由后坐行程约为8.88 mm。

电磁炮弹沿膛内运动时期结束后，后坐部分即进入后坐惯性运动时期。假定没有反后坐装置，后坐阻力仅包括摩擦力，后坐部分获得的最大动能将以摩擦阻力做功的形式消耗掉。在平角状态，则有：

$\frac{1}{2}M{V^2} = \mu Mgs{\text{，}}$

(6)

$s = \frac{1}{{2\mu g}}{V^2}{\text{。}}$

(7)

式中： $\mu $ 为后坐部分与其滑动配合副的摩擦系数； $s$ 为摩擦阻力作用下的最大后坐位移； $g$ 为重力加速度。

在平角状态及摩擦阻力作用下，不同摩擦系数下对应的最大后坐行程如表1所示。

可以看出，摩擦系数越小，后坐行程越长。后坐行程越长对提高电磁轨道炮的发射率越不利。为此，需要设置反后坐装置减小后坐行程，同时储存一定能量，用于后坐部分复位，使得电磁轨道炮再次处于初始待发位置。

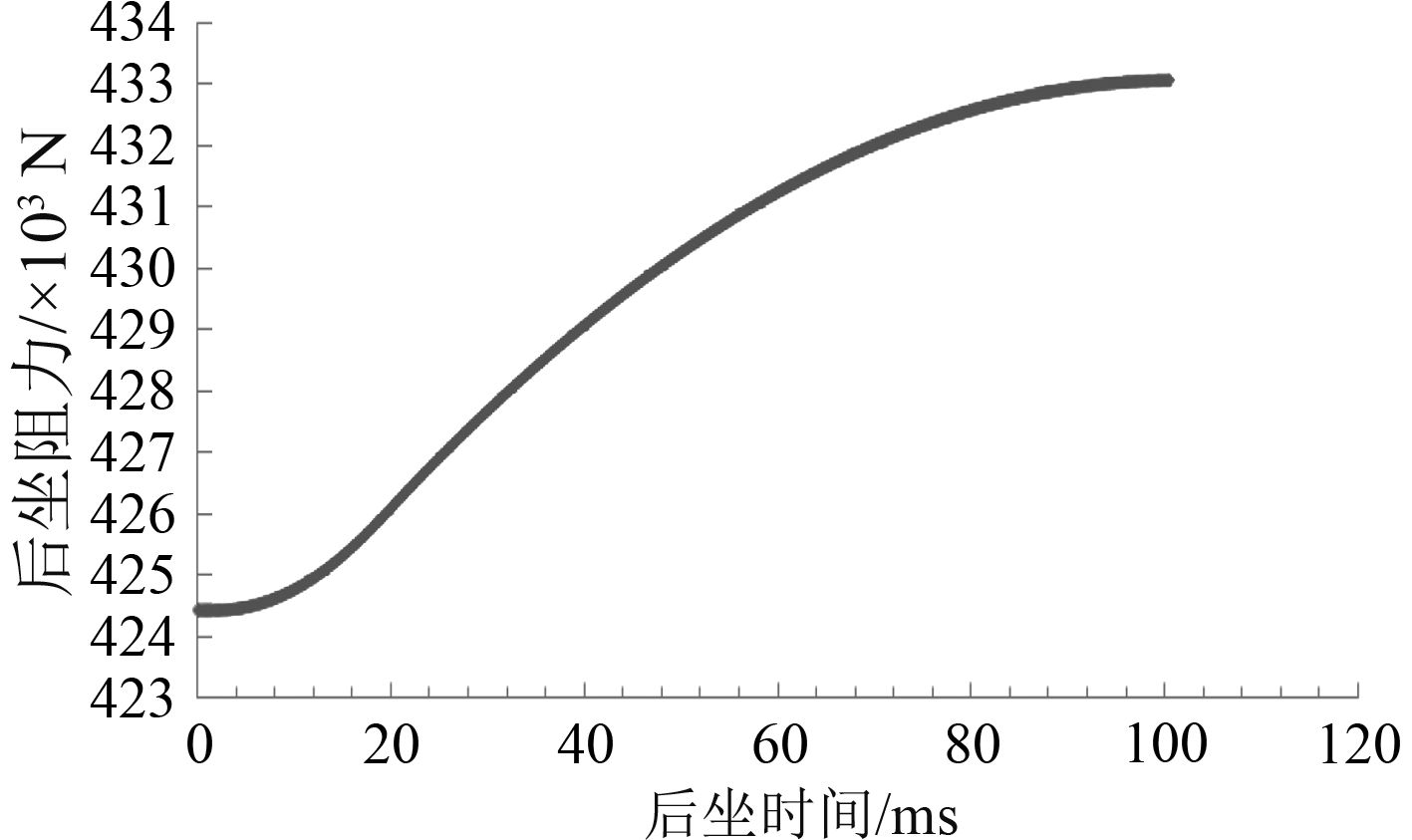
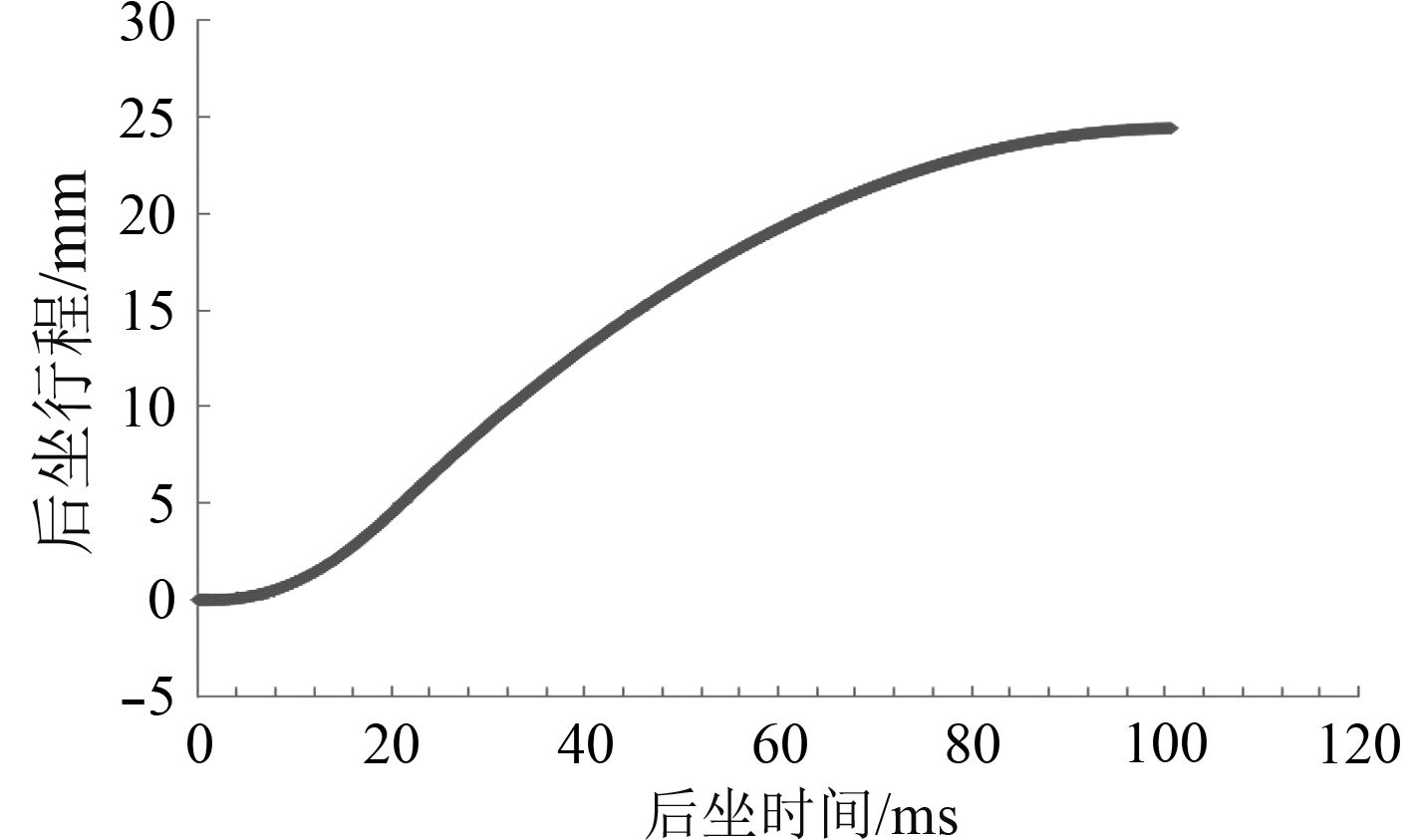
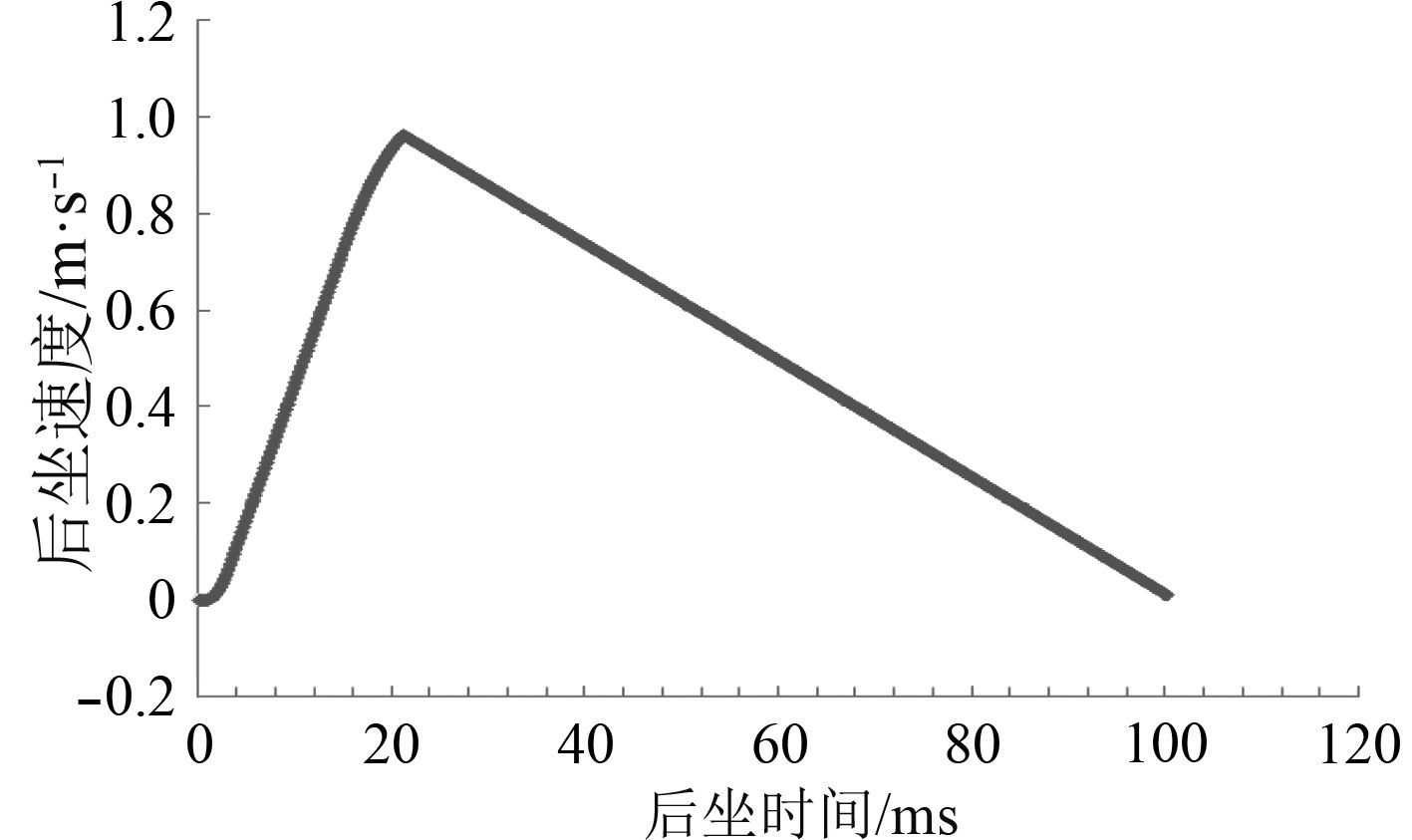
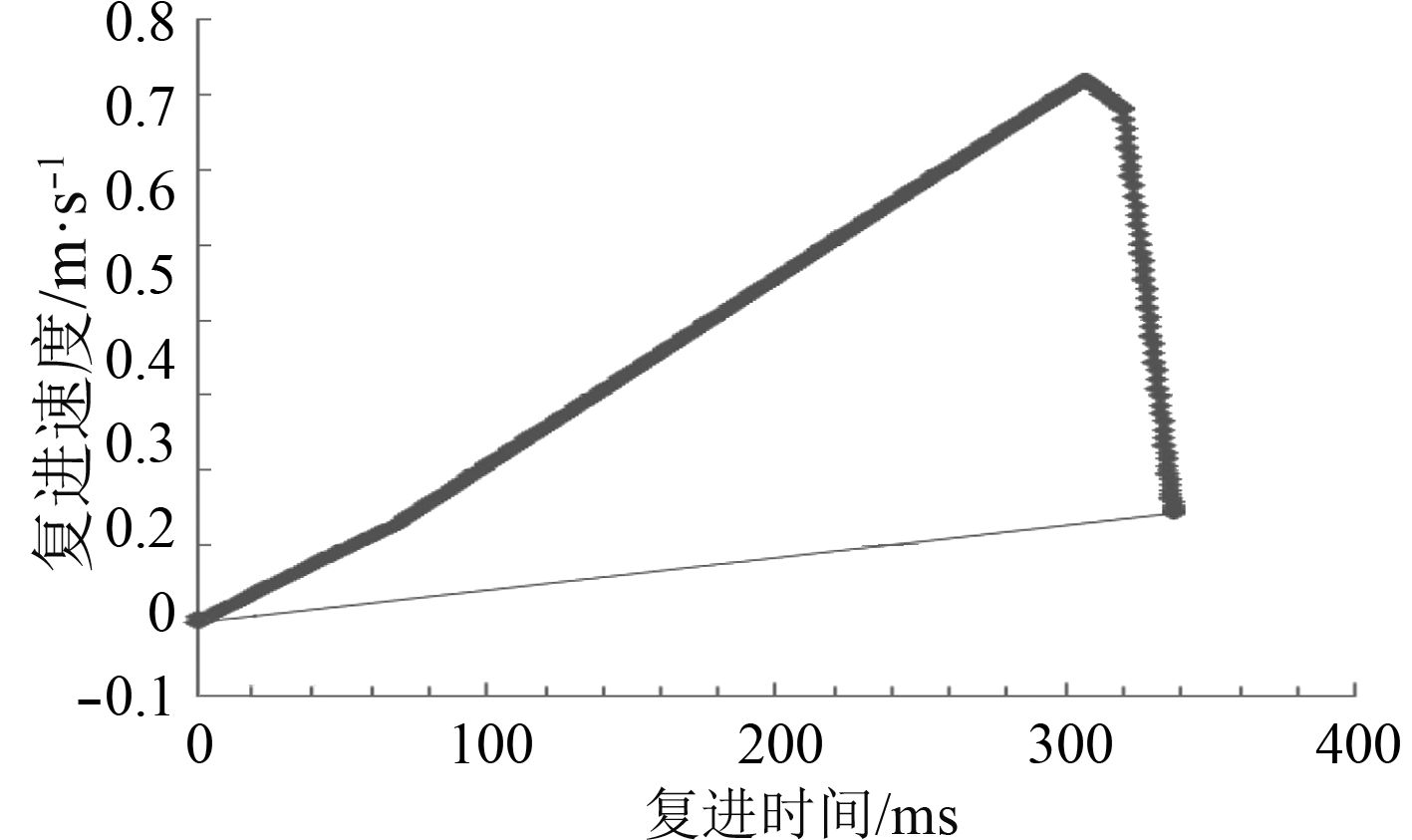
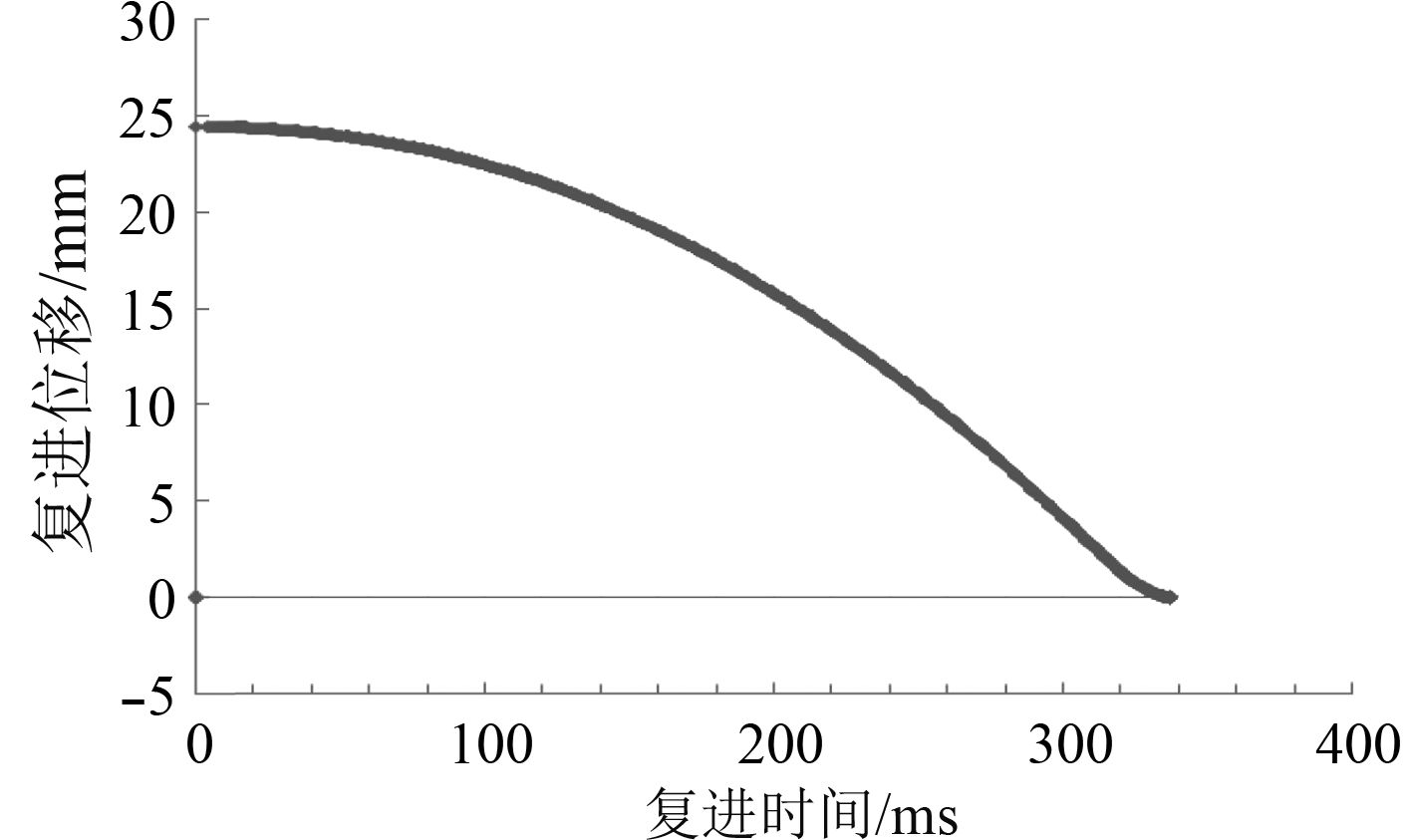
4 电磁轨道炮反后坐装置的设计研究

对于电磁轨道炮的反后坐装置，可以利用制退机和复进机进行组合，根据电磁轨道炮大后坐质量的特殊条件，按照式（4）、式（5）推导相关后坐运动诸元。得到高低零度射角时，后坐时间与后坐阻力曲线（见图2）、后坐时间与后坐位移曲线（见图3）、后坐时间与后坐速度曲线（见图4）、复进时间与复进速度曲线（见图5）、复进时间与复进位移曲线（见图6）。可以看出，后坐时间为50.3 ms，最大后坐阻力43.31 t，最大后坐行程24.4 mm，最大后坐速度0.96 m/s，复进时间336.8 ms。后坐行程与复进行程一致，复进终了时复进速度约为0.1 m/s，满足后坐复进要求。

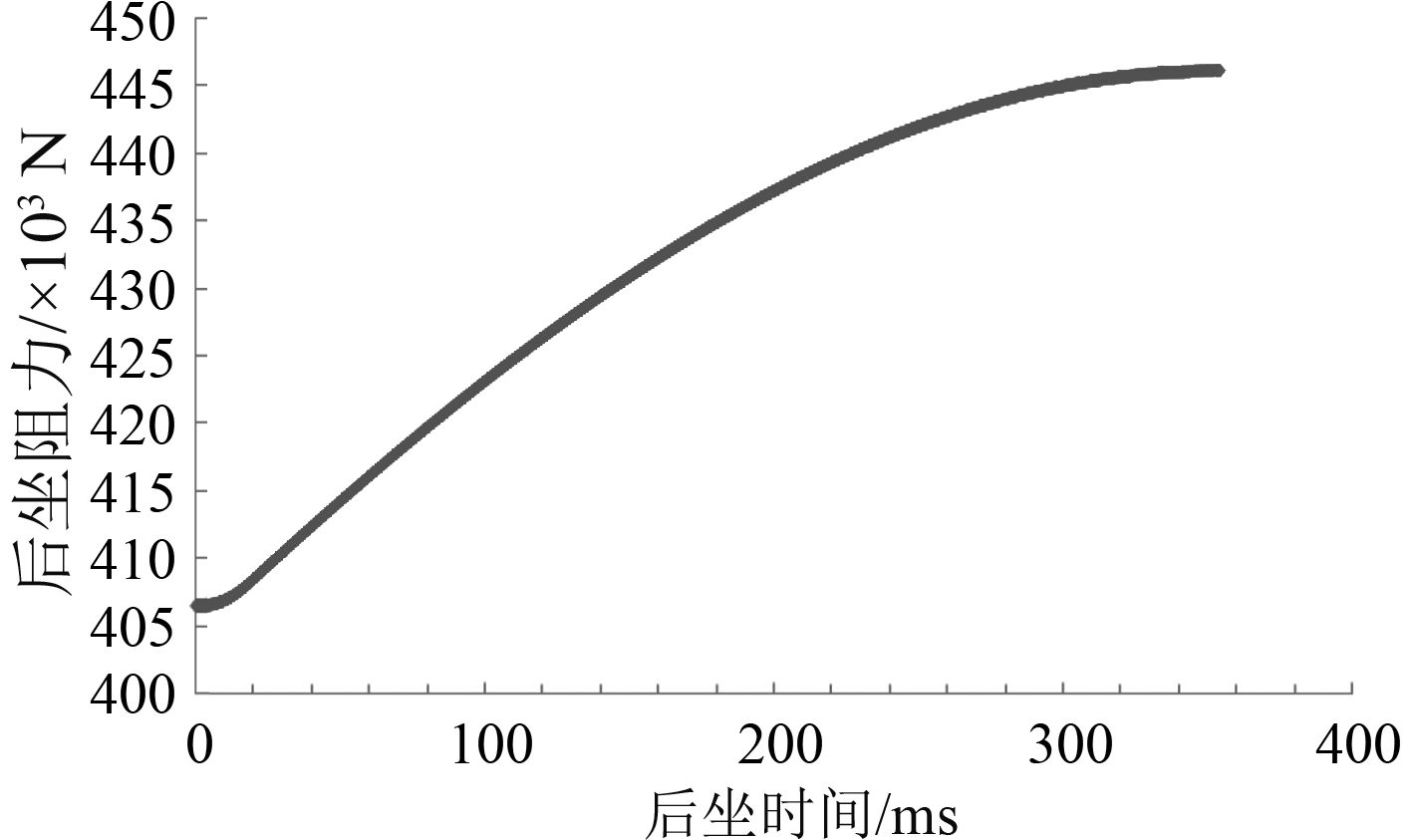
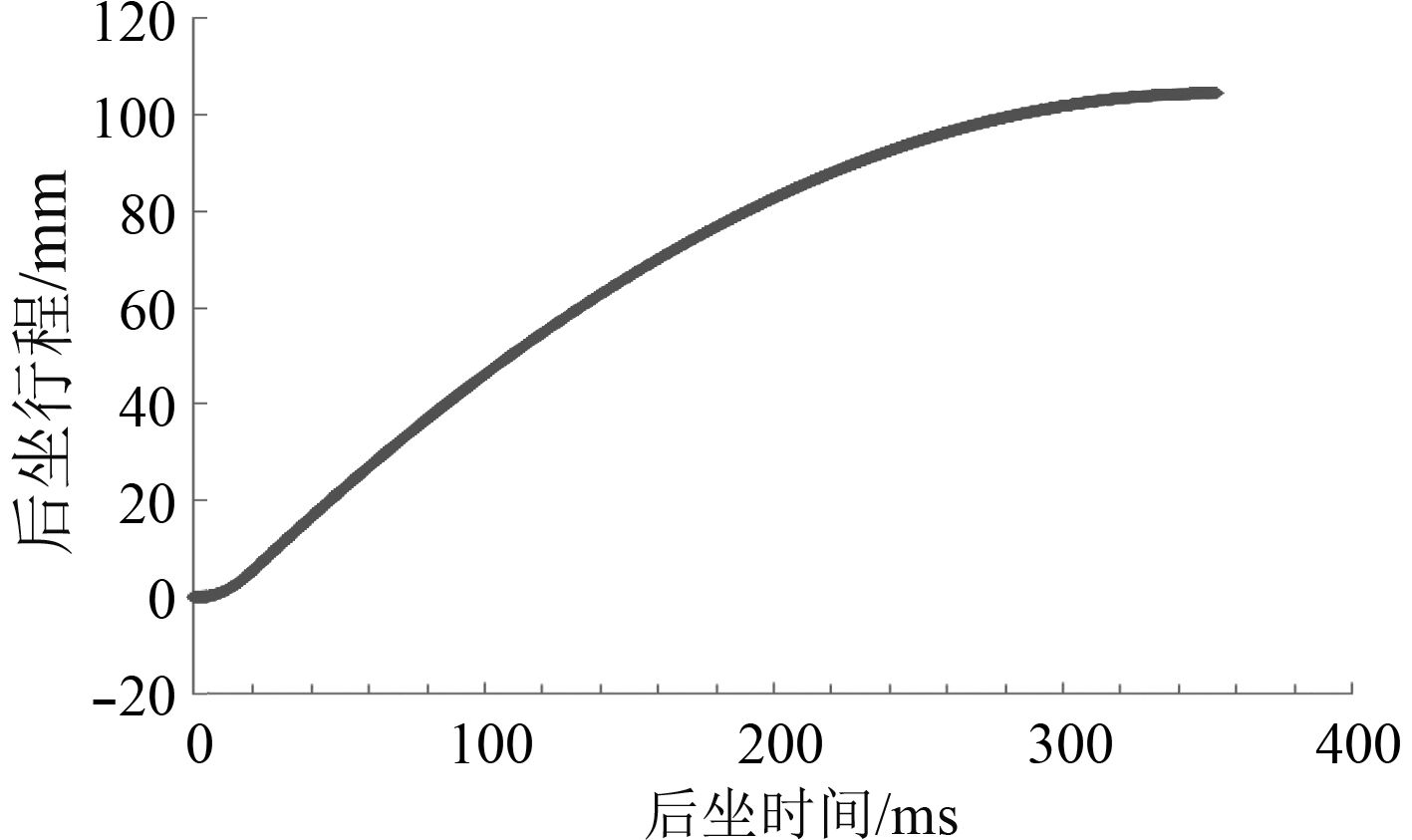
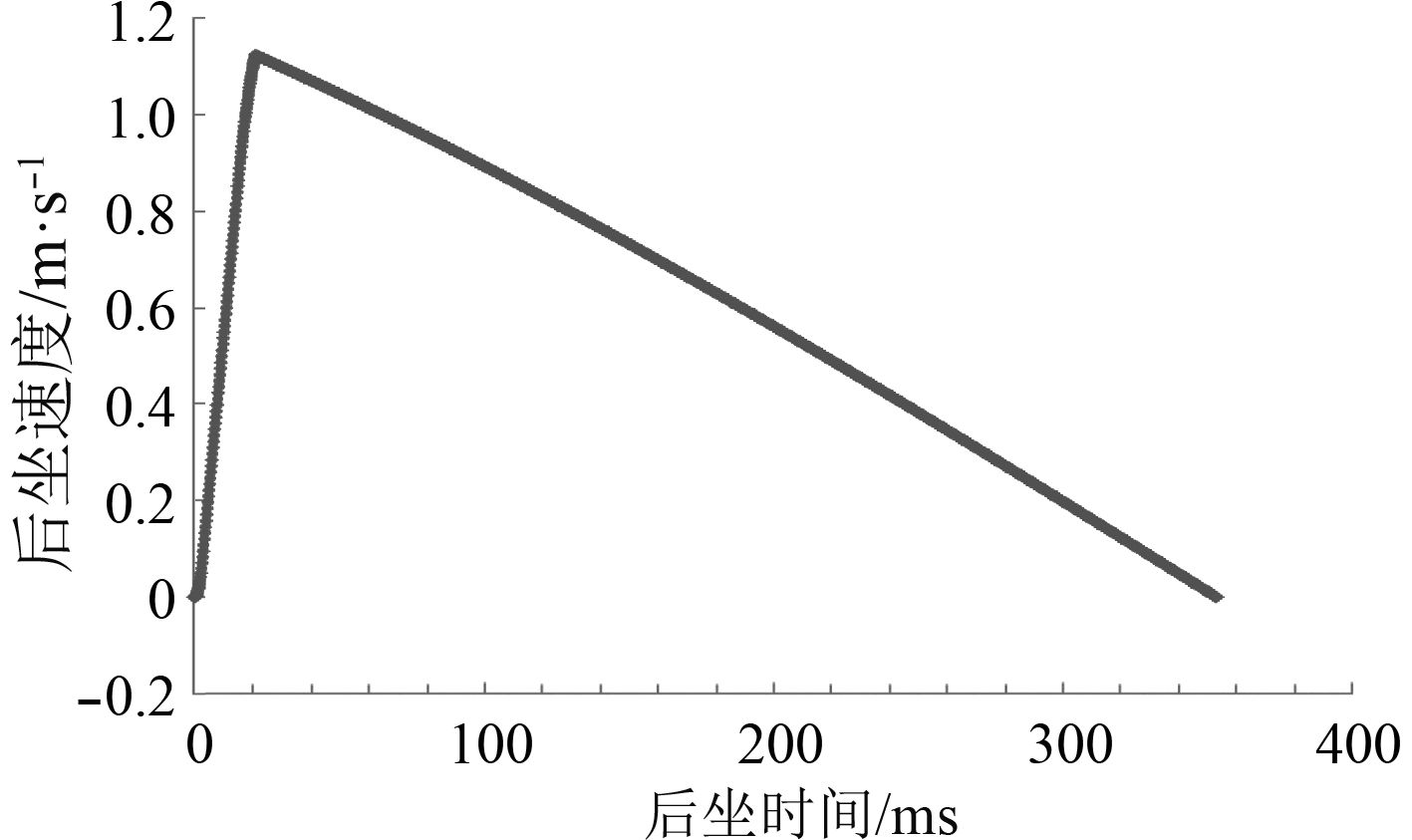
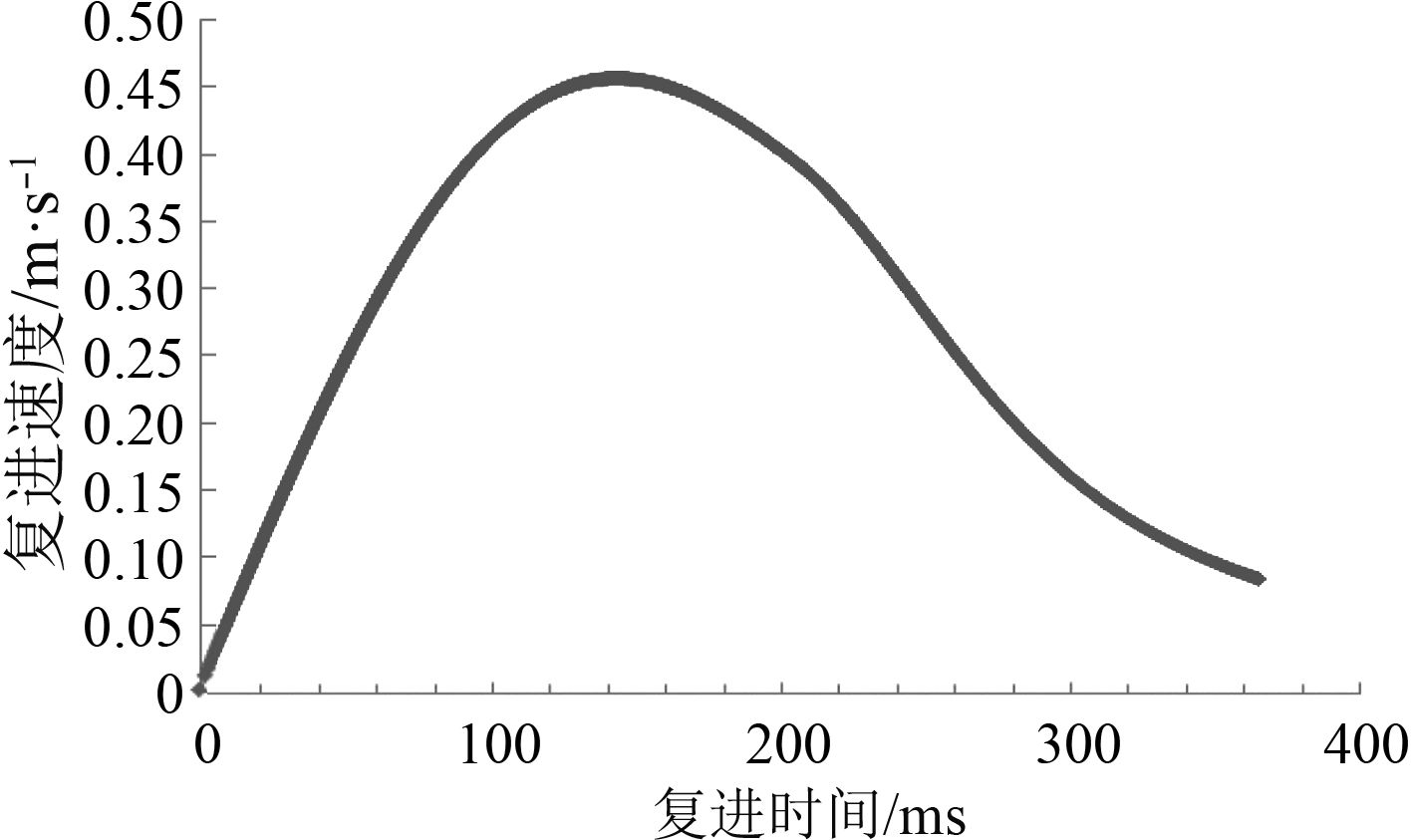
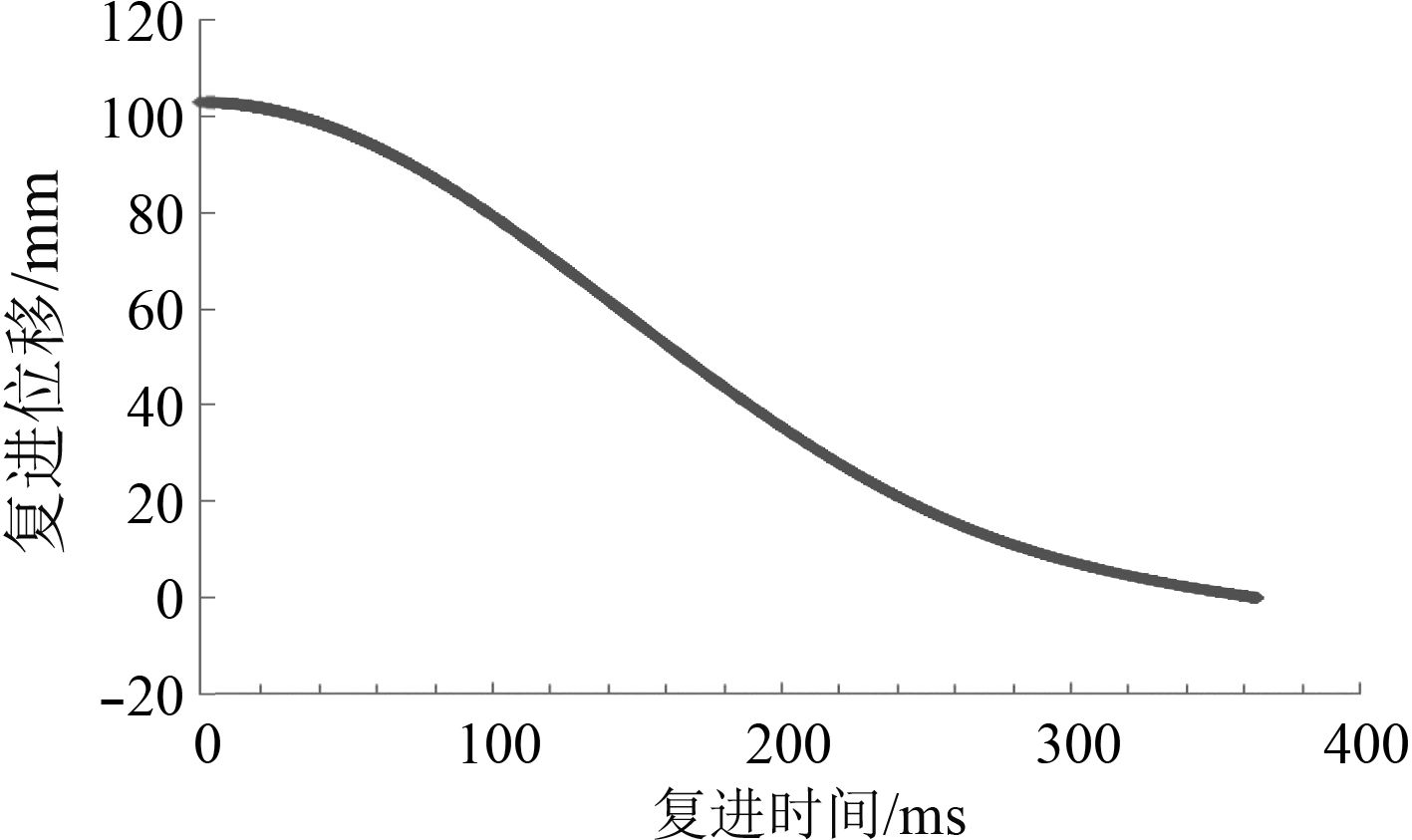
高角时由于后坐部分重力分力作用，后坐主动力增大，带来后坐加速度增大，相应地后坐阻力、行程都需要相应增大，后坐复进总时间也相应增大。以高角60°为例，通过计算得到后坐时间与后坐阻力曲线（见图7）、后坐时间与后坐位移曲线（见图8）、后坐时间与后坐速度曲线（见图9）、复进时间与复进速度曲线（见图10）、复进时间与复进位移曲线（见图11）。可以看出，后坐时间为350 ms，最大后坐阻力44.6 t，最大后坐行程104 mm，最大后坐速度1.12 m/s，复进时间365.4 ms。后坐行程与复进行程一致，复进终了时复进速度约为0.08 m/s，满足后坐复进要求。

5 结　语

与传统火炮类似，电磁轨道炮也存在后坐现象。不同的是，电磁轨道炮的后坐运动时期可视为2个运动时期，没有火药发射的后效期。电磁轨道炮后坐部分的特点是后坐质量大、后坐最大速度相对较小，为此需要结合其他技术指标合理设计反后坐装置，使得电磁轨道炮能够按预定后坐、复进规律进行运动，从而达到与全炮总体技术指标的匹配。