0 引　言

声呐目标跟踪技术作为水下UUV关键技术，是计算机视觉的重点研究课题之一^[1]。目标跟踪技术可获取监测目标感兴趣的特征信息和运动状态，同时对目标的识别和分割技术发展起到了重要推动作用。声呐图像序列目标跟踪技术通过利用提取目标的图像信息，对环境噪声和混响等干扰因素进行一定抑制，以实现对水下目标的有效跟踪。水声图像目标跟踪技术起步略晚，但目前正处于快速发展阶段。各个国家都围绕着水下目标开展相关研究，其中美欧都有成立相关的研究机构，例如美国Florida Atlantic大学海洋工程系，其利用自研水下UUV进行水下目标探测、目标跟踪等试验，取得了一些进展^[2]；在国内，如中科院声学所、哈尔滨工程大学等，也在水下目标处理相关领域开展了研究工作^{[3 – 5]}。其中，中科院声学所研制了一种单波束侧扫声呐，并以此为基础开展了水下目标识别及检测等工作，取得了一定的成果；哈尔滨工程大学在小平台探测声呐展开了相关研究，己研制出二维高分辨率成像声呐、三维成像声呐等多类样机，在水下声图像处理领域也取得了一定程度的进展。

声呐图像处理相较于光学图像，由于其受海底噪声、环境噪声干扰严重，给声呐图像处理带来了很多不便。相比传统线性模型，粒子滤波在水下非线性系统的应用中具有独特优势^[6]。与非线性模型相比，粒子滤波目标跟踪模型是一种非线性模型，具有更好的适用性、估计精度及灵活性，能够适应复杂的水下环境。但由于水下环境噪声干扰更强烈，将粒子滤波直接用于声呐图像跟踪并不能取得理想效果。本文针对以上问题，首先提出一种Curvelet变换的图像增强改进算法；该算法在有效降低声呐图像噪声的同时，对目标边缘也进行了一定的增强；在此基础上提出了一种新的基于粒子滤波的目标跟踪方法，在保证鲁棒性的同时，提高了跟踪精度。与传统声呐目标跟踪方法相比，本文所提方法在保证鲁棒性的同时，提高了跟踪精度，具有更好的适应性。

1 声呐图像的预处理

海洋水下环境复杂多变，声呐图像受到噪声的随机干扰严重，使得原本均匀连续变化的灰度突然增大或减小，噪声的产生因素很多，主要由换能器灵敏度差异、温度变化、电磁影响等因素产生。可能形成高斯噪声、椒盐噪声、斑点噪声等多种形式的噪声^[7]。而且，气泡散射、多径干扰以及海洋中特有的声现象也是噪声的重要来源。为了确保目标检测及后续的跟踪精度，就必须对声呐图像进行一定的预处理，以降低海洋噪声，混响等干扰因素的影响。

Curvelet变换，即曲波变换。是Donoho等于1988年以小波变换和瘠波变换为理论基础提出的一种多尺度图像增强算法。Curvelet变换能够克服小波变换和瘠波变换在图像边缘和奇异特性等方面的不足，具有一定优势。

声呐图像随机噪声干扰严重，故声呐图像增强的关键问题在于如何降低噪声干扰的同时有效保留目标边缘，自适应的调节动态范围。针对声呐图像序列特点，本文提出一种自适应阈值的Curvelet变换算法抑制噪声干扰，采用一种非线性映射来有效调节各个通道的变换系数，对目标边缘进行增强，拉伸对比度，以提高图像的边缘表现。

对于高频通道，采用定义非线性映射函数：

${\hat C_{\left( {s, d, m, n} \right)}} = \left\{ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} \!\!\!\!\!\! {0, }&{\left| {{C_{\left( {s, d, m, n} \right)}}} \right| < {T_{\left( {s, d} \right)}}}{\text{，}} \end{array}} \\ {\begin{array}{*{20}{c}} \!\!\!\!\!\! {{C_{\left( {s, d, m, n} \right)}}sign\left( {{C_{\left( {s, d, m, n} \right)}}} \right)}&{\left| {{C_{\left( {s, d, m, n} \right)}}} \right| \geqslant {T_{\left( {s, d} \right)}}} {\text{，}} \end{array}} \end{array}} \right.$

(1)

高频子带自适应阈值为：

${T_{\left( {s, d} \right)}} = k \cdot {\sigma _n}{\text{，}}$

(2)

其中： $k$ 为阈值调节系数，取 $k = 3$ ； ${\sigma _n}$ 为噪声标准差估计，采用鲁棒中值估计：

${\sigma _n} = median\left( {abs\left( C \right)} \right)/0.674\;5{\text{，}}$

(3)

其中， $C$ 为最细子带的Curvelet变换系数。

对低频子带（s=1），定义非线性映射函数：

${\hat C_{s, d, m, n}} = q \times {C_{\left( {s, d, m, n} \right)}}sign\left( {{C_{\left( {s, d, m, n} \right)}}} \right){\left[ {\sin \left( {\frac{\text π}{2}\frac{{\left| {{C_{\left( {s, d, m, n} \right)}}} \right|}}{{{C_{\max \left( {s, d} \right)}}}}} \right)} \right]^{\frac{1}{q}}}{\text{，}} $

(4)

其中， $q = \displaystyle\frac{{{{\bar C}_{\left( {s, d} \right)}} + {\sigma _{\left( {s, d} \right)}}}}{{{{\bar C}_{\left( {s, d} \right)}}}}{\text{。}}$

式中： ${C_{\left( {s, d, m, n} \right)}}$ 为原始s尺度d方向上 $\left( {m, n} \right)$ 处的变换系数； ${\hat C_{\left( {s, d, m, n} \right)}}$ 为处理后对应的变换系数（对于低频子带，s=1）； ${C_{\max \left( {s, d} \right)}}$ 为s尺度和d尺度方向变换系数绝对值的最大值：

${C_{\max \left( {s, d} \right)}} = \max \left[ {abs\left( {{C_{s, d}}} \right)} \right]{\text{，}}$

(6)

${\bar C_{\left( {s, d} \right)}}$ 为s尺度d方向上变换系数绝对值的平均值：

${\bar C_{\left( {s, d} \right)}} = mean\left[ {abs\left( {{C_{\left( {s, d} \right)}}} \right)} \right]{\text{，}}$

(7)

${\sigma _{\left( {s, d} \right)}}$ 为s尺度d方向上变换系数绝对值的标准差：

${\sigma _{\left( {s, d} \right)}} = {\left[ {\frac{1}{{MN}}\sum\limits_{m = 1}^M {\sum\limits_{n = 1}^N {\left( {\left| {{C_{\left( {s, d, m, n} \right)}}} \right| - {{\bar C}_{\left( {s, d} \right)}}^2} \right)} } } \right]^{1/2}}{\text{。}}$

(8)

2 声呐图像的目标分割

图像分割的目的是根据不同特性，将图像区域分为若干个子区域。对声呐图像而言，海底混响、环境噪声以及环能器自噪声等多种因素影响，声呐图像半点噪声强、信噪比低，这些均给声呐图像的分割造成了极大困难。声呐图像目标跟踪的关键在于如何将目标与背景有效的分割，以便之后的特征提取奠定基础。

图像分割是一种病态问题，根据贝叶斯理论，分割的关键在于利用图像自身特征信息，结合一定的先验知识，提出合适的分割函数；并且分割的结果应对应图像相关特征并且符合先验约束条件。基于水平集模型的分割算法所采用的活动轮廓模型的能量泛函易于迭代运算，具有集成各种约束的灵活性，求解方便等特点。

LBF水平集模型是Li C为解决水平集重复初始化问题，提出的一种高精准度分割结果的分割模型^[9]。水平集分割的核心思想将闭合曲线视为高维曲面中水平集函数的零水平集，通过求解曲线方程的演化来确定分割边界，具有拓扑变化自由、求解灵活的优点。

LBF水平集模型是一种区域可扩展性的能量拟合模型。非负核函数参数的大小决定了水平集拟合的灰度区域范围。为了使得当前点的拟合能量达到最小，就需要演化曲线到达目标边界且灰度值接近区域内曲线内外的灰度值。即要求对整个区域上的点的拟合能量达到最小。

LBF水平集分割步骤为：1）采用合适的能量函数以确认分割边界；2）利用拉格朗日乘数法求出能量泛函的全局极小值以确定最优的分割边界；3）利用变分法或者梯度下降法等算法，得到能量最小化的演化方程；4）采用某种数值迭代算法求解演化方程。

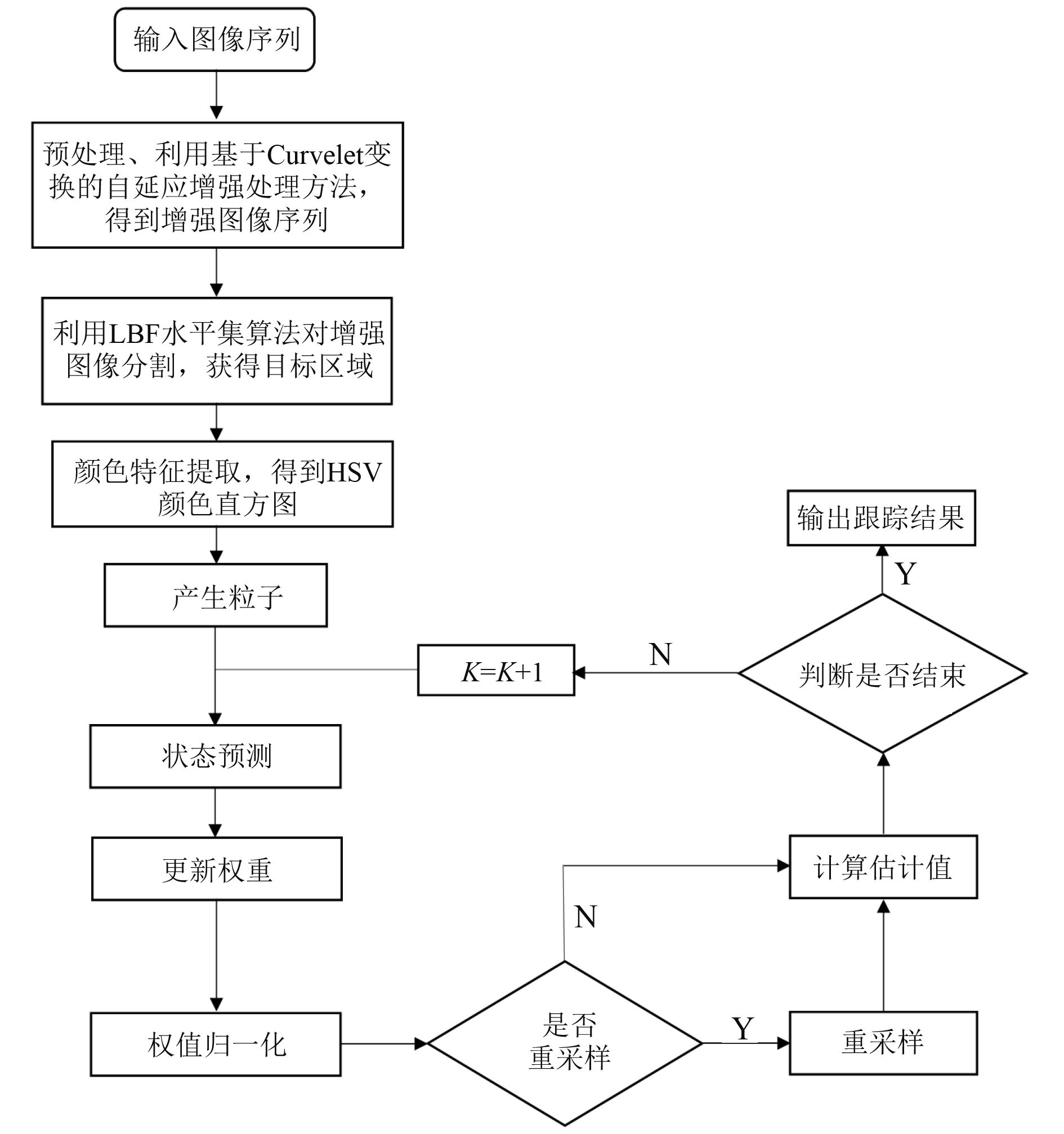
3 基于粒子滤波目标跟踪器的实现

基于粒子滤波的目标跟踪器可以从含有噪声的目标模型中估计目标的运动状态，在状态空间中，通过散布的大量离散随机变量（即粒子）以近似模拟后验概率分布。当粒子个数趋于无穷时，理论上可以无限逼近真实概率密度函数。粒子滤波的关键在于通过权值粒子集合来近似估计分布概率。每个粒子代表了对目标状态的预测，本文的目标特征取为彩色分布模型，处理流程如图1所示。

3.1 目标模型的色彩特征描述

本文采用颜色概率分布直方图作为目标模型特征描述，利用LBF水平集分割从初始声呐图像中将目标与背景有效分割开，确定目标跟踪的区域。对选中区域进行离散统计得到目标区域的HSV彩色分布直方图。为了避免目标边缘像素遮挡的影响，对于目标边缘区域赋予小的权值；对于目标中心区域，赋予较大的权值，保证跟踪的准确性。确定核函数为：

$k\left( r \right) = \left\{ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {1 - {r^2}}{\text{，}}&{r < 1}{\text{，}} \end{array}}\\ {\begin{array}{*{20}{c}} 0{\text{，}}& {\text{其他}}{\text{。}} \end{array}} \end{array}} \right.$

(9)

其中r为像素点距离区域中心的距离。位于y处的像素点颜色分布概率密度函数 ${p_y} = {\left\{ {{p_y}\left( u \right)} \right\}_{u = 1, ..., m}}$ 可以表示为：

$p_y^{\left( u \right)} = f\sum\limits_{i = 1}^n {k\left( {\frac{{\left\| {{y_i} - {x_0}} \right\|}}{a}} \right)} \delta \left[ {h\left( {{y_i}} \right) - u} \right]{\text{，}}$

(10)

其中：

$f = \frac{1}{{\sum\limits_{i = 1}^n {k\left( {\frac{{\left\| {y - {x_i}} \right\|}}{\alpha }} \right)} }}{\text{，}}$

(11)

$\alpha {{ = }}\sqrt {H_x^2 + H_y^2} {\text{。}}$

(12)

式中： $n$ 为目标区域内包含像素个数； ${x_0}$ 为目标区域的中心坐标； $f$ 为归一化因子； ${H_x}$ 和 ${H_y}$ 分别表示目标区域的宽和高； $\delta \left[ {h\left( {{y_i}} \right) - u} \right]$ 函数判断目标区域中像素 ${y_i}$ 处是否为颜色直方图的第 $u$ 个单元。在跟踪过程中，目标状态根据观测向量进行实时更新，采用Bhattacharyya距离衡量颜色特征的相似度。

3.2 目标粒子模型的建立

彩色分布的粒子模型定义为 $s = \left\{ {x, y, {\nu _x}, {\nu _y}, {H_x}, {H_y}, a} \right\}$ ，其中， $x, y$ 是粒子的中心位置； ${\nu _x}$ 和 ${\nu _y}$ 为粒子在 $x, y$ 方向的运动速度； ${H_x}$ 和 ${H_y}$ 表示粒子所在区域的宽与高； $a$ 为尺度因子。通过系统状态转移方程确定粒子样本集合的更新。

3.3 基于颜色直方图的粒子滤波算法

1）预处理。针对声呐图像序列，对每一帧图像进行子带划分，得到Curvelet变换系数。对低频子带，采取非线性映射以增强图像的边缘，得出低频子带增强变换系数；估计得到噪声标准差 ${\sigma _n}$ 得出自适应阈值 ${T_{\left( {s, d} \right)}}$ ，利用自适应阈值计算得到高频子带增强系数；进行Curvelet反变换，得到增强图像序列。

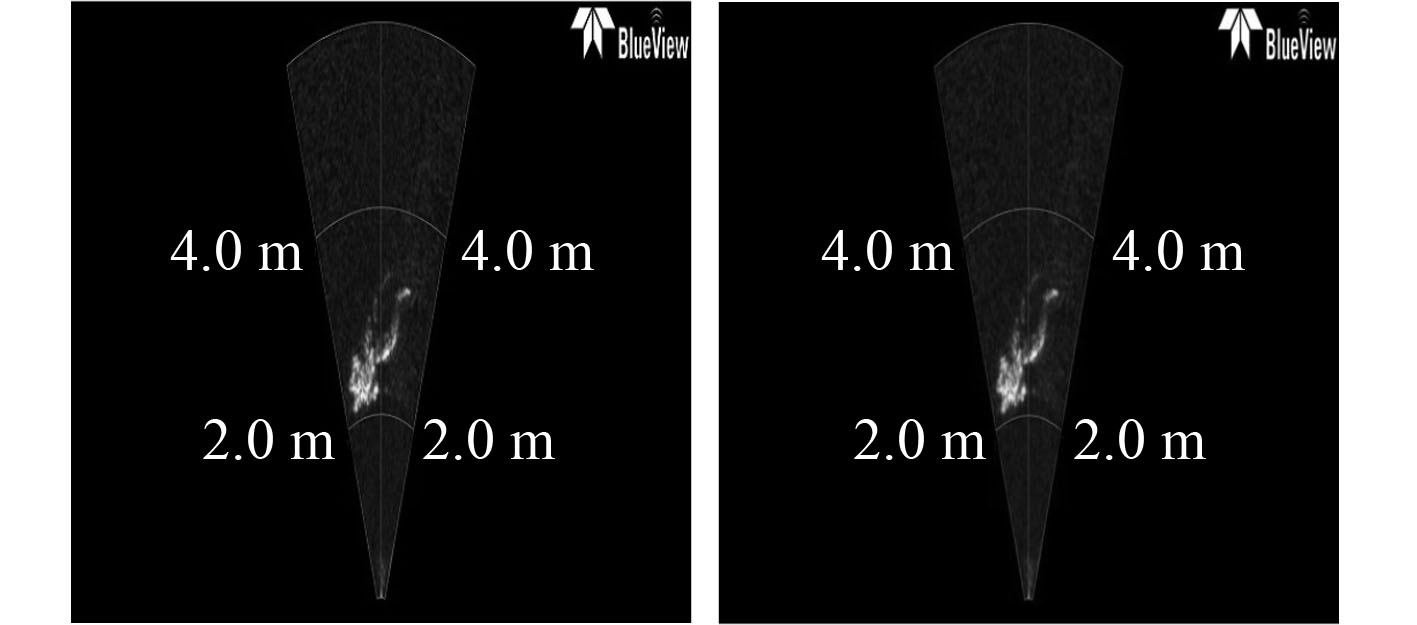
处理输出图像如图2所示。

2）目标分割。输入初始序列图像，利用高斯核函数建立曲线演化方程，进行水平集演化，通过迭代算法使得演化曲线逼近目标边界，从而得到目标区域。

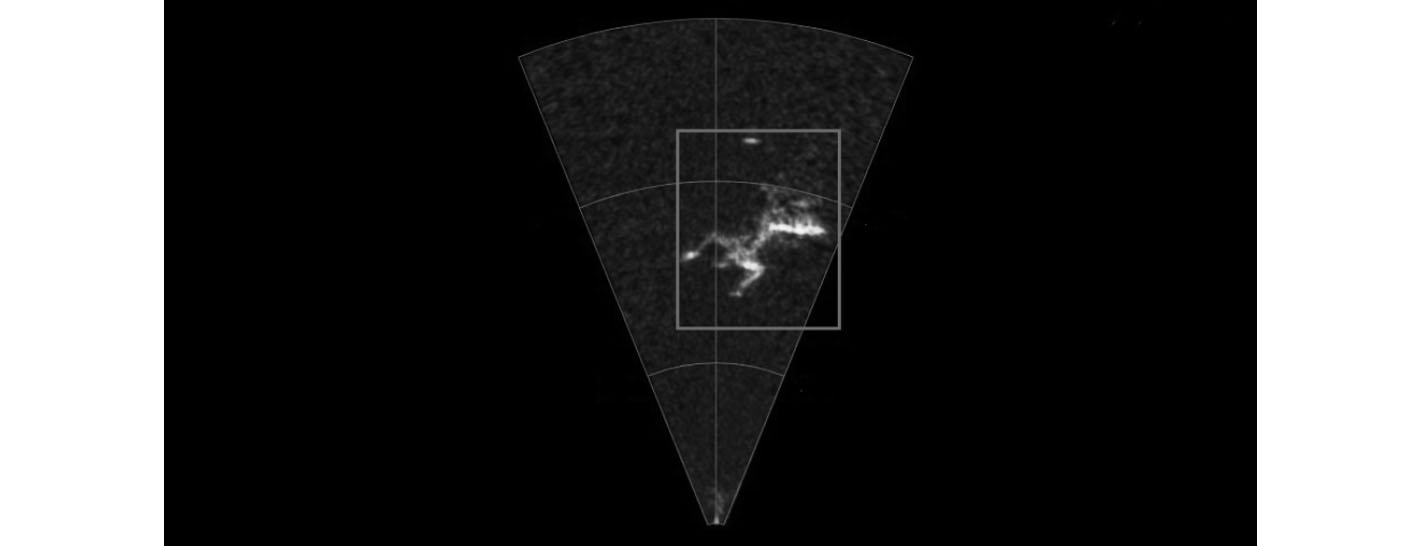
分割处理后得到目标区域如图3所示。

3）基于颜色直方图的粒子滤波算法。提取目标区域的颜色直方图，建立相应特征向量，设置粒子数为N，粒子初始权重均设定为1/N，给定 $t - 1$ 时刻粒子样本集合为 ${S_{t - 1}}$ 。

① 重采样。从集合 ${S_{t - 1}}$ 根据权重 $\pi _{t - 1}^{\left( n \right)}$ 挑选N个样本。

对权重数组计算可得归一化累计概率 $c_{t - 1}^k$ ：

$c_{t - 1}^k = \frac{{\displaystyle\sum\limits_{i = 1}^k {{\pi_i}} }}{{\displaystyle\sum\limits_{i = 1}^N {{\pi_i}} }}\text{，}$

(13)

产生 $N$ 个 $\left[ {0, 1} \right]$ 间满足均匀分布的粒子，构成数组 $r$ 。

对 $r$ 中每个元素用二分查找法搜索归一化累计数组，得到含 $N$ 个最小索引的数组 $j$ ， $j$ 满足 $c_{t - 1}^{j\left[ i \right]} \geqslant r\left[ i \right]$ 。

更新样本粒子集合， $S_{t - 1}^i = S_{t - 1}^{j\left[ i \right]}$ 。

② 传播。根据系统的状态转移方程 ${S_t} = A{S_{t - 1}} + {w_{t - 1}}$ ，计算新的粒子集合 ${S_t}$ ，估计新粒子的位置。

③ 观测。根据状态合集 ${S_t}$ 中的每一个采样样本，观测颜色直方图，更新估计，得到新的权重概率分布。

对于状态集合 ${S_t}$ 中每个粒子计算其颜色分布直方图分布：

$p_{S_t^{\left( n \right)}}^u = f\sum\limits_{i = 1}^n {k\left( {\frac{{\left\| {S_t^{\left( n \right)} - {x_0}} \right\|}}{a}} \right)} \delta \left[ {h\left( {S_t^{\left( n \right)}} \right) - u} \right] \text{，}$

(14)

计算集合中每个粒子颜色分布与目标模型的Bhattacharyya系数：

$\rho \left[ {{p_{S_t^{\left( n \right)}}}, q} \right] = \sum\limits_{u = 1}^m {\sqrt {p_{S_t^{\left( n \right)}}^{\left( u \right)}{q^{\left( u \right)}}} }\text{，} $

(15)

对集合 ${S_t}$ ，根据计算得到的Bhattacharyya系数计算各个权值：

$\pi _t^{\left( n \right)} = \frac{1}{{\sqrt {2{\text π} \sigma } }}{e^{ - \frac{{\left( {1 - \left[ {{\rho _{S_t^{\left( n \right)}}}, q} \right]} \right)}}{{2{\sigma ^2}}}}}\text{。}$

(16)

④ 估计。根据权重，估算集合 ${S_t}$ 的平均值，提取坐标位置，作为目标跟踪输出：

$E\left[ {{S_t}} \right] = \sum\nolimits_{n = 1}^N {{\text π} _t^{\left( n \right)}} S_t^{\left( n \right)}\text{。}$

(17)

⑤ 模型更新。在跟踪输出位置，重新计算目标的彩色直方图，作为下一帧目标的色彩分布。计算当前目标颜色分布与上一帧颜色分布的Bhattacharyya系数，更新权重，将新的权值作为下一帧的初始 $\pi _t^{\left( n \right)}$ 。

4 实验结果及分析

为了验证算法增强的效果，本节对本文跟踪算法和传统算法进行实验对比。传统算法取均值漂移算法和传统粒子滤波算法。本文使用声呐为blueviewm450，声呐图像序列来源为水下25 m。试验平台为Windows，仿真软件为Matlab2012b，跟踪效果如图4所示。

自上至下依次为均值漂移算法、传统粒子滤波算法和本文跟踪算法。由第2帧、第14帧、第26帧的对比可以看到，均值漂移算法的跟踪效果较差，目标在14帧和26帧时没有进入跟踪框；传统粒子滤波效果强于均值飘逸算法，但粒子散布过于离散，不能准确反映目标的位置信息；相较于前2种跟踪方法而言，本文算法取得了良好的跟踪效果，目标运动基本被框定在跟踪框以内，粒子的分布也很集中而均匀。

为了定量评价几种跟踪算法的跟踪效果，引入跟踪精确度以及算法运行时间以检验算法的实时效果。结果如表1所示。

由表1可以看到，相较于传统算法，本文算法在跟踪精确度方面有明显提高。与之相对的是，由于增加前期处理以及算法复杂度，本文算法在实时性方面有一定下降。

5 结　语

本文针对声呐图像序列噪声干扰严重、背景复杂等问题，提出一种基于粒子滤波的声呐图像跟踪算法。对声呐图像的预处理进行深入研究和分析，采用一种自适应阈值的Curvelet变换声呐图像增强算法，有效降低了环境噪声，减小了目标背景干扰。对粒子滤波算法进行了深入分析研究，采用一种基于HSV颜色特征模型的粒子滤波算法，对声呐图像序列进行跟踪仿真实验，并且与传统目标跟踪算法以及传统粒子滤波算法进行了对比实验。

实验结果表明，该算法在跟踪精确度方面有很大提升，而相对的则是增加了运算的复杂程度，实时性略有欠缺。今后的改进工作应针对实时性降低的问题，对算法加以改进和强化，做到实时性和准确性的平衡统一。