近年来,随着国家对海洋开发的重视,水下定位服务的需求日益迫切,以惯性导航为代表的航位推算系统(Dead Reckoning,DR)长时间使用后会引入较大的累积误差,而声波是水下唯一可以进行远距离传播的信号形式,利用水声导航系统校正惯导累积误差成为研究热点。单信标同步式测距定位系统参考了OWTT(one-way travel-time)导航的原理,利用单程传播时间TOF(time-of-flight)进行测距,利用单个信标可以实现水下航行器隐蔽无源定位,极大地降低应用成本,拓展作用范围,同时可以扩展通信指挥功能,是未来发展的趋势[1 – 2]。
文献[3]给出一种航位推算轨迹平移策略的水下航行器初始位置确定方法,文献[4]在水下航行器变向机动的前提下利用最小二乘法解算其水平初始位置,文献[5]利用粒子滤波和扩展卡尔曼滤波实现了单信标测距定位。以上算法针对的是信标固定的假设,实际情况中,信标受洋流的影响不断在运动。文献[6]利用移动的母船给水下航行器提供位置信息,水下航行器采用信息滤波方法实现了单信标同步式测距定位。文献[7]将移动矢径的概念引入水下自主航行器(AUV)的协同定位中,文献[8]考虑了水下未知定常洋流的影响,设计了一种基于单移动领航者仅依靠距离量测的主从式AUV协同定位方法,文献[9]分析了移动矢径对AUV协同定位精度的影响。
基于移动矢径的定位方法在AUV协同定位中得到了广泛应用,本文将移动矢径的的概念应用到移动单信标测距定位系统中,基于扩展卡尔曼滤波(EKF)算法提出一种信标运动场景下的定位算法,用于对航位推算系统的累积误差和定位海域未知声速误差进行估计和滤除。仿真和试验结果表明,该算法可以对未知声速误差进行估计,明显减小了初始位置误差,大大提高了定位精度。
1 基于移动矢径的单信标测距定位模型基于单信标的同步式测距定位系统通过水声通信测量单程传播时延OWTT,其定位示意图如图1所示,水下航行器需要进行定位时,对水声导航信标授时后将其发射出去,信标上浮至水面后接收GNSS(Global Navigation Satellite System)定位信号,信标成功捕获卫星信号实现自定位后以固定频率向外发送水声导航信号,通过水声通信将自身位置和时间发送给水下航行器,由于初始时刻信标和水下航行器时钟同步,水下航行器接收水声导航信号后结合自身时钟测得单程传播时延,并基于单程传播时延进行定位。

|
图 1 单信标同步式测距定位示意图 Fig. 1 Map of single beacon synchronous range measurement location |
水下航行器在该定位场景下已知条件为:水声导航信号单程传播时延,海区平均声速经验信息,信标位置(信标经纬度坐标和信标发射换能器深度),自身运动信息,航行深度等。
将水下航行器第1次捕获到的水声导航信号对应的发射时间记为
| $ {{({{x}_{k}}-{{X}_{k}})}^{2}}+{{({{y}_{k}}-{{Y}_{k}})}^{2}}+{{({{z}_{k}}-{{Z}_{k}})}^{2}}={{(c{{\tau }_{k}})}^{2}} {\text{。}} $ | (1) |
其中:
| $ \left\{ \begin{align} & {{({{x}_{k}}-{{X}_{k}})}^{2}}+{{({{y}_{k}}-{{Y}_{k}})}^{2}}={{r}_{k}}^{2}{\text{,}} \\ & {{r}_{k}}^{2}={{(c{{\tau }_{k}})}^{2}}-{{({{z}_{k}}-{{Z}_{k}})}^{2}}{\text{。}} \\ \end{align} \right. $ | (2) |
假设水下航行器自身航位推算系统精度较高,短时间内运动轨迹推算信息作为不含误差的准确信息,由此建立基于移动矢径的单信标测距定位系统,其定位模型如图2所示。
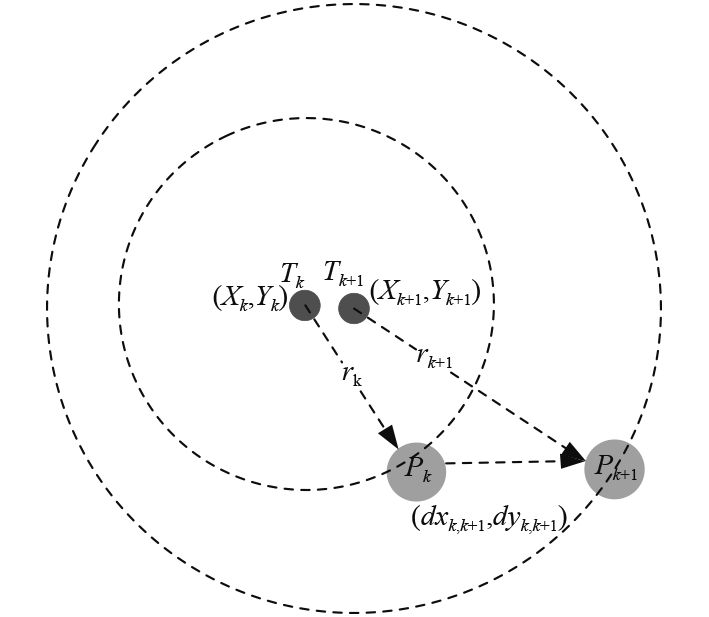
|
图 2 基于移动矢径的单信标测距定位模型 Fig. 2 Single beacon synchronous range measurement location model based on MRV |
参考文献[7]的定义,移动矢径(Moving Radius Vector,MRV)指的是接收机在相邻采样时刻经由自身航位推算获得的相对位移向量。记水下航行器从第
| $ \left\{ \begin{align} & {{x}_{k+1}}{\rm{=}}{{x}_{k}}+d{{x}_{k,k+1}} {\text{,}}\\ & {{y}_{k+1}}{\rm{=}}{{y}_{k}}+d{{y}_{k,k+1}}_{k}{\text{。}} \\ \end{align} \right. $ | (3) |
进而可根据两次测得的距离信息建立如下定位方程:
| $ \left\{ \begin{aligned} & {{({{x}_{k+1}} -d{{x}_{k,k+1}}-{{X}_{k}})}^{2}}+{{({{y}_{k+1}}-d{{y}_{k,k+1}}_{k}-{{Y}_{k}})}^{2}}\\ & \quad\quad ={{(c{{\tau }_{k}})}^{2}}-{{({{z}_{k}}-{{Z}_{k}})}^{2}} {\text{,}}\\ & {{({{x}_{k+1}}-{{X}_{k+1}})}^{2}}+{{({{y}_{k+1}}-{{Y}_{k+1}})}^{2}}\\ &\quad\quad ={{(c{{\tau }_{k+1}})}^{2}}-{{({{z}_{k+1}}-{{Z}_{k+1}})}^{2}} {\text{。}}\\ \end{aligned} \right. $ | (4) |
解上述方程即可获得水下航行器在第
水下航行器抛弃信标进行同步式测距定位的目的是为了对航位推算系统的累积误差进行滤除,缩小定位误差。卡尔曼滤波算法根据建立的系统方程和观测方程对需要处理的信号做出满足最小均方误差的估计,实时性好,鲁棒性强,适合应用于该定位场景下的定位滤波算法。
同步式测距需要信标发送较多的导航信息,信号时间较长,为了避免水声信道的多途效应造成前后两次信号发生互相串扰,通常将信标水声导航信号的发送间隔设置的步长较长。由于水下航行器与信标距离的变化,传播时间在不断变化,信标等时间间隔向外发送导航信号,水下航行器接收到水声导航信号的时间间隔并非固定不变,而是随着距离的变化在连续变化。以水中声速1 500 m/s为例,相对距离变化1 500 m,时间间隔即可变化约1 s,误差不可忽略。
因此,在设计卡尔曼滤波算法时应当考虑水声传播时间的变化,系统状态的更新频率为非等间隔,避免状态方程采样时间与观测方程不同步的问题。此外,水下航行器掌握的海区平均声速并不一定准确,通常含有一定的偏差,在建立滤波模型时也要将其考虑进去。
建立卡尔曼定位算法的过程如下:
定义状态向量为
| $ {{{X}}_{k+1}}={{[{{x}_{k+1}},{{y}_{k+1}},\Delta c]}^{\rm{T}}}{\text{,}} $ |
其中,
| $ \left\{ \begin{align} & {{x}_{k+1}}{\rm{=}}{{x}_{k}}+d{{x}_{k,k+1}} {\text{,}}\\ & {{y}_{k+1}}{\rm{=}}{{y}_{k}}+d{{y}_{k,k+1}}_{k}{\text{,}} \\ & \Delta c=\Delta c {\text{。}}\\ \end{align} \right. $ | (5) |
参考文献[8]将误差项分离的建模方法,定义状态方程含噪声的项为
| $ {{{\omega }}_{{k}}}={{[{{x}_{k}},{{y}_{k}},d{{x}_{k,k+1}},d{{y}_{k,k+1}},\Delta c]}^{\rm{T}}}{\text{,}} $ |
假设状态方程中噪声为相互独立的高斯白噪声,
| $ {{{Q}}_{{k}}}=E[{{{\omega }}_{{k}}}-{{{\hat{\omega }}}_{{k}}}]{{[{{{\omega }}_{{k}}}-{{{\hat{\omega }}}_{{k}}}]}^{\rm{T}}}{\text{。}} $ | (6) |
定义量测向量为
根据式(4)可得量测方程为
| $ \left\{ \begin{aligned} & \tau _k^2{\rm{ = [}}{({x_k} - {X_k})^2} + {({y_k} - {Y_k})^2} + {({z_k} - {Z_k})^2}]/{(c + \Delta c)^2}{\text{,}}\\ &\tau _{k + 1}^2{\rm{ = [}}{({x_k} + d{x_{k,k + 1}} - {X_{k + 1}})^2} + {({y_k} + d{y_{k,k + 1}} - {Y_{k + 1}})^2} \\ & \quad\;\;\; + {({z_{k + 1}} - {Z_{k + 1}})^2}]/{(c + \Delta c)^2}{\text{。}} \end{aligned} \right. $ | (7) |
由于深度传感器测量精度较高,在水平远距离条件下,其误差对测距来说可以忽略。因此定义
| $ {{{v}}_{{k}}} = {[{x_k},{y_k},d{x_{k,k + 1}},d{y_{k,k + 1}},{X_k},{Y_k},{X_{k + 1}},{Y_{k + 1}},\Delta c]^{\rm{T}}}{\text{,}} $ |
为量测方程含噪声的项,
| $ {{{R}}_{{k}}} = E[{{{v}}_{{k}}} - {{{\hat v}}_{{k}}}]{[{{{v}}_{{k}}} - {{{\hat v}}_{{k}}}]^{\rm{T}}}{\text{。}} $ | (8) |
从模型上看,状态方程是线性的,量测方程是非线性的,因此单信标同步式测距定位是一个非线性估计问题,通常的处理方法是将其线性化转化为一个近似的线性滤波问题,常用的非线性卡尔曼滤波算法有扩展卡尔曼滤波(EKF)、无迹卡尔曼滤波(UKF)、粒子滤波(PF)、容积卡尔曼滤波(CKF)等。虽然EKF的近似精度只有1阶,但没有引进其他额外的高阶项,不需要选取任何参数,比UKF,CKF和PF等确定采样型滤波算法更容易预测[10]。因此,本文采用EKF进行定位算法设计。
根据式(5)确定的状态方程和式(7)确定的量测方程,可得系统的滤波方程为
| $ \left\{ \begin{array}{l} {{{X}}_{k + 1}} = f({{{X}}_k},{{{\omega }}_{{k}}}){\text{,}}\\ {{{Z}}_{k + 1}}{\rm{ = }}h({{{X}}_k},{{{v}}_{{k}}}){\text{,}} \end{array} \right. $ | (9) |
则状态转移矩阵为
| $ {{{F}}_{k,k + 1}} = {\left. {\frac{{\partial f({{{X}}_k},{{{\omega }}_{{k}}})}}{{\partial {{{X}}_k}}}} \right|_{{{{X}}_k}{\rm{ = }}{{{{\hat X}}}_k},{{{\omega }}_{{k}}} = {{{{\hat \omega }}}_{{k}}}}}{\text{,}} $ | (10) |
系统噪声驱动矩阵为
| $ {{{W}}_{k,k + 1}} = {\left. {\frac{{\partial f({{{X}}_k},{{{\omega }}_{{k}}})}}{{\partial {{{\omega }}_{{k}}}}}} \right|_{{{{X}}_k}{\rm{ = }}{{{{\hat X}}}_k},{{{\omega }}_{{k}}} = {{{{\hat \omega }}}_{{k}}}}}{\text{,}} $ | (11) |
量测矩阵为
| $ {{{H}}_{k,k + 1}} = {\left. {\frac{{\partial h({{{X}}_k},{{{v}}_{{k}}})}}{{\partial {{{X}}_k}}}} \right|_{{{{X}}_k}{\rm{ = }}{{{X}}_{k + 1|k}},{{{v}}_{{k}}}={{{{\hat v}}}_{{k}}}}}{\text{,}} $ | (12) |
量测噪声驱动矩阵为
| $ {{{V}}_{k,k + 1}} = {\left. {\frac{{\partial h({{{X}}_k},{{{v}}_{{k}}})}}{{\partial {{{v}}_{{k}}}}}} \right|_{{{{X}}_k}{\rm{ = }}{{{X}}_{k + 1|k}},{{{v}}_{{k}}}={{{{\hat v}}}_{{k}}}}}{\text{。}} $ | (13) |
其中,
| $ \begin{array}{l} {{{F}}_{k,k + 1}} = \left[ {\begin{array}{*{20}{c}} 1\!\!&\!\!0\!\!&\!\!0\\ 0\!\!&\!\!1\!\!&\!\!0\\ 0\!\!&\!\!0\!\!&\!\!1 \end{array}} \right]{\text{,}}\\ {\rm{}}\\ {{{W}}_{k,k + 1}} = \left[ {\begin{array}{*{20}{c}} 1\!\!&\!\!0\!\!&\!\!1\!\!&\!\!0\!\!&\!\!0\\ 0\!\!&\!\!1\!\!&\!\!0\!\!&\!\!1\!\!&\!\!0\\ 0\!\!&\!\!0\!\!&\!\!0\!\!&\!\!0\!\!&\!\!1 \end{array}} \right]{\text{,}}\\ {\rm{}}\\ {{{H}}_{k,k + 1}} = \left[ {\begin{array}{*{20}{c}} {H(1,1)}\!\!&\!\!{H(1,2)}\!\!&\!\!{H(1,3)}\\ {H(2,1)}\!\!&\!\!{H(2,2)}\!\!&\!\!{H(2,3)} \end{array}} \right]{\text{,}}\\ {\rm{}}\\ {\begin{aligned} {{{V}}_{k,k + 1}} =& \left[\!\!{\begin{array}{*{20}{c}} {V(1,1)}\!\!&\!\!{V(1,2)}\!\!&\!\!0\!\!&\!\!0\!\!&\!\!{V(1,5)}\!\!&\!\! \\ {V(2,1)}\!\! &\!\!{V(2,2)}\!\!&\!\!{V(2,3)}\!\!&\!\!{V(2,4)}\!\!&\!\!0\!\!\end{array}}\right.\\ & \left.{\begin{array}{*{20}{c}}{V(1,6)}\!\!&\!\!0\!\!&\!\!0\!\!&\!\!{V(1,9)}\\ 0\!\!&\!\!{V(2,7)}\!\!&\!\!{V(2,8)}\!\!&\!\!{V(2,9)} \end{array}}\!\right]{\text{。}} \end{aligned}} \end{array} $ |
其中:
| $ \begin{array}{l} H(1,1){\rm{ = }}2({x_k} - {X_k})/{(c + \Delta c)^2}{\text{,}}\\ H(1,2){\rm{ = }}2({y_k} - {Y_k})/{(c + \Delta c)^2}{\text{,}}\\ H(1,3){\rm{ = - }}2{\rm{[}}{({x_k} - {X_k})^2} + {({y_k} - {Y_k})^2} + {({z_k} - {Z_k})^2}]/{(c + \Delta c)^3}{\text{,}}\\ H(2,1){\rm{ = }}2({x_k} + d{x_{k,k + 1}} - {X_{k + 1}})/{(c + \Delta c)^2}{\text{,}}\\ H(2,2){\rm{ = }}2({y_k} + d{y_{k,k + 1}} - {Y_{k + 1}})/{(c + \Delta c)^2}{\text{,}}\\ H(2,3){\rm{ = - }}2{\rm{[}}{({x_k} + d{x_{k,k + 1}} - {X_{k + 1}})^2} + \\ \quad\quad \cdots {({y_k} + d{y_{k,k + 1}} - {Y_{k + 1}})^2} + {({z_{k + 1}} - {Z_{k + 1}})^2}]/{(c + \Delta c)^3}{\text{,}} \end{array} $ |
| $ \begin{array}{l} V(1,1){\rm{ = }}2({x_k} - {X_k})/{(c + \Delta c)^2}{\text{,}}\\ V(1,2){\rm{ = }}2({y_k} - {Y_k})/{(c + \Delta c)^2}{\text{,}}\\ V(1,5){\rm{ = }}2({X_k} - {x_k})/{(c + \Delta c)^2}{\text{,}}\\ V(1,6){\rm{ = }}2({Y_k} - {y_k})/{(c + \Delta c)^2}{\text{,}}\\ V(1,9){\rm{ = - }}2{\rm{[}}{({x_k} - {X_k})^2} + {({y_k} - {Y_k})^2} + {({z_k} - {Z_k})^2}]/{(c + \Delta c)^3}{\text{,}}\\ V(2,1){\rm{ = }}2({x_k} + d{x_{k,k + 1}} - {X_{k + 1}})/{(c + \Delta c)^2}{\text{,}}\\ V(2,2){\rm{ = }}2({y_k} + d{y_{k,k + 1}} - {Y_{k + 1}})/{(c + \Delta c)^2}{\text{,}}\\ V(2,3){\rm{ = }}2({x_k} + d{x_{k,k + 1}} - {X_{k + 1}})/{(c + \Delta c)^2}{\text{,}}\\ V(2,4){\rm{ = }}2({y_k} + d{y_{k,k + 1}} - {Y_{k + 1}})/{(c + \Delta c)^2}{\text{,}}\\ V(2,7){\rm{ = - }}2({x_k} + d{x_{k,k + 1}} - {X_{k + 1}})/{(c + \Delta c)^2}{\text{,}}\\ V(2,8){\rm{ = - }}2({y_k} + d{y_{k,k + 1}} - {Y_{k + 1}})/{(c + \Delta c)^2}{\text{,}}\\ V(2,9){\rm{ = - }}2{\rm{[}}{({x_k} + d{x_{k,k + 1}} - {X_{k + 1}})^2} + \\ \begin{array}{*{20}{c}} {}&{}& \cdots \end{array}{({y_k} + d{y_{k,k + 1}} - {Y_{k + 1}})^2} + {({z_{k + 1}} - {Z_{k + 1}})^2}]/{(c + \Delta c)^3}{\text{。}} \end{array} $ |
定位算法的迭代更新过程如下:
状态一步预测方程为
| $ {{{X}}_{k + 1|k}} = f({{{\hat X}}_k},{{{\hat \omega }}_{{k}}}){\text{,}} $ | (14) |
状态预测方差阵
| $ {{{P}}_{k + 1|k}} = {{{F}}_{k,k + 1}}{{{P}}_k}{{F}}_{k,k + 1}^{\rm{T}} + {{{W}}_{k,k + 1}}{{{Q}}_{{k}}}{{W}}_{k,k + 1}^{\rm{T}}{\text{,}} $ | (15) |
量测值预测
| $ {{{Z}}_{k + 1|k}}{\rm{ = }}h({{{\hat X}}_k},{{{\hat v}}_{{k}}}){\text{,}} $ | (16) |
滤波增益
| $ \begin{split} {{{K}}_{k + 1}} = {{{P}}_{k + 1|k}}{{H}}_{k,k + 1}^{\rm{T}}({{{V}}_{k,k + 1}}{{{R}}_{{k}}}{{V}}_{k,k + 1}^{\rm{T}} + \\ {{{H}}_{k,k + 1}}{{{P}}_{k + 1|k}}{{H}}_{k,k + 1}^{\rm{T}}{)^{ - 1}}{\text{,}} \end{split} $ | (17) |
状态估计方差阵
| $ {{{P}}_{k + 1}} = ({{I}} - {{{K}}_{k + 1}}{{{H}}_{k,k + 1}}){{{P}}_{k + 1|k}}{\text{,}} $ | (18) |
状态估计
| $ {{{\hat X}}_{k + 1}}{\rm{ = }}{{{X}}_{k + 1|k}} + {{{K}}_{k + 1}}({{{Z}}_{k + 1}} - {{{Z}}_{k + 1|k}}){\text{。}} $ | (19) |
针对前文所述的应用场景,设计一道仿真题目用于测试算法的性能。如图3所示,水下航行器航速2 m/s;信标以10 s为间隔向外发送水声导航信号,受海流影响以0.3 m/s的速度匀速航行;设置真实声速误差服从均值为30,方差为1的高斯分布,含有[500 m,500 m]的初始位置误差。仿真时间为1 500 s。滤波参数设置为:
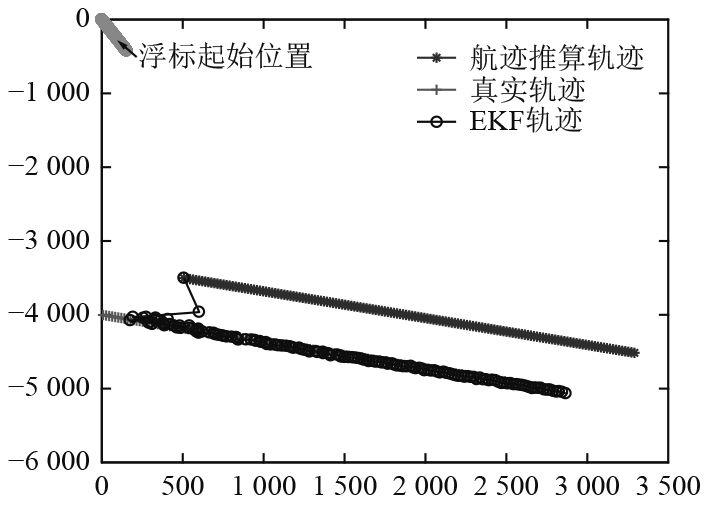
|
图 3 仿真航迹 Fig. 3 Simulation track |
| $ \left\{\begin{array}{l} {{{X}}_1} = {[{x_1} + 500,{y_1} + 500,0]^{\rm{T}}}{\text{,}}\\ {Q_0} = {\rm diag}(1,1,1,1,16){\text{,}}\\ {R_0} = {\rm diag}(\!1,\!1,\!1,\!1,\!0.001,\!0.001,\!0.001,\!0.001,\!16\!)\!{\text{,}}\\ {P_0} = {\rm diag}({10^6},{10^6},{10^2}){\text{。}} \end{array}\right. $ | (20) |
式中:
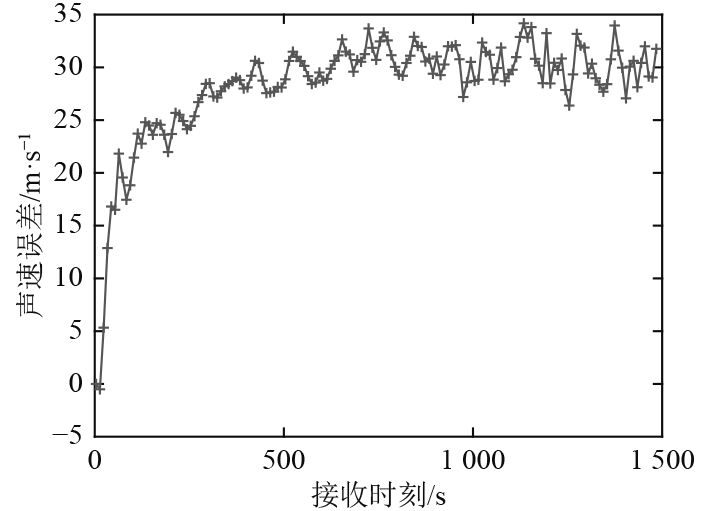
|
图 4 声速误差估计 Fig. 4 Error estimation of sound velocity |

|
图 5 定位误差 Fig. 5 Positioning error |
为检验算法在实际应用中的性能,2017年8月,在丹江口水库进行了水声导航科学试验。试验平台为某型UUV(Unmanned Underwater Vehicle),试验设备包括:GNSS定位系统、惯性导航系统、深度传感器和NCART长基线定位系统等。信标随水流漂移,其水面浮体装备有北斗定位系统,起始坐标(0,0)。UUV惯导记录航迹如图6所示,航行速度2 m/s,由于UUV携带的惯导精度较高,且下潜前在水面利用GNSS定位系统对惯导进行了校正,本次试验以惯导推算航迹作为基准。试验中间隔10 s进行一次测距定位,整个过程持续700 s。对采集回来的数据进行离线处理,并给惯导记录数据增加[500 m,500 m]的误差作为UUV航迹推算轨迹。

|
图 6 试验航迹 Fig. 6 Experiment track |
滤波参数设置同式(20),应用本文算法对增加误差后的试验数据进行处理,定位误差如图7所示,声速误差估计如图8所示。由图7可知,本文算法处理实际数据时同样取得了较好的效果,中间出现了一次定位波动是因为在转向过程中传播时延观测量出现了粗差,这也造成图8中声速误差估计并不准确。

|
图 7 定位误差 Fig. 7 Positioning error |
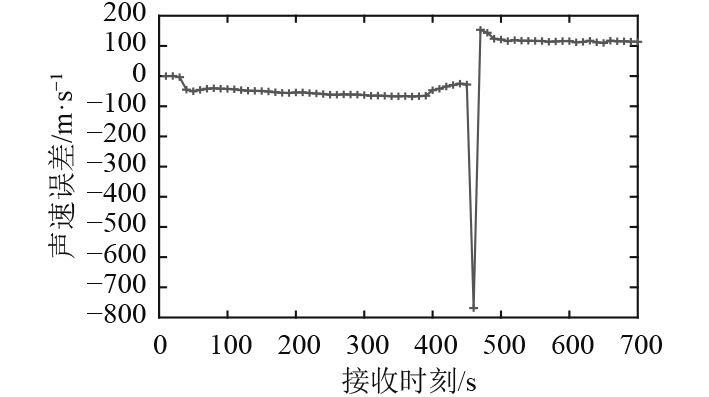
|
图 8 声速误差估计 Fig. 8 Error estimation of sound velocity |
本文借助移动矢径的概念建立了移动单信标同步式测距定位模型,并基于EKF设计了该定位模型下的定位滤波算法,然后通过解算仿真算例和试验数据,验证了该定位滤波算法的有效性,实现了利用单个移动信标为水下航行器提供定位服务。水下航行器长时间航行后航位推算系统会累积较大的误差,本文算法可以在未知声速干扰下有效约束这种初始位置误差,提高定位精度,并对声速误差进行估计。算法定位性能会受观测值粗差的影响,如何提升算法的抗差性能是下一步的研究工作。
| [1] |
张光普, 梁国龙, 王燕, 等. 分布式水下导航、定位、通信一体化系统设计[J]. 兵工学报, 2007, 28(12): 1455-1462. DOI:10.3321/j.issn:1000-1093.2007.12.011 |
| [2] |
孙大军, 郑翠娥. 水声导航、定位技术发展趋势探讨[J]. 海洋技术学报, 2015, 34(3): 64-68. |
| [3] |
张延顺, 郭雅静, 黄小娟, 等. 水下运载体航位推算系统初始位置确定方法[J]. 北京航空航天大学学报, 2006, 32(8): 946-949. DOI:10.3969/j.issn.1001-5965.2006.08.017 |
| [4] |
ALEXANDER P S.The AUV positioning using ranges from one transponder LBL[C]//Proceedings of the 1995 MTS/IEEE Oceans Conference, San Die-go, CA, USA, IEEE, 1995: 1620–1623.
|
| [5] |
FERREIRA B, MATOS A, CRUZ N. Single beacon navigation: Localization and control of the MARES AUV[J]. Oceans, 2010, 58(1): 1-9. |
| [6] |
SARAH E. WEBSTER C J C. Decentralized single beacon acoustic navigation : communication and navi-gation for underwater vehicles[D]. Washington D.C.: The Johns Hopkins University , 2010, 6–22.
|
| [7] |
LI Wen-bai, LIU Ming-yong, LIU Fu-qiang, et al. Coop-erative navigation for autonomous underwater vehicles based on estimation of motion radius vectors[J]. Defence Technology, 2011, 07(1): 9-14. |
| [8] |
刘明雍, 张加全, 张立川. 洋流影响下基于运动矢径的AUV协同定位方法[J]. 控制与决策, 2011, 26(11): 1632-1636. |
| [9] |
张加全, 刘明雍, 胡俊伟. 运动矢径对AUV协同定位精度影响的仿真[J]. 火力与指挥控制, 2012, 37(1): 43-46. DOI:10.3969/j.issn.1002-0640.2012.01.011 |
| [10] |
王小旭, 潘泉, 黄鹤, 等. 非线性系统确定采样型滤波算法综述[J]. 控制与决策, 2012, 27(6): 801-812. |
 2019, Vol. 41
2019, Vol. 41
