2. 低速机国家工程试验室,上海 201108
2. Low Speed National Engineering Laboratory, Shanghai 201108, China
船用柴油机结构复杂、体积庞大,其安全性、可靠性要求比车用发动机更高,但船用柴油机整机试验费用高、周期长、风险系数大,故硬件在环测试在船用柴油机电控系统的开发过程中显得尤为重要。硬件在环测试的可靠性依赖于可靠的硬件设备和准确的模型。硬件设备有很多厂家如dSPACE,NI,ETAS等[1],都能提供成熟可靠的标准化产品。模型通常需要根据被测系统的要求以及被控对象的特点定制开发。模型的准确度决定了硬件在环测试的正确度。
船用柴油机电控系统功能越来越复杂,需要验证的功能项也越来越多。目前,柴油机实时模型大多采用平均值模型,但它难以模拟柴油机真实工作过程,很多功能无法在硬件在环测试阶段得到验证,且模型准确度不高。对于缸数较多的柴油机,若采用准维模型,模型精度高预测性好,但难以满足实时性要求。本文采用基于缸内过程热力学计算的零维柴油机模型,满足测试对象功能性要求的同时,兼顾模型准确度和实时性。
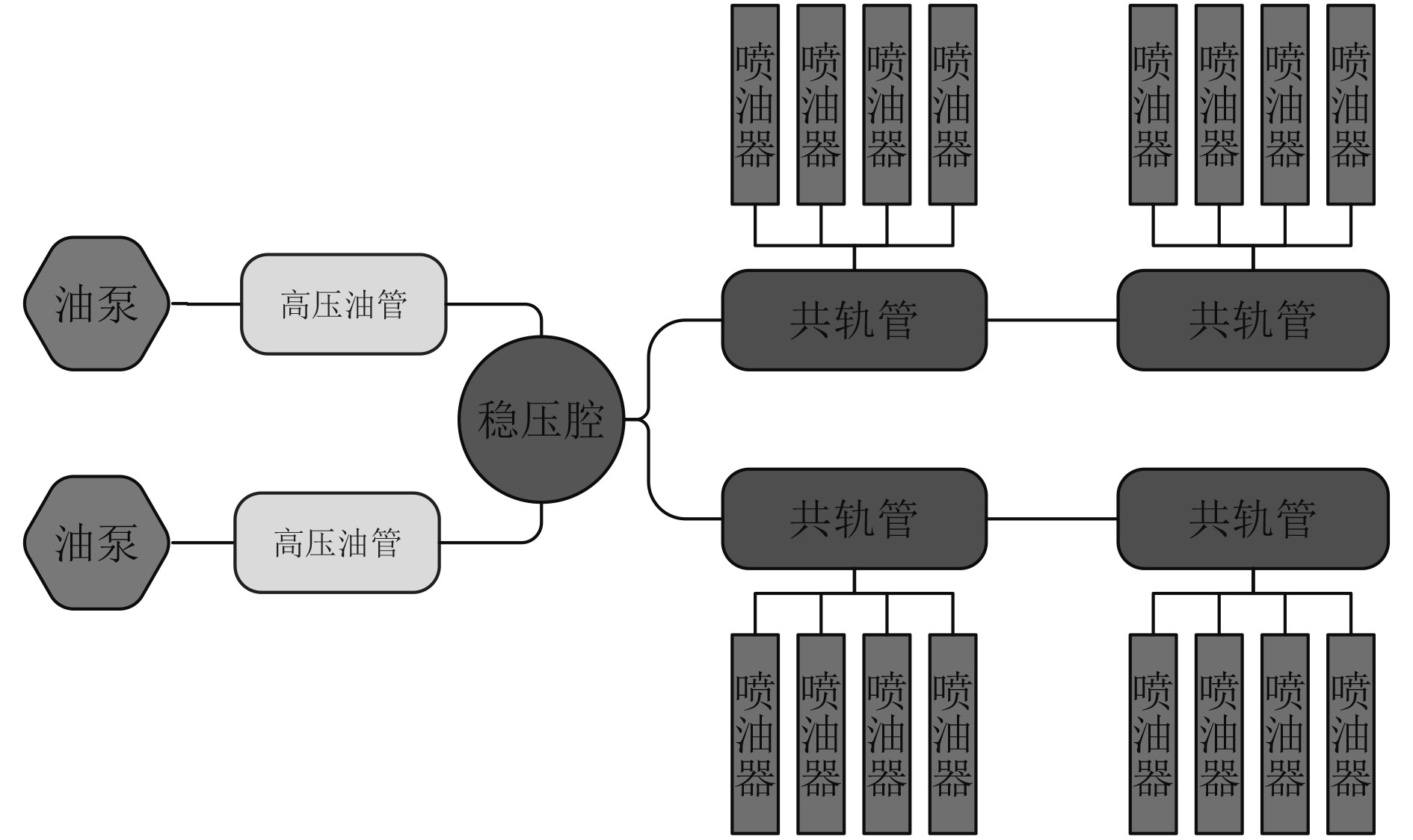
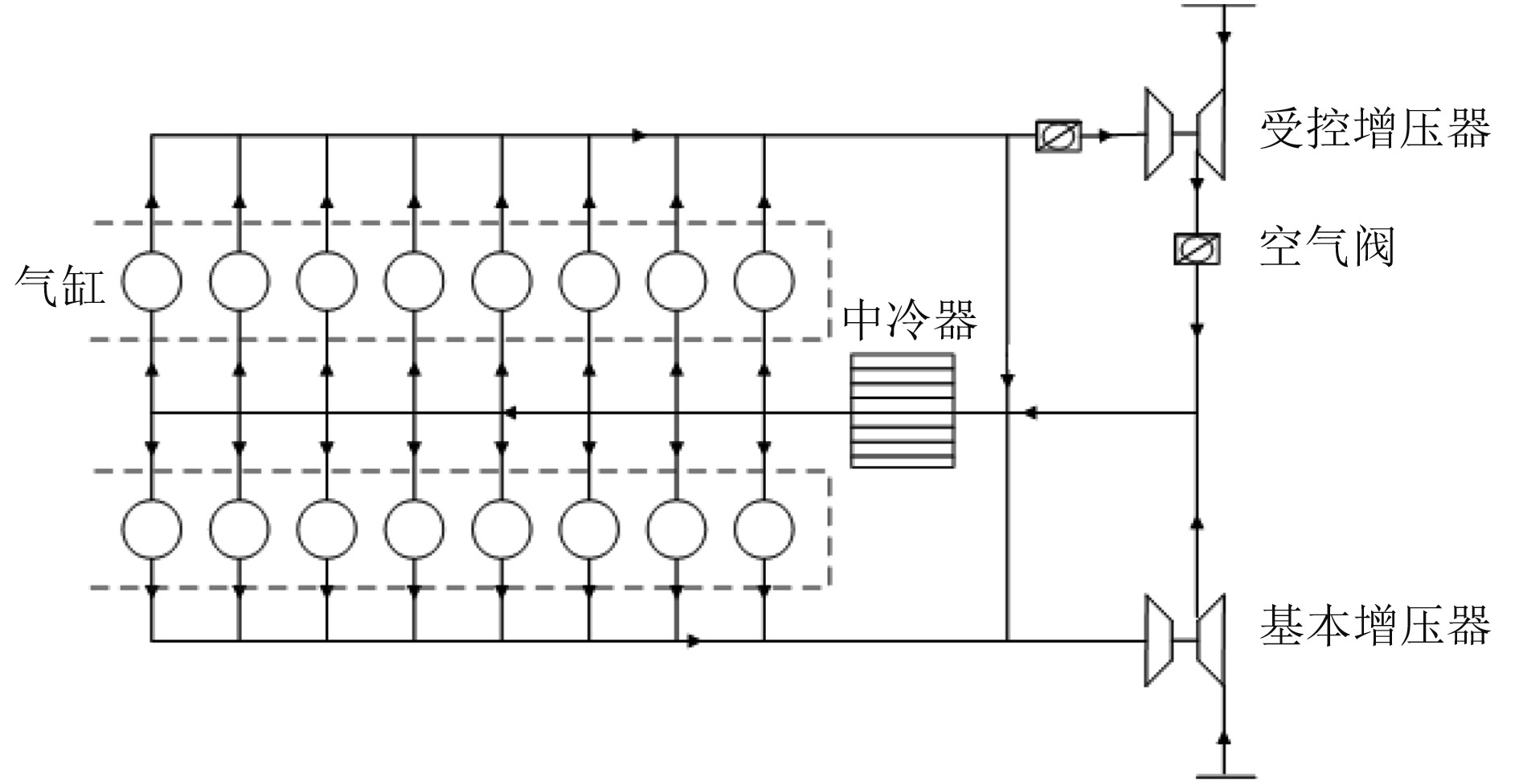
1 建模对象建模原型机为船用16缸共轨增压中冷柴油机。燃油系统结构如图1所示。气缸进排气系统结构如图2所示。
|
图 1 燃油系统结构示意图 Fig. 1 Schematic diagram of fuel system structure |
|
图 2 气缸和进排气系统结构示意图 Fig. 2 Schematic diagram of the structure of cylinders and intake and exhaust system |
考虑模型的兼容性,采用Matlab/Simulink软件建立仿真模型。气缸建模采用基于热力学的零维模型,体现不同时刻缸内压力变化对柴油机特性的影响。被测对象具有多次喷射控制功能,故采用了多个韦伯模型计算燃烧放热率[2]。进排气管、共轨管、油管等部件,被测对象只关注油压、轨压稳态值的变化,故可简化采用容积法建立均值模型。为验证被测对象相继增压控制功能,采用热力学公式建立2个增压模型,模拟增压器实际工作过程。
2 柴油机实时仿真模型建模建立柴油机模型主要包括共轨燃油系统模型、气缸模型、进排气系统模型、动力传动系统模型以及虚拟控制器模型。
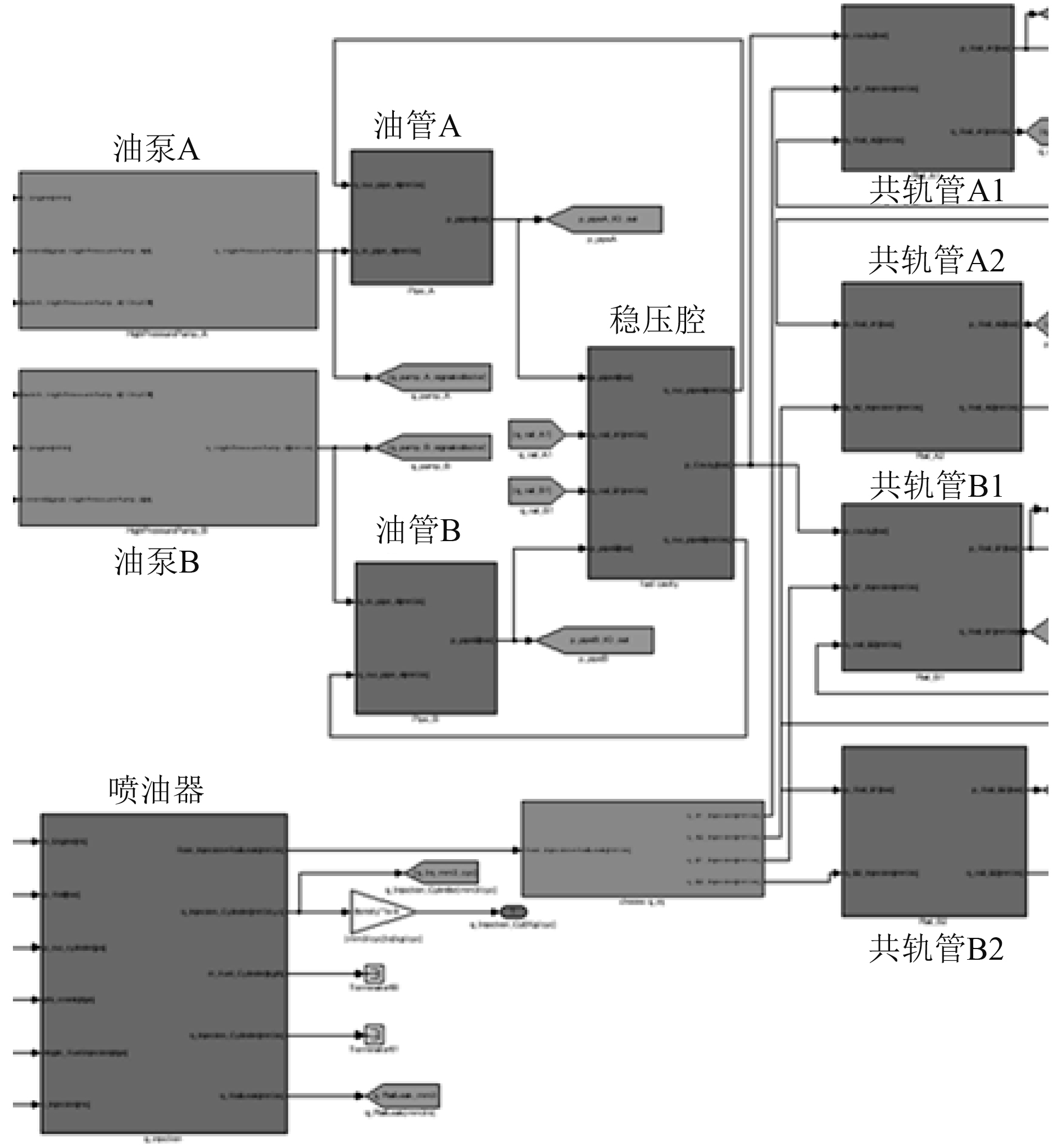
2.1 共轨燃油系统模型建模按照共轨燃油系统结构划分模型,包括高压油泵模型、油管模型、稳压腔模型、共轨管和喷油器模型。共轨燃油系统模型如图3所示。
|
图 3 共轨燃油系统模型示意图 Fig. 3 Schematic diagram of common-rail fuel system model |
通过改变油泵入口驱动电流改变油泵流量。忽略燃油温度、压力等物理性质的变化对于泵油效率的影响,按式(1)计算油泵泵油量。通过油泵泵油体积流量计算公式、ηp修正效率和ηc油泵泵油效率数值MAP来模拟实际油泵的泵油特性曲线。
泵油量计算公式如下:
| $ {\rm{}}{{{q}}_{{p}}} ={{{V}}_1}{\rm{*}}{{{N}}_{{p}}}{{*n*}}{{{Z}}_{{p}}}{\rm{*}}{{\rm{\eta }}_{{p}}}{\rm{*}}{{\rm{\eta }}_{{c}}}{\text{。}} $ | (1) |
式中:qp油泵泵油流量,mm3/s;V1为单个柱塞腔体积,m3;Np为柱塞腔数目;n为柴油机转速,r/min;Zp为泵速比;ηp为修正效率;ηc为油泵泵油效率[3]。
2.1.2 稳压腔模型高压油管、稳压腔、共轨管建模方法相同。忽略压力波的传播,采用容积法计算内部压力。计算公式如下:
| $ {\rm{}}{{{P}}_{{\rm{rail}}}} =\frac{{{{{E}}_{{\rm{fuel}}}}}}{{{{{V}}_{{\rm{rail}}}}}}\mathop \smallint \nolimits {{q}}\left( {{t}} \right){\rm{d}}t =\frac{1}{{{{{C}}_{{H}}}}}\mathop \smallint \nolimits {\rm{\Sigma }}{{{q}}_{{t}}}{\rm{d}}t\text{。} $ | (2) |
式中:Prail为油腔内燃油压力,Pa;Vrail为稳压腔体积,m3;q(t)为稳压腔内流进、流出的燃油体积流量,m3/s;Efuel为柴油体积弹性模量,Pa;用经验公式进行计算,公式如下:
| $ {{{E}}_{{\rm{fuel}}}} ={{{C}}_0}{\rm{*}}{\left( {{{p}} + {{{C}}_1} - {{T*}}{{{C}}_2}} \right)^{{{{C}}_3}}}{\rm{}}\text{。} $ | (3) |
式中:C0=34.74;C1=111 061 456.8;C2=469 742.34;C3=0.947;p为燃油压力,Pa;T为燃油温度,℃。
2.1.3 喷油器模型喷油量是共轨压力和喷油脉宽的函数。通过试验数据标定数据MAP计算每缸每循环喷油量,再根据喷油量查MAP得到动态回油量和静态回油量。
根据缸内压力、喷油压力和喷油器的结构参数计算喷油速率(kg/s),公式如下:
| $ {}^{{\rm d}m}\!\!\diagup\!\!{}_{{\rm d}t}\;=\frac{{{d}_{0}}^{2}*{\text{π}} *{{N}_{noz}}*\mu }{4}*\sqrt{2*\Delta P*\rho } \text{。} $ | (4) |
式中:d0为喷孔直径,m;Nnoz为每个喷油器的喷孔个数;μ为喷孔阻力系数;ΔP为共轨压力与缸内压力差;ρ为柴油的密度,kg/m3[4]。
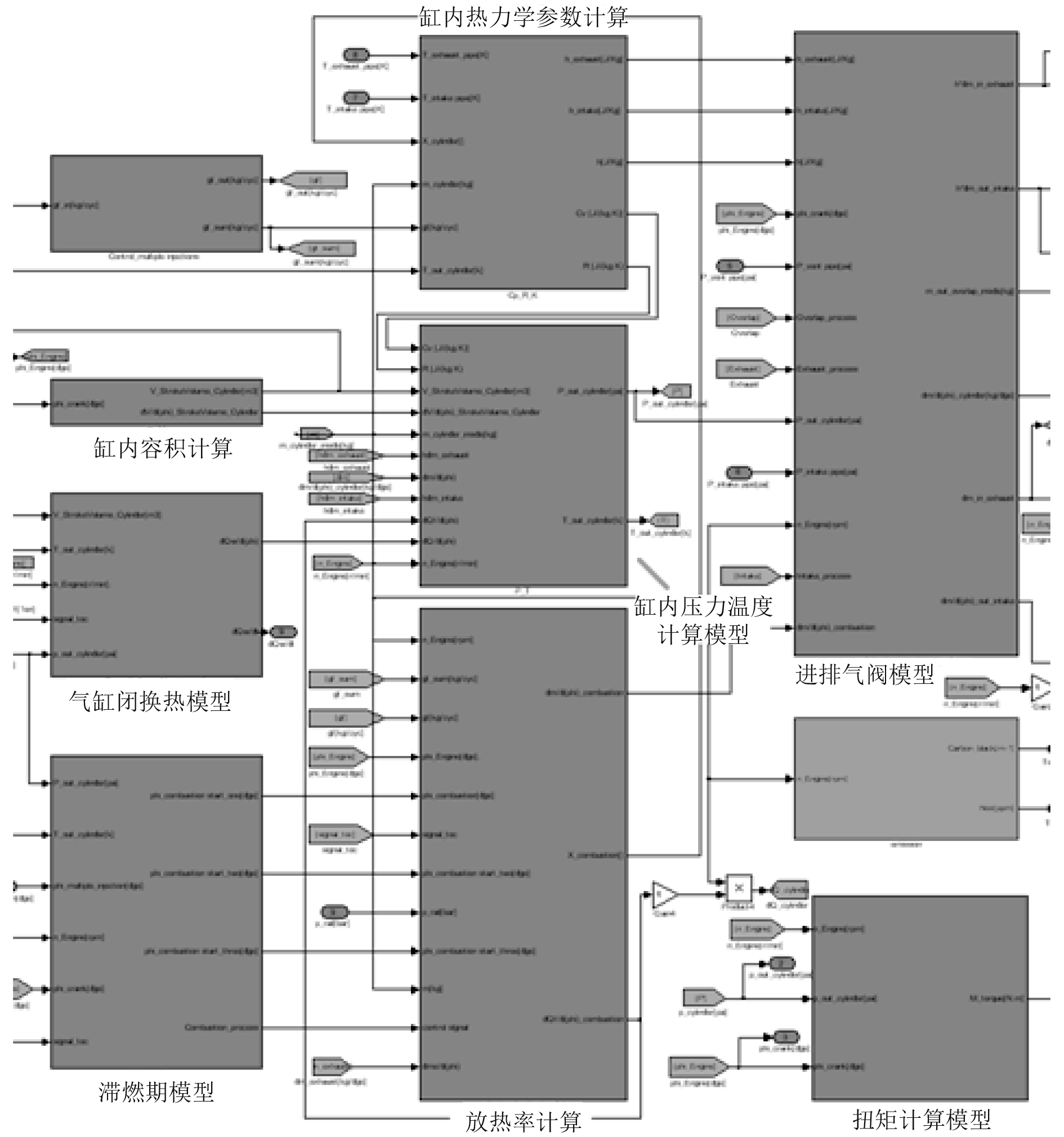
2.2 气缸模型假设缸内气体为理想气体,进排气过程近似为准维态过程,缸内气体变化过程为稳态过程,建立零维稳态气缸模型。将缸内工作过程分为压缩、燃烧、膨胀、排气、气阀重叠和进气6个过程循环[5]。气缸模型如图4所示,主要包括缸内容积计算模型、气缸壁换热模型、滞燃期模型、进排气阀模型、放热率计算模型等。
|
图 4 气缸模型示意图 Fig. 4 Schematic diagram of cylinders model |
按照动力学公式,计算随着活塞往复运动,气缸容积的变化。计算公式如下:
| $ \frac{{\rm d}V}{{\rm d}\varphi }=\left[ \sin \left( \frac{{\text{π}}}{180}\varphi \right)+\frac{\lambda }{2}\cdot \frac{\sin \left(\displaystyle\frac{{\text{π}}}{180}\cdot 2\varphi \right)}{\sqrt{1-{{\lambda }^{2}}{{\sin }^{2}}\left( \displaystyle\frac{{\text{π}} }{180}\varphi \right)}} \right]\text{,} $ | (5) |
| $ \begin{split} & \ \ \ \ \ \ \ \ {V}=\frac{{\text{π}} {{D}^{2}}}{4}\left[ \frac{S}{\varepsilon -1} \right.+\frac{S}{2}\left[ \left( 1+\frac{1}{\lambda } \right) \right.- \\ & \left. \left. \cos \left( \frac{{\text{π}}}{180}\varphi \right)-\frac{1}{\lambda }\sqrt{1-{{\lambda }^{2}}{{\sin }^{2}}\left( \frac{{\text{π}} }{180}\varphi \right)} \right] \right]\text{。} \end{split} $ | (6) |
式中:D为缸内直径,m;S为气缸冲程,m;λ为曲柄连杆比;ε为压缩比。
2.2.2 气缸换热计算模型计算气缸换热
| $ \frac{{{\rm d}{Q_w}}}{{{\rm d}\varphi }} =\mathop \sum _{i =1}^3 \frac{{{\rm d}{Q_{wi}}}}{{{\rm d}\varphi }} =\mathop \sum _{i =1}^3 {\alpha _g} \cdot {A_i}\left( {T - {T_{wi}}} \right)\text{。} $ | (7) |
式中:αg为瞬时平均换热系数,J/(m2.K.CA°);A为换热面积,m2;Tw为壁面的平均温度,K;i=1,2,3,分别表示气缸盖、活塞和气缸套。
为了减少计算量,导热系数αg采用Woschni模型的优化算法:
| $ {\alpha _g} =\mu {D^{ - 0.214}}{\left( {p \cdot n \cdot s} \right)^{0.786}}{T^{ - 0.53}}\text{。} $ | (8) |
式中:μ为用于标定的导热修正系数;n为发动机转速,r/min[6]。
2.2.3 滞燃期计算模型计算滞燃期确定燃烧起始时刻,计算公式如下:
| $ {\tau _{{\rm{ig}}}} =0.1 + 1.194 \times {10^{ - 4}}{p^{ - 0.87}}{e^{\frac{{1967}}{T}}}{C_{ig}}\text{。} $ | (9) |
式中:τig为着火的延迟期,s;Cig为滞燃期的修正系数。
2.2.4 缸内热力学参数计算模型根据质量守恒、能量守恒和气体状态方程计算缸内热力学参数,如:定容比热cV、定压比热cp、气体常数R、气体焓值h和绝热系数k等。绝热系数k和气体常数R由下式拟合计算:
| $ \begin{split} k =1.4373 - 1.318 \times {10^{ - 4}} \cdot T + .12 \times \\ {10^{ - 8}} \cdot {T^2} - 4.8 \times {10^{ - 2}}/{\alpha _\varphi }\text{,} \end{split} $ | (10) |
| $ {\rm{R}} =9.81 \times \left( {29.2647 - 0.0402 / {\alpha _\varphi }} \right)\text{。} $ | (11) |
式中:αφ为瞬时过量空气系数,αφ=
| $ {c_v} =\frac{R}{{k - 1}}\text{,} $ | (12) |
| $ {c_p} =\frac{{k \cdot R}}{{k - 1}}\text{,} $ | (13) |
| $ {{h}} ={c_P} \cdot T\text{,} $ | (14) |
缸内温度、压力计算公式如下:
| $ \begin{split} \frac{{{\rm d}T}}{{{\rm d}\varphi }} =&\frac{1}{{m{c_V}}}\left[ {{g_f}{H_u}\frac{{{\rm d}x}}{{{\rm d}\varphi }}} \right. - \frac{{{\rm d}{Q_w}}}{{{\rm d}\varphi }} - p\frac{{{\rm d}V}}{{{\rm d}\varphi }} + {h_s}\frac{{{\rm d}{m_s}}}{{{\rm d}\varphi }} - \\ &{h_e}\frac{{{\rm d}{m_e}}}{{{\rm d}\varphi }} - \left. {u\frac{{{\rm d}m}}{{{\rm d}\varphi }}} \right]\text{,} \end{split} $ | (15) |
| $ {{pv}} ={{mRT}}\text{。} $ | (16) |
采用韦伯模型计算缸内燃烧过程的放热率,计算公式如下:
| $ \begin{split} \frac{{d{\rm{x}}}}{{d\varphi }} =&\left( {m + 1} \right) \times 6.908{\left( {\frac{1}{{\varphi z}}} \right)^{{m_p} + 1}} \cdot (\varphi - {\varphi _B}{)^{{m_p}}} \times\\ & {e^{ - 6.908{{\left( {\frac{1}{{{\varphi _{{Z_p}}}}}} \right)}^{m + 1}} \cdot {{\left( {\varphi - {\varphi _B}} \right)}^{m + 1}}}}\text{。} \end{split} $ | (17) |
式中:m为燃烧品质指数;φ为瞬时曲轴转角;φZ为燃烧持续角;为了能够模拟多次喷射,模型采用多个韦伯模型,每次喷射过程采用一次韦伯模型计算[7]。
2.2.6 进排气阀模型建立进排气模型,模拟流入流出气缸工质的质量和焓值变化。质量流量的变化计算下式:
| $ \frac{{{\rm d}{m_e}}}{{{\rm d}\phi }} =\frac{1}{{6n}}{\mu _e} \cdot {F_e}\frac{p}{{\sqrt {RT} }}{\left( {\frac{2}{{k + 1}}} \right)^{\frac{1}{{k - 1}}}} \cdot \sqrt {\frac{{2k}}{{k + 1}}} \text{。} $ | (18) |
式中:
计算指示扭矩。
1)计算作用于活塞顶端的作用力P
| $ {{{P}}_{g}}=\frac{{\text{π}}{{D}^{2}}}{4}\left( p-\overset{\acute{\ }}{\mathop{p}}\, \right)\text{。} $ | (19) |
式中:p为缸内压力,Pa;
2)计算连杆与活塞之间的往复惯性力
| $ {{{P}}_{{j}}} = - \left( {{{{m}}_{{p}}} + {{{m}}_1}} \right){{*a}}\text{。} $ | (20) |
式中:mp为单个气缸的活塞组质量,kg;m1为单个连杆小段的替代质量,kg;a为活塞运动加速度,m/s2,
计算公式为
| $ {{a}} =R{{\rm{\omega }}^2}\left( {\cos {\rm{\alpha }} + {\rm{\gamma }}\frac{{\cos 2{\rm{\alpha }}}}{{\cos {\rm{\beta }}}} + \frac{{{{\rm{\gamma }}^3}}}{4}\frac{{{\rm{si}}{{\rm{n}}^2}2{\rm{\alpha }}}}{{{\rm{co}}{{\rm{s}}^2}{\rm{\beta }}}}} \right)\text{。} $ | (21) |
式中:R为曲柄半径,m;ω为旋转角速度,1/s;γ为曲柄连杆比;α为曲轴转角;β为连杆与气缸中心线之间的夹角,其中有sinβ=γsinα
3)计算扭矩:
| $ {{{M}}_1} =\frac{{\sin \left( {{\rm{\alpha }} + {\rm{\beta }}} \right)}}{{{\rm{cos\beta }}}}\left( {{{{P}}_{{g}}} + {{{P}}_{{j}}}} \right){{*R}}\text{。} $ | (22) |
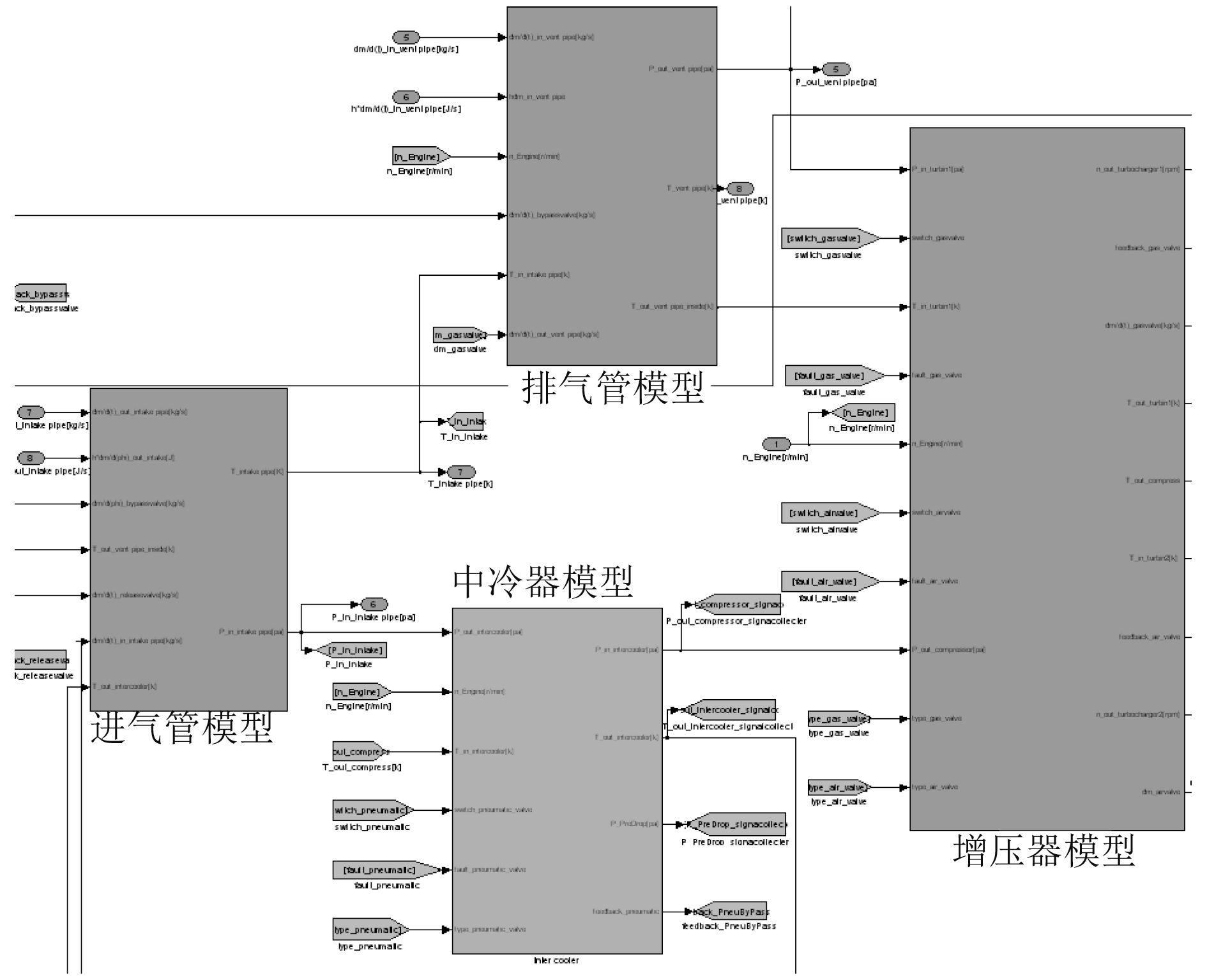
进排气系统主要由进气管、排气管、中冷器和涡轮增压器组成,根据进排气系统的结构和工作原理建立模型,如图5所示。
|
图 5 进排气系统模型示意图 Fig. 5 Schematic diagram of intake and exhaust system model |
假设进气管、排气管内气体为准稳态流动,忽略管内压力波的传播、反射、叠加等现象,采用定容积法建模。计算公式如下:
| $ {{pv}} ={{mRT}}\text{,} $ | (23) |
| $ \frac{{{\rm{d}}m}}{{{\rm{d\varphi }}}} =\mathop \sum _{{{i}} =1}^{{n}} \left( {\frac{{{\rm{d}}{{{m}}_{{i}}}}}{{{\rm{d\varphi }}}}} \right) + \frac{{{\rm{d}}{{{m}}_{{T}}}}}{{{\rm{d\varphi }}}}\text{,} $ | (24) |
| $ \frac{{{\rm{d}}T}}{{{\rm{d\varphi }}}} =\frac{{\left(\mathop \sum \nolimits_{{{i}} =1}^{{n}} \left( {{{{h}}_{{i}}}\displaystyle\frac{{{\rm{d}}{{{m}}_{{i}}}}}{{{\rm{d\varphi }}}}} \right) + {{{h}}_{{T}}}\displaystyle\frac{{{\rm{d}}{{{m}}_{{T}}}}}{{{\rm{d\varphi }}}} + \displaystyle\frac{{{\rm{d}}{{{Q}}_{{w}}}}}{{{\rm{d\varphi }}}} - {{{c}}_{{v}}}{{T}}\displaystyle\frac{{{\rm{d}}{{{m}}_{{T}}}}}{{{\rm{d\varphi }}}}\right)}}{{{{\rm{c}}_{\rm{v}}}{\rm{m}}}}\text{。} $ | (25) |
式中:
排气管需要考虑冷却散热问题,故排气管建模时需要加入冷却系数影响。
2.3.2 增压器建模柴油机低负荷运行时,基本增压器工作,高负荷运行时,通过燃气阀、空气阀控制受控增压器切入,2个增压器一起工作。增压器的工作过程简化为等熵压缩和等熵膨胀过程。将增压器简化为压气机、涡轮和连接轴3部分建模。
压气机扭矩计算公式如下:
| $ {W_{Kad}} =\frac{k}{{k - 1}}{\rm{*R}}{T_0}\left( {{\text{π}}_k^{\frac{{k - 1}}{k}} - 1} \right)\frac{{{\rm d}m}}{{{\rm d}t}}\text{。} $ | (26) |
式中:WKad为等熵压缩功,Nm;k为绝热系数;T0为压气机入口温度,K;πk为压气机压比;
压气机出口温度计算如下:
| $ {T_K} = {\rm{}}{T_0} + {T_0}\left( {{\text{π}} _k^{\frac{{k - 1}}{k}} - 1} \right)\frac{1}{{{\eta _{kad}}*\tau }}\text{。} $ | (27) |
式中:TK为压气机出口温度,K;τ为修正系数。
涡轮输出扭矩计算公式如下:
| $ {M_T} = {\eta _T}\frac{{{\rm{d}}m}}{{{\rm{d}}t}}{\rm{*}}\frac{k}{{k - 1}}{\rm{*R}}{T_T}\left( {1 - {\text{π}} _k^{\frac{{k - 1}}{k}}} \right)\frac{{30}}{{3.14*{n_T}}}\text{。} $ | (28) |
式中:MT为涡轮的膨胀扭矩,Nm;ηT为涡轮的绝热膨胀效率;TT为涡轮入口温度,K;πT为涡轮膨胀比。
涡轮出口温度计算公式为:
| $ {T_{0T}} = {\tau _T}{T_T}\left\{ {1 - {\eta _T}\left[ {1 - {{\left( {\frac{1}{{{{\text{π}} _T}}}} \right)}^{\frac{{k - 1}}{k}}}} \right]} \right\}{\rm{}}\text{。} $ | (29) |
式中:T0T为压气机出口温度,K;τT为出口温度的修正系数。
连接轴连接压气机和涡轮,根据压气机与涡轮之间的扭矩平衡关系,按转子动力学公式计算增压器转速。
试验数据标定MAP,根据柴油机转速和负荷获取中冷器效率和压降。
根据柴油机实际运行工况,查标定MAP确定燃气阀和空气阀的控制状态,完成受控增压器切入、切出过程模拟。
2.4 动力传动系统建模依据摩擦扭矩、瞬时扭矩、指示扭矩、平均扭矩等,采用动力学公式计算柴油机转速。
| $ {\rm{d}}n/{\rm{d}}t = \frac{{{{{T}}_{{i}}} + {{{T}}_{{s}}} - {{{T}}_{{f}}} - {{{T}}_{{p}}}}}{{{{{J}}_{{e}}}}}\frac{{60}}{{2{\rm{{\text{π}} }}}}\text{。} $ | (30) |
式中:dn/dt为柴油机加速度,r/s2;Ti为指示扭矩,Nm;Ts为起动扭矩,Nm;Tf为摩擦扭矩,Nm;Tp为负载扭矩,Nm;Je为转动惯量,kg/m2。
2.5 虚拟控制器模型建立虚拟控制器模型替代真实控制器,在建模阶段验证模型功能。虚拟控制器能够实现真实控制器的主要功能,如柴油机调速控制、轨压控制、燃油喷射控制、相继增压器控制功能。采用PID算法,实现轨压和转速闭环控制;根据油量、轨压获取喷油脉宽,根据转速和油量获取喷油正时,控制燃油喷射;手动输入阀门控制信号,实现相继增压控制[8]。
3 模型仿真验证本文采用dSPACE硬件设备,模型下载到硬件设备中,设置仿真步长为0.2 ms,仿真验证模型功能、精度以及实时性是否满足要求。
3.1 模型功能验证本文研究的被测对象具有起动控制、停车控制、转速控制、轨压控制、相继增压控制、多次喷射等功能。模型能够根据控制信号的变化,模拟柴油机的动态特性,以验证被测对象功能的正确性。
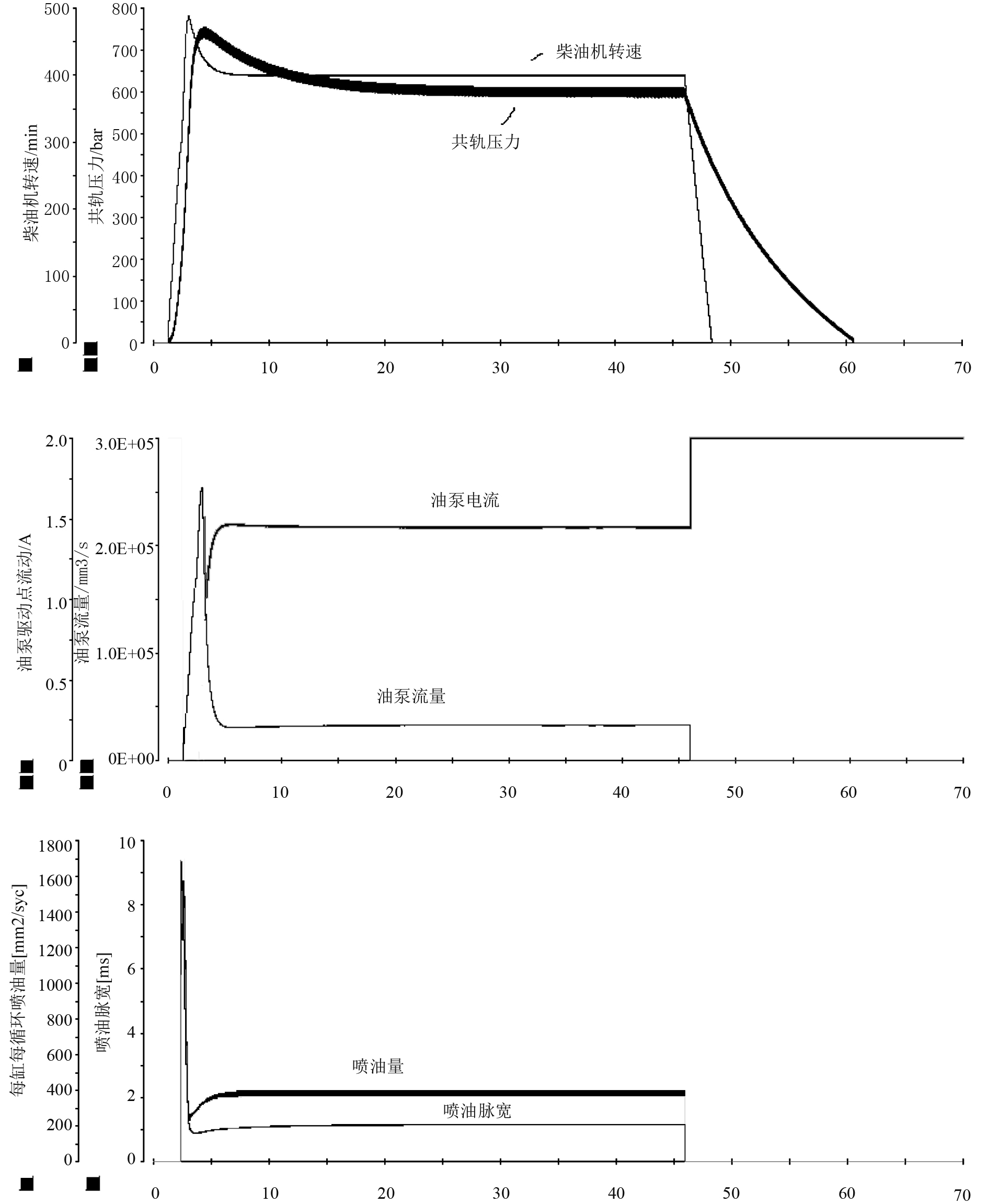
3.1.1 验证起动、停车控制功能控制器收到起动信号,控制柴油机起动,起动成功后,转速闭环控制怠速运行。收到停车信号,控制停止喷油柴油机停车。仿真验证结果如图6所示。
|
图 6 起动停车功能验证结果图 Fig. 6 Result diagram of start and stop function verification |
由图6可知,模型能够根据喷油脉宽、油泵驱动电流的变化,模拟柴油机起动、停车过程的动态特性,可用于控制器起动、停车控制功能测试。
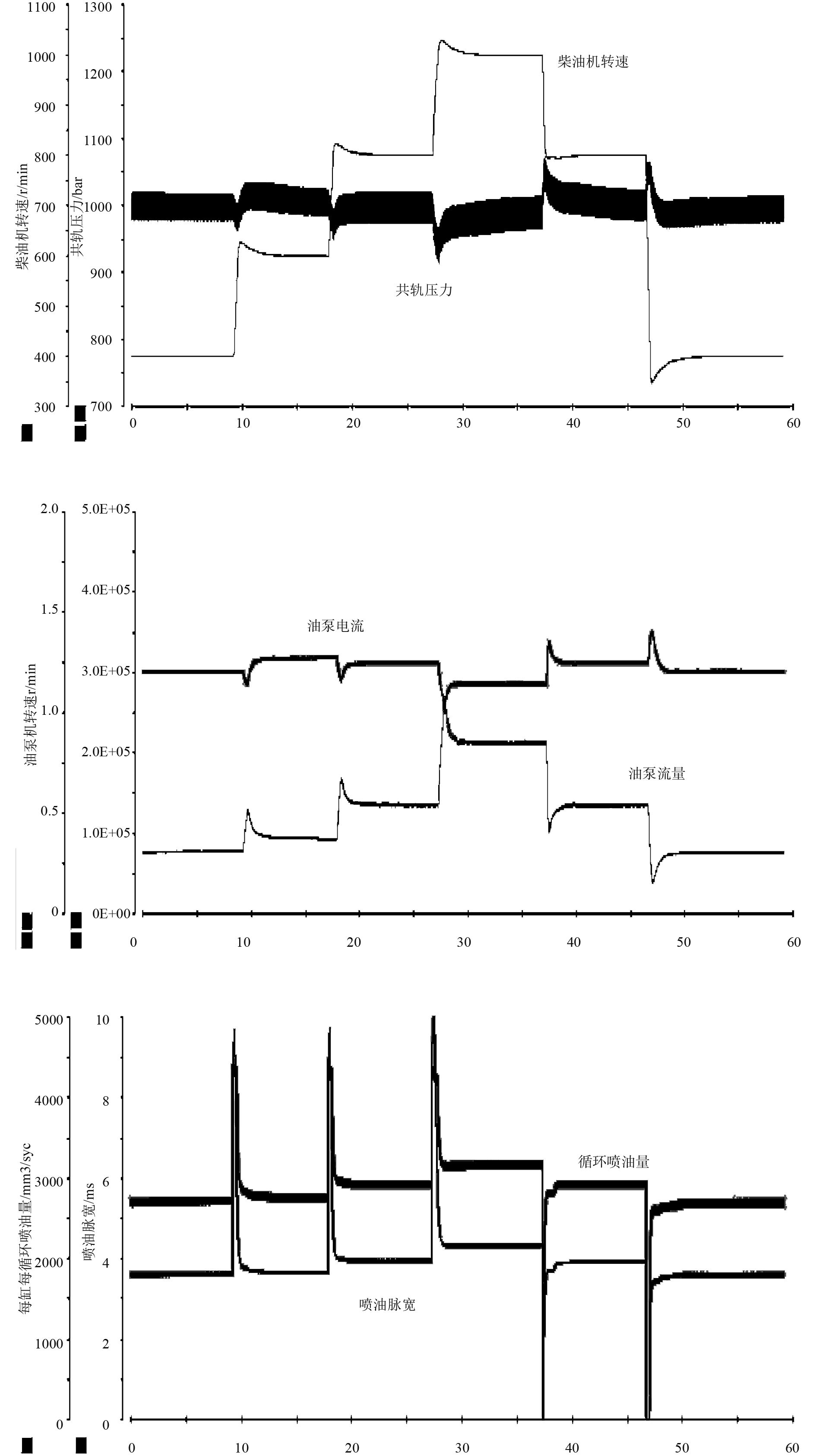
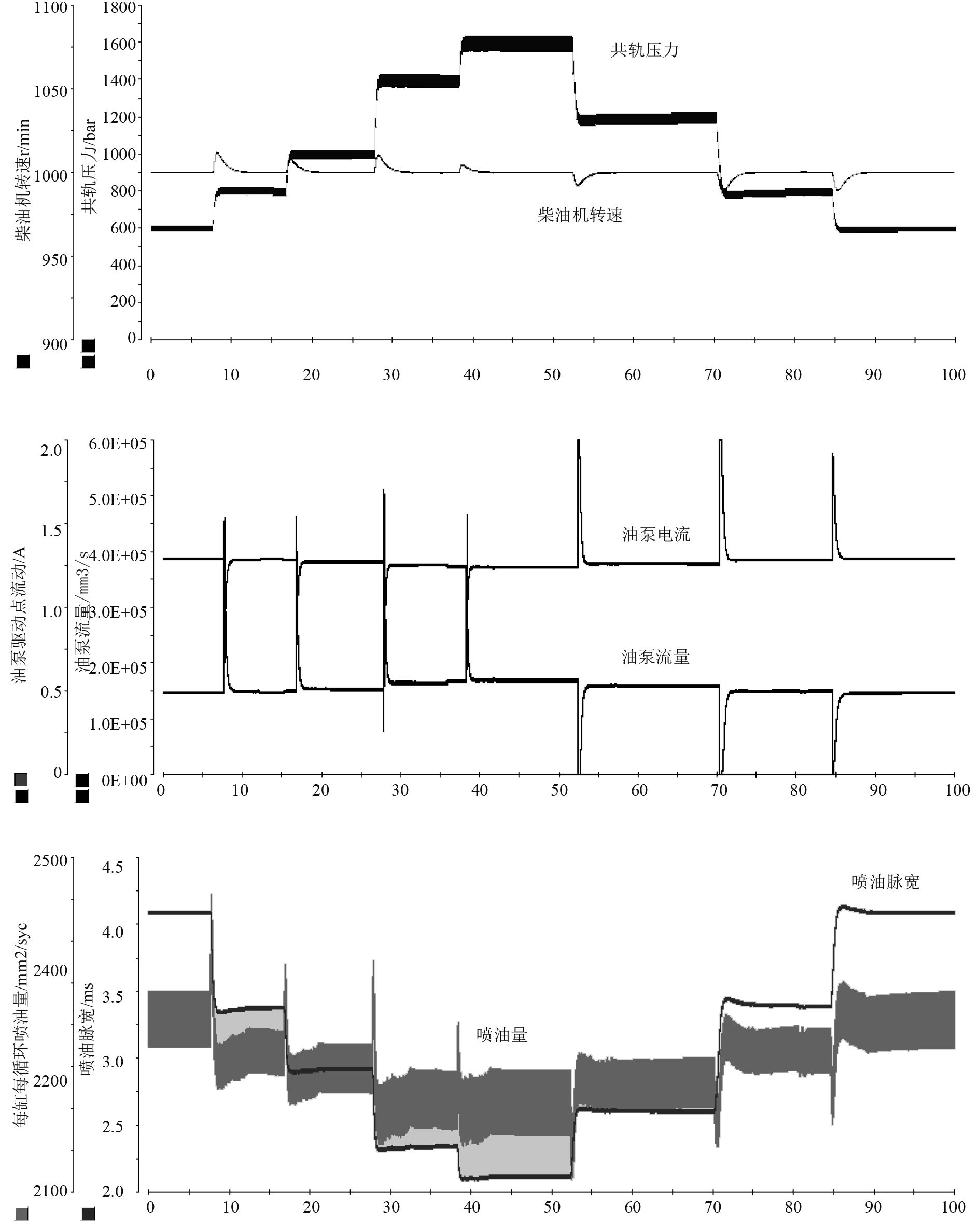
3.1.2 转速、轨压闭环功能验证在轨压1 000 bar时,设置设定转速值为400,600,800,1000,800,400 r/min,观测实际转速、喷油和油泵信号的变化,验证转速闭环控制功能,如图7所示。在转速1 000 r/min时,设置目标轨压值为600,800,1 000,1 400,1 600,1 200,800,600 bar,观测实际轨压、喷油和油泵信号的变化,验证轨压闭环控制功能如图8所示。
|
图 7 转速闭环功能验证结果图 Fig. 7 Result diagram of speed closed loop function verification |
|
图 8 轨压闭环控制验证结果图 Fig. 8 Result diagram of rail pressure closed loop function verification |
由图7可知,设定转速值的每次变化都引起喷油脉宽和油泵电流的变化,从而使模型计算喷油量和油泵流量变化,导致转速跟随设定转速变化,实现转速闭环控制。轨压闭环同样。模型能够模拟转速和轨压闭环时柴油机的动态响应特性,可用于转速、轨压闭环功能测试。
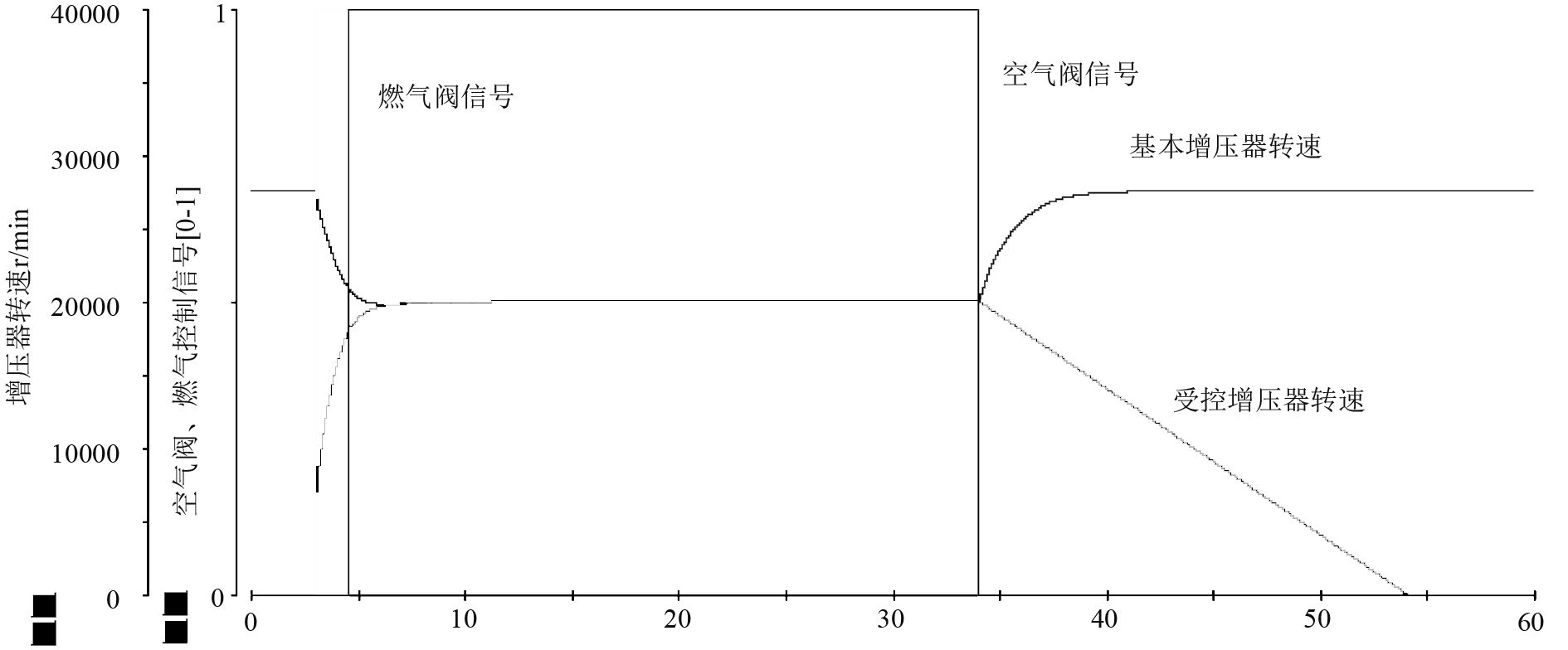
3.1.3 相继增压功能验证设置空气阀、燃气阀开启、关闭信号,观测增压器动态特性,验证结果如图9所示。
|
图 9 相继增压功能验证结果图 Fig. 9 Result diagram of sequential supercharging function verification |
由图9可知,燃气阀、空气阀开启时,受控增压器切入工作,基本增压器转速降低,受控增压器转速由0增大,最终两增压器转速一样。燃气阀、空气阀关闭时,受控增压器切出。模型能够模拟相继增压切换动态过程,可用于该功能验证。
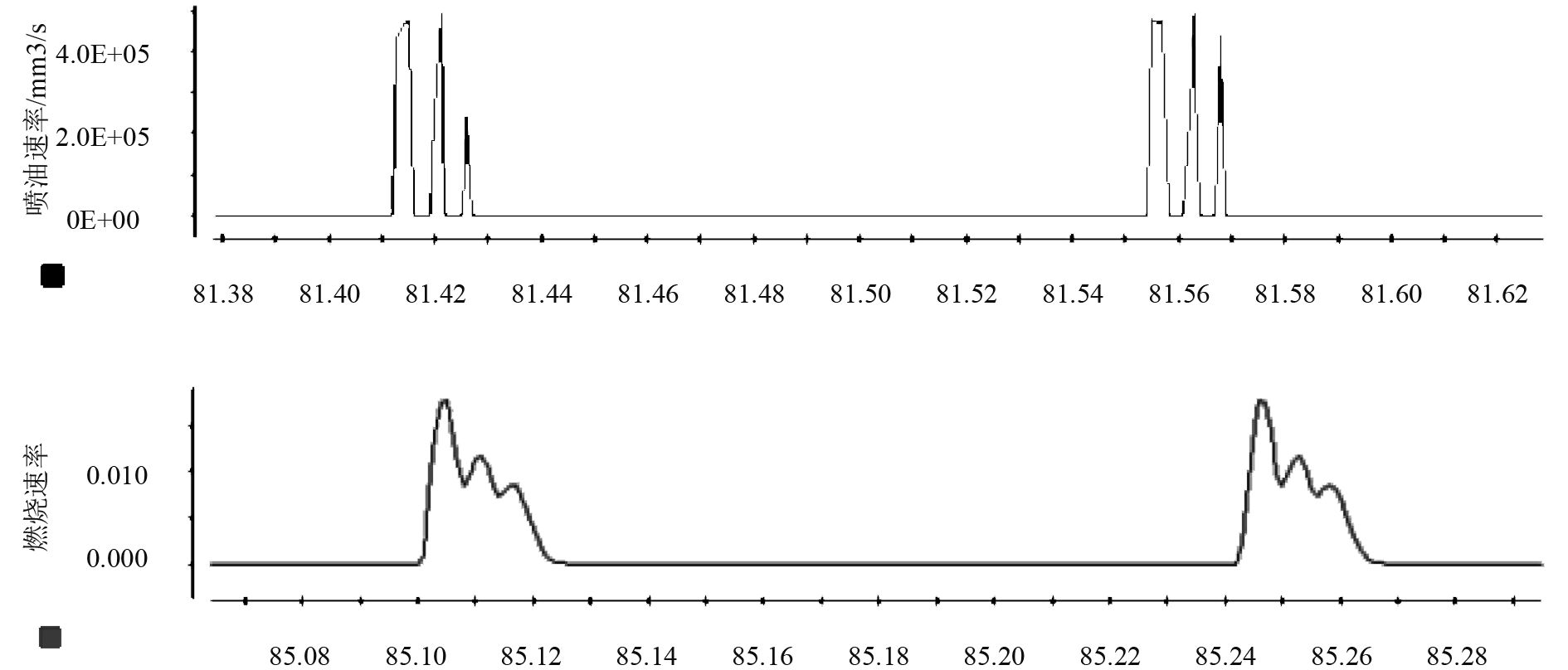
3.1.4 多次喷射功能验证设置多次喷射控制,观测模型是否能够根据喷射信号,模拟多次喷射,验证结果如图10所示。
|
图 10 多次喷射功能验证结果图 Fig. 10 Result diagram of multiple injections function verification |
图10显示3次喷射时,喷油速率和燃烧速率的变化,可见模型能够根据3次喷射信号,模拟柴油机3次喷射燃烧的动态特性。
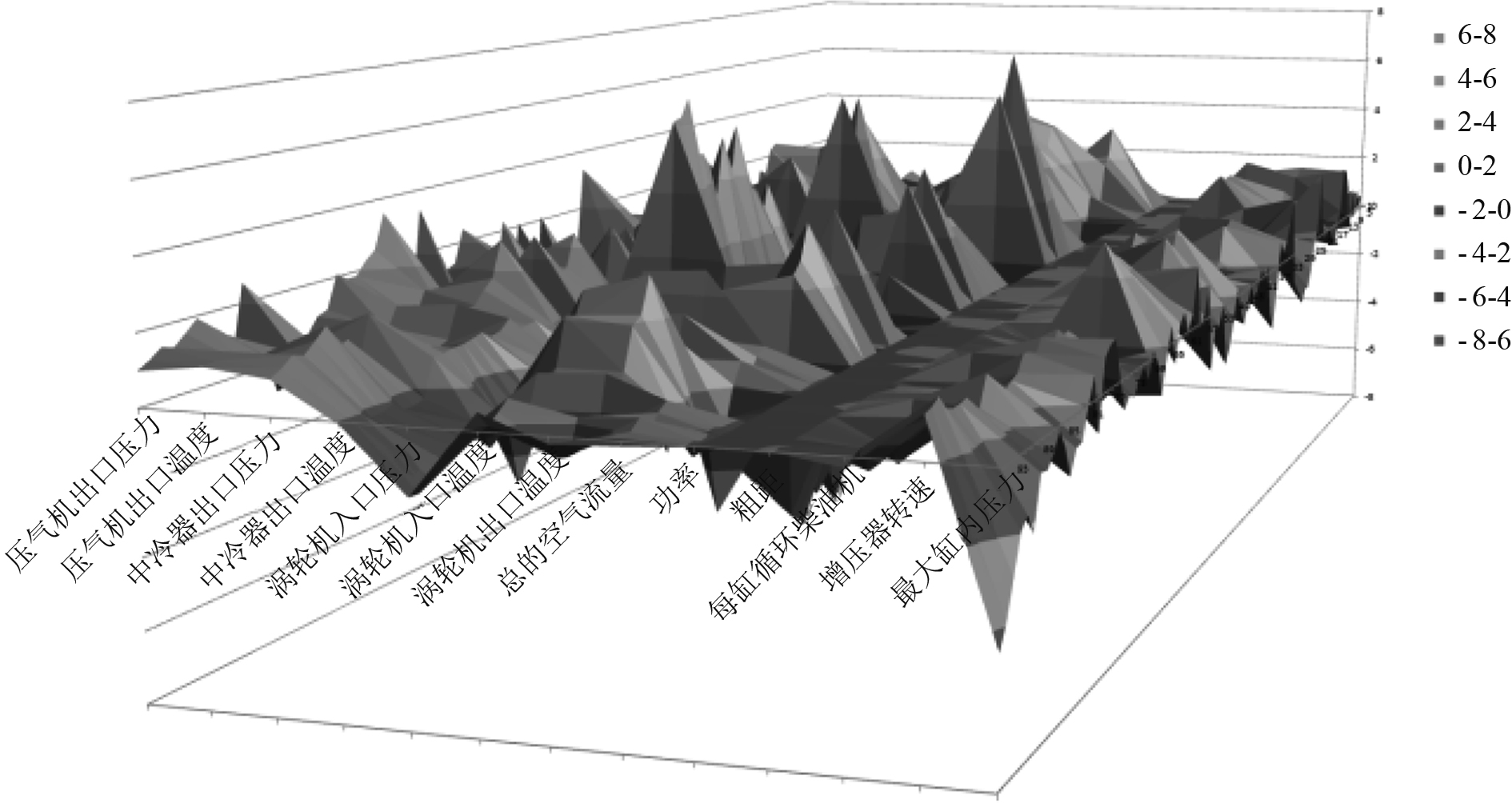
3.2 模型精度和实时性验证 3.2.1 模型精度验证选取覆盖柴油机整个运行特性的稳态工况点,对比试验数据与仿真计算数据,验证模型精度。对比工况点参数试验与仿真数据偏差,如图11所示。
|
图 11 试验与仿真数据偏差曲线图 Fig. 11 Deviation curve diagram of experiment and simulation data |
由图11可知,对比参数的最大偏差在6%~8%之间,精度在90%以内,模型精度较高,满足测试要求。
3.2.2 模型实时性验证设置仿真步长为0.2 ms,16缸柴油机单步长计算时间为0.082 ms,占单步长仿真时间的41%,满足实时性要求。
4 结 语本文针对某16缸船用高压共轨增压中冷柴油机建立了零维实时仿真模型。该模型比平均值模型功能更加丰富,准确度也更高,比准维模型实时性好。仿真验证结果表明,模型能够根据控制信号变化,实时反映柴油机动态响应特性,满足功能测试要求。仿真与试验数据对比结果表明,模型精度较高,在90%以内,符合精度要求。实时仿真步长占设定单位步长的41%,表明模型实时性符合要求。
综上,模型功能、精度和实时性,均满足被测电控系统测试要求,为后续船用柴油机硬件在环测试环境建设准备好软件基础。
| [1] |
杜剑维. 基于dSPACE的相继增压柴油机硬件在环仿真[D]. 哈尔滨: 哈尔滨工程大学, 2007.
|
| [2] |
蒋方毅. 基于模型的柴油机硬件在环仿真与控制研究[D]. 武汉: 华中科技大学, 2009.
|
| [3] |
杨闻睿, 敖国强, 等. 高压共轨柴油机ECU硬件在环仿真系统软件设计[J]. 内燃机工程, 2009, 30(5): 41-45. DOI:10.3969/j.issn.1000-0925.2009.05.009 |
| [4] |
凌健, 刘希, 谢晖. 高压共轨柴油机ECU硬件在环实时仿真及测试平台的开发[C]//. 中国内燃机学会燃烧节能净化分会2009年学术年会. CSICE2009-091.
|
| [5] |
齐鲲鹏, 隆武强, 冯立岩. 硬件在环仿真系统中柴油机工作过程建模研究[J]. 内燃机工程, 2007, 28(6): 49-52. DOI:10.3969/j.issn.1000-0925.2007.06.012 |
| [6] |
DEEPA R, RYAN M S S. A case study in hardware-in-the-loop testing: development of an ecu for a hybrid electric vehicle[J]. SAE Technical Paper Series, 2004-01-0303(2004).
|
| [7] |
岳继光, 董延超. 汽车发动机模型硬件在环仿真研究[J]. 系统仿真技术, 2008(4): 85-89. |
| [8] |
王文成. 高压共轨柴油机轨压控制策略的研究[D]. 北京: 中国舰船研究院. 2017
|
 2019, Vol. 41
2019, Vol. 41
