直翼推进器又称摆线推进器(Cycloidal Propeller)或竖轴推进器,与其他推进器不同的是,它由一组伸向水中并绕垂直于船体轴线做圆周运动的叶片组成。叶片在绕着船体轴线做圆周运动的同时,还绕自身的固定轴转动[1]。通过控制推进器的偏心率和偏心方向,可在垂直于旋转轴平面内产生任意方向和大小的力,从而使得直翼推进器具有良好的操纵性和动力定位性能。目前国外大多应用在拖船、渡轮、海洋平台和扫雷艇等,而国内船舶领域在应用直翼推进器方面几乎空白。为了满足国内今后某些船舶的特殊需求,使用直翼推进器作为船舶推进器成为一种比较好的方案选择。本文通过建立船机桨仿真模型,研究直翼推进器与船体和主机之间的匹配性能,进一步提高直翼推进器的实船应用水平。
为了提高船舶经济性和安全性,使船机桨系统达到最佳配合,就需要研究船机桨在不同的工况和海况下的匹配特性。在匹配理论研究方面,胡安康对沪东型螺旋桨进行了研究,建立了桨的水动力性能预报模型,并进行数值计算。实船试航结果表明,船机桨匹配良好,航速预报准确。覃峰和詹志刚等[2]把遗传算法应用到船舶设计中,实践证明遗传算法具有收敛快,精度高的特点;刘莹建立了经过优化的船舶、汽轮机和螺旋桨匹配模型,表明汽轮机和螺旋桨的效率均有所提高;黄斌等建立全柴联合动力装置的Matlab/Simulink仿真模型,并利用MFC对模型进行集成和改进,提出该模型推进系统均匀加速和非均匀加速过程“机—桨”联控方法[3]。以上这些方法都只是针对基于螺旋桨的船机桨匹配研究,并无对采用直翼推进器的船机桨匹配特性研究。
本文针对以上不足之处,以采用直翼推进器的船舶为研究对象,通过分析直翼推进器的水动力特性,分析船机桨之间的能量转化关系,研究采用直翼推进器的船机桨匹配特性,为进一步的实船应用提供参考。
1 直翼推进器动力装置简介如图1所示,直翼推进系统一般构成包括直翼推进器、传动轴、齿轮箱和主机等,由于技术复杂及应用的问题,国内对直翼推进器的研究较少。

|
图 1 某直翼推进器动力装置简图 Fig. 1 The propulsion system with cycloidal propeller |
本文以某进口1 400 吨级船舶为研究对象,该船采用双机双桨直翼推进的结构,直翼推进器型号为28 GH/210,额定转速为400 r/min,主机功率为2 000 kW,该船舶具有机动性高,操纵性好,动力定位能力强,低噪声等特点,其最高航速要求不小于15 kn。图2为直翼推进器的结构简图。

|
图 2 直翼推进器结构图 Fig. 2 The structure of cycloidal propeller |
本文新研究的直翼推进系统构成特点,其动力装置模型主要包括柴油机模型,传动系模型,直翼推进器模型以及船体运动模型等。图3为船机推进器匹配模型结构。

|
图 3 船机桨匹配模型结构简图 Fig. 3 The model of ship-diesel-propeller matching |
由图3可知,船机推进器匹配过程是一个能量转换过程,柴油机将燃油的化学能转化为机械能,通过传功装置和轴系将力矩传递给直翼推进器,使其旋转产生力矩,用于克服船体所受的阻力。
根据能量守恒原理和运动平衡,得到柴油机和直翼推进器之间的平衡关系:
| $ \left\{ \begin{split} & {{M}_{D}}i-{{M}_{f}}-{{M}_{P}}=\left( J+{{J}_{S}} \right)\displaystyle\frac{{\rm{d}}{{\omega }_{P}}}{{\rm{d}}t}{\text{,}} \\ & {{n}_{D}}={{n}_{P}}i{\text{。}} \\ \end{split} \right. $ |
式中:MD为柴油机转矩;i为减速比;Mf为推进装置阻力矩;MP为直翼推进器转矩;J为轴系转动惯量;JS为直翼推进器附连水转动惯量;ωP,nP分别为直翼推进器角速度和转速;nD为柴油机转速。
同理可得推进器和船体的平衡关系:
| $ \left\{ \begin{split} & {{Z}_{P}}T\left( 1-{{t}_{P}} \right)-R=\left( m+{{m}_{s}} \right)\displaystyle\frac{d{{V}_{S}}}{{\rm{d}}\rm{t}}{\text{,}} \\ & {{V}_{A}}=\left( 1-\omega \right){{V}_{S}} {\text{。}} \\ \end{split} \right. $ |
式中:ZP为直翼推进器数量;T为单推进器推力;R为船舶阻力:m为船舶质量;ms为船舶附加质量;VA,VS分别为推进器进速和船速;tP,ω分别为推力减额和伴流系数。
2.1 柴油机模型柴油机根据建模的原理、难易程度、使用范围的不同选择合适的模型,大致分准稳态非线性模型、容积法和线性化模型。根据建模过程对模型精度、准确度以及反应速度的要求,本文采用准稳态法对柴油机进行建模。
准稳态模型将动态过程看作多个过程组成,是由柴油机各部分的稳态特性、流体力学和热力学方程以及基于试验的经验公式表达。柴油机本体模型应用牛顿第二定律,利用柴油机输出扭矩、负载扭矩和摩擦扭矩之间的平衡,得到柴油机的转速等参数。
2.2 直翼推进器数学模型如图4所示,建立同原点的2个坐标系xoy和ξoς,控制点N在y正方向上,且2个坐标系夹角为β,设来流速度为VA,诱导速度为un,合速度为VR,盘面半径为R,圆盘角速度为ω,叶片轨迹角为θ,偏心方向角为β,叶片冲角为α,叶片方向角为φ,则由几何关系可得叶片单位长度上的推力和扭矩[4]:
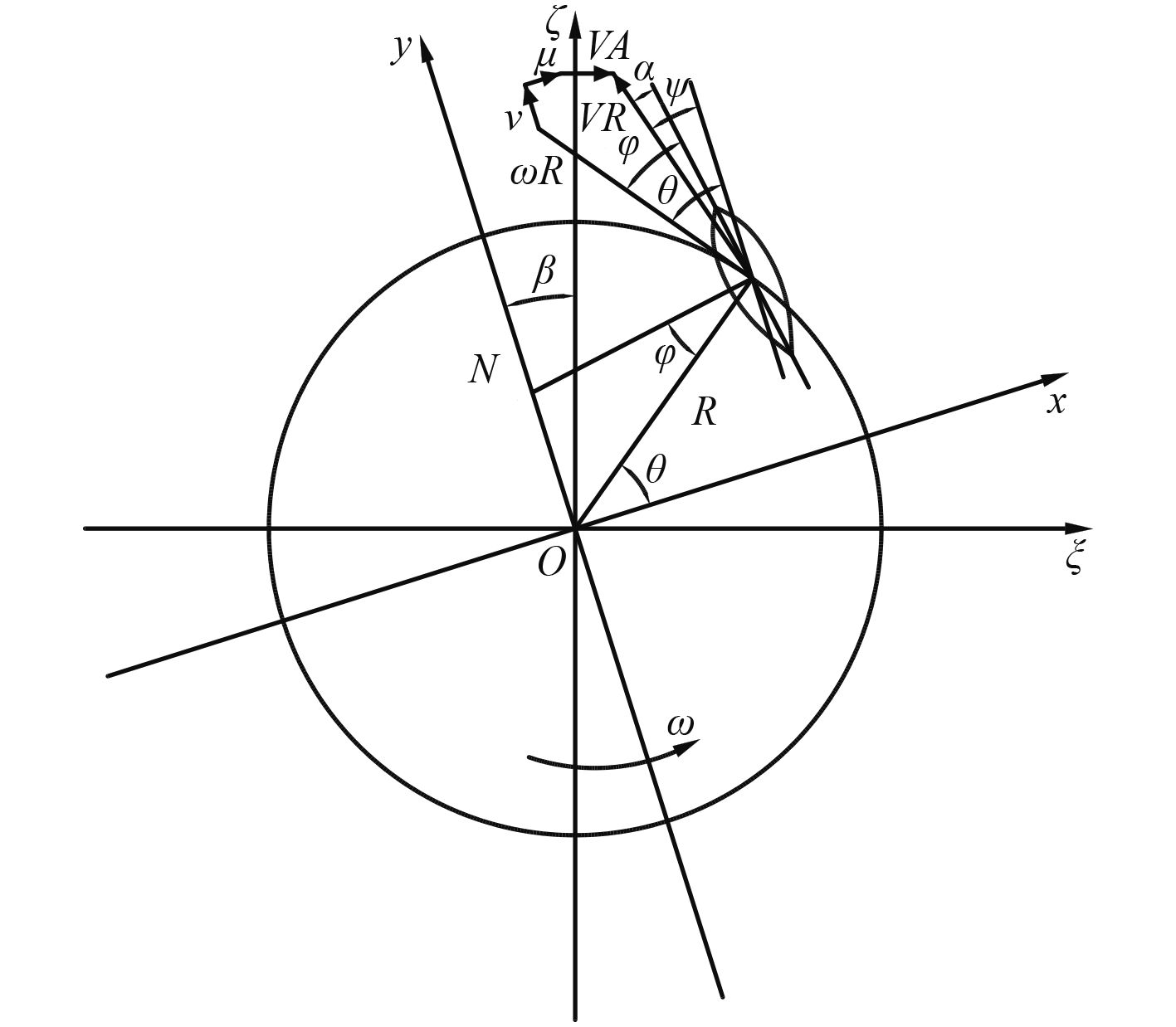
|
图 4 水动力分析图 Fig. 4 The analysis of force |
| $ \left\{ \begin{split} & {{t}_{X}}\left( \theta \right)=L\cos \left( \theta -\varphi +\alpha \right)+D\sin \left( \theta -\varphi +\alpha \right) {\text{,}} \\ & {{t}_{Y}}\left( \theta \right)=L\sin \left( \theta -\varphi +\alpha \right)-D\cos \left( \theta -\varphi +\alpha \right) {\text{,}} \\ & m\left( \theta \right)=\left[ L\sin \left( \varphi -\alpha \right)+D\cos \left( \varphi -\alpha \right) \right]R{\text{。}} \end{split} \right. $ |
式中:升力
由上述公式沿叶片长进行积分,得到单个直翼叶片在任意轨迹角圆周上的水动力,然后对其进行圆周积分并取平均值,乘上叶片数可得直翼推进器平均水动力,具体结果如下:
| $ \begin{aligned} & {T_X} = \frac{Z}{{4{\text{π}} }}\rho cb\int_{ - \text{π} }^\text{π} {{V_R}} \left[ \begin{aligned} & {C_L}\left( {\omega R\cos (\theta ) + (v - {V_A}\sin (\beta ))} \right) + \\ & {C_D}\left( {\omega R\sin (\theta ) - (u + {V_A}\cos (\beta ))} \right) \end{aligned} \right]{\rm{d}}\theta {\text{,}}\\ & {T_Y} = \frac{Z}{{4\text{π} }}\rho cb\int_{ - \text{π} }^\text{π} {{V_R}} \left[ \begin{aligned} & {C_L}\left( {\omega R\sin (\theta ) - (u + {V_A}\cos (\beta ))} \right) + \\ & {C_D}\left( {\omega R\cos (\theta ) + (v - {V_A}\sin (\beta ))} \right) \end{aligned} \right]{\rm{d}}\theta{\text{,}} \\ & \begin{aligned} & M = \frac{Z}{{4\text{π} }}\rho cb\int_{ - \text{π} }^\text{π} {{V_R}}\;\times\\ & \left\{ \begin{aligned} & {C_L}\left[ {(u + {V_A}\cos (\beta ))\cos (\theta ) + (v - {V_A}\sin (\beta ))\sin (\theta )} \right] + \\ & {C_D}\left[ {\omega R - (u + {V_A}\cos (\beta ))\sin (\theta ) + (v - {V_A}\sin (\beta ))\cos (\theta \!)} \right] \end{aligned}\! \right\}{\rm{d}}\theta {\text{,}} \end{aligned} \end{aligned} $ |
则单桨总推力为
| $ {{T}_{P}}=\sqrt{T_{X}^{2}+T_{Y}^{2}}{\text{,}} $ |
对
| $ \left\{ \begin{split} {{K}_{X}}=\displaystyle\frac{{{T}_{X}}}{\rho n_{P}^{2}D_{P}^{3}b}{\text{,}} \\ {{K}_{Y}}=\displaystyle\frac{{{T}_{Y}}}{\rho n_{P}^{2}D_{P}^{3}b}{\text{,}} \\ {{K}_{M}}=\displaystyle\frac{M}{\rho n_{P}^{2}D_{P}^{4}b}{\text{。}} \\ \end{split} \right. $ |
由于上述KX,KY,KM是在XOY坐标系中求得的,需要投影到ξ坐标和ς坐标中,则转换关系如下:
| $ \left\{ \begin{matrix} {{K}_{T}}={{K}_{X}}\cos \beta -{{K}_{Y}}\sin \beta {\text{,}} \\ {{K}_{S}}={{K}_{X}}\sin \beta +{{K}_{Y}}\cos \beta {\text{。}} \\ \end{matrix} \right. $ |
转矩KM在2个坐标系中相同。
推进器效率由下式计算:
| $ \eta =\frac{{{V}_{A}}T}{2{\text{π}} nM}=\frac{J}{2{\text{π}} }\cdot \frac{{{K}_{T}}}{{{K}_{S}}}{\text{。}} $ |
式中
直翼推进器作为船机桨匹配过程中的重要组成部分,根据直翼推进器的工作原理和工作状态建立Simulink模型,为船机桨匹配研究做准备。
2.3 船体数学模型 2.3.1 伴流系数和推力减额系数估算通常情况下,可通过实验得到精确的伴流系数和推力减额系数。由于缺乏采用直翼推进船舶的相关实验数据。在不需要精确计算的情况下,本文采用估算螺旋桨船舶的经验公式用以估算伴流系数和推力减额系数。
1)伴流系数估算。
常见的经验公式包括汉克歇尔公式、越智重信公式和巴甫米尔公式,其中估算结果和实测结果比较接近的是汉克歇尔公式。本文采用适用双桨船的汉克歇尔公式,公式如下:
| $ {{\omega }_{p0}}=0.7{{C}_{P}}-0.3{\text{。}} $ |
2)推力减额系数估算
对于双桨船,推力减额系数tp0计算方法有汉克歇尔估算式、哥铁堡公式、商赫公式和霍尔特洛泼公式。本文采用汉克歇尔估算式和哥铁堡公式的平均值。
①汉克歇尔估算式
| $ {{t}_{p0}}=0.5{{C}_{P}}-0.18{\text{;}} $ |
②哥铁堡公式
| $ {{t}_{p0}}=1.67-2.3\frac{{{C}_{b}}}{{{C}_{WP}}}+1.5{{C}_{b}}{\text{。}} $ |
式中:CP为菱形系数;Cb为方形系数;CWP水线面面积系数。
2.3.2 船体运动模型根据日本操纵性模型小组MMG建模思想,船舶所受的外力和外力矩分为裸体船、直翼推进器力和力矩,裸体船上的力和力矩分为粘性类和惯性类:
| $ \left\{ \begin{split} & m\left( \dot{u}-vr \right)={{X}_{I}}+{{X}_{H}}+{{X}_{P}}{\text{,}} \\ & m\left( \dot{v}+ur \right)={{Y}_{I}}+{{Y}_{H}}+{{Y}_{P}}{\text{,}} \\ & {{I}_{Z}}\dot{r}={{M}_{I}}+{{M}_{H}}+{{M}_{P}} {\text{。}} \\ \end{split} \right. $ |
式中:下标I为船体惯性类;H为船体粘性类;P为直翼推进器;XH,YH,MH分别为船舶纵向水动力,横向水动力和力矩;XP,YP,MP分别为直翼推进器推力,横向力和力矩。
1)船体惯性类水动力和力矩。由周昭明对元良诚三图谱进行多元回归分析,其估算公式如下[5]:
| $ \begin{split} &{\displaystyle\frac{{{m_x}}}{m} = \frac{1}{{100}}\left[ \begin{aligned} & 0.398 + 11.97{C_b}\left(1 + 3.73\frac{d}{B}\right) - 2.89{C_b}\frac{L}{B} \times \\ &\left(1 + 1.13\frac{d}{B}\right) + 0.175{C_b}{\left(\displaystyle\frac{L}{B}\right)^2}\left(1 + 0.541\frac{d}{B}\right)- \\ & 1.107\frac{L}{B}\frac{d}{B} \end{aligned} \right]}{\text{,}}\\ &{\displaystyle\frac{{{m_y}}}{m} = 0.882 - 0.54{C_b}\left(1 - 1.6\frac{d}{B}\right) - 0.156\frac{L}{B}(1 - 0.673{C_b})}+\\ &\quad{ 0.826\frac{d}{B}\frac{L}{B}\left(1 - 0.678\frac{d}{B}\right) - 0.638{C_b}\displaystyle\frac{d}{B}\frac{L}{B}\left(1 - 0.669\frac{d}{B}\right)}\times\\ &{\sqrt {\displaystyle\frac{{{J_Z}}}{m}} = \frac{L}{{100}}\left[\begin{aligned} & 33 - 76.85{C_b}\left(1 - 0.784{C_b}\right)\\ & + 3.43\displaystyle\frac{L}{B}\left(1 - 0.63{C_b}\right) \end{aligned}\right]} {\text{。}}\end{split} $ |
式中:mx,my,JZ为附加质量和附加惯性矩;d,B,L,Cb分别为船舶吃水,型宽,船长和方型系数。
2)船体粘性类水动力和力矩。目前对粘性水动力计算模型是按漂角β的大小选取的,本文选择贵岛模型进行计算:
| $ \left\{ \begin{aligned} & {{X}_{H}}=X\left( u \right)+{{X}_{vv}}{{v}^{2}}+{{X}_{vr}}vr+{{X}_{rr}}rr {\text{,}} \\ & {{Y}_{H}}={{Y}_{v}}v+{{Y}_{r}}r+{{Y}_{vv}}\left| v \right|v+{{Y}_{rr}}\left| r \right|r+{{Y}_{vvr}}{{v}^{2}}+{{Y}_{vrr}}v{{r}^{2}}{\text{,}} \\ & {{M}_{H}}={{M}_{v}}+{{M}_{r}}r+{{M}_{vv}}\left| v \right|v+{{M}_{rr}}\left| r \right|r+{{M}_{vvr}}{{v}^{2}}r+{{M}_{vrr}}v{{r}^{2}} {\text{。}}\end{aligned} \right. $ |
3)直翼推进器推力、横向力和力矩。直翼推进器具有优良的操纵性,其纵向推力是主动力,横向推力是起到舵的作用。图5为推进器控制点N在任意位置与推力关系的示意图。
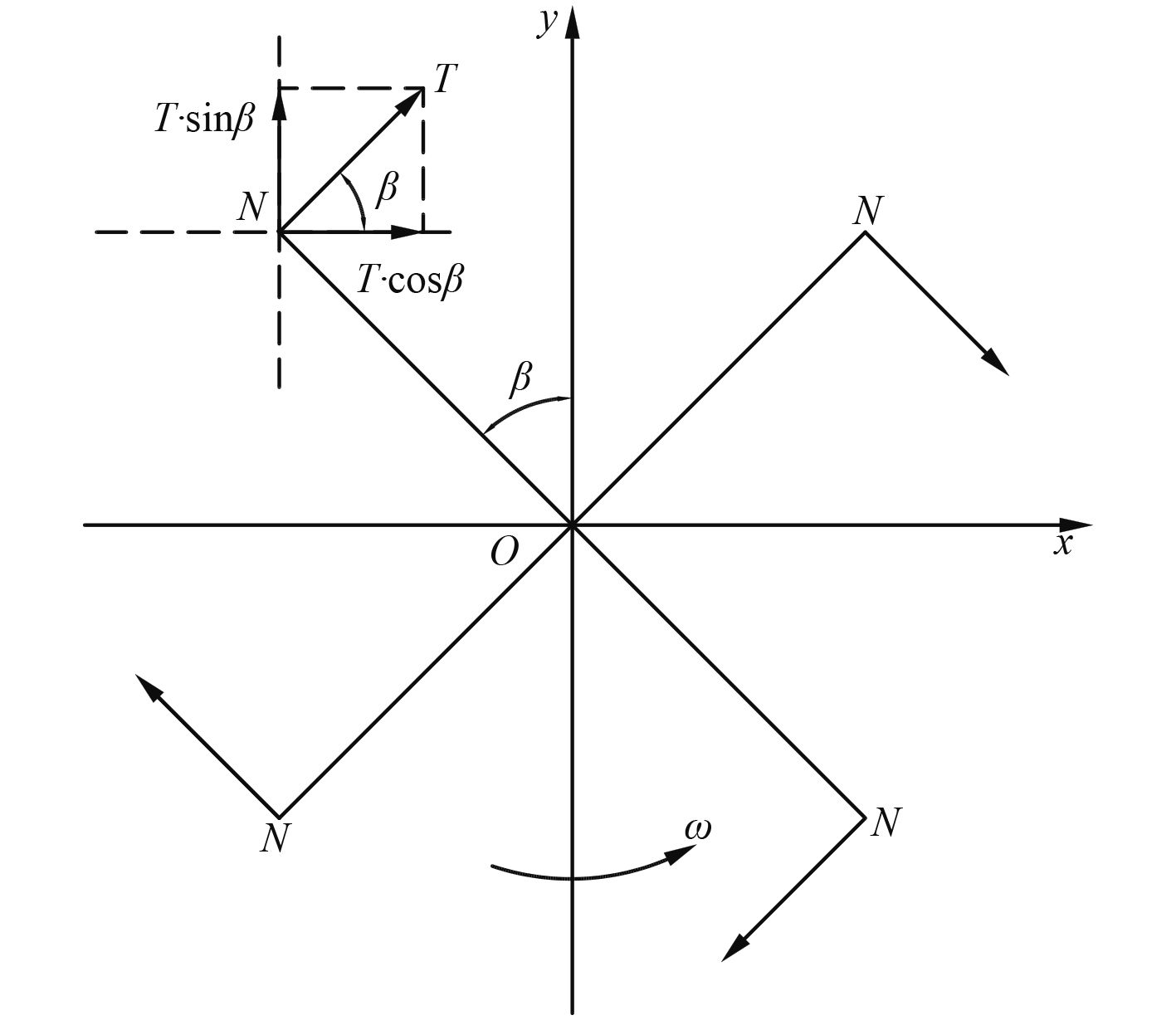
|
图 5 N点位置与推力方向示意图 Fig. 5 Relation between position N and thrust direction |
由图可知,推力可分解为x、y方向上分力,如下式:
| $ \left\{ \begin{matrix} {{T}_{x}}=T\cos \beta {\text{,}} \\ {{T}_{y}}=T\sin \beta {\text{,}} \\ \end{matrix} \right. $ |
设船舶在某运动状态下,左桨偏转角度为δP,转速为nP,本文直接采用以下公式计算左桨的有效推力:
| $ {{T}_{P}}=\left( 1-{{t}_{P}} \right)\rho n_{P}^{2}D_{P}^{3}{{L}_{P}}{{K}_{t}}\left( {{J}_{P}} \right){\text{。}} $ |
式中:TP为左桨推力;Kt(JP)为桨的推力系数;tP为推力减额系数;ρ为流体密度;nP为左桨转速;DP为桨的直径;LP为桨叶长度。
右桨的有效推力公式如下:
| $ {{T}_{S}}=\left( 1-{{t}_{P}} \right)\rho n_{S}^{2}D_{P}^{3}{{L}_{P}}{{K}_{t}}\left( {{J}_{P}} \right){\text{。}} $ |
式中:TS为右桨推力;其他参数同上。
船舶所受总推力及转矩为:
| $ \left\{ \begin{aligned} & {{X}_{P}}={{T}_{P}}\cos \left( {{\delta }_{P}} \right)+{{T}_{S}}\cos \left( {{\delta }_{S}} \right){\text{,}} \\ & {{Y}_{P}}={{T}_{P}}\sin \left( {{\delta }_{P}} \right)+{{T}_{S}}\sin \left( {{\delta }_{S}} \right){\text{,}} \\ & {{M}_{P}}=\left( {{T}_{P}}\cos \left( {{\delta }_{P}} \right)-{{T}_{S}}\cos \left( {{\delta }_{S}} \right) \right)\frac{{{L}_{PS}}}{2}-{{Y}_{P}}\frac{{{L}_{OP}}}{2}{\text{,}} \\ & {{K}_{P}}={{Y}_{P}}{{Z}_{P}} {\text{。}} \end{aligned} \right. $ |
式中:nS为右桨转速;δS为右桨偏转角度;LPS为左右桨之间的横向距离;LOP为直翼推进器纵向位置;ZP为直翼推进器的垂向位置。
将上述公式代入MMG公式中,并运用龙格库塔计算方法,可解得操纵运动参数u(t),v(t),r(t),则可求出船舶在固定坐标系中轨迹和艏向角ψ。
| $ \left\{ \begin{aligned} & \psi \left( t \right)=\int_{0}^{t}{r{\rm{d}}t}{\text{,}} \\ & x=\int_{0}^{t}{{{V}_{x}}{\rm{d}}t}=\int_{0}^{t}{\left( u\cos \psi -v\sin \psi \right){\rm{d}}t}{\text{,}} \\ & y=\int_{0}^{t}{{{V}_{y}}{\rm{d}}t}=\int_{0}^{t}{\left( u\sin \psi +v\cos \psi \right){\rm{d}}t} {\text{。}} \end{aligned} \right. $ |
柴油机Simulink仿真模型如图6所示。
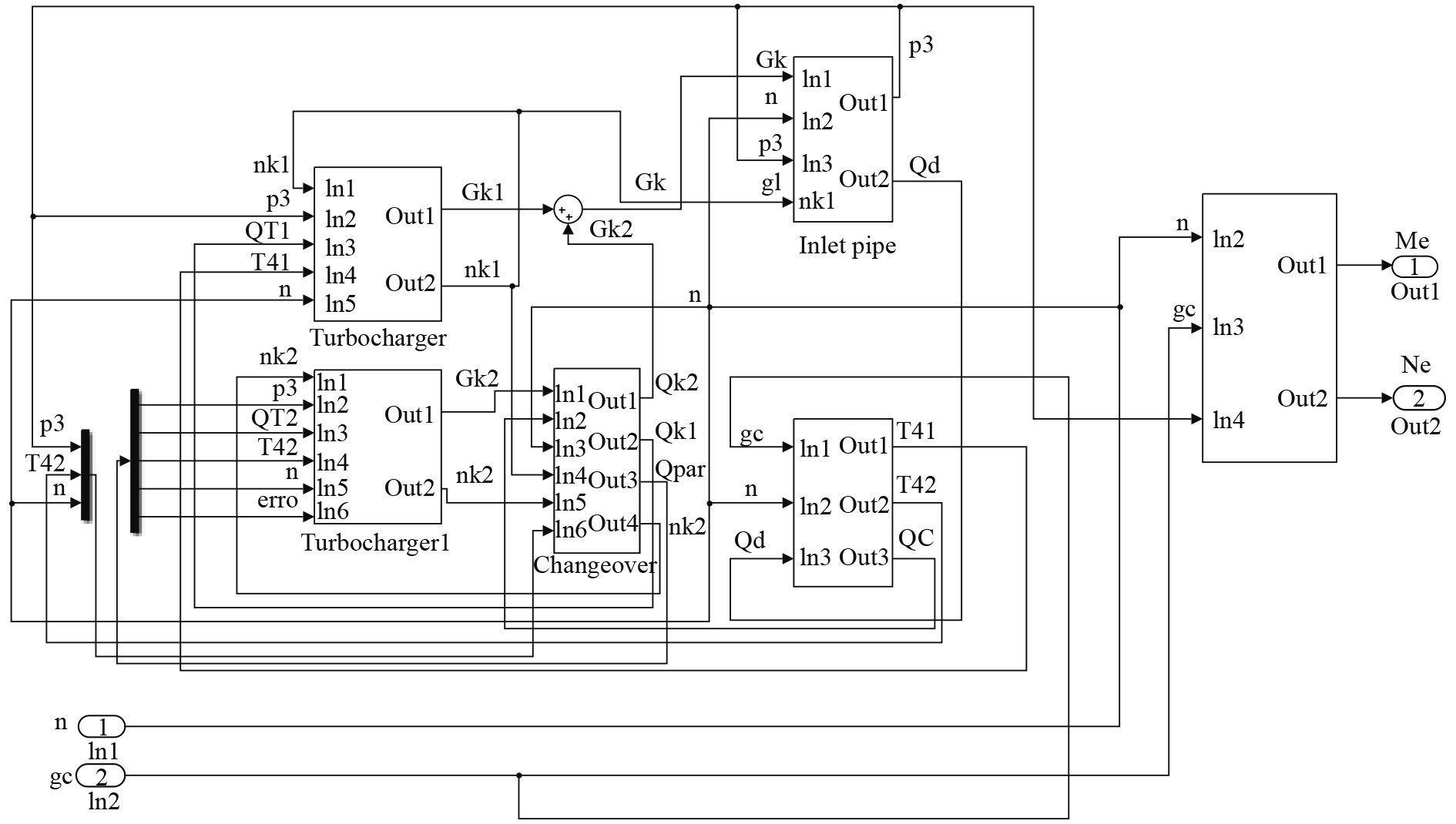
|
图 6 柴油机Simulink模型图 Fig. 6 The Simulink model of diesel |
直翼推进器Simulink仿真模型如图7所示。

|
图 7 直翼推进器Simulink模型图 Fig. 7 The Simulink model of cycloidal propeller |
图8为基于Simulink的船舶直航运动仿真模型。
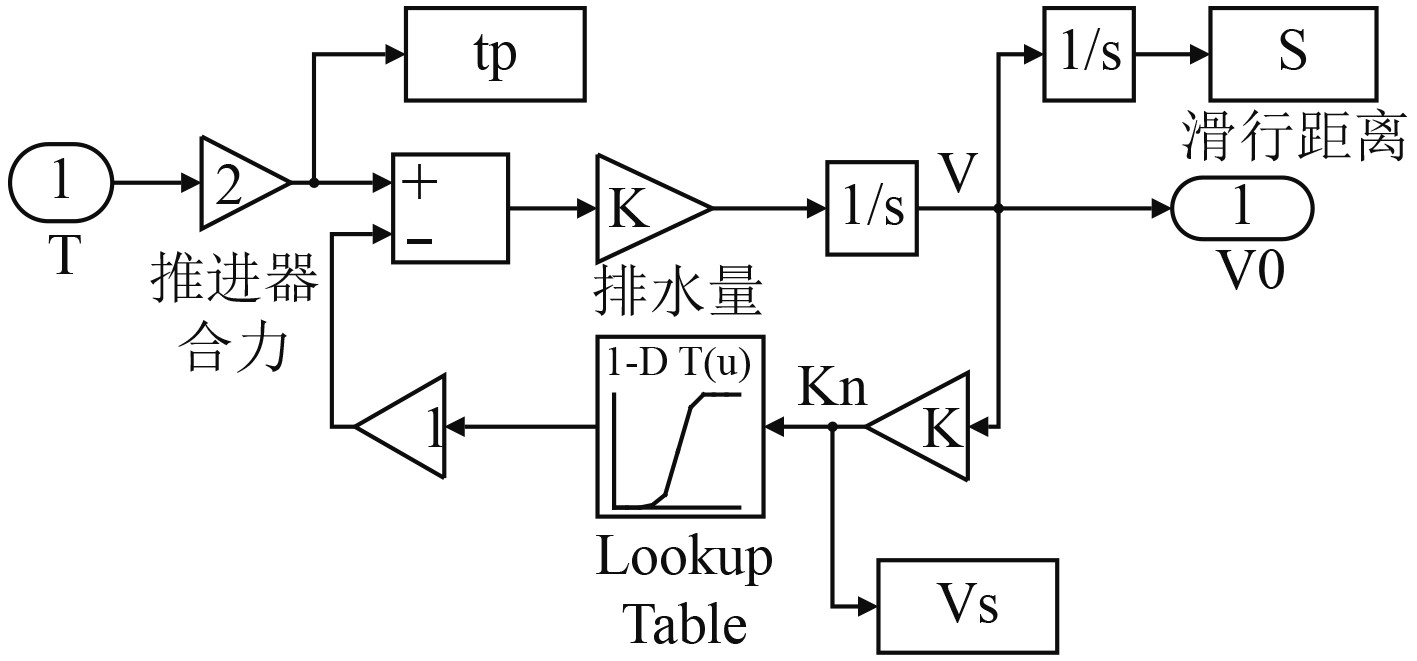
|
图 8 基于Simulink船舶直航运动仿真模型 Fig. 8 The Simulink model of ship motion |
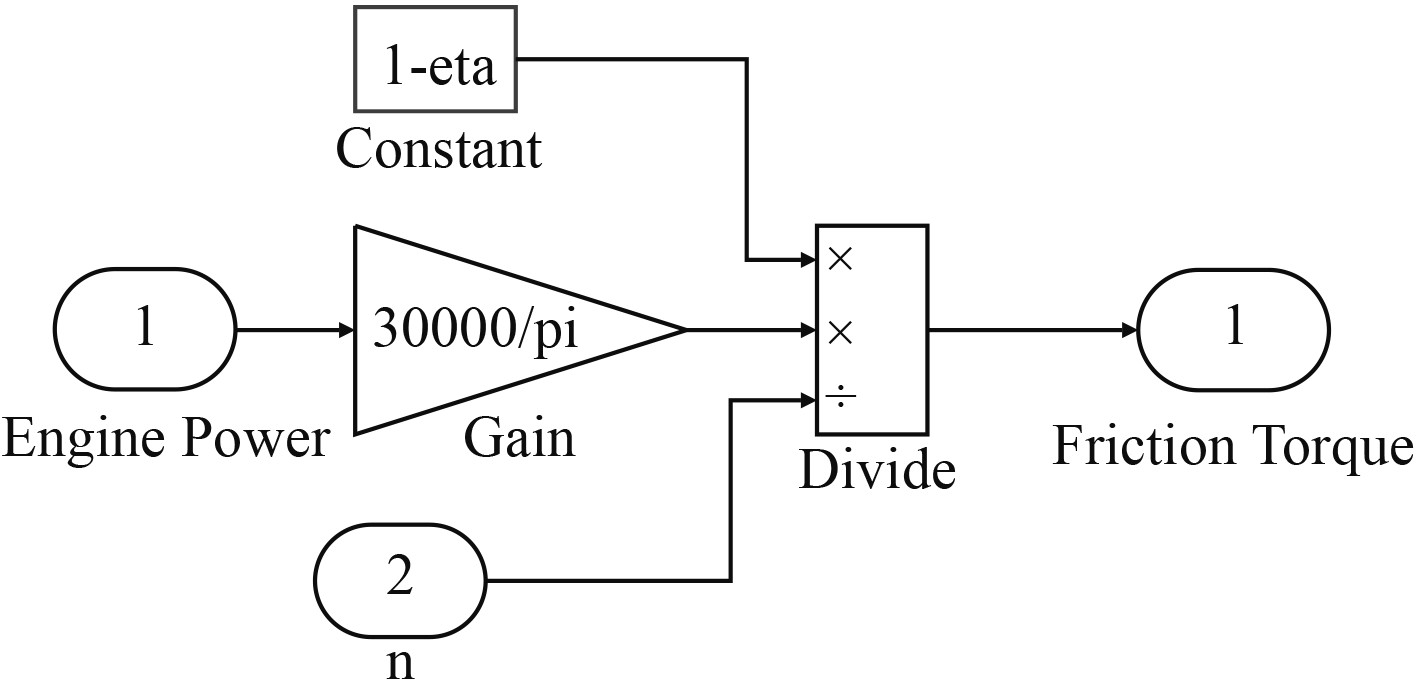
图9为轴系摩擦损失仿真模型,图10为减速齿轮箱摩擦损失仿真模型。

|
图 9 轴系摩擦损失仿真模型 Fig. 9 The model of friction loss of shaft |
|
图 10 齿轮箱摩擦损失仿真模型 Fig. 10 The model of friction loss of gearbox |
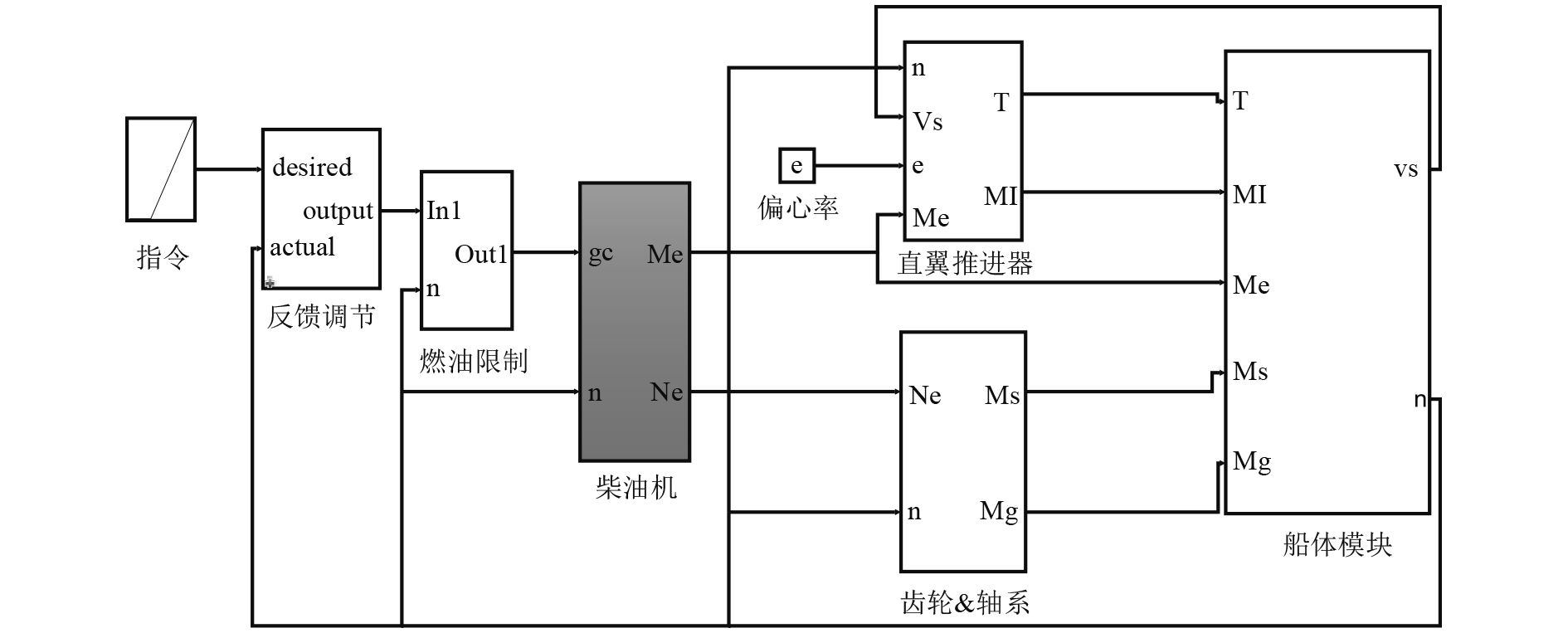
图11为基于Simulink的船机桨匹配仿真模型。
|
图 11 船机桨匹配仿真模型 Fig. 11 The model of ship-diesel-propeller matching |
船舶运动过程中,船舶各个状态量都在发生变化,本文通过建立1组1阶常微分方程,并运用4阶龙格库塔进行求解,具体解法如下:
| $ \left\{ \begin{aligned} & \dot{u}={{f}_{1}}\left( t,u,v,r,\varphi ,x,y \right) {\text{,}}\\ & \dot{v}={{f}_{2}}\left( t,u,v,r,\varphi ,x,y \right) {\text{,}}\\ & \dot{r}={{f}_{3}}\left( t,u,v,r,\varphi ,x,y \right) {\text{,}}\\ & \dot{\varphi }={{f}_{4}}\left( t,u,v,r,\varphi ,x,y \right){\text{,}} \\ & \dot{x}={{f}_{5}}\left( t,u,v,r,\varphi ,x,y \right) {\text{,}}\\ & \dot{y}={{f}_{6}}\left( t,u,v,r,\varphi ,x,y \right) {\text{。}}\\ \end{aligned} \right. $ |
设tj时刻,初值为uj,vj,rj,φj,xj,yj,则t=tj+1=tj+h时,各参数值的标准4阶龙格库塔公式为:
| $ \left\{ \begin{aligned} & {{u}_{j+1}}={{u}_{j}}+h/6\left( {{K}_{11}}+2{{K}_{12}}+2{{K}_{13}}+{{K}_{14}} \right) {\text{,}}\\ & {{v}_{j+1}}={{v}_{j}}+h/6\left( {{K}_{21}}+2{{K}_{22}}+2{{K}_{23}}+{{K}_{24}} \right) {\text{,}}\\ & {{r}_{j+1}}={{r}_{j}}+h/6\left( {{K}_{31}}+2{{K}_{32}}+2{{K}_{33}}+{{K}_{34}} \right) {\text{,}}\\ & {{\varphi }_{j+1}}={{\varphi }_{j}}+h/6\left( {{K}_{41}}+2{{K}_{42}}+2{{K}_{43}}+{{K}_{44}} \right) {\text{,}}\\ & {{x}_{j+1}}={{x}_{j}}+h/6\left( {{K}_{51}}+2{{K}_{52}}+2{{K}_{53}}+{{K}_{54}} \right){\text{,}} \\ & {{y}_{j+1}}={{y}_{j}}+h/6\left( {{K}_{61}}+2{{K}_{62}}+2{{K}_{63}}+{{K}_{64}} \right){\text{。}} \\ \end{aligned} \right. $ |
式中:
为验证搭载直翼推进器的船机桨匹配仿真模型的正确性,运行仿真模型,并对仿真结果进行分析。
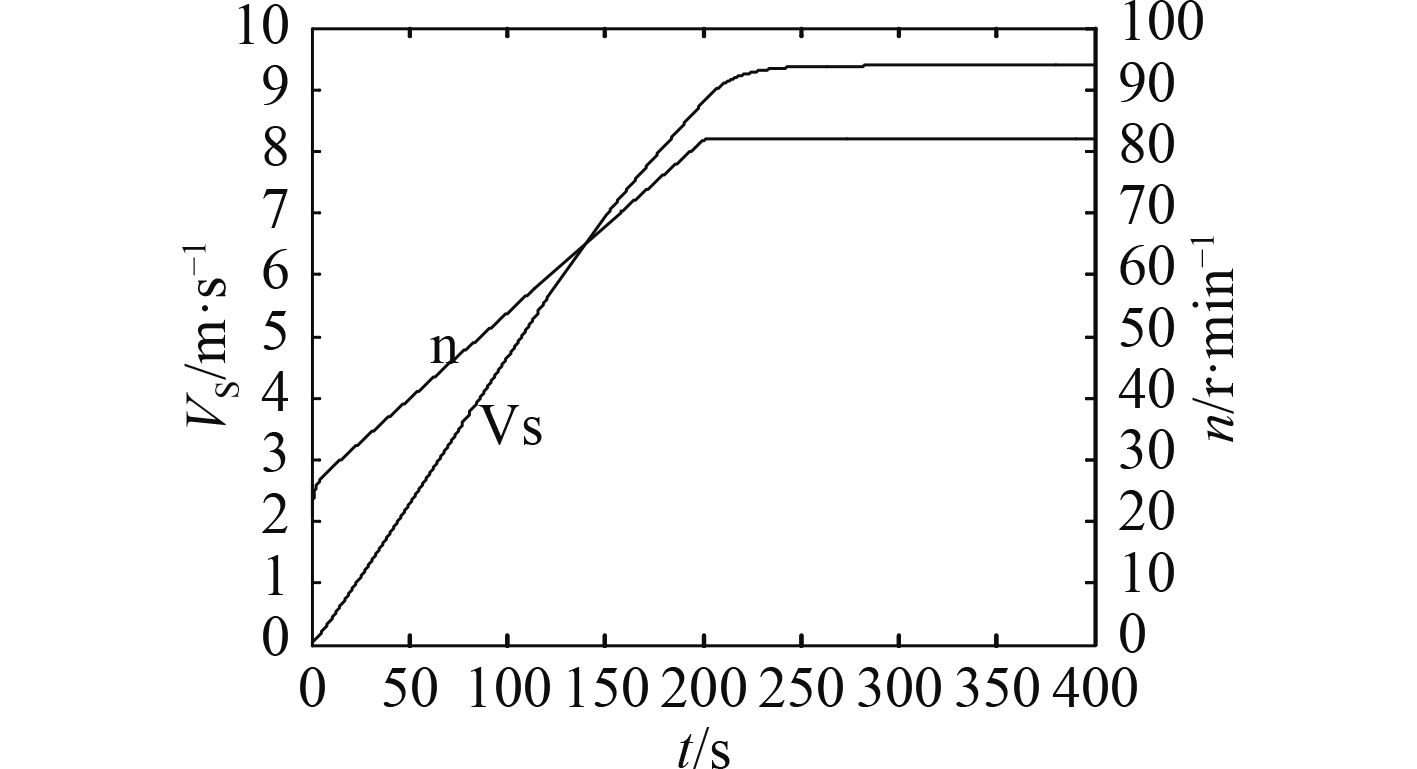
4.2.1 直航运动仿真船舶直航时,主机转速以6.5 r/min/s的加速速率从600 r/min增加到1 900 r/min,左右桨偏心率为0.9,方向角为,初始纵向速度为0 m/s,其他初始条件为0。仿真结果如图12所示。
|
图 12 船舶航速、推进器转速与时间曲线 Fig. 12 Speed of ship and rotating speed of propeller curves |
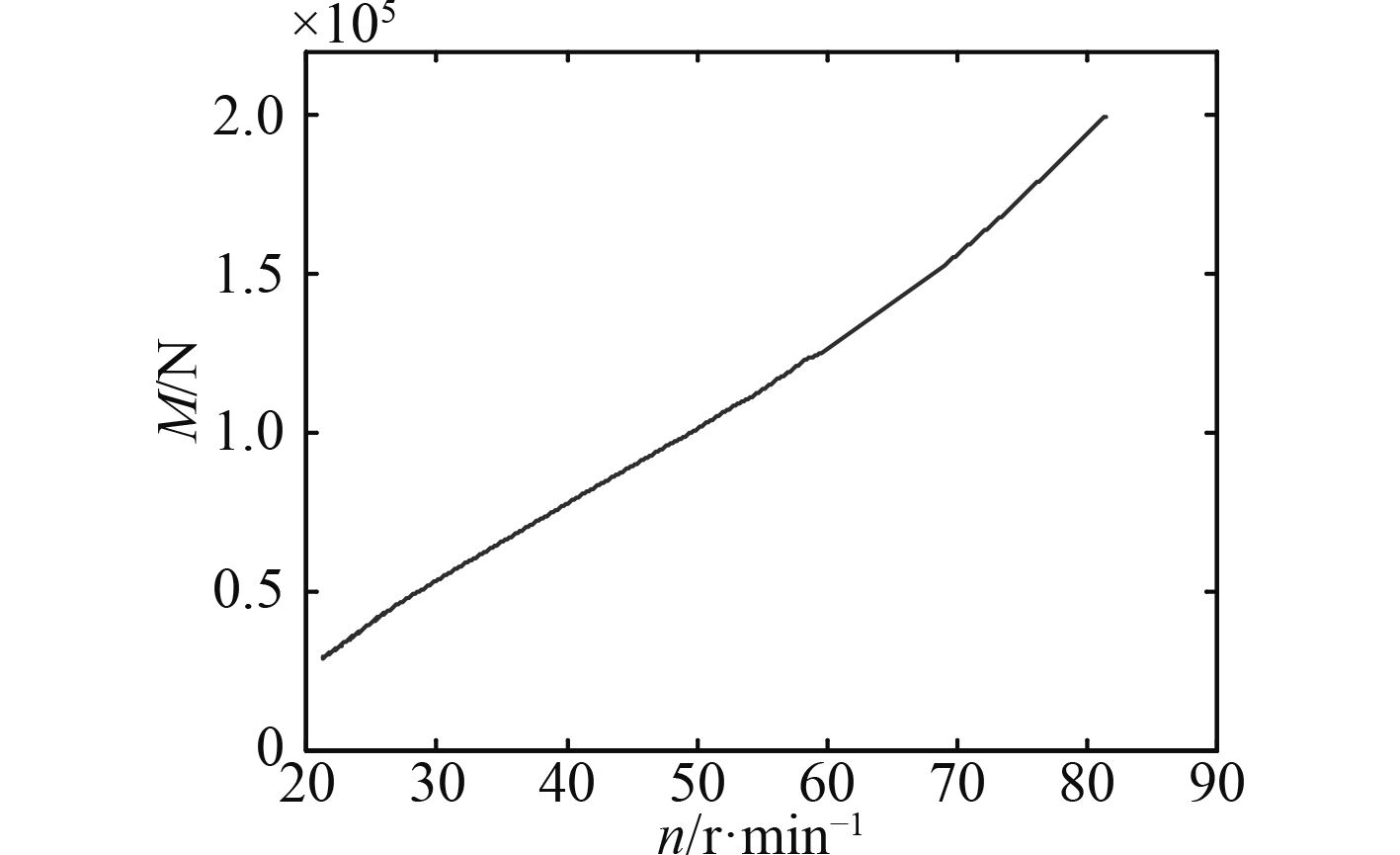
由图12可看出,仿真模型运行结果显示船舶达到最大航速18.3 kn,与船舶实际最大航速相近。图13为直翼桨扭矩与转速关系曲线,图14为船舶推力、阻力与时间的关系曲线。根据仿真结果分析,模型仿真结果较为准确。
|
图 13 直航运动时直翼桨扭矩与转速曲线 Fig. 13 Torque of propeller with rotating speed curve |

|
图 14 直航运动时船舶推力、阻力与时间曲线 Fig. 14 Thrust of propeller and resistance of ship curves |
由图12可知,船舶可在较短的时间内,迅速从初速为0加速到最大航速,提高了舰艇的机动性。同时,在保证一定航速的情况下,直翼推进器能以较低的转速运行,这在减少噪声方面具有极大的优势,特别是能够极大提高舰艇生命力。
4.2.2 回转运动仿真船舶回转运动时,左右直翼桨偏心率为0.5,方向角为22.5°,初始纵向速度为4.65 m/s,其他初始条件为0。仿真结果如图15所示。
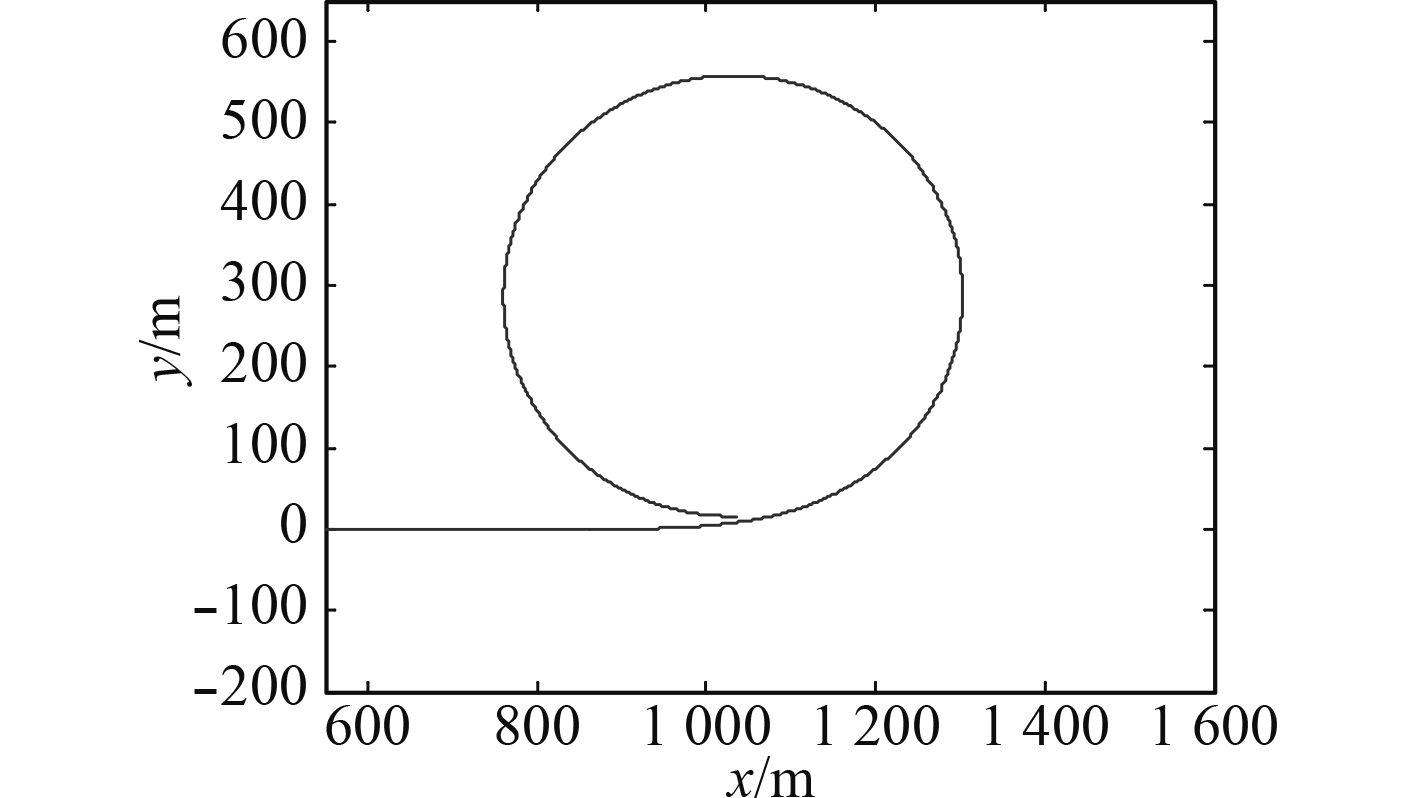
|
图 15 船舶回转运动轨迹曲线 Fig. 15 The turning trajectory of ship |
根据仿真模型的运行结果,船舶回转直径为554 m,与船舶实际回转半径接近。图16和图17分别为船舶回转运动的纵向速度和横向速度。对仿真结果进行分析,该模型的回转运动结果比较准确,验证了该模型的正确性。
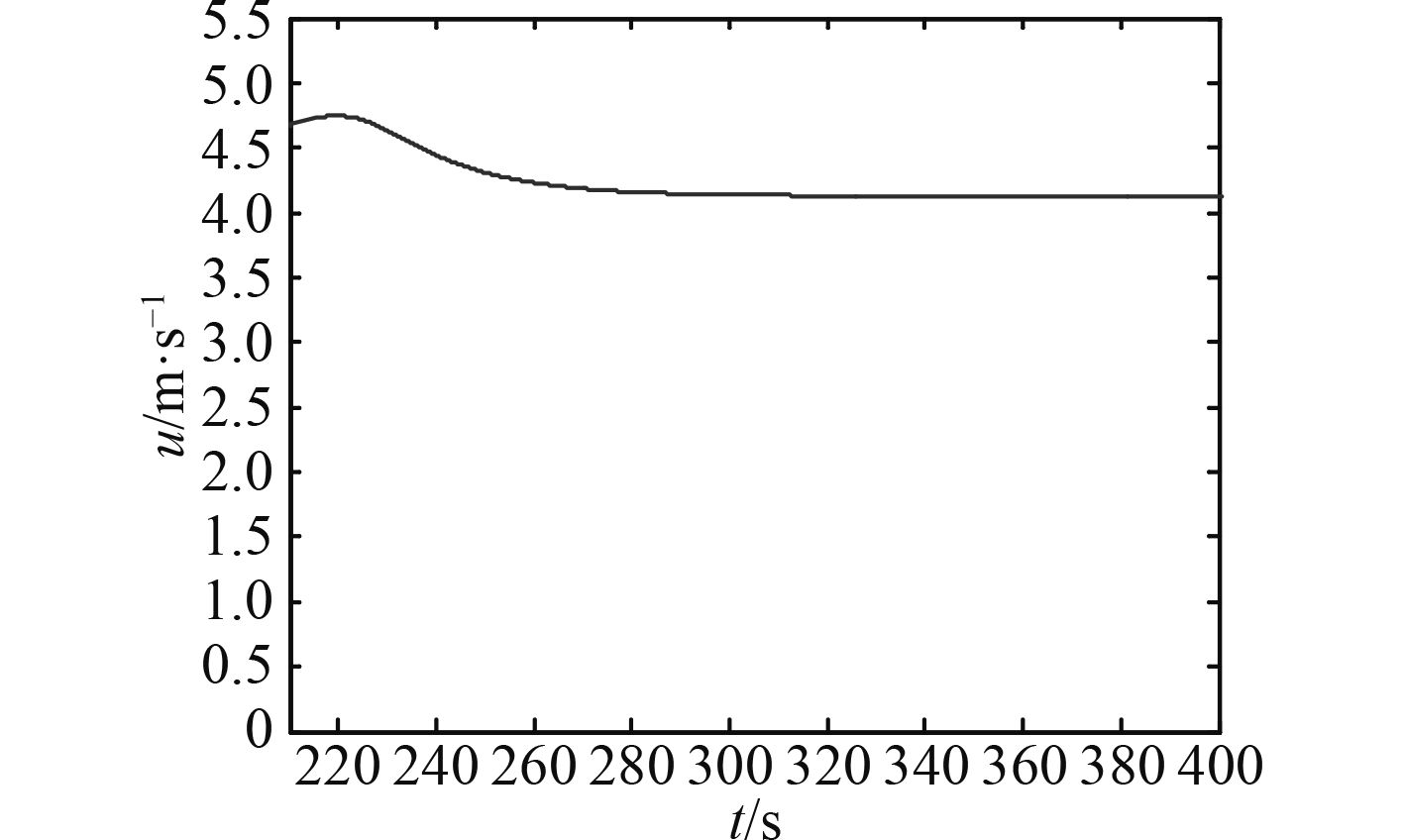
|
图 16 船舶纵向速度曲线 Fig. 16 The curve of advance speed |
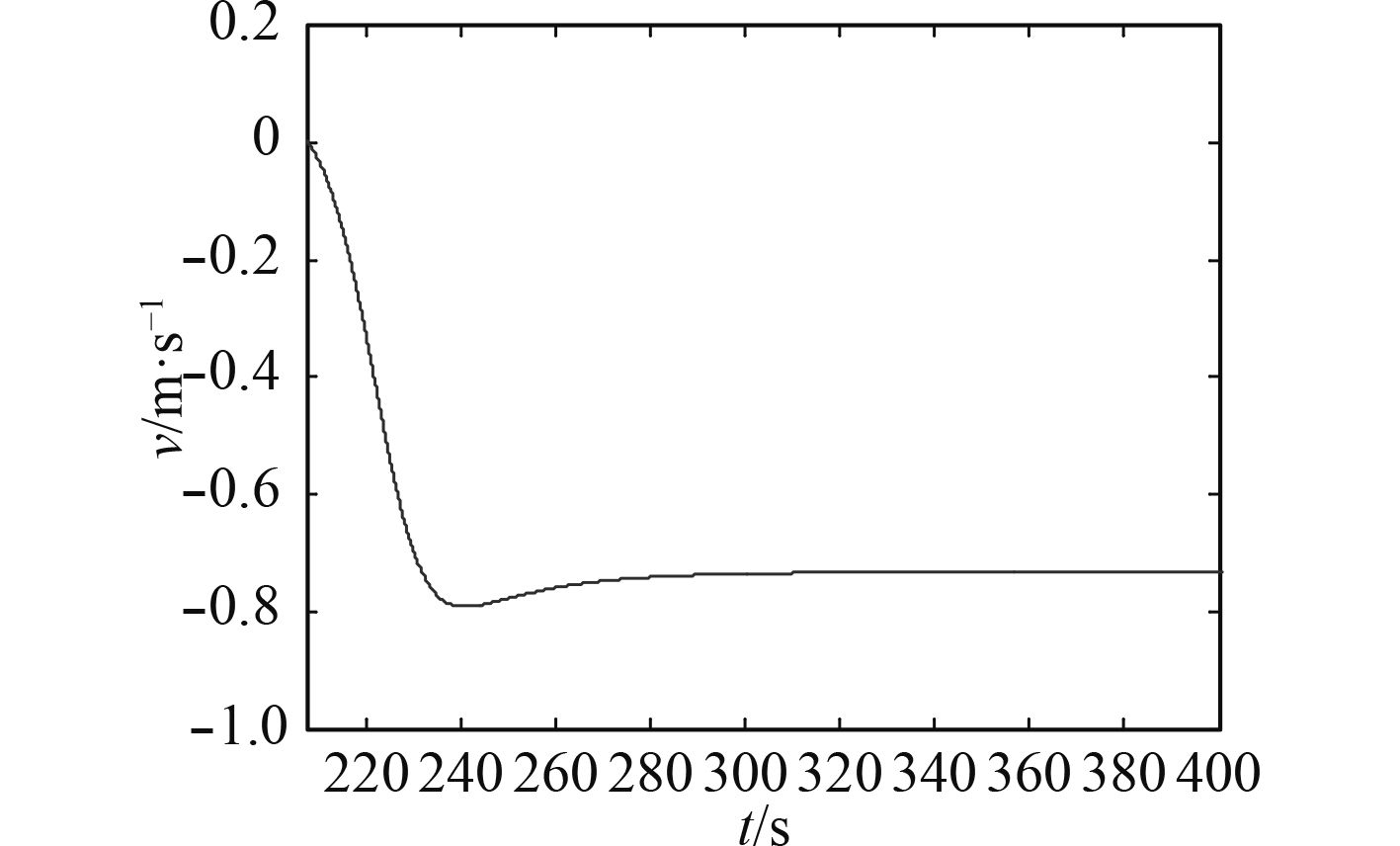
|
图 17 船舶横向速度曲线 Fig. 17 The curve of transverse speed |
由图15可知,船舶能够在很小的回转半径内完成回转,直翼推进器的应用极大提高了舰艇的操纵性和机动性,同时,也提高了舰艇的动力定位性能,降低了定位误差,为某些特种舰艇提高了战场生命力。
5 结 语本文通过研究分析船体、柴油机、直翼推进器之间的能量转换,建立船舶动力学方程,采用MMG数学模型建立船舶运动方程,并参考经验公式,利用4阶龙格库塔求解方法,建立并分析船机桨Matlab/Simulink仿真模型。通过对运行结果的分析,本文所建模型的准确性较高。
仿真结果显示,搭载直翼推进器的舰船具有机动性高、操纵性好、低噪声和动力定位精确等特点,极大地提高了舰艇的生命力。因此,加大对直翼推进器的研究应用成为舰船动力领域的一个新方向。本文所建立的直翼推进动力装置模型为实船搭载直翼推进器提供理论支持,为直翼推进船舶的安全操纵提供参考。
| [1] |
陈先进. 摆线推进器结构及性能优化研究[D]. 杭州: 浙江大学, 2013.
|
| [2] |
覃峰, 肖金生, 詹志刚, 等. 基于遗传算法的船舶推进系统船、机、桨匹配优化设计[J]. 武汉理工大学学报, 2003, 27(1): 22-25. |
| [3] |
王永生, 黄斌. 船舶加速过程最优机-桨联控方法仿真研究[J]. 四川大学学报, 2011, 43(1): 246-251. |
| [4] |
邢国英. 摆线推进器任意方向角的水动力计算方法研究[J]. 水动力学研究与进展, 2005(4): 472-478. DOI:10.3969/j.issn.1000-4874.2005.04.010 |
| [5] |
高孝日. 平旋推进拖船的运动建模与仿真[D]. 大连: 大连海事大学, 2008.
|
 2019, Vol. 41
2019, Vol. 41
