0 引　言

小管径微肋管以其经济高效和节能的显著特点，已得到广泛应用。自1977年日立公司^[1]正式提出微肋管想法后，国内外很多学者^{[2 – 5]}对其进行改进研究。图1为微肋管的结构图。目前国内外的空调公司均推出了自己的微肋管产品，在家用和车用空调中得到广泛应用。

作为舰船保障系统的一部分，空调系统能够为各级用户提供适宜的温湿度，其安全稳定的运行具有重要意义。随着舰船向小型化、紧凑化发展，船用空调系统换热器也面临很多挑战，通过强化换热来减少体积是其中一个发展方向。

关于换热管强化换热实验研究的较多^{[2 – 10]}，但在蒸发管沸腾换热数值模拟方面研究较少。作为R22的在家用空调中的替代工质，R410A在舰船空调中研究较少。基于此，本文通过数值模拟研究了R22和R410A在外径为5 mm的微肋管管内沸腾过程中的换热特性，与已有的实验结果进行对照，以期通过数值模拟手段进行新型换热管开发及制冷工质替换研究。

1 物理模型

模拟的微肋管管外径为5 mm，螺旋角为0°（以下简称直肋管），其他几何参数如表1所示。

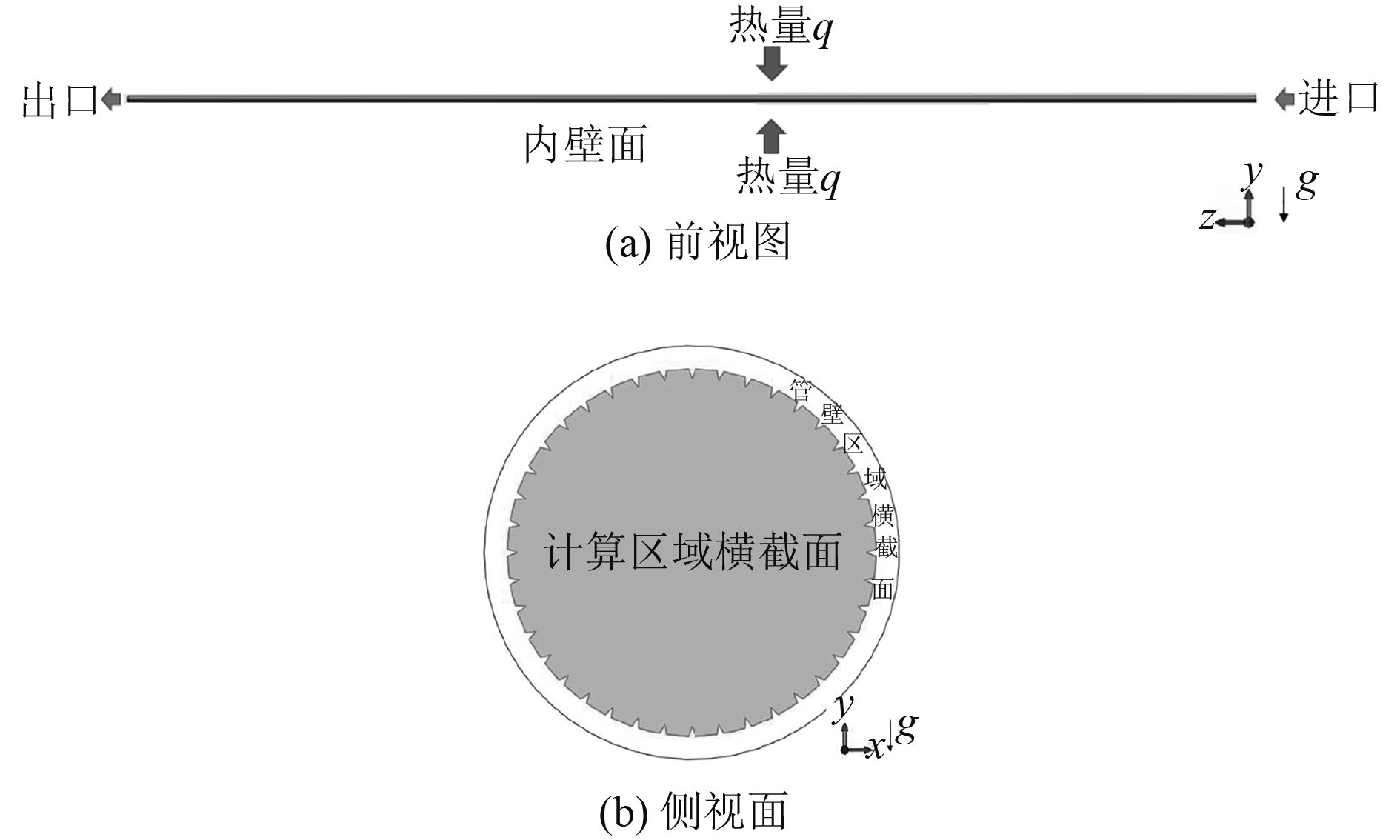
实际换热过程中，直肋管是有一定管壁厚度的强化管，在管壁中是一个金属材料稳态导热的过程，稳态换热过程中管壁温度不发生变化，只是将外加的热量传递给管内的沸腾过程，从数值计算角度是一个耦合问题，即管壁温度与流体温度需要同时计算；由于沸腾换热一般给定热流密度作为边界条件，为了计算过程的简化，将加热量直给定到管内壁面上。基准直肋管在管内沸腾过程中的计算区域的物理模型图如图2所示。

2 数值方法及沸腾换热模型 2.1 数值方法

本节中直肋管管内的流动沸腾过程的数值模拟是采用Eulerian-Eulerian多相流数值模拟方法中的欧拉模型，在欧拉模型中制冷工质的液相被设置为连续相，气相当作分散相，连续相采用湍流模型，分散相采用零方程模型湍流模型，对流项采用二阶迎风格式处理、扩散项采用中心差分格式。轴方向为主流方向，入口设置为Inlet边界，入口流体是温度为5 ℃的饱和液相制冷工质R22及R410A，给定质量流量为100 kg·m^–2·s^–1；出口设置为Outlet边界；在周向按照外壁面热流密度为5 kW·m^–2均匀折算到直肋管内壁面，内壁面为等热流WALL边界条件，计算采用Ansys CFX 14.0完成，分别计算了直肋管不同入口干度条件下沸腾换热特性。

下边分别介绍管内沸腾换热过程中的控制方程：

1）连续性方程

$ \nabla \cdot \left( {{\gamma _\alpha }{\rho _\alpha }{U_\alpha }} \right) = \varGamma _{\alpha \beta }^ + - \varGamma _{\beta \alpha }^ + \text{。} $

(1)

式中： $\gamma $ 为相的体积分数； $U$ 为速度向量； $\varGamma _{\alpha \beta }^ + $ 为单位体积空间内 $\alpha$ 相向 $ \beta$ 相正向的质量传递速率； $\varGamma _{\beta \alpha }^ + $ 为单位体积空间内 $\alpha$ 相向 $\beta$ 相正向的质量传递速率，式（1）对气液相均成立，式中下标 $\alpha$ 可以代表液相或气相， $\beta$ 就代表气液两相中除 $\alpha$ 相外的另一相，这一定义方式对所有控制方程均成立。实际上需分别求解气相与液相2个控制方程。

2）动量守恒方程

$ \begin{split} & \nabla \cdot \left( {{\gamma _\alpha }\left( {{\rho _\alpha }{U_\alpha } \otimes {U_\alpha }} \right)} \right) + {\gamma _\alpha }\nabla p= \\ & \nabla \cdot \left( {{\gamma _\alpha }{\eta _\alpha }} \right)\left( {\nabla {U_\alpha } + {{\left( {\nabla {U_\alpha }} \right)}^{\rm T}}} \right) + {\gamma _\alpha }{\rho _\alpha }g + {M_\alpha }\text{。} \end{split} $

(2)

式中： $p$ 为流场中的压力； $ \otimes $ 为张量积的符号； $M$ 为气液相界面作用力的总和，包含曳力、浮升力、湍流耗散力等几种作用力，可分别通过对应的公式进行计算； $\eta $ 为当量动力粘度系数，对于液相和气相，可分别通过下式进行计算获得：

$ {\eta _{ld}} = {\eta _l} + {\eta _{lt}} + {\eta _{lv}}\text{，} $

(3)

$ {\eta _{vd}} = {\eta _v} + {\eta _{vt}}\text{。} $

(4)

式中：液相当量动力粘度系数 ${\eta _{ld}}$ 由液相动力粘度系数 ${\eta _{l}}$ 、液相湍流动力粘性系数 ${\eta _{lt}}$ 和气泡诱导动力粘性系数 ${\eta _{lv}}$ 三项组成，可分别通过物性表、 $k - \varepsilon $ 湍流模型及Sato^[11]公式获取；气相当量动力粘度系数 ${\eta _{vd}}$ 由气相动力粘度系数 ${\eta _{v}}$ 、气相湍流动力粘性系数 ${\eta _{vt}}$ 两项组成，可分别通过物性表和零方程湍流模型获得。动量方程也需分别对气相与液相求解。

3）能量守恒方程

$ \begin{split} & \nabla \cdot \left( {{\gamma _\alpha }\left( {{\rho _\alpha }{U_\alpha }{h_\alpha }} \right)} \right) =\\ & \quad \nabla \cdot \left( {{\gamma _\alpha }{\lambda _\alpha }\left( {\nabla {T_\alpha }} \right)} \right) + \left( {\varGamma _{\alpha \beta }^ + {h_{\beta {\rm{s}}}} - \varGamma _{\beta \alpha }^ + {h_{\alpha {\rm{s}}}}} \right) + {q_\alpha }\text{。} \end{split} $

(5)

式中： $h$ 为工质的焓值； $T$ 为流场中的温度； $h_s$ 为工质饱和状态的焓值； $q$ 为单位体积内外加热功率，本节中管内沸腾过程中气液相制冷工质的外加热功率的分配将在沸腾模型中予以介绍。能量方程也需分别对气相与液相求解。

4）体积守恒方程

$ {\gamma _\alpha } + {\gamma _\beta } = 1\text{。} $

(6)

在整个管内沸腾换热过程中，管内的任何区域内气液相制冷工质的体积分数为1，即充满整个空间。

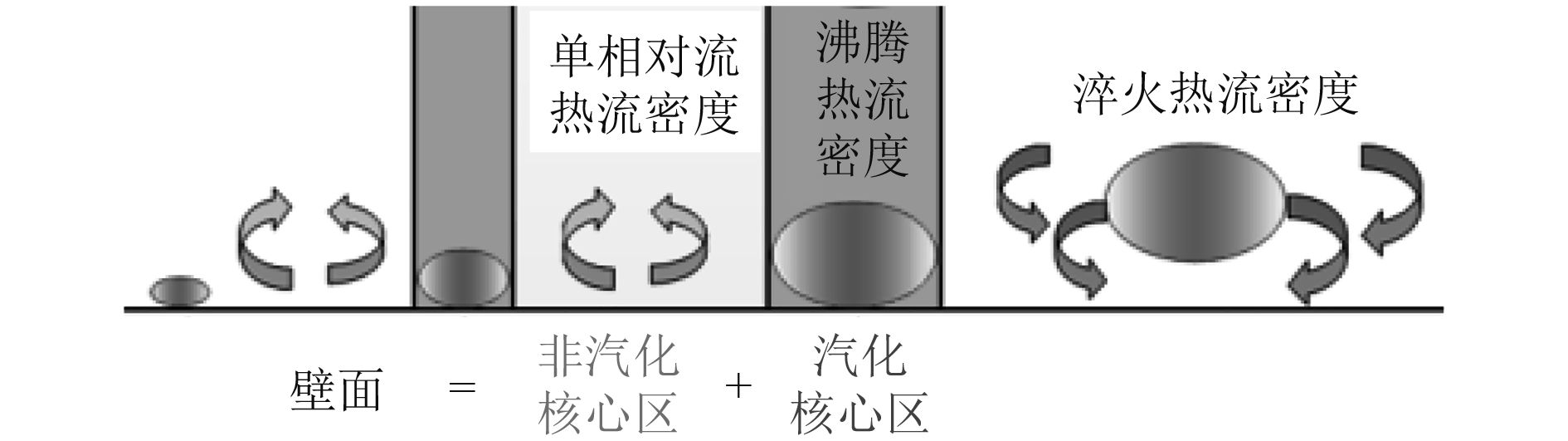
2.2 沸腾换热模型

本节微肋管管内沸腾过程中数值模拟研究中的沸腾换热模型采用商业软件自带的RPI沸腾模型（由Kural和Pidowski^[12]在Rensselaer Polytechnic Institute首次提出）。RPI沸腾模型假设沸腾过程中壁面处的网格尺寸大于汽化核心区域的物理尺寸，它不分析沸腾机理中汽化核心区域产生气泡的过程，而是研究在已有气泡产生基础上的沸腾换热过程。RPI沸腾模型的核心思想是对沸腾过程中的外加热量进行分配，对于过冷沸腾过程，外加热流密度可通过下式分配：

$ {q_w} = {q_c} + {q_q} + {q_e}\text{。} $

(7)

式中： ${q_w}$ 为壁面外加的热流密度，是整个管内沸腾过程中吸收的热量； ${q_c}$ 为液相工质单相对流过程中的热流密度； ${q_q}$ 为淬火热流密度，是指汽化核心区域中从上一个气泡脱离到下一个气泡产生过程中等待过程中液相工质被加热过程中吸收的热量； ${q_e}$ 为沸腾热流密度，是用来促使气泡脱离的热量。热流密度的分配过程图3所示。

按照沸腾换热RPI模型中的假设，3种热流密度可分别通过式（8）～式（10）求解得出：

$ {q_c} = {A_1}{h_c}\left( {{t_w} - {t_l}} \right)\text{，} $

(8)

$ {q_q} = {A_2}{h_q}\left( {{t_w} - {t_l}} \right)\text{，} $

(9)

$ {q_e} = \dot m\left( {{h_v} - {h_l}} \right)\text{。} $

(10)

式中： $A_1$ 为壁面非汽化核心区域的面积分数； $h_c$ 为单相对流换热系数； $t_w$ 和 $t_l$ 分别为壁面温度和壁面附近液相工质的温度； $A_2$ 为壁面汽化核心区域的面积分数； $h_q$ 为淬火换热系数； $h_v$ 和 $h_l$ 分别为气相和液相工质的焓值， ${\dot m}$ 为单位壁面面积上的气相工质的产生量。

从以上分析中可以看到，采用RPI沸腾换热模型计算的结果好坏与汽泡面积分数 $F_2$ 、气泡成核密度 $n$ 、气泡脱离直径 $d_w$ 、气泡脱离频率 $f$ 、气泡等待时间 $t_{wait}$ 、液相温度的取值处 $Y^+$ 六个参数在计算过程中的取值息息相关，计算中应用的Ansys CFX 14.0软件均采用了文献中认可度较高的经验计算公式来计算6个参数的数值^[13]，尽量提高计算结果的可信度。

3 计算结果 3.1 网格独立性考核

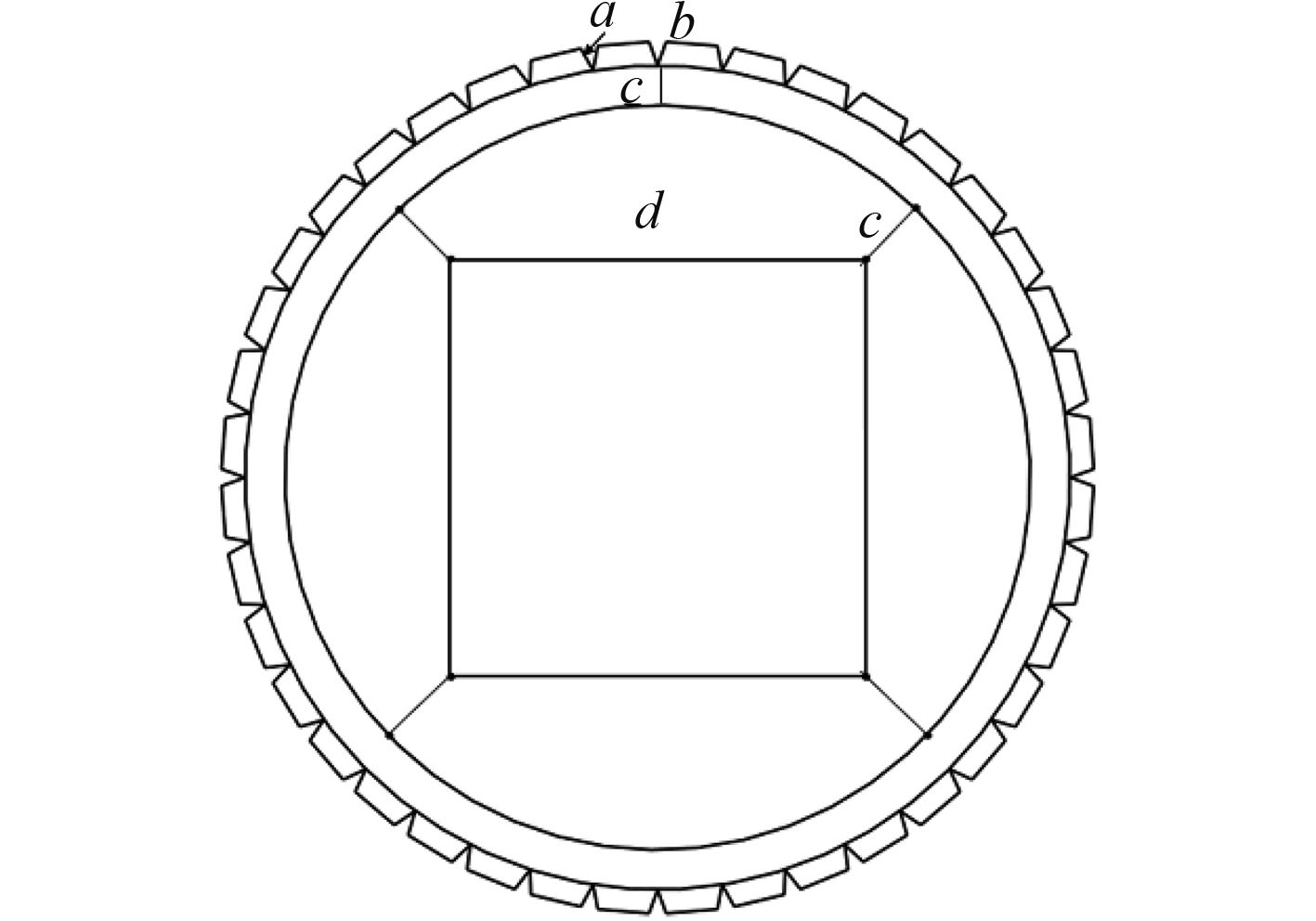
直肋管在数值模拟中的网格采用Gambit 2.3.16划分，六面体结构化网格。在进行正式分析前，首先对网格的独立性进行考核，验证过程中总共采用了8套网格，网格数最小为68.4万，最大为380万。直肋管横截面的网格划分示意图如图4所示，通过将横截面切割成46个不同的区域，将每个区域用结构化的四面体网格进行划分，图中的a，b，c，d分别为齿斜坡、齿间距、径向、中心区域边长方向上的网格数，通过a，b，c，d可以决定横截面上的网格数量。

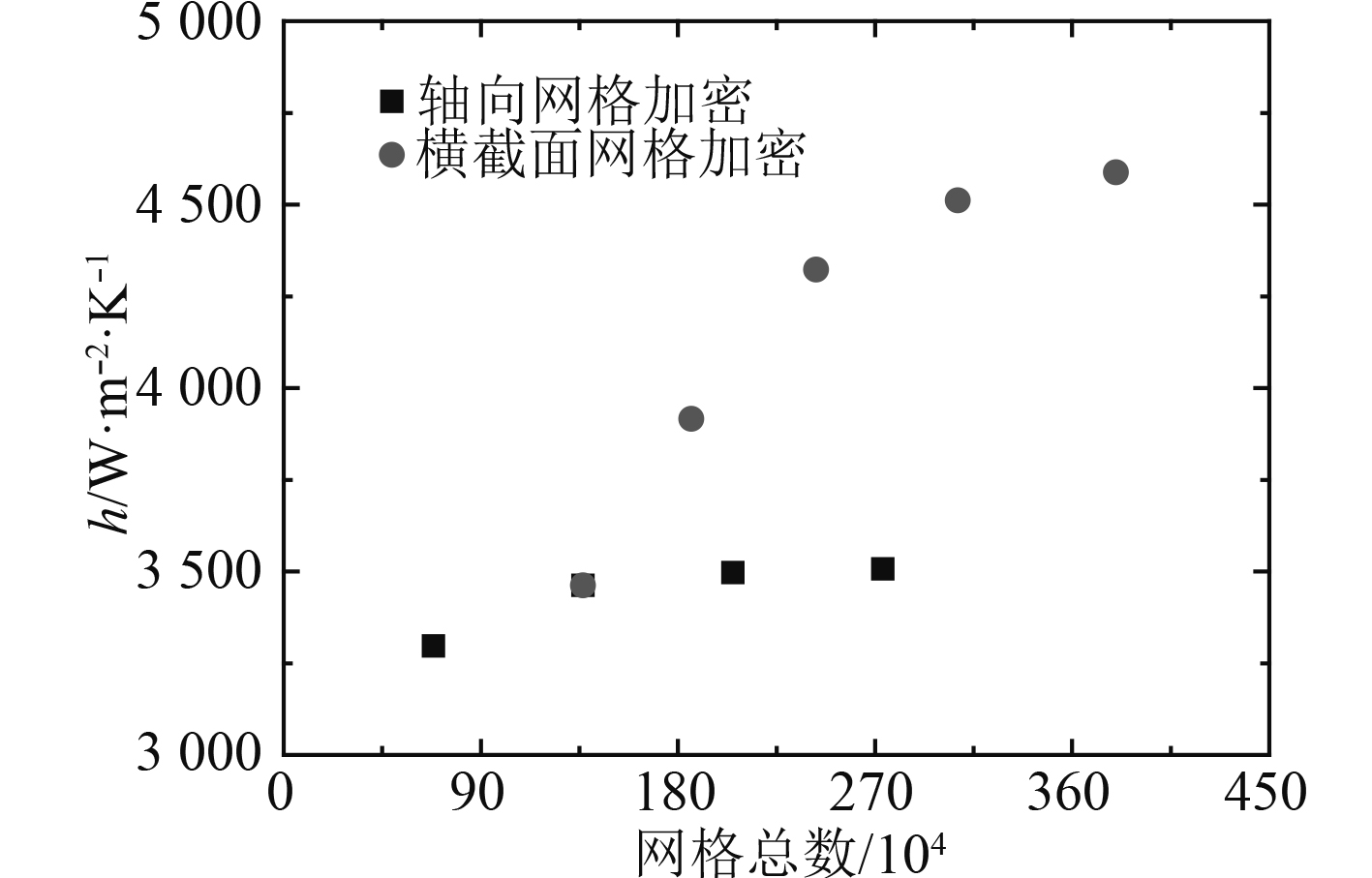
对于工质R410A，直肋管管内沸腾中的平均干度为0.5的整个管长的平均换热系数随网格数量的变化如图5所示，横截面网格数目的变化对换热系数影响要比轴向网格变化大。由于横截面上的网格变化引起网格数量急剧增大，因此首先固定横截面上的网格数目，根据轴向网格不同换热系数的变化规律，选定轴向网格数量为200，此时与轴向网格数量为300，400的换热系数计算结果误差在1.3%之内；固定轴向网格数为200，改变横截面的网格数目，选定齿上网格数目为9，此时换热系数计算结果误差为1.7%，最终选择307万的网格用于直肋管管内沸腾的计算。

3.2 数值计算换热结果

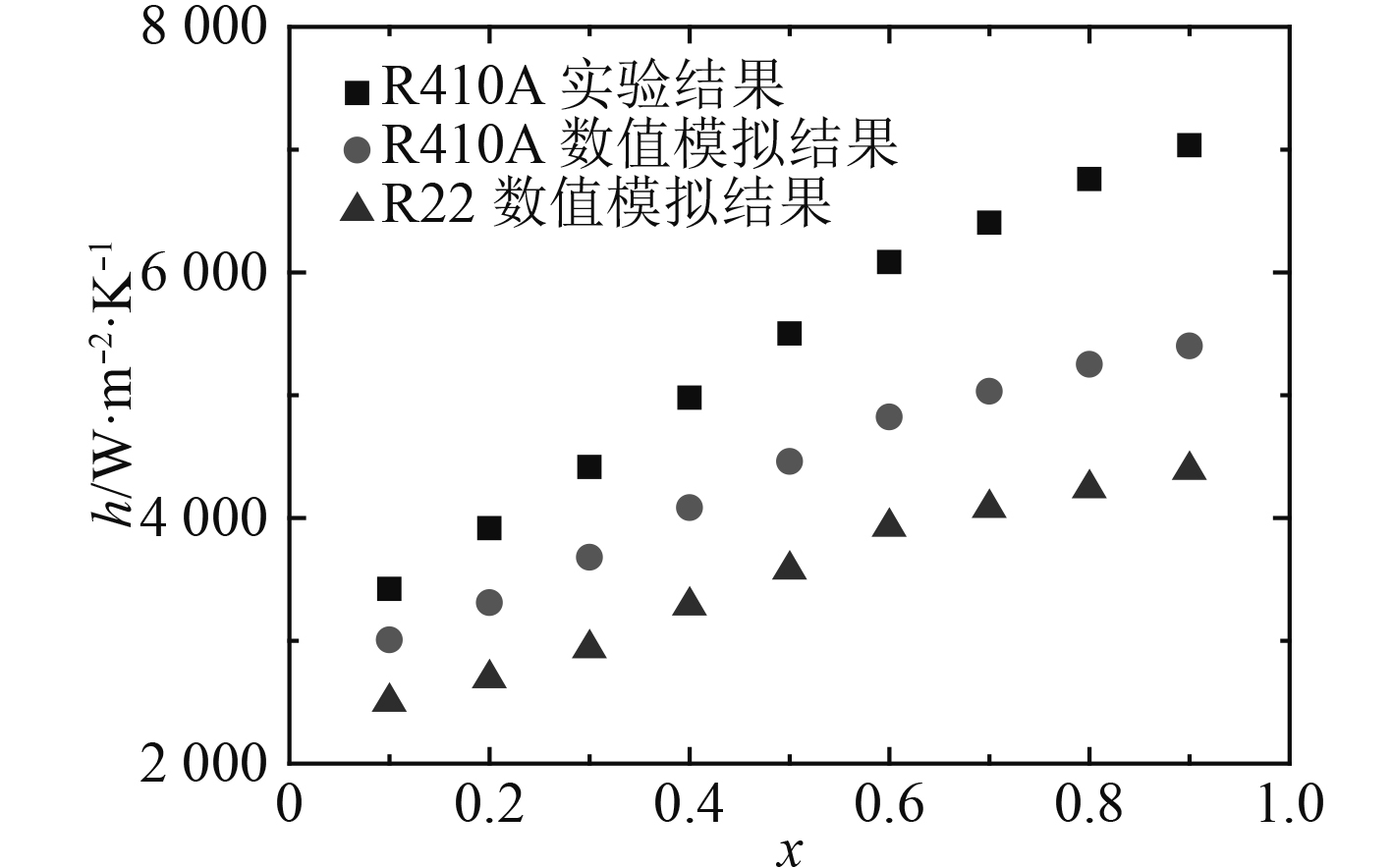
R410A在不同干度条件下的换热系数随干度变化的数值模拟结果与相同工况下实验结果^[14]进行比较并列于图6中。从图中可以看出，换热系数数值模拟结果均要比实验结果小一些。负偏差产生的原因可能与模型本身有关，因为现有的RPI模型的参数主要是从平表面的实验结果中提取的，对于带微肋表面的微肋管由于汽化核心区域的增加，换热系数会得到一定程度的提高从而减少模型误差。实验过程中换热系数的数值模拟结果与实验结果的平均偏差为–18%而最大偏差为–26%。考虑到沸腾换热实验数据本身的不确定性，总体上采用Euler多相流模型和RPI沸腾模型的计算结果基本能够反映直肋管管内沸腾过程中的换热特性。从图中可以看出，不同干度条件下R410A的换热系数要比R22小，大约要高30%～40%，在进行制冷剂替换过程应考虑两种制冷工质的换热特性。

4 结　语

本文应用Euler多相流模型及RPI沸腾换热模型计算了R22和R410A在外径为5 mm的直肋管管内沸腾过程中的换热特性，研究表明：数值计算结果基本能够反映直肋管管内沸腾过程中的换热特性，与文献中实验结果差距不大；相同条件下R410A的换热特性要比R22高，约是1.3～1.4倍，在舰船空调换热器进行制冷工质替换及设计优化过程要予以考虑。