2. 中国舰船研究设计中心,湖北 武汉 430064;
3. 哈尔滨工程大学 动力与能源工程学院,黑龙江 哈尔滨 150001
2. China Ship Development and Design Center, Wuhan 430064, China;
3. College of Power and Energy Engineering, Harbin Engineering University, Harbin 150001, China
船舶轴系是推进系统中的重要部分,在实际运转中受到各种冲击和周期激振力作用,影响船舶运行的安全性[1]。针对轴系、轴承、弹性联轴器的适配性设计是保障轴系安全可靠运行的关键因素。
目前一些船舶为了减少主机振动到船体的传递,普遍对主机进行了隔振处理[2-4],在船舶摇摆环境下对轴系提出了大位移补偿要求,同时显著增加了主机端传递到轴系的扰动力。由于对主机隔振后,支撑刚度降低,主机轴系与推进轴系产生耦合作用,改变了轴系的动力学特性,直接影响到轴系的低噪声性能及安全性。
国内外学者针对这一问题,已经开展了一些研究,取得一定的成果。张亚洲[5]采用了气囊隔振器对主机进行隔振,分析了隔振后轴系的校中状态及其对轴系振动的影响,得出加载气囊隔振器后可以提高轴系抗横向干扰的能力,并有效地减小轴承支座的侧向移动。卜文俊[6]对船舶推进装置气囊隔振系统对中可控性问题进行研究,提出了根据可控性进行控制系统工作参数自主调整的方法,并进行了试验验证。Arvid Naess[7]提出了一种计算船体振动的二阶理论,该方法可以适应随机海况下船体的弹性变形,并且对计算机的性能要求不高,具有一定的普适性。J.Juncher Jensen[8]则基于非线性切片理论,推导了随机波浪中船体附加质量,阻尼和水线变化中的非线性影响,得出在短波长波浪激励下,非线性因素不可忽略。Alok K.Jha[9]进一步研究了近海的情况,应用非线性传递函数,分析了波浪载荷下船体的振动响应,得到较为准确的结果,但是这种方法耗时很高,仍需要改进。郭全丽[3]建立了包括主机及其隔振系统的有限元模型和运动微分方程,分析了隔振刚度对冲击响应的影响,研究表明隔振刚度与轴系抗冲击性能相互抵触,如何平衡二者之间的关系是设计的关键。刘树鹏[10]对舰船发生纵、横摇摆运动时,舰船动力装置转子-系统进行了建模,对其动力学特性进行深入的分析和研究,并考虑了线性和非线性油膜力的作用。
可以看出,目前国内外学者的主要研究方向还集中于船体在简化的波浪环境下的振动状态,并未针对摇摆运动本身,对推进轴系振动的影响进行分析。本文正是基于这一角度,首先建立纵摇环境的简化方法,然后建立带有主机隔振系统的推进轴系动力学模型,进行纵摇环境下轴系动力响应的计算,分析轴系各轴承的适配性,为轴系设计提供指导。
1 纵摇环境简化方法船舶在航行过程中,受到风力、不规则波浪或发射武备后坐力等因素影响,会产生各种摇荡运动,其中纵摇运动是最危险的运动之一,是船舶失速、砰击、上浪的主要原因,严重影响航行的安全性,因此本文主要考虑纵摇环境下推进轴系的动力响应。
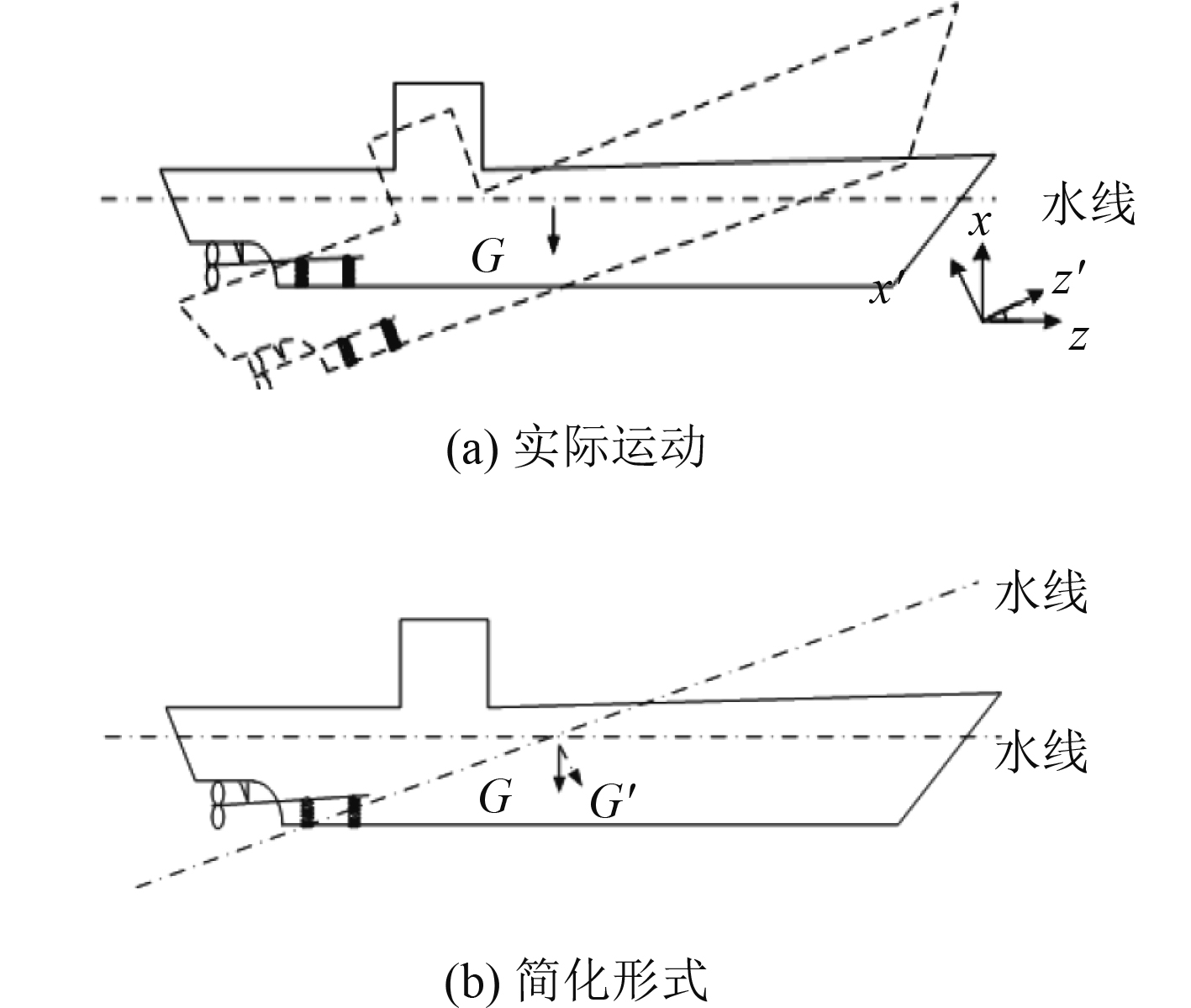
纵摇是船体绕横轴的回转振荡运动。考虑纵摇环境时,常规思路是将船体整体的结构位置进行改变,这就要求在每一步计算之前,都要重新建立模型,操作起来十分复杂。因此本文考虑对施加载荷的方式进行简化,由于船舶的纵摇运动是一个整体性运动,其每一部分的运动幅度都相同,因此考虑将船体结构作为静止项,改变其重力场的方式,再将纵摇运动产生的加速度考虑进去,最终其动力学参数可以近似以重力加速度与纵摇加速度的合成来等效计算。纵摇运动等效示意图如图1所示。
|
图 1 纵摇简化示意图 Fig. 1 Predigestion of pitching |
根据《舰船通用规范》的要求,船舶纵摇时的最大角度为±15°,最长周期为10 s,因此假定纵摇角θ随时间t变化的方程为:
| $ \theta = \frac{{\text{π}} }{{12}} \times \sin \frac{{2{\text{π}} t}}{{10}}{\text{,}} $ | (1) |
式中,t为时间,角位移单位为弧度。
纵摇的等效加速度由重力加速度和纵摇运动加速度合成所得。定义图1所示的船体剖面为XOZ平面,L为船体重心至纵摇所绕横轴的距离,则等效重力加速度可由式(2)表示。
令
| $ \begin{align} {g_v} =& \left [g + \frac{{\text{π}}}{{12}}{\omega ^2}L \left(\frac{{\text{π}}}{{12}}{B^2}D - AC\right)\right]D +\\ & \left[\frac{\text{π} }{{12}}{\omega ^2}L \left( - \frac{{\text{π}}}{{12}}{B^2}C - AD\right)\right]C{\text{,}}\\ {g_A} =& \left[g + \frac{{\text{π}}}{{12}}{\omega ^2}L \left(\frac{{\text{π}} }{{12}}{B^2}D - AC\right)\right]C -\\ & \left[\frac{\text{π} }{{12}}{\omega ^2}L\left( - \frac{{\text{π}} }{{12}}{B^2}C - AD\right)\right]D{\text{,}}\\ & \overrightarrow g = ({g_V},0,{g_A}){\text{。}} \end{align} $ | (2) |
由于本文主要进行方法与机理的研究,假定L=10。
2 轴系动力学模型 2.1 模型建立基于某典型船舶推进轴系试验台,建立轴系动力学模型。该推进轴系全长5 m,由3个轴承支撑,分别为尾后轴承、尾前轴承、推力轴承,其中推力轴承为油润滑轴承,尾后轴承和尾前轴承为水润滑橡胶轴承,各轴承均采用独立的润滑系统,尾部安装有螺旋桨。应用有限元法,建立的轴系动力学模型如图2所示。

|
图 2 轴系台架模型 Fig. 2 Model of shafting test bench |
对该轴系试验台进行模态测试,并与仿真结果进行对比分析,对比结果如表1和图3所示。
|
|
表 1 轴系弯曲振动固有频率 Tab.1 Natural frequencies of shafting transverse vibration |
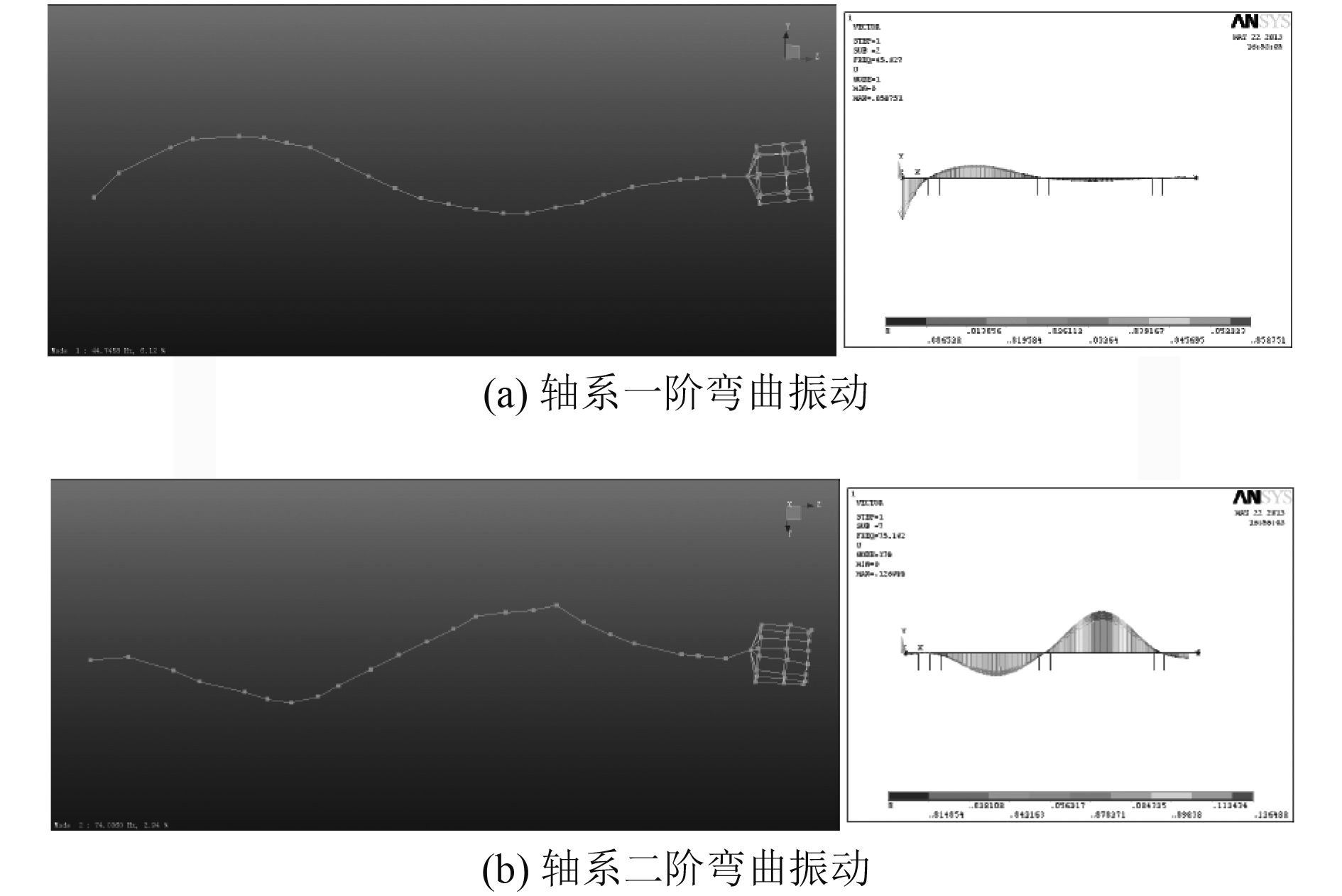
|
图 3 轴系模态振型试验与仿真的比较 Fig. 3 Comparison of shafting modes by tests and computation |
可以看出,轴系弯曲振动固有频率的试验值和计算值一致性较好,振型基本一致,说明该模型建立的参数准确,方式合理,可以应用于下一步的计算中。
3 计算分析 3.1 载荷输入将纵摇环境的各参数代入式(2),得到各方向的等效重力加速度,对轴系动力学模型进行瞬态响应分析,计算时取4个周期,以保证计算结果的稳定性。输入的等效重力加速度曲线如图4所示。

|
图 4 纵摇环境等效重力加速度 Fig. 4 Equivalent gravity of pitching |
可以看出,垂直方向的等效重力加速度在重力加速度附近波动,这是由于纵摇的运动形式产生的惯性加速度与重力加速度合成的结果,与此同时,由于纵摇运动是一种类似圆周的运动,因此也产生了轴向的加速度。弹性联轴器对轴系的附加激励结果如图5所示。

|
图 5 弹性联轴器激励力 Fig. 5 Excitation forces at coupling |
可以看出,对主机进行隔振后,纵摇环境下弹性联轴器处的激励明显增大,最大值均出现在纵摇角度最大的时刻,说明由于轴段侧和主机侧运动的不同步,弹性联轴器激励已经成为了一个主要激励。
3.2 隔振刚度对轴承负荷的影响1)分析不同方向的刚度变化对轴系适配性的影响
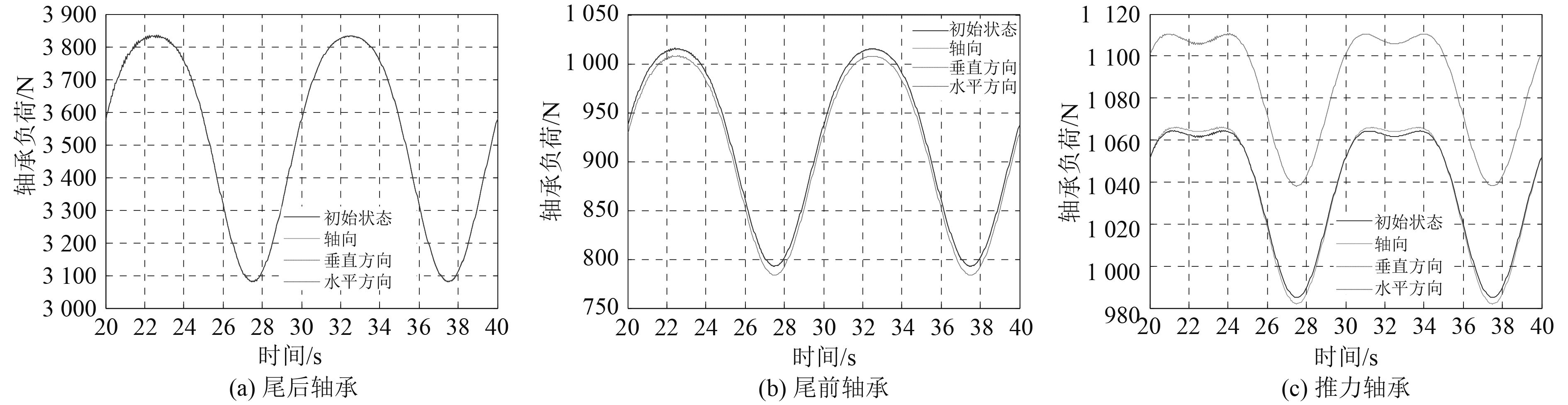
选取基准隔振刚度,将其设置为K,分别将主机隔振轴向、垂直方向和水平方向的刚度变为0.8K,计入纵摇环境边界条件进行计算,提取各轴承的负荷,进行对比说明,结果如图6所示。
|
图 6 各轴承的负荷 Fig. 6 Bearing loads of each bearing |
可以看出,当主机垂向隔振刚度变化时,尾前轴承和推力轴承的各方向轴承负荷受其影响最大,亦即尾前轴承和推力轴承的负荷对主机垂直方向隔振刚度最为敏感。
2)分析不同大小的刚度变化对轴系适配性的影响
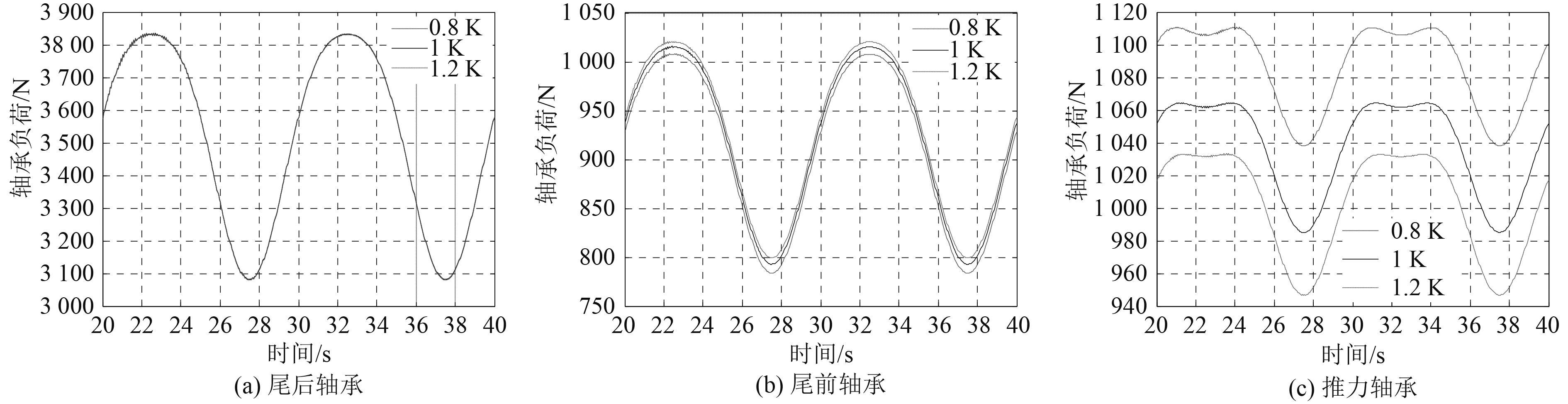
由于轴承负荷对主机垂直方向隔振刚度最敏感,因此选取基准隔振刚度K后,将主机隔振垂直方向的刚度变为0.8 K,1.2 K,计入纵摇环境边界条件进行计算,结果如图7所示。
|
图 7 各轴承的负荷 Fig. 7 Bearing loads of each bearing |
可以看出,随着轴承位置越靠近主机,其轴承负荷受主机垂直方向隔振刚度变化的影响越大。主机垂向隔振刚度增大时,尾后轴承垂向负荷变化很小,尾前轴承垂向负荷增大,推力轴承轴向和垂直方向的负荷减小。
3.3 适配性规律由以上的计算可以看出,纵摇环境下,主机垂向刚度的变化对轴承负荷的影响尤为明显。从船舶推进轴系设计的角度来说,尾后轴承和尾前轴承承担着支撑轴系总重的作用,而推力轴承的作用主要是承担轴向的推力,因此应尽量增大尾前轴承的负荷,减小推力轴承的负荷,因此应增大动力装置垂向隔振刚度。但同时垂向隔振刚度又是影响主机的隔振性能的主要因素,在对主机进行隔振设计后,其垂向隔振刚度就被限定到了一定范围内,因此应综合以上两方面的因素考虑。本文给出一种建议,纵摇环境下,为了降低轴系的振动,增强轴系运转的安全性,应优先调整主机垂直方向隔振刚度,在给定范围内,尽量选择较大的值。
4 结 语本文以典型轴系试验台架为研究对象,建立轴系有限元模型,考虑纵摇环境下,船舶主机的隔振对轴系产生的附加激励,对轴系进行瞬态响应计算,分析了主机隔振刚度对轴系适配性的影响。计算结果表明:计入纵摇环境后,弹性联轴器处的激励明显增大,已经成为了一个主要激励。当主机垂向隔振刚度变化时,尾前轴承和推力轴承的各方向轴承负荷受其影响最大,随着轴承位置越靠近主机,这种影响越明显,而在进行总体设计时,应综合考虑隔振刚度对轴系振动和隔振效果的影响。
值得注意的是,针对不同的船型,轴系的布置差别很大,然而纵摇环境下,主机隔振会使推进轴系振动恶化,本文旨在提供一种考虑纵摇环境的分析方法,并对轴系适配性进行了初步的探讨。在船舶推进轴系设计阶段,应考虑纵摇条件的影响,以保证轴系安全高效的运转。
| [1] |
陈之炎. 船舶推进轴系振动[M]. 上海: 上海交通大学出版社, 1987.
|
| [2] |
徐伟, 李桐桥. 推进电机新型隔振装置设计研究[J]. 舰船科学技术, 2006, 28(2): 86-88. XU W, LI T Q. Design study of a new mounting system for marine propulsion electrical machine[J]. Ship Science and Technology, 2006, 28(2): 86-88. |
| [3] |
郭全丽, 祝长生, 邓轶. 主机隔振器刚度对船舶推进轴系冲击特性的影响[J]. 中国舰船研究, 2008, 3(3): 38-41. GUO Q L, ZHU C S, DENG Y. Effects of the stiffness of vibration isolators on anti-shock dynamics for propulsion shafting of ship[J]. Chinese Journal of Ship Research, 2008, 3(3): 38-41. DOI:10.3969/j.issn.1673-3185.2008.03.009 |
| [4] |
王永远.船舶动力系统隔振技术研究[D]. 武汉: 武汉理工大学, 2008.
|
| [5] |
张亚洲.船舶推进装置-气囊隔振系统校中特性研究[D]. 西安: 西安科技大学, 2013.
|
| [6] |
卜文俊, 何琳, 施亮. 船舶推进装置气囊隔振系统对中可控性问题研究[J]. 振动与冲击, 2015, 34(5): 56-60. BU W J, HE L, SHI L. Alignment controllability of air spring vibration isolation system of a ship propulsion plant[J]. Journal of Vibration and Shock, 2015, 34(5): 56-60. |
| [7] |
ARVID Naess. A second-order theory for the response statistics of wave induced ship hull vibrations in random seas[J]. Maritime Structures, 1996, 9: 389-408. DOI:10.1016/0951-8339(95)00029-1 |
| [8] |
J. JUNCHER JENSEN. Wave-induced ship hull vibrations in stochastic seaways[J]. Maritime Structures, 1996, 9: 353-387. DOI:10.1016/0951-8339(95)00031-3 |
| [9] |
ALOK K. Jha. Nonlinear stochastic models for ocean wave load and responses of offshore structures and vessels[D]. USA:Stanford University, 1997.
|
| [10] |
刘树鹏.舰船纵横倾作用下转子轴承系统动力学特性研究[D]. 哈尔滨: 哈尔滨工业大学, 2011.
|
 2019, Vol. 41
2019, Vol. 41
