2. 华中科技大学,湖北 武汉 430074
2. Huazhong University of Science and Technology, Wuhan 430074, China
风洞试验的早期阶段主要应用于航空航天工程。随着现代科学技术的快速发展,空气动力学特别是低速空气动力学领域已经完全跨出了航空航天的范畴,扩散到国民经济的方方面面,诸如交通运输工具、建筑物构筑物,以及地球环境等领域的工程问题[1]。洞壁干扰和安装支架干扰[2] 是风洞测试中的2种主要干扰,也是引起测试不确定度的2个重要因素。在风洞试验的领域,1987年AGARD召开会议建议推行风洞试验的数据不确定度评估方法,随之美国建立了相关的评估方法与标准[3]。美国的一些研究机构如NASA、波音公司等也都根据自己的设备和要求进行此项研究[4]。国内方面,随着配套不确定度评价理论的逐步推广与完善,中国合格评定国家认可委员会(CNAS)采用了系统的认可标准,明确指出检测实验室必须建立并实施所有各类校准测量不确定度的评定程序[5]。采用数值计算不确定度分析也开展了相应的研究,在国外方面,Simonsen等[6]应用ITTC的推荐规程对游轮的数值模拟不确定度进行研究,Van等[7]对潜艇标模Suboff的流场数值模拟进行了不确定度分析。国内方面,朱德祥等[8]对Suboff裸艇体的压力分布数值计算不确定度进行了研究,张楠等[9]对Suboff全附体阻力和流场模拟进行了不确定度的分析。
本文采用数值方法对风洞洞壁和安装支架对测试结果的影响进行分析修正,对提高风洞测试时数据分析精度起到积极的作用。
1 理论基础 1.1 控制方程采将NS方程和连续方程中的瞬时值用时均值和脉动值来替代和简化方程即RANS方程,达到大幅度缩减计算资源耗费的目的。连续性方程和RANS方程表达如下:
| $ \frac{{\partial {{\bar u}_i}}}{{\partial {x_i}}} = 0{\text{,}} $ | (1) |
| $ \frac{{\partial {{\bar u}_i}}}{{\partial t}} + \frac{{\partial {{\bar u}_i}{{\bar u}_j}}}{{\partial {x_j}}} = {F_i} - \frac{1}{\rho }\frac{{\partial \bar p}}{{\partial {x_i}}} + \nu \frac{{{\partial ^2}{{\bar u}_i}}}{{\partial {x_j}\partial {x_j}}} - \frac{{\partial \overline {u_i'u_j'} }}{{\partial {x_j}}}{\text{。}} $ | (2) |
引入漩涡粘性理论将雷诺应力模化,可得到二阶封闭的漩涡粘性模型,不同的封闭方程构建形式,形成了不同的湍流模型。双方程湍流模型建立湍动能与湍流频率的输运方程,优点在于低雷诺数流动的近壁区处理。本文采用的标准湍流模型对应的方程组如下:
| $ \frac{\partial }{{\partial t}}\left( {\rho k} \right) + \frac{\partial }{{\partial {x_i}}}\left( {\rho k{u_i}} \right) = \frac{\partial }{{\partial {x_j}}}\left( {{\varGamma _k}\frac{{\partial k}}{{\partial {x_j}}}} \right) + {G_k} - {Y_k} + {S_k}{\text{,}} $ | (3) |
| $ \frac{\partial }{{\partial t}}\left( {\rho \omega } \right) + \frac{\partial }{{\partial {x_i}}}\left( {\rho \omega {u_i}} \right) = \frac{\partial }{{\partial {x_j}}}\left( {{{\varGamma }_\omega }\frac{{\partial \omega }}{{\partial {x_j}}}} \right) + {G_\omega } - {Y_\omega } + {S_\omega }{\text{。}} $ | (4) |
采用有限体积法对方程进行离散,基于线性重构方法,支持多重几何形状的计算单元,对流项均采用二阶迎风格式离散,速度压力的耦合迭代采用SIMPLEC算法。
1.3 边界条件对Suboff光体模型数值模拟的边界条件进行设置。
入口条件:入口处边界条件设置为速度入口,速度大小设置随工况逐步改变。
出口条件:出口处边界条件设置为压力出口,认为流动在该处已经充分发展。
艇身、洞壁及支架系统:艇身、洞壁及支架系统表面的边界条件设置为无滑移壁面条件。
无限流场边界:无限流场边界设置为不影响内部流场的条件。
对称面:对称面的边界条件设为镜像对称条件。
2 研究对象及其干扰分析方法 2.1 研究对象计算对象为相比Suboff标模缩尺比为1∶2的光体模型,模型总长为2.178 m,最大直径处为0.254 m。由于模型几何造型简单,本文的模型直接在ICEM软件的建模环境之下完成建模,如图1所示。
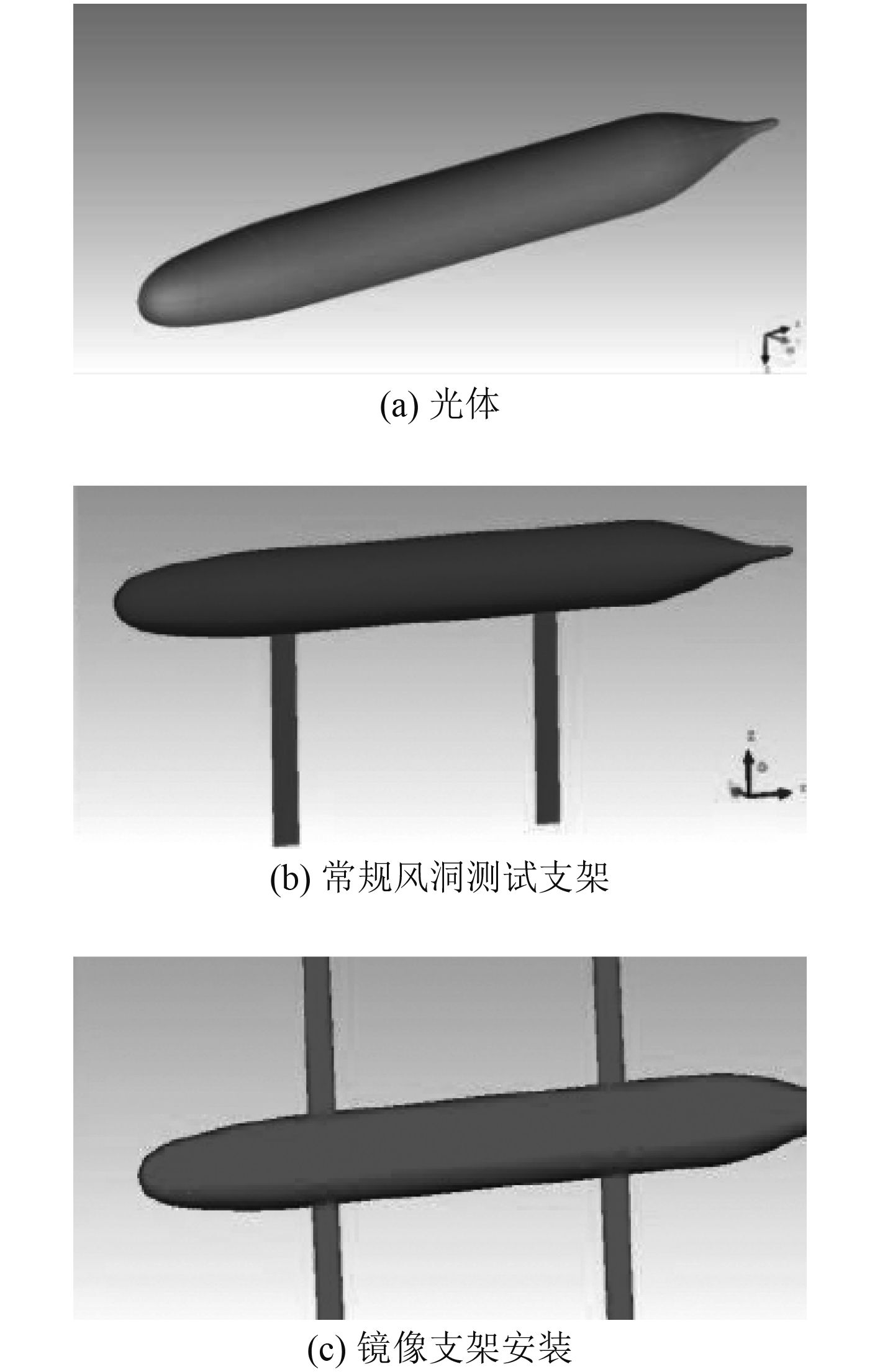
|
图 1 Suboff模型及安装示意图 Fig. 1 Suboff model and installation |
安装支架选择流线型断面,可以将支架本身的阻力降低一个数量级,减少支架对测试对象的干扰。
2.2 洞壁干扰处理方法洞壁干扰处理方法主要是考虑计算域无限大,根据文献资料,一般取大于测试对象10倍直径,四周去对称边界,而有洞壁干扰的,以某一有限尺寸的风洞为例,本文中取5倍直径,四周取壁面边界,对比2种计算结果,并采用映像法对风洞洞壁干扰进行修正。主要原理为:
| $ {C_{{D_c}}} = {C_{{D_u}}}\left( {1 - 2\varepsilon } \right) + \Delta {C_D} + \Delta {C_{DW}}{\text{,}} $ | (5) |
其中下标c代表修正之后的值,下标u代表未修正的量值。ε为阻塞干扰因子,可以被分解为模型尾流阻塞干扰因子和模型实体阻塞干扰因子两部分。∆CD和∆CDW则为下洗作用产生的影响,本计算对象是直航1:2 Suboff模型,无升力影响,可不考虑∆CD因素影响。其中阻塞因子可采用如下方法计算:
| $ {\rm{\varepsilon }} = {\varepsilon _S} + {\varepsilon _W} {\text{,}}$ | (6) |
其中
| $ {{\varepsilon }_{S}}=K\tau \frac{V}{{{A}^{{}^{3}\!\!\diagup\!\!{}_{2}\;}}}{\text{。}} $ | (7) |
作为Suboff潜艇的光体,可以视为旋成体,取
而
| $ {\varepsilon _W} = \frac{S}{{4A}}{C_{D{0_u}}}{\text{,}} $ | (8) |
其中S为力和力矩系数的参考面积1.489 2 m2,A为试验段横截面积2.31 m2,
| $ \Delta {C_{DW}} = - {\varepsilon _S} \cdot {C_{D{0_u}}}{\text{,}} $ | (9) |
其中
当支架系统存在时,模型区附近的气流速度因支架系统而导致阻塞效应比单独只存在模型时大一个增量,即耦合干扰。通常状态之下这种附加的干扰是线性的,也被称之为支架的洞壁干扰。通过镜像法中的叠加法可以证明,两步法所测出的支架干扰中自然包括了支架的洞壁干扰。因而,测力数据经由两步法修正后,就已经将支架的直接干扰和支架的洞壁干扰全部修正。只剩下模型的洞壁干扰待修正。所以,两步法修正后的测力数据理论上应该等于只有模型洞壁干扰作用下的测力数据。有洞壁有支架的常规风洞试验状态的修正数据和有洞壁无支架的理想风洞试验状态的数据和无限流场下的数据的三者综合对比。
3 计算结果及其分析 3.1 洞壁干扰表1为洞壁干扰修正前后的阻力系数计算表格。
|
|
表 1 洞壁干扰修正结果与无限流场对比 Tab.1 Comparison of wall interference correction results and infinite flow field |
有洞壁干扰的试验状态之下测得的数据,在进行映像法的修正之后,获得的阻力系数与无限流场状态下的阻力系数最大偏差不超过4.0%,吻合程度良好。其中对于摩擦阻力系数而言,洞壁干扰的影响很小,基本可以忽略不计;而对于粘压阻力而言,洞壁干扰的影响就比较大,是进行修正工作时的主要修正对象。对于光体Suboff这类几何外形简单的模型来说,经典的映像修正法仍具有较高的可靠性。
3.2 安装支架干扰针对同时有支架干扰和洞壁干扰耦合作用下的数值仿真结果,首先采用镜像两步法来修正支架的干扰,再引用映像法来修正洞壁干扰的作用。表2为修正的过程及结果。
|
|
表 2 镜像法修正数据与理想风洞试验、无限流场的综合对比 Tab.2 Comparison of correction data of image method with ideal wind tunnel test and infinite flow field |
在镜像两步法的测试环境中,模型添加了另一套支架系统后,其阻力系数又产生了很大的变化。风洞测试时一般测力传感器安装在风洞洞壁以外,壁面安装传感器破坏艇体表面形状,因此实际测试的阻力包含了支架阻力及其支架对艇体阻力的影响。安装了镜像支架以后摩擦阻力和粘压阻力都有不同程度的增大。而经典的镜像两步法对支架干扰的修正效果良好,修正后的数据与无支架的理想风洞试验结果吻合良好;而进一步修正洞壁干扰后,与无限流场下的测定数据一致性良好。运用镜像法结果与常规风洞阻力系数的差值作为修正值去修正常规风洞的阻力系数。修正后的结果与只有洞壁干扰下的理想风洞试验状态的数据吻合比较好,也证明了叠加法推导的合理性和镜像修正法的可靠性。
将试验数据运用镜像法修正了支架干扰之后,再使用映像法修正数据中的洞壁干扰,获得的结果与无限流场相对比来看,最大偏差不超过3.8%,一致性良好。
4 结 语1)通过数值方法对风洞测试过程中2个主要干扰因素进行修正,修正结果表明对于洞壁干扰效应,从阻力测定的角度来说,只要洞壁与模型的相对尺寸选择合理,洞壁干扰对于测定结果的影响比较有限,而其影响均可以通过适当的手段进行修正。
2)对于支架干扰效应,从阻力测定的角度来说,即使支架的截面选择为对阻力系数影响相对较小的流线型,支架系统的存在对测定结果中阻力系数的影响仍然非常大。镜像两步法的修正效果对于本文的研究对象来说具有很高的可靠性。
数据的修正过程不仅需要对阻力系数进行修正,还需要对来流速度以及雷诺数进行洞壁干扰的修正,但是修正后的来流速度不再与无限流场的来流速度一致,缺乏了可比性。考虑到修正的系数比较小,只在2%的量级,因而文中为了方便比较,对来流速度和雷诺数的修正选择了忽略不计。严格来说,应该把修正了来流速度和雷诺数的情形重新设置工况进行数值仿真计算。
| [1] |
王勋年等. 《低速风洞试验》第1版. 北京: 国防工业出版社 2002: 1–2.
|
| [2] |
程厚梅等. 《风洞实验干扰与修正》第1版. 北京: 国防工业出版社 2003: 4–5.
|
| [3] |
UNCERTAINTY E, APPLICATION W, TESTING W T. Standard: assessment of experimental uncertainty with application to wind tunnel testing (AIAA S-071A-1999)[M]. 1999.
|
| [4] |
MEYN L. A new method for integrating uncertainty analysis into data reduction software[C]//Aiaa Aerospace Sciences Meeting and Exhibit. 2013.
|
| [5] |
全国认证认可标准化技术委员会. GB/T27025-2008检测和校准实验室能力的通用要求理解与实施[M]. 中国标准出版社, 2009: 94.
|
| [6] |
SIMONSEN C D, STERN F. Verification and validation of RANS maneuvering simulation of Esso Osaka: effects of drift and rudder angle on forces and moments[J]. Computers & Fluids, 2003, 32(10): 1325-1356. |
| [7] |
KIM J, PARK I R, VAN S H, et al. Calculation of Turbulent Flows around a Submarine for the Prediction of Hydrodynamic Performance[J]. Journal of Ship & Ocean Technology, 2003, 7(4). |
| [8] |
朱德祥, 张志荣, 吴乘胜, 等. 船舶CFD不确定度分析及ITTC临时规程的初步应用[J]. 水动力学研究与进展, 2007, 22(3): 363-370. DOI:10.3969/j.issn.1000-4874.2007.03.015 |
| [9] |
张楠, 沈泓萃, 姚惠之. 阻力和流场的CFD不确定度分析探讨[J]. 船舶力学, 2008, 12(2): 211-224. DOI:10.3969/j.issn.1007-7294.2008.02.007 |
 2019, Vol. 41
2019, Vol. 41
