管路结构在船舶等工程领域有着广泛的应用,其主要连接方式包括刚性连接(如焊接)和弹性连接(弹性管接头连接),不同连接方式对结构声传递有着不同的抑制效果。
管路中结构声的主要来源,一方面为获取传输液体的动力,管路与泵机、柴油机等相连,动力源在工作时产生的振动,将不可避免的传递给管路系统;另一方面,船体振动会通过管支架传递给管道。而在管路结构中,振动能量将从上游管路传递给下游管路,因此,有必要对连接管路进行振动能量传递的研究,改善其工作状态。根据波动理论[1],这些振动都可以等效为不同类型结构波的入射,其中弯曲波占主导。本文仅是在理论方面就管路不同连接方式对结构声传递的影响进行分析。
目前,对管道结构常用的结构振动计算方法主要有有限元法、阻抗分析法、传递矩阵法和模态综合法等[2]。潘国雄等[3]利用有限元软件Ansys建立阀组单元结构模型,计算了阀组单元结构在不同频率载荷激励下的振动响应频谱。王勇等[4]通过实验研究验证了弹性支承是控制舰用管路振动噪声的有效途径;何琳等[5]研究了阻振质量对杆类结构中弯曲波传递的影响,结果表明阻振质量可阻抑弯曲波的传递,管路结构同是杆类构件,适用于此理论,但其未考虑波形转换及振动能量传递关系;L.Cremer与Heckl[6]在其著作《Structure-Borne Sound》中指出,结构振动可以看作是沿不同方向传递的不同类型结构波的互相叠加,且结构波在传递过程中遇到任何阻抗突变都会发生反射与透射,同时伴随波形转换;R. M. Grice和R. J. Pinnington[1]采用波分析法研究了梁结构波传递规律;车驰东和陈端石等[7]对成任意角度连接的两块板进行了弯曲波振动能量传递分析,通过改变阻振质量起到了良好的阻振效果,对本文研究振动能量在管路之间传递的研究有一定的指导作用。在舰船运行过程中,振动能量从动力源持续传递给管路结构,并在管路结构中进行传递。综合各类研究发现,对管路结构中振动波形转换及能量传递的研究涉及较少,本文将管路结构进行简化,建立了2根成任意角度连接的半无限长管道纵弯耦合振动模型,利用波分析法,在弯曲波入射条件下,对系统振动能量传递进行理论和数值分析,得到管道在不同连接方式下,波形转换及透射和反射系数,为管路结构减振降噪的研究提供参考。
1 理论分析 1.1 模型描述考虑2根半无限长的管道结构,以任意角度

|
图 1 半无限长管道局部坐标及受力示意图 Fig. 1 Local coordinate and force diagram of semi-infinite long pipelines |
考虑到管路与柴油机、压缩机等动力源相连,所承受的载荷主要来源于动力源引起的弯曲(回旋)振动,因此,可将对管路的激励等效为弯曲波入射的形式,对于简谐平面弯曲波入射的情况,某一特定激励频率
| $ {v_{y1}}({x_1}) = {e^{ - j{k_{B1}}{x_1}}} + {r_b}{e^{ + j{k_{B1}}{x_1}}} + {r_j}{e^{ + {k_{B1}}{x_1}}},{x_1} < 0\text{,} $ | (1) |
| $ {v_{y2}}({x_2}) = {\tilde v_{y1}}({t_b}{e^{ - j{k_{B2}}{x_2}}} + {t_j}{e^{ - {k_{B2}}{x_2}}}),{x_2} > 0\text{,} $ | (2) |
| $ {v_{x1}}({x_1}) = {r_L}{e^{ + j{k_{L1}}{x_1}}},{x_1} < 0\text{,} $ | (3) |
| $ {v_{x2}}({x_2}) = {t_L}{e^{ - j{k_{L2}}{x_2}}},{x_2} > 0\text{。} $ | (4) |
式中:
如图1所示,当两管道间存在扭转刚度和连接刚度时,在
1)力平衡
| $ {F_{x1}} = {k_x} \cdot \frac{1}{{j\omega }}({v_{x2}} \cdot \cos \theta - {v_{y2}} \cdot \sin \theta - {v_{x1}})\text{,} $ | (5) |
| $ {F_{y1}} = {k_y} \cdot \frac{1}{{j\omega }}({v_{y2}} \cdot \cos \theta + {v_{x2}} \cdot \sin \theta - {v_{y1}})\text{,} $ | (6) |
| $ {F_{x1}} = {F_{x2}} \cdot \cos \theta + {F_{y2}} \cdot \sin \theta \text{,} $ | (7) |
| $ {F_{y1}} + {F_{x2}} \cdot \sin \theta = {F_{y2}} \cdot \cos \theta \text{;} $ | (8) |
2)力矩平衡
| $ {M_1} = {k_r} \cdot ({\alpha _1} - {\alpha _2})\text{,} $ | (9) |
| $ {M_1} = {M_2}\text{。} $ | (10) |
式中:
将式(1)~式(4)代入式(5)~式(10)中,可得到2组弯曲波入射下,反射系数和透射系数的方程,将该方程无量纲化后,可得到式(11);当2根管道间扭转刚度极小可以忽略时,即
| $\small\begin{split} &\left[ {\begin{array}{*{20}{c}} \!\! \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!0\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!&\!\!\!\!\!\!\!\!\!\!0\!\!\!\!\!\!\!\!&\!\!\!\!\!\!\!\!{1 + {\eta _1}}\!\!\!\!\!\!\!\!\!&\!\!\!\!\!\!\!\!\!{{\eta _1}\sin \theta }\!\!\!\!\!\!\!\!\!&\!\!\!\!\!\!\!\!\!{{\eta _1}\sin \theta }\!\!\!\!\!\!\!\!&\!\!\!\!\!\!\!\!{ - {\eta _1}\cos \theta }\!\!\!\!\!\!\!\!\!\\ {1 - {\eta _2}}&{j - {\eta _2}}&0&{{\eta _2}\cos \theta }&{{\eta _2}\cos \theta }&{{\eta _2}\sin \theta } \\ {j{\eta _3}{\rm{ + 1}}}&{{\eta _3}{\rm{ - 1}}}&0&{j\chi {\eta _3}}&{\chi {\eta _3}}&0 \\ { - 1}&1&0&\psi &{ - \psi }&0 \\ 0&0&1&{ - {\beta _{\rm{1}}}\sin \theta }&{j \cdot {\beta _{\rm{1}}}\sin \theta }&{\alpha \cos \theta } \\ { - {\beta _{\rm{2}}}}&{ - j \cdot {\beta _{\rm{2}}}}&0&{ - {\gamma _{\rm{2}}}\cos \theta }&{ - j \cdot {\gamma _{\rm{2}}}\cos \theta }&{ - \sin \theta } \end{array}} \right] \times\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! \\ &\quad \left[ {\begin{array}{*{20}{c}} {{r_b}} \\ {{r_j}} \\ {{r_l}} \\ {{t_b}} \\ {{t_j}} \\ {{t_l}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 0 \\ {1 + {\eta _2}} \\ {j{\eta _3}{\rm{ - 1}}} \\ 1 \\ 0 \\ { - {\beta _{\rm{2}}}} \end{array}} \right]\text{,} \end{split} $ | (11) |
| $\small \begin{split} &\left[ {\begin{array}{*{20}{c}} \!\!\!\! 0\!\!\!\!&\!\!\!\!0\!\!\!\!&\!\!\!\!{1 + {\eta _1}}\!\!\!\!&\!\!\!\!{{\eta _1}\sin \theta }\!\!\!\!&\!\!\!\!{{\eta _1}\sin \theta }\!\!\!\!&\!\!\!\!{ - {\eta _1}\cos \theta } \!\!\!\!\\ {1 - {\eta _2}}&{j - {\eta _2}}&0&{{\eta _2}\cos \theta }&{{\eta _2}\cos \theta }&{{\eta _2}\sin \theta } \\ {\rm{1}}&{{\rm{ - }}1}&0&{\rm{0}}&{\rm{0}}&0 \\ {{\rm{ - 1}}}&{\rm{1}}&0&\psi &{{\rm{ - }}\psi }&0 \\ 0&0&1&{ - {\beta _{\rm{1}}}\sin \theta }&{j \cdot {\beta _{\rm{1}}}\sin \theta }&{\alpha \cos \theta } \\ { - {\beta _{\rm{2}}}}&{ - j \cdot {\beta _{\rm{2}}}}&0&{ - {\gamma _{\rm{2}}}\cos \theta }&{ - j \cdot {\gamma _{\rm{2}}}\cos \theta }&{ - \sin \theta } \end{array}} \right]\times \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\\ &\quad\left[ {\begin{array}{*{20}{c}} {{r_b}} \\ {{r_j}} \\ {{r_l}} \\ {{t_b}} \\ {{t_j}} \\ {{t_l}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 0 \\ {1 + {\eta _2}} \\ {{\rm{ - 1}}} \\ {\rm{1}} \\ 0 \\ { - {\beta _{\rm{2}}}} \end{array}} \right]\text{,} \end{split} $ | (12) |
| $ \small \begin{split} &\left[ {\begin{array}{*{20}{c}} 0&0&{\rm{1}}&{\sin \theta }&{\sin \theta }&{ - \cos \theta } \\ { - {\rm{1}}}&{ - {\rm{1}}}&0&{\cos \theta }&{\cos \theta }&{\sin \theta } \\ j&{\rm{1}}&0&{j\chi }&\chi &0 \\ { - 1}&1&0&\psi &{ - \psi }&0 \\ 0&0&1&{ - {\beta _{\rm{1}}}\sin \theta }&{j \cdot {\beta _{\rm{1}}}\sin \theta }&{\alpha \cos \theta } \\ { - {\beta _{\rm{2}}}}&{ - j \cdot {\beta _{\rm{2}}}}&0&{ - {\gamma _{\rm{2}}}\cos \theta }&{ - j \cdot {\gamma _{\rm{2}}}\cos \theta }&{ - \sin \theta } \end{array}} \right]\times\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! \\ &\quad\left[ {\begin{array}{*{20}{c}} {{r_b}} \\ {{r_j}} \\ {{r_l}} \\ {{t_b}} \\ {{t_j}} \\ {{t_l}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 0 \\ 1 \\ j \\ 1 \\ 0 \\ { - {\beta _{\rm{2}}}} \end{array}} \right]\text{。} \end{split} $ | (13) |
式中:
在两管连接处,反射波、近场波与入射波相比,幅值和相位会发生改变,因此
在工程上,振动将以能量的形式由管路传递给船体,为更直观地表现弯曲波的透射和反射现象,通常将其转化为能量传递效率,用以表示各种形式的波在入射波能量中的占比。
弯曲波-弯曲波透射能量效率:
| $ {\tau _{BB}} = \frac{{{P_{BT}}}}{{{P_{BI}}}} = \frac{{{\beta _{\rm{1}}}}}{{{\gamma _{\rm{1}}}}}{\left| {{t_b}} \right|^2}{\rm{ = }}\frac{{{c_{B2}}{\rho _2}{A_2}}}{{{c_{B1}}{\rho _1}{A_1}}}{\left| {{t_b}} \right|^2}\text{,} $ | (14) |
弯曲波-弯曲波反射能量效率:
| $ {\rho _{BB}} = \frac{{{P_{BR}}}}{{{P_{BI}}}} = {\left| {{r_b}} \right|^2}\text{,} $ | (15) |
弯曲波-纵波透射能量效率:
| $ {\tau _{BL}} = \frac{{{P_{LT}}}}{{{P_{BI}}}} = \frac{1}{{2{\beta _2}}}{\left| {{t_l}} \right|^2}{\rm{ = }}\frac{{{c_{L2}}{\rho _2}{A_2}}}{{{\rm{2}} \cdot {c_{B1}}{\rho _1}{A_1}}}{\left| {{t_l}} \right|^2}\text{,} $ | (16) |
弯曲波-纵波反射能量效率:
| $ {\rho _{BL}} = \frac{{{P_{LR}}}}{{{P_{BI}}}} = \frac{1}{{2{\gamma _1}}}{\left| {{r_l}} \right|^2}{\rm{ = }}\frac{{{c_{L1}}}}{{2 \cdot {c_{B1}}}}{\left| {{r_l}} \right|^2}\text{。} $ | (17) |
式中:P为波的功率,下标B表示弯曲波,L表示纵波;下标I/R/T分别表示入射/反射/透射;
| $ {\rho _{BB}} + {\rho _{BL}} + {\tau _{BB}} + {\tau _{BL}} = 1\text{。} $ | (18) |
为研究管路结构连接刚度等参数的变化对振动能量转换和传递的影响,可用数值分析的方法模拟能量在半无限长管路结构中的传递。设两管均采用40Cr钢材,且截面内外径相同,外径均为60 mm,内径为50 mm,图2和图3分别代表扭转刚度为

|
图 2 能量透射与反射效率曲线 Fig. 2 Energy transmission and reflection efficiencies |

|
图 3 忽略扭转刚度时能量透射与反射效率曲线 Fig. 3 The energy efficiencies without rotation rigidity |
由图2和图3可以看出,每张图中的0~1均被3条曲线分为4段,自下而上分别代表
1)在计算频率范围内,相同连接方式下,4种能量系数和为1,符合式(18),即能量守恒定律;
2)2根管道间存在扭转刚度时,在计算范围内,透射波总能量曲线随频率的增加既可能产生波峰又可能产生波谷;
3)弯曲波能量(
4)2根管道之间不存在扭转刚度时,在计算范围内,透射波总能量,即
能量效率除了随频率改变之外,还与管道连接方式的物性参数有关,在上文的计算中,管道的刚度、密度、横截面积及连接刚度等物性参数均保持一致。
可以看出,弯曲波能量(
| $ TL = 10\log \left(\frac{1}{{{\tau _{BB}}}}\right)\text{。} $ | (19) |
保持两管夹角不变,在3种极限情况下:
1)连接刚度一定(1E8 N/m),扭转刚度为0;
2)连接刚度一定(1E8 N/m),扭转刚度为无穷大;
3)连接刚度和扭转刚度均为无穷大,即两管焊接。
弯曲波传递损失曲线变化如图4所示,图中曲线由细到粗分别代表上述3种情况。
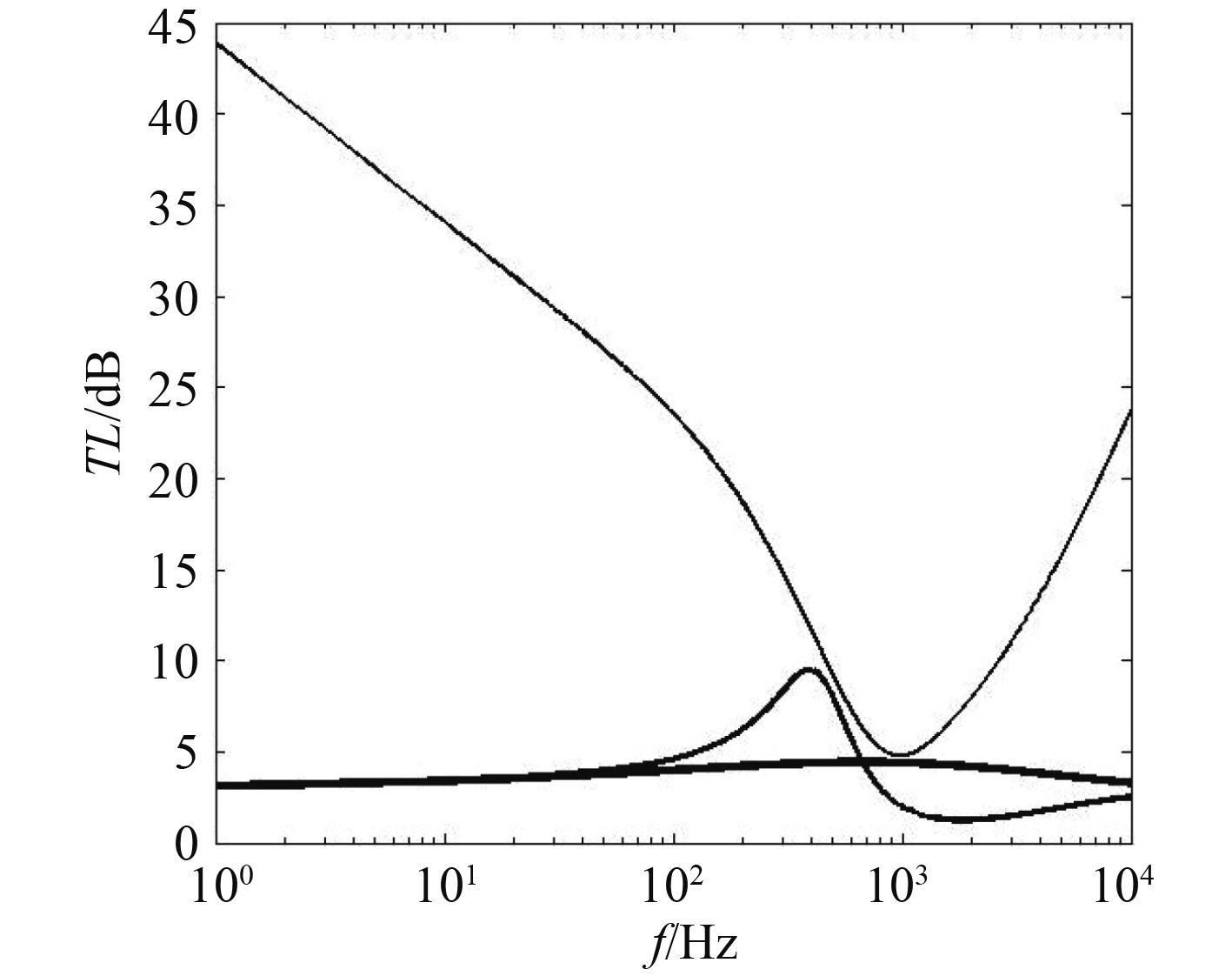
|
图 4 特殊边界下的弯曲波传递损失系数变化曲线 Fig. 4 TL under special boundary condition |
由图4可以看出,当2管焊接时,弯曲波能量传递损失极小,弯曲波的大部分能量都将传递到下游管路中。
为研究连接刚度与扭转刚度对管路中弯曲波能量传递的影响,可作以下分析:
当连接刚度一定(1E8 N/m)时,仅改变扭转刚度,弯曲波传递损失曲线变化如图5和图6所示(图例值对应扭转刚度值)。
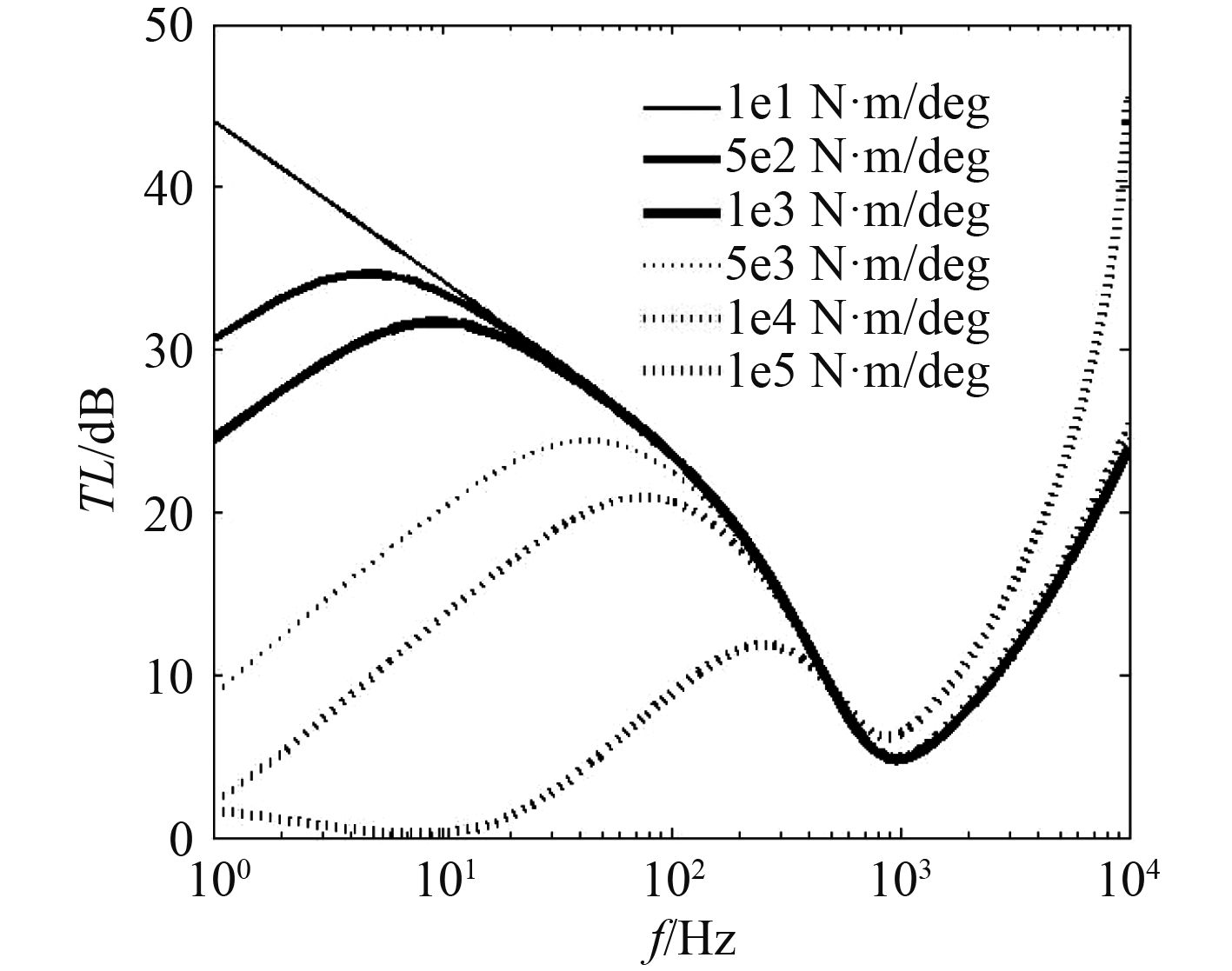
|
图 5 弯曲波传递损失系数随扭转刚度变化曲线 Fig. 5 TL curves with the change of rotation rigidity |
由图5可以看出,当扭转刚度较低时,随着扭转刚度增大,弯曲波传递损失系数在低频范围内降低,在高频段内变化较小;传递损失系数产生的波峰峰值降低,所对应频率增大,而波谷对应频率则变化不大。
由图6可以看出,当扭转刚度较高时,弯曲波传递损失系数随扭转刚度变化很小。极限情况下,当两管间扭转刚度为无穷大时,弯曲波传递损失系数曲线变化同样不明显。
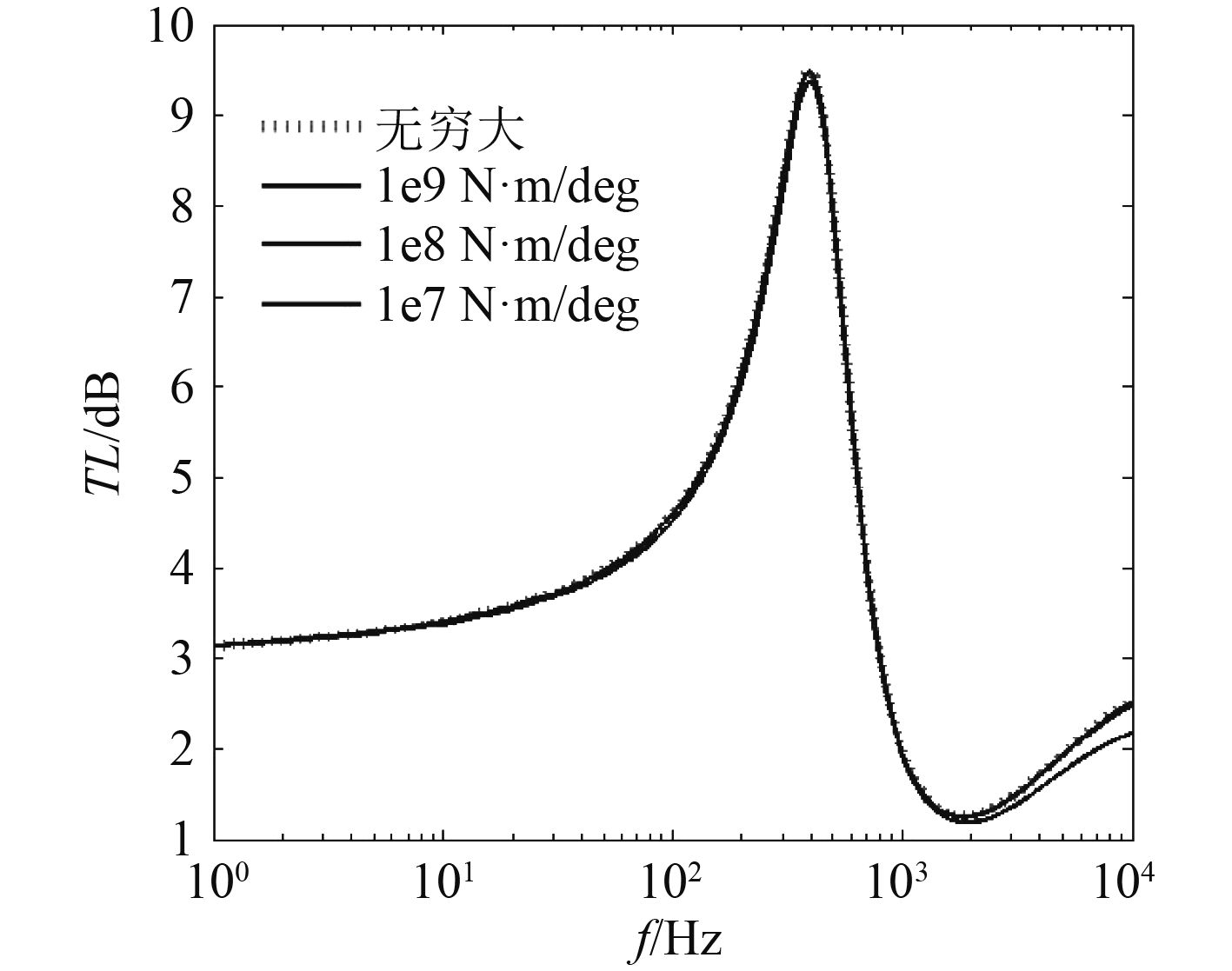
|
图 6 弯曲波传递损失系数随扭转刚度变化曲线 Fig. 6 Bend waves TL with the change of rotation rigidity |
当扭转刚度一定时,仅改变连接刚度,弯曲波传递损失系数曲线如图7所示。
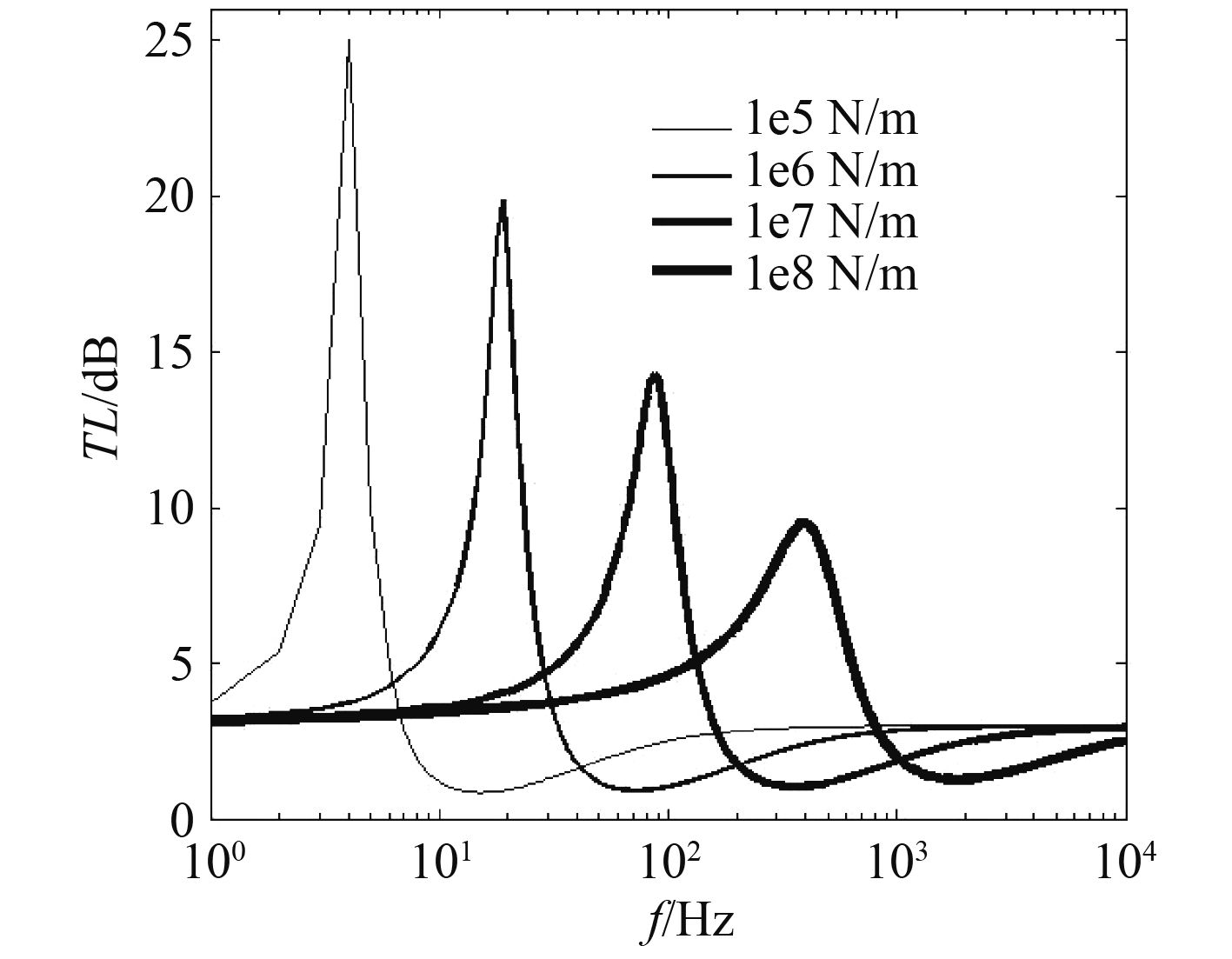
|
图 7 弯曲波传递损失系数随连接刚度变化曲线 Fig. 7 Bend waves TL with the change of connecting rigidity |
由图7可以看出,随着连接刚度的增大,弯曲波能量传递损失系数曲线峰值降低明显,谷值变化不大,峰值谷值所对应的频率将增大。
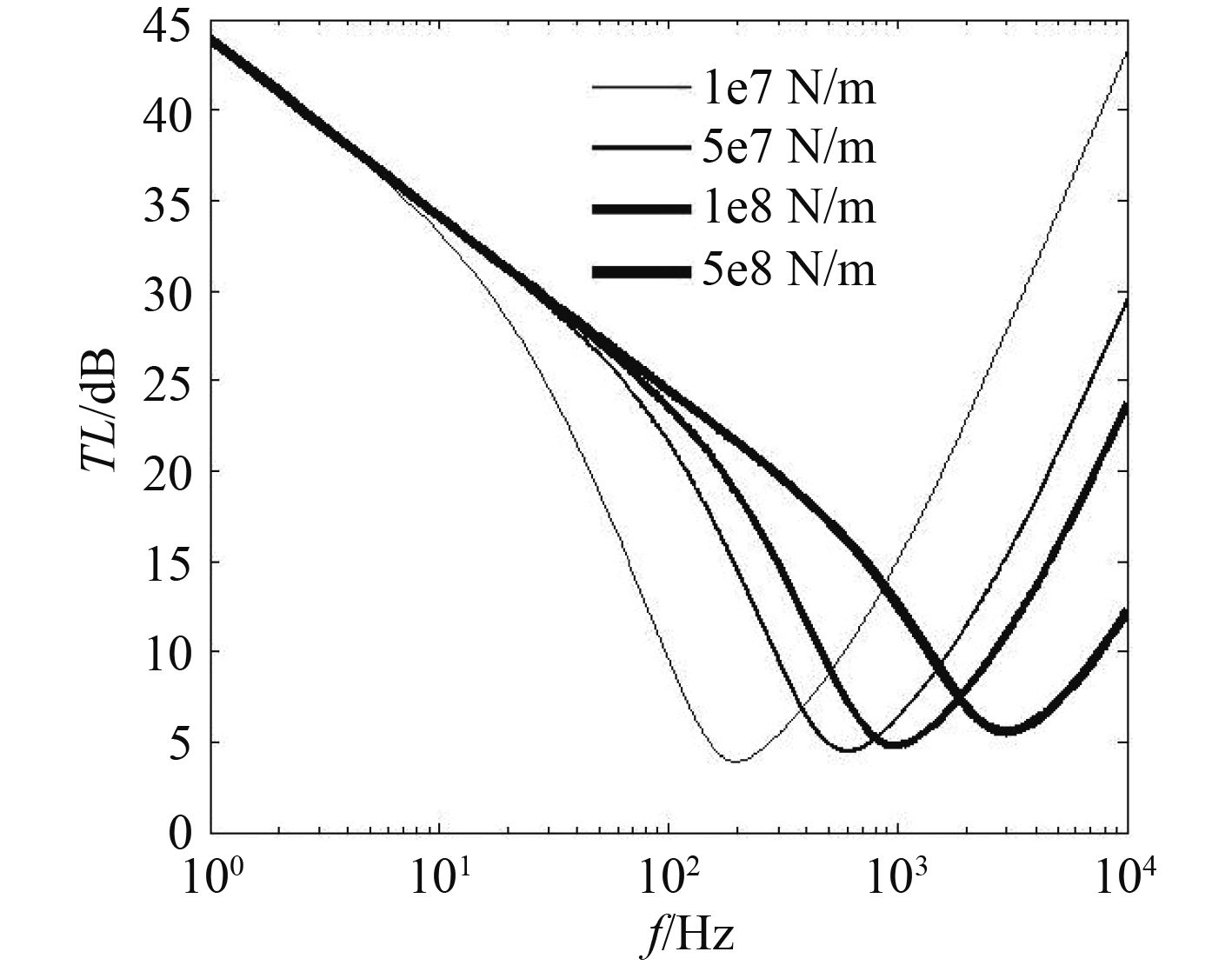
极限情况下,当扭转刚度极小可忽略时,TL曲线如图8所示(图例值对应连接刚度)。
|
图 8 弯曲波传递损失系数随连接刚度变化曲线 Fig. 8 Bend waves TL with the change of connecting rigidity |
由图8可以看出,弯曲波传递损失系数曲线波峰消失,仅存在波谷,其对应频率随连接刚度增大而增大;当连接刚度增加到一定数值后,连接刚度对低频段的传递损失系数影响较小,主要影响高频段。
在实际工程中,应根据激励频率来选择适当的管道连接刚度和扭转刚度,降低不平衡扰动引起的弯曲波传递。
当两根管道间的连接刚度为

|
图 9 扭转刚度极小时TL随两管夹角变化曲线 Fig. 9 The angle change curve of the non-rotating rigidity |
由图9可以看出,角度变化对TL曲线的影响主要在于低频段,传递损失参数会随着夹角增大而增大;对高频段影响较小。
当两管间连接刚度值和扭转刚度值均为

|
图 10 带有扭转刚度时TL随两管夹角变化曲线 Fig. 10 The angle change curve of the rotating rigidity |
由图10可以看出,夹角对TL曲线的影响主要在于波峰附近的频段,对远离波峰的频段影响较小。在工程中,通过改变2根管道间的夹角,起到减振降噪的作用。
3 结 语本文基于波分析法,对2根半无限长管道纵弯耦合振动的能量传递进行理论研究和数值分析,总结得到了在不同参数下能量传递规律,可以得出以下结论:
1)2根管道连接会产生一定的连接和扭转刚度,其刚度值会影响振动能量的传递。
2)两管间能量的传递弯曲波能量占主导地位,在工程中,更关注透射弯曲波对下游管道的工作状态影响,通过改变传动参数可以改善管道工作状态。
3)扭转刚度会使弯曲波能量传递效率曲线产生波谷,当扭转刚度较低时,扭转刚度对弯曲波能量透射传递效率低频段影响较大;当扭转刚度较高时,增加到一定数值之后,对弯曲波能量透射效率的影响将极小。
4)连接刚度主要影响高频弯曲波透射能量传递效率。
5)忽略扭转刚度时,两管夹角的变化对高频弯曲波的传递损失影响较小,对低频段影响较大;存在扭转刚度时,角度变化影响效率曲线波峰附近的频段。
6)本文理论分析中引入的无量纲数,将管道振动透射和反射系数与管道特征阻抗联系在一起,简化了公式表达,有利于进一步研究管道物性参数对振动能量传递的影响。
| [1] |
GRICE R M, PINNINGTON R J. A method for the vibration analysis of built-up structures, part Ⅰ: introduction and analytical analysis of the plate-stiffened beam[J]. Journal of Sound and Vibration, 2000, 230(4): 825-849. DOI:10.1006/jsvi.1999.2657 |
| [2] |
王川. 海洋工程管路减振降噪研究[D].中国海洋大学, 2015.
|
| [3] |
潘国雄, 张盛, 周赤奇, 等. 管路阀组结构制造工艺参数的振动特性影响[J]. 舰船科学技术, 2013, 35(4): 131-136. DOI:10.3404/j.issn.1672-7649.2013.04.031 |
| [4] |
王勇, 黄映云, 吕志强, 等. 一种舰用管路振动传递控制的工程方法[J]. 舰船科学技术, 2007(4): 75-77+85. |
| [5] |
何琳, 何世平. 阻隔质量对杆类结构弯曲波隔离的工程应用研究[J]. 声学技术, 2007(1): 153-158. DOI:10.3969/j.issn.1000-3630.2007.01.031 |
| [6] |
CREMER L, HECKL M, PETERSSON B A T. Structure-Borne Sound[M]. Springer Berlin Heidelberg, 2005.
|
| [7] |
车驰东, 陈端石. 成任意角度连接的两块平板转角处阻振质量对平面弯曲波传递的影响分析[J]. 声学学报, 2007(3): 282-288. DOI:10.3321/j.issn:0371-0025.2007.03.014 |
 2019, Vol. 41
2019, Vol. 41
