铝合金具有密度低、比弹模量大和比强度高的特点,而且价格较低、工艺性较好,且铝合金材质的船舶相比钢质船重量减轻了15%以上,因此是建造高速舰船的理想材质[1-2]。对于高速舰船,波浪载荷将随着航速的提高而增大,并且会在船舶首底部、外飘区域等位置发生更严重的砰击现象[3]。砰击是船舶在航行过程中,由于剧烈的摇荡产生的波浪与船体的冲撞现象,遭受砰击的区域可能会发生局部破坏或导致船上仪器设备不能正常使用[4]。随着铝合金越来越广泛的用于建造高速舰船,为了更好地评估铝合金船体结构的安全性能[5],对铝合金质船体结构在砰击载荷作用下的结构动响应进行研究是有必要的。
文中以某船的铝合金板架为研究对象,基于Patran/Nastran大型有限元分析软件,采用材料非线性的瞬态响应分析方法,分析了关键参数对仿真结果的影响,并分析了铝合金板架对砰击载荷的响应规律。因为铝合金材料在高应变率下的应力响应与在准静态下拉伸应力响应存在差异[6],有必要讨论应变率对数值计算结果的影响,另外,由于阻尼的机理十分复杂[7],在阻尼影响很小的情况下,可以不计入阻尼的影响,以简化求解过程。为此,文中分析了阻尼对板架响应的影响。实际航行时,砰击载荷连续且存在变化,分析铝合金板架对砰击载荷的响应规律,对于实际的船体砰击响应计算有参考价值。
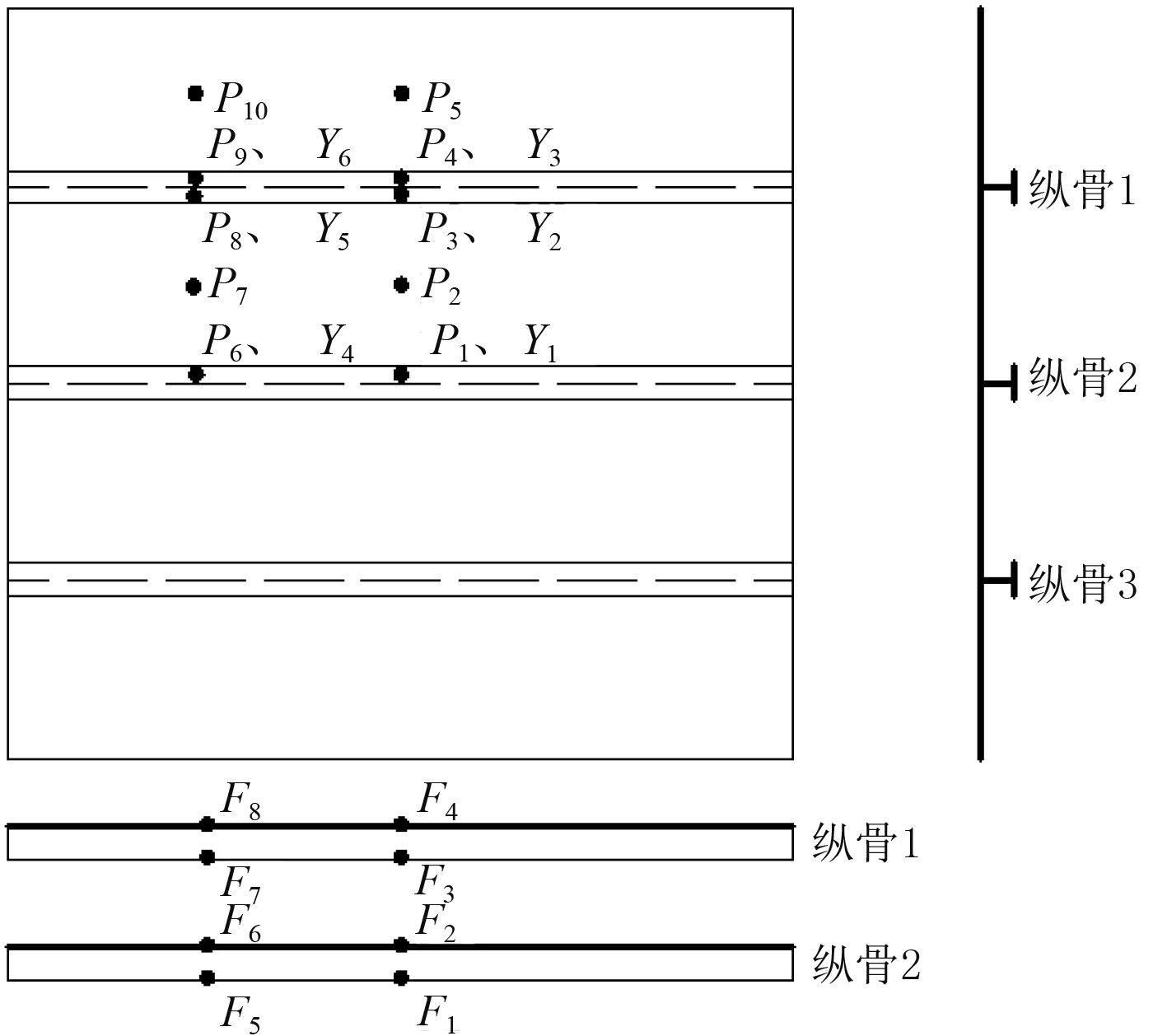
1 计算模型的建立 1.1 板架模型在实船试验中发现该铝合金艇某处受到砰击,参考该船此处的结构形式,船体板材料为5083型铝合金,纵骨材料为6082型铝合金,密度均为2 857,弹性模量均为70 000,泊松比均为0.3。板架几何模型如图1所示,取跨距为1 200 mm,板厚6 mm,骨材为3根,尺寸为
|
图 1 单跨三纵骨板架几何模型 Fig. 1 The plate geometric model of single span with three vertical bone |
系统的阻尼包括材料阻尼和粘性阻尼,铝合金板架结构的材料阻尼是由铝合金内部晶粒相互摩擦产生的,粘性阻尼是运动过程中由结构干摩擦及粘性流体摩擦产生的。对于铝合金板架结构,在砰击载荷瞬时作用的过程中,粘性阻尼的产生的影响很小,结构阻尼主要为材料阻尼[8]。粘性阻尼
文中采用理想弹塑性本构模型,材料的应变率效应由Cowper-Symonds模型描述,动态屈服强度
| $ {\sigma _d} = {\sigma _0}\left[ {1 + {{\left( {\frac{{\dot \varepsilon }}{D}} \right)}^{1/n}}} \right]{\text{。}} $ |
式中:
将Cowper-Symonds模型进行转化,得到:
| $ \ln \dot \varepsilon = \ln D + n \cdot \ln \left( {\frac{{{\sigma _y}}}{{{\sigma _0}}} - 1} \right){\text{。}} $ |
对于应变率,人们认为铝合金材料具有低的应变率敏感性,研究者发现,应变率超过1 000 s–1时,铝的应变率敏感性会增加,高宁等[1]利用CRIMS RPL100试验机和分离式霍普金森压杆开展了不同应变率下的拉伸试验,得到了0.0002 s–1,0.0010 s–1,10 s–1,4 000 s–1,10 650 s–1应变率下5083铝合金的应力应变曲线。高宁等通过拉伸试验得到结论:5083铝合金在0.0010 s–1(准静态)~20 000 s–1的应变速率范围内,应变率敏感性较低,材料的屈服强度和抗拉强度随应变率的增加而增大。在对6082铝合金力学性能的研究方面,王誉瑾等[6]对90个试件做了拉伸试验,得到了较为详细的力学参数,张云峰[9]通过拉伸试验得到了2 000 s–1,2 200 s–1,2 500 s–1,2 800 s–1应变率下6082铝合金的应力应变曲线。参考以上文献,可得5083铝合金和6082铝合金在不同应变率下的屈服应力,如表1所示。
|
|
表 1 两种铝合金在不同应变率下的屈服应力 Tab.1 Yield stress of two kinds of aluminum alloys at different strain rates |
由表1可得到5083铝合金对应的Cowper-Symonds模型的参数为D=24 123 s–1,n=2.3;6082铝合金对应的参数为D=4 719 s–1,n=0.27。
1.3 砰击载荷砰击是由气-流-固三者相互耦合作用产生的水动力效应,由于砰击的动力特征和耦合效应相当复杂,通过试验得到结构的砰击压力仍是目前最为可靠的方法[10-11],图2是某次试验中得到的0.22s时长的砰击载荷时间历程曲线,可以看出该艇受到的砰击载荷与常规结构入水砰击压力不同,该艇砰击载荷具有双峰值的特点,单个峰值作用时间为0.11s,将得到的真实载荷作为输入载荷,对阻尼效应和应变率效应进行分析。

|
图 2 真实砰击载荷 Fig. 2 True slamming load |
基于大型有限元分析软件Patran/Nstran对真实砰击载荷作用下铝合金板架的瞬态响应进行了仿真计算,首先对仿真进行了验证,之后考虑到结构和计算的对称性,分别取位于图1中的P1~P10点、Y1~Y6点和F1~Y8点作为特征点,对这些点位置处的变形情况进行比较分析,得到板架的最大变形和发生在P2点,在以下分析中,将P2点作为分析点,通过分析P2点的变形时历曲线,得到计算参数对仿真结果的影响。
2.1 瞬态响应仿真验证对祝伟[12]运用Abaqus软件求解的方板模型进行计算验证:长宽均为1 000 mm,材料密度为7.8 t/mm3,弹性模量E为
| $ \left[ { M} \right]\left\{ {{{\ddot u}_{(t)}}} \right\} + \left[ { B} \right]\left\{ {{{\dot u}_{(t)}}} \right\} + \left[ { K} \right]\left\{ {{u_{(t)}}} \right\} = \left\{ {{P_{(t)}}} \right\}{\text{,}} $ |
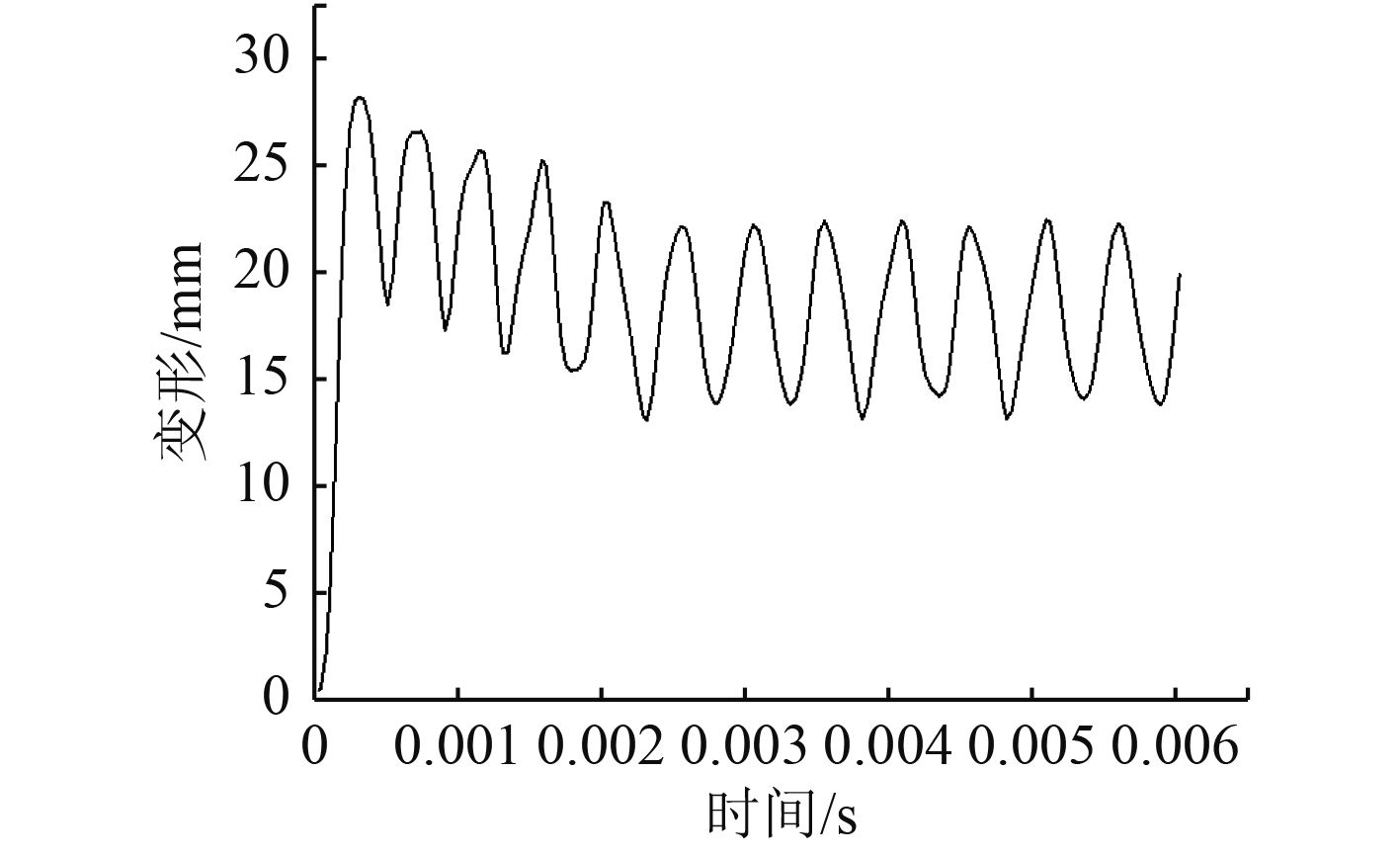
得到的仿真结果如图3所示。
|
图 3 钢质方板的瞬态响应分析 Fig. 3 Transient response analysis of steel square plate |
考虑应变率效应时,板中心的最大变形为28.01 mm,与祝伟给出的28.0 mm一致,因此文中采用Patran/Nstran对弹塑性材料进行瞬态响应动力分析是有效的。
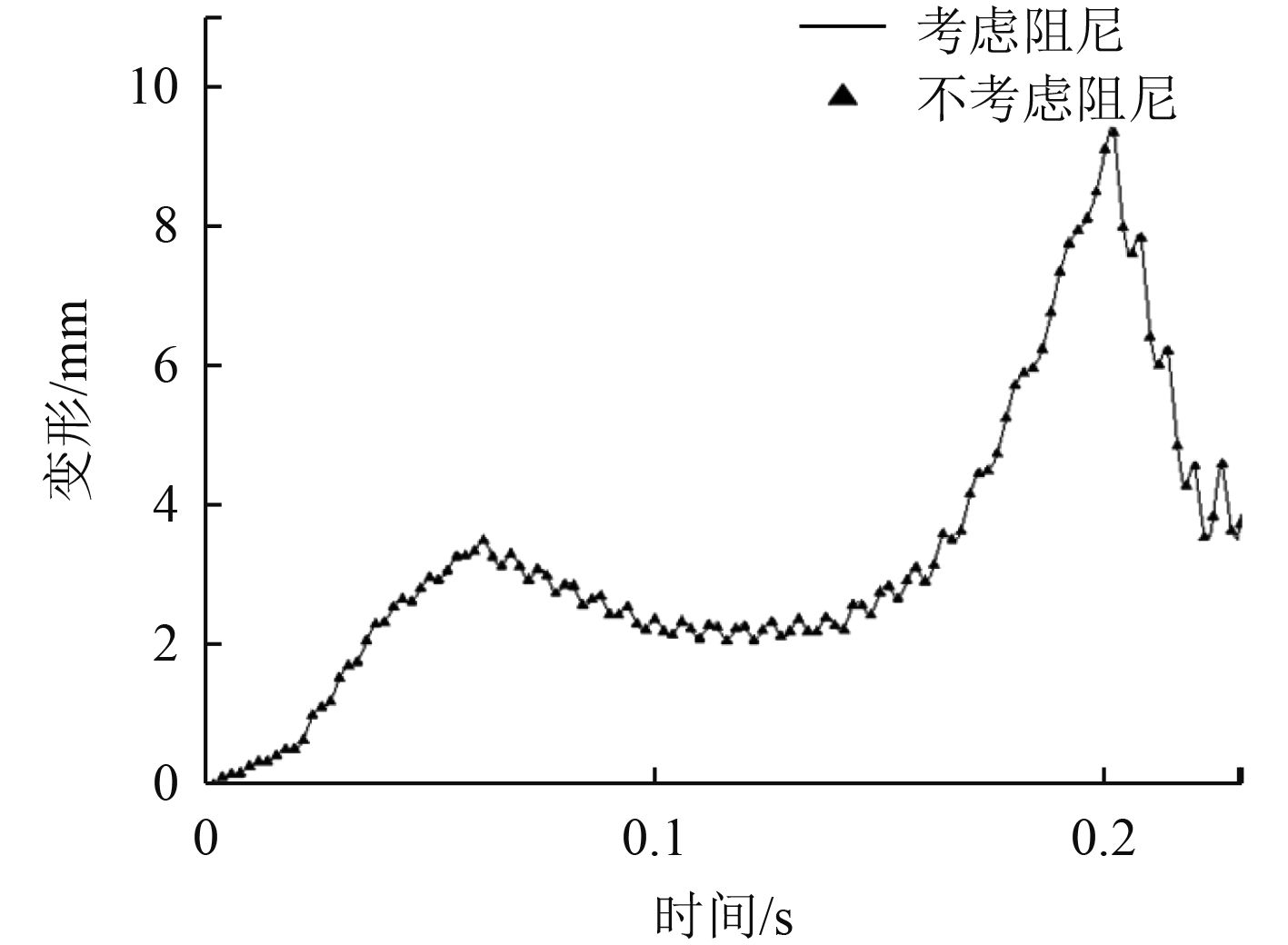
2.2 阻尼的影响对板架的面板上施加真实的砰击载荷,板架在有、无阻尼的情况下的变形情况如图4所示。
|
图 4 阻尼对板架瞬态响应的影响 Fig. 4 Influence of damping on transient response of frame |
由图4可以看出,2种情况下板架的变形基本一致,可以判断在铝合金板架的瞬态响应分析中阻尼的影响很小,计算时可以不予考虑,以简化求解过程。
2.3 应变率的影响利用得到的5083铝合金和6082铝合金对应的Cowper-Symonds参数,对比分析在有、无应变率效应下结构的瞬态响应,板架的变形情况如图5所示。

|
图 5 应变率对板架瞬态响应的影响 Fig. 5 Effect of strain rate on transient response of plate |
由图5可以看出,在真实载荷作用下,不考虑应变率时铝合金板架的最大变形为9.4 mm,考虑应变率时铝合金板架的最大变形为9.2 mm,减小了2.12%,应变率效应不明显,可以不计入应变率对铝合金板架瞬态响应的影响。
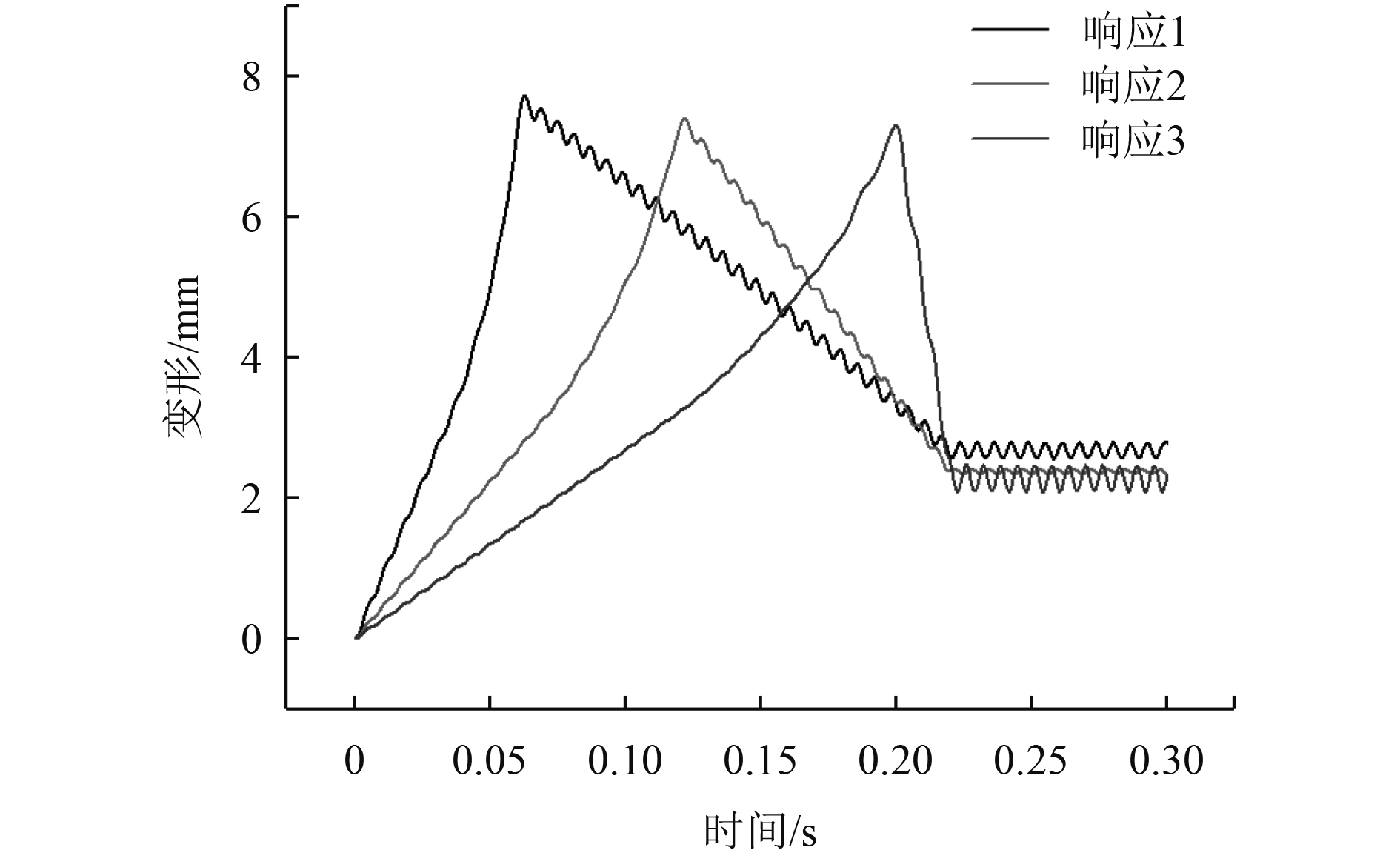
3 铝合金板架的砰击响应规律 3.1 载荷峰值出现时间对结构响应的影响将试验得到的砰击载荷简化为Ochi等提出的三角形载荷[13],载荷值从0到峰值又回到0,保持三角形载荷与真实载荷的作用时间相同及冲量相等,对比分析板架在不同载荷形式下的瞬态动力响应。三角形载荷如图6所示,载荷峰值为0.078,峰值出现时间分别取0.06 s,0.12 s和0.20 s,仿真计算结果如图7所示。

|
图 6 真实载荷与三角形载荷 Fig. 6 Actual load and triangle load |
|
图 7 不同载荷作用下结构响应 Fig. 7 Response of structures under different loads |
可以看出,变形曲线与载荷曲线同步,载荷1作用下板架最大变形为7.83 mm,永久变形为2.68 mm;载荷2作用下板架的最大变形为7.49 mm,永久变形为2.36 mm;载荷3作用下板架最大变形为7.36 mm,永久变形为2.27 mm。可以看出载荷在越短的时间内达到最大值,即峰值出现时间越早,板架的最大变形越大,永久变形也越大。
3.2 连续载荷作用下的结构响应在船舶实际航行中,会受到连续砰击的作用,因此有必要分析在连续砰击载荷作用下的结构响应,将图1中的砰击载荷连续施加到板架上,加载次数为
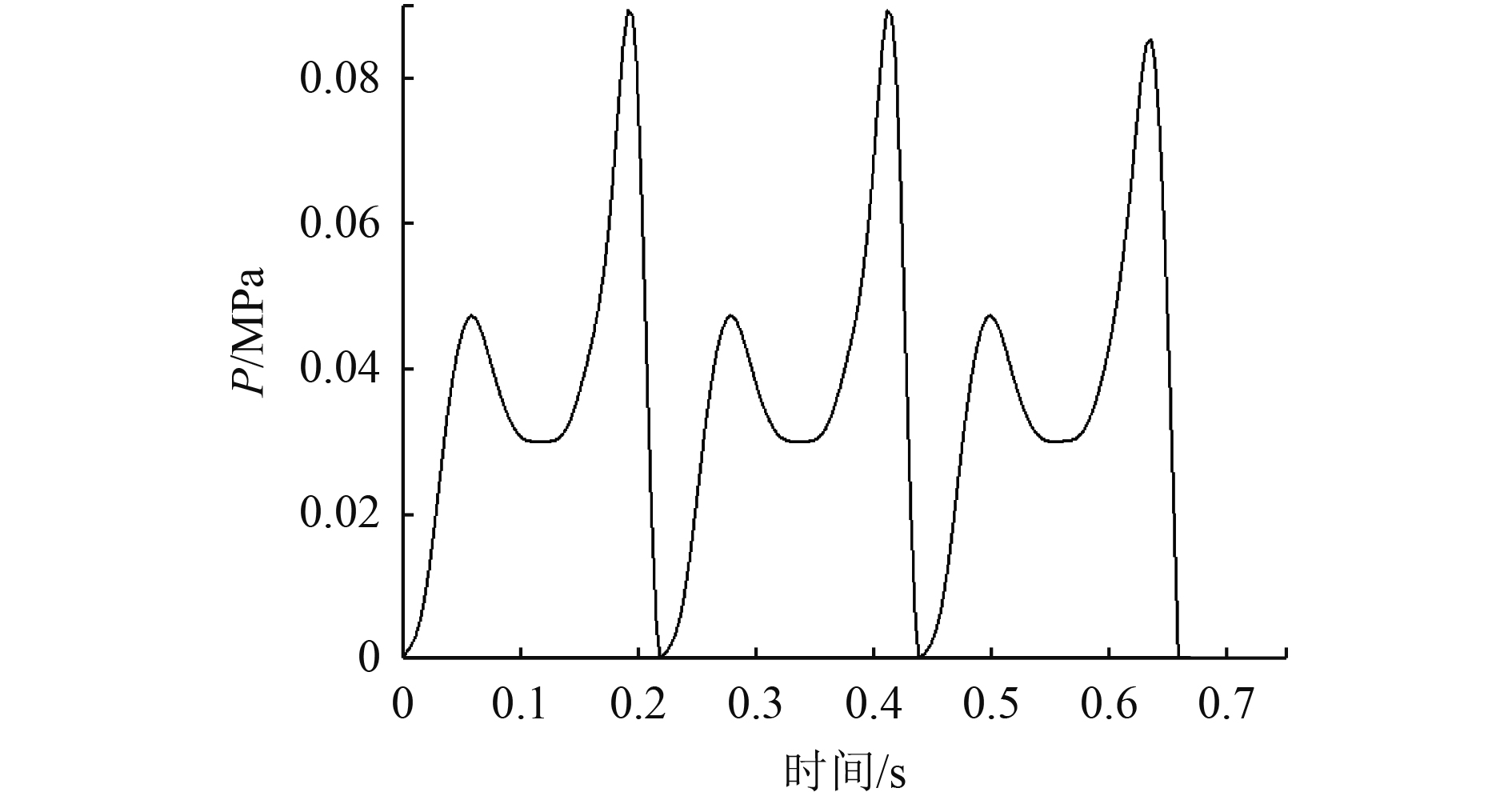
|
图 8 三次连续砰击载荷 Fig. 8 Three consecutive Slamming Loads |
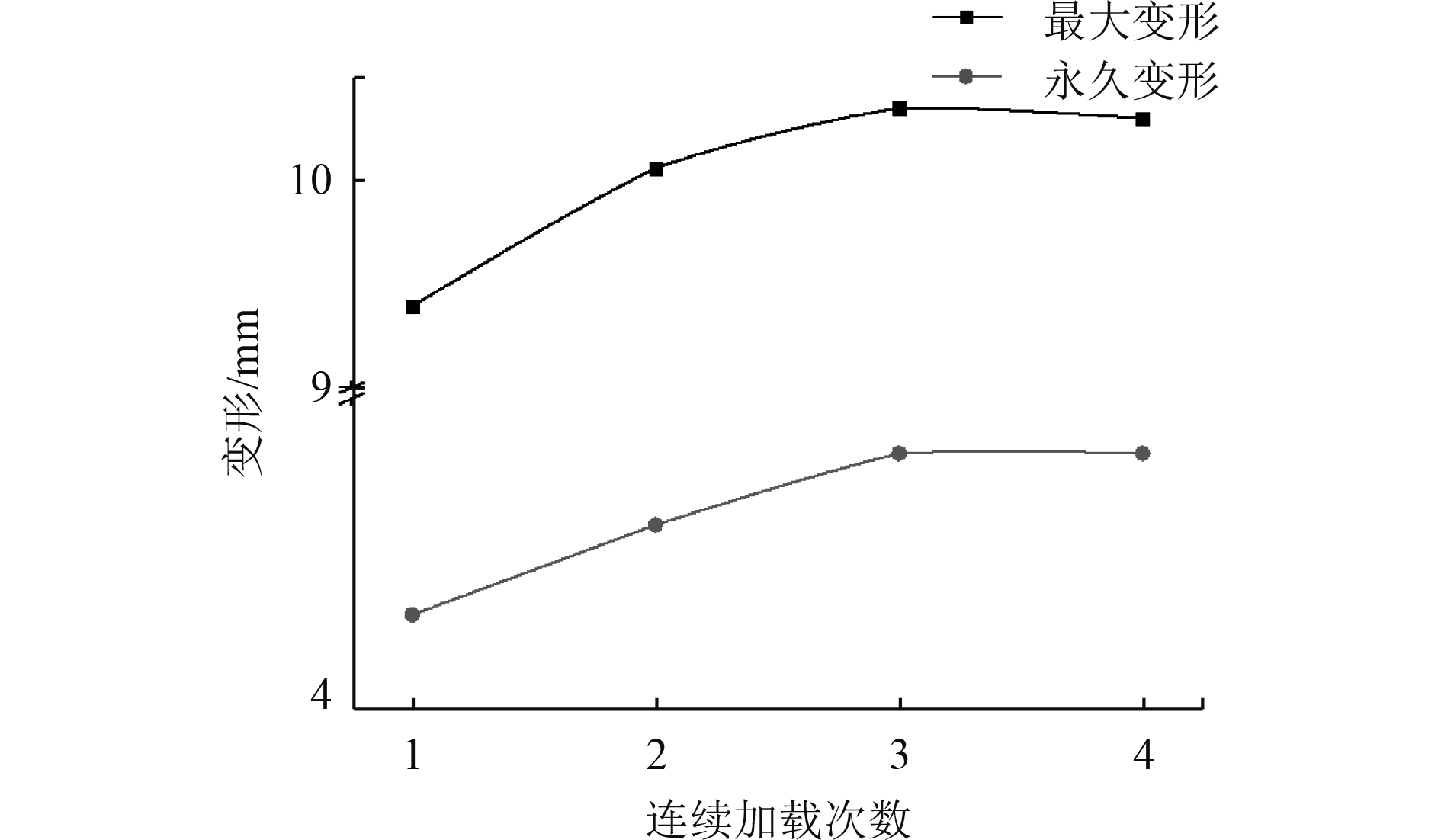
|
图 9 变形与加载次数曲线 Fig. 9 Deformation and loading times curve |
|
|
表 2 连续加载下结构响应 Tab.2 Response of structures under continuous loading |
由图9和表2可以看出,板架的最大变形和永久变形随着加载连续加载次数的增加而增大,与只加载一次相比,当连续加载3次时,板架最大变形值增大10.22%,永久变形值增大12.09%,可以看出,加载次数对板架结构瞬态响应影响较大;加载次数大于3时,变形值趋于稳定,因此在对铝合金结构进行砰击强度计算时,需要计算前3次砰击载荷下结构的响应。
4 结 语本文分析了铝合金艇板架的砰击瞬态响应,比较了阻尼和应变率在仿真计算过程中的影响,分析了板架在不同砰击载荷作用下的响应规律,得到以下结论:
1)在对铝合金板架进行瞬态响应分析时,可以不考虑应阻尼和应变率效应。
2)在峰值出现时间越早三角形载荷作用下的板架发生的最大变形越大,永久变形也越大。
3)连续砰击作用下板架的最大变形会增大,永久变形也会增大,在船舶航行时,应避免连续砰击的发生,以减少砰击对结构造成的损伤。
4)板架的在第3次砰击后变形趋于稳定,在对船体进行砰击强度计算时,需要对前3次砰击下的结构响应进行分析。
| [1] |
高宁, 朱志武. 5083铝合金宽应变率实验与基于损伤的本构模型研究[J]. 高压物理学报, 2017(1): 51-60. |
| [2] |
MARCINB C, STANISZEWSKI. Simulation of tri-axially braided composites half-cylinder behavior during balistic impact[J]. Anesthesiology, 2007, 94(5): 790-792.2007. |
| [3] |
夏齐强, 陈志坚. 波浪载荷与砰击载荷联合作用下SWATH船结构动态响应[J]. 上海交通大学学报, 2012(3): 352-357. DOI:10.3969/j.issn.1674-8115.2012.03.025 |
| [4] |
邹勇, 张佳宁, 郑镜华, 等. 砰击载荷对大型铝合金船舶结构强度的影响[J]. 大连海事大学学报, 2014(1): 45-48. DOI:10.3969/j.issn.1006-7736.2014.01.012 |
| [5] |
ROBERT K GOLDBERG, BRINA J BLINZLER, WIESLAW K. BINIENDA.. Modification of a macromechanical finite element–based model for impact analysis of triaxially braided composites[J]. Journal of Aerospace Engineering, 2012, 25(3): 383-394. DOI:10.1061/(ASCE)AS.1943-5525.0000135 |
| [6] |
王誉瑾, 钱宏亮, 范峰. 结构用铝合金6082-T6材料本构关系及力学参数试验研究[J]. 工程力学, 2013(S1): 309-313+319. |
| [7] |
张世联, 王能扬, 肖熙. 砰击载荷作用下板结构动力响应的参数分析[J]. 上海交通大学学报, 2001(4): 562-564. DOI:10.3321/j.issn:1006-2467.2001.04.019 |
| [8] |
杨旭东, 张世联. 有限元分析结构瞬态响应中的结构阻尼问题[J]. 中国海洋平台, 2004(2): 32-36. |
| [9] |
张云峰. 6082-T6铝合金材料力学性能研究[J]. 科技创新与应用, 2016(33): 5-6. |
| [10] |
任慧龙, 翟帅帅, 于鹏垚, 等. 砰击载荷作用下船艏结构瞬态响应研究[J]. 中国舰船研究, 2013(6): 14-19. |
| [11] |
戴仰山, 沈进威, 宋竞正.船舶波浪载荷[M].北京: 国防工业出版社, 2007.
|
| [12] |
祝伟, 刘敬喜. 爆炸冲击载荷下加筋板塑性动力响应分析[J]. 船海工程, 2011(6): 28-30. DOI:10.3963/j.issn.1671-7953.2011.06.008 |
| [13] |
OCHI M.K, MOTTER L.E. Prediction of slamming characteristics and hull responses for ship design[J]. Transactions SNAME, 1973, 81: 144-177. |
 2019, Vol. 41
2019, Vol. 41
