2. 国家水运安全工程技术研究中心可靠性工程研究所,湖北 武汉 430063
2. Reliability Engineering Institute, National Engineering Research Center for Water Transport Safety (WTS), Wuhan 430063, China
当今AUV的应用越来越广泛,涉及军事应用、地质勘探、考古等多个领域。其中推进系统是AUV的重要组成部分,它不仅与AUV的快速性和机动性有关,还关系到AUV的续航力[1]。如今螺旋桨推进仍然是AUV主流的推进形式,其中对转螺旋桨(Counter-Rotating Propellers)属于组合推进器中的一种,它不仅具有较高的效率,而且前后两桨的扭矩可以相互抵消,具有较高的稳定性,因此将对转螺旋桨应用在AUV上具有一定的实际意义[2 – 3]。
对转螺旋桨的前后两桨同轴且转向相反,其两桨的流场存在很大的相互干扰。本文基于CFD方法对AUV的对转螺旋桨进行水动力计算,分别运用SolidWorks和Ansys ICEM进行建模和网格划分,并分析计算结果,得到最佳湍流模型。运用最佳湍流模型来计算,对对转桨的最佳配合参数展开研究,并分析其尾流的变化规律。
1 螺旋桨基本参数本文的计算模型为MAU型4叶螺旋桨,其主要参数如表1所示。对转桨由2个MAU型单桨组成,其基本配合参数包括桨距比L/D(两桨0.7 R处的轴向距离与螺旋桨直径的比值,L表示两桨0.7 R处的轴向距离,R表示螺旋桨半径,D表示直径)和直径比Da/Df(后桨直径与前桨直径的比值,Da为后桨直径,Df为前桨直径),L/D和Da/Df的变化对对转桨的性能有重要影响。
|
|
表 1 MAU螺旋桨基本参数 Tab.1 Basic propeller parameters |
数值模拟的是螺旋桨在一定来流速度的水中匀速旋转,在轴向上没有位移,把流体看作不可压的,则流场的连续性方程和动量方程[4]为:
| $ \frac{{\partial {u_i}}}{{\partial {x_i}}} = 0{\text{,}} $ | (1) |
| $ \rho \frac{{\partial \left( {{u_i}{u_j}} \right)}}{{\partial {x_j}}} = - \frac{{\partial P}}{{\partial {x_j}}} + \rho {g_i} + \rho \frac{\partial }{{\partial {x_j}}} \cdot \left[ {\mu \left( {\frac{{\partial {u_i}}}{{\partial x}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right) - \overline {{{u'}_i}{{u'}_j}} } \right]{\text{。}} $ | (2) |
式中:
| $\begin{split} \frac{{\partial \rho k}}{{\partial t}} + \frac{{\partial \rho ku}}{{\partial x}} + \frac{{\partial \rho kv}}{{\partial y}} + \frac{{\partial \rho kw}}{{\partial z}} = \frac{\partial }{{\partial x}}\left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _k}}}} \right)\frac{{\partial k}}{{\partial x}}} \right] +\\ \frac{\partial }{{\partial y}}\left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _k}}}} \right)\frac{{\partial k}}{{\partial y}}} \right] + \frac{\partial }{{\partial z}}\left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _k}}}} \right)\frac{{\partial k}}{{\partial z}}} \right] + {P_k} - \rho {\beta ^ * }k\omega \hfill{\text{,}} \end{split} $ | (3) |
| $\begin{split} \frac{{\partial \rho \omega }}{{\partial t}} + \frac{{\partial \rho \omega u}}{{\partial x}} + \frac{{\partial \rho \omega v}}{{\partial y}} + \frac{{\partial \rho \omega w}}{{\partial z}} = \frac{\partial }{{\partial x}}\left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _\omega }}}} \right)\frac{{\partial \omega }}{{\partial x}}} \right] + \\ \!\! \frac{\partial }{{\partial y}}\left[ {\left( {\mu \!+\! \!\frac{{{\mu _t}}}{{{\sigma _\omega }}}} \right)\frac{{\partial \omega }}{{\partial y}}} \right]\! +\! \!\frac{\partial }{{\partial z}}\left[ {\left( {\mu\! +\! \!\frac{{{\mu _t}}}{{{\sigma _\omega }}}} \right)\frac{{\partial \omega }}{{\partial z}}} \right] \!+ \!\!\alpha \frac{\omega }{k}{P_k} - \beta \rho {\omega ^2}{\text{。}}\\ \end{split} $ | (4) |
其中湍流动能生成项Pk为:
| $\begin{split}{P_k} = {\mu _t}{S^2},S = \sqrt {\sum\limits_i {\sum\limits_j {{S_{ij}}{S_{ij}}} } } ,{S_{ij}} = \\ \frac{1}{2}\left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right){\text{。}}\end{split}$ | (5) |
计算中各参数可取为:
根据1957 ITTC标准公式[6],得到对转桨的计算公式如式(6)~式(8):
| $ {\text{前桨}}\left\{ \begin{gathered} J = \frac{{{V_A}}}{{n{D_f}}},{K_{Tf}} = \frac{{{T_f}}}{{\rho {n^2}{D_f}^4}}{\text{,}} \hfill \\ {K_{Qf}} = \frac{{{Q_f}}}{{\rho {n^2}{D_f}^5}},{\eta _f} = \frac{{{K_{Tf}}}}{{{K_{Qf}}}} \cdot \frac{J}{{2{\text{π}}}} \hfill {\text{。}}\\ \end{gathered} \right. $ | (6) |
| $ {\text{后桨}}\left\{ \begin{gathered} {K_T}_a = \frac{{{T_a}}}{{\rho {n^2}{D_f}^4}},{K_Q}_a = \frac{{{Q_a}}}{{\rho {n^2}{D_f}^5}}{\text{,}} \hfill \\ {\eta _f} = \frac{{{K_T}_a}}{{{K_Q}_a}} \cdot \frac{J}{{2{\text{π}}}}{\text{。}} \hfill \\ \end{gathered} \right. $ | (7) |
| $ {\text{对转桨}}\left\{ \begin{gathered} T = \left| {{T_f}} \right| + \left| {{T_a}} \right|,Q = \left| {{Q_f}} \right| + \left| {{Q_a}} \right|{\text{,}} \hfill \\ \eta = \frac{{{K_T}}}{{{K_Q}}} \cdot \frac{J}{{2{\text{π}} }}{\text{,}} \hfill \\ {K_T} = {K_{Tf}} + {K_{Ta}},{K_Q} = {K_{Qf}} + {K_{Qa}}{\text{。}} \hfill \\ \end{gathered} \right. $ | (8) |
基于MAU型螺旋桨的二维型值点坐标,利用Excel函数将其转化为三维空间坐标,导入到Solidworks中生成桨叶曲线,依次通过填充曲面、放样、缝合等命令生成桨叶曲面,然后通过圆周阵列来生成其他桨叶[7]。最后根据毂径比绘制桨毂,得到完整的螺旋桨,如图1所示。

|
图 1 MAU型螺旋桨 Fig. 1 The MAU propeller |
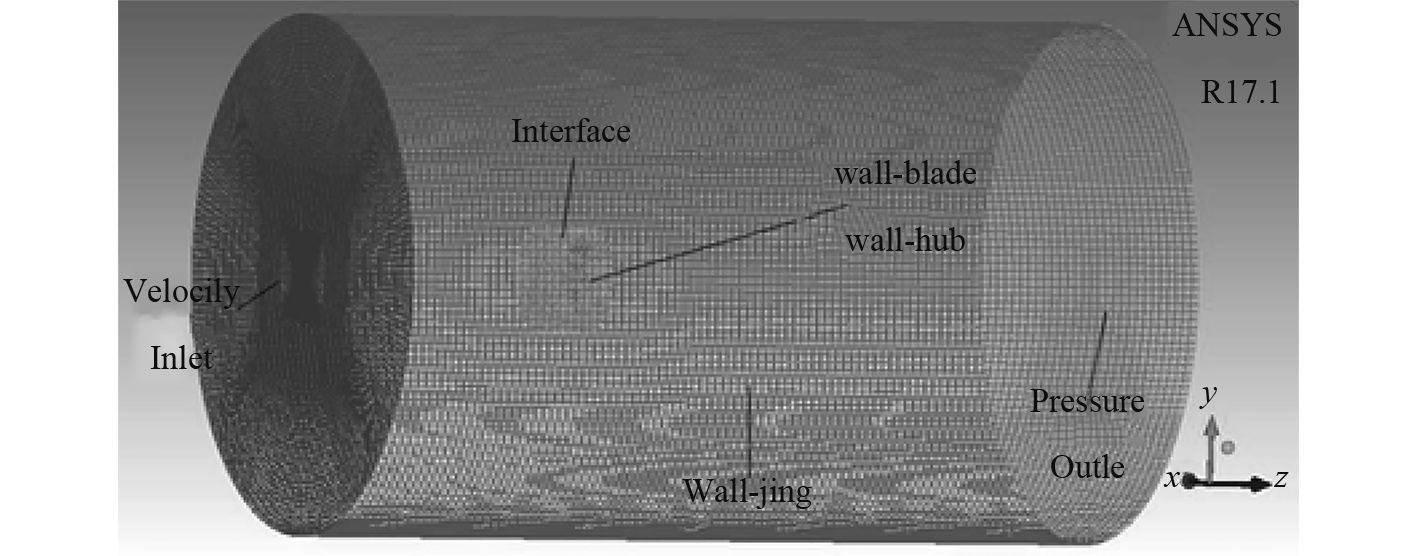
本文选取的计算域为圆柱体,计算域模型在建模软件SolidWorks中完成,分为静止域和旋转域两部分[8 – 9]。静止域直径为6D,长度为10D,旋转域直径为1.2D,长度为D。利用ICEM进行网格划分,首先对静止域和旋转域单独划分网格,然后进行网格合并。静止域的几何形状为规则的圆柱形,故采用结构网格划分;旋转域的内壁面为螺旋桨的表面,曲率较大且几何形状较为复杂,只能采用非结构网格划分,对叶梢等尺寸较小的部分进行网格加密;然后利用ICEM中的merge命令将两者合并[10],得到总体网格及边界命名如图2所示。
|
图 2 网格划分及计算域设置情况 Fig. 2 Grid division and computing domain Settings |
为了得到最佳湍流模型,选择Standard
|
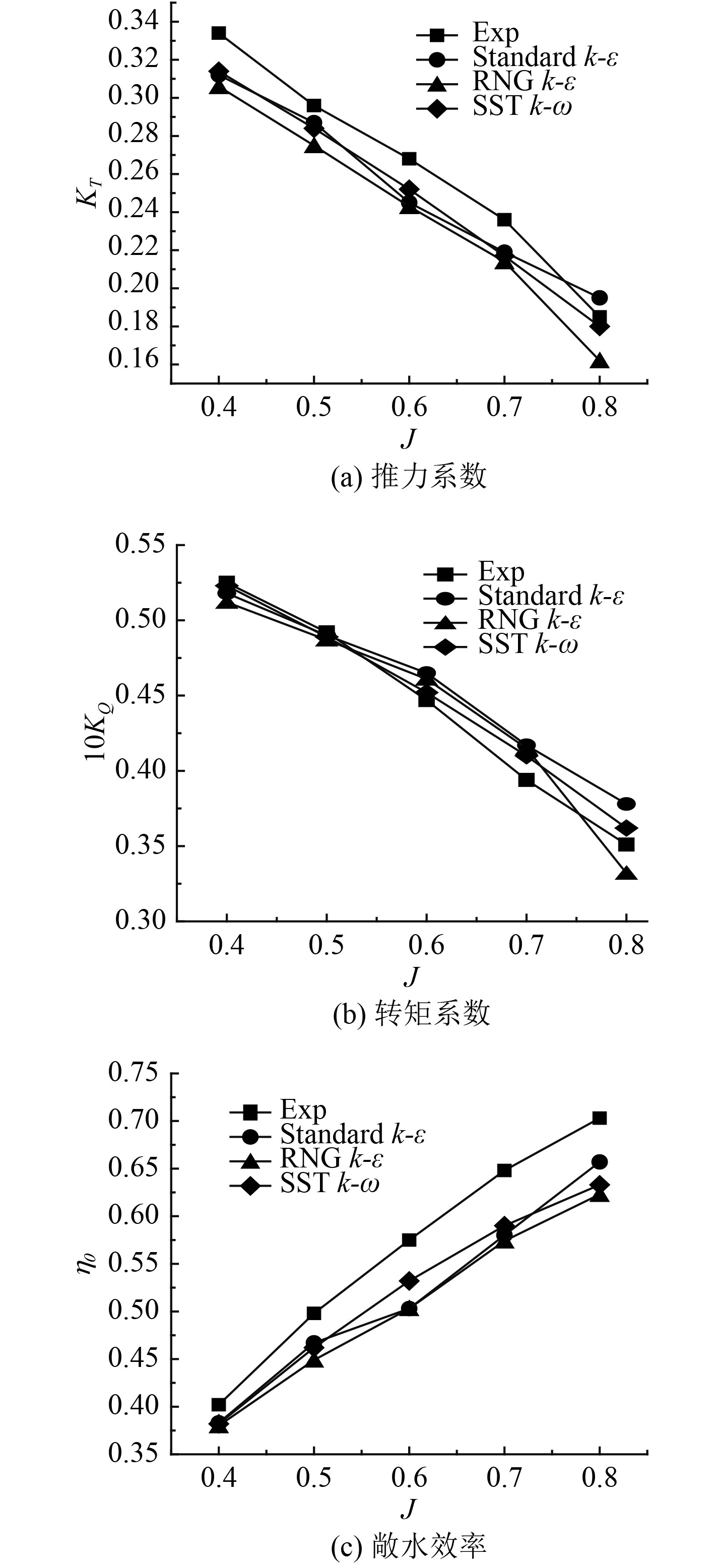
图 3 不同湍流模型计算的敞水特性曲线 Fig. 3 Open water characteristic curves calculated by different turbulence models |
通过分析可以看出:对于推力系数KT,Standard
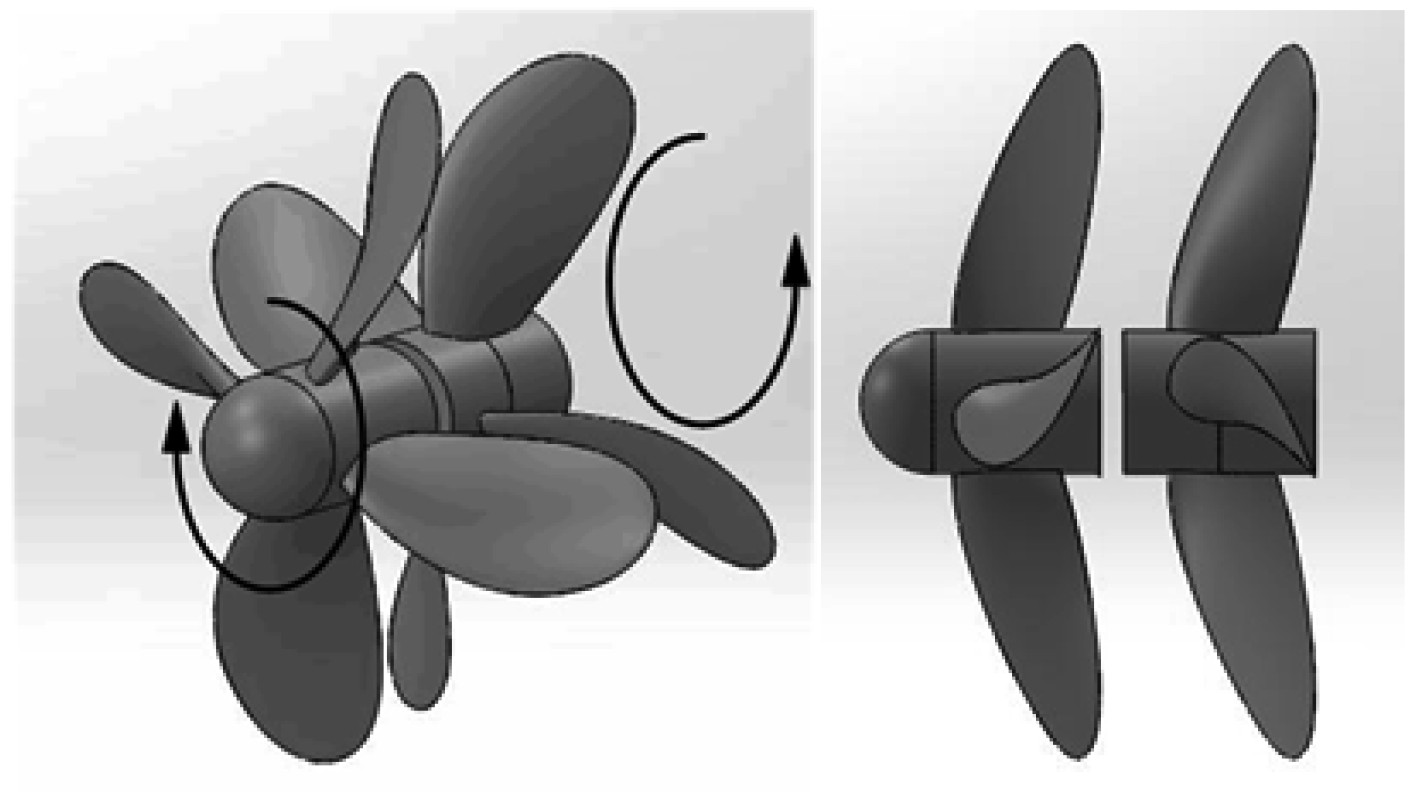
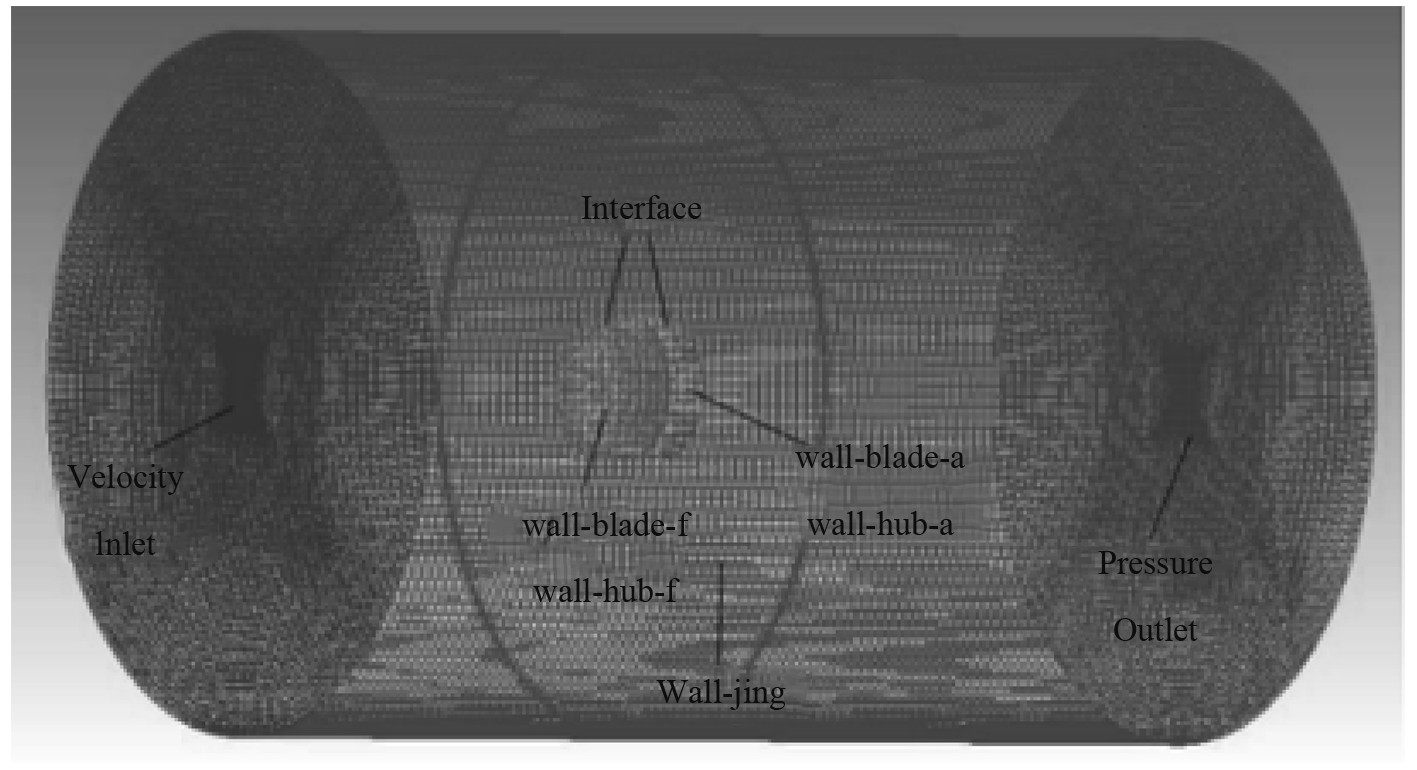
本节主要探讨对转桨主要配合参数L/D和Da/Df的变化对对转桨的性能的影响,通过改变参数建立不同的对转桨模型,并进行仿真计算,得到最优结果。关于建模和网格划分与单桨基本相同,不同之处在于对转桨的前后2个桨单独建立旋转域。通过建模得到的对转桨模型如图4所示,网格划分情况如图5所示。
|
图 4 对转桨模型 Fig. 4 The counter-rotating propeller model |
|
图 5 网格划分情况 Fig. 5 Computational domain meshing |
在计算桨距比L/D时,先取两桨的直径Da=Df,对于Da/Df的最优值将在下一步中研究。为了确定最优桨距比,分别取L/D=0.233,0.267,0.283,0.300,0.333,对应不同的模型a,b,c,d,e。将计算结果表示为敞水性能曲线,如图6所示。
从图6可以看出,KT,KQ随着L的增加而增大,且逐渐趋于一个稳定值,可以推测当L足够大时,两桨就成为独立的单桨,其KT,KQ也不再变化。敞水效率
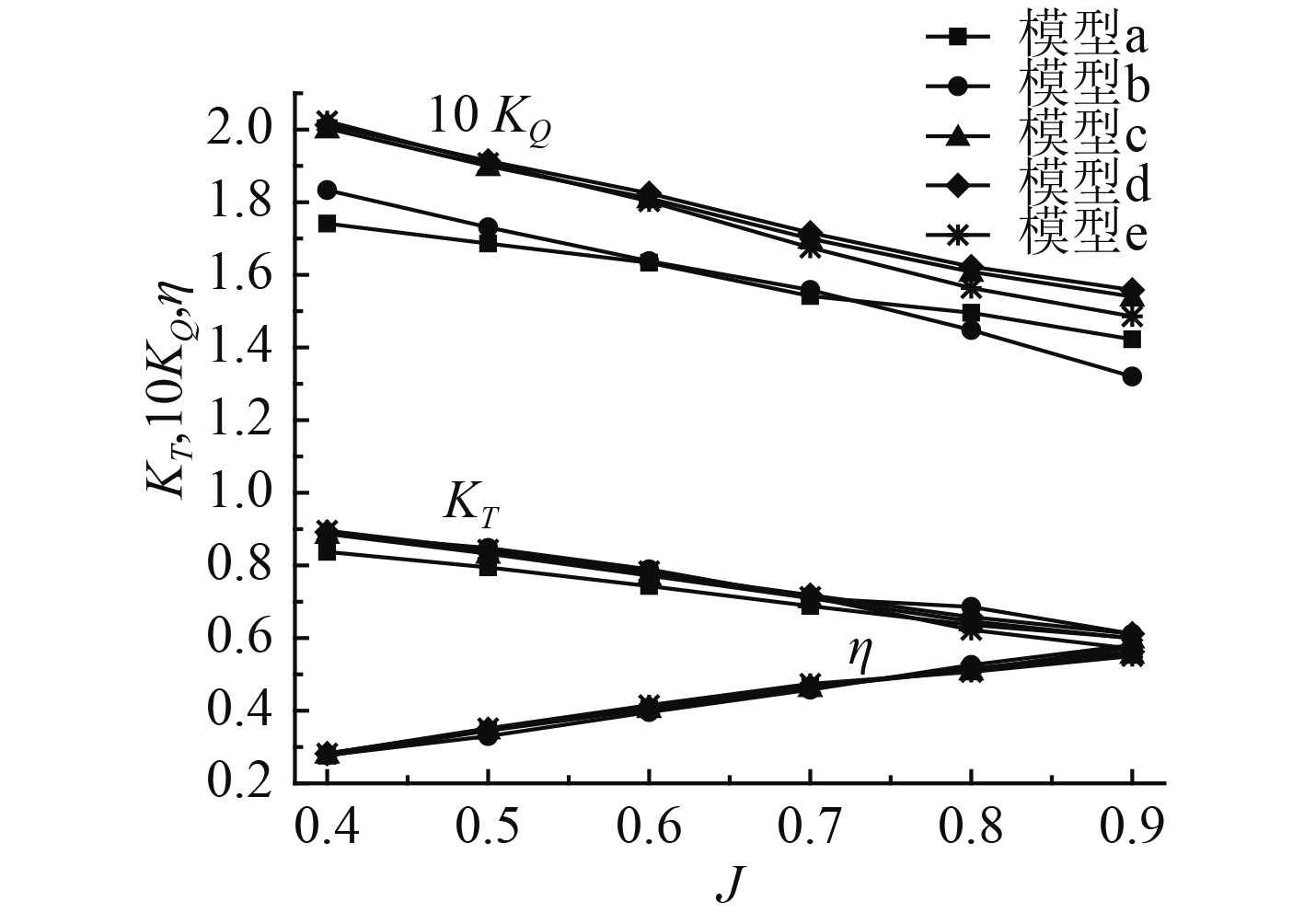
|
图 6 不同桨距比下对转桨敞水性能曲线 Fig. 6 The open water performance curves of counter-rotatong propellers under different L/D |
采用控制变量法,选取不同的直径比作为变量,桨距比选择上一节中确定的最佳值,即取L/D=0.267。建立4组模型a,b,c,d,分别对应Da/Df=1.00,0.98,0.94,0.90。将计算结果绘制为敞水性能曲线,如图7所示。
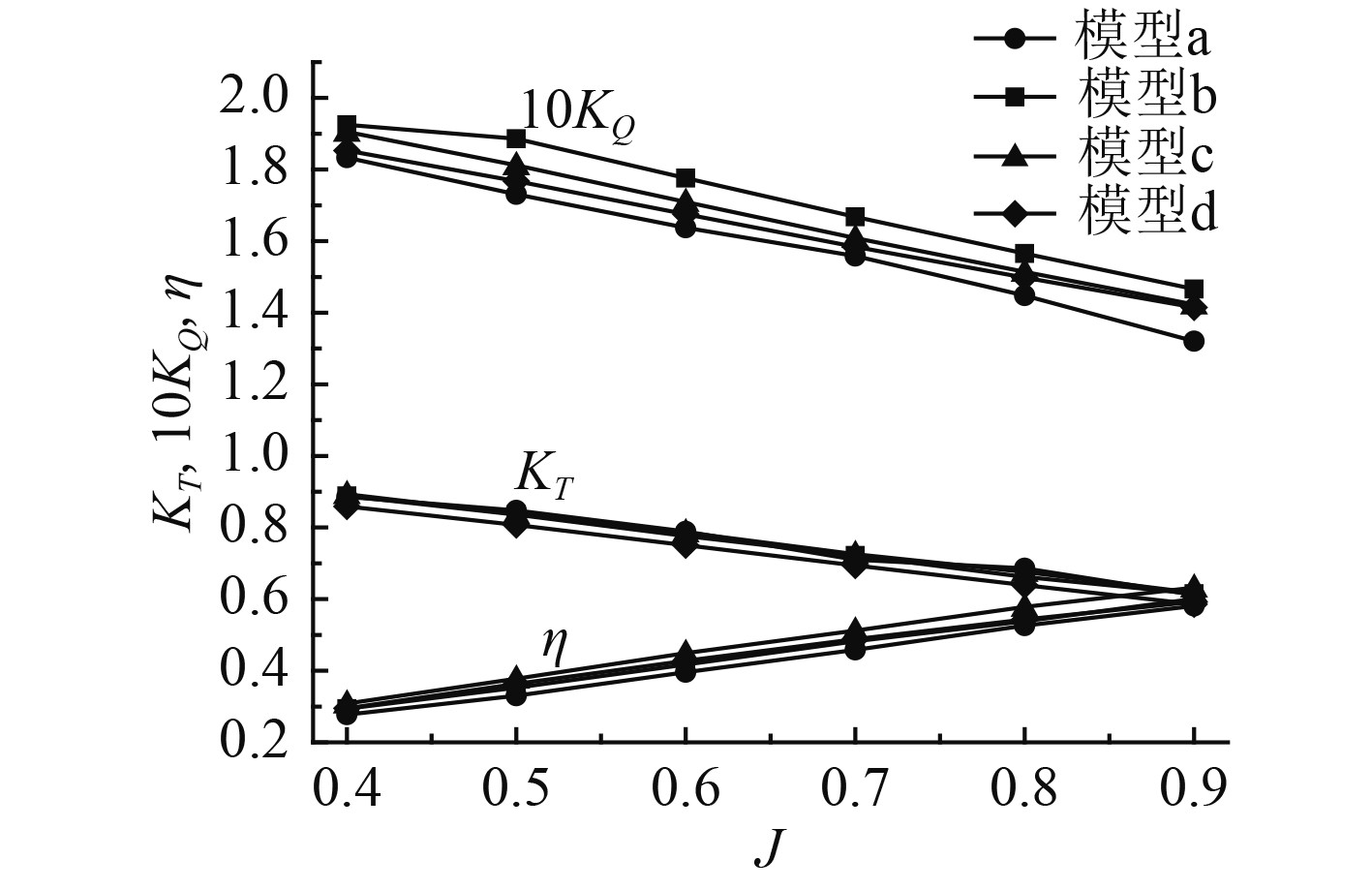
|
图 7 不同直径比下的对转桨敞水曲线 Fig. 7 The open water performance curves of counter-rotating propellers under different diameter ratio |
可以看出,KT,KQ,
为了直观地反映对转桨前后桨之间的相互影响,利用后处理软件进行处理,做出了进速系数为0.6时各模型的流线图,如图8所示。

|
图 8 对转桨尾流线图(J=0.6) Fig. 8 The wake flow of counter-rotating propellers |
可以看出,模型a和模型b由于后桨直径较大,前桨的尾流线直径大于后桨,尾流发散比较严重,后桨吸收的效果不太好;对于模型c,前桨产生的尾流线直径与后桨比较接近,刚好把后桨充分包裹在内,前桨的尾流存在比较明显的收缩,这说明后桨对前桨的尾流吸收较好,效率较高,两者配合产生的水动力性能较好;对于模型d,可以看出其后桨的直径小于前桨的尾流直径,因此对前桨的吸收效率没有模型c高,结合上一节中分析的结果,选择最优直径比Da/Df=0.94。
4.4 对转桨与等效单桨性能对比对转桨有很多优点,其中最重要的一点就是与工况相同的单桨相比具有较高的效率。为了比较单桨和对转桨的效率,可以选择在相同的进速下比较,但是这样没有考虑螺旋桨的收到功率,也就是说在相同的进速下,两者的螺旋桨收到功率不同,这样得到的效率没有参考意义。这里选择转速n和螺旋桨收到功率P为定值,为了便于比较,引入功率系数Bp,在相同的Bp下比较两者的效率[11]。Bp表达式为:
| ${B_p} = \frac{{{P_D}^{0.5}n}}{{{V_A}^{2.5}}} = 33.30\frac{{{K_Q}^{0.5}}}{{{J^{2.5}}}}{\text{。}}$ | (9) |
关于单桨的选择,理论上应该选与对转桨等效的单桨,由参考文献知,在前后桨螺距相同的时,只需单桨的伸张轮廓面积与对转桨相同即可,即
|
|
表 2 等效单桨主要参数 Tab.2 The main parameters of the equivalent single propeller. |
|
|
表 3 对转桨主要参数(模型c) Tab.3 The main parameters of counter-rotating propeller |
经过三维建模、网格划分和仿真计算,得到等效单桨的各水动力参数。结合对转桨的计算结果,可作出对转桨和等效单桨的Bp-
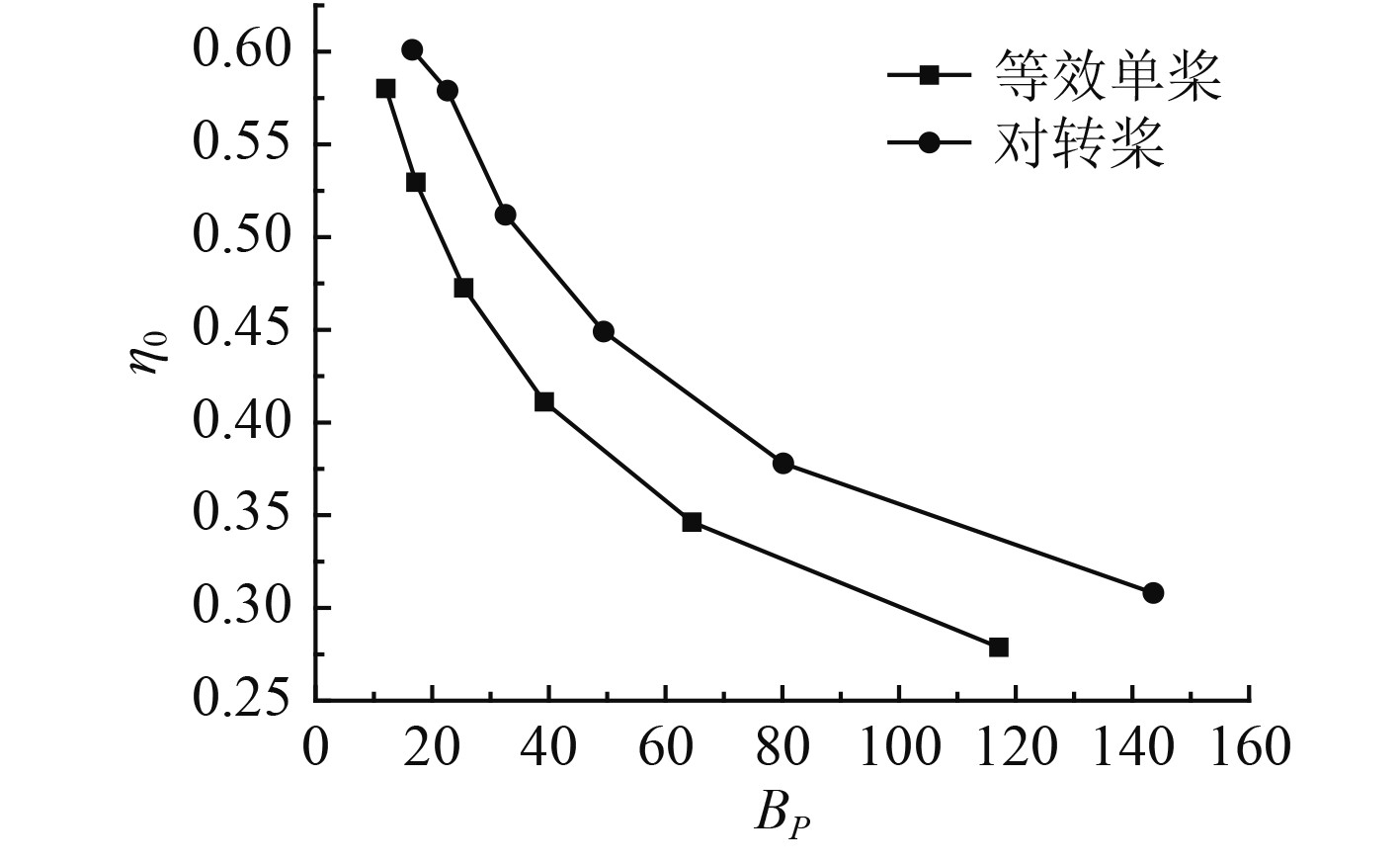
|
图 9
对转桨和单桨的
|
|
|
表 4 对转桨和单桨效率对比 Tab.4 Efficiency comparison of the counter-rotating propellers and the single propeller |
由表4中数据可以看出,对转桨的效率比单桨的效率有较大的提高,最大时提升了9.307%,可以证明在相同的功率系数下,对转桨的效率比单桨更高。而CFD计算的结果存在5%的误差,因此理想状态下对转桨的效率提升可能会更高。
5 结 语通过对MAU型螺旋桨和对转桨的水动力性能研究,得到如下结论:
1)基于RANS方程,计算得到螺旋桨的敞水性能,并与图谱试验值对比发现,Standard
2)通过CFD仿真计算,得到对转桨的最佳配合参数,L/D=0.267,Da/Df=0.94。尾流分析的结果也支持了得到的最佳桨距比和直径比的结果。
3)将对转桨和等效单桨的敞水性能在相同的功率系数下作对比,发现对转桨的效率比单桨最大提高9.307%,从而证明了对转桨的优越性。
| [1] |
孙承亮, 赵江滨. AUV动力电池技术的应用现状及展望[J]. 船舶工程, 2017(7): 65-70. |
| [2] |
常煜, 洪方文, 张志荣, 等. 对转桨水动力性能的数值分析[C]//船舶水动力学学术会议暨中国船舶学术界进入ittc30周年纪念会. 2008.
|
| [3] |
HAYATI A N, HASHEMI S M, SHAMS M. A study on the behind-hull performance of marine propellers astern autonomous underwater vehicles at diverse angles of attack[J]. Ocean Engineering, 2013, 59(1): 152-163. |
| [4] |
LAUNDER B E, SPALDING D B. Lectures in mathematical models of turbulence[J]. Von Karman Institute for Fluid Dynamics, 1972. |
| [5] |
董世汤. 船舶推进器水动力学[M]. 北京: 国防工业出版社, 2009.
|
| [6] |
GHASSEMI H, TAHERINASAB M. Numerical calculations of the hydrodynamic performance of the counter-rotating propeller (CRP) for high speed vehicle[J]. Polish Maritime Research, 2013, 20(2): 13-20. DOI:10.2478/pomr-2013-0012 |
| [7] |
申毅莉. 船用螺旋桨桨叶建模分析研究[J]. 组合机床与自动化加工技术, 2013(4): 113-117. DOI:10.3969/j.issn.1001-2265.2013.04.030 |
| [8] |
薛侠峰, 严天宏, 何波. MAU型螺旋桨建模与水动力性能分析[J]. 船舶工程, 2016(1): 38-42. |
| [9] |
安邦, 朱汉华, 范世东, 等. 基于流固耦合的螺旋桨性能分析及参数优化[J]. 舰船科学技术, 2017, 39(15): 41-46. |
| [10] |
王福军. 计算流体动力学分析:CFD软件原理与应用[M]. 北京: 清华大学出版社, 2004.
|
| [11] |
余欣. 基于CFD方法的串列螺旋桨水动力性能研究[D]. 大连: 大连理工大学, 2014.
|
 2019, Vol. 41
2019, Vol. 41
