船舶在恶劣海况中航行时,由于剧烈的摇荡运动,会与波浪产生猛烈的砰击现象。在砰击瞬时,船体底部受到巨大的冲击力,船体垂向加速度会突然改变,并且紧接着出现高频振动。严重的砰击,一方面使冲击区域承受巨大的压力,局部结构可能会发生破坏;另一方面将引起整个船体剧烈的颤振,产生较大的弯矩,当与低频波浪弯矩叠加,可能导致船舶总纵强度的丧失。
自Von-Karman[1]和Wagner[2]对物体入水砰击进行研究以来,该问题越来越引起人们的关注,各国学者对此进行了大量的试验和理论研究。Faltinsen[3]采用正交异性板理论建立加筋板的弯曲微分方程,加筋板在X方向的变形取一阶振动模态,在Y方向的变形取前二阶振动模态;采用广义Wagner方法,并考虑物体入水时加筋板的振动变形对速度势及砰击压力的影响,采用Galerkin法建立加筋板Y方向的前2阶振动的主坐标微分方程,最终得到加筋板的结构响应。实船试验验证了该方法的合理性,研究结果表明楔形体入水角越小、入水速度越大,入水过程中物体的弹性变形对结构响应的影响也就越大,结构变形相较准静态计算结果也就越小。I.Stenius[4]对楔形体入水问题开展了研究,研究了物体弹性、边界条件、入水速度、入水角对砰击载荷的影响。研究发现,当入水速度增大到一定程度时,楔形体固支无纵向约束比固支有纵向约束的变形大;入水角越小,水弹性影响越明显;由于水弹性的影响,2种楔形体的砰击载荷分布有较大差异。在冲击过程中,楔形体会发生变形,影响入水速度及入水角的变化,从而使得砰击载荷发生变化,变化的砰击载荷反过来影响楔形体的变形,冲击过程是流体与结构的相互影响过程。Hermundstad[5] 和Torgeir Moan等采用非线性切片理论计算船体相对运动,将计算得到的船波相对垂向和横摇速度作为输入,计算船体受到的砰击载荷,并对船模在波浪中的砰击现象进行了试验研究。考虑非线性影响,垂荡、纵摇及船体与波浪之间相对运动的理论计算与试验结果吻合很好。砰击压力对于航速、横摇角及浪向角都非常敏感,在计算外飘砰击压力时,一定要考虑横摇运动。研究发现,船体向前运动时,在船的首部会产生水堆效应,这会大大增加砰击压力的量值,对计算的砰击压力进行三维效应的修正之后,所计算得到的砰击压力与试验值吻合得较好。Daniele Dessi[6]对1艘高速渡轮的砰击问题进行试验研究,研究发现,与Ochi的假设不同,砰击的发生并非相互独立的,而是有相关性的。砰击现象往往以集群的方式出现,且在该时间段内,砰击发生的周期接近船体纵摇运动的周期。因此,该种情况下,砰击引起的船体结构响应可能更具有威胁,前一次砰击引起的船体振动还没结束,下一次砰击开始发生,前后2次砰击引起的船体振动可能会叠加在一起。Hanbing Luo[6]对V形楔加筋板的入水问题开展了试验研究,测量了V形楔入水过程中的加速度、砰击压力与结构响应;用匹配渐进法计算了V形楔为刚体时入水冲击的运动及砰击压力,将该砰击压力施加在有限元模型上,计算了V形楔的结构响应。
本文对船首的砰击压力进行研究,采用“两步走”的方法,首先计算船体在波浪中的运动,得到砰击瞬时船体与波浪之间的相对速度;接着计算该相对速度条件下船体受到的砰击压力;将压力施加在船体结构上,计算在砰击压力作用下船体结构的响应,对船体结构设计提供支持。
1 砰击载荷根据国内外的大量研究,一致认为砰击压力与船体入水的速度平方呈正比,即
| $ p = k{v^2}{\text{。}} $ | (1) |
求砰击载荷可以转化为求解砰击系数和砰击瞬时船体与波浪之间的相对速度。本文采用两步走的方法,分别求出砰击压力系数和砰击瞬时船舶与波浪之间的相对速度,根据式(1)便可得到砰击载荷。
1.1 砰击系数的确定随着计算机技术的发展,CFD技术也取得了长足进步,可以采用大型软件模拟具有复杂型线的物体入水砰击问题。本文基于Fluent计算船体入水砰击压力系数,选取需要计算的船体剖面,在Gambit中建立有限元模型,在有限元模型中,测量点附近采用细网格,离测量点较远区域采用稀疏网格。流体域上表面定义为PRESSURE_OUTLET,其余各表面定义为刚性墙WALL,利用Fluent中提供的宏命令DEFINE_CG_MOTION, 定义船体入水速度。因为船体砰击压力与物体入水速度的平方成正比,砰击压力系数几乎不随入水速度的变化而变化,故本文计算船体结构以10 m/s速度匀速进入到水中时受到的砰击压力,进而求出各个测量点的砰击压力系数。
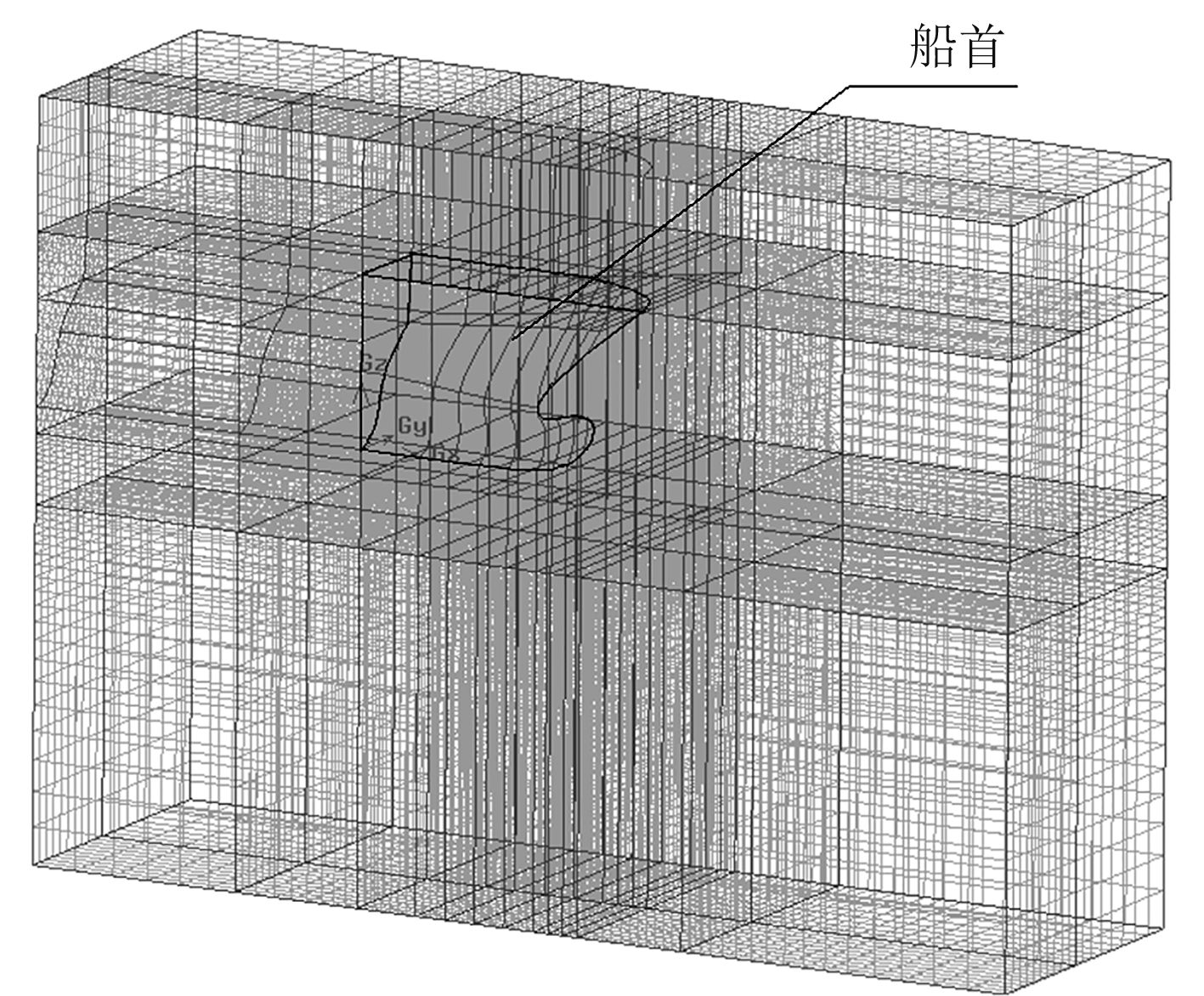
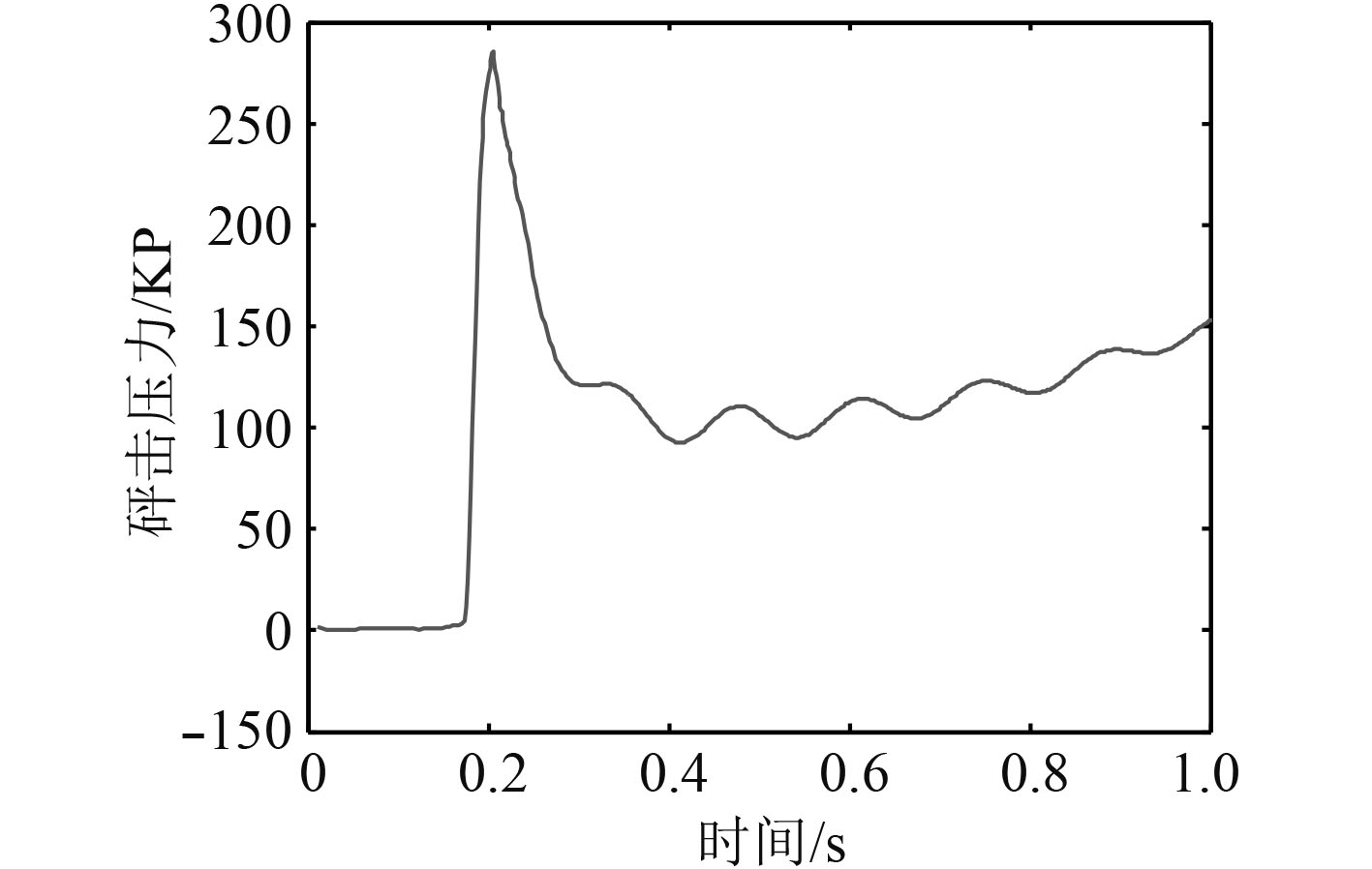
图1为船首入水模型,图2为P1点的砰击压力曲线,表1为各个计算点的坐标及砰击压力系数,由计算结果可以看出,由于P1~P4处的入水角较小,故砰击压力系数较大,其余各点的入水角较大,砰击压力系数较小。
|
图 1 船首入水模型 Fig. 1 Water entry model of bow |
|
图 2 P1砰击压力时历曲线 Fig. 2 Slamming pressure |
|
|
表 1 测点坐标及砰击压力系数 Tab.1 Slamming coefficient |
本文采用Sesam计算砰击瞬时船体与波浪之间的相对运动速度。波高为13.6 m,浪向角为180°,航速为0 kn。对船体及其流域进行三维建模,船体湿表面模型如图3所示。

|
图 3 SESAM三维计算模型(湿表面) Fig. 3 Wetted surface |
船体测量点的静吃水为d,则该点发生底部砰击的数学表达式为:
| $ \left\{ {\begin{aligned} & {{Z_R} = d}\text{,} \\ & {{{\dot Z}_R}\text{≤} - {{\dot Z}_{R * }}} \text{。} \end{aligned}} \right. $ | (2) |
其中:
|
|
表 2 各点入水速度及砰击压力 Tab.2 Relative velocity between ship and wave and slamming pressure |
由计算结果可知,砰击瞬时,各点的相对入水速度有较大的差异。在船体纵向方向,越靠近船首的位置,相对入水速度越大;在垂向方向,入水速度呈现先增大后减小的趋势。入水速度最大值为15.81 m/s。
1.3 砰击压力时历曲线大量研究结果表明,砰击压力与入水速度的平方呈正比。本文假设同一个物体、相同姿态、不同速度入水的砰击压力时历曲线也呈正比关系,即
| $ P\left( t \right) = {P_0}\left( t \right){V^2}/V_0^2\text{。} $ | (3) |
式中:

|
图 4 砰击压力时历曲线 Fig. 4 Slamming pressure |
船体结构受到的砰击压力与船体型线有着直接的关系,研究表明,船体某点入水角越小,相同速度下所受到的砰击压力越大,入水角越大,相同速度下受到的砰击压力越小。船首区域入水角较小,所受到的砰击压力较大,砰击瞬时,对船体结构响应会产生较大的影响。从船首向后,入水角逐渐增大,所受到的砰击压力大小及砰击发生次数都逐渐减小,产生的砰击压力对船体结构的影响也逐渐减小,当入水角增大到某一程度时,其产生的砰击压力可忽略不计。
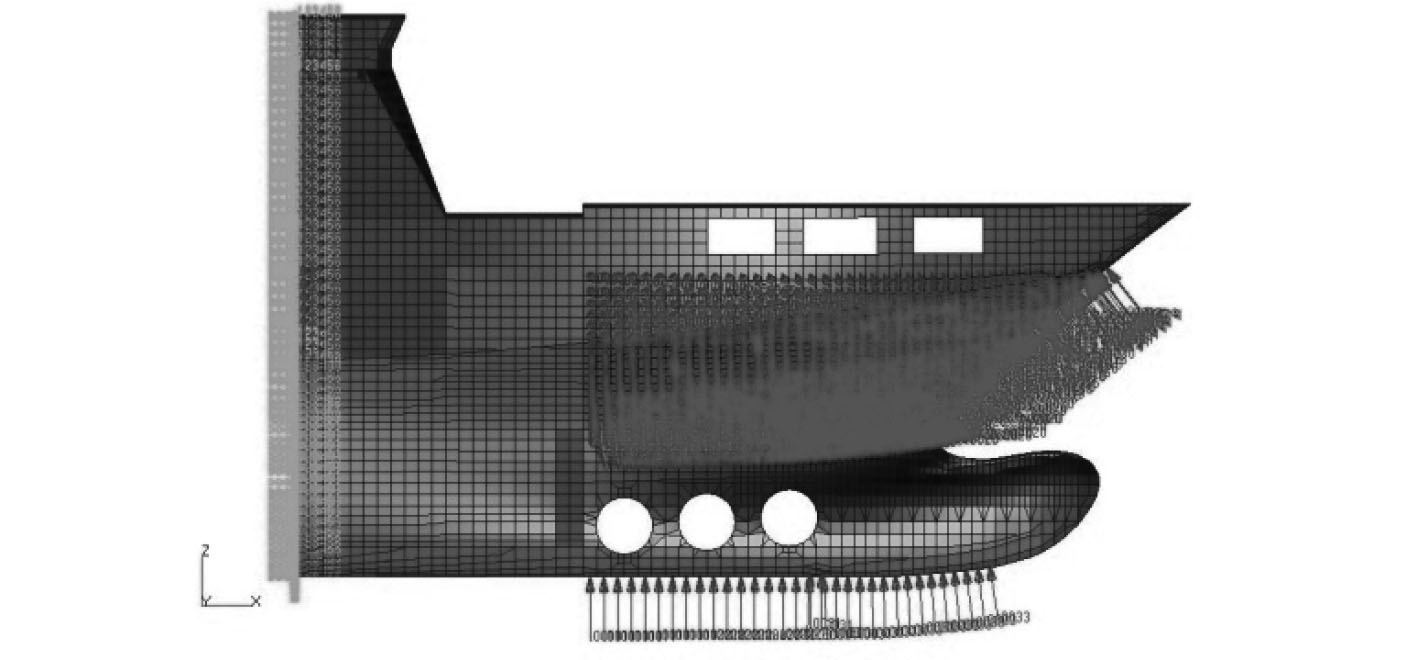
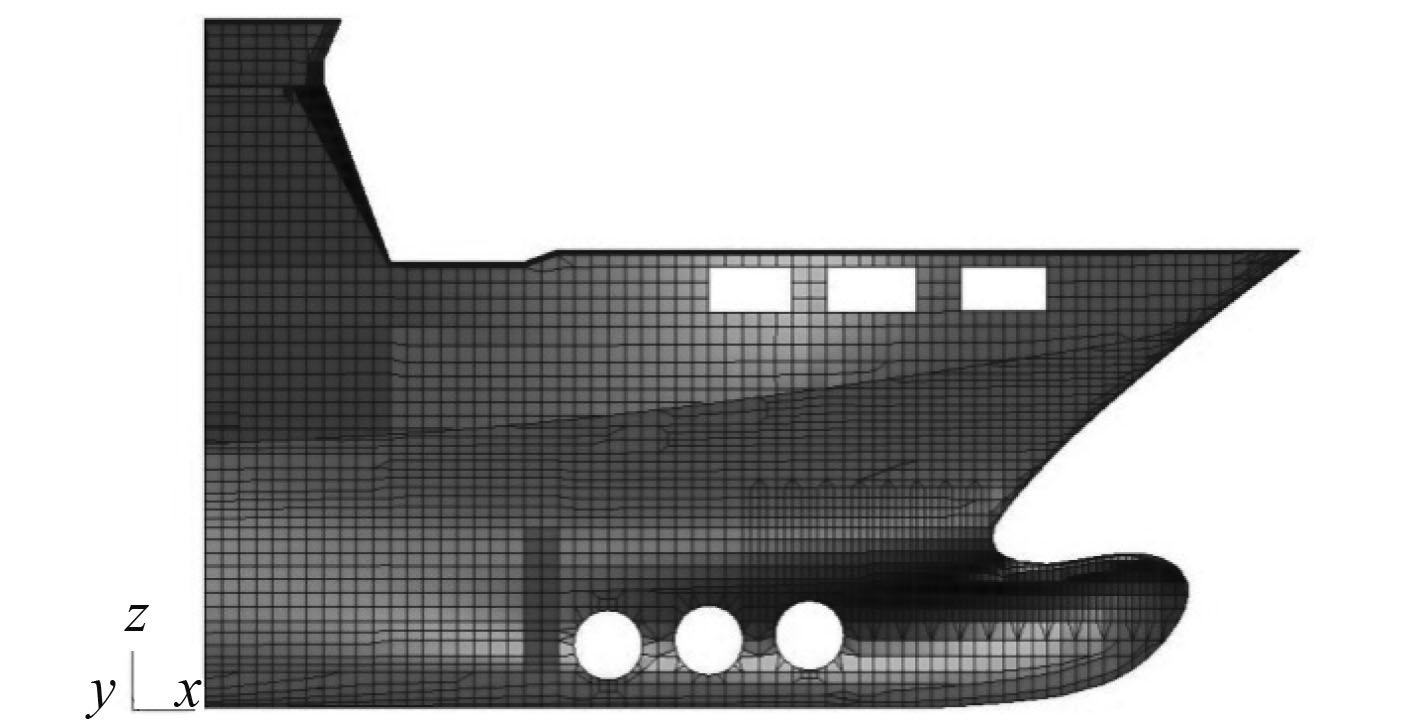
选取156#向前至船首部位建立有限元模型(见图5和图6)。参考该船的船体横剖面图,177#肋位向后的船体入水角均较大,产生的砰击压力较小,对船体结构的影响在本文中忽略不计。本文选择177#肋位向前至首部包括船首底部和水线以上的外飘较为显著部分作为砰击压力加载区。图5方框内部即为砰击压力加载区。

|
图 5 砰击压力加载区及区域划分 Fig. 5 Domain of slamming pressure |
|
图 6 船首有限元模型 Fig. 6 Finite element model of bow |
3)砰击压力加载方法
以表1中的计算砰击点为中心将船体外板砰击压力加载区划分成若干区域,在同一区域,本文假设船体外板所受到的砰击压力时历相同,即该区域中心砰击点的砰击压力时历。砰击压力时历根据式(3)得到。
4)约束条件
在船体结构有限元模型端部施加刚性约束。
2.2 船体结构响应

|
图 7 外板应力云图 Fig. 7 Stress distribution of ship hull plate |

|
图 8 03甲板以下纵舱壁应力云图 Fig. 8 Stress distribution of longitudinal bulk head under 03 deck |
由表3计算结果可以看出,砰击载荷作用下,在垂向,从03甲板到船底,结构响应逐渐减小。03甲板以下纵舱壁的结构响应最大,在177#肋位处达到了580 MPa,这主要是因为在177#肋位船体剖面出现突变,产生了应力集中,使得船体结构产生了较大的应力。
|
|
表 3 船体结构响应 Tab.3 Ship structure response |
需对177# 肋位处有突变的局部区域进行优化,本文采用平滑过渡的方法对该区域进行优化设计。按照平滑过渡段包含的肋位数的不同分为3个方案,3个方案分别为包含2个肋位、5个肋位和8个肋位,重新建立有限元模型,分别计算这3个优化方案在第5节中得到的砰击载荷作用下的结构响应。
|
图 9 有限元模型(包含2个肋位) Fig. 9 Finite element model |
|
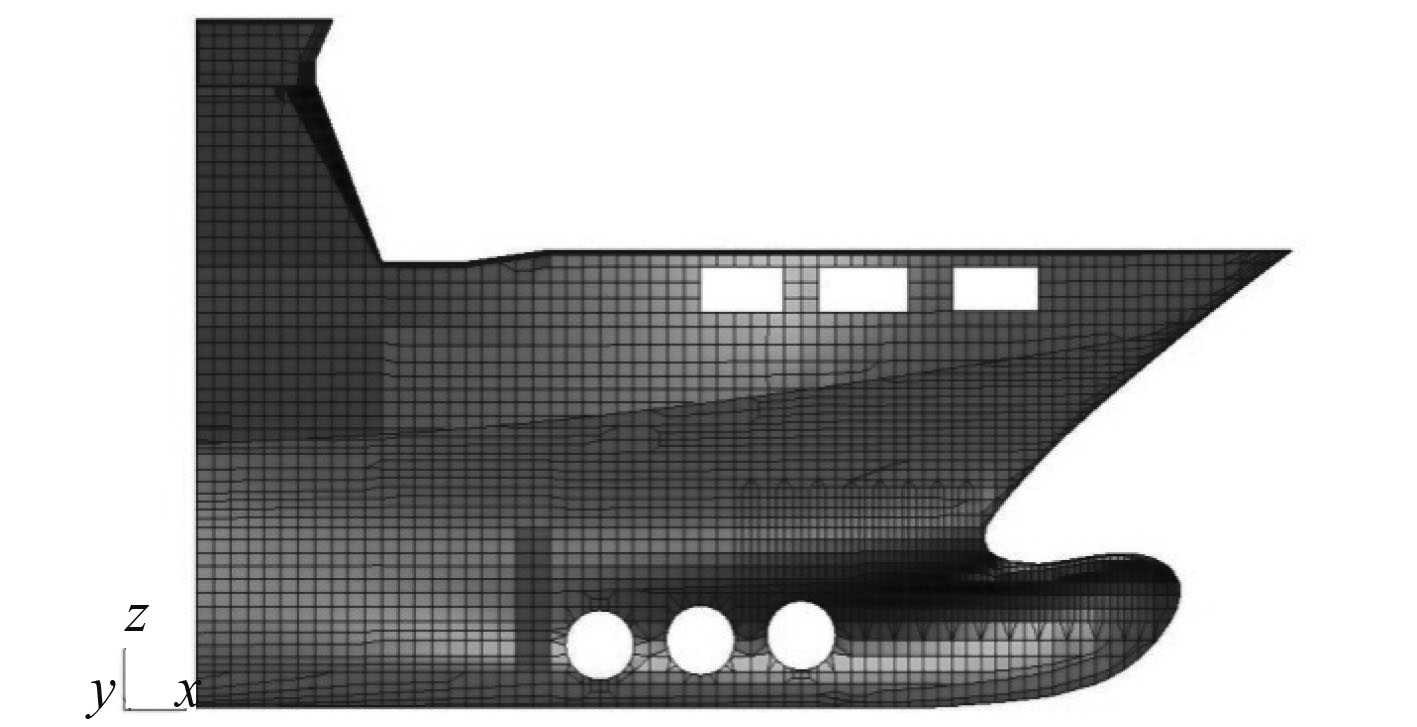
图 10 有限元模型(包含5个肋位) Fig. 10 Finite element model |
|
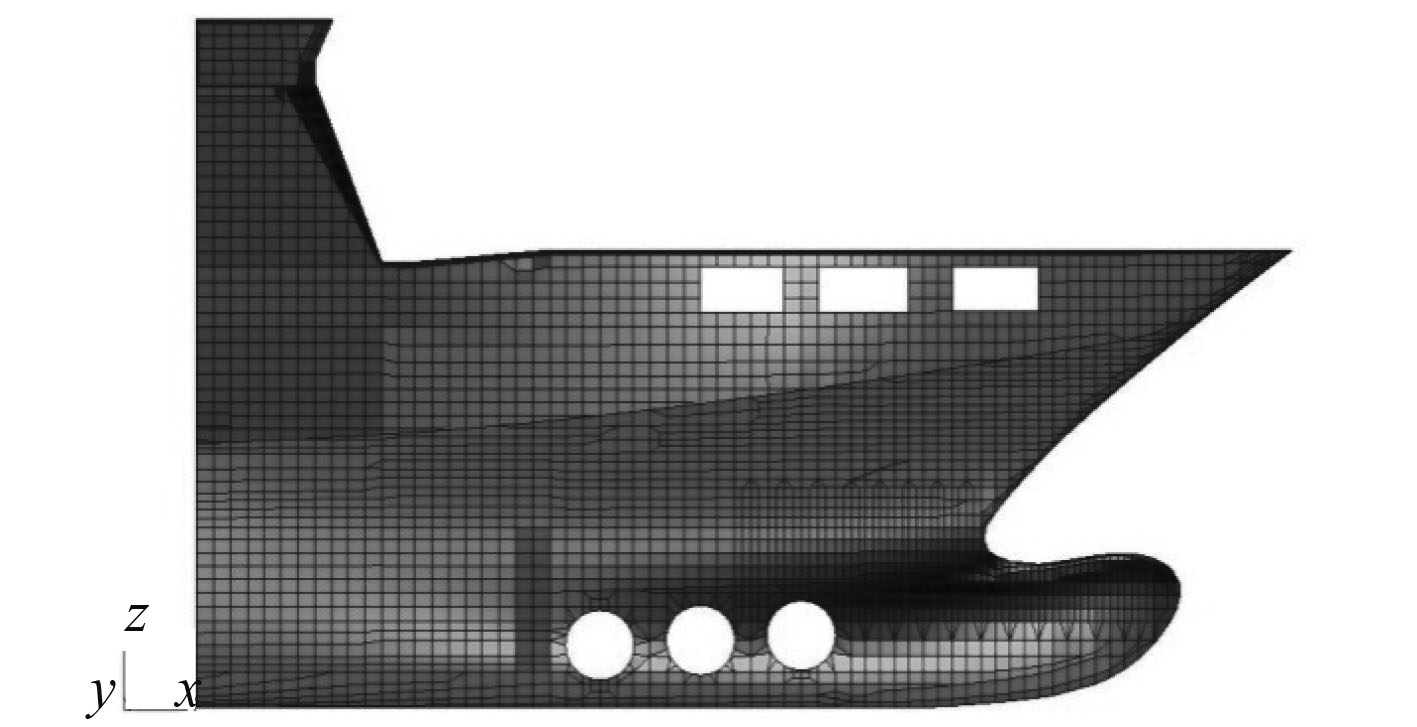
图 11 有限元模型(包含8个肋位) Fig. 11 Finite element model |
|
|
表 4 船体结构响应 Tab.4 Ship structure response |
由计算结果可以看出,随着平滑过渡段的延长,外板、01甲板、01甲板纵舱壁、01甲板纵桁、02甲板、02甲板纵舱壁、02甲板纵桁变化并不太明显,平滑过渡段的长度对这些结构的影响并不太大。
由于应力集中的作用,对于方案1,03甲板和03甲板纵舱壁、03甲板纵桁处的最大应力都较大,但随着平滑过渡段的延长,在方案2和方案3中,这些区域的结构最大应力明显降低。对于方案3,所有结构应力响应均较小。对于结构设计,本文建议采用第3种方案。
4 结 语本文采用“两步走”的方法对船首区域的砰击载荷进行研究,计算了该砰击载荷作用下船体结构强度,并对船首局部结构进行了优化设计,研究结果表明:
1)砰击瞬时,各点的相对入水速度有较大的差异。在船体纵向方向,越靠近船首的位置,相对入水速度越大;在垂向方向,入水速度呈现先增大后减小的趋势;
2)对于原始结构,在177#肋位船体剖面出现突变,因为应力集中,03甲板以下纵舱壁的结构响应较大,达到了580 MPa;
3)对船首局部结构进行优化设计,随着平滑过渡段的延长,外板、01甲板、01甲板纵舱壁、01甲板纵桁、02甲板、02甲板纵舱壁、02甲板纵桁变化并不太明显,平滑过渡段的长度对这些结构的影响并不太大;但对03甲板、03甲板纵舱壁及03甲板纵桁的影响较大,随着平滑过渡段的延长,在方案2和方案3中,这些区域的结构最大应力明显降低。对于结构设计,本文建议采用第3种方案。
| [1] |
VON KARMAN T. The impact on sea plane floats during landing[R]. Advisory Committee for Aeronatics. Techinical note No. 321, 1929: 309–313.
|
| [2] |
WAGNER H. Uber stoss-und gleitvergange an der oberflache von flussigkeiten[J]. ZAMM, 1932, 12(4): 193-235. DOI:10.1002/(ISSN)1521-4001 |
| [3] |
ODD M.. Faltinsen water entry of a wedge by hydroelastic orthotropic plate theory[J]. Journal of ship research, 1999, 43(3): 180-193. |
| [4] |
I STENIUS, A ROSEN, J.. Kuttenkeuler hydorelastic interaction in panel-water impacts of high-speed craft[J]. Ocean Engineer, 2011, 38: 371-381. DOI:10.1016/j.oceaneng.2010.11.010 |
| [5] |
Ole Andreas Hermundstad, Torgeir Moan. Numerical and experimental analysis of bow flare slamming on a Ro-Ro vessel in regular oblique waves[J]. Journal of Marine Science and Technology, 2005, 10: 105-122. DOI:10.1007/s00773-005-0192-3 |
| [6] |
DANIELE DESSI, ELENA CIAPPI. Slamming clustering on fast ships: from impact dynamics to globle response analysis[J]. Ocean Engineering, 2013, 62: 110-122. DOI:10.1016/j.oceaneng.2012.12.051 |
| [7] |
HANBING LUO, HUI WANG, C. Guedes soares numerical and experimental study of hydrodynamic impact and elastic response of one free-drop wedge with stiffened panels[J]. Ocean Engineering, 2012, 40: 1-14. DOI:10.1016/j.oceaneng.2011.11.004 |
 2019, Vol. 41
2019, Vol. 41
