2. 中国船舶科学研究中心,江苏 无锡 214000
2. China Ship Science Research Center, Wuxi 214000, China
船舶在服役过程中会受到碰撞、搁浅、疲劳和结构腐蚀等因素的影响产生损伤,而裂纹是船舶结构中常见的一种损伤。根据裂纹生成的原因及裂纹的大小,可以将裂纹分为微观裂纹和宏观裂纹。当裂纹存在时,船舶结构的极限承载能力会降低,若此时船舶受到恶劣环境工况的作用,外部载荷超过船舶的极限承载能力时,船舶结构会发生崩溃,而产生灾难性的后果。对于裂纹一般的措施是在出现裂纹的结构处进行修补或者更换受损的局部结构,但是这种方法的成本较高,并且在船舶航行过程中修补难度较大,不易实现。因此,需要对受损后的船舶极限强度进行评估分析,实现对含裂纹结构极限承载能力的预报,从而避免事故发生。
在船舶结构强度分析中,船体甲板通常被等效为平板和加筋板组成的板格进行分析。对于含裂纹结构的强度分析,通常采用的是考虑临界应力强度因子准则的断裂力学裂纹扩展研究方法或者是基于J积分准则的研究方法[1]。为了简化计算,胡勇[2]以矩形平板为研究对象,采用材料的极限拉伸强度σb代替σs,提出具有初始裂纹的极限强度弹塑性有限元模型。王芳[3]在Paik J K等[4]提出的一种非常直观的简化公式基础上,通过有限元计算,对结果进行分析,修正了含裂纹平板在拉伸载荷作用下的极限强度简化公式。师桂杰[5]探究了裂纹对舱段结构的影响因素并将平板裂纹简化公式运用在舱段结构上。本文以典型舱段结构为研究对象,开展在扭转、弯曲荷载分别作用下的极限强度研究,提出了考虑厚度影响的含裂纹舱段结构剩余极限强度评估公式。
1 含裂纹结构剩余极限强度评估方法 1.1 含裂纹平板结构极限强度评估结构极限强度的评估方法很多,有基于屈服极限σs的极限强度评估公式,也有基于强度极限σb的极限强度评估公式。
Paik(2002)以含裂纹平板结构(见图1)为研究对象,基于屈服极限σs,提出了在拉伸载荷作用下含穿透裂纹的矩形平板的极限强度简化计算公式,认为含裂纹平板的拉伸极限载荷值等于破坏后的有效横截面积乘以材料屈服强度,即
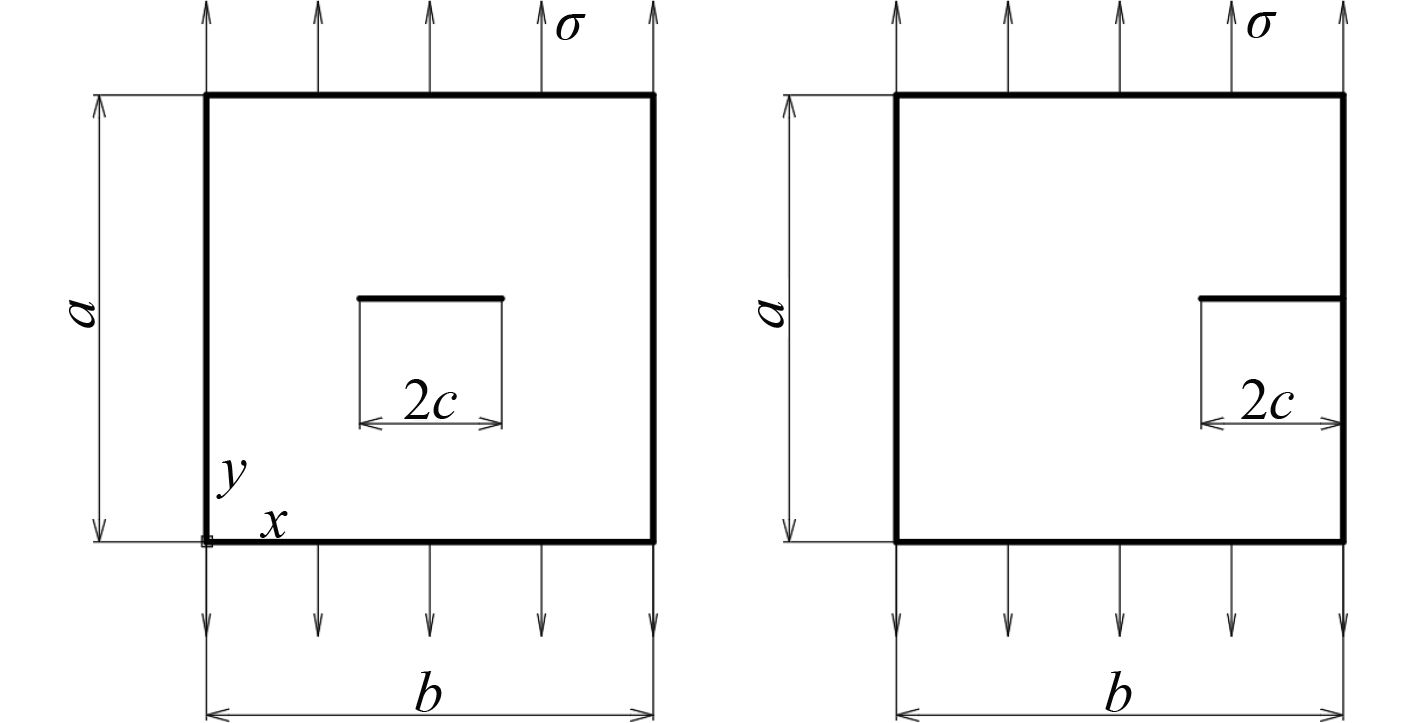
|
图 1 含裂纹的矩形平板结构 Fig. 1 Rectangular plate structure with cracks |
| $ {\sigma _u} = \frac{{{{{A}}_{\rm{c}}}}}{{{{{A}}_{\rm{0}}}}}{\sigma _s}\text{。} $ | (1) |
将Ac=(b-2c)t,A0=bt代入式(1)简化得
| $ {\sigma _u} = \left(1{\rm{ - }}\frac{{{\rm{2}}c}}{b}\right){\sigma _s}\text{。} $ | (2) |
其中:
胡勇采用材料的极限拉伸强度
| $ {\sigma _u} = \left(1{\rm{ - }}\frac{{{\rm{2c}}}}{b}\right){\sigma _b}\text{。} $ | (3) |
其中:σb为材料极限强度;σu为在拉伸载荷作用下,含中心裂纹平板结构的极限强度;c为裂纹半长;b为矩形板宽;2c/b为相对裂纹长度。
为验证含裂纹极限强度评估公式的准确性,Paik以含裂纹等厚度平板结构为研究对象,预制了不同平板厚度和不同裂纹长度的模型,开展了平板拉伸试验,获得结果如图2所示。
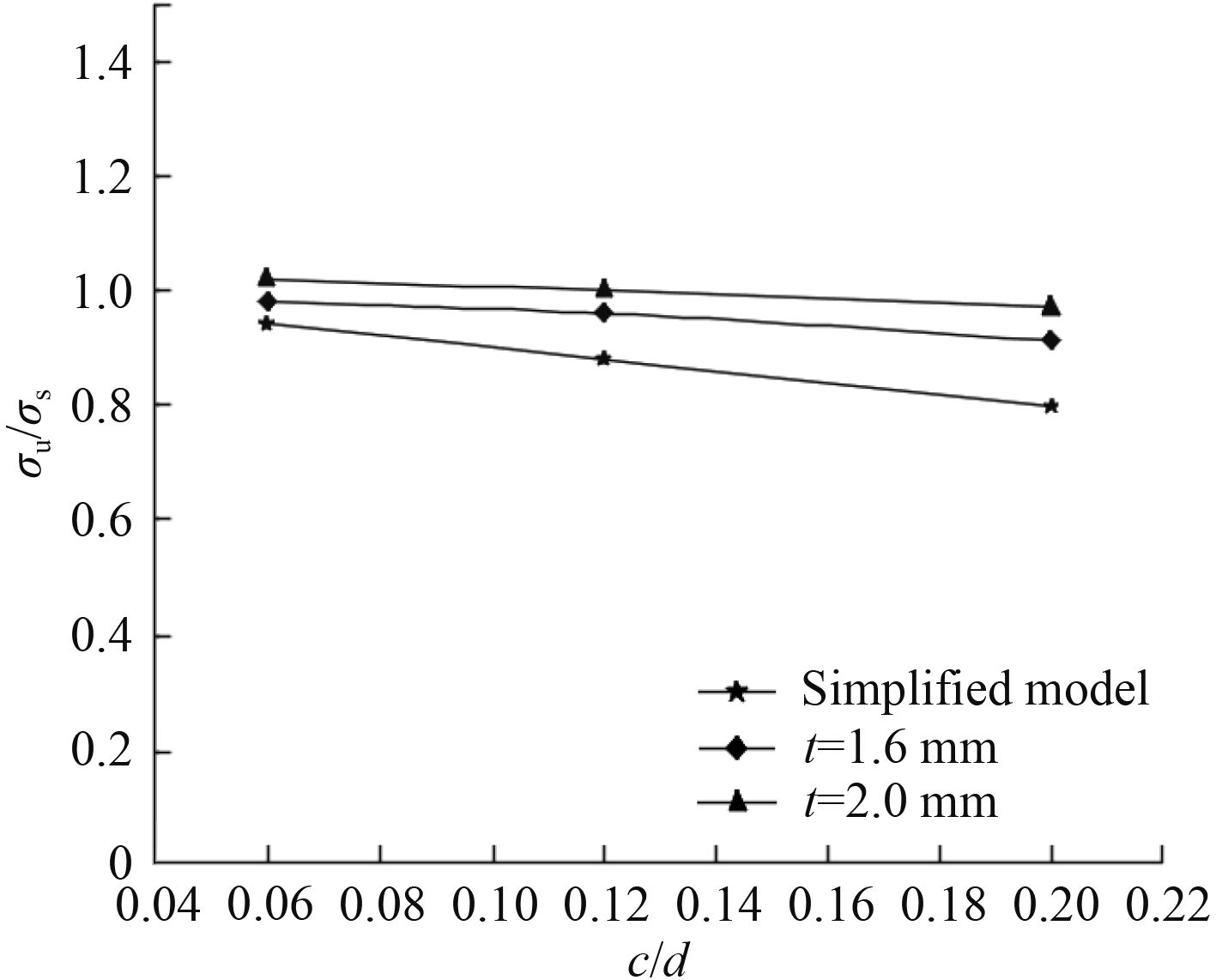
|
图 2 实验所得出的名义极限变化曲线 Fig. 2 The nominal limit change curve obtained from the experiment |
由图2可知,当板厚一定时,平板结构极限强度随着裂纹长度的增加而减小,厚度越厚,裂纹长度对结构极限强度的降低作用越显著;当裂纹长度一定时,平板结构极限强度随着板厚的增加而降低,裂纹长度越长,板厚对极限强度的降低越明显。而平板拉伸极限强度简化公式所得到的预报结果较为保守,与试验结果对比具有较大的分散性,其原因是没有考虑到厚度对裂纹结构的影响。
1.2 含裂纹损伤舱段剩余极限强度评估由于平板结构与舱段结构在结构特征上存在差异性,而实际问题中载荷状态较为复杂,而基于净截面屈服理论所提出的简化公式不再适用于含裂纹舱段结构的极限强度预测。
王芳等在研究舱段结构剩余极限强度时,在Paik的基础上提出了在扭转作用下剩余强度公式:
| $ \frac{{{\tau _\mu }}}{{{\tau _{\mu 0}}}} = \frac{{{{{A}}_{\rm{c}}}}}{{{{{A}}_0}}} = \frac{{4\left( {{{b - }}2{{c}}} \right){{t}}}}{{4{{bt}}}} = 1{\rm{ - }}\frac{{2{{c}}}}{{{b}}}\text{。} $ | (4) |
其中:
| $ {\tau _\mu } = \frac{{{{{T}}_\mu }}}{{2At}}; \ {\tau _{\mu 0}} = \frac{{{{{T}}_{\mu 0}}}}{{2At}}\text{。} $ |
用
| $ \frac{{{{{T}}_\mu }}}{{{{{T}}_{\mu {\rm{0}}}}}} = 1 - \frac{{2{{c}}}}{{{b}}}\text{。} $ | (5) |
式中:
在扭转算例模型两端扭心处施加中拱弯矩,舱段发生中拱弯曲变形,顶部结构受拉,底部结构受压。舱段中的最大弯曲应力定义为
| $ \frac{{{{{M}}_\mu }}}{{{{{M}}_{\mu {\rm{0}}}}}} = 1 - \frac{{2{{c}}}}{{{b}}}\text{。} $ | (6) |
式中:
将平板理论运用于舱段结构时需要考虑到板厚方向上约束的情况,由Paik的平板拉伸试验可以得出,板厚对极限强度有较大的影响。但是含裂纹结构极限强度简化计算公式,没有考虑厚度t的影响,因此本文将为研究裂纹长度和厚度对舱段结构极限强度的影响,以含裂纹T型梁舱段结构为研究对象,选取具有典型裂纹型式的舱段作为算例模型,进行大变形弹塑性计算,对扭转和弯曲载荷作用下的含裂纹损伤舱段极限强度进行研究。
2 含裂纹舱段算例 2.1 有限元模型本文主要采用弹塑性有限元方法,假定裂纹为静态贯穿裂纹,不考虑裂纹尖端的扩展。裂纹宽度设定为10 mm,为的是消除自由边之间的摩擦作用。通过载荷位移曲线来表示舱段的极限强度。
以含典型裂纹缺陷(中心裂纹,双边裂纹和单边裂纹)的舱段为分析对象,开展对裂纹特征(长度、位置)、材料特性(屈服极限、弹性模量、泊松比)和结构几何尺寸(长宽高、板厚)等影响因素的研究,舱段模型如图3所示。
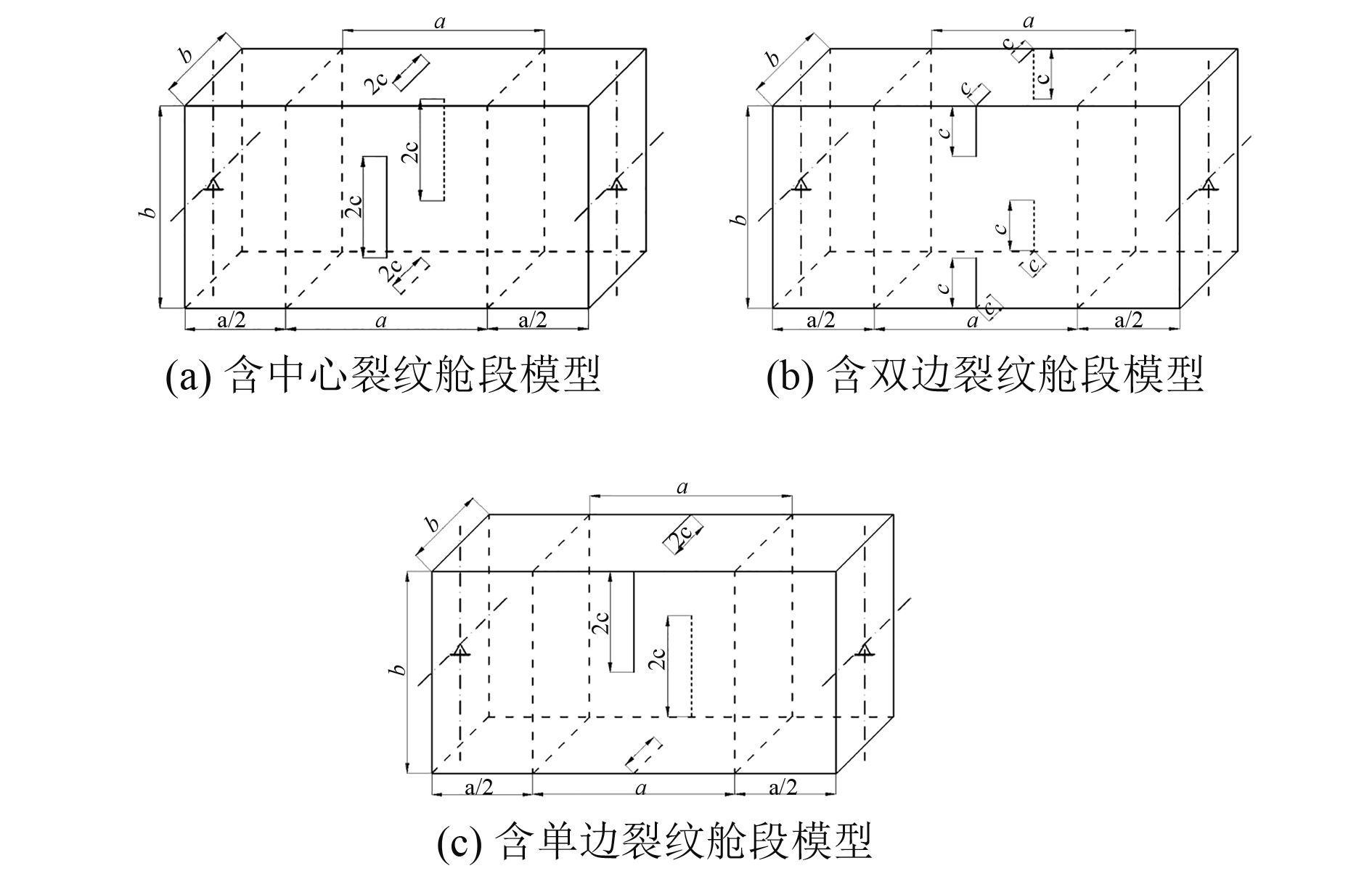
|
图 3 典型裂纹型式的舱段模型 Fig. 3 Cabin model with typical crack types |
舱段截面的宽度b=800 mm,舱段的长度2a=1600 mm,舱段上板的厚度分别取t=10 mm,15 mm和20 mm。假定材料为理想弹塑性,材料的弹性模量E=205.8 GPa,泊松比
在对舱段结构作极限强度分析的时候,一般是将结构等效为简支梁,即在运动耦合点RP-1上施加线位移约束Uy=0和Uz=0转角约束URx=0,URz=0在另一端的运动耦合点RP-2上施加线位移约束Ux=0,Uy=0和Uz=0转角约束URx=0,URz=0。载荷则是在两端的耦合控制点上施加大小相同、方向相反,在加载时间内从0缓慢、均匀增加到

|
图 4 算例模型加载方式 Fig. 4 The loading method of example model |
本文工况选择的是弯曲荷载和扭转荷载。弯曲工况是在运动耦合点处基于长-高平面施加一对能使结构破坏的相反转角;扭转工况是假定舱段的初始变形为扭转屈曲模态,初始变形的幅值
| $ {\omega _0} = 0.1{\beta ^2}t\text{,} $ | (7) |
式中,
舱段出现裂纹损伤,改变裂纹的类型、长度和舱段上板厚,利用Abaqus进行弹塑性大变形分析,研究裂纹对弯曲、扭转极限强度的影响。
图5为3种不同的裂纹型式和不同板厚舱段在弯曲作用下剩余极限强度随着裂纹长度变化的情况。可以看出,当厚度相同时,随着裂纹长度的增加中心裂纹对弯曲作用下的剩余极限强度影响程度降低;而双边裂纹和单边裂纹随着裂纹长度增加对弯曲作用下的剩余极限强度影响程度增大,并且双边裂纹与单边裂纹对极限强度的影响趋势十分相似。从整体的趋势可以得到板厚对极限强度的影响有着较为明显的作用。
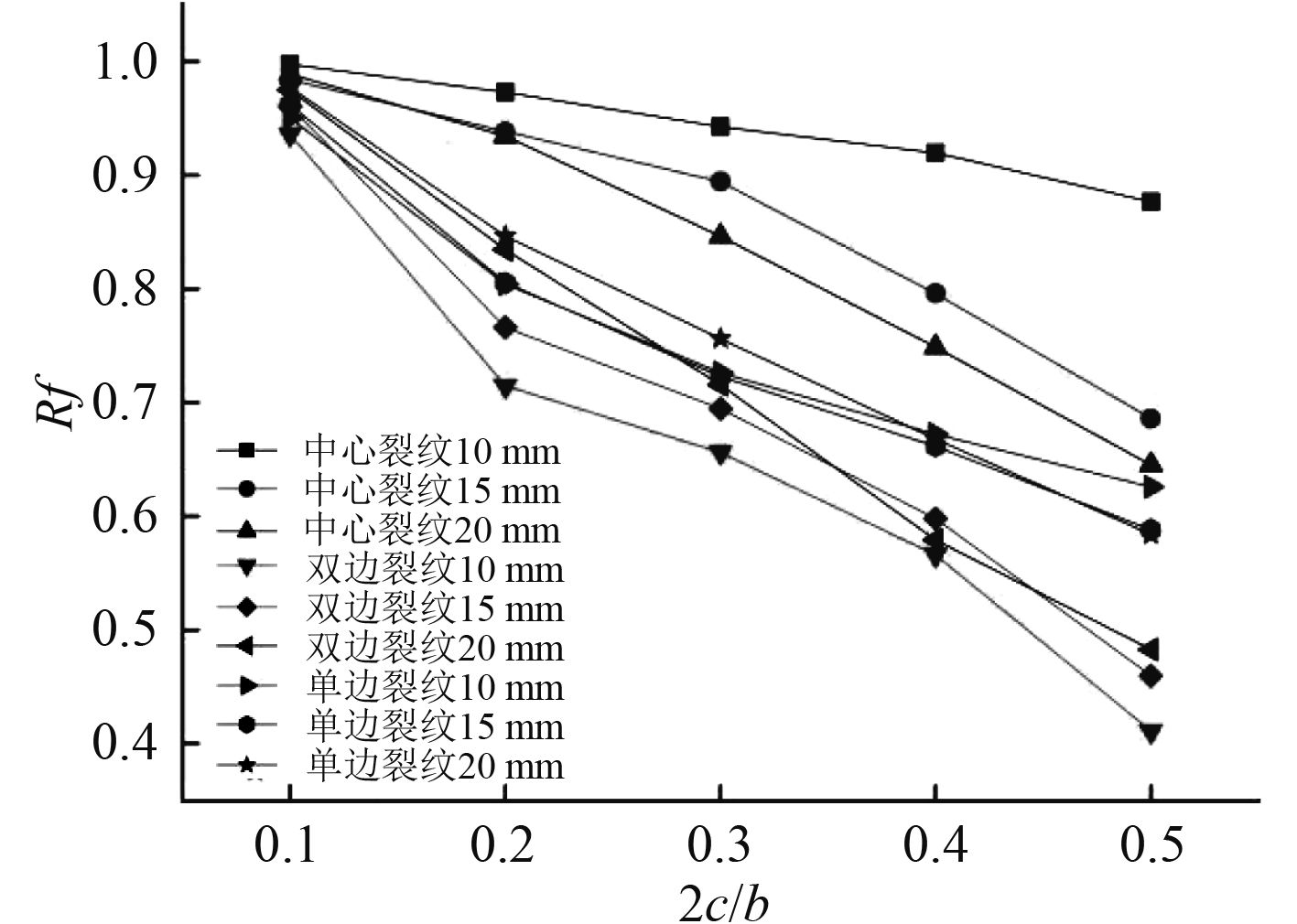
|
图 5 含不同裂纹和不同板厚的舱段弯曲剩余极限强度 Fig. 5 Bending residual ultimate strength of cabin with different cracks and different plate thicknesses |
图6为3种不同的裂纹型式舱段在扭转作用下剩余极限强度随着裂纹长度变化的情况。由图可以看出,当厚度相同时,随着裂纹长度的增加3种裂纹型式对扭转作用下的剩余极限强度影响不大。同时随着壁厚的变化,Rf-2c/b斜率基本一致。这说明板厚对含裂纹损伤的舱段扭转剩余极限强度影响不大。
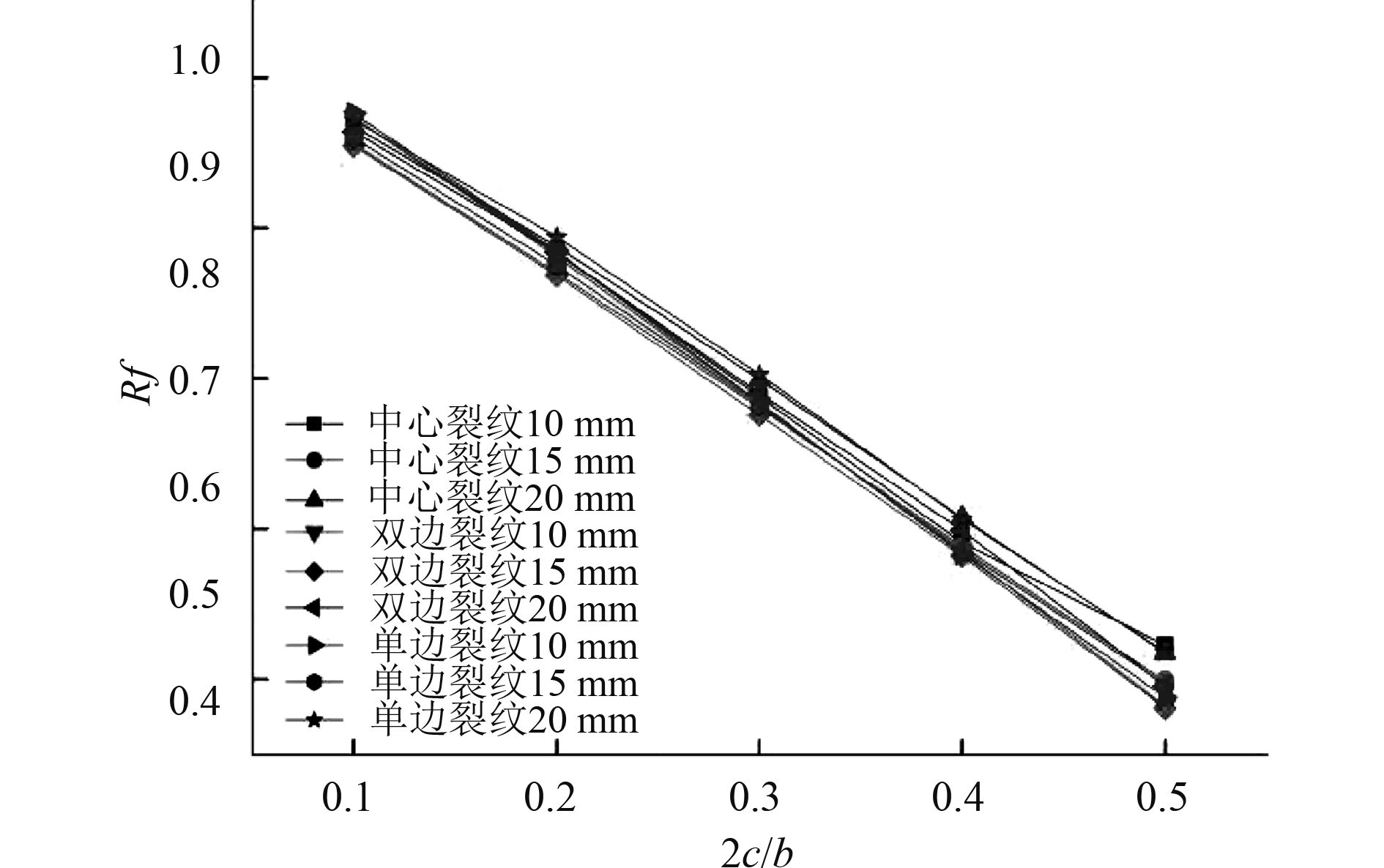
|
图 6 含不同裂纹和不同板厚的舱段扭转剩余极限强度 Fig. 6 Torsional residual ultimate strength of cabin with different cracks and different plate thicknesses |
上文讨论了含裂纹的平板拉伸极限强度和压缩极限强度预报公式是否在舱段上的适用性,为的是之后更进一步提出更为精确的预报公式。以壁厚为15 mm的舱段为例,将完整舱段弯曲、扭转作用下的剩余极限强度代入式(5)与式(6),与数值模拟得到的3种裂纹型式的剩余极限强度数值作比较(见表1~表6和图7)。
|
|
表 1 弯曲作用下中心裂纹极限强度 Tab.1 Center crack bending ulti-strength |
|
|
表 2 扭转作用下中心裂纹极限强度 Tab.2 Center crack torsional ulti-strength |
|
|
表 3 弯曲作用下双边裂纹极限强度 Tab.3 Double-side crack bending ulti-strength |
|
|
表 4 扭转作用下双边裂纹极限强度 Tab.4 Double-side crack torsional ulti-strength |
|
|
表 5 弯曲作用下单边裂纹极限强度 Tab.5 Single-side crack bending ulti-strength |
|
|
表 6 扭转作用下单边裂纹极限强度 Tab.6 Single-side crack torsional ulti-strength |
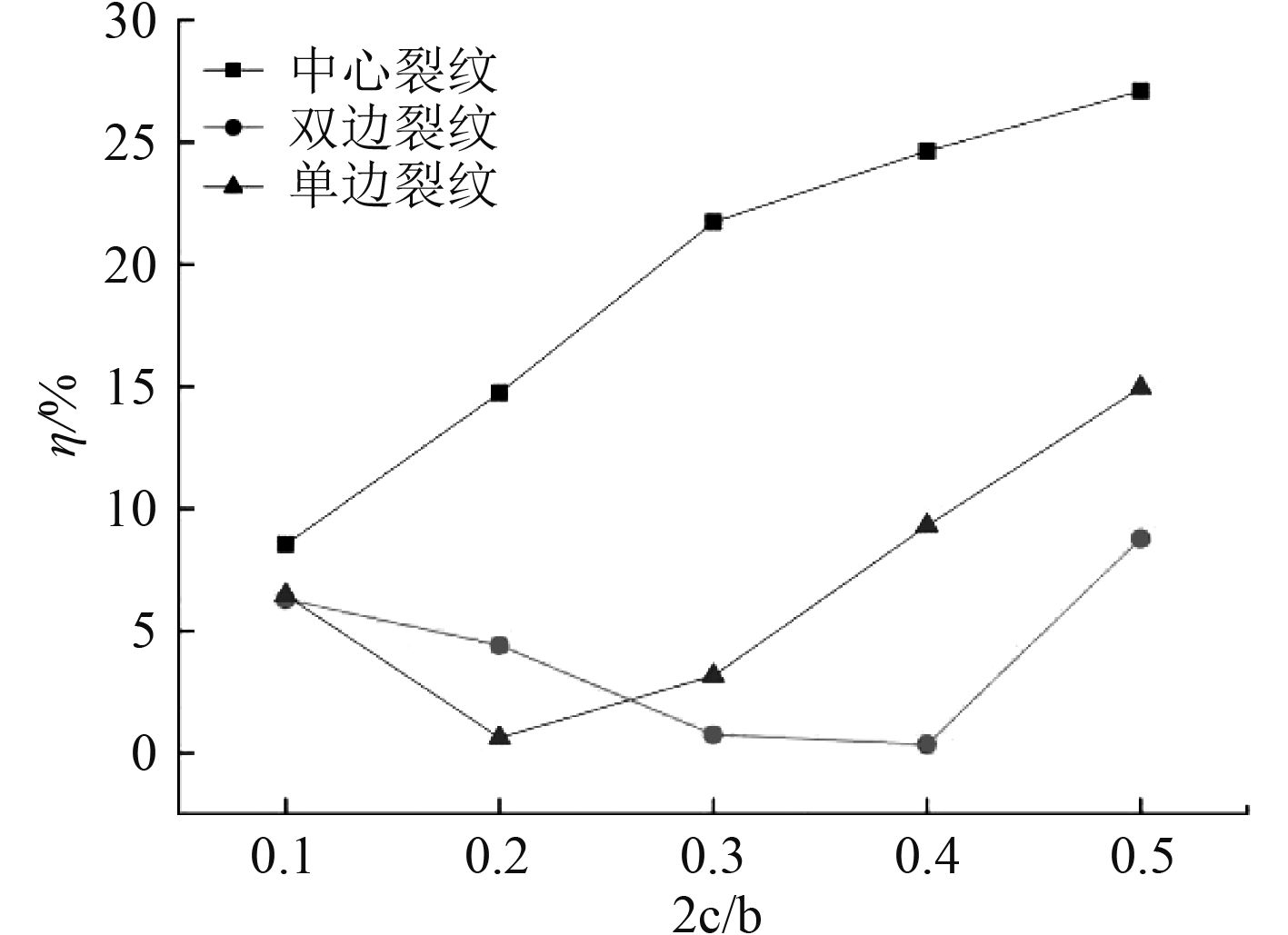
|
图 7 简化公式预报弯曲剩余极限强度情况 Fig. 7 Simplified formula predicts bending residual ultimate strength |
可以看出3种裂纹型式的舱段在扭转作用下的扭转极限强度有限元结果与预报公式得到理论结果较为接近,都是随着裂纹长度的增加η也随之增加,但上升趋势平缓。而对于3种裂纹型式舱段在弯曲作用下的扭转极限强度有限元结果与预报公式得到理论结果η波动比较大。含中心裂纹的舱段弯曲极限强度随着裂纹长度的增加,离散性较大。双边裂纹型式与单边裂纹型式的舱段弯曲极限强度相似,η变化趋势翻转,整体趋势在15%以内,当裂纹长度在0.2~0.3之间时剩余极限强度的预报最为精确。
3.2 考虑板厚影响的舱段剩余极限强度评估公式可以看出,在含裂纹缺陷的舱段极限强度受板厚影响较大。并且通过图表可以得到,板厚对扭转作用下的极限强度呈线影响,板厚对弯曲作用下的极限强度呈指数影响同时裂纹类型不同其影响程度也不同。因此在这小节中,将分别提出在扭转作用下和弯曲作用下关于板厚t的预测公式。
基于准牛顿法(BFGS)和通用全局优化法,提出参数k1,k2用于表示扭转作用下板厚对舱段极限强度带来的线性影响,如下式:
| $ \frac{{{T_u}}}{{{T_{u0}}}} = {k_1} - {k_2} \cdot \frac{{2c}}{b}\text{。} $ | (8) |
式中:Tu为含裂纹舱段端部的极限扭矩;Tu0为不含裂纹舱段端部的极限扭矩;b为平板宽度;2c为裂纹长度。
提出参数k3,k4,k5,k6用于表示弯曲作用下板厚对舱段极限强度带来的指数影响,如下式:
| $ \frac{{{M_u}}}{{{M_{u0}}}} = {k_3} - {k_4} \cdot {\left( {\frac{{2c}}{b}} \right)^{{k_5}}} \cdot {t^{{k_6}}}\text{。} $ | (9) |
式中:Mu为含裂纹舱段模型端部的极限扭矩;Mu0为不含裂纹舱段模型端部的极限扭矩;b为平板宽度;2c为裂纹长度;t为板厚。
通过将有限元计算结果代入到式(8)和式(9)中,使用回归计算方法得到,适用于具有中心裂纹,双边裂纹和单边裂纹型式的舱段极限强度评估公式。
扭转作用下具有中心裂纹,双边裂纹和单边裂纹缺陷的舱段极限强度评估公式:
| $ \frac{{{T_u}}}{{{T_{u0}}}} = 1.05 - 0.92 \cdot \frac{{2c}}{b}\text{。} $ | (10) |
弯曲作用下具有中心裂纹,双边裂纹和单边裂纹缺陷的舱段极限强度评估公式:
| $ \frac{{{M_u}}}{{{M_{u0}}}} = \left\{ \begin{array}{l} 1.01{\rm{ - }}0.03 \cdot {\left( {\displaystyle\frac{{2c}}{b}} \right)^{1.65}} \cdot {t^{1.22}},\;\;{\text{中心裂纹}}\text{;}\\ 1.27{\rm{ - }}1.72 \cdot {\left( {\displaystyle\frac{{2c}}{b}} \right)^{0.57}} \cdot {t^{{\rm{ - }}0.14}},\;\;{\text{双边裂纹}}\text{;}\\ 1.68{\rm{ - }}1.51 \cdot {\left( {\displaystyle\frac{{2c}}{b}} \right)^{0.22}} \cdot {t^{{\rm{ - }}0.07}},\;\;{\text{单边裂纹}}\text{。} \end{array} \right. $ | (11) |
式中:
可以粗略的通过以上评估公式计算结果与有限元计算结果的比较来检验其有效性。这里将板厚为10 mm,15 mm和20 mm的舱段模型完整舱段模型扭转、弯曲作用下的参数分别代入式(10)与式(11),把评估公式得到的结果与有限元计算得到的3种裂纹型式的极限强度作比较(见表7~表12)。
|
|
表 7 中心裂纹弯曲载荷预报精度 Tab.7 The forecast accuracy of bending center crack |
|
|
表 8 中心裂纹扭转载荷预报精度 Tab.8 The forecast accuracy of resduialcenter crack center crack |
|
|
表 9 双边裂纹弯曲载荷预报精度 Tab.9 The forecast accuracy of bending double-side crack |
|
|
表 10 双边裂纹扭转载荷预报精度 Tab.10 The forecast accuracy of resduialdouble-side crack double-side crack |
|
|
表 11 双边裂纹弯曲载荷预报精度 Tab.11 The forecast accuracy of bending single-side crack |
|
|
表 12 双边裂纹扭转载荷预报精度 Tab.12 The forecast accuracy of resduialsingle-side crack single-side crack |
根据裂纹型式的不同而提出的修正公式,对弯曲荷载作用下舱段剩余极限强度预报,其η都在7%以内,精确性较高;根据扭转载荷作用下的预报情况发现,预报公式与厚度无关,因此提出仅与裂纹长度相关的预报公式,η都在5%以内,精确度较高(见图8和图9)。

|
图 8 两种预报公式预报弯曲作用下剩余极限强度对比 Fig. 8 Two forecast formulas predicting residual ultimate strength contrast under bending |

|
图 9 两种预报公式预报扭转作用下剩余极限强度对比 Fig. 9 Two forecast formulas predicting residual ultimate strength contrast under torsion |
根据以上对比表和图可以得到,通过式(8)与式(9)得到的计算结果与算例中有限元计算结果更加接近。而考虑板厚对剩余极限强度的影响在实际工程应用中也是需要的。因此考虑板厚影响的舱段剩余极限强度预报公式是具有实际意义的。
4 结 语本文主要对含裂纹损伤的舱段在弯曲和扭转作用下的剩余极限强度的影响因素研究。基于对2种预报公式预报在舱段上的预报情况分析,可以得到以下结论:
1)一定范围内,裂纹宽度对含裂纹舱段结构极限度影响不大。舱段结构板厚对弯曲极限强度影响较大,而对扭转极限强度的影响趋势不大,影响效果呈线性趋势。
2)裂纹类型对舱段结构弯曲极限强度的影响都比较小,但对舱段结构扭转极限强度的影响程度就较为明显。当裂纹长度2c/b≤0.1时,扭转作用下结构极限强度受裂纹损伤的影响较小。然而,裂纹长度2c/b≥0.2时,扭转作用下结构极限强度受到裂纹损伤有明显的降低作用。对比3种典型的裂纹型式,当裂纹长度2c/b≤0.3时,扭转作用下结构极限强度受单边裂纹损伤的降低作用最显著;当裂纹长度2c/b≥0.4时,扭转作用下结构极限强度受双边裂纹损伤的降低作用明显。
3)本文提出了分别在扭转和弯曲作用下考虑板厚影响的含裂纹舱段结构极限强度评估公式,数值分析结果验证了公式在评估舱段结构极限强度时的准确性。
| [1] |
王芳, 黄小平, 崔维成. 具有中心穿透裂纹缺陷的矩形板极限拉伸强度分析[J]. 中国造船, 2006(1): 12-18. DOI:10.3969/j.issn.1000-4882.2006.01.002 |
| [2] |
胡勇. 基于" 第一原理”的船体结构强度评估系统[D]. 上海: 上海交通大学, 2004.
|
| [3] |
王芳. 具有裂纹损伤的船舶结构剩余极限强度分析[D].上海: 上海交通大学, 2007.
|
| [4] |
PAIK J K, THAYAMBALLI A K. Ultimate strength of aging ships[J]. Proceedings of the Institution of Mechanical Engineers. Part M, Journal of Engineering for the Maritime Environment, 2002, 216(M 1): 57~77.
|
| [5] |
师桂杰. 集装箱船船体结构极限强度研究[D].上海: 上海交通大学, 2011.
|
| [6] |
陈俊丹, 王德禹. 含裂纹损伤箱型梁剩余扭转极限强度研究[J]. 舰船科学技术, 2016, 38(7): 12-16. |
| [7] |
赵南, 顾学康. 船体结构极限强度研究综述[J]. 舰船科学技术, 2015, 37(11): 1-7. DOI:10.3404/j.issn.1672-7649.2015.11.001 |
| [8] |
李景阳, 崔维成, 王芳. 中心穿透裂纹板在复杂载荷作用下的剩余极限强度分析[J]. 舰船科学技术, 2009, 31(8): 44-50. |
 2019, Vol. 41
2019, Vol. 41
