环肋双层圆柱壳是潜艇的主要结构形式,在艇体敷设阻尼材料是降低其振动与辐射噪声的有效手段。目前,国内外许多学者对敷设阻尼材料圆柱壳的振动与声辐射特性进行研究。Ramasamy[1]分析了流体载荷下约束阻尼层圆柱壳的振动特性,采用迭代法求解了结构的复特征值。陈炜等[2]在Laulagnet B和 Guyader J [3~5]所做研究的基础上系统地分析了敷设阻尼材料的环肋圆柱壳振动与声辐射性能。陈美霞等[6-7]采用Flügge微分算子描述壳体振动,采用Helmholtz方程和壳体表面边界条件求解壳间流场,采用Navier方程描述粘性阻尼层的运动,建立了敷设阻尼材料的圆柱壳振动方程,研究了阻尼层厚度、弹性模量、损耗因子和静水压缩因子以及阻尼材料敷设方式对双层圆柱壳振动与声辐射特性的影响。刘向东等[8]对辐射阻尼材料的加筋双层圆柱壳进行振动和声辐射实验,测量了壳体的响应和水中辐射声压,对比分析了双层圆柱壳内、外壳敷设隔声去耦材料后的近场声压变化。窦松然[9]采用有限元迭代法对粘弹性复合结构进行了模拟仿真,并对圆柱壳振动控制中的约束阻尼结构进行了优化研究。
目前,对于敷设阻尼材料的双层圆柱壳的振动与声辐射特性研究大多集中在中、低频。在高频,由于结构的模态密度增大,不确定性更加明显,结构细微的差异会导致响应的大幅改变,传统的模态叠加法、有限元法等方法很难准确计算结构的响应。统计能量法是分析结构高频振动与声辐射问题的有效手段。王献忠等[10]采用统计能量分析对敷设阻尼材料圆柱壳进行了建模分析,通过仿真结果与实验值对比验证了SEA方法计算敷设阻尼结构的圆柱壳声辐射特性的有效性。本文在此基础上,采用统计能量法,分析了敷设阻尼材料对环肋双层圆柱壳振动与声辐射特性的影响。首先研究了内、外壳分别敷设阻尼材料时双层圆柱壳的振动与声辐射特性,然后研究了阻尼材料的杨氏模量、损耗因子和阻尼层厚度对其降噪效果的影响,最后研究了阻尼材料对不同结构形式的圆柱壳降噪效果的差异。对于合理使用阻尼材料降低水下结构的振动与辐射噪声有一定参考作用。
1 基本原理 1.1 统计能量法Lyon研究发现对于2个线性耦合的单一频率振子,它们之间的能量流动满足关系:
| $ {\rm{ < }}{{{P}}_{12}}{\rm{ > = }}{\tau _{12}}(\left\langle {{{{E}}_1}} \right\rangle - \left\langle {{{{E}}_2}} \right\rangle ){\text{。}} $ | (1) |
其中:
| $ {P_{ij}} = \omega {\eta _{{\rm{ij}}}}{E_i} - \omega {\eta _{ji}}{E_j}{\text{。}} $ | (2) |
其中:
根据能量守恒,子系统
| $ {P_{i,in}} = {\dot E_i} + {P_{id}} + \sum\limits_{j = 1,j \ne i}^N {{P_{ij}}} {\text{。}} $ | (3) |
其中:
将式(1)~式(3)写成矩阵形式:
| $ \left[\!\!\!\! \!{\begin{array}{*{20}{c}} {\displaystyle\sum\limits_{k \!=\! 1}^N {{\eta _{1k}}} }&{ - {\eta _{21}}}&{...}&{ - {\eta _{N1}}}\\ { - {\eta _{12}}}&{\displaystyle\sum\limits_{k \!= \!1}^N {{\eta _{2k}}} }&{...}&{ - {\eta _{N2}}}\\ {...}&{...}&{...}&{...}\\ { - {\eta _{1N}}}&{...}&{...}&{\displaystyle\sum\limits_{k \!= \!1}^N \!{{\eta _{Nk}}} } \end{array}} \!\!\!\!\!\right]\left\{ \!\!{\begin{array}{*{20}{c}} {{E_1}}\\ {{E_2}}\\ {...}\\ {{E_N}} \end{array}}\!\! \right\} \!= \!\frac{1}{\omega }\left\{\!\! {\begin{array}{*{20}{c}} {{P_1}}\\ {{P_2}}\\ {...}\\ {{P_N}} \end{array}}\!\! \right\}{\text{,}} $ | (4) |
根据互易定理,对保守耦合系统,
| $ \begin{split} \left[\!\!\!\!\!\! {\begin{array}{*{20}{c}} {\displaystyle\sum\limits_{k = 1}^N {{\eta _{1k}}{n_1}} }&{ - {\eta _{21}}{n_1}}&{...}&{ - {\eta _{N1}}{n_1}}\\ { - {\eta _{21}}{n_1}}&{\displaystyle\sum\limits_{k = 1}^N {{\eta _{2k}}{n_2}} }&{...}&{ - {\eta _{N2}}{n_2}}\\ {...}&{...}&{...}&{...}\\ { - {\eta _{N1}}{n_1}}&{...}&{...}&{\displaystyle\sum\limits_{k = 1}^N {{\eta _{Nk}}{n_N}} } \end{array}} \!\!\!\!\!\!\!\right]\left\{\!\! {\begin{aligned} {\displaystyle\frac{{{E_1}}}{{{n_1}}}}\\ {\displaystyle\frac{{{E_2}}}{{{n_2}}}}\\ \!{...}\!\\ {\displaystyle\frac{{{E_N}}}{{{n_N}}}} \end{aligned}}\!\!\right\} \!\!=\!\!\frac{1}{\omega }\left\{\!\!\!\!{\begin{array}{*{20}{c}} {{P_1}}\\ {{P_2}}\\ \!{...}\!\\ {{P_N}} \end{array}} \!\!\!\! \right\}{\text{。}} \end{split} $ | (5) |
根据子系统的行进波传播特性获得内损耗因子、模态密度、耦合损耗因子等参数,根据激励获得每个子系统的输入功率,解方程(5)得到每个子系统的能量
阻尼材料是覆盖在振动结构上抑制结构振动及结构声传播与声辐射的材料,目前主要是高分子材料[11]。通过在结构表面敷设阻尼材料,可以大大提高结构表面的阻尼,结构振动时周期性不同程度的拉紧阻尼材料,通过材料的“滞后阻尼”损耗结构的振动能量。不同结构形式的阻尼材料的特性相差很大,文献[12]对大量阻尼材料的结构形式进行分析,将其主要归为两类:自由阻尼层和有约束阻尼层。自由阻尼层是将一定厚度的阻尼材料直接敷设在结构表面,结构变形时阻尼材料跟随变形,主要承受拉伸形变。有约束阻尼层是在阻尼材料上再增加一层弹性材料,当结构振动时,由于约束层阻止阻尼层伸长,阻尼材料主要承受剪切形变。相对于自由阻尼层,有约束阻尼层的阻尼效果较好,但是制备工艺相对复杂。
本文采用自由阻尼层结构,阻尼材料采用橡胶,厚度为50 mm。阻尼材料和基体的特性如表1所示[13]。
|
|
表 1 材料参数 Tab.1 Data of the material |
圆柱壳敷设阻尼材料后的内损耗因子为[14]:
| $ \eta _{}^{free} = {\eta _1} + \frac{{{\eta _2}{E_2}{h_2}\left(r_2^2 + h_{21}^2\right)}}{{{E_1}r_1^2{h_1}}}{\text{。}} $ | (6) |
其中:
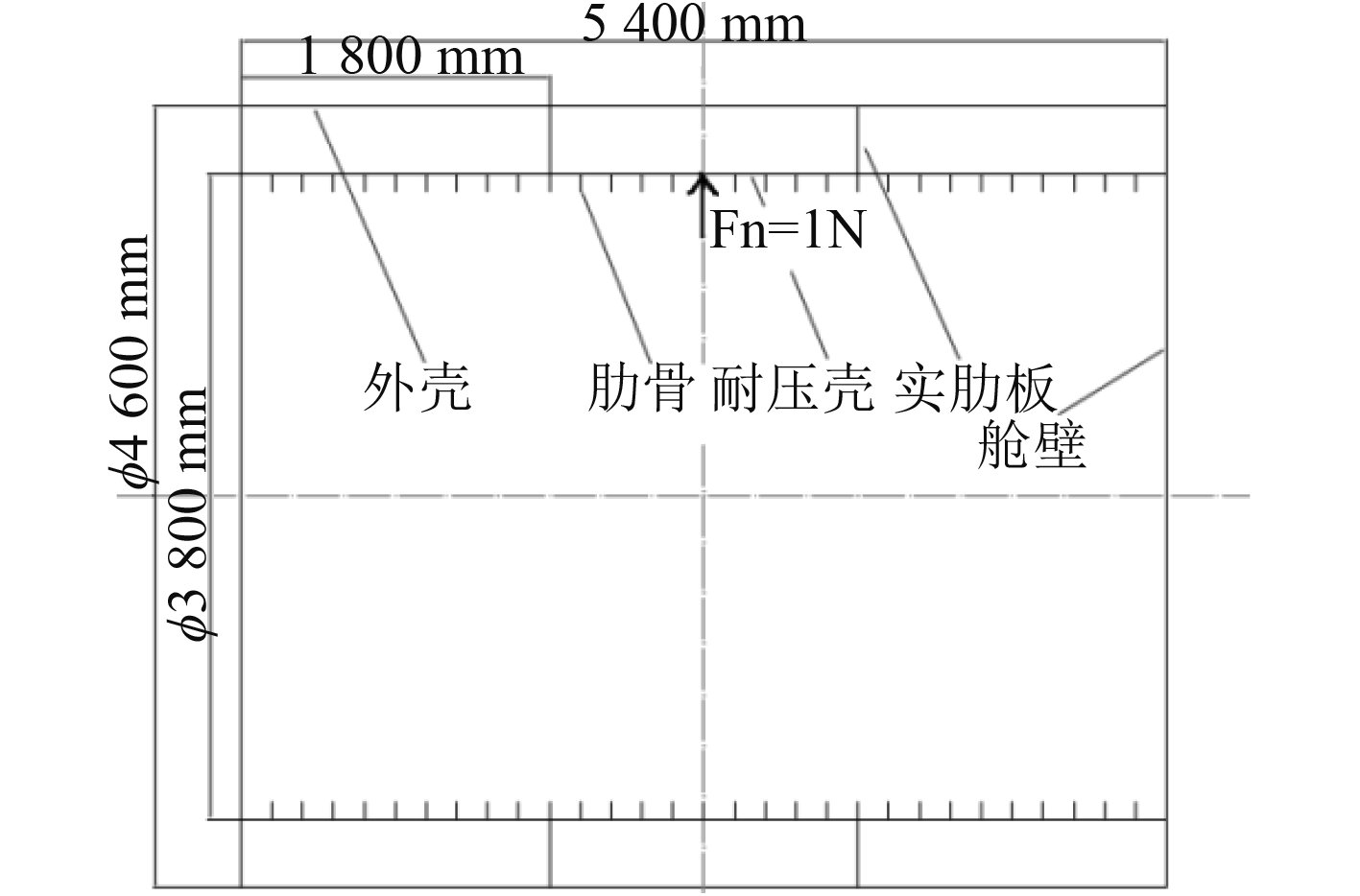
如图1所示,模型为双层圆柱壳,外壳和耐压壳之间采用实肋板连接,壳间介质为空气,其结构参数如表2所示。激励为作用在耐压壳上的径向力,大小为1 N,计算频带为100~100 000 Hz的1/3倍频程,测点位于距离圆柱壳中心轴线15 m处。在耐压壳上采用T型肋骨强化,肋骨间距0.6 m。
|
图 1 双层圆柱壳模型 Fig. 1 Double cylindrical shell model |
|
|
表 2 圆柱壳结构参数 Tab.2 Data of the cylindrical shell model and material |
图2为圆柱壳的SEA模型,根据自然几何边界条件和材料介质特性以及满足模态相似、弱耦合等条件,将模型划分为21个子系统。耐压壳、外壳分别划分为3个壳体子系统,舱壁划分为2个平板子系统,实肋板划分为8个平板子系统,还有4个声腔子系统和测点处的半无限流域子系统。

|
图 2 双层圆柱壳的SEA模型 Fig. 2 The SEA model of double cylindrical shell |
对于双层圆柱壳,可以在耐压壳和外壳敷设阻尼材料,但是两者的减振降噪效果不同。分别计算在耐压壳和外壳敷设阻尼材料前后,耐压壳2和外壳2的平均振动速度以及双层圆柱壳的辐射声压级,研究耐压壳和外壳敷设阻尼材料的减振降噪效果。
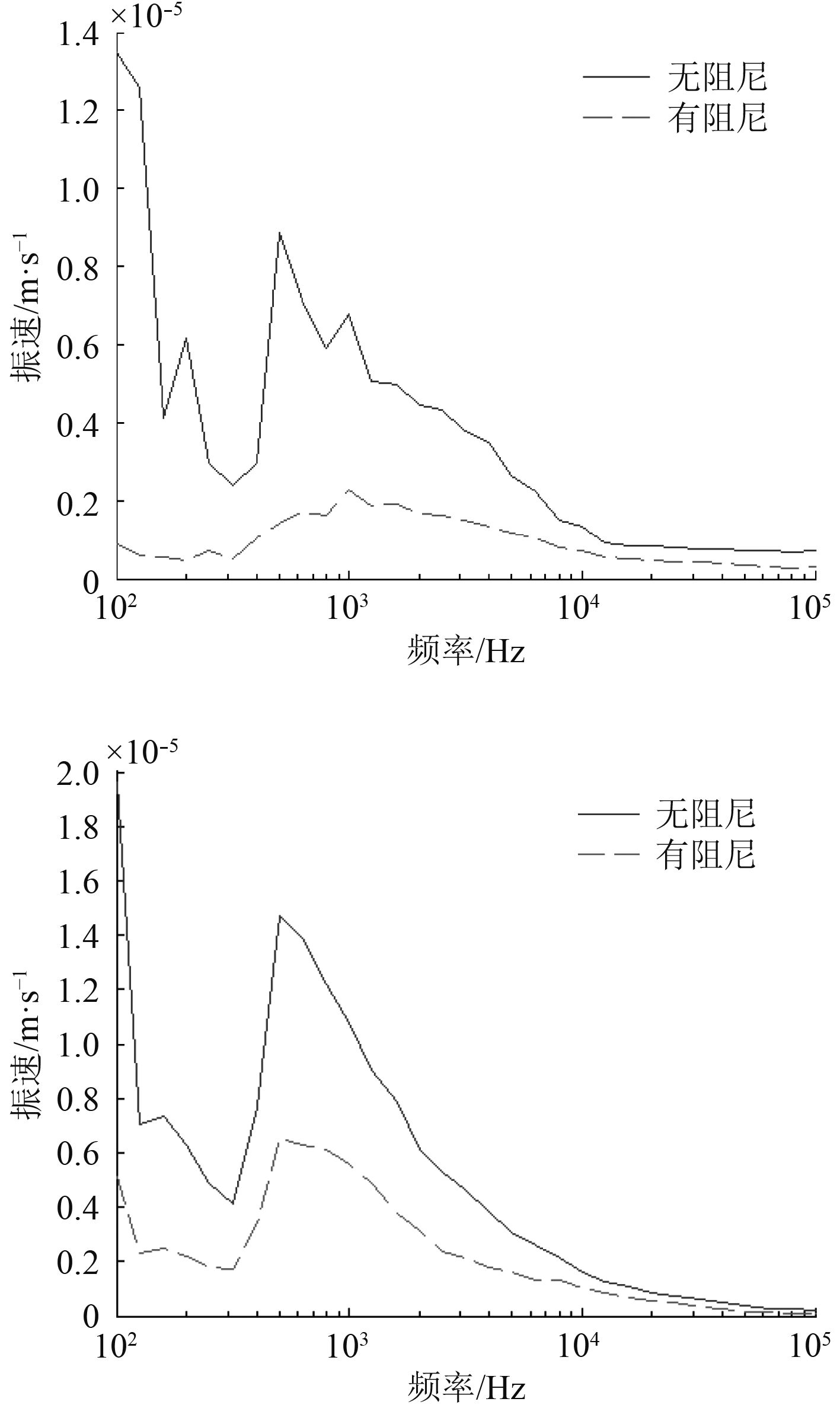
3.1 耐压壳敷设阻尼材料双层环肋圆柱壳的耐压壳敷设阻尼材料前后,其内、外壳的整体平均振速和辐射声压级,如图3和图4所示。
|
图 3 耐压壳2和外壳2的平均振速 Fig. 3 The average speed of the pressure shell and the outer shell |
|
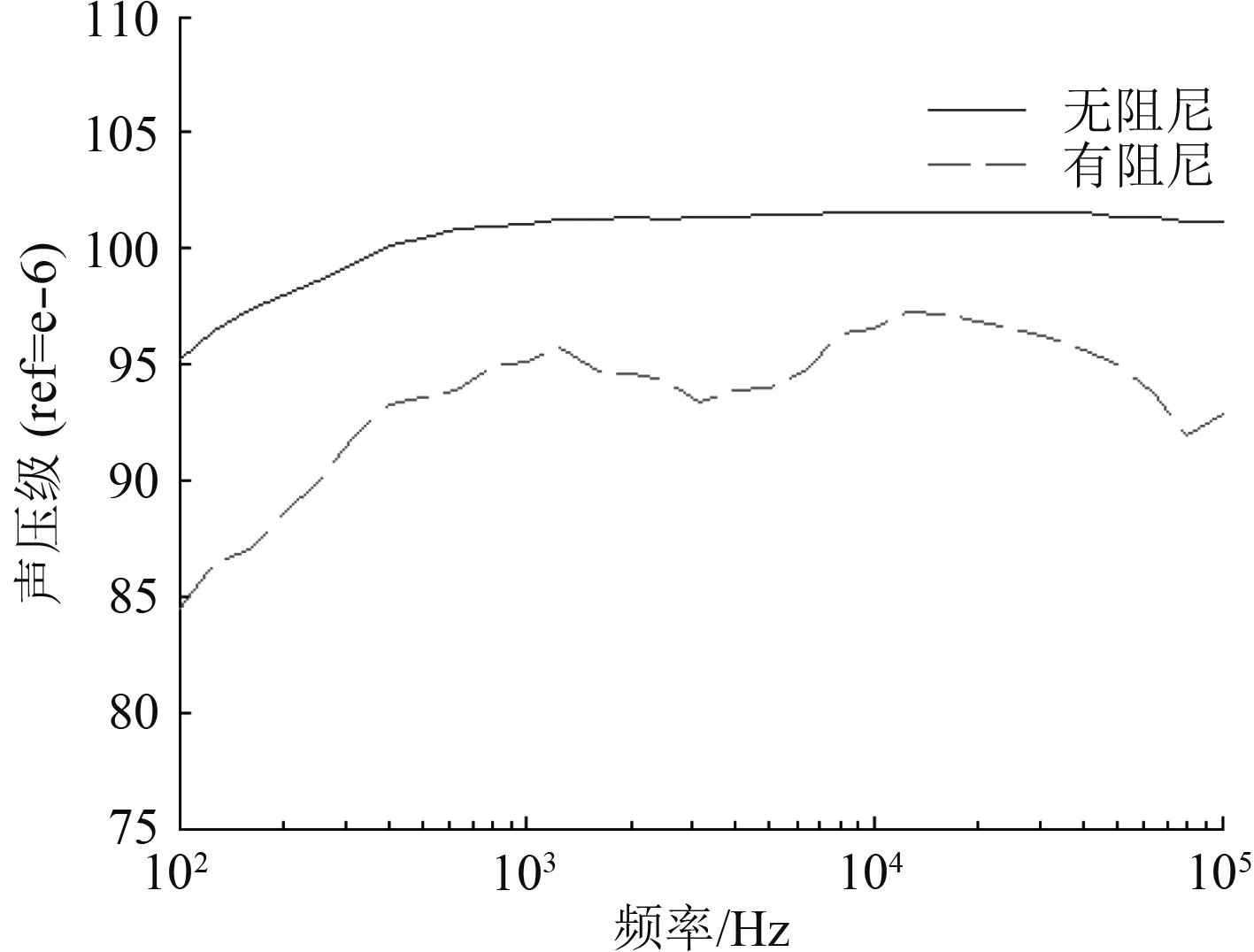
图 4 辐射声压级 Fig. 4 Radiation sound pressure level |
在耐压壳敷设阻尼材料后,耐压壳和外壳的振速都有所下降。对于耐压壳,由于增加阻尼材料,使结构的阻尼增大,振动能量被阻尼材料大量消耗,振动速度在整个频带上大幅下降,速度曲线上的峰值处振速大大降低,整个曲线变得平滑。由于耐压壳振动速度下降,向外壳传递的振动也随之降低,外壳振动速度也有明显降低,外壳的振动速度曲线形状改变不大,近似于向下平移。耐压壳增加阻尼材料后圆柱壳的辐射声压在整个频带上都有所降低,在100~1 000 Hz上辐射声压下降约10 dB,在1 000 Hz之后辐射声压下降约5 dB。
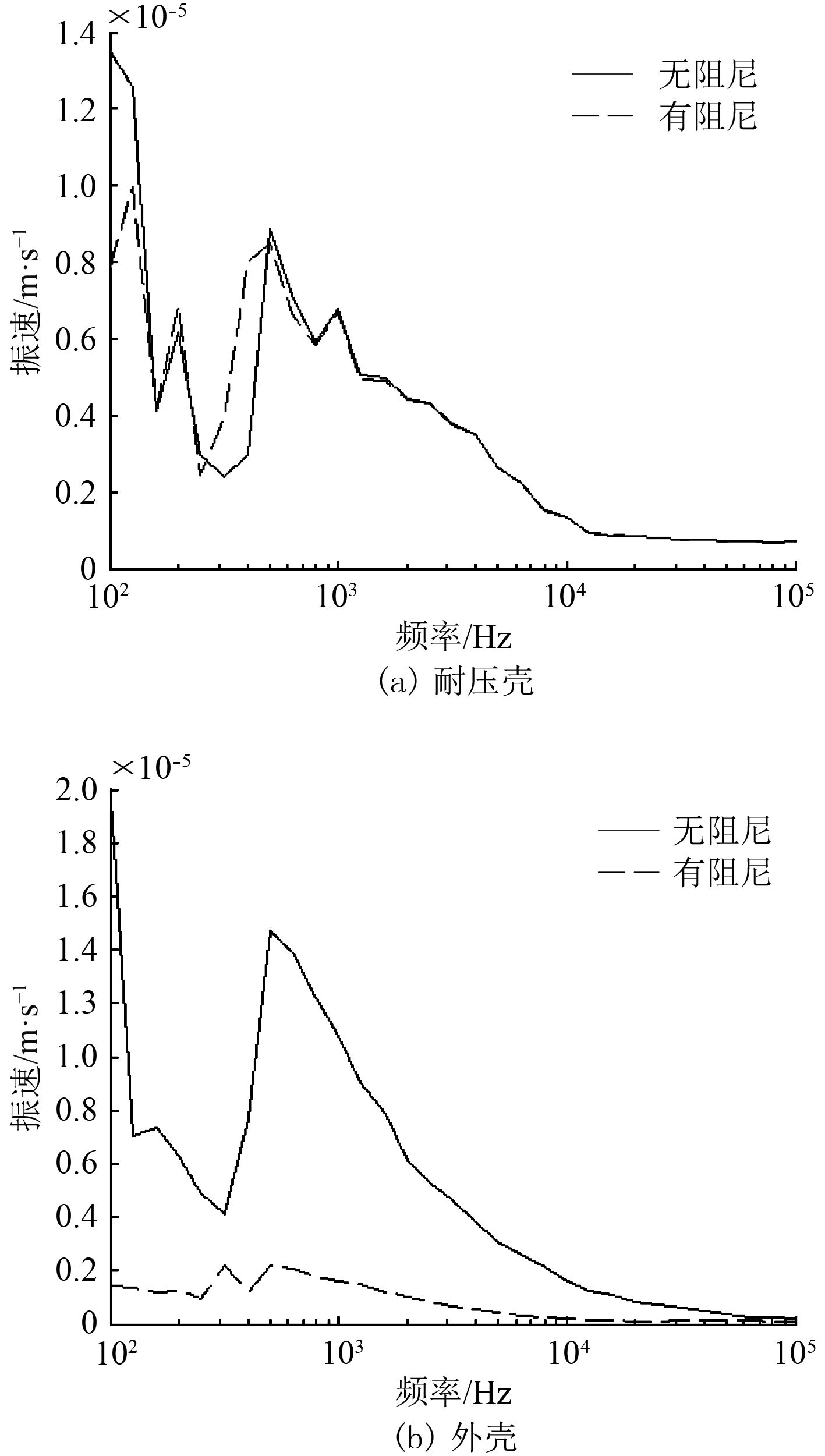
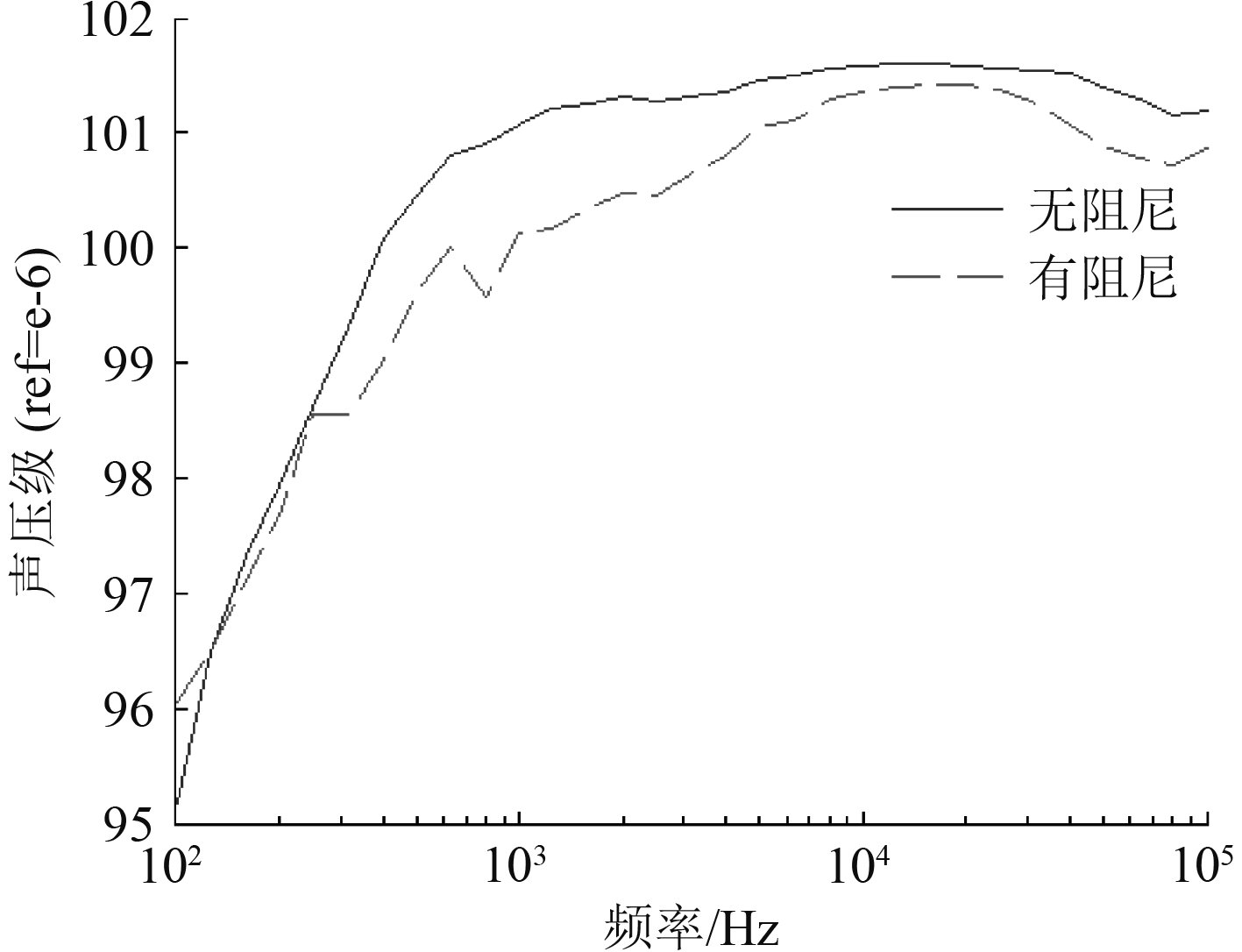
3.2 外壳敷设阻尼材料外壳敷设阻尼材料前后,耐压壳2和外壳2的平均振速以及双层圆柱壳的辐射声压级,如图5和图6所示。与耐压壳敷设阻尼不同,外壳敷设阻尼后,耐压壳的振速除了在低频时略微下降外几乎没有改变,但是外壳振速在整个频带内大幅下降。由于外壳较薄,同样厚度的阻尼材料能够增加更大的结构损耗,因此相对与较厚的耐压壳在外壳敷设相同厚度的阻尼材料能够更好抑制结构的振动。但是由于双层圆柱壳的振动主要是耐压壳的振动通过实肋板和壳间介质向外传递从而带动外壳的振动,因此外壳敷设阻尼材料对双层圆柱壳的降噪效果相对较差。如图6所示,外壳敷设阻尼材料后,圆柱壳辐射噪声降低较小,在1 dB左右。在环频率处,辐射噪声下降最大为2 dB左右。
|
图 5 耐压壳2和外壳2的平均振速 Fig. 5 The average speed of the pressure shell and the outer shell |
|
图 6 辐射声压级 Fig. 6 Radiation sound pressure level |
杨氏模量、损耗因子和阻尼层厚度是阻尼材料非常重要的参数,不同参数的阻尼材料,其减振降噪效果也不同。分别计算耐压壳敷设不同参数的阻尼材料前后圆柱壳的辐射噪声,研究阻尼材料特性对其降噪效果的影响。
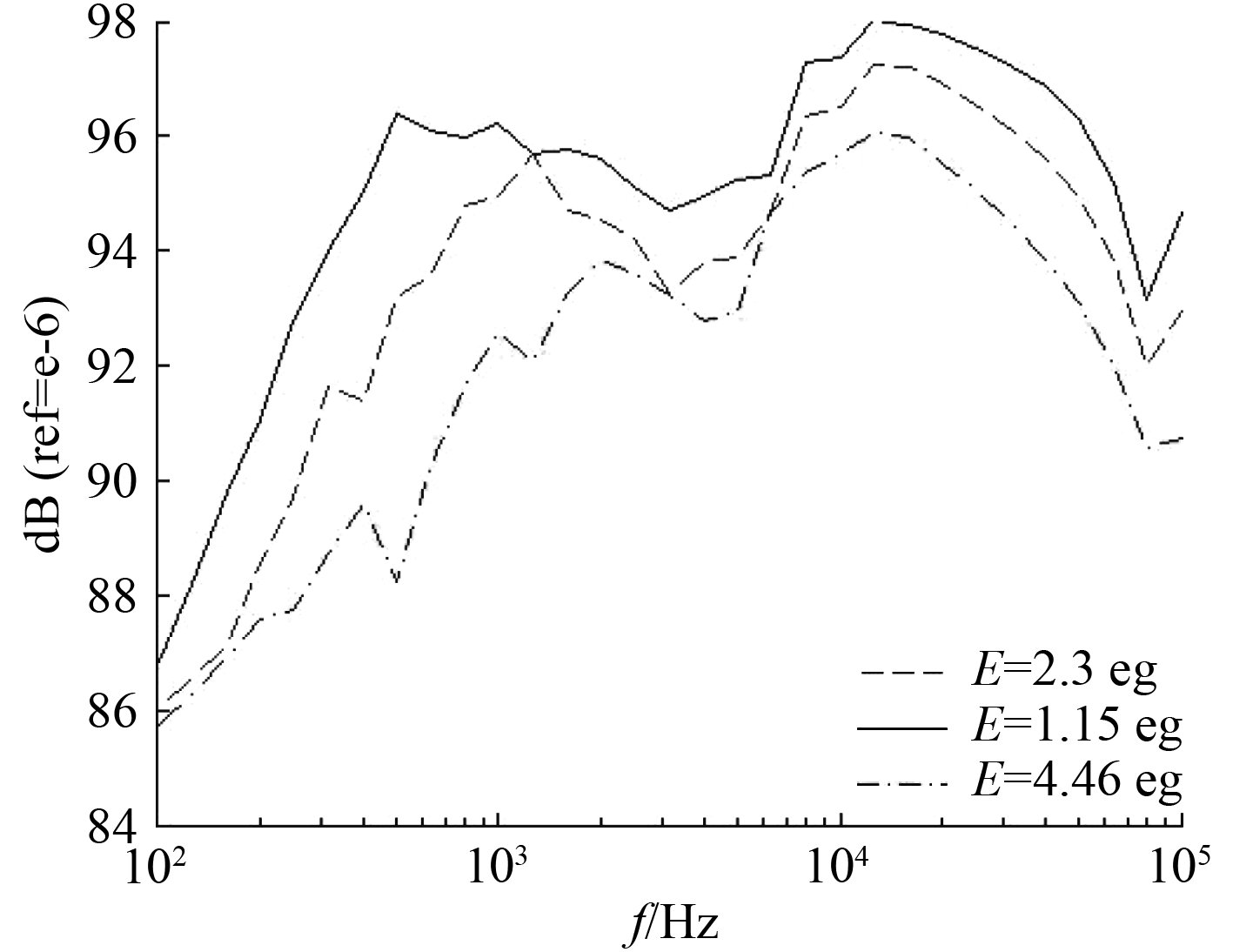
4.1 杨氏模量的影响计算阻尼材料的杨氏模量分别为1.15E9,2.3E9,4.6E9时双层圆柱壳的辐射噪声,如图7所示。
|
图 7 辐射声压级 Fig. 7 Radiation sound pressure level |
由式(6)可知,阻尼材料的杨氏模量会影响敷设阻尼材料结构的内损耗因子,杨氏模量增大时结构的内损耗因子也一定程度增大;阻尼材料的杨氏模量还会影响结构的模态密度,增大杨氏模量会使结构的模态密度降低。如图7所示,阻尼材料的杨氏模量是影响其减振降噪效果的重要因素,增大阻尼材料的杨氏模量可以增加内损耗因子,同时减小结构的模态密度,更好地抑制结构的振动从而降低辐射噪声。从图7可以看出,100~1 000 Hz之间,阻尼材料的杨氏模量对辐射噪声的影响随着频率增高逐步增大;在环频率和临界频率处,杨氏模量对辐射噪声的影响较小;临界频率之后,杨氏模量对辐射噪声的影响基本不变。
4.2 损耗因子的影响分别计算阻尼材料损耗因子为0.3,0.5和0.7时,双层圆柱壳的辐射噪声,如图8所示。

|
图 8 辐射声压级 Fig. 8 Radiation sound pressure level |
阻尼材料的损耗因子主要影响敷设阻尼材料后结构的内损耗因子,阻尼材料拥有较高的损耗因子时,相同的激励下结构能够吸收更多的振动能量,更加有效的抑制结构的振动,从而降低辐射噪声。由图8可知,在300 Hz之前,阻尼材料的损耗因子对辐射噪声的影响非常小,因为低频时结构中的波长较长,属于“刚度控制区”,此时结构的阻尼对结构振动特性影响较小。300 Hz之后,阻尼材料的损耗因子对辐射噪声有较大影响,并且在整个频带上的降噪效果相似。
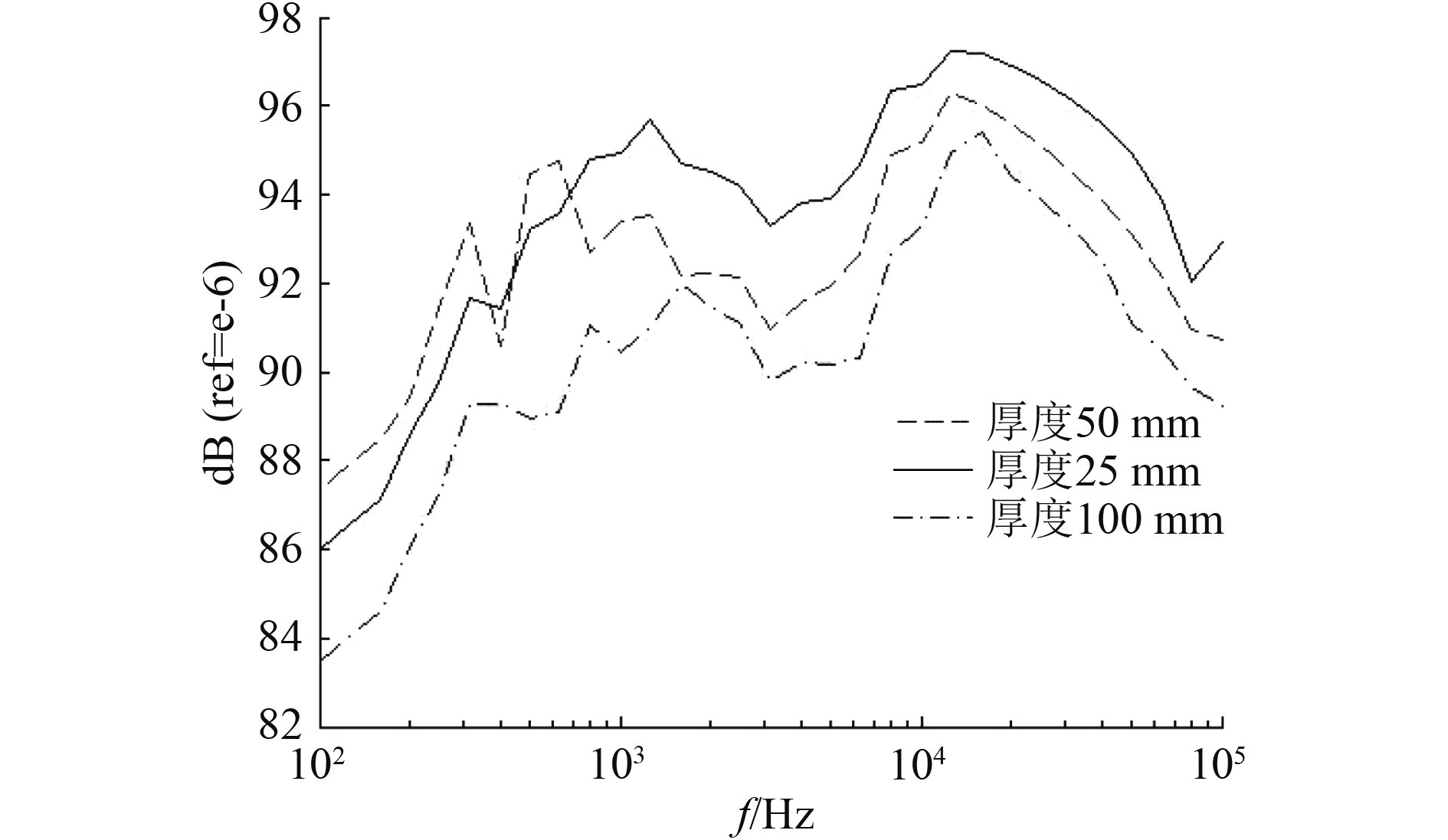
4.3 厚度的影响分别计算阻尼层厚度为25 mm,50 mm和100 mm时,双层圆柱壳的辐射噪声,如图9所示。
|
图 9 辐射声压级 Fig. 9 Radiation sound pressure level |
阻尼材料的厚度会影响整个结构的刚度,阻尼和质量,增加阻尼材料的厚度可能减小结构的刚度,增大结构的阻尼和质量,从而改变结构的振动特性,影响辐射噪声大小。由图9可知,在300 Hz之前,阻尼层的厚度从25 mm变为50 mm时辐射噪声反而增大,在低频时结构的刚度对其振动特性有较大影响,增大阻尼层厚度可能导致结构刚度的降低,使振动更加剧烈,导致辐射噪声增大,在300 Hz之后,增大阻尼层厚度辐射噪声有明显降低;阻尼层厚度对辐射噪声的影响,在整个频带上的基本相同。
5 阻尼材料对不同结构形式圆柱壳的降噪效果阻尼材料对于不同结构形式的圆柱壳,降噪效果可能有所不同。分别建立了实肋板、托板、无连接件的3个双层圆柱壳模型,分析了耐压壳敷设阻尼材料对3种形式的双层圆柱壳的降噪效果。
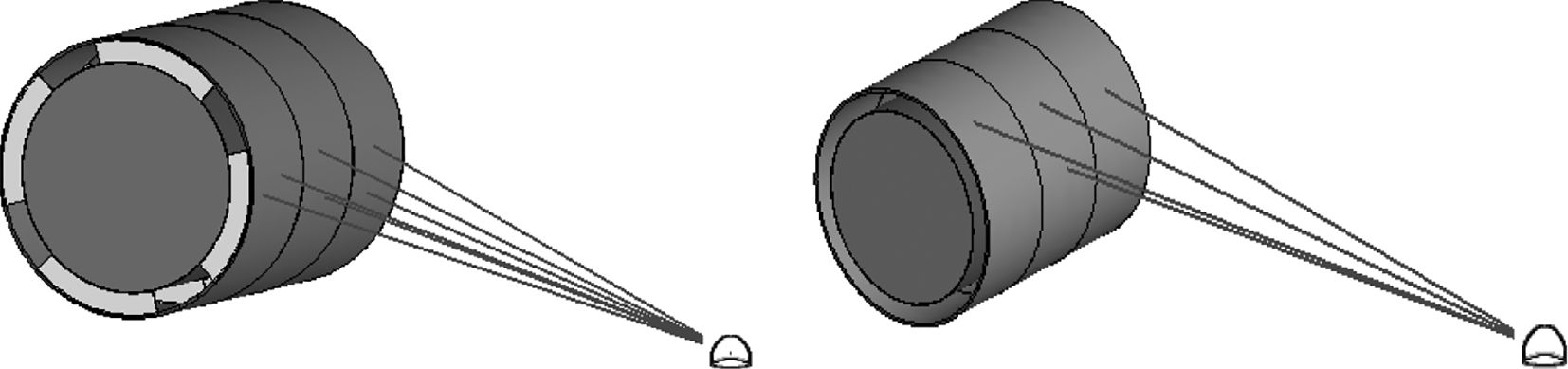
实肋板连接的双层圆柱壳模型如图2所示,托板和无连接件的双层圆柱壳模型如图10所示。耐压壳敷设阻尼材料后3个圆柱壳辐射噪声下降量如图11所示。
|
图 10 托板连接和无连接件圆柱壳 Fig. 10 Pallet connection and connectionless cylindrical shell |
|
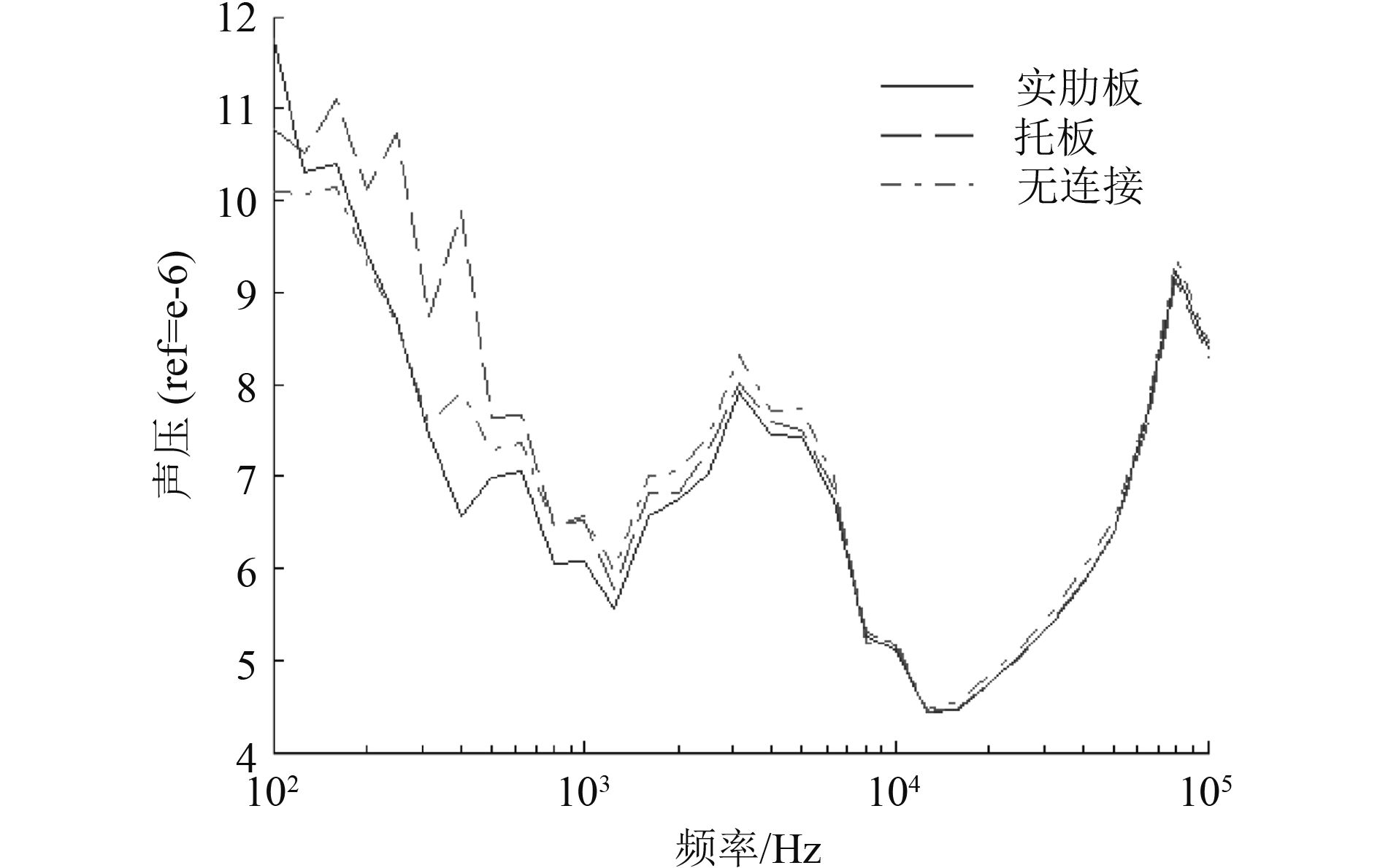
图 11 辐射声压级 Fig. 11 Radiation sound pressure level |
可知,对于3种不同结构形式的圆柱壳,耐压壳敷设阻尼材料后降噪效果比较相似,都能一定程度上降低辐射噪声,但是在不同的频段降噪效果有一定的差异。在1 000 Hz之前,托板连接时阻尼材料的降噪效果最好,比实肋板和无连接件的圆柱壳多降低1 dB左右;1 000~7 000 Hz时,不同结构形式的圆柱壳,阻尼材料降噪效果相差较小,阻尼材料对无连接件的圆柱壳降噪效果最好;在7 000 Hz以后阻尼材料对3种结构的圆柱壳降噪效果几乎相同。
6 结 语本文运用统计能量法及其相应软件AutoSEA2,研究了阻尼材料对双层圆柱壳声辐射特性的影响,得到如下结论:
1)阻尼材料厚度相同时,在耐压壳敷设阻尼材料比在外壳敷设阻尼材料更能抑制结构的振动,降低辐射噪声。
2)增大阻尼材料的杨氏模量能降低结构的辐射噪声;在低频,随着频率的增大,杨氏模量对辐射噪声的影响逐渐增大;在高频,杨氏模量对辐射噪声的影响基本相同。
3)在低频,阻尼材料的损耗因子对结构的辐射噪声影响很小;在高频,增大阻尼材料的损耗因子能够明显降低结构的辐射噪声。
4)在低频,增加阻尼材料的厚度反而可能导致结构辐射噪声的增大;在高频,增加阻尼材料的厚度能够有效的降低结构的辐射噪声。
5)在较低频率时,阻尼材料对托板连接的圆柱壳降噪效果比实肋板和无连接件的圆柱壳好;达到一定频率后对于不同结构形式的圆柱壳,阻尼材料降噪效果相差很小,几乎相同。
| [1] |
RAMASAMY R, GANESAN N. Vibration and damping analysis of fluid filled orthotropic cylindrical shells with constrained viscoelastic damping[J]. Computers & Structures, 1999, 70(3): 363-376. |
| [2] |
陈炜, 骆东平, 张书吉, 等. 敷设阻尼材料的环肋柱壳声辐射性能分析[J]. 声学学报, 2000(1): 27-32. DOI:10.3321/j.issn:0371-0025.2000.01.006 |
| [3] |
LAULAGNET B, GUYADER J L. Sound radiation from finite cylindrical coated shells, by means of asymptotic expansion of three‐dimensional equations for coating[J]. Journal of the Acoustical Society of America, 1994, 96(96): 277-286. |
| [4] |
LAULAGNET B, GUYADER J L. Sound radiation from finite cylindrical shells, partially covered with longitudinal strips of compliant layer[J]. Journal of Sound & Vibration, 1995, 186(186): 723-742. |
| [5] |
LAULAGNET B, GUYADER J L. Sound radiation from a finite cylindrical shell covered with a compliant layer[J]. Journal of Vibration & Acoustics, 1991, 113(2): 267. |
| [6] |
陈美霞, 骆东平, 彭旭, 等. 敷设阻尼材料的双层圆柱壳声辐射性能分析[J]. 声学学报, 2003(6): 486-493. DOI:10.3321/j.issn:0371-0025.2003.06.002 |
| [7] |
陈美霞, 骆东平, 周锋, 等. 阻尼材料敷设方式对双层壳体声辐射性能的影响[J]. 声学学报, 2005(4): 296-302. DOI:10.3321/j.issn:0371-0025.2005.04.002 |
| [8] |
刘向东, 庞福振, 姚熊亮. 敷设阻尼材料的圆柱壳声辐射性能实验分析[J]. 船海工程, 2009(3): 26-31. DOI:10.3963/j.issn.1671-7953.2009.03.009 |
| [9] |
窦松然. 壳体结构振动及声辐射的粘弹性阻尼控制技术研究[D]. 哈尔滨: 哈尔滨工业大学, 2015.
|
| [10] |
王献忠, 孙龙泉, 邱忠辉, 等. 部分敷设阻尼材料的水下结构声辐射分析[J]. 振动与冲击, 2012, 31(18): 122-127. |
| [11] |
田宝晶. 敷设阻尼层的加肋圆柱壳辐射性能及噪声特性分析[D]. 哈尔滨: 哈尔滨工程大学, 2006.
|
| [12] |
UNGAR E E. Loss factors of viscoelastically damped beam structures[J]. Journal of the Acoustical Society of America, 1962, 34(8): 1082-1089. DOI:10.1121/1.1918249 |
| [13] |
姚德源. 统计能量分析原理及其应用[M]. 北京: 北京理工大学出版社, 1995.
|
| [14] |
LYON R H, DEJONG R G, HECKL M. Theory and application of statistical energy analysis, second edition[J]. Journal of the Acoustical Society of America, 1995, 98(6): 3021. |
 2019, Vol. 41
2019, Vol. 41
