基于阻力图谱的船型参数敏感度分析

引用本文

陈佳宝, 徐青, 田斌斌. 基于阻力图谱的船型参数敏感度分析. 舰船科学技术, 2019, 41(2): 14-18 复制到剪切板

CHEN Jia-bao, XU Qing, TIAN Bin-bin. Sensitivity analysis of ship hull parameters based on resistance altas. Ship Science and Technology, 2019, 41(2): 14-18 复制到剪切板

基于阻力图谱的船型参数敏感度分析

陈佳宝, 徐青, 田斌斌

中国舰船研究设计中心，湖北武汉 430064

收稿日期: 2018-05-29.

作者简介: 陈佳宝(1994 – )，男，硕士研究生，研究方向为舰船水动力优化

摘要: 目前，已定性掌握船舶主尺度及主要船型系数对船舶阻力性能的影响趋势，但各个船型参数对阻力性能的具体影响程度仍不明确。为了确定各船型参数对阻力数值的贡献率，基于泰洛系列剩余阻力系数图谱，通过回归分析法，利用Isight软件在不同航速下对棱形系数、排水量长度系数以及宽度吃水比进行对剩余阻力系数的敏感度分析。结果得出各参数对剩余阻力的敏感度指数，并验证了已知船型参数对阻力的影响趋势。结果表明，敏感度分析结果具有较高的可信度，对于船舶设计具有一定的指导意义。

关键词: 船型参数阻力图谱敏感度分析

Sensitivity analysis of ship hull parameters based on resistance altas

CHEN Jia-bao, XU Qing, TIAN Bin-bin

China Ship Development and Design Center, Wuhan 430064, China

Abstract: At present, we have qualitatively grasped the trend of ship's main scale and main ship hull coefficient on the ship's resistance performance, but the specific influence degree of each ship hull parameter on resistance performance is still not clear. In order to determine the contribution rate of each ship hull parameter to the resistance value, based on Taylor's series of residual resistance coefficient altas, through the regression analysis method, the residual coefficient of resistance was calculated using the Isight software at different speeds for sensitivity of the prismatic coefficient, the displace -ment length coefficient and the width draft ratio. The results obtained the sensitivity index of each parameter to the residual resistance, and verified the already known influence of the ship parameters on the resistance. The results show that the sensitivity analysis results have high credibility and have certain guiding significance for ship design.

Key words: ship hull parameters resistance altas sensitivity analysis

0 引　言

现如今，由于能源及环保问题日益突出，船舶作为高耗能行业，节能降耗的要求也日益迫切^[1]。因此，在船舶设计及相关研究中，降低阻力以实现节能降耗一直是研究热点。船型优化作为降低船舶阻力的主要手段，近年来得到了极大关注，很多研究人员在该领域取得了较大的成就。为更好推进船型优化的进一步发展，需要明确所研究的船型参数对阻力性能的影响程度，确定哪些参数对阻力性能影响较大，哪些参数影响不明显，从而为船型优化提供指导方向，敏感度分析可确定上述船型参数对阻力性能的影响程度，采用不同的敏感度分析方法，可定性得出各参数的敏感性排序，或定量得出敏感度数值。

虽然敏感度分析方法已经得到了很大的发展，但其在船舶领域尤其是船舶阻力性能领域应用较少。在公开发表的文献中，国内外相关研究都很少出现。在国外，Valorani等^[2]在2003年根据敏感度公式和伴随方法估算了成本函数梯度，可降低基于阻力最小的船型优化的计算成本。在国内，张恒等对该方向进行了研究，并取得了一定成果，其中2015年，张恒等^[3]基于径向基神经网络利用回归分析法研究船型主尺度参数对阻力性能的敏感度，得到了主尺度参数的敏感度排序；2017年，将基于Kriging模型的TPBF方法和改进的Sobol′s方法用于船型优化，确定了无影响变量，并验证了2种方法的精确度和鲁棒性^[4]。

本文主要研究棱形系数、排水量长度系数以及宽度吃水比在不同航速下对剩余阻力的敏感性，定量得出各参数对剩余阻力的数值。泰洛系列剩余阻力图谱是根据泰洛标准系列船模试验结果整理得到的，可用于船舶剩余阻力近似估算。通过采用泰洛图谱，相比于仿真计算，可保证用于敏感度分析数据的准确性。定量得出敏感度数值，在验证各参数对阻力性能影响趋势的同时，可确定各参数对剩余阻力数值的贡献程度。

1 泰洛系列剩余阻力图谱

为了满足船舶工程师手工计算的需要，各国船模试验水池在过去几十年开展了大量的船模系列试验。在这些船模试验中，经常以直观的图谱形式展示系列试验的结果。在这些图谱中，比较著名的有泰洛系列、陶德系列（又称系列60）等用于分析船型对阻力性能影响的图谱，它们通常根据傅汝德假定将阻力分为摩擦阻力和剩余阻力，通过相当平板摩擦阻力公式计算摩擦阻力，而剩余阻力则通过图谱求得^[5]。

泰洛系列剩余阻力图谱（见图1）最初是由泰洛（Taylor）绘制的单位排水量剩余阻力等值线构成，盖脱勒（Gertler）于1954年将阻力数据重新分析整理，通过修正限制航道、水温及层流的影响，最终整理出1套无量纲剩余阻力系数表。本文选用的敏感度分析数据均来自该系数表。

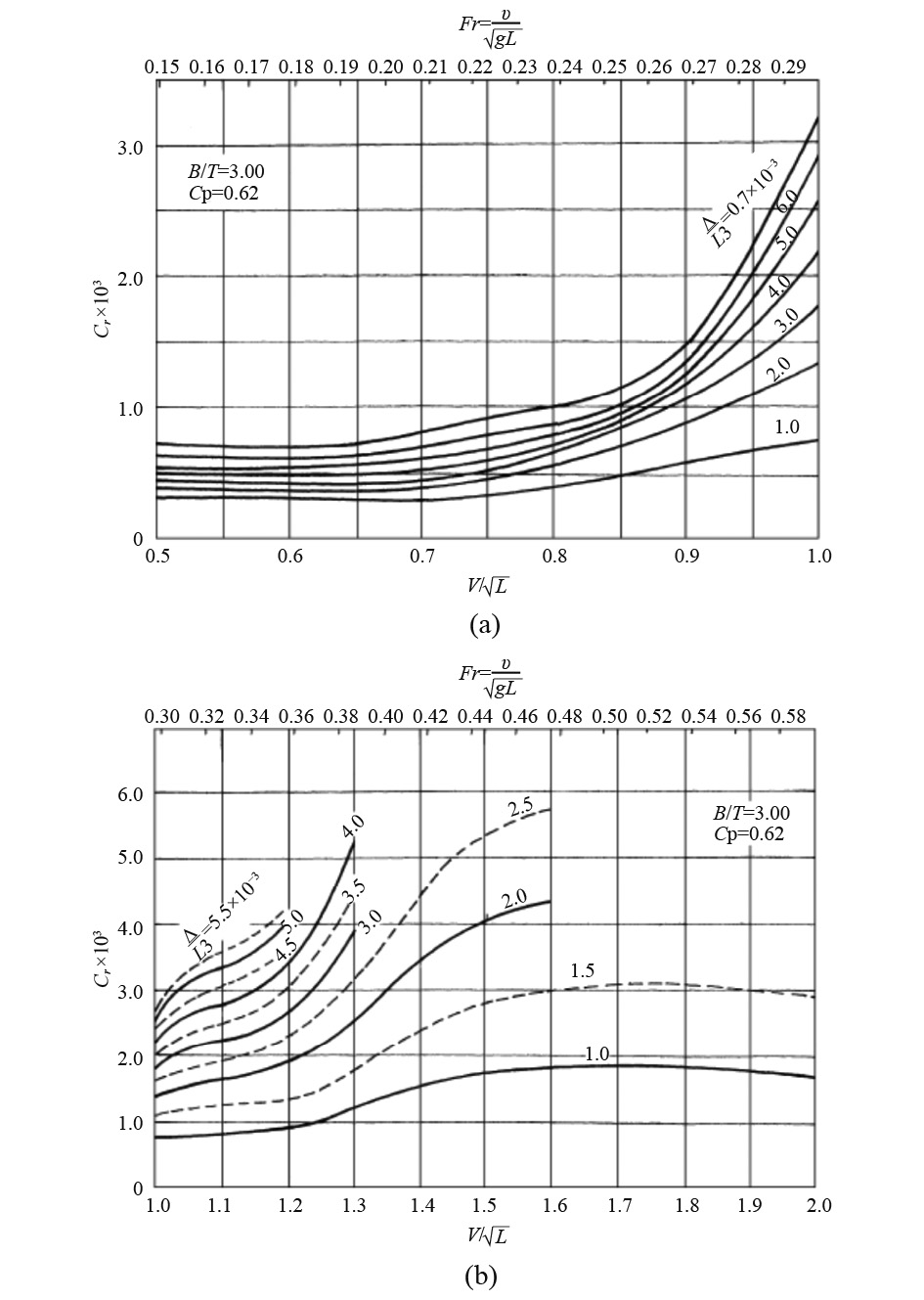
图 1 泰洛系列剩余阻力系数图谱 Fig. 1 Atlas of residual resistance coefficients of Tylor series

目前关于泰洛图谱中的棱形系数、排水量长度系数以及宽度吃水比对剩余阻力的影响已基本了解：棱形系数C_P主要表征排水体积沿船长方向的分布，对剩余阻力具有较大影响，且与航速紧密相关；排水量长度系数 ${{1000\Delta }}/{{{L^3}}}$ 主要表征船舶的瘦长程度，其对剩余阻力的影响需要考虑船长变化和排水量变化2种情况，且与航速有关;宽度吃水比 ${B}/{T}$ 用于表征船体的扁平程度，其对剩余阻力的影响亦需要分别考虑B和T的影响，由泰洛试验结果知，剩余阻力随着 ${B}/{T}$ 减小而趋于减小，但在部分速度范围却增大。以上3个系数包括船舶主尺度数据和船型系数，基本可用于表征船型变化对剩余阻力的影响，但目前主要了解各系数对阻力的影响趋势，通过敏感度分析则可确定各系数对阻力的具体影响程度。

2 船型参数敏感度分析

本文主要针对棱形系数C_P、排水量长度系数 ${{1000\Delta }}/{{{L^3}}}$ 以及宽度吃水比 ${B}/{T}$ 对剩余阻力在不同航速下的影响进行敏感度分析，分析数据以泰洛标准剩余阻力系数图谱为基础，理论方法为最小二乘回归分析法，分析手段为利用Isight软件得到敏感度分析结果。

首先以均匀抽样的原则，从类似表1的泰洛标准剩余阻力系数表中选取相应航速下的部分数据。

表 1 泰洛标准系列剩余阻力系数 $\left(\frac{B}{T} = 2.25 \right)$ Tab. 1 Tylor standard series of residual resistance coefficients $\left(\frac{B}{T} = 2.25\right)$

${C_r} \times {10^3}$ 值
${C_p}$	$\frac{{1000\Delta }}{{{L^3}}}$	Fr
${C_p}$	$\frac{{1000\Delta }}{{{L^3}}}$	0.18	0.20	0.22	0.24	0.26	0.28	0.30	0.32
0.50	1.0	0.20	0.20	0.20	0.20	0.20	0.20	0.24	0.40
	2.0	0.27	0.28	0.28	0.32	0.37	0.40	0.44	0.72
	3.0	0.31	0.32	0.36	0.43	0.50	0.53	0.61	1.00
	4.0	0.36	0.38	0.42	0.52	0.59	0.64	0.77	1.26
	5.0	0.42	0.44	0.49	0.60	0.70	0.73	0.93	1.54
	6.0	0.47	0.49	0.55	0.68	0.82	0.88	–	–
	7.0	0.53	0.56	0.64	0.80	0.99	1.04	–	–
0.60	1.0	0.23	0.23	0.23	0.25	0.28	0.38	0.45	0.46
	2.0	0.28	0.29	0.30	0.37	0.50	0.73	1.01	1.03
	3.0	0.33	0.33	0.38	0.47	0.66	1.02	1.45	1.54
	4.0	0.38	0.40	0.46	0.56	0.80	1.32	1.86	2.00
	5.0	0.45	0.47	0.53	0.64	0.90	1.49	2.18	2.41
	6.0	0.50	0.52	0.60	0.71	1.01	1.67	–	–
	7.0	0.56	0.59	0.68	0.81	1.10	1.82	–	–
0.70	1.0	0.23	0.23	0.28	0.40	0.55	0.81	1.13	1.23
	2.0	0.30	0.32	0.47	0.71	0.97	1.46	2.30	2.47
	3.0	0.37	0.42	0.60	0.87	1.22	1.97	3.26	3.77
	4.0	0.42	0.52	0.71	1.01	1.43	2.48	4.28	5.02
	5.0	0.49	0.59	0.82	1.10	1.56	2.88	–	–
	6.0	0.56	0.68	0.90	1.20	1.68	3.20	–	–
	7.0	0.64	0.77	0.97	1.28	1.82	3.50	–	–
0.80	1.0	0.45	0.62	0.91	1.30	1.45	1.70	2.21	2.18
	2.0	0.53	0.80	1.29	1.94	2.32	2.63	3.77	4.36
	3.0	0.60	0.96	1.58	2.30	3.02	–	5.38	6.64
	4.0	0.67	1.13	1.80	2.54	3.43	–	–	–
	5.0	0.75	1.22	1.96	2.75	–	–	–	–
	6.0	0.83	1.31	2.10	–	–	–	–	–
	7.0	0.90	1.41	2.23	–	–	–	–	–

表 1 泰洛标准系列剩余阻力系数 $\left(\frac{B}{T} = 2.25 \right)$ Tab.1 Tylor standard series of residual resistance coefficients $\left(\frac{B}{T} = 2.25\right)$

本文主要研究低、中、高速下的敏感度，对应的傅汝德数分别选取Fr=0.18，0.24，0.32。由于泰洛系数表中， ${B}/{T}$ 只有2.25，3.00，3.75三个值，因此C_P， ${{1000\Delta }}/{{{L^3}}}$ 也均匀选取3个数值，表2为Fr=0.24时选取的参数及阻力数据。

表 2 船型参数及阻力数据（Fr=0.24） Tab. 2 Ship hull parameters and resistance data (Fr=0.24)

B/T	2.25	2.25	2.25	2.25	2.25	2.25	2.25	2.25	2.25
Cp	0.5	0.5	0.5	0.6	0.6	0.6	0.7	0.7	0.7
1000Δ/L³	2	4	6	2	4	6	2	4	6
Cr×10³	0.32	0.52	0.68	0.37	0.56	0	0.71	1.01	1.2
B/T	3	3	3	3	3	3	3	3	3

Cp	0.5	0.5	0.5	0.6	0.6	0.6	0.7	0.7	0.7
1000Δ/L³	2	4	6	2	4	6	2	4	6
Cr×10³	0.52	0.74	0.96	0.58	0.71	0.86	0.82	1.24	1.4
B/T	3.75	3.75	3.75	3.75	3.75	3.75	3.75	3.75	3.75

Cp	0.5	0.5	0.5	0.6	0.6	0.6	0.7	0.7	0.7
1000Δ/L³	2	4	6	2	4	6	2	4	6
Cr×10³	0.55	0.83	1.12	0.56	0.77	0.97	0.91	1.26	1.48

表 2 船型参数及阻力数据（Fr=0.24） Tab.2 Ship hull parameters and resistance data (Fr=0.24)

将选取的上述数据导入到Isight软件中，利用其中的DOE（试验设计）模块，将参数数据设为因子，阻力数据设为响应，进行拟合回归分析。回归分析法根据上述数据建立多元二次回归模型^{[6 – 7]}：

$ y = {\beta _0} + \sum {{\beta _i}} {x_i} + \sum {{\beta _i}} x_i^2 + \sum\limits_{i \ne j} {{\beta _{ij}}{x_i}{x_j}}{\text{。}} $

式中：y为上述的响应；x为上述的因子；β则可反映对应因子项对响应的贡献率，也即敏感度。

通过回归分析可得到上述回归系数表，并能得到对应的Pareto图、主效应图以及交互效应图，如图2～图10所示。

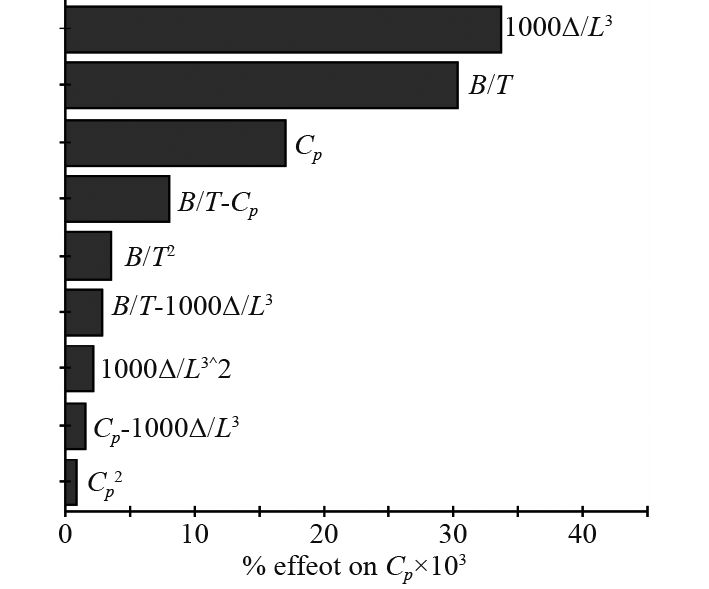
图 2 Pareto图（Fr=0.18） Fig. 2 Pareto diagram (Fr=0.18)

图 10 ${C_P} - \displaystyle\frac{{1000\Delta }}{{{L^3}}}$ 交互效应图 Fig. 10 ${C_P} - \displaystyle\frac{{1000\Delta }}{{{L^3}}}$ Interaction effect diagram

Pareto图可直观反映回归模型中各因子项对响应的贡献率，其值为系数表中的规范化值，深色表示贡献为正，浅色表示贡献为负。主效应图反映因子对响应的主效应，也即因子在某一水平时所有试验中响应的平均值。交互效应图主要反映2个因子的交互对响应的影响，如2条线平行，意为无交互效应，反之，则有交互效应，不平行度反映了交互的强弱程度。回归模型的拟合精确度可通过R²进行验证，R²越接近1，则表示模型越精确^[8]。上述图表均在下列结果分析中出现，并加以分析。

3 敏感度结果及分析 3.1 不同航速下船型参数敏感度分析

本文选取Fr=0.18，0.24，0.32分别代表低、中、高速下的数据进行分析，分析结果如表3所示。

表 3 不同航速下船型参数的敏感度 Tab. 3 Sensitivity of ship hull parameters at different speeds

E/%	F_r
E/%	$\displaystyle\frac{B}{T}$	$ {C_P}$	$\displaystyle\frac{{1000\Delta }}{{{L^3}}}$	${\left( {\displaystyle\frac{B}{T}} \right)^2}$	${\left( {{C_P}} \right)^2}$	${(\displaystyle\frac{{1000\Delta }}{{{L^3}}})^2}$	$\displaystyle\frac{B}{T} - {C_P}$	$\displaystyle\frac{B}{T} - \displaystyle\frac{{1000\Delta }}{{{L^3}}}$	${C_P} - \displaystyle\frac{{1000\Delta }}{{{L^3}}}$
0.18	30.267	16.914	33.68	0.89	0.89	2.226	8.012	2.893	1.558
0.24	13.699	21.907	23.352	–6.532	23.642	–3.237	–2.168	3.121	2.341
0.32	2.267	32.09	27.94	–1.4	14.543	4.108	–0.884	0.709	16.06
表中E/%表示主效应值，也即敏感度； ${\left( {\displaystyle\frac{B}{T}} \right)^2}$ 表示 $\displaystyle\frac{B}{T}$ 的二阶项； $\displaystyle\frac{B}{T} - {C_P}$ 表示 $\displaystyle\frac{B}{T}$ 与 ${C_P}$ 的交互项。

表 3 不同航速下船型参数的敏感度 Tab.3 Sensitivity of ship hull parameters at different speeds

图 3 主效应图（Fr=0.18） Fig. 3 Main effect diagram (Fr=0.18)

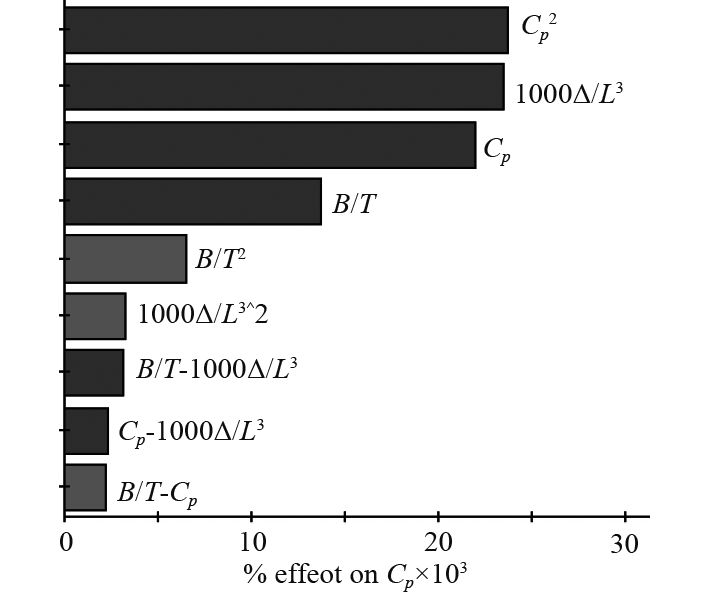
图 4 Pareto图（Fr=0.24） Fig. 4 Pareto diagram (Fr=0.24)

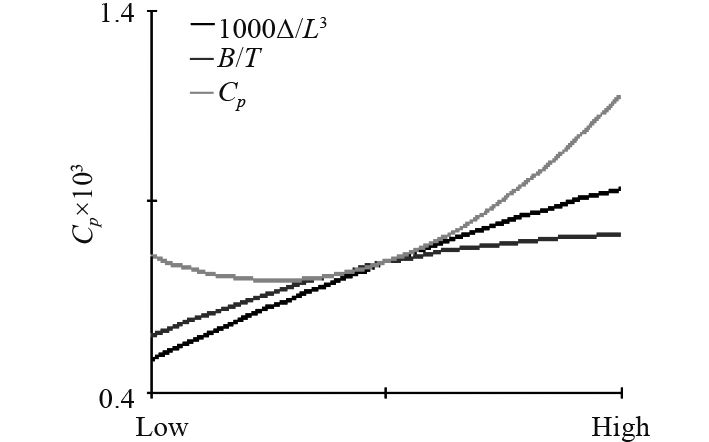
图 5 主效应图（Fr=0.24） Fig. 5 Main effect diagram (Fr=0.24)

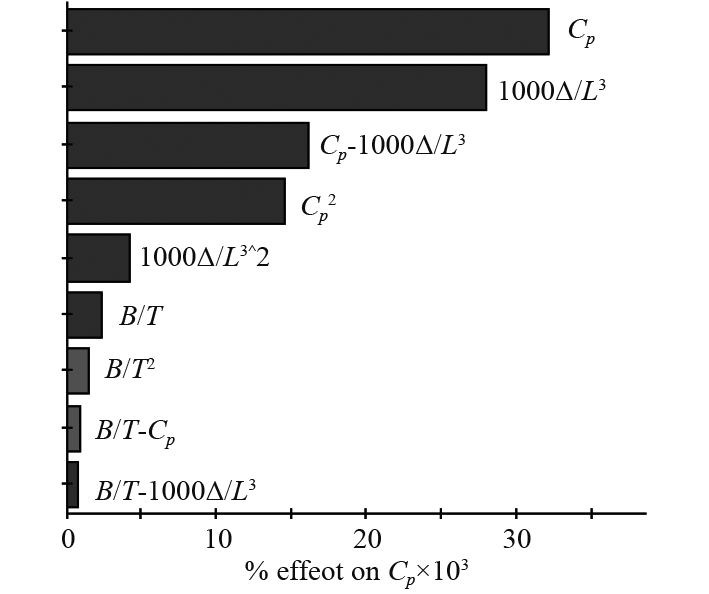
图 6 Pareto图（Fr=0.32） Fig. 6 Pareto diagram (Fr=0.32)

图 7 主效应图（Fr=0.32） Fig. 7 Main effect diagram (Fr=0.32)

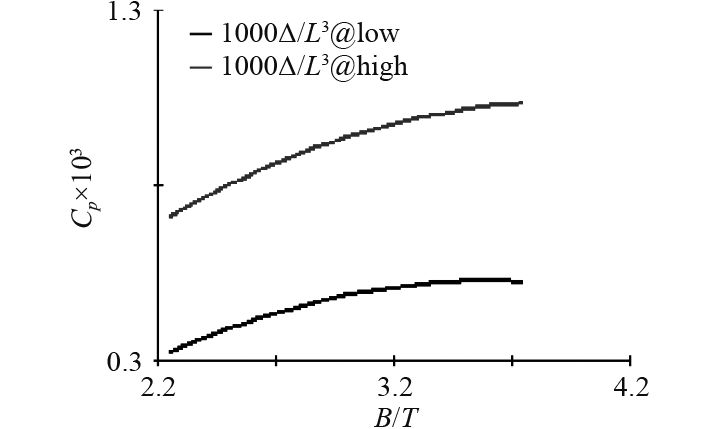
图 8 $\displaystyle\frac{B}{T} - \frac{{1000\Delta }}{{{L^3}}}$ 交互效应图 Fig. 8 $\displaystyle\frac{B}{T} - \frac{{1000\Delta }}{{{L^3}}}$ Interaction effect diagram

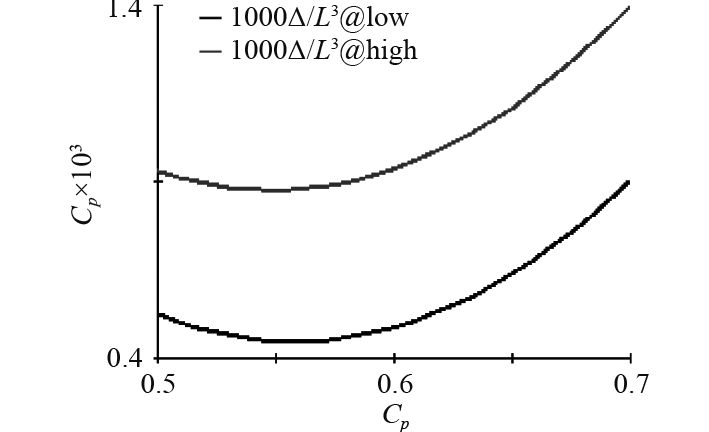
由于交互效应图过多，本文仅展示Fr=0.24时的交互效应图，并对其进行简要分析。

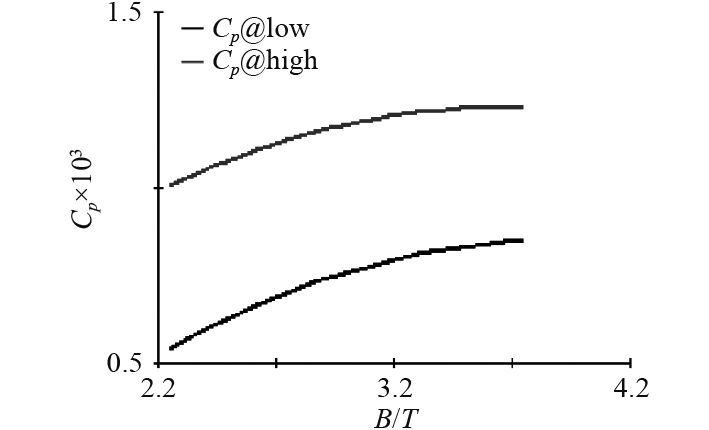
图 9 $\displaystyle\frac{B}{T} - {C_P}$ 交互效应图 Fig. 9 $\displaystyle\frac{B}{T} - {C_P}$ Interaction effect diagram

通过对上述图表进行对比分析，可得出以下结论：

1）棱形系数 ${C_P}$ 、宽度吃水比 ${B}/{T}$ 以及排水量长度系数 ${{1000\Delta }}/{{{L^3}}}$ 的主效应均为正效应，验证了剩余阻力与在这3个系数在一定范围内呈正相关关系。由于这3个参数增加都会使船舶变得肥大，因此剩余阻力会增大。

2）对于棱形系数 ${C_P}$ ，随着航速的升高， ${C_P}$ 的一阶项的主效应逐渐增大，表明 ${C_P}$ 的敏感度随着航速升高逐渐显著。

3）对于宽度吃水比 ${B}/{T}$ ，一阶项的主效应随着航速的升高逐渐减小，表明 ${B}/{T}$ 的敏感度随着航速升高逐渐减弱。

4）对于排水量长度系数 ${{1000\Delta }}/{{{L^3}}}$ ，一阶项的主效应随着航速升高基本不变，均保持一个较高的数值，表明航速对 ${{1000\Delta }}/{{{L^3}}}$ 的敏感度的影响很小，且在不同航速下， ${{1000\Delta }}/{{{L^3}}}$ 均对剩余阻力影响较大。

5）交互效应图中的曲线均趋近于平行，且Pareto图中的交互项数值都很小，表明这3个参数在Fr=0.24的航速下相互影响很小。

3.2 敏感度分析结果精确度验证

回归模型拟合的精确度可通过拟合精确度R²进行验证，以上3个模型的R²如表4所示。

表 4 回归模型拟合精确度R² Tab.4 Regression model fitting accuracy R²

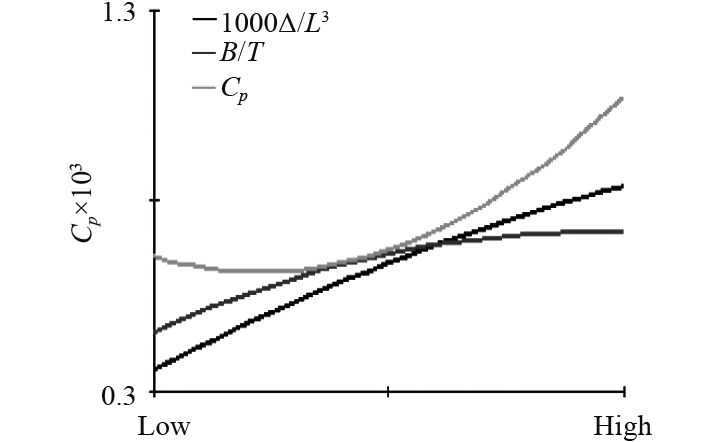
由表4可知，拟合精确度R²均接近于1，故回归模型满足精度要求。但是，由于用于敏感度分析的数据较少，每次分析只有27组样本点，分析的准确度还需要加以验证。由于 ${B}/{T}$ 只有3个值，而 ${{1000\Delta }}/{{{L^3}}}$ 有7个值1～7，按照均匀分布的原则，上述分析均选取了2、4、6，以下将对Fr=0.24， ${{1000\Delta }}/{{{L^3}}}$ 选取1，3，5时的参数敏感度进行分析，并与上述结果进行比较。分析结果如图11和图12所示。

图 12 主效应图（ $\displaystyle\frac{{1000\Delta }}{{{L^3}}}$ 取1，3，5） Fig. 12 Main effect diagram ( $\displaystyle\frac{{1000\Delta }}{{{L^3}}}$ takes 1, 3, 5)

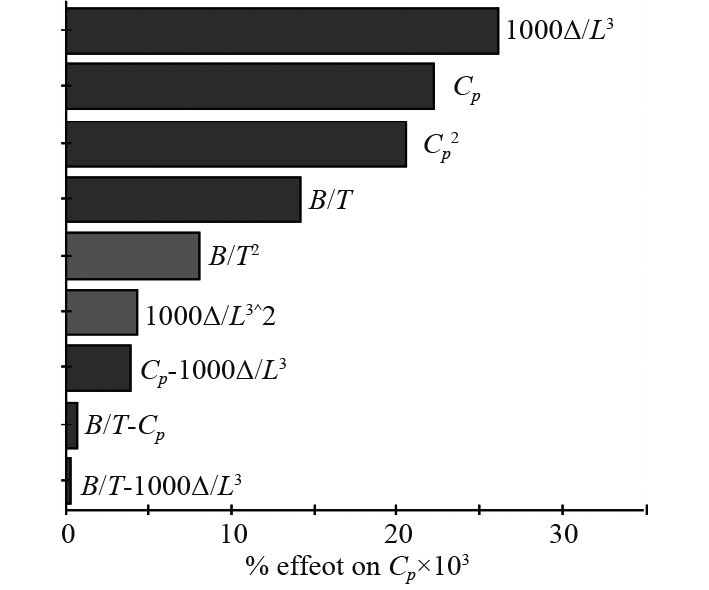
图 11 Pareto图（ $\displaystyle\frac{{1000\Delta }}{{{L^3}}}$ 取1，3，5） Fig. 11 Pareto diagram ( $\displaystyle\frac{{1000\Delta }}{{{L^3}}}$ takes 1, 3, 5)

通过对比Fr=0.24， ${{1000\Delta }}/{{{L^3}}}$ 取2，4，6时的Pareto图和主效应图，发现2种情况下的各参数项的主效应基本相同，说明 ${{1000\Delta }}/{{{L^3}}}$ 取1，3，5与取2，4，6时的敏感度分析结果基本一致，从而从侧面验证了上述敏感度分析结果的准确性。

4 总结与展望

本文基于泰洛标准系列剩余阻力系数图谱采用回归分析法对棱形系数C_P、排水量长度系数 ${{1000\Delta }}/{{{L^3}}}$ 以及宽度吃水比 ${B}/{T}$ 对剩余阻力在不同航速下的影响进行了敏感度分析，分别得出了低、中、高航速下各参数对剩余阻力系数的贡献率。通过分析Pareto图、主效应图以及交互效应图，验证了剩余阻力与3个参数的正相关关系，确定了航速对3个参数的敏感度的影响，并得出了Fr=0.24时3个参数间的交互效应很小的结论。3个航速下，回归模型的拟合精确度R²均接近于1，且在Fr=0.24时 ${{1000\Delta }}/{{{L^3}}}$ 取1，3，5与取2，4，6时的敏感度分析结果基本一致，一定程度上验证了结果的精确度。

由于本文的数据基于泰洛图谱，可供分析的参数和阻力数据较少，且参数局限于船型系数和主尺度，阻力局限于剩余阻力。后续将通过仿真计算结合试验验证，分析更多的船型特征，并针对总阻力及每一个阻力成分进行敏感度分析，从而确保结果具有更高的普适性。

参考文献

[1]	LU Y, CHANG X, HU A. A hydrodynamic optimization design methodology for a ship bulbous bow under multiple operating conditions[J]. Engineering Applications of Computational Fluid Mechanics, 2016, 10(1): 331-346.
[2]	VALORANI M, PERI D, CAMPANA E F. Sensitivity analysis methods to design optimal ship hulls[J]. Optimization & Engineering, 2003, 4(4): 337-364.
[3]	张恒, 詹成胜, 刘祖源, 等. 基于船舶阻力性能的船型主尺度参数敏感度分析[J]. 船舶工程, 2015(6): 11-14. Zhang H, Zhan C, Liu Z, et al. Sensitivity analysis of ship hull dimensions based on ship resistance performance[J]. Ship Engineering, 2015(6): 11-14.
[4]	LIU Q, FENG B, LIU Z, et al. The improvement of a variance-based sensitivity analysis method and its application to a ship hull optimization model[J]. Journal of Marine Science & Technology, 2017(10): 1-16.
[5]	盛振邦, 刘应中. 船舶原理[M]. 上海: 上海交通大学出版社, 2004. Sheng Zhenbang, Liu Yingzhong. Ship principle[M]. Shanghai Jiao Tong University press, 2004.
[6]	赖宇阳. Isight参数优化理论与实例详解[M]. 北京: 北京航空航天大学出版社, 2012. Lai Yuyang. Isight parameter optimization theory and case study[M]. Beihang University press, 2012.
[7]	罗鹏程, 傅攀峰. 武器装备敏感性分析方法综述[J]. 计算机工程与设计, 2008, 29(21): 5546-5549. Luo Pengcheng, Fu Panfeng. Summary of sensitivity analysis methods for weapon and equipment[J]. Computer Engineering and Design, 2008, 29(21): 5546-5549.
[8]	李睿. Sobol′灵敏度分析方法在结构动态特性分析中的应用研究[D]. 长沙: 湖南大学, 2003. Li Rui. Sobol'sensitivity analysis method applied in structural dynamic characteristics analysis[D]. Hunan University, 2003.


舰船科学技术 2019, Vol. 41 Issue (2): 14-18	PDF