2. 沈阳新松机器人自动化股份有限公司 移动机器人事业部,辽宁 沈阳 110169
2. Business Group of Mobile Robot, SIASUN Robot and Automation Co., Ltd., Shenyang 110169, China
船舶与海洋工程结构在建造和营运过程中不可避免地存在一些裂纹,这些裂纹在交变载荷作用下将会发生扩展,最终可能会导致结构发生断裂失效,严重影响结构的安全使用。采用数值方法预报含裂纹结构裂纹扩展形貌及扩展寿命具有重要的工程应用价值,可为结构裂纹检测周期的确定、疲劳寿命评估及抗疲劳设计提供支撑。结构裂纹前缘应力强度因子(SIF)是含裂纹结构疲劳裂纹扩展形貌及寿命数值预报方法中的关键参数,一些学者提出了采用奇异单元求解裂纹尖端应力强度因子的有限元模型,并以裂纹最深点及裂纹端点处的应力强度因子作为计算参量模拟简单焊接接头裂纹面内扩展形貌[1 – 5]。然而,由于工程结构承受载荷复杂性及结构中裂纹分布随机性致使结构最大主应力与裂纹平面并不垂直,裂纹扩展形貌将不再保持平面。结构三维裂纹前缘各个位置处应力强度因子准确计算将是模拟真实裂纹扩展形貌的前提。
文中基于20节点奇异单元1/4节点位移法,提出三维裂纹网格划分方法及裂纹前缘不同位置、不同类型应力强度因子的计算方法。采用平板表面裂纹研究三维裂纹整个裂纹前缘各个位置应力强度因子随裂纹网格划分参数变化情况,通过整个裂纹前缘应力强度因子数值计算结果与Newman-Raju解析公式[6]计算结果的对比分析,验证了数值计算方法的准确性,最终提出裂纹网格划分参数取值范围。为了验证文中提出的数值计算方法计算其他类型裂纹前缘应力强度因子的准确性,采用数值计算方法计算分析了疲劳裂纹扩展三点弯曲试样裂纹扩展过程中裂纹前缘应力强度因子,并与解析解进行对比分析,验证了数值计算方法计算穿透性裂纹前缘应力强度因子的准确性。
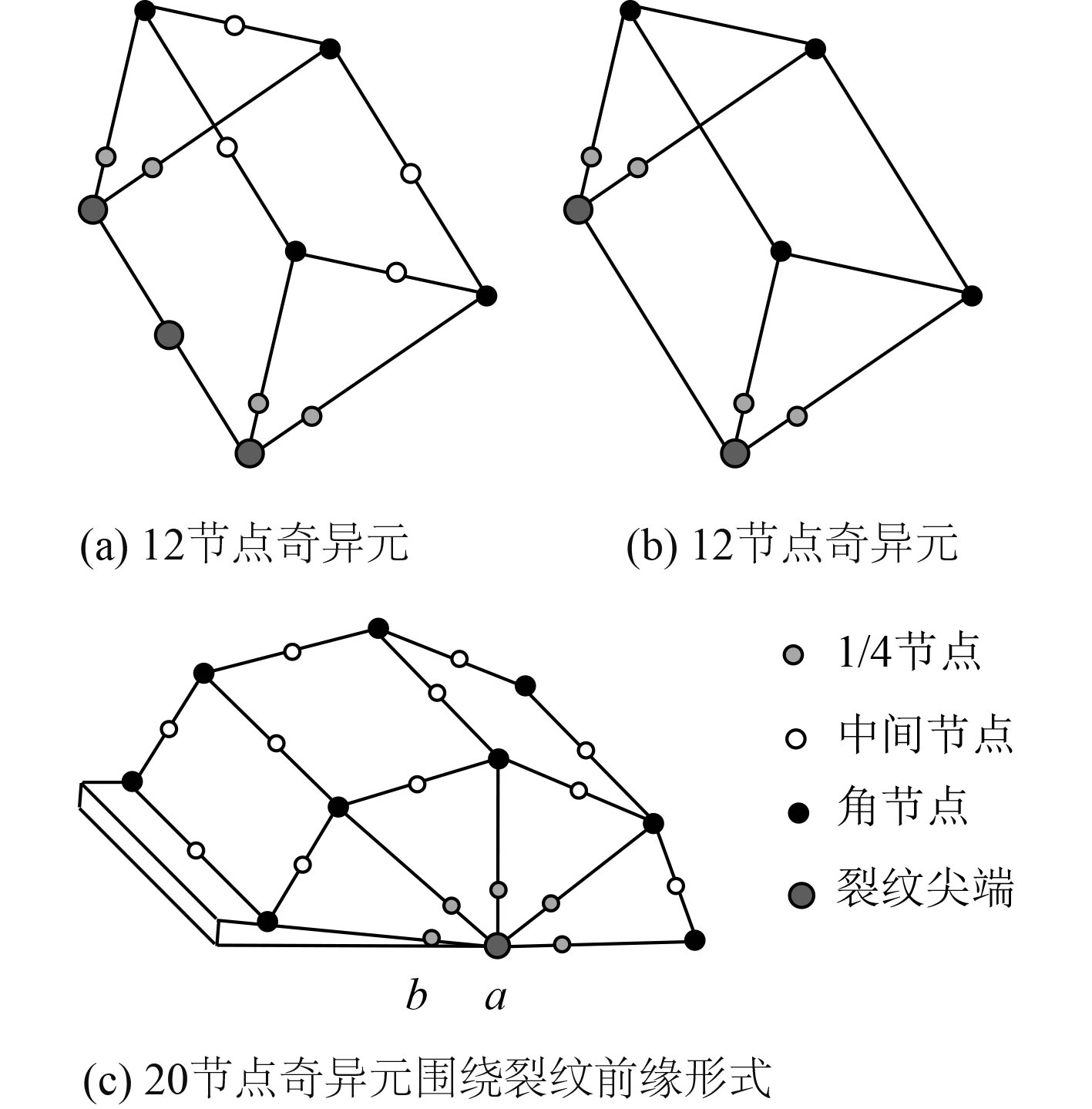
1 三维裂纹应力强度因子有限元法相比于应力外推法,位移法是裂纹前缘应力强度因子计算相对较稳定的方法。位移法采用蜕化的20节点或12节点等参单元奇异单元描述裂纹前缘的应力和应变场的奇异性,通常将裂纹前缘第1层单元设置为奇异单元,围绕第1层奇异单元的其余各层单元为相应等参单元,形式如图1所示。
|
图 1 奇异单元类型及其围绕裂纹前缘形式 Fig. 1 Singular element types and form of singular elements around crack tip |
Shaw和Henshell[7]以及Barsoum等[8]证明了通过将蜕化的20节点等参单元的中间节点移动至1/4位置处便可以获得
直角坐标系下应力裂纹前缘位移张量矩阵为
| $\begin{split} &\left[ {{u_i}} \right] = \left[ {\begin{array}{*{20}{c}} {{u}}\\ {{v}}\\ {{w}} \end{array}} \right] =\\ &\quad \left[ \begin{aligned} & \displaystyle\frac{{{K_I}}}{{4\mu }}\sqrt {\displaystyle\frac{r}{{2{\text{π}} }}} \left[ {\left( {2\kappa \!-\! 1} \right)\cos \displaystyle\frac{\theta }{2} - \cos \displaystyle\frac{{3\theta }}{2}} \right] \!+\!\\ &\quad \displaystyle\frac{{{K_{II}}}}{{4\mu }}\sqrt {\displaystyle\frac{r}{{2{\text{π}} }}} \left[ {\left( {2\kappa \!+\! 3} \right)\sin \displaystyle\frac{\theta }{2} \!+\! \sin \frac{{3\theta }}{2}} \right]\\ & \displaystyle\frac{{{K_I}}}{{4\mu }}\sqrt {\displaystyle\frac{r}{{2{\text{π}}}}} \left[ {\left( {2\kappa \!+\! 1} \right)\sin \displaystyle\frac{\theta }{2} \!-\! \sin \frac{{3\theta }}{2}} \right] \!-\!\\ &\quad \displaystyle\frac{{{K_{II}}}}{{4\mu }}\sqrt {\frac{r}{{2{\text{π}} }}} \left[ {\left( {2\kappa \!-\! 3} \right)\cos \frac{\theta }{2} + \cos \frac{{3\theta }}{2}} \right]\\ & \!-\! \displaystyle\frac{{\upsilon ''z}}{E}\left( {{\sigma _{xx}} \!+\! {\sigma _{yy}}} \right) \!+\! \displaystyle\frac{{2{K_{III}}}}{\mu }\sqrt {\left( {\frac{r}{{2{\text{π}} }}} \right)} \sin \frac{\theta }{2} \end{aligned} \right]{\text{,}} \end{split}$ | (1) |
其中:KI,KII和KIII分别为Ⅰ型、Ⅱ型和Ⅲ型应力强度因子;r为距离裂纹前缘的距离;E为杨氏模量;μ为剪切模量;υ"为材料参数,平面应力状态υ"=υ为泊松比,平面应变状态υ"=0;κ为材料参数,平面应力状态κ=(3-υ)/(1+υ),平面应变状态κ=3−4υ;σxx和σyy为直角坐标系下裂纹前缘应力分量。
在式(1)中令r=ra-b,那么通过求解θ=π平面上裂纹尖端点a和1/4位置处节点b处y方向位移便可求得KΙ,通过求解θ=π平面上裂纹尖端点a和1/4位置处节点b处x方向位移便可求得KΙΙ,通过求解θ=π平面上裂纹尖端点a和1/4位置处节点b处z方向位移便可求得KΙΙΙ。
3种类型应力强度因子表达式分别为:
| $ {K_I} = \frac{{2\mu }}{{\kappa + 1}}\sqrt {\frac{{2{\text{π}}}}{{{r_{a - b}}}}} \left( {{{\rm{v}}_b} - {{\rm{v}}_a}} \right){\text{,}} $ | (2) |
| $ {K_{II}} = \frac{{2\mu }}{{\kappa + 1}}\sqrt {\frac{{2{\text{π}} }}{{{r_{a - b}}}}} \left( {{{\rm{u}}_b} - {{\rm{u}}_a}} \right){\text{,}} $ | (3) |
| $ {K_{III}} = \mu \sqrt {\frac{{\text{π}} }{{2{r_{a - b}}}}} \left( {{{\rm{w}}_b} - {w_a}} \right){\text{。}} $ | (4) |
其中:ua,ub分别为裂纹前缘端点及1/4位置处节点直角坐标系下x方向位移;va,vb分别为裂纹前缘端点及1/4位置处节点直角坐标系下y方向位移;wa,wb分别为裂纹前缘端点及1/4位置处节点直角坐标系下z方向位移。
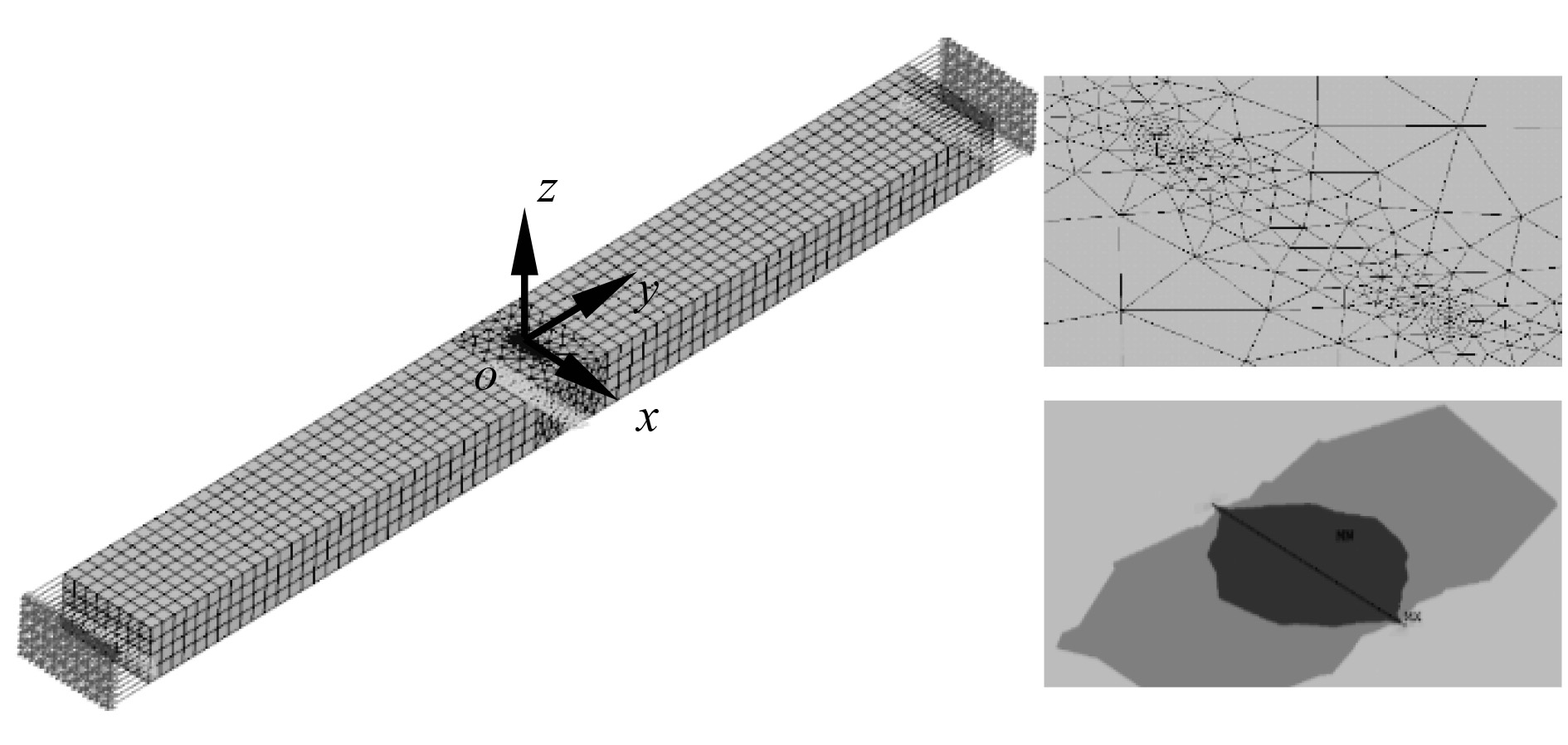
2 三维裂纹体有限元模型本文采用Ansys中20节点solid95单元建立含半椭圆表面裂纹平板有限元模型,深入研究裂纹网格剖分方式,分析裂纹前缘应力强度因子计算结果对网格划分参数的敏感性,最终确定计算裂纹前缘应力强度因子稳定可靠的奇异单元网格划分形式。建立的含有半椭圆表面裂纹的有限元模型如图2所示,平板长度600 mm,宽度60 mm,厚度35 mm,裂纹长度为2c=10 mm,裂纹深度为a=10 mm。平板长度两端承受垂直裂纹面方向的100 MPa均匀拉伸载荷作用。坐标原点位于裂纹长度中心,x轴为裂纹长度方向,y轴为平板长度方向。
|
图 2 含半椭圆表面裂纹平板结构有限元模型 Fig. 2 Surface cracked plate finite element model |
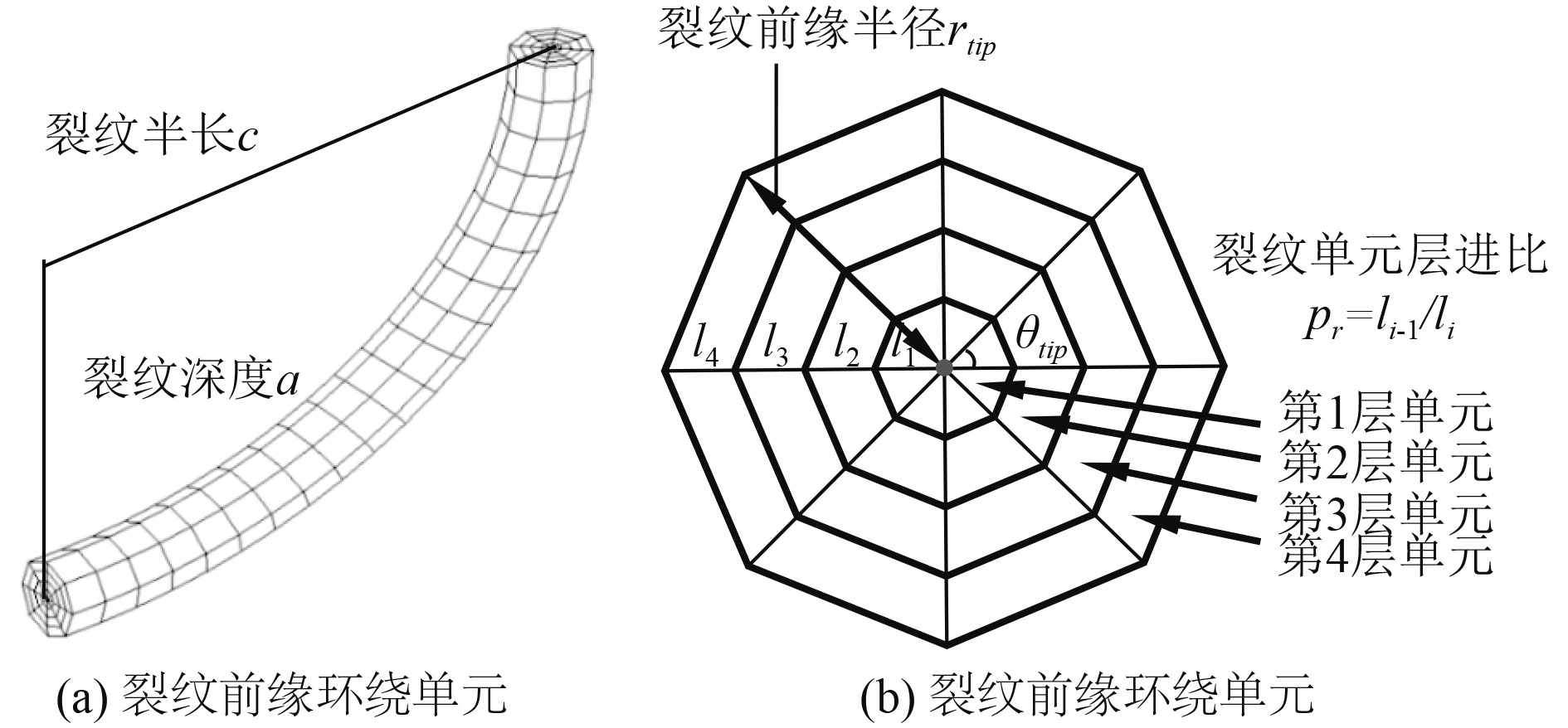
裂纹前缘网格剖分方式及裂纹前缘截面形状如图3所示,影响裂纹前缘应力强度因子计算精度的主要参数有裂纹前缘单元层数ntip、裂纹前缘单元夹角θtip、裂纹前缘单元层渐比pr以及裂纹前缘半径rtip。
|
图 3 裂纹前缘有限元网格划分示意图 Fig. 3 Mesh around crack front |
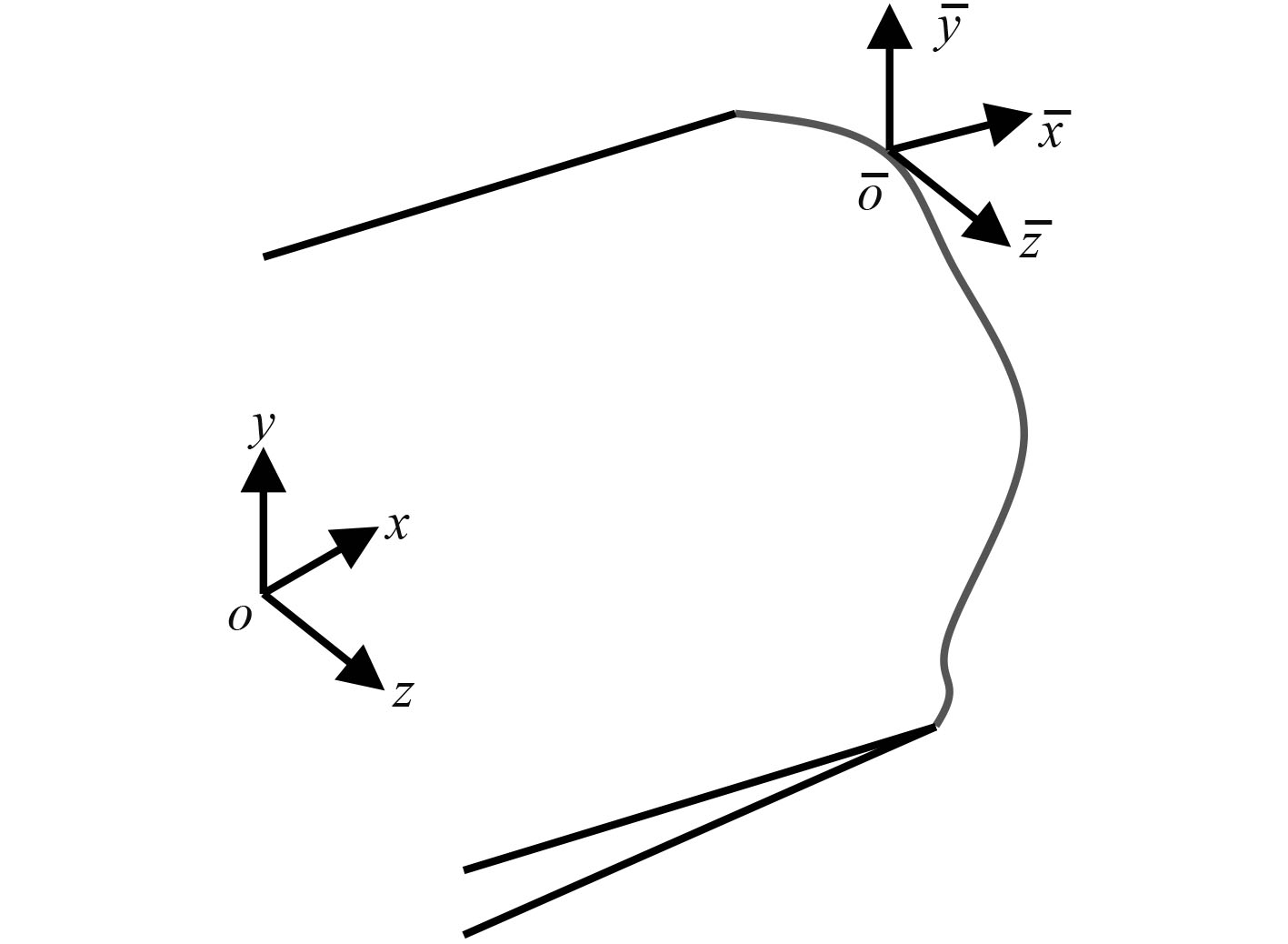
三维裂纹整个裂纹前缘各节点应力强度因子的计算是在以裂纹前缘各个节点自身位置为坐标原点所建立的局部坐标系中进行的,整个裂纹前缘各节点局部坐标系如图4所示。其中裂纹前缘各节点局部坐标系的
|
图 4 裂纹前缘各节点局部坐标系 Fig. 4 Local coordinate of the crack front |
针对所建立的含裂纹平板结构有限元模型,分析整个裂纹前缘各个节点应力强度因子随裂纹网格划分参数的变化情况,并与经典的Newman-Raju平板表面裂纹应力强度因子解析公式(5)进行对比,以验证求解应力强度因子数值方法的准确性,并给出网格划分参数范围建议值。
| $ {K_I} = Y\left( {\frac{a}{t},\frac{a}{c},\frac{c}{{2W}},\varphi } \right)\left( {{\sigma _t} + H{\sigma _b}} \right)\frac{{\sqrt {{\text{π}} a} }}{{E\left( k \right)}}{\text{,}} $ | (5) |
式中:Y为裂纹几何修正因子;σt为名义拉伸应力;σb为名义弯曲应力;H为弯曲载荷应力梯度修正系数;a为裂纹深度;E(k)为第2类椭圆积分。
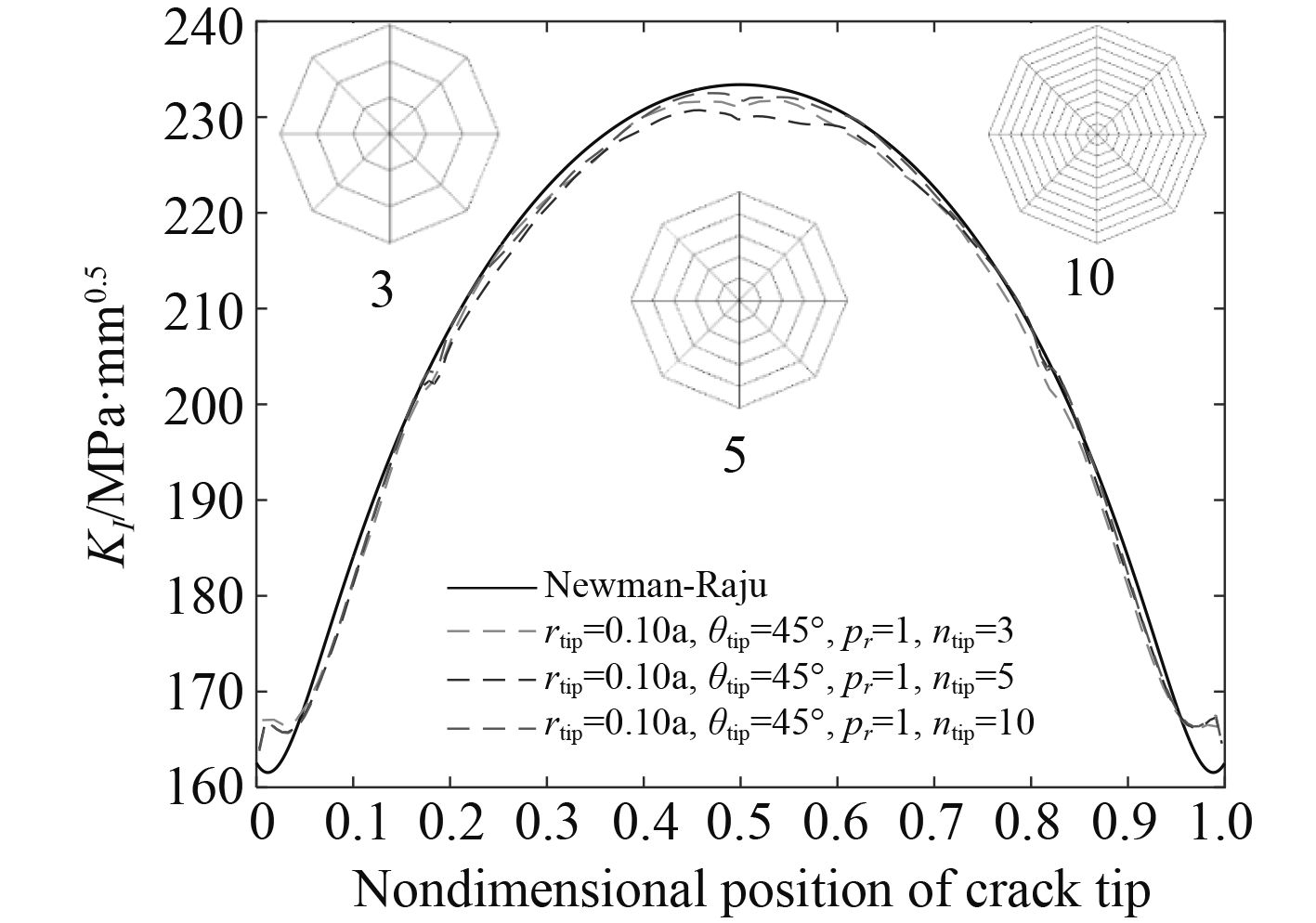
3.1 单元层数ntip对SIF计算结果的影响取裂纹前缘半径rtip=0.1a,裂纹前缘单元夹角θtip=45°,裂纹前缘环绕单元层渐比pr=1.0,裂纹前缘单元层数ntip分别取3,5和10。不同单元层数时裂纹前缘截面及100 MPa均匀拉应力作用下裂纹前缘应力强度因子如图5所示。
|
图 5 不同单元层数裂纹前缘应力强度因子分布 Fig. 5 SIFs along crack front for different ntip |
采用20节点奇异元计算应力强度因子时,环绕裂纹前缘单元层数ntip的变化对应力强度因子的影响很小,整个裂纹前缘应力强度因子有限元值均在理论值附近,最大相对误差不超过2%(裂纹最深点)。因此,建立裂纹有限元模型时,ntip可取3~10之间的任意值。
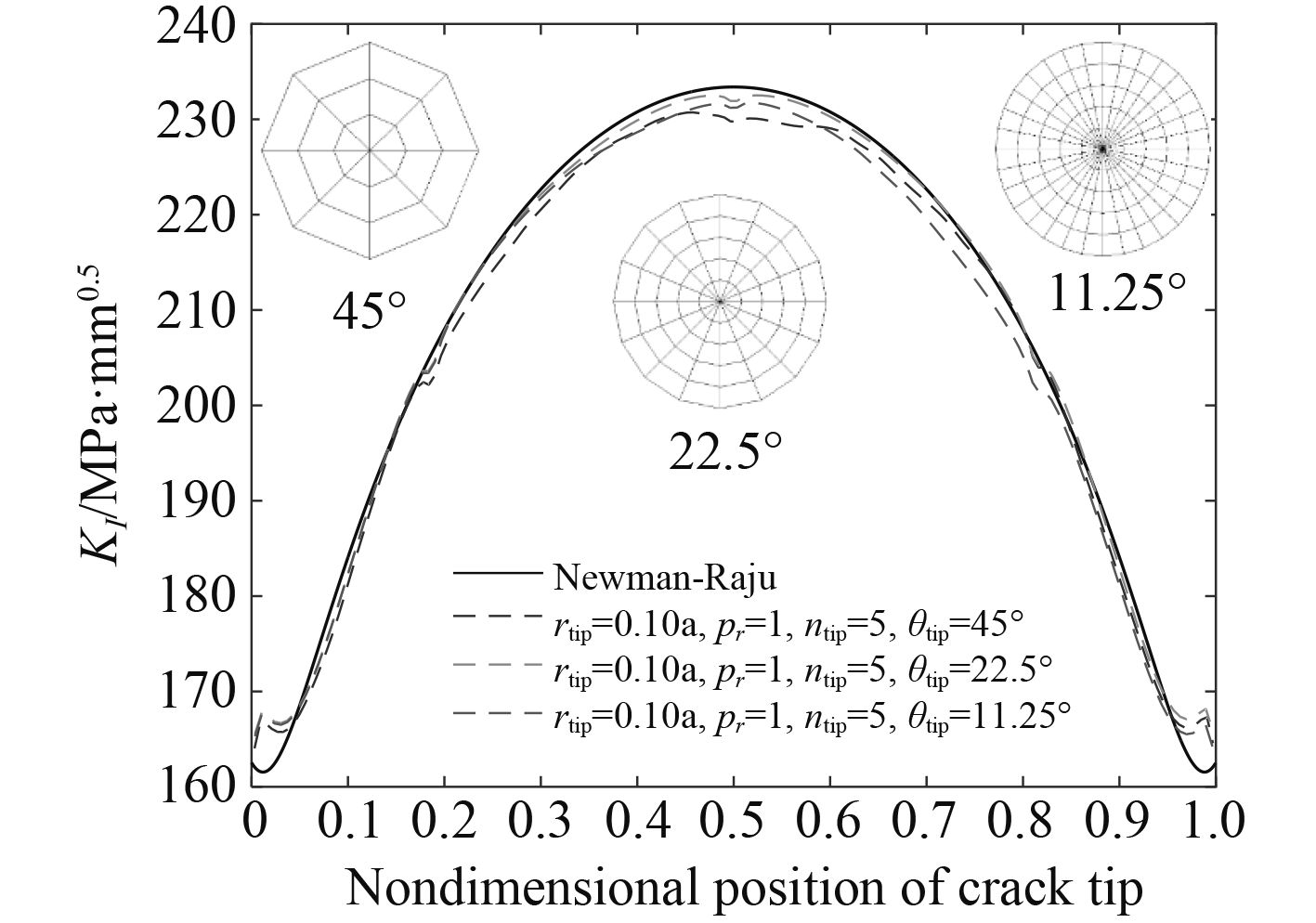
3.2 单元夹角θtip对SIF计算结果的影响取裂纹前缘半径rtip=0.1a,裂纹前缘环绕单元层渐比pr=1.0,裂纹前缘单元层数ntip=5,裂纹前缘单元夹角θtip分别取为45°(每层环绕单元数为8),22.5°(每层环绕单元数为16)和11.25°(每层环绕单元数为32)。不同单元夹角时裂纹前缘截面及100 MPa均匀拉应力作用下裂纹前缘应力强度因子如图6所示。
|
图 6 不同单元夹角裂纹前缘应力强度因子分布 Fig. 6 SIFs along crack front for different θtip |
采用20节点奇异元计算应力强度因子时,裂纹前缘单元层数ntip的变化对应力强度因子的影响很小,整个裂纹前缘应力强度因子有限元值均在理论值附近,最大相对误差不超过2%(裂纹最深点)。建立有限元模型时,为了提高计算效率,建议θtip取45°,即环绕裂纹前缘的每层单元数目为8个。
3.3 单元层渐比pr对SIF计算结果的影响如图3(b)所示,定义裂纹前缘层渐比为相邻两层单元之间长度比值:
| $ {p_r} = \frac{{{l_{i - 1}}}}{{{l_i}}}\left( {2 \text{≤} i \text{≤} {n_{tip}}} \right){\text{。}} $ | (6) |
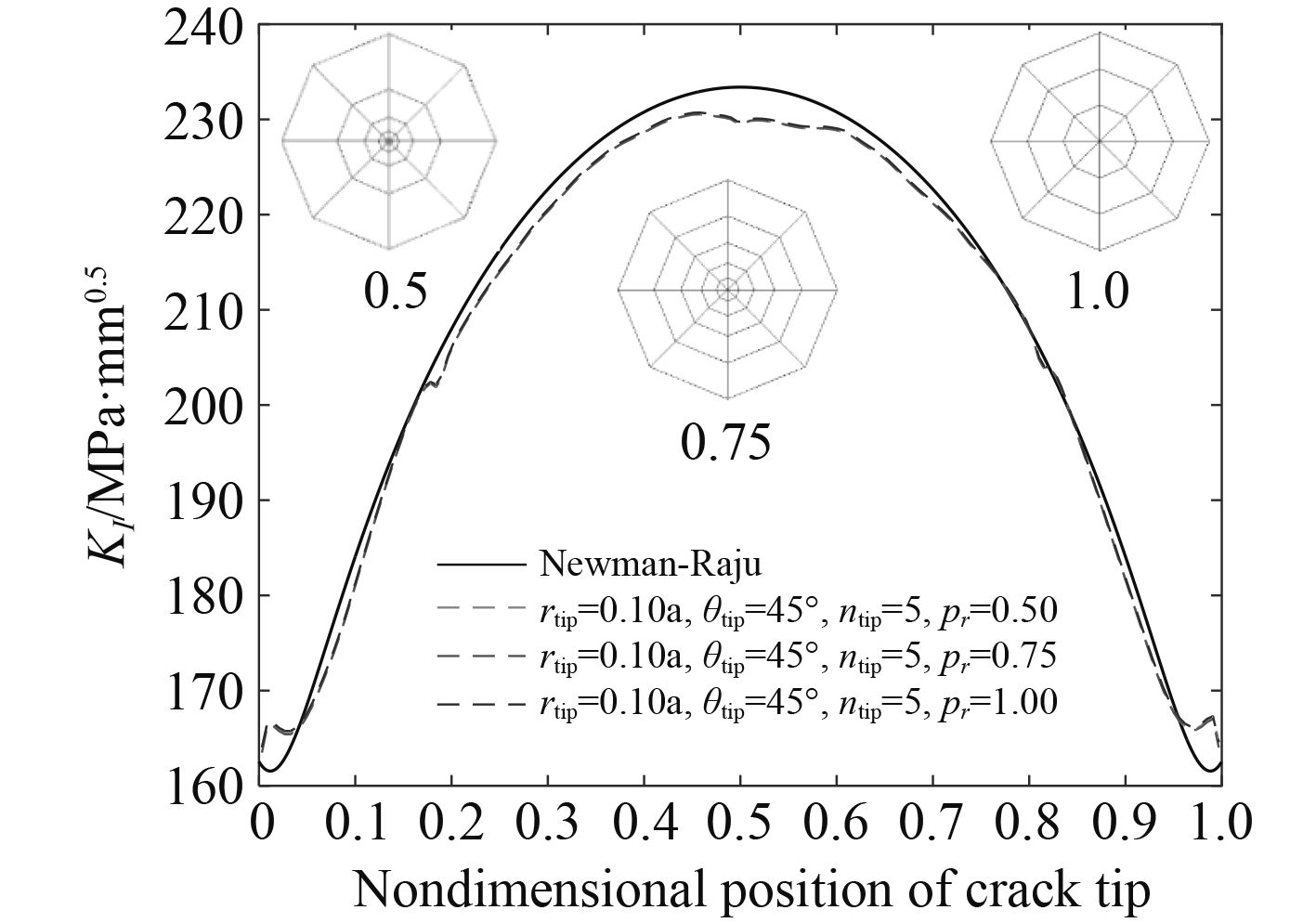
取裂纹前缘半径rtip=0.1a,裂纹前缘单元层数ntip=5,裂纹前缘单元夹角θtip=45°,裂纹前缘环绕单元层渐比pr分别取为0.5,0.75和1.0。不同单元层渐比时裂纹前缘截面及100 MPa均匀拉应力作用下裂纹前缘应力强度因子如图7所示。
|
图 7 不同单元层渐比裂纹前缘应力强度因子分布 Fig. 7 SIFs along crack front for different pr |
采用20节点奇异元计算应力强度因子时,裂纹前缘单元层渐比pr的变化对应力强度因子几乎没有影响,整个裂纹前缘应力强度因子有限元值均在理论值附近,最大相对误差不超过2%(裂纹最深点)。建立有限元模型时,建议pr取1.0。
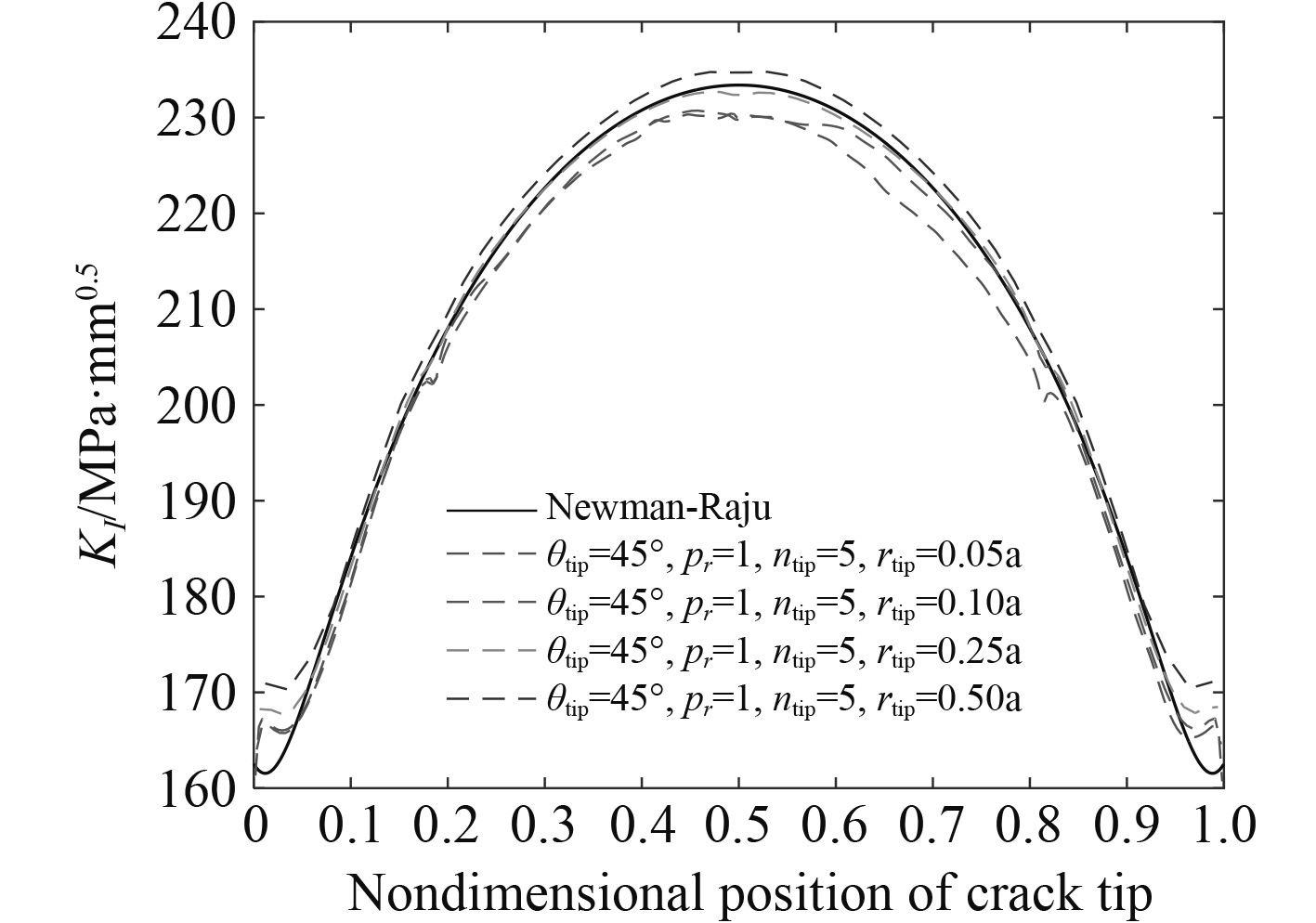
3.4 裂纹前缘半径rtip对SIF计算结果的影响裂纹前缘环绕单元层渐比pr=1.0,裂纹前缘单元层数ntip=5,裂纹前缘单元夹角θtip=45°,裂纹前缘半径rtip分别取为0.05a,0.10a,0.25a和0.50a。不同裂纹前缘半径时裂纹前缘截面及100 MPa均匀拉应力作用下裂纹前缘应力强度因子如图8所示。
|
图 8 不同前缘半径裂纹前缘应力强度因子分布 Fig. 8 SIFs along crack front for different rtip |
采用20节点奇异元计算应力强度因子时,裂纹前缘应力强度因子随裂纹前缘半径rtip的增大而变大,整个裂纹前缘应力强度因子有限元值均在理论值附近,最大相对误差不超过2%(裂纹最深点)。建立有限元模型时,裂纹前缘半径rtip可在0.05~0.50a之间取值。
4 三点弯曲试样SIF计算结果验证文中第3节验证了所建立的有限元模型求解表面裂纹应力强度因子的有效性,为进一步验证文中建立的三维裂纹有限元计算应力强度因子的准确性,选取标准裂纹扩展速率三点弯曲试样建立有限元模型求解单边穿透裂纹应力强度因子进行分析。
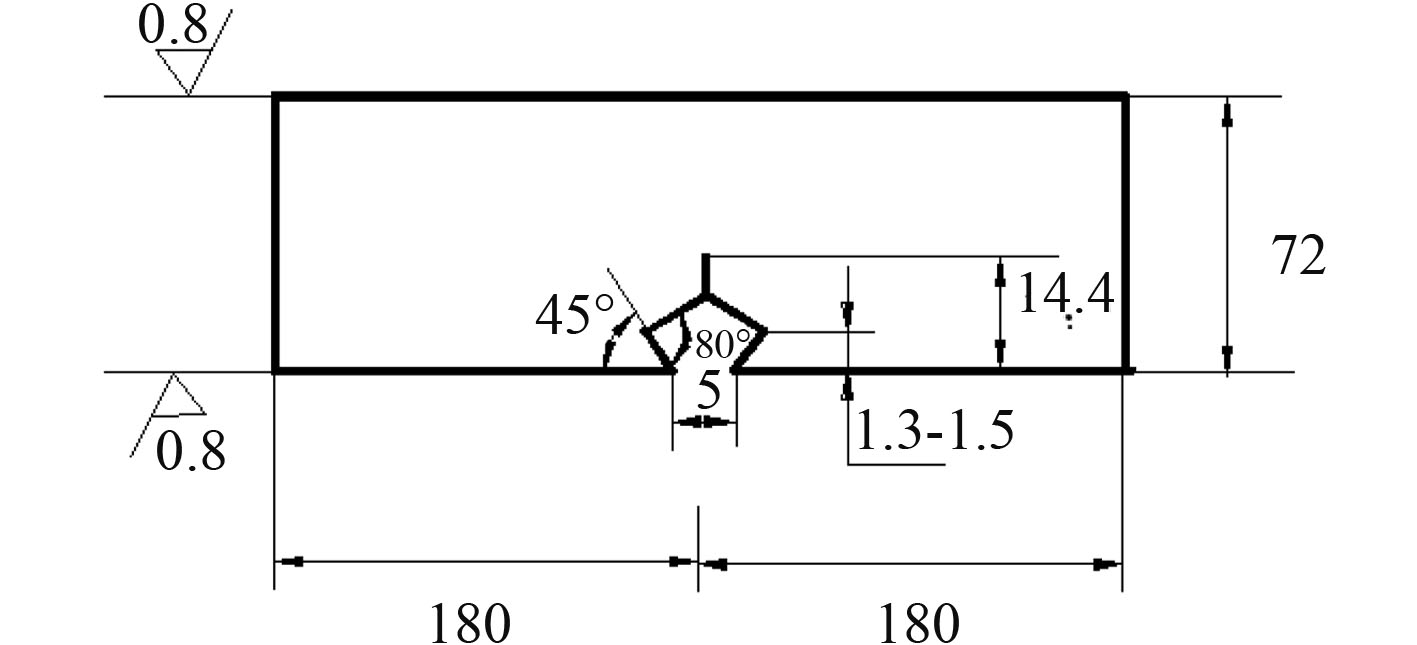
三点弯曲试样主尺度如图9所示。试样总长为360 mm,试样宽度为72 mm,支撑跨距为288 mm,试样厚度为36 mm,初始裂纹长度为16 mm(其中14.4 mm为机加工,1.6 mm为疲劳试验机上预制)。
|
图 9 SE(B)试样图 Fig. 9 SE(B) specimen |
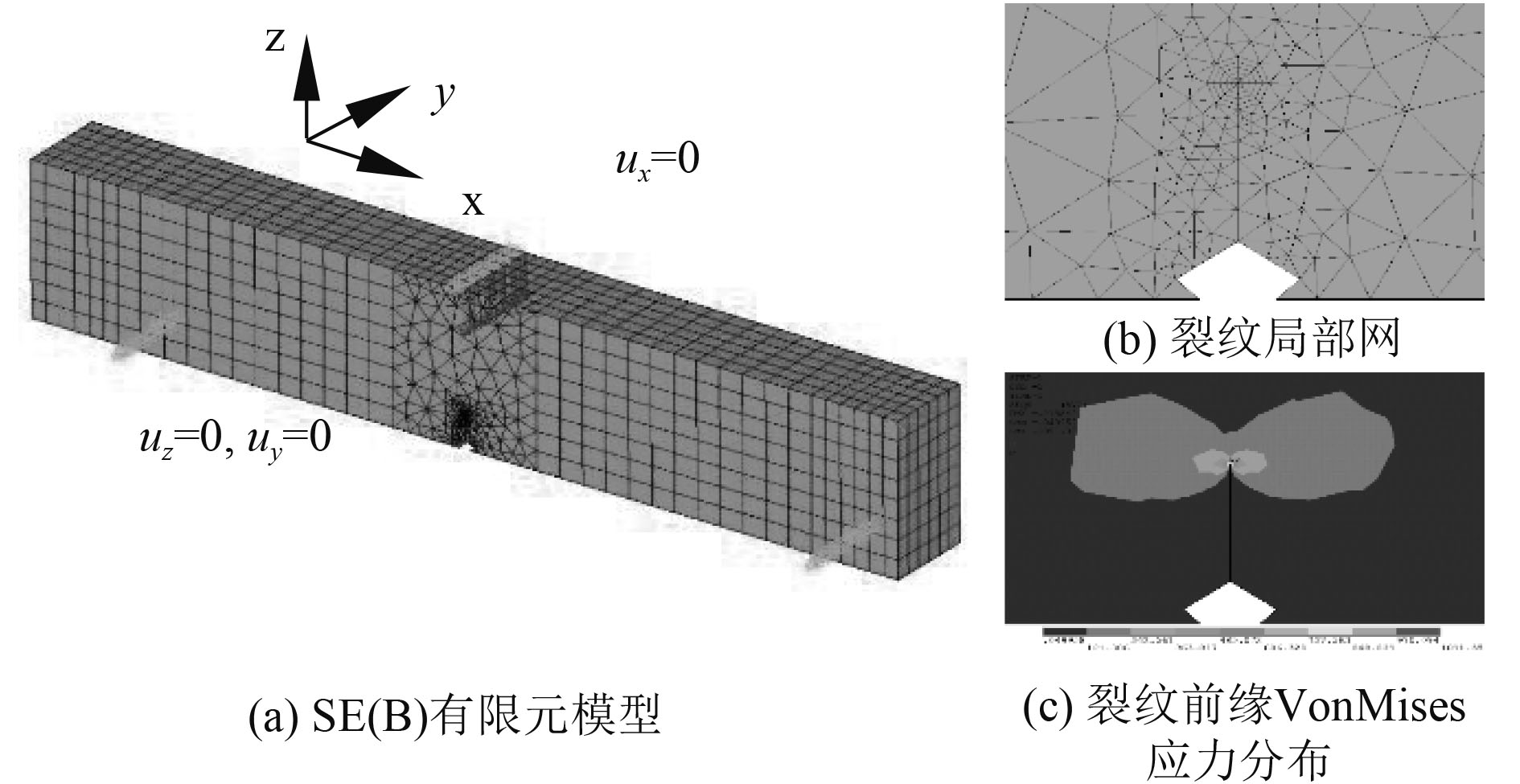
建立的SE(B)试样有限元模型如图10所示,初始裂纹尺寸为16 mm。坐标原点位于试样底面中心,x轴平行于试样长度方向,y轴平行于试样厚度方向,z轴平行于试样宽度方向。在试样顶面节点均匀施加总载荷55kN,并约束其x方向自由度;约束底面支撑位置处z方向自由度,并约束支撑中心处的y方向自由度。
|
图 10 SEB试样模型及应力分布 Fig. 10 FE model, stress contour of the specimen |
采用SE(B)试样应力强度因子解析公式(7)计算得到初始裂纹16 mm对应的应力强度因子数值为897.6 MPa
| $ \begin{split} {K_I} =& \frac{F}{{t\sqrt W }}\left[ {\frac{{6{{\left( {\displaystyle\frac{a}{W}} \right)}^{1/2}}}}{{\left( {1 + 2\displaystyle\frac{a}{W}} \right){{\left( {1 - \displaystyle\frac{a}{W}} \right)}^{3/2}}}}} \right]\times\\ & \left[ {1.99 \!-\! \frac{a}{W}\left( {1 \!-\! \frac{a}{W}} \right)\left( {2.15 \!-\! 3.93\frac{a}{W} \!+\! 2.7{{\left( {\frac{a}{W}} \right)}^2}} \right)} \right] {\text{。}} \end{split} $ | (7) |
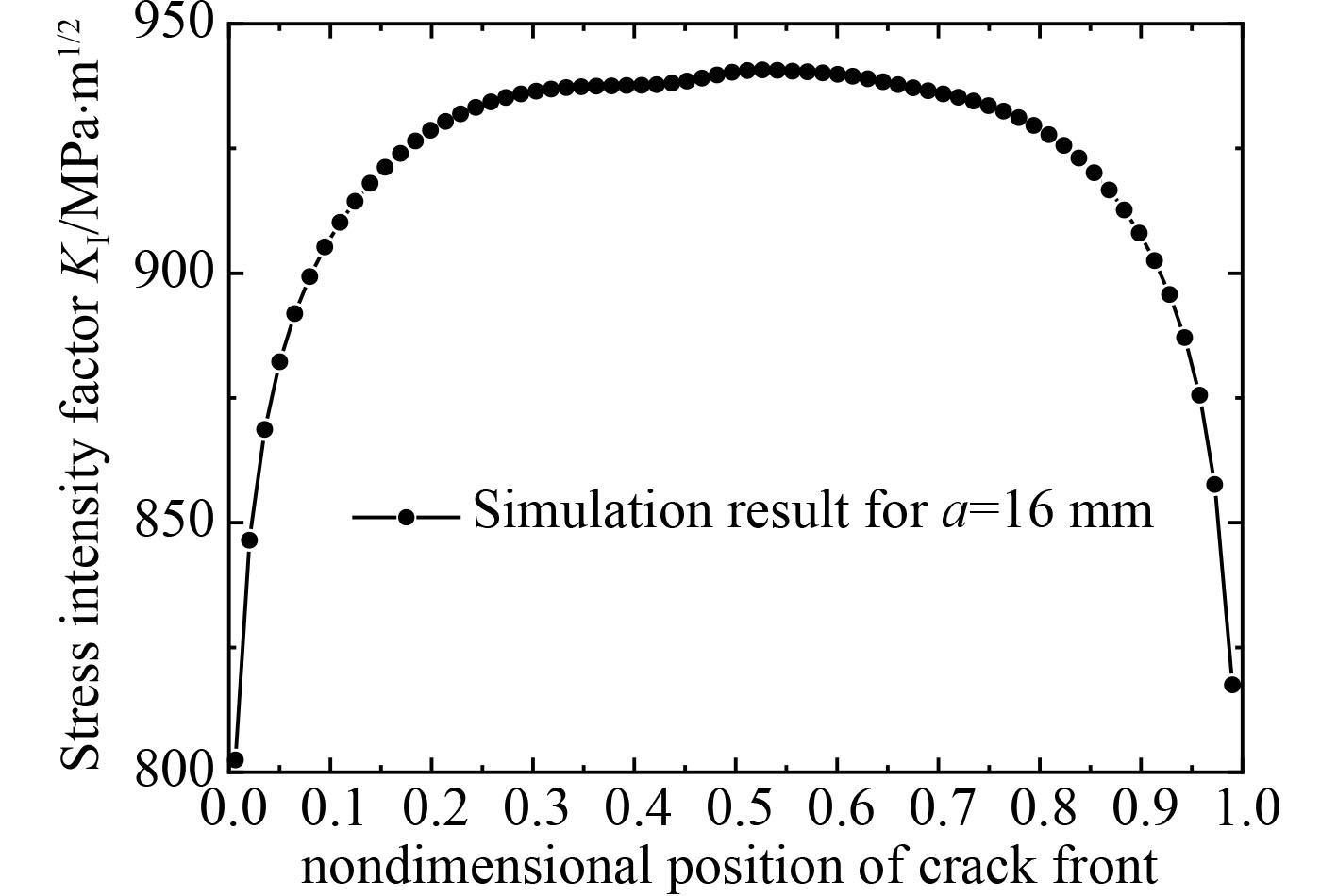
基于建立的有限元模型求解得到的SE(B)试样裂纹前缘应力强度因子分布如图11所示。
由图11可知,应力强度因子最大值位于裂纹前缘中点位置(平面应变状态),大小为940.7 MPa
|
图 11 裂纹前缘应力强度因子分布曲线(a=16 mm) Fig. 11 SIF of crack front for a=16 mm |
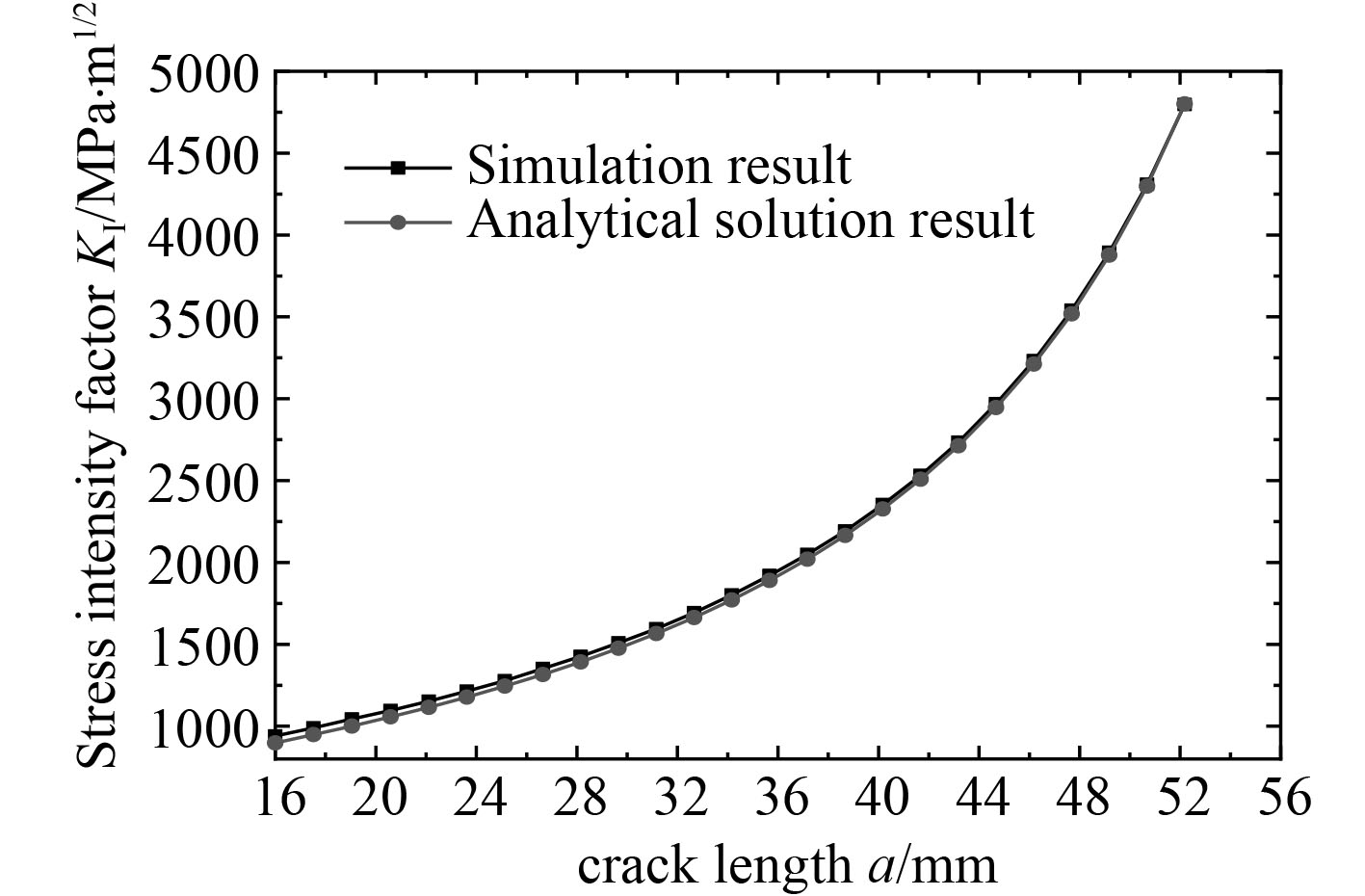
三点弯曲试样裂纹由初始16 mm扩展到52 mm过程中裂纹前缘中点应力强度因子解析解和数值解如图12所示。
由图12可知,随着三点弯曲试样裂纹扩展,应力强度因子解析解和数值解更加接近,二者最大误差为4.7%。
|
图 12 裂纹前缘中点应力强度因子计算结果 Fig. 12 SIF results of middle point of crack front |
文中采用有限元法建立三维裂纹前缘应力强度因子数值计算方法,给出三维裂纹体网格划分参数范围建议值,为船舶与海洋工程结构局部含裂纹构件三维裂纹前缘应力强度因子的有效计算提供支撑,可用于结构三维裂纹扩展形貌的数值预报中。本文得到结论如下:
1)提出的20节点奇异单元裂纹网格划分方法计算裂纹前缘应力强度因子结果精度高,研究结果表明网格划分参数对应力强度因子的计算结果影响不大;
2)表面裂纹应力强度因子数值计算结果与Newman-Raju解析结果的最大误差不超过2%,具有很高的计算精度;
3)三点弯曲试样单边穿透裂纹应力强度因子数值计算结果与解析结果的最大误差为4.7%,且随着裂纹扩展,误差越来越小;
4)裂纹前缘单元层数ntip可取3~10之间的任意整数值,裂纹前缘单元夹角θtip取45°,即环绕裂纹前缘的每层单元数目为8个,裂纹前缘单元层渐比pr取1.0,裂纹前缘半径rtip可在0.05~0.50 a之间取值。
| [1] |
王永伟, 林哲. 表面裂纹的三维模拟及应力强度因子计算[J]. 中国海洋平台, 2006, 26(3): 23-26. DOI:10.3969/j.issn.1001-4500.2006.03.004 |
| [2] |
陈景杰, 黄一, 刘刚. 基于奇异元计算分析裂纹尖端应力强度因子[J]. 中国造船, 2010, 51(3): 56-64. DOI:10.3969/j.issn.1000-4882.2010.03.007 |
| [3] |
吴志学. 表面裂纹疲劳扩展形状演化预测[J]. 应用力学学报, 2010, 27(4): 783-786. |
| [4] |
黄如旭, 黄进浩, 万正权. 焊接结构纵向及横向表面裂纹扩展特性有限元数值模拟[J]. 大连海事大学学报, 2015, 41(1): 49-53. |
| [5] |
黄如旭, 黄进浩, 万正权. T型接头横向埋藏裂纹扩展特性[J]. 舰船科学技术, 2015, 37(4): 29-33. HUANG RX, HUANG JH, WAN ZQ. Research of T welded joint embedded transverse crack propagation behavior[J]. Ship Science and Technology, 2015, 37(4): 29-33. DOI:10.3404/j.issn.1672-7649.2015.04.006 |
| [6] |
NEWMAN JC, RAJU IS. An empirical stress intensity factor equation for surface crack[J]. Engineering Fracture Mechanics, 1981, 15: 185-192. DOI:10.1016/0013-7944(81)90116-8 |
| [7] |
HENSHELL RD, SHAW KG. Crack tip finite elements are unnecessary[J]. International Journal of Numerical Method Engineering[J], 1975, 9: 495-507. DOI:10.1002/(ISSN)1097-0207 |
| [8] |
BARSOUM RS. On the use of isoparametric finite elements in linear fracture mechanics[J]. International Journal of Numerical Method Engineering, 1976, 10: 25-37. DOI:10.1002/(ISSN)1097-0207 |
 2019, Vol. 41
2019, Vol. 41
