无线电能传输技术是指通过非接触的形式或者说是无线连接的形式来实现电能传输的技术[1],是近年较为热门的研究方向,无线电能传输技术主要分为磁场感应式、磁场耦合谐振式以及微波辐射式等[2 – 5]。由于磁场感应式传输电能的距离比较近并且其传输的效率非常低;微波辐射式传输电能时的辐射比较大,对人体的危害不言而喻。因此根据实际需要以及设计要求等因素考虑,本文主要研究磁耦合谐振式无线电能传输天线[6]。
磁耦合谐振式无线电能传输系统有着传输效率高、传输距离远以及传输功率大等特点,但该天线结构复杂,这些性能的好坏都与其天线的参数息息相关。考虑到HFSS是一款三维电磁仿真软件,它可以计算天线的基本电磁场数值解和开边界问题、端口特征阻抗、传输常数和S参数等[7]。因此可以用HFSS软件对磁耦合谐振式无线电能传输天线的仿真设计方面进行分析。
该天线应用于小型无人艇的电池充电方面。对于一般的小型无人艇而言,当电池电量耗尽时必须将小型无人艇拿到岸边以有线的方式充电,而本文的设计理念是当无人艇出去巡逻至电池电量快用完时,它会自动返回岸边的无线充电装置处,此时就可以通过岸边的发射天线向无人艇上的接收天线传输电能。
1 耦合模型理论磁耦合谐振式无线电能传输技术的原理利用近场“耦合”来进行能量传输,其基本原理是利用2个完全相同的或者说是2个具有相同工作频率的天线之间进行高效的能量传输[8]。与之相比而言,2个谐振频率不一样的天线之间的能量传递效率就很低。因此可以看出磁耦合谐振式无线电能传输的关键是2个达到“谐振”状态的天线。
对于磁耦合谐振式无线电能传输技术而言,它的基础知识方面比较复杂,其涉及的学科也比较广泛,主要运用在电磁场与电磁波、微波技术与天线、高频电子线路、电子电力技术和数值分析等领域[9 – 10]。磁耦合谐振式目前还处于初步的理论研究阶段,它相对应的理论方面的知识尚不明确,所对应的分析方法十分有限[11]。
1.1 耦合模基本理论一般而言,当系统处在均匀的无源状态且每个单元间又相互正交的情况下是不存在能量传递的;只有在系统进入耦合状态时也就是说当2个具有相同谐振频率的天线在相互耦合的情况下才会产生能量传输的现象。下面是Kurs A在文献[12]中给出的耦合模理论的相关公式:
| $\frac{{{\rm d}{a_m}(t)}}{{{\rm d}t}} = (j{\omega _m} - {\Gamma _m}){a_m}(t) + \sum j{k_{mn}}{a_n}(t) + {S_m}(t)\text{。}$ | (1) |
式中:
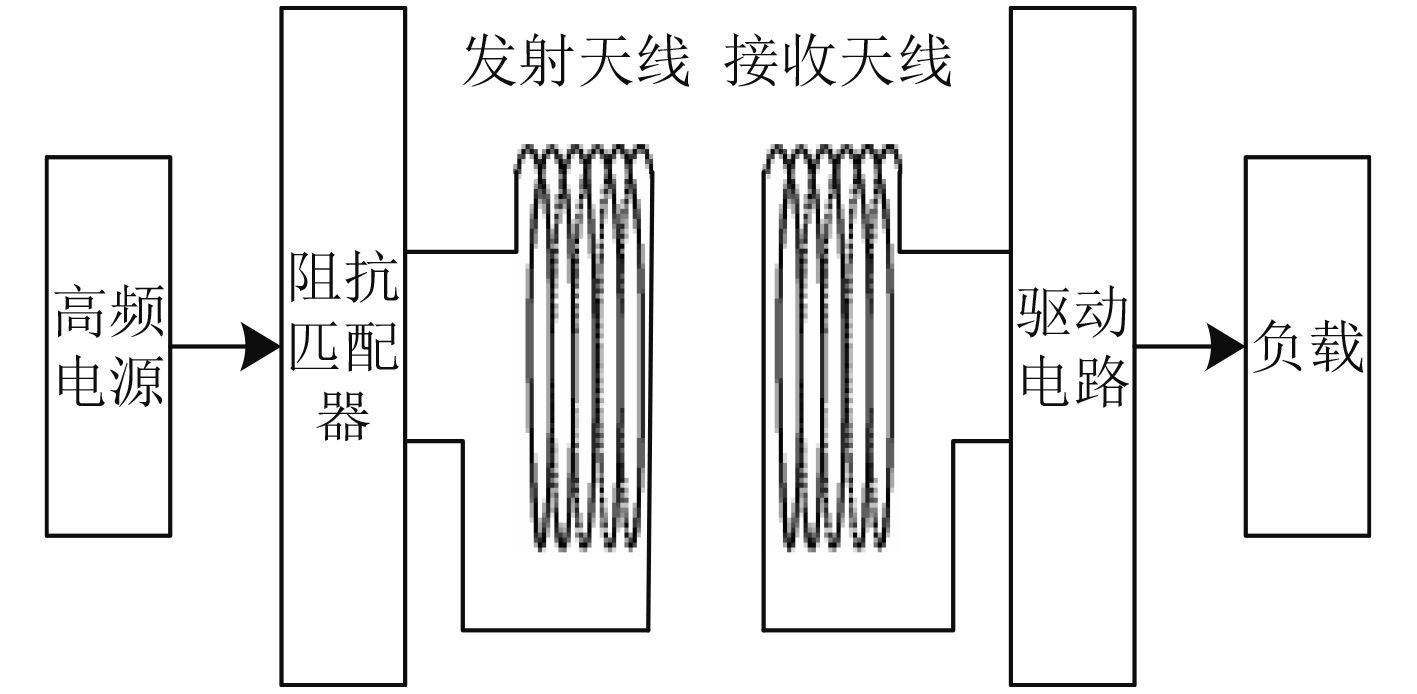
磁耦合谐振式无线电能传输系统一般由高频电源、阻抗匹配器、发射天线、接收天线、驱动电路以及负载构成,其原理框图如图1所示。在该系统工作时,高频电源输出高频交流电至发射天线处,在阻抗匹配器的作用下,接收天线与发射天线发生耦合谐振从而实现了无线电能的传输过程,此后接收到的电能经过驱动电路进行整流滤波后便可以直接给负载供电[13 – 15]。根据等效电路理论,建立成的磁耦合谐振式无线电能传输系统的等效电路图如图2所示。该系统的耦合模公式可表示为下式:
|
图 1 磁耦合谐振式无线电能传输原理框图 Fig. 1 Flow chart of magnetic coupling resonant radio energy transmission |
|
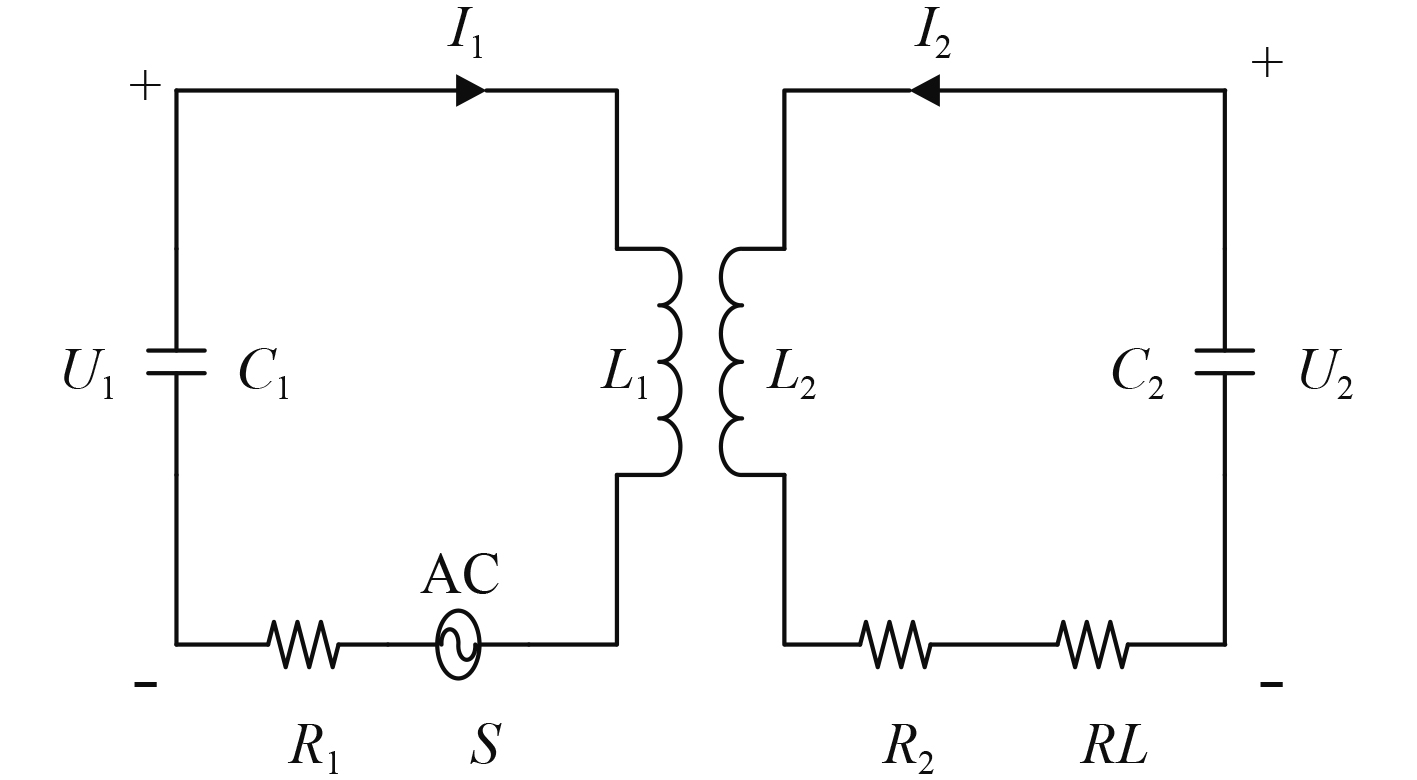
图 2 磁耦合谐振式无线电能传输系统等效电路图 Fig. 2 Flow chart of magnetic coupling resonant radio energy transmission system equivalent circuit |
| $\left\{ \begin{aligned} & \frac{{{\rm d}{a_1}}}{{{\rm d}t}} = - (j{\omega _1} + {\Gamma _1}){a_1} + j{k_{12}}{a_1} + s \text{,} \\ & \frac{{{\rm d}{a_2}}}{{{\rm d}t}} = - (j{\omega _2} + {\Gamma _2} + {\Gamma _L}){a_2} + j{k_{21}}{a_2} \text{。} \end{aligned} \right.$ | (2) |
其中,s为驱动项。
由于激励源的存在,可以调整其输出功率与系统消耗的功率相等,这样系统所包含的总能量不变,即
| $\frac{{{\rm d}{W_1}}}{{{\rm d}t}} + \frac{{{\rm d}{W_2}}}{{{\rm d}t}} = 0\text{。}$ | (3) |
发射天线中的能量变化率为下式:
| $ \begin{split} & \frac{{{\rm d}{W_1}}}{{{\rm d}t}} = \frac{{{\rm d}{{\left| {{a_{1 \pm }}} \right|}^2}}}{{{\rm d}t}} = j{k_{12}}({a_{2 + }}{a_{1 - }} - {a_{1 + }}{a_{2 - }})-\\ & 2{\Gamma _1}{\left| {{a_{1 \pm }}} \right|^2} + s({a_ + } + {a_ - }) \text{,} \end{split} $ | (4) |
接收天线中的能量变化率为下式:
| $ \begin{split} & \frac{{{\rm d}{W_2}}}{{{\rm d}t}} = \frac{{{\rm d}{{\left| {{a_{2 \pm }}} \right|}^2}}}{{{\rm d}t}}=\\ & j{k_{21}}({a_{1 + }}{a_{2 - }} - {a_{1 - }}{a_{2 + }}) - 2({\Gamma _2} + {\Gamma _L}){\left| {{a_{2 \pm }}} \right|^2}\text{。} \end{split} $ | (5) |
当
| $ \begin{aligned}{l} P = s({a_{1 + }} + {a_{1 - }}) = 2{\Gamma _1}{\left| {{a_{1 \pm }}} \right|^2} + 2({\Gamma _2} + {\Gamma _L}){\left| {{a_{2 \pm }}} \right|^2} = \\ 2{\Gamma _1}{W_1} + 2({\Gamma _2} + {\Gamma _L}){W_2}\text{,}\;\;\;\quad\quad\quad\quad\quad\quad\quad\quad\quad \end{aligned} $ | (6) |
假设负载RL功率为
| ${P_L} = 2{\Gamma _L}{W_2}\text{,}$ | (7) |
因此,系统的效率
| $\eta = \frac{{{P_L}}}{P} = \frac{{{\Gamma _L}{W_2}}}{{{\Gamma _1}{W_1} + ({\Gamma _2} + {\Gamma _L}){W_2}}}\text{,}$ | (8) |
进一步表示为:
| $\eta = \frac{{{R_L}{L_1}{W_2}}}{{{R_1}{L_2}{W_1} + ({R_1} + {R_L}){L_1}{W_2}}}\text{。}$ | (9) |
式中:
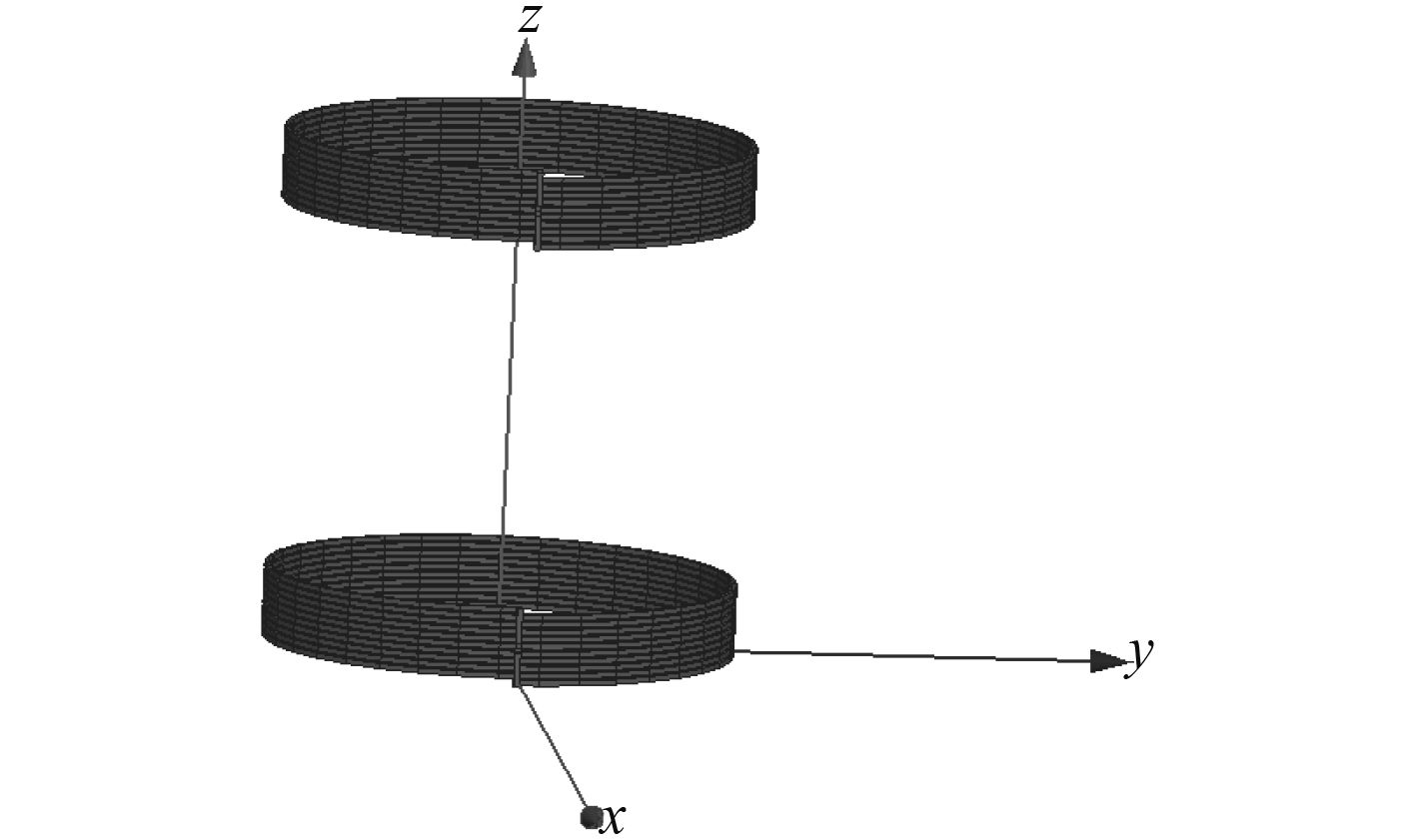
本文仿真设计的发射天线和接收天线是一种螺旋式线圈天线[13],该天线由铜管线圈绕制而成,为了确保发射天线和接收天线的谐振频率相同,将发射天线和接收天线的参数设置为相同值,它的谐振频率一般都在MHz处。通过HFSS软件根据耦合模理论的相关知识建立了螺旋半径50~100 mm的6组天线模型图。天线的具体参数如表1所示,天线模型如图3所示。图中下方是发射天线,上方是接收天线。考虑到该天线实际应用于无人艇电池的充电中,为模拟无人艇离岸边的距离100 mm左右,仿真时将发射天线与接收天线之间的距离设定为100 mm,在此基础上研究天线传输效率与螺旋半径之间关系。
|
|
表 1 天线的具体参数 Tab.1 The specific parameters of the antenna |
|
图 3 HFSS仿真模型图 Fig. 3 Flow chart of simulation model based on HFSS |
对于磁耦合谐振式无线电能传输而言,其天线工作在过耦合状态的时候,就会存在多个谐振频率,该现象被称作为频率分裂。频率分裂现象主要由天线阻抗不匹配造成。发生频率分裂时,接收和发射天线间的传输效率会受到影响。本节通过磁耦合谐振式无线电能传输天线的仿真来分析频率分裂现象,主要分析螺旋半径为100 mm的发射天线与接收天线的频率分裂现象。
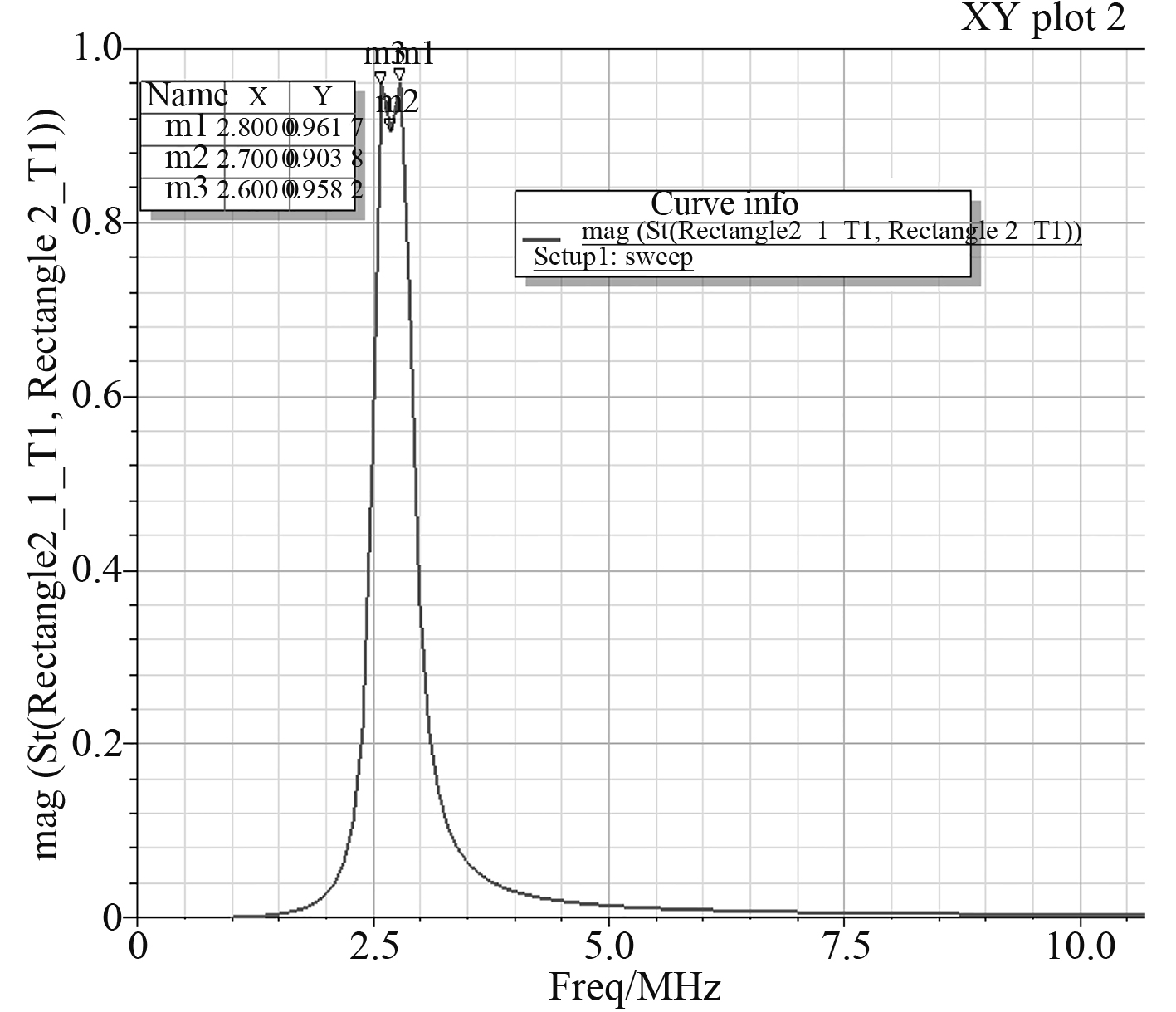
在HFSS仿真模型中,根据耦合模理论为其添加电容值,现设定电容值大小为85 pF,设置好激励和端口后仿真出天线的S21参数如图4所示。
|
图 4 电容85 pF时天线的S21参数 Fig. 4 The S21 parameters of the antenna when the capacitor’s value is 85 pF |
从图中可以看出,天线工作时存在频率分裂现象。当谐振频率为2.8 MHz时,此时的S21值为0.961 7,效率约为92.49%;当谐振频率为2.6 MHz时,此时的S21值为0.958 2,效率约为91.81%;然而原有的谐振频率在2.7 MHz处,此时的S21值为0.903 8,效率约为81.69%。由此可见发生频率分裂现象的时候,天线在原有谐振频率点处的效率没有在其分裂处的效率高。
2.2 调节电容值上面提到了频率分裂现象,在天线的实际设计中应该抑制频率分裂现象。在设计磁耦合谐振式无线电能传输天线的过程中,天线的具体参数已经给出,则该天线的电感值已经是一个确定值,因此要解决发射天线与接收天线的谐振频率相关的问题或者说是阻抗匹配的问题,只能通过调节电容值来完成。仍然以螺旋半径100 mm的天线为例,通过电容值调节的方法使发射和接收天线达到良好匹配,从而解决了频率分裂问题,提升传输效率。
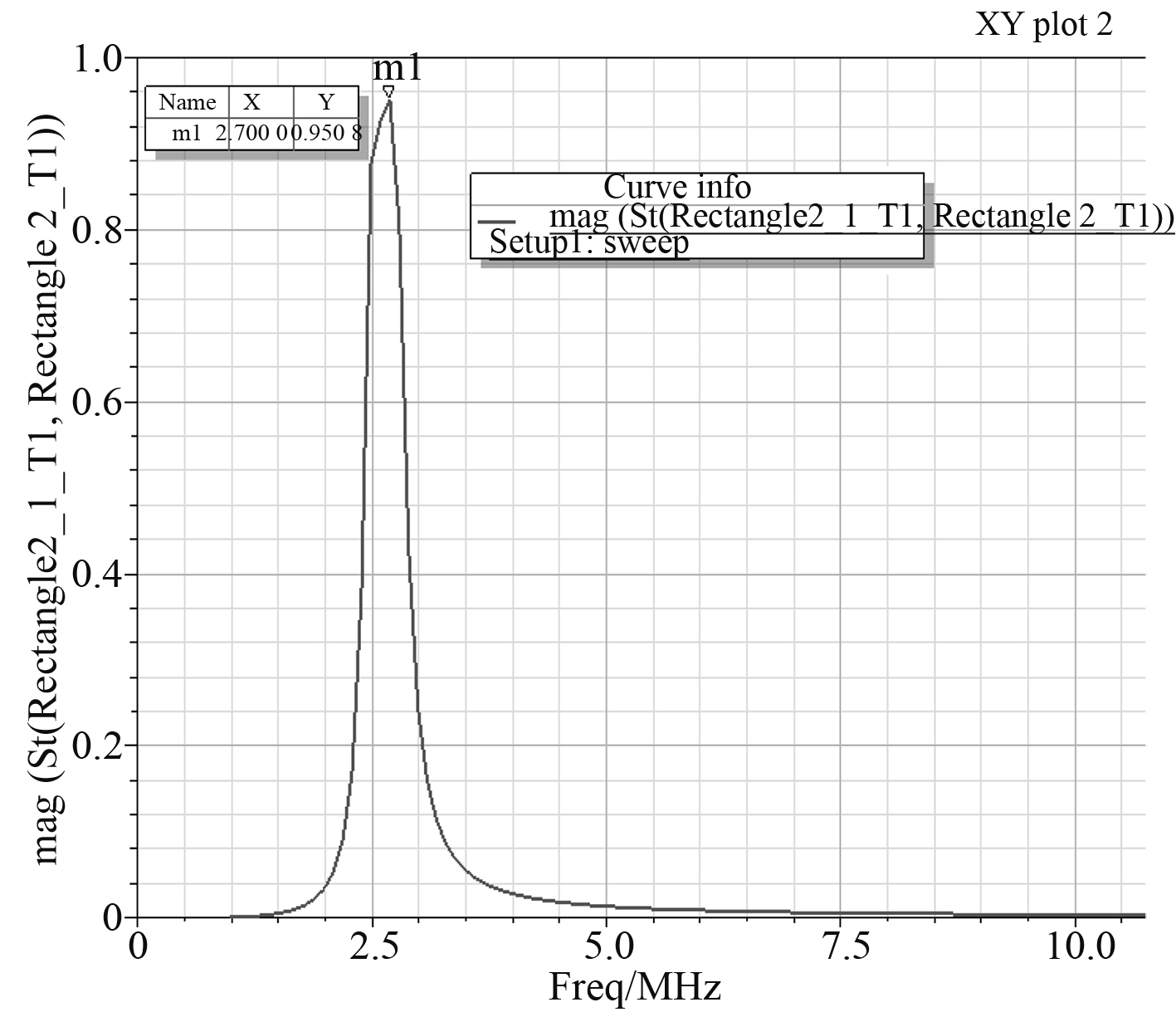
将电容值设定在80~95 pF之间,仿真出天线的S21参数,期间根据仿真出的频率分裂的情况来人为经验判断增大或减小电容值。最终发现电容值为90 pF时,发射天线与接收天线达到良好匹配,对应的S21参数如图5所示。可以看出,当谐振频率为2.7 MHz时,此时的S21值最大,达到0.950 8,效率约为90.40%。
|
图 5 电容90 pF时天线的S21参数 Fig. 5 The S21 parameters of the antenna when the capacitor′s value is 90 pF |
利用电容值调节的方法,最终使表1中的6组接收天线与发射天线都达成良好匹配,具体参数如表2所示。可以看出,天线的螺旋半径越大,所需达成良好匹配的电容值也越大,其工作频率越小;当发射天线与接收天线相距100 mm时,天线的传输效率与螺旋半径的相关性较小。
|
|
表 2 良好匹配的天线参数 Tab.2 Well matched antenna parameters |
本文从耦合模基本理论分析了磁耦合谐振式无线电能传输的原理以及其传输效率。设计了6组螺旋半径50~100 mm的磁耦合谐振式无线电能传输天线,仿真时通过HFSS软件分析了天线工作时频率分裂的现象以及频率分裂对天线传输效率的影响,对于频率分裂现象通过电容值调节的方法,完成了6组接收天线与发射天线良好匹配。分析了接收天线和发射天线相距100 mm时的螺旋半径与匹配电容值、谐振频率、以及传输效率之间的关系:天线的螺旋半径越大,所需达成良好匹配的电容值也越大,其工作频率越小;当发射天线与接收天线相距100 mm时,天线的传输效率与螺旋半径的相关性较小。
| [1] |
毛赛君. 非接触感应电能传输系统关键技术研究[D]. 南京: 南京航空航天大学, 2006.
|
| [2] |
李阳. 大功率谐振式无线电能传输方法与实验研究[D]. 河北: 河北工业大学, 2012.
|
| [3] |
赵争鸣, 张艺明, 陈凯楠. 磁耦合谐振式无线电能传输技术新进展[J]. 中国电机工程学报, 2013, 33(3): 1-13. |
| [4] |
黄学良, 谭林林, 陈中, 等. 无线电能传输技术研究与应用综述[J]. 电工技术学报, 2013(10): 1-10. DOI:10.3969/j.issn.1000-6753.2013.10.001 |
| [5] |
范兴明, 莫小勇, 张鑫. 无线电能传输技术的研究现状与应用[J]. 中国电机工程学报, 2015, 35(10): 2584-2600. |
| [6] |
陈文杰, 王浩陈, 张懿, 等. 基于磁耦合谐振的无线电能传输研究[J]. 江苏科技大学学报(自然科学版), 2015, 29(6): 555-559. DOI:10.3969/j.issn.1673-4807.2015.06.009 |
| [7] |
谢拥军. Ansoft HFSS基础及应用[M]. 西安: 西安电子科技大学出版社, 2007.
|
| [8] |
BEH T C, KATO M, IMURA T, et al. Automated impedance matching system for robust wireless power transfer via magnetic resonance coupling[J]. IEEE Transactions on Industrial Electronics, 2013, 60(9): 3689-3698. DOI:10.1109/TIE.2012.2206337 |
| [9] |
ZHONG W, LEE C. HUI, et al.. R General analysis on the use of tesla′s resonators in domino forms for wireless power transfer[J]. IEEE Transactions on Industrial Electronics, 2013, 60(1): 261-270. DOI:10.1109/TIE.2011.2171176 |
| [10] |
SHIN J, SHIN S, KIM Y, et al. Design and implementation of shaped magnetic resonance based wireless power transfer system for roadway-powered moving electric vehicles[J]. IEEE Transactions on Industrial Electronics, 2014, 61(3): 1179-1192. DOI:10.1109/TIE.2013.2258294 |
| [11] |
迟浩坤. 基于HFSS的PCB线圈无线传能系统仿真分析[D]. 青岛: 中国海洋大学, 2015.
|
| [12] |
KURS A, KARALIS A, MOFFATT R, et al. Wireless power transfer via strongly coupled magnetic resonances[J]. Science, 2007, 317(5834): 83-86. DOI:10.1126/science.1143254 |
| [13] |
KURS A, MOFFATT R, SOLJACIC M, et al. Simultaneous mid-range power transfer to multiple devices[J]. Applied Physics Letters, 2010, 96(4): 23-30. |
| [14] |
李中启, 黄守道, 易吉良. 磁耦合谐振式无线电能传输系统频率分裂抑制方法[J]. 电力系统自动化, 2017, 41(2): 21-27. |
| [15] |
刘东, 王兆尹, 田雨波, 等. 基于MOPSO算法的小型化复合结构槽螺旋天线设计[J]. 江苏科技大学学报(自然科学版), 2014, 28(5): 480-484. DOI:10.3969/j.issn.1673-4807.2014.05.013 |
 2019, Vol. 41
2019, Vol. 41
