海洋核动力平台是搭载有核动力装置的非自航船式浮动平台,长期单点系泊于渤海指定作业海域,可根据用户需要提供电能和淡水。
海洋核动力平台搭载核动力装置,不仅需要满足用户不间断能源供应需求,同时还要保证核安全要求。因此海洋核动力平台的设计重现期比同样采用单点系泊型式的FPSO高,对船体的稳性要求更高,抗风浪能力更强。
FPSO是海洋油气开发中应用最广泛的海洋工程装备,例如作业于渤海海域的“明珠”号和“长青”号,采用塔架软刚臂单点系泊装置系泊,使得FPSO具有风标效应,能使FPSO处于风、浪、流等外界环境联合作用下,位于最小环境力的位置上[1]。
本文针对1艘作业于渤海海域的海洋核动力平台,采用数值方法对平台的耐波性进行计算,并结合模型试验结果,对比数值计算与试验数据的频域和时域结果。
1 理论概述平台频域运动方程为:
| $\left[ { - {\omega ^2}\left( {{ M} + {{ M}_a}\left( \omega \right)} \right) - i\omega B + { K}} \right]x\left( \omega \right) = F\left( \omega \right)\text{。} $ | (1) |
式中:
时域运动方程为:
| $ \begin{split} & \left( {{ M} + {{ M}_a}} \right)\ddot x\left( t \right) + \int_0^t {{ K}\left( {t - \tau } \right)} \dot x\left( \tau \right){\rm{d}}\tau + Cx\left( t \right)=\\ & \quad{F_w}\left( t \right) + {F_{wind}}\left( t \right) + {F_{cur}}\left( t \right) + {F_m}\left( t \right){\text{。}} \end{split} $ | (2) |
式中:
依据API RP 2SK[3]规范采用模块法计算风力和流力[3]。风力计算公式为:
| $ {F_{wind}} = {C_w}{C_s}{C_h}{A_w}V_z^2{\text{。}} $ | (3) |
式中:
流力计算公式为:
| ${F_{cur}} = {C_{ss}}{C_d}{A_c}V_{cur}^2\text{。} $ | (4) |
式中:
模型试验与数值计算分别选取了2种典型的装载工况,即压载工况和满载工况。平台主尺度和2种载况下的主要参数如表1所示。
|
|
表 1 平台主要参数 Tab.1 Main parameters of FPSO |
时域计算工况分为作业工况与自存工况,作业工况为船上设备保持作业状态时能够承受的最恶劣工况,自存工况为在该工况下保证平台总体安全和船上设备不损坏[4],环境条件如表2所示。
|
|
表 2 环境条件 Tab.2 Environmental conditions |
风浪流不同方向的组合对平台的运动性能影响很大。平台运动的最大值可能出现在:风、浪同向,流与风、浪成0°,30°,45°或90°角;风、浪同向且无流;浪、流同向,风与浪、流成30°,45°或90°角。一般情况下,取风与浪同向,流与风浪成0°,30°,45°和90°角为基本工况,再增加无流且风与浪同向和浪与流同向、风与浪流成某一夹角2种工况。因此,模型试验与数值计算中风浪流方向组合如表3所示。
|
|
表 3 风浪流方向组合 Tab.3 Directions combinations of wind, wave and current |
平台试验模型如图1所示,由4根水平放置的带有弹簧的软绳系泊,以提供足够大的纵荡、横荡和首摇固有周期,这样既可以把平台模型限制在一定的运动范围内,又不影响平台的波频运动。数值计算水动力网格如图2所示。

|
图 1 模型试验频域模型 Fig. 1 Frequency domain model of model test |

|
图 2 数值计算频域模型 Fig. 2 Frequency domain model of numerical calculation |
塔架软刚臂单点系泊系统由系泊塔架、旋转接头、系泊机构和平台支撑结构4部分组成。该装置适用于浅水海域,如渤海海域。模型试验和数值计算中时域模型分别如图3和图4所示,平台由单点系泊装置系泊,并由软钢臂的配重提供系泊恢复力。

|
图 3 模型试验时域模型 Fig. 3 Time domain model of model test |

|
图 4 数值计算时域模型 Fig. 4 Time domain model of numerical calculation |
数值计算采用三维势流理论,波浪频率范围选取0.2~1.2 rad/s,步长0.05 rad/s,浪向角选取0°~180°,步长15°。为了提高试验效率,模型试验只针对典型波浪频率和浪向角进行单位规则波频域试验。由2种方法计算得到的平台在压载状态下的RAO曲线如图5~图7所示,在满载状态下的RAO曲线如图8~图10所示。
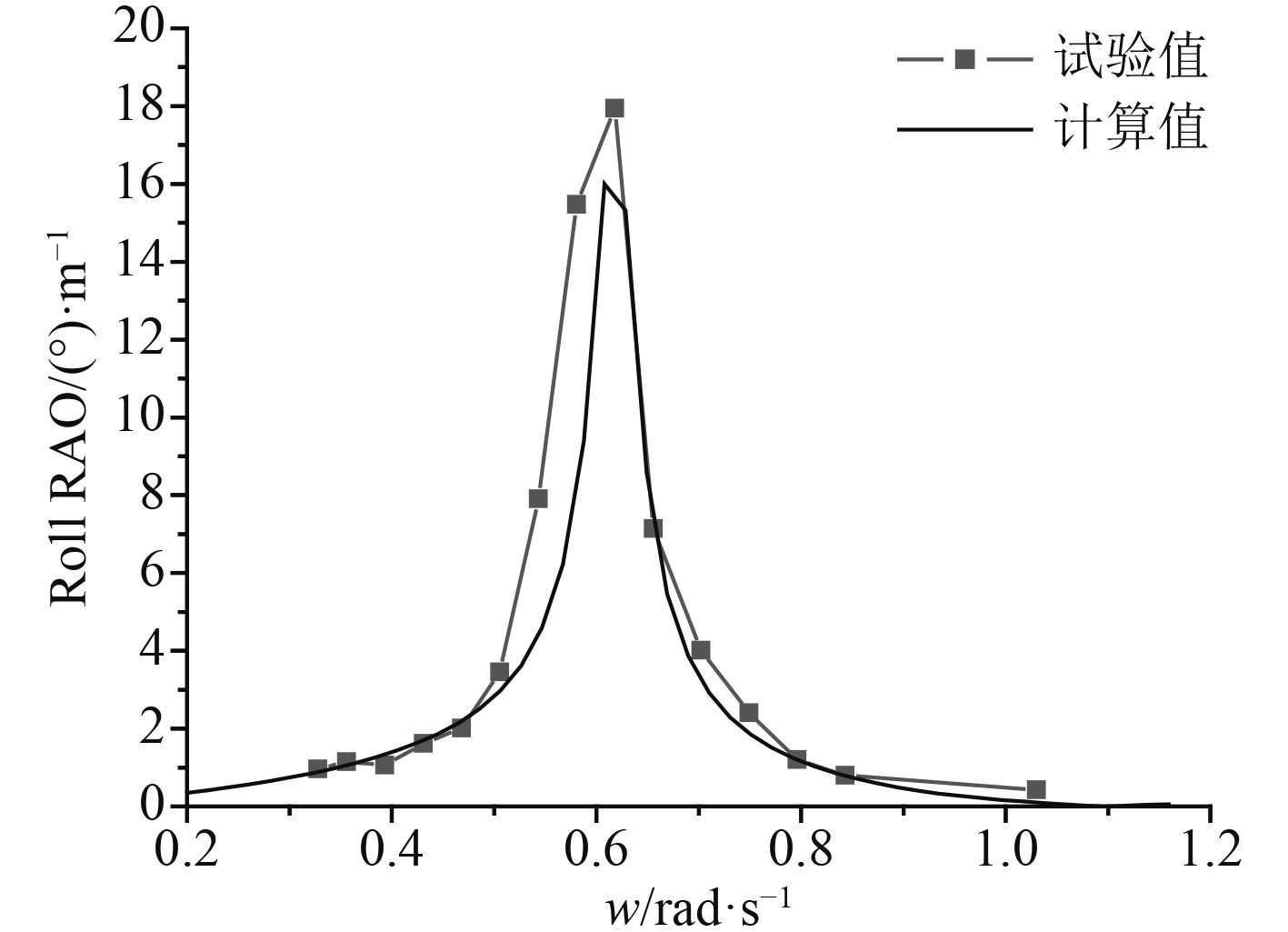
|
图 5 浪向角为90°时的横摇RAO Fig. 5 Roll RAO in 90° wave direction |
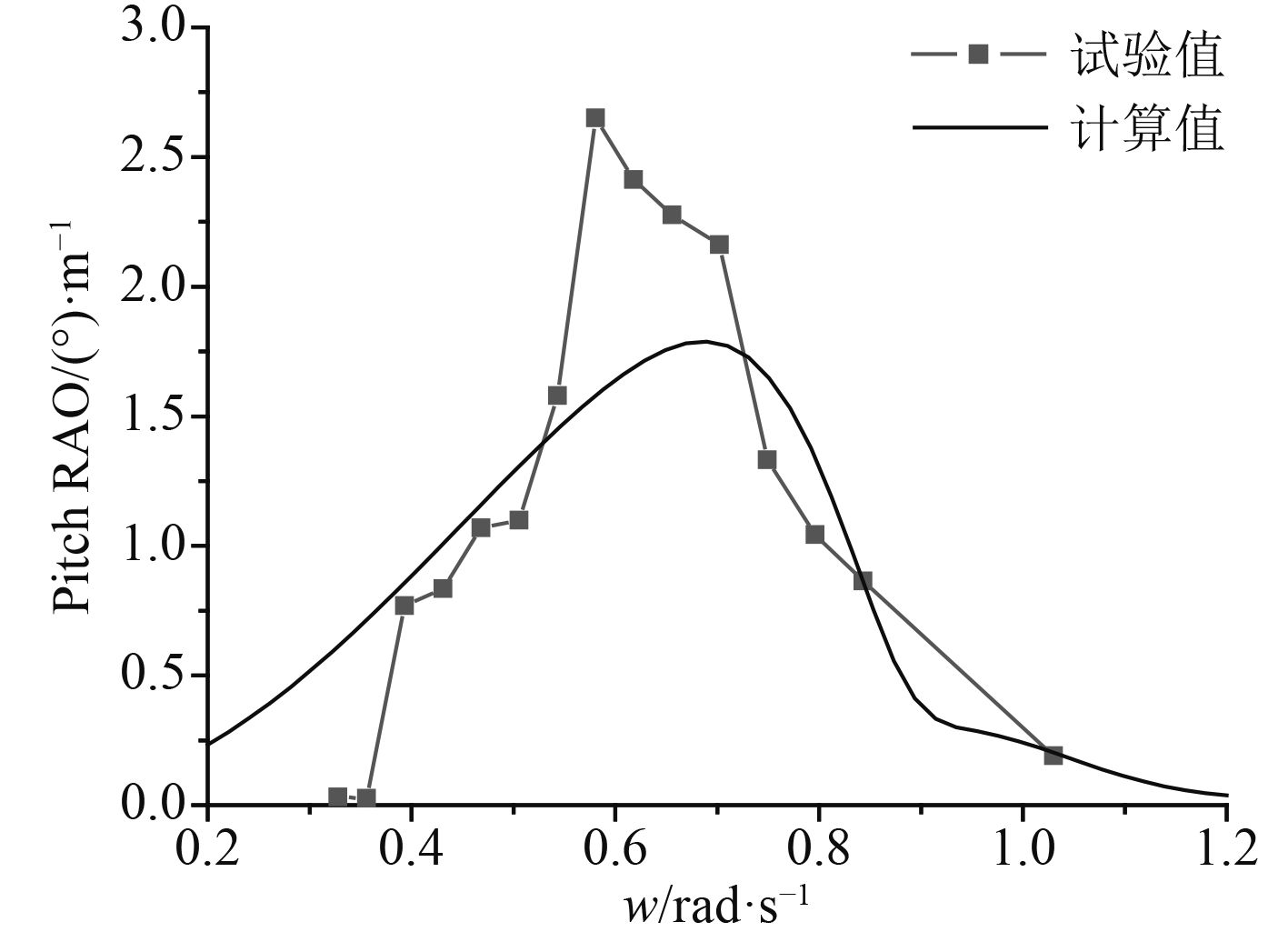
|
图 6 浪向角为180°时的纵摇RAO Fig. 6 Pitch RAO in 180° wave direction |
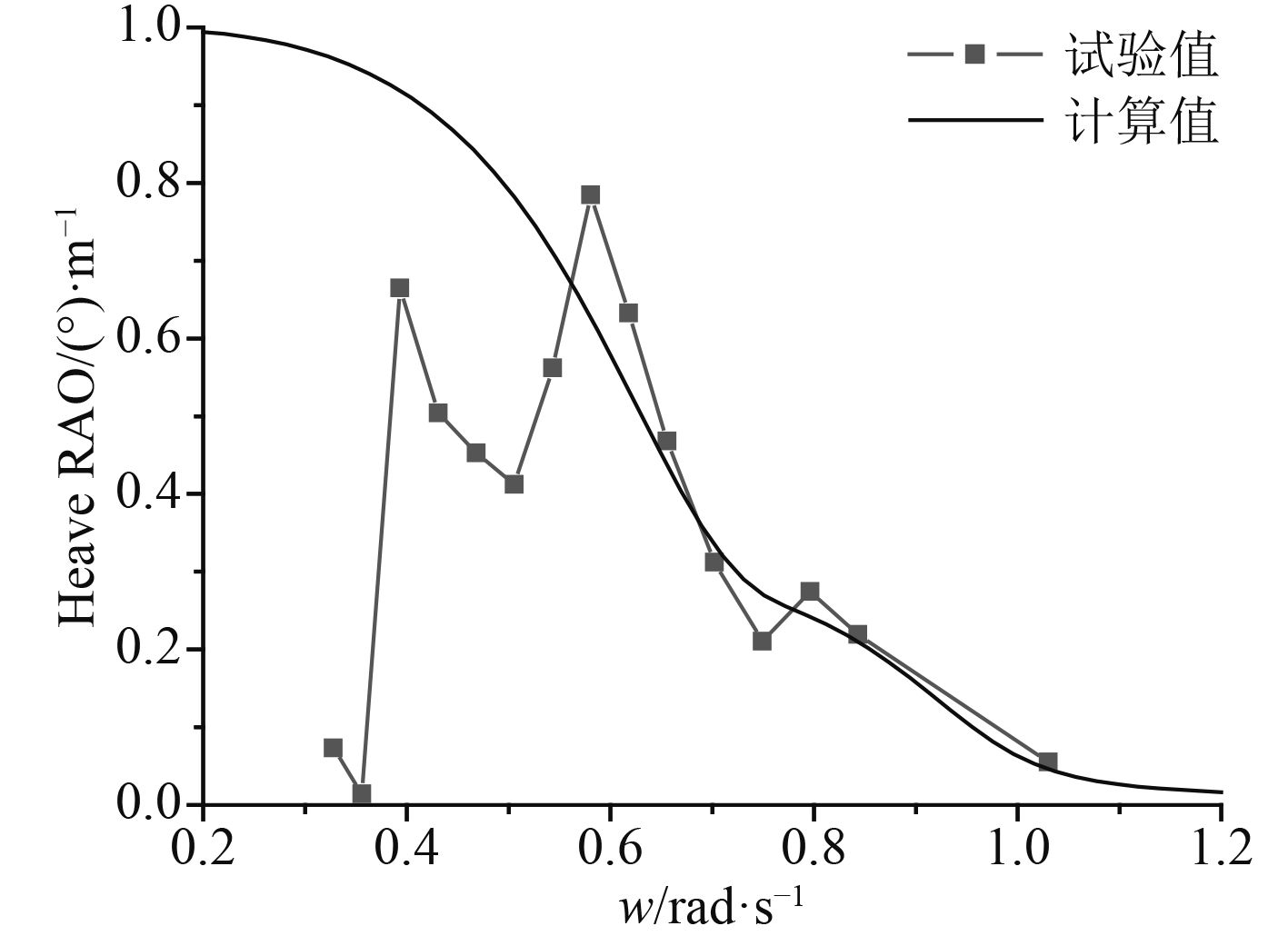
|
图 7 浪向角为180°时的升沉RAO Fig. 7 Heave RAO in 180° wave direction |
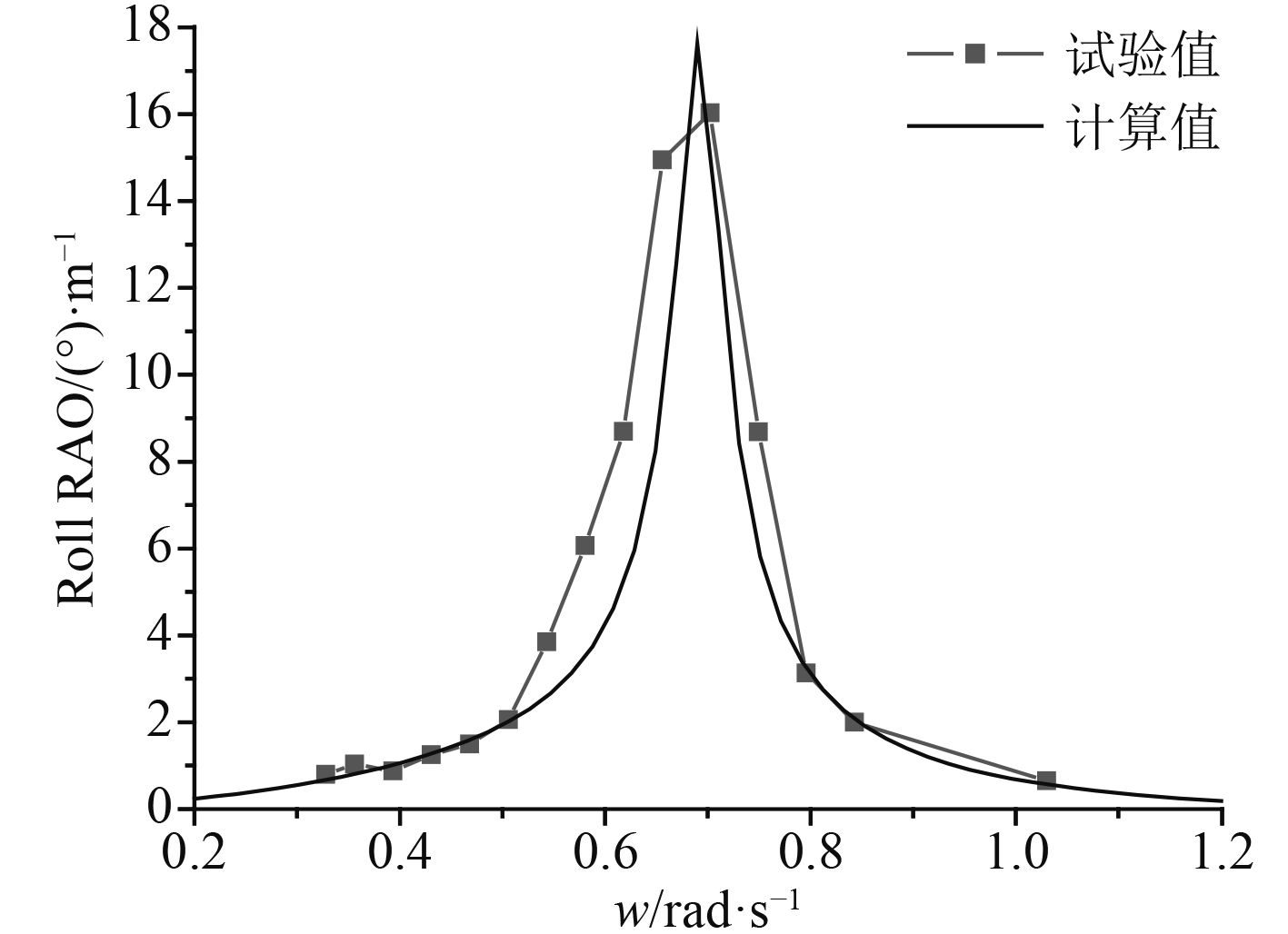
|
图 8 浪向角为90°时的横摇RAO Fig. 8 Roll RAO in 90° wave direction |
|
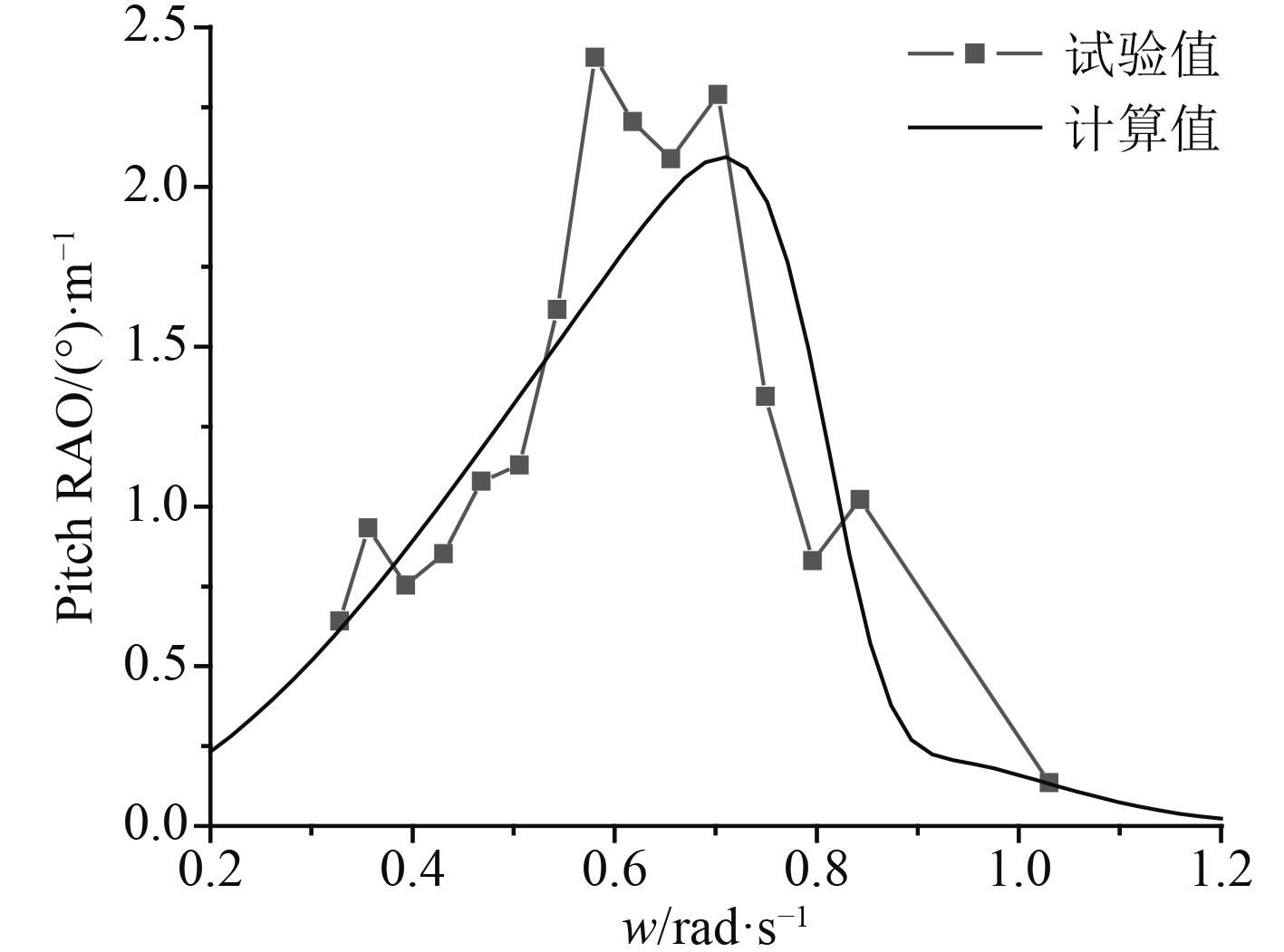
图 9 浪向角为180°时的纵摇RAO Fig. 9 Pitch RAO in 180° wave direction |
|
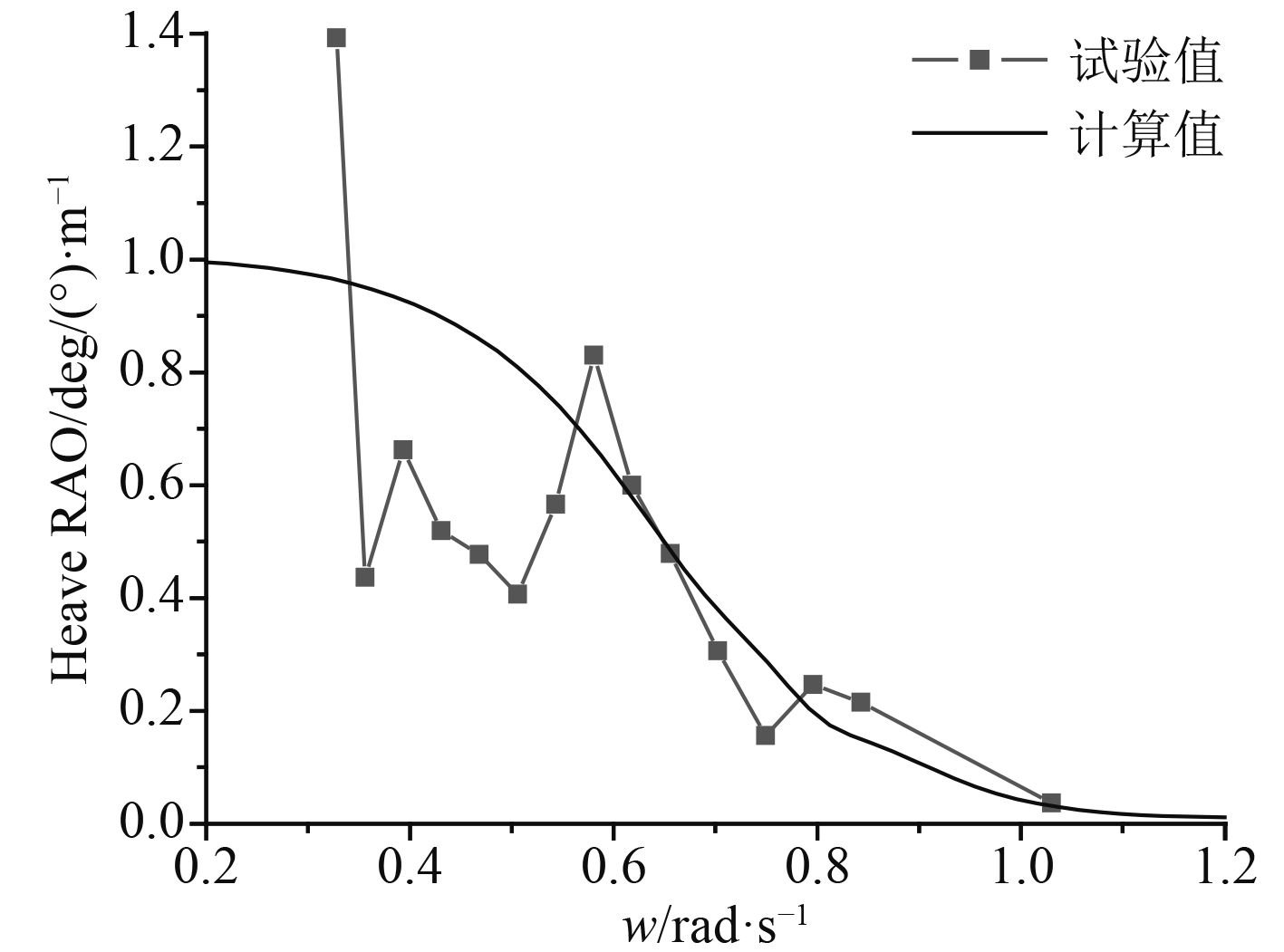
图 10 浪向角为180°时的升沉RAO Fig. 10 Heave RAO in 180° wave direction |
模型试验和数值计算得到平台时域运动的时历曲线,提取运动的有义值和最大值(见表4~表7)。有义值为所有最大幅值按绝对值从大到小按序排列,对前1/3最大幅值取平均值。最大值采用Weibull分布进行统计,得到累计概率为99.9%时对应的幅值。
|
|
表 4 压载工况有义值统计 Tab.4 Significant values in ballast condition |
|
|
表 5 压载工况最大值统计 Tab.5 Maximum valuesin ballast condition |
|
|
表 6 满载工况有义值统计 Tab.6 Significant valuesin full load condition |
|
|
表 7 满载工况最大值统计 Tab.7 Maximum values in full load condition |
对比由数值计算与模型试验2种方法计算得到的频域RAO结果可知:
1)由2种方法计算得到的RAO曲线吻合较好;
2)数值计算由于选取波浪频率较密,得到的RAO曲线更加光顺;
3)由于选取频率较少或外界环境等因素,模型试验结果出现折线起伏。
对比在不同风浪流方向组合工况下的时域运动统计结果可知:
1)与模型试验结果相比,数值计算结果在垂荡、横摇和纵摇运动统计值上相对较小;
2)由2种方法计算得到的运动统计值在不同风浪流方向组合工况下的大小趋势相同;
3)在极端恶劣海况下,平台未出现稳性丧失,安全性能够得到满足。
5 结 语本文通过数值计算和模型试验对由单点系泊装置系泊的核动力平台的水动力运动性能进行分析。结果表明,由2种方法计算得到的频域和时域结果相近,相互验证了2种方法的正确性,可为核动力平台的设计提供有力的支撑。
| [1] |
祁祺, 张涛, 文攀, 等. 基于AQWA的FPSO系泊系统响应数值模拟[J]. 舰船科学技术, 2011, 33(12): 14-18. QI Qi, ZHANG Tao, WEN Pan, et al. Numerical simulation of FPSO mooring systems based on AQWA[J]. Ship Science and Technology, 2011, 33(12): 14-18. DOI:10.3404/j.issn.1672-7649.2011.12.003 |
| [2] |
刘元丹, 刘敬喜, 谭安全. 单点系泊FPSO风浪流载荷下运动及其系泊力研究[J]. 船海工程, 2011, 40(6): 146-149. DOI:10.3963/j.issn.1671-7953.2011.06.038 |
| [3] |
API. Recommended practice for design and analysis of stationkeeping systems for floating structures[S]. 1997.
|
| [4] |
李欣, 杨建民, 范模. 渤海油田浅水软刚臂系泊FPSO触底分析[J]. 海洋工程, 2004, 22(2): 51-57. LI Xin, YANG Jian-min, FAN Mo. Investigation on the touch of sea bottom by a FPSO in bohai oil field with shallow water[J]. The Ocean Engineering, 2004, 22(2): 51-57. |
 2019, Vol. 41
2019, Vol. 41
