作为海洋油气资源开发重要前提和必要保证之一的水下安装吊放模块,随着水下开发水深的增加和吊装作业要求的不断提高,其作业范围由数十米的浅水(500 m以下)区域发展至数百米的深水(500~1 500 m)海域,甚至达到近2 000 m的超深水海域,同时其吊载质量也随水下安装模块的高度集成化与一体化由数吨增至数百吨[1]。深水、重载时吊缆在外部激励作用下的运动响应,特别是垂向运动,与浅水、轻载时的运动响应呈现很大的不同,其原因为浅水、轻载时的吊缆可视为刚体,吊缆的运动响应与力学特性可看作是线性的;随着作业水深的增加和吊载质量的不断增大,吊缆自身弹性变形引起的伸缩将不可忽视,此时的吊缆应视为弹性体,其运动响应与力学特性亦已超出线性范围而进入非线性区域[2 – 3]。
缪国平等[4]指出水下缆索可看作挠性部件;Gault[5]采用悬链线法计算得到系泊缆索的几何构型和缆张力;Webster[6]采用非线性有限元方法,对系泊缆索在上端点简谐激励下的动力特性和系泊阻尼做了广泛的参数敏感性研究;Yang & Teng [7]采用基于索单元的几何非线性有限元方法对一个具有非线性应力-应变关系的合成缆索进行了动力分析。一般对轻载、浅水时吊缆进行研究时多将其视为刚体,采用牛顿定律分析其运动而忽略了吊缆自身的变形。对于水下吊装缆索而言,随着长度的增加,其自身的弹性性能表现的异常突出。在突变载荷的作用下,吊索变形并非整体保持均匀,其运动也不会整体一致,变形和运动是一个不断发展和传播的过程,此过程可看作类似波动的微观过程,显然此类问题已超出了经典力学的求解范畴,而采用弹性动力学中的弹性波理论可有效解决此类问题[8 – 9]。
1 深水吊缆动力学建模以弹性波理论为基础,考虑吊缆的自身特点及弹性力学性能,忽略其弯曲、剪切及扭转刚度,用
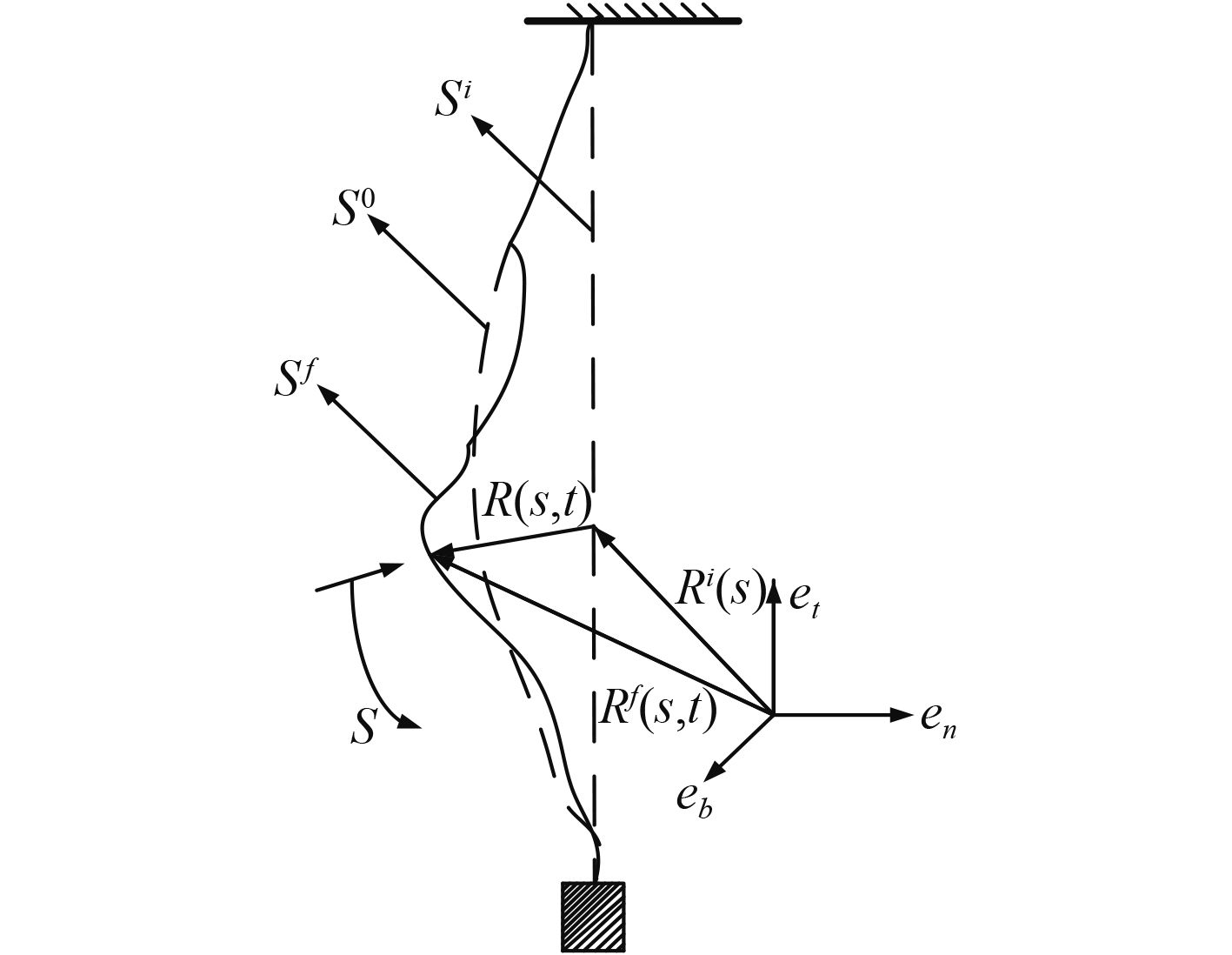
|
图 1 吊缆动态几何构型示意图 Fig. 1 The dynamic geometry of hoisting cable |
建立弧坐标
| $R(s,t) = {R^f}(s,t) - {R^i}(s)\text{。}$ | (1) |
将
| $R\left( {s,t} \right) = {R_1}\left( {s,t} \right)\vec \tau + {R_2}\left( {s,t} \right)\vec n + {R_3}\left( {s,t} \right)\vec b\text{。}$ | (2) |
根据Hamilton原理,认为吊缆的总能量由其自身的应变能、动能、重力势能及外力所做的功几部分组成,则描述吊缆瞬态应变能的表达式为
| ${e^f} = \frac{1}{2}\frac{{{{\left( {d{s^f}} \right)}^2} - {{\left( {d{s^{\circ}}} \right)}^2}}}{{{{\left( {d{s^{\circ}}} \right)}^2}}} = \frac{1}{2}\left( {\frac{{\partial {R^f}}}{{\partial {s^{\circ}}}} \cdot \frac{{\partial {R^f}}}{{\partial {s^{\circ}}}} - 1} \right)\text{。}$ | (3) |
其中:
则吊缆在瞬态构型
| $\begin{split} \varPsi _s^f = \varPsi _s^i + \frac{1}{2}\int\limits_0^{{L^i}} {[2{P^i}\left( {{s^i},t} \right)\varepsilon \left( {{s^i},t} \right)} \times \\ \left( {1 + 2{e^i}} \right)\left. { + E{A^i}{\varepsilon ^2}{{\left( {1 + 2{e^i}} \right)}^2}} \right]{\rm{d}}{s^i} \end{split} \text{,}$ | (4) |
其中:
当不考虑吊缆周围流体时,其重力势能可表示为:
| $\varPsi _g^f = \varPsi _g^i + \int\nolimits_{{\varOmega ^i}} {\rho {A^i}g\left( { - {l_\tau }{R_1} - {l_n}{R_2}} \right)} {\rm d}{\varOmega ^i}\text{。}$ | (5) |
其中:
由浮力产生的势能可表示如下:
| $\varPsi _b^f = \varPsi _b^i + \int\nolimits_{{\varOmega ^i}}^{} {{\rho _w}{A^i}g\left( { - {l_t}{U_1} - {l_n}{U_2}} \right)} {\rm d}{\varOmega ^i}\text{。}$ | (6) |
式中:
吊缆在瞬态构型
| $\varPsi _k^f = \frac{1}{2}\int_0^{{L^i}} {\rho {A^i}\left( {{V^f} \cdot {V^f}} \right)} {\rm d}{s^i}\text{,}$ | (7) |
其中
| $\begin{split} {V^f} = & \frac{{{\rm d}R\left( {{s^i},t} \right)}}{{{\rm d}t}} = {R_{1,t}}\left( {s,t} \right){e_1} + {R_{2,t}}\left( {s,t} \right){e_2}+ \\ & {R_{3,t}}\left( {s,t} \right){e_3} \text{。} \end{split} $ | (8) |
作用于吊缆上的外力
| $\varPsi _f^f = \int\nolimits_{{\varOmega ^i}}^{} {F \cdot U} {\rm d}{\varOmega ^i} = \int\nolimits_{{\varOmega ^i}}^{} {\left( {{F_1}{R_1} + {F_2}{R_2} + {F_3}{R_3}} \right)} {\rm d}{\varOmega ^i}\text{,}$ | (9) |
其中外力
根据Hamilton原理,有
| $\delta \int\nolimits_{{t_1}}^{{t_2}} {\left( {\varPsi _k^f - \varPsi _s^f - \varPsi _g^f + \varPsi _b^f + \varPsi _f^f} \right)} {\rm d}t = 0\text{。}$ | (10) |
将表达式(4)~式(9)代入式(10),可得3个方向吊缆三维非线性运动方程。
切向运动方程:
| $\begin{split} - \rho {A^i}{R_{1,tt}} = & {\left[ {\left( {{P^i} + E{A^i}\varepsilon } \right)\left( {1 + {R_{1,s}} - {\kappa ^i}{R_2}} \right)} \right]_{,s}} \\ & \left[ {\left( {{P^i} + E{A^i}\varepsilon } \right)\left( {1 + {R_{1,s}} - {\kappa ^i}{R_2}} \right)} \right] - \\ & {\kappa ^i}\left( {{P^i} + E{A^i}\varepsilon } \right)\left( {{R_{2,s}} - {\kappa ^i}{R_1}} \right) - \\ & \left( {\rho - {\rho _w}} \right){A^i}g{l_t} + {F_1} \text{,} \end{split}$ | (11) |
法向运动方程:
| $\begin{split} - \rho {A^i}{R_{2,tt}} = & {\left[ {\left( {{P^i} + E{A^i}\varepsilon } \right)\left( {{U_{2,s}} - {\kappa ^i}{R_1}} \right)} \right]_{,s}} - \\ & {\kappa ^i}\left( {{P^i} + E{A^i}\varepsilon } \right)\left( {1 + {R_{1,s}} - {\kappa ^i}{R_2}} \right) - \\ & \left( {\rho - {\rho _w}} \right){A^i}g{l_n} + {F_2} \text{,} \end{split} $ | (12) |
副法向运动方程:
| $ - \rho {A^i}{U_{3,tt}} = {\left[ {\left( {{P^i} + E{A^i}\varepsilon } \right){U_{3,s}}} \right]_{,s}} + {F_3}\text{。}$ | (13) |
假设吊缆的本构关系为线性的,并仅考虑面内运动,忽略与副法向有关的项,结合弹性波的基本方程,可得吊缆非线性运动方程为:
| $\begin{split} - {R_{1,tt}} + & \frac{{{F_1}}}{{\rho A}} + \left[ { - 2g - \frac{E}{\rho }\lambda + \frac{E}{\rho }{\lambda ^3}{s^2}} + \right. \\ & \left. { g{\lambda ^2}{s^2}} \right]{R_{2,s}} + \left[ {\frac{{{P_0}}}{{\rho A}} + \frac{E}{\rho } + \frac{g}{2}\lambda {s^2}} + \right. \\ & \left. { 2\frac{E}{\rho }{R_{1,s}} + 2\frac{E}{\rho }{\lambda ^3}{s^2}{R_2} - 2\frac{E}{\rho }\lambda {R_2}} \right]{R_{1,ss}} + \\ & g\lambda s{R_{1,s}} + g\lambda s + \left( {2\frac{E}{\rho }{\lambda ^3}s + g{\lambda ^2}s} \right){R_2} +\\ & \left( {\frac{3}{2}g{\lambda ^3}{s^2} - g\lambda } \right){R_1} = 0 \text{,} \end{split}$ | (14) |
| $\begin{split} &- {R_{2,tt}} + \frac{{{F_2}}}{{\rho A}} + \left[ {\frac{{{P_0}}}{{\rho A}} + \frac{g}{2}\lambda {s^2} + \left( {{\lambda ^3}{s^2} - \lambda } \right)\frac{E}{\rho }{R_2}} + \right. \\ & \left. { \frac{E}{\rho }{R_{1,s}}} \right]{R_{2,ss}} - g{\lambda ^2}s{R_1} + g\lambda s{R_{2,s}} + \left( {g - \frac{g}{2}{\lambda ^2}{s^2}} \right) + \\ & \left( {2g - g{\lambda ^2}{s^2} - \frac{E}{\rho }{\lambda ^3}{s^2} + \frac{E}{\rho }\lambda } \right){R_{1,s}} + \\ & \left( { - \frac{E}{\rho }{\lambda ^2} - g\lambda + \frac{3}{2}g{\lambda ^3}{s^2}} \right){R_2} = 0 \text{。} \end{split}$ | (15) |
考虑到求解速度与求解规模,对于大位移的吊缆内在固有非线性问题,有限差分法是较为适宜的一种方法。但由于通用的差分格式无法适应非线性较高的方程,因此根据泰勒展开推导得到更为适用的差分格式,如式(16)和式(17)所示。
| $\frac{{{\rm d}\bar u}}{{{\rm d}x}} = \frac{1}{{\left( {4!\Delta x} \right)}}\left[ {\begin{array}{*{20}{c}} { - 50}&{96}&{ - 72}&{32}&{ - 6} \\ { - 6}&{ - 20}&{36}&{ - 12}&2 \\ 2&{ - 16}&0&{16}&{ - 2} \\ { - 2}&{12}&{ - 36}&{20}&6 \\ 6&{ - 32}&{72}&{ - 96}&{50} \end{array}} \right]\bar u + {\rm O}\left( {\Delta {x^4}} \right)\text{,}$ | (16) |
| $ \begin{array}{l} \displaystyle\frac{{{\rm d}{u^2}}}{{{\rm d}{x^2}}} = \displaystyle\frac{1}{{4!\Delta {x^2}}}\left[ {\begin{array}{*{20}{c}} { - \displaystyle\frac{{415}}{3}} & {192} & { - 72} & {\displaystyle\frac{{64}}{3}} & { - 3} & 0\\ {20} & { - 30} & { - 8} & {28} & { - 12} & 2\\ { - 2} & {32} & { - 60} & {32} & { - 2} & 0\\ {20} & { - 30} & { - 8} & {28} & { - 12} & 2\\ { - \displaystyle\frac{{415}}{3}} & {192} & { - 72} & {\displaystyle\frac{{64}}{3}} & { - 3} & 0 \end{array}} \right]u + \\ \left[ {\begin{array}{*{20}{c}} {100\displaystyle\frac{{{\rm d}u}}{{{\rm d}{x_1}}}}\\ 0\\ 0\\ 0\\ {100\displaystyle\frac{{{\rm d}u}}{{{\rm d}{x_n}}}} \end{array}} \right] + {\rm O}\left( {\Delta {x^4}} \right)\text{,} \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad(17) \end{array}$ |
与时间相关的位移和速度的差分格式为[11]:
| $\left\{ \begin{gathered} {\left( {{U_1}} \right)_j}^{i + 1} = {\left( {{U_1}} \right)_j}^i + \left( {{v_1}} \right)_j^i\Delta t + \frac{1}{2}\Delta {t^2}\left[ {{\beta _1}\left( {{a_1}} \right)_j^i + {\beta _2}\left( {{a_1}} \right)_j^{i + 1}} \right] \text{,} \\ {\left( {{U_2}} \right)_j}^{i + 1} = {\left( {{U_2}} \right)_j}^i + \left( {{v_2}} \right)_j^i\Delta t + \frac{1}{2}\Delta {t^2}\left[ {{\beta _1}\left( {{a_2}} \right)_j^i + {\beta _2}\left( {{a_2}} \right)_j^{i + 1}} \right] \text{,} \\ \left( {{v_1}} \right)_j^{i + 1} = \left( {{v_1}} \right)_j^i + \frac{1}{2}\Delta t\left[ {{\alpha _1}\left( {{a_1}} \right)_j^i + {\alpha _2}\left( {{a_1}} \right)_j^{i + 1}} \right] \text{,} \quad\quad\quad\;(18)\\ \left( {{v_2}} \right)_j^{i + 1} = \left( {{v_2}} \right)_j^i + \frac{1}{2}\Delta t\left[ {{\alpha _1}\left( {{a_2}} \right)_j^i + {\alpha _2}\left( {{a_2}} \right)_j^{i + 1}} \right] \text{。} \quad\quad\quad\quad\quad \end{gathered} \right.$ |
其中,
式(18)中不同节点处法向和切向的加速度与吊缆非线性运动方程(14)和式(15)中的外部力
| $ M{A^{i + 1}} + C\left| {{V^i}} \right|{V^i} + K{U^i} = {\left( {{F^{excit}}} \right)^i}\text{。} $ | (19) |
式中:
采用空间差分格式(16)、式(17)和时间差分格式(18)求解深水吊缆非线性运动微分方程(14)和式(15),分析不同吊缆长度及吊载时吊缆的运动特性。
2.2.1 深水吊缆非线性运动响应计算及验证|
|
表 1 计算参数 Tab.1 Calculation parameters |
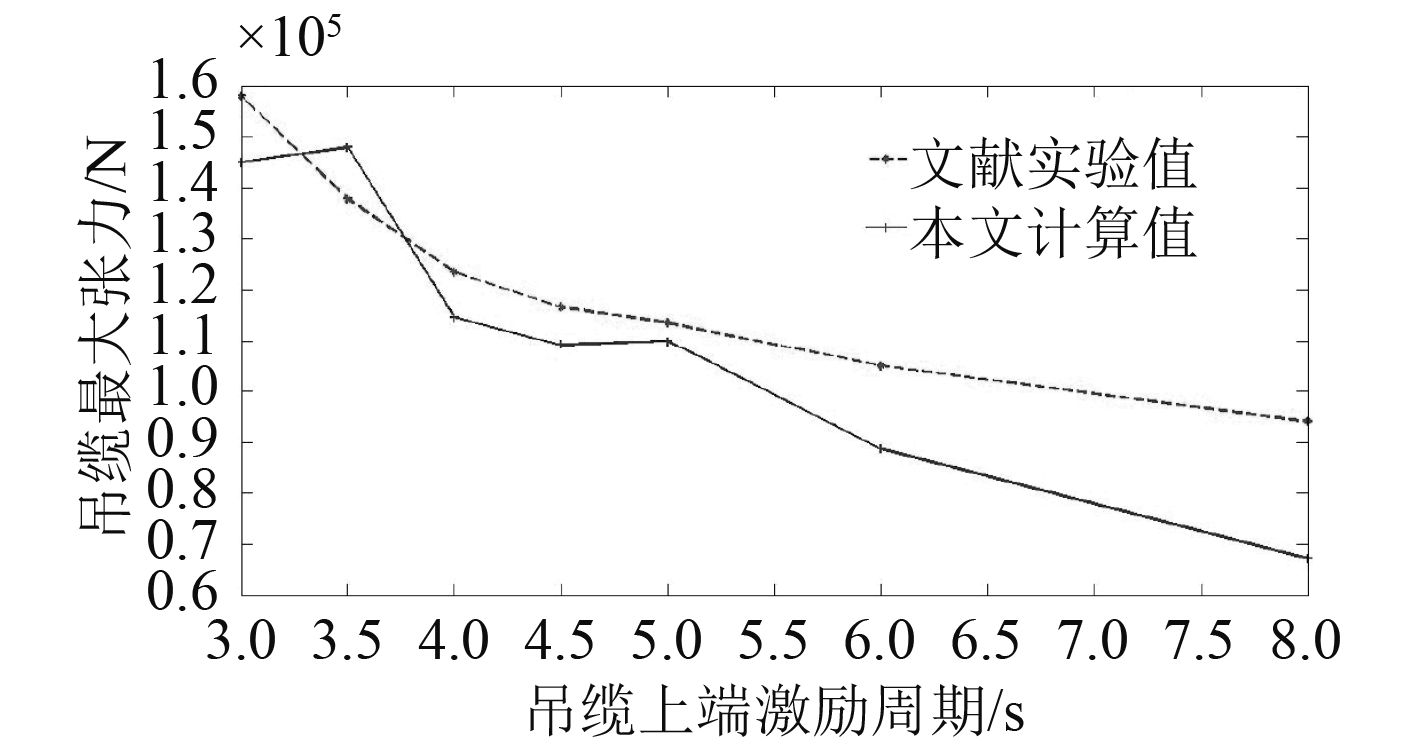
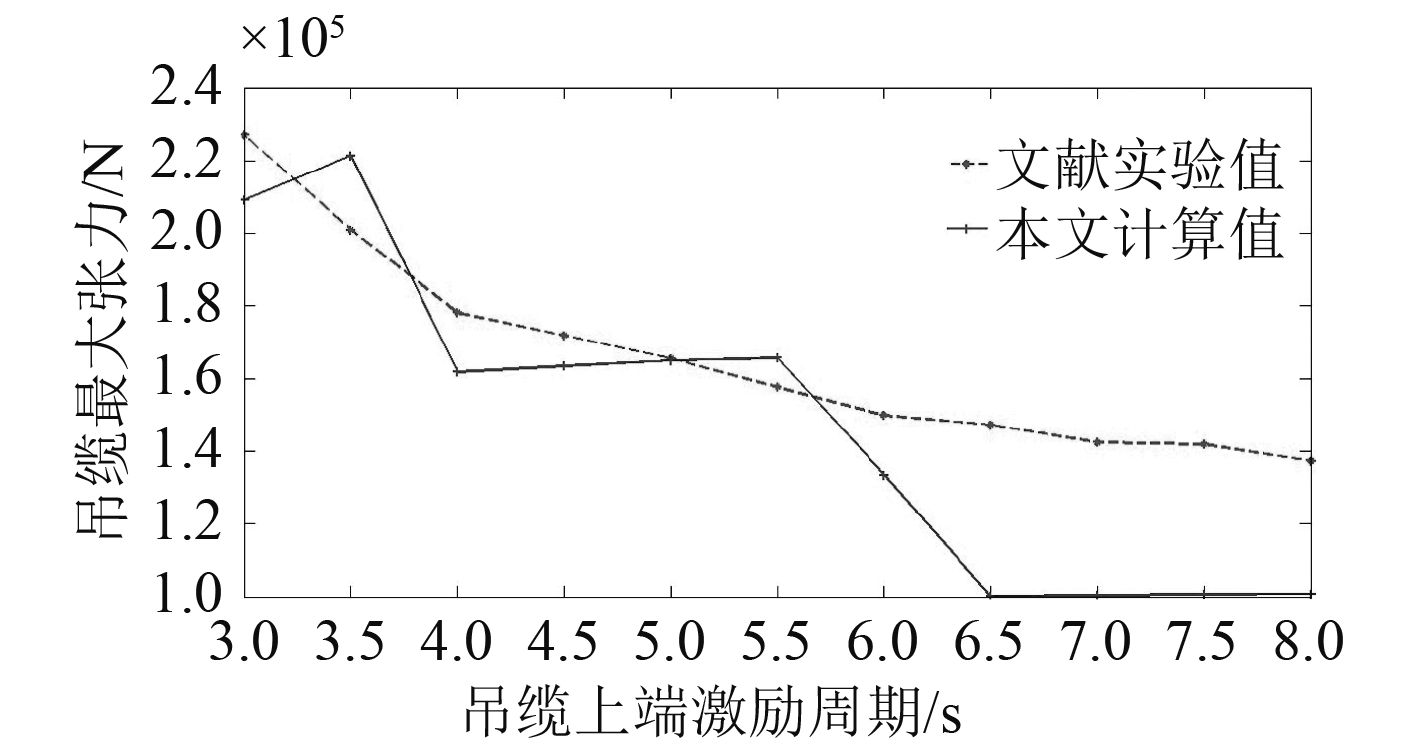
采用表1中的计算参数,通过编程求解式(14)和式(15),分别计算4 500 m和3 000 m时不同上端激励周期时吊缆的最大张力值,与试验值进行对比,一并列于表2和表3中,并根据表中数据绘制图2和图3。
|
|
表 2 3 000 m时不同激励周期时吊缆张力值比较 Tab.2 The comparison of cable tension with different inspiring period when the length is 3 000 m |
|
|
表 3 4 500 m时不同激励周期下吊缆张力值比较 Tab.3 The comparison of cable tension with different inspiring period when the length is 4 500 m |
|
图 2 3 000 m时不同激励周期时吊缆张力值比较 Fig. 2 The comparison of cable tension with different inspiring period when the length is 3 000 m |
|
图 3 4 500 m时不同激励周期时吊缆张力值比较 Fig. 3 The comparison of cable tension with different inspiring period when the length is 4 500 m |
从计算结果可以看出,无论是4 500 m水深还是3 000 m水深,本文计算结果与试验值的变化趋势相同,特别是在周期低于6 s时,误差较小,计算结果与试验值吻合较好。当上端激励周期超过6 s时,2种水深情况下计算值都比试验值偏小,误差甚至达到30%以上。对此问题的解释,首先看到无论是计算结果还是试验值,随着上端激励周期的不断增加,缆张力呈现逐渐减小的趋势,其原因为当上端激励周期较小时,此时的激励频率较高,上端激励可以看作是“突变载荷”,“突变载荷”的作用效果使得吊缆中存在瞬间变化的冲击张力,随着上端激励周期的逐渐增加,此时的激励可以看作是缓慢变化的,上端激励的“突变效应”逐渐减小,吊缆内的冲击张力逐渐减小,在表面看来吊缆的张力也会响应减小。文献中采取等效截断方法进行试验,吊缆的长度为12 m,此时吊缆的张力与变形的关系仍符合胡克定律,呈线性关系。而本文计算考虑了吊缆的非线性效应,随着上端激励周期的逐渐增加,吊缆的非线性程度也逐渐变大,因此吊缆张力计算结果随着上端激励增加而减小的程度势必会增大,这说明是否考虑由吊缆弹性伸缩引起的非线性对于缆张力影响的差异还是较大的。由此可以看出,采用本文中的计算方法是准确可靠的,可以作为后续理论分析与仿真计算的有效工具。
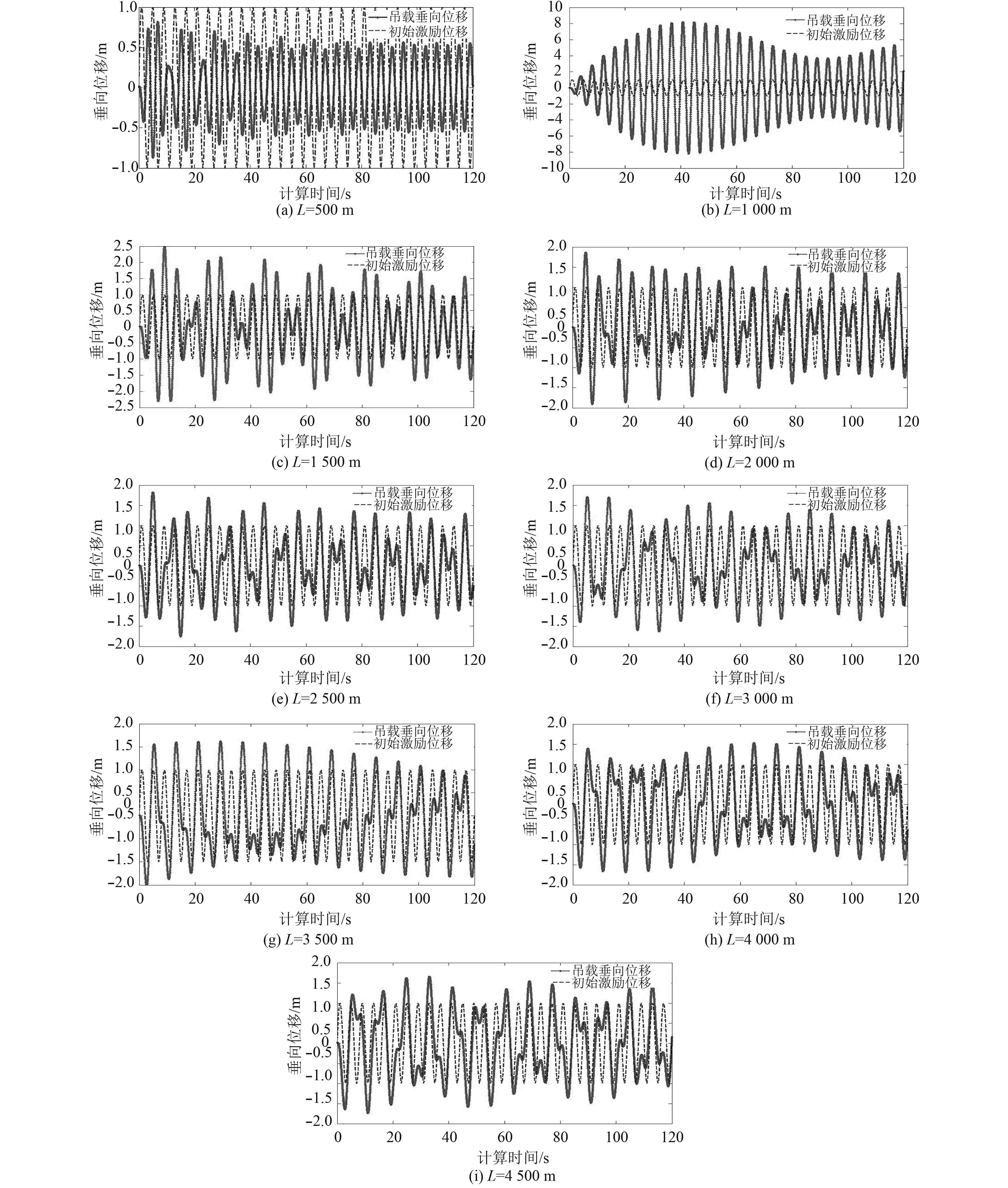
2.2.2 深水吊缆非线性运动响应分析不失一般性,为准确掌握吊载在不同水深时的垂向运动特性,分析由吊缆长度的不同引起的吊缆伸缩性的变化对吊缆非线性运动的影响,考虑深水吊装的实际作业海况及工作母船运动响应特性,选取幅值为1 m,周期为4 s的谐波运动作为初始激励,吊缆参数与表1相同,吊载质量为10 t,计算时间为120 s,对不同水深时的吊载垂向运动响应特性进行计算,计算结果如图4所示。由图4可以看出,初始激励为线性运动,吊载的垂向运动响应时历呈现随机状态,为明显的非线性运动。而且,当吊缆长度为1 000 m时,吊载的垂向位移响应呈现一定的规律性,其响应周期与初始激励极为接近,幅值明显超过初始激励,甚至可以达到初始激励的数倍,这说明当前吊缆在选取的计算参数和初始激励下出现了共振现象,因此在实际作业过程中应尽量避免在此工况下进行施工。
|
图 4 不同缆长时初始激励位移与吊载垂向位移时历 Fig. 4 The initial motivation displacement and load vertical displacement of cable under the different cable length |
为了更为清晰的得到吊缆垂向运动响应周期与初始激励的关系,将图4中的运动时历进行频谱分析,结果如图5所示。由图5可以看出,吊缆上端初始激励的主频率为一特定的值,为线性运动;而吊载响应的主频率有2个(L=1 000 m除外),大体分布于吊缆上端激励频率的两侧,由此亦可以说明吊载运动响应是非线性的。其中一个主频率为0.3,另一频率的值随着吊缆长度的增加逐渐减小,且频率0.3所对应的谱密度峰值逐渐减小,另一频率的峰值逐渐增加,这说明吊载垂向运动响应周期随吊缆长度的变化而发生改变,也就是说吊缆长度是影响吊载垂向运动响应周期的重要因素之一。
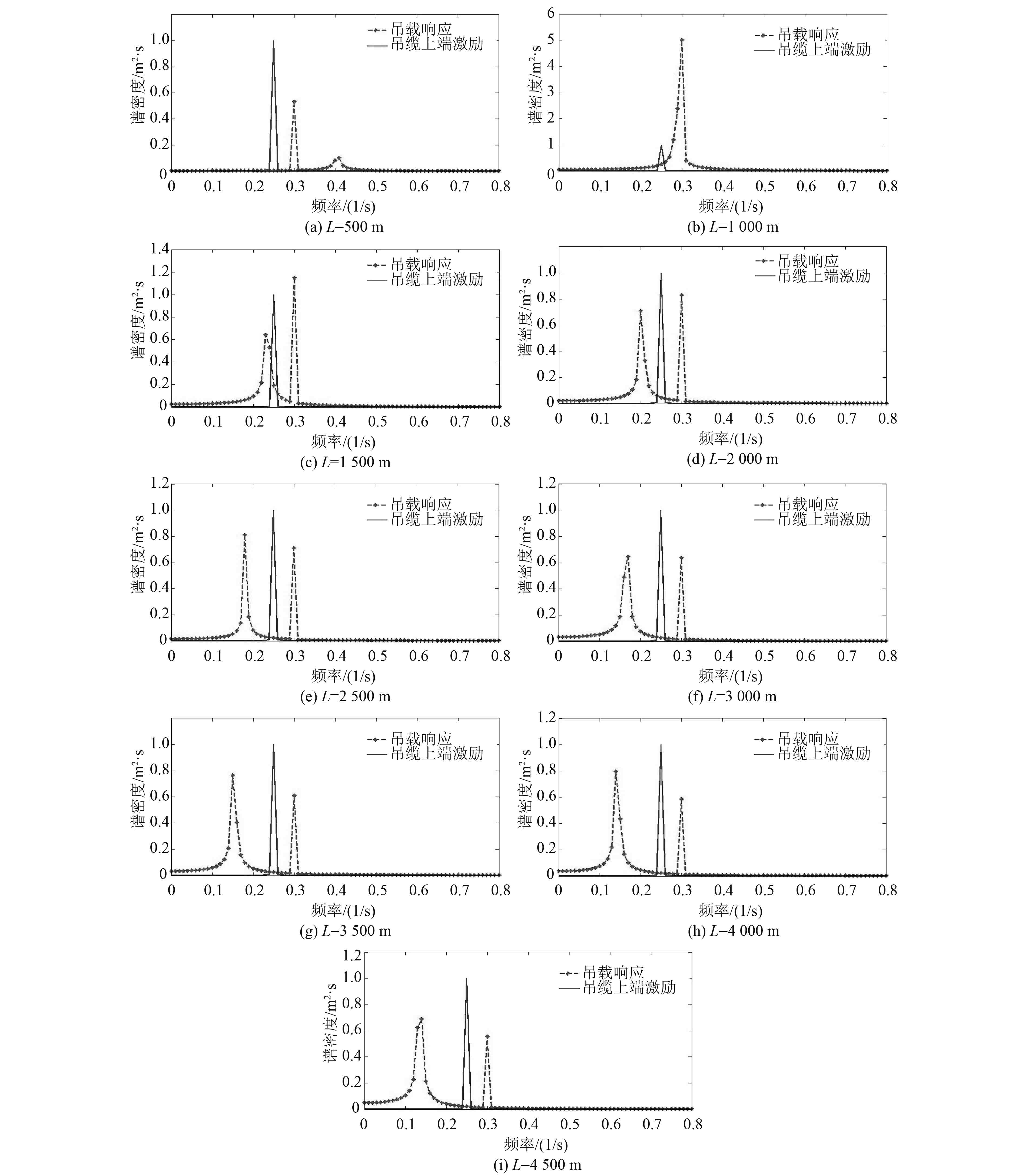
|
图 5 不同缆长时吊载响应频谱分析 Fig. 5 The response spectrum analysis of hoisting load under the different cable length |
将缆长3 000 m和4 500 m时吊载处垂向位移幅值的计算结果绘制成图6。通过分析计算结果可以发现,激励周期在4 s以内时,缆长3 000 m和4 500 m吊载处的垂向位移幅值基本保持一致,随着激励周期增加,3 000 m时吊载处的垂向位移幅值要大于4 500 m,且相差程度越来越大,这与缆长的变化引起吊缆自身弹性伸缩量的不同有直接关系。计算结果表明,吊缆上端激励周期影响吊缆垂向运动响应的重要因素之一,故在考察上端激励对吊缆非线性运动响应的影响时,除考虑激励幅值等因素外,还需关注上端激励周期。
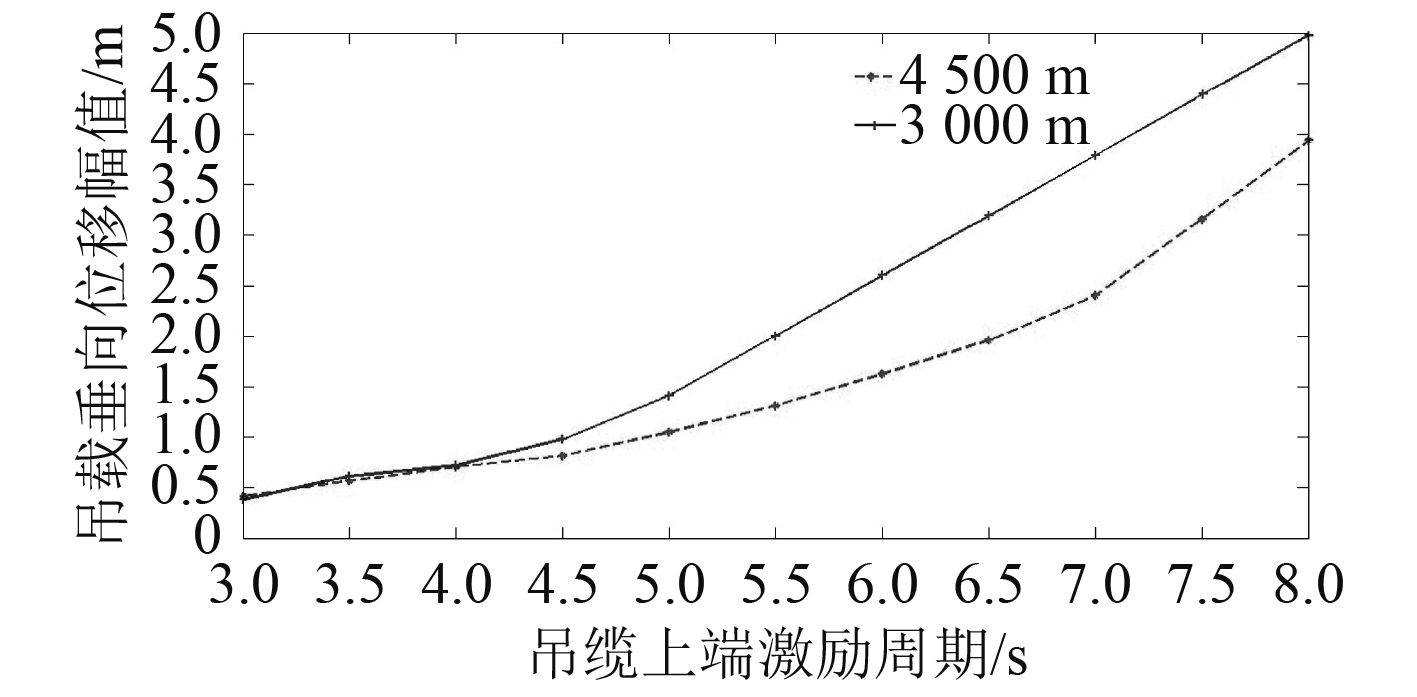
|
图 6 不同吊缆长度的吊载垂向位移随吊缆上端激励变化情况 Fig. 6 The variation of load vertical displacement with different inspiring period and cable length |
以弹性波理论为基础,从能量的角度出发,根据Hamilton原理建立了吊缆的动态模型,推导出吊缆在法向、切向和副法向3个方向的三维非线性运动方程,考虑平面运动,通过泰勒展开得到各自的非线性表达,根据方程的特点,采用有限差分方法进行求解,参照文献中给定的参数对深水吊缆的非线性运动响应进行计算,通过与文献中不同上端激励周期时缆张力试验值的比较,验证了求解方法的准确性和可靠性,同时分析了出现误差的原因;以谐波运动作为初始激励,计算不同水深时的吊载垂向运动响应并进行频谱分析,结果表明初始激励为只有一个主频率的线性运动,但吊载的垂向运动响应时历呈现随机状态,出现2个主频率,为明显的非线性运动;同时给出了缆长4 500 m和3 000 m吊载处的垂向位移的计算结果,发现随着激励周期增加,3 000 m时吊载处的垂向位移幅值要大于4 500 m,且相差程度越来越大。
| [1] |
曾一非.海洋工程环境[M].上海:上海交通大学出版社.2007年.
|
| [2] |
李润培, 谢永和, 舒志. 深海平台技术的研究现状与发展趋势[J]. 中国海洋平台, 2003, 18(3): 1-5. LI Run-pei, XIE Yong-he, SHU Zhi. Research status and development trend of deep-sea platform technology[J]. China Offshore Platform, 2003, 18(3): 1-5. DOI:10.3969/j.issn.1001-4500.2003.03.001 |
| [3] |
苏斌, 冯连勇, 王思聪, 等. 世界海洋石油工业现状和发展趋势[J]. 中国石油企业, 2006, 2(2): 138-141. SU Bin, FENG Liang-yong, WANG Si-cong, et al. The current situation and development trend of the world's offshore oil industry[J]. Petro China Enterprise, 2006, 2(2): 138-141. |
| [4] |
缪国平, 刘应中.挠性部件力学导论[M]. 上海: 上海交通大学出版社. 1995.
|
| [5] |
GAULT A J. COX W R. Method for predicting geometry and loading distribution in an anchor chain from a single point mooring buoy to a buried anchorage[C]//OTC, 1973(1):309–318.
|
| [6] |
WEBSTER W C. Mooring induced damping[J]. Ocean Engineering, 1995, 22: 571-591. DOI:10.1016/0029-8018(94)00027-5 |
| [7] |
YANG Min-dong, TENG Bin. Static and dynamic analysis of mooring lines by nonlinear finite element method[J]. China Ocean Engineering, 2010, 24(3): 417-430. |
| [8] |
陈雯,窦义粟. 世界海洋工程产业发展现状分析[J]. 中国水运, 2007, 7(8): 190-200. CHEN Wen, DOU Yi-su. Analysis of the current situation of the world's ocean engineering industry[J]. China Water Transport, 2007, 7(8): 190-200. |
| [9] |
陶永宏. 我国海洋工程发展现状[J]. 中外船舶科技, 2009(3): 6-9. TAO Yong-hong. China's marine engineering development status[J]. Shipbuilding Science and Technology, 2009(3): 6-9. |
| [10] |
M. Freely propagating waves in elastic cables[J]. Journal of Sound and Vibration, 1996, 196(2): 189-202. |
| [11] |
MAHAMMAD Behbahan, Nejad, Wave propagation in elastic cables with and without fluid interaction[D], Doctor Degree, the University of Michigan, 1997.
|
| [12] |
吴开塔,ROV被动式升沉补偿系统理论及试验研究[D].上海:上海交通大学,2011.
|
| [13] |
袁鑫.系泊缆索动力分析数值方法研究[D].哈尔滨:哈尔滨工程大学.2010.
|
| [14] |
陆金甫,关冶.偏微分方程数值解法[M].北京:清华大学出版社, 2004.
|
| [15] |
李荣画,冯果忱.偏微分方程数值解法[M].北京:高等教育出版社, 1996.
|
| [16] |
RICHARD Haberman, 郇中丹, 李援南等译. 实用偏微分方程[M]. 北京: 机械工业出版社, 2007. 2, S2.
|
| [17] |
PETTER Andreas Berthelsen, Dynamic response analysis of a truss spar in waves[J].Newcastle;University Of Newcastle, 2000.
|
| [18] |
H. Analytical solution on the dragged surge vibration of tension leg platforms (TLPS) with wave large body and small body multi-interactions[J]. Journal of Sound and Vibration, 2001, 248(3): 533-556. DOI:10.1006/jsvi.2001.3803 |
| [19] |
CHATJIGEORGION,L. Comparative evaluation of numerical schemes for 2D mooring dynamics[J]. International journal of offshore and polar engineering, 2010, 10(4): 301-309. |
 2019, Vol. 41
2019, Vol. 41
