舰艇作战态势判断模型是舰艇作战指挥系统的核心模型之一,处于舰艇作战指挥过程的前段,为后续指挥提供决策依据,其可信度直接决定作战指挥决策的成败。目前,评估模型可信度的方法比较多,主要有定性评估、定量评估和定性与定量结合式评估[1 – 3]3种方式。评审法是定性式评估的一种典型方法,主要用于解决评估项目多且难于指标化处理的评估内容,即直接将评估项目分解成若干个子项目,然后由相关人员对其进行一一评估,此种方法常用于模型的验证过程。定量式评估的方法主要有相似度评判法,这种方法需要模型具体的数据输出,通过在相同的输入状态下考察模型输出与理论输出的相似程度来确定模型的可信度。定性与定量结合式评估的方法主要有模糊综合评判法、灰色综合评估法[4 – 6]、多属性决策分析法[7 – 8]等,这些方法需要对评估项目建立评估系统的指标体系,并组织相关专家对各指标进行打分,然后对其进行数理方法的处理,最后将可信度量化成具体的数值来供使用者参考。而舰艇作战态势判断模型并不像工程模型那样有特定的数据输入输出,为此,只能通过建立指标体系,由相关评审人员对指标体系的主观评分而进行,但这种评估方法主观性强,参考价值不大,那么如何才能综合评审专家的意见又能进行定量分析,客观的得出评估结论呢?模糊综合评判法就为解决这类问题提供了解决途径。
1 建立舰艇作战态势判断模型的可信度评估指标体系模型可信度评估指标体系是进行可信度评估的前提条件,直接影响评估方法和评估结果。在建立评估指标体系时必须从分析评估对象的本质属性入手,将这一属性的外观表现确定为指标,建立模型可信度的指标体系应该遵循以下几个原则[9 – 11]:
1)可度量原则,即评估指标的度量能够依据模型本身而得出,是对模型原始状态的客观反映,而不是主观确定的;
2)完整性原则,即评估指标要尽量涵盖模型的每个方面,要形成一个相对完善的系统;
3)相互独立性原则,即各个指标之间要尽可能的避免涵义交集,便于独立的对指标进行处理;
4)本质属性体现原则,即评估指标要能体现评估对象的本质和主要方面,能够把评估对象的关键因素反映出来;
5)目的关联性原则,即所选择的评估指标一定要与评估目的紧密相关。
舰艇作战态势判断是根据敌我双方当前的战斗状态而做出对将来战斗状态发展的预测,便于指挥员做出指挥决策的过程。根据“基于当下预判未来”的特点,结合上述5项原则,可以建立舰艇作战态势判断模型可信度评估的指标体系如图1所示。
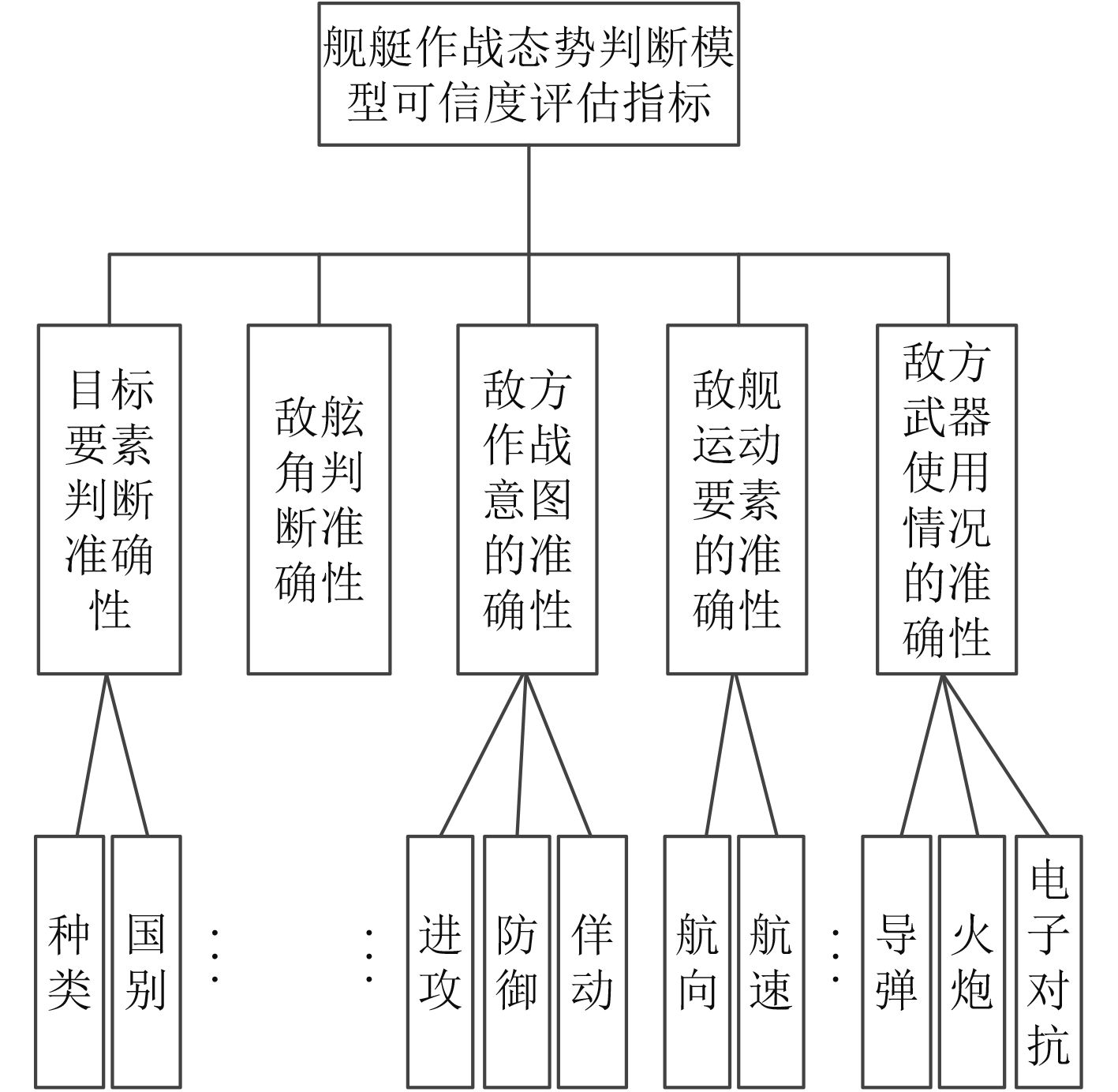
|
图 1 舰艇作战态势判断模型可信度评估的指标体系 Fig. 1 The reliability index system of warship combat situation judgement modle |
1)目标要素判断准确性:目标要素是态势判断中对我方战斗部署影响较大的一方面,其准确性会直接影响态势判断的结果,是态势判断模型中可信度评价的一个重要指标;
2)敌舷角判断准确性:敌舷角是预测敌我双方有利阵位的关键,在态势判断中是我方必须分析的一个重要因素,对态势判断模型的可信度影响不言而喻;
3)敌方作战意图的准确性:敌方的作战意图会关系到我作战策略的实施,是控制作战态势向有利于我方发展的关键,是决定态势判断模型可信度的又一重要环节。
4)敌舰运动要素的准确性:敌舰运动要素是辅助揣测敌方作战意图及对我方威胁程度的基础性因素,是影响态势判断模型可信度的基础。
5)敌方武器使用情况的准确性:敌方武器使用情况将间接决定我方战术战法,确保我方用最少的战略资源有效歼灭敌方。
2 舰艇作战态势判断模型的评估方法要获得态势判断模型的可信度必须对上述5项指标展开分析,由于衡量这些评价指标时常常具有不确定性,在一定程度上会使评审人员给出一个带有模糊性质的评估结果,为了将模糊的结果定量化,本文以模糊数学为理论依据,运用模糊综合评判法对态势判断模型进行可信度评估。具体步骤如下[12]:
1)建立态势判断模型的可信度评价指标集
2)根据评估的需要,确定评价等级
3)由评审人员给出各指标对应与各评价等级的得分
| ${ R} = \left| {\begin{array}{*{20}{c}} {f({x_{1m}})} \\ {f({x_{2m}})} \\ \vdots \\ {f({x_{nm}})} \end{array}} \right| = \left| {\begin{array}{*{20}{c}} {{r_{11}}}&{{r_{12}}}& \cdots &{{r_{1m}}} \\ {{r_{21}}}&{{r_{22}}}& \cdots &{{r_{2m}}} \\ \vdots & \vdots & \ddots & \vdots \\ {{r_{n1}}}&{{r_{n2}}}& \cdots &{{r_{nm}}} \end{array}} \right|{\text{,}}$ | (1) |
式中,
4)确定权重集
5)进行可信度评估计算,根据可信度评估需要,选取乘积有界和的模糊算子,并进行归一化处理后,得到
| $ Y = Q \cdot R{\rm{ = }}\left( {{y_1}, {y_2}, {y_3}, {y_4}} \right)\text{,} $ | (2) |
式中,y1~y4分别为态势判断子模型属于完全可信、比较可信、基本可信、不可信的程度,这里取完全可信与比较可信的和作为态势判断模型的可信度。
3 构建评价指标与评价等级的S型隶属度函数在上述模糊综合评判法评估舰艇作战态势判断模型可信度的分析中,可以知道指标集与评判集的隶属度函数的确定是该方法的核心部分,其结果直接影响评估结果。目前,各类隶属度函数已经非常的多,不同指标不同评价目的使用的隶属度函数就不同,常见的隶属度函数有梯形分布、K次抛物型分布、T型分布、正态分布、柯西分布、岭型分布[12 – 15]等,但是通过作战实际和理论分析发现,这些隶属度函数并不适用于舰艇作战态势判断模型的指标与可信度评价等级的隶属关系,这就需要建立一种新的适用于该模型的隶属度函数。
为了研究合理的隶属关系,本文以舰艇作战态势判断模型中的目标要素判断准确性这项指标与可信度评价等级的隶属度关系进行了调查,通过部队使用人员、领域专家的反馈,整理得到了如表1所示的数据,调查的指标分值采用百分制,隶属度值为0~1之间。
|
|
表 1 目标要素判断准确性与可信度评价等级的隶属度关系 Tab.1 The relationship between the accuracy of judgment of objective elements and reliability evaluation level |
从表1中的数据中可以发现,当指标评分在低于60分内增长时,对隶属度影响程度较小,表明在这个范围内使用者认为模型的可信度不高;当指标评分高于95时,其分值增长对隶属度影响也较小,表明该指标已经达到了使用者对模型的期望程度,基于以上数据分析,由表1运用数据拟合的方法得到了S型隶属度函数关系:
| $ f(x) = \left\{ \begin{aligned} & 1, x \in (95, 100] \text{,}\\ &1 - {e^{ - {{(\frac{x}{\lambda })}^3}}}, x \in (20, 95] \text{,}\\ & 0, x \in [0, 20) \text{。} \end{aligned} \right. $ | (3) |
式中,
运用数学方法证明该隶属度函数的正确性。
要证明增长率先增大后减小,即要证明其导数值是先增大后减小的变化趋势,容易想到对
为此,这里利用泰勒公式对原函数做等价变换,由于f(x)在
| $ f(x) \cong {\left(\frac{x}{\lambda }\right)^3} - \frac{1}{{2!}}{\left(\frac{x}{\lambda }\right)^6} + \frac{1}{{3!}}{\left(\frac{x}{\lambda }\right)^9} - \frac{1}{{4!}}{\left(\frac{x}{\lambda }\right)^{12}} + \frac{1}{{5!}}{\left(\frac{x}{\lambda }\right)^{15}} - \cdots \cdots $ |
为了计算方便,取其前四项得到

|
图 2 指标得分与隶属度的增长率的变化关系 Fig. 2 The change relationship between Index score and growth rate of membership |
通过几种典型的隶属度函数与表1中的样本数据进行拟合比较。
图3为正态分布函数的拟合图像,图中曲线基本符合样本数据的走向,但曲线坡度还不够,不能正确反映隶属度函数关系。
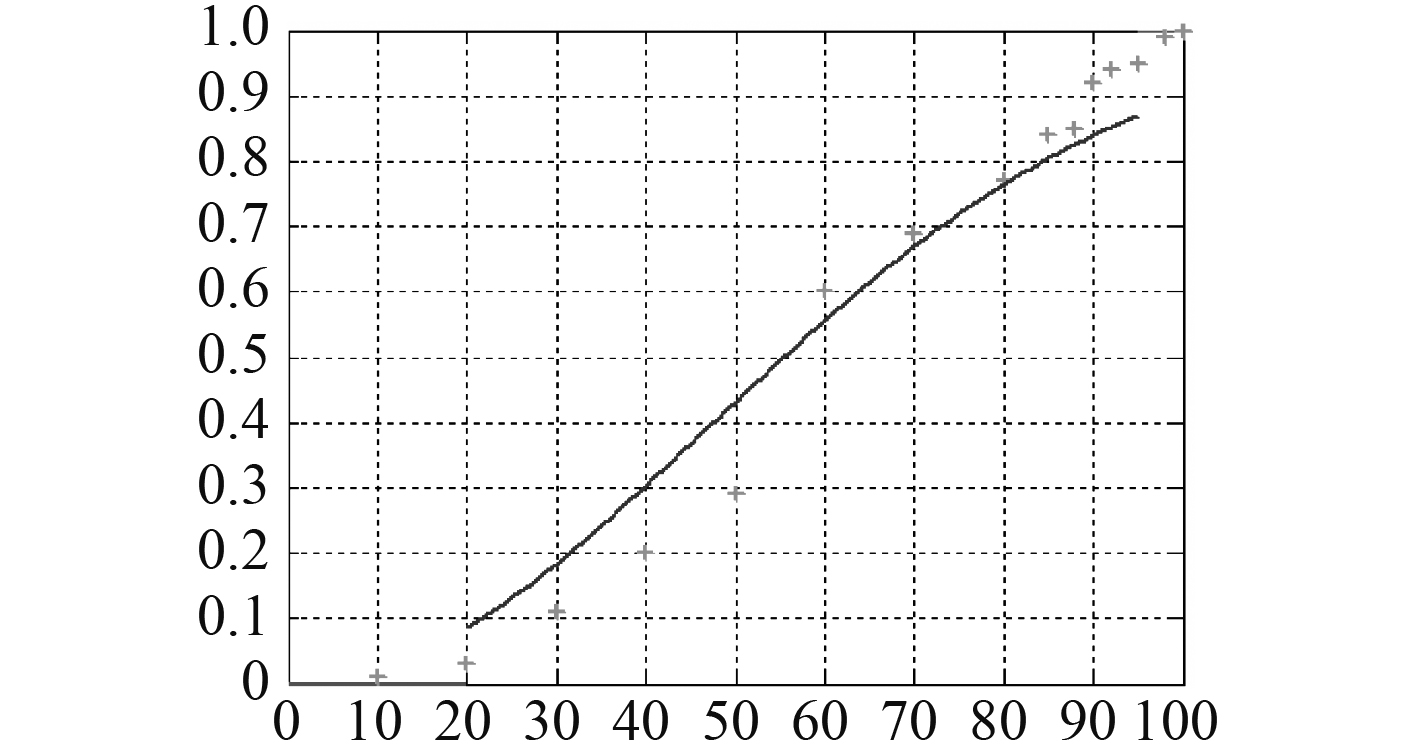
|
图 3 正态分布函数拟合图 Fig. 3 The fitting graph of normal distribution function |
图4和图5分别为二次抛物型和T型分布的函数拟合图,从图中直观反映出2种函数已经严重偏离样本数据的发展趋势,完全不符合本文需要建立的隶属度函数;
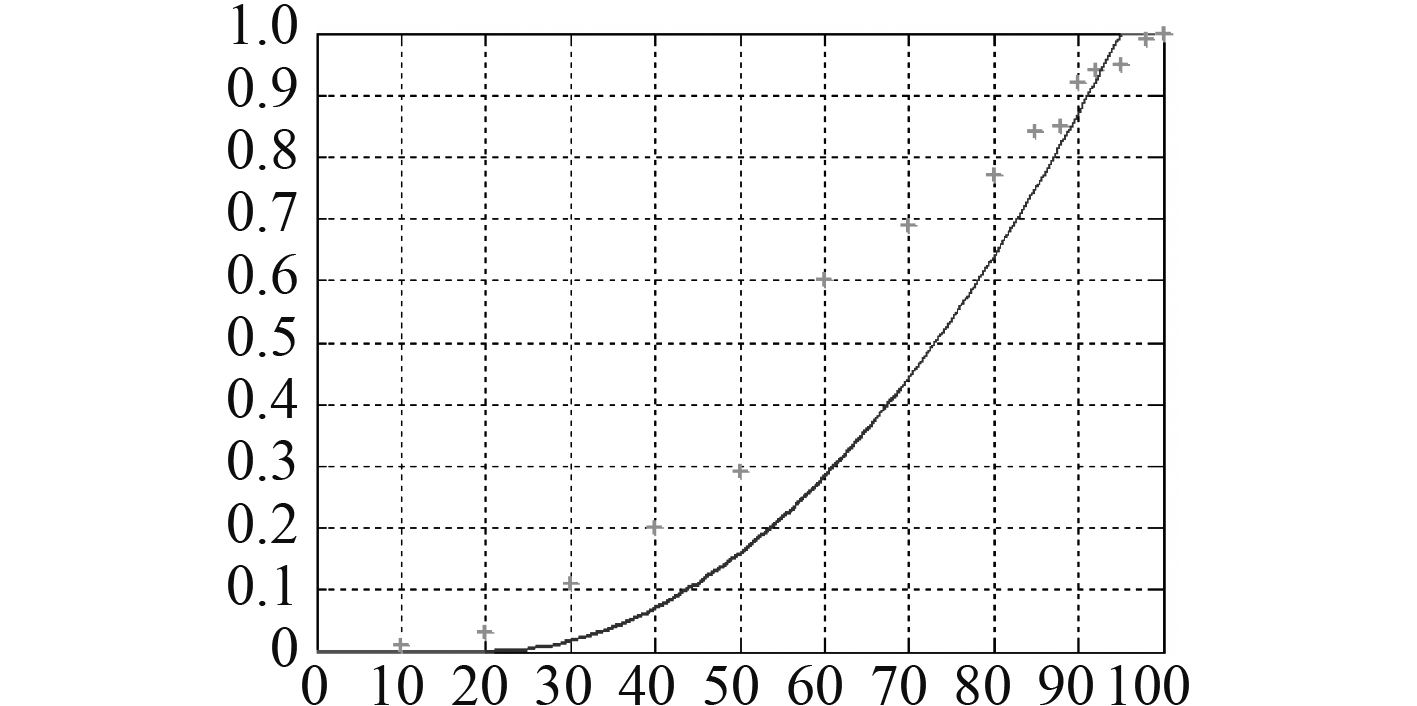
|
图 4 二次抛物型拟合图 Fig. 4 The fitting graph of two parabolic function |
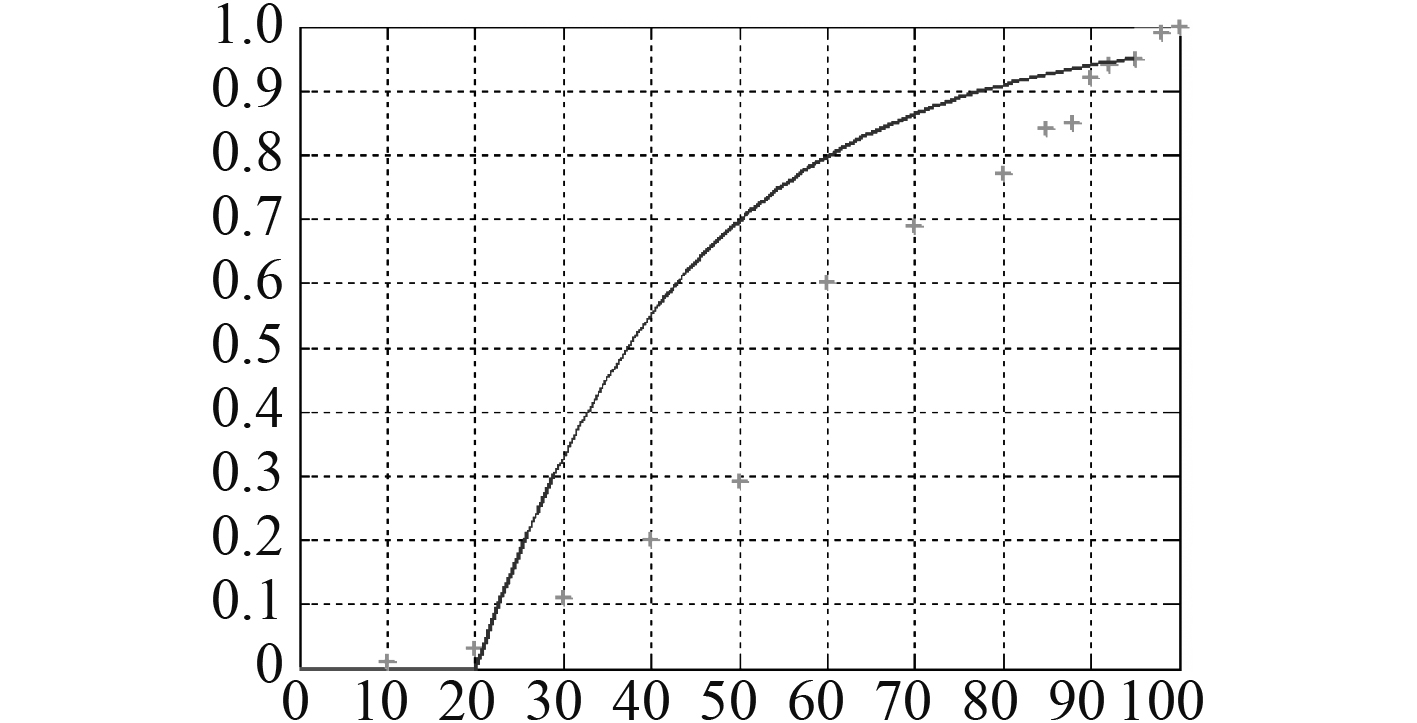
|
图 5 T型分布拟合图 Fig. 5 The fitting graph of T type distribution |
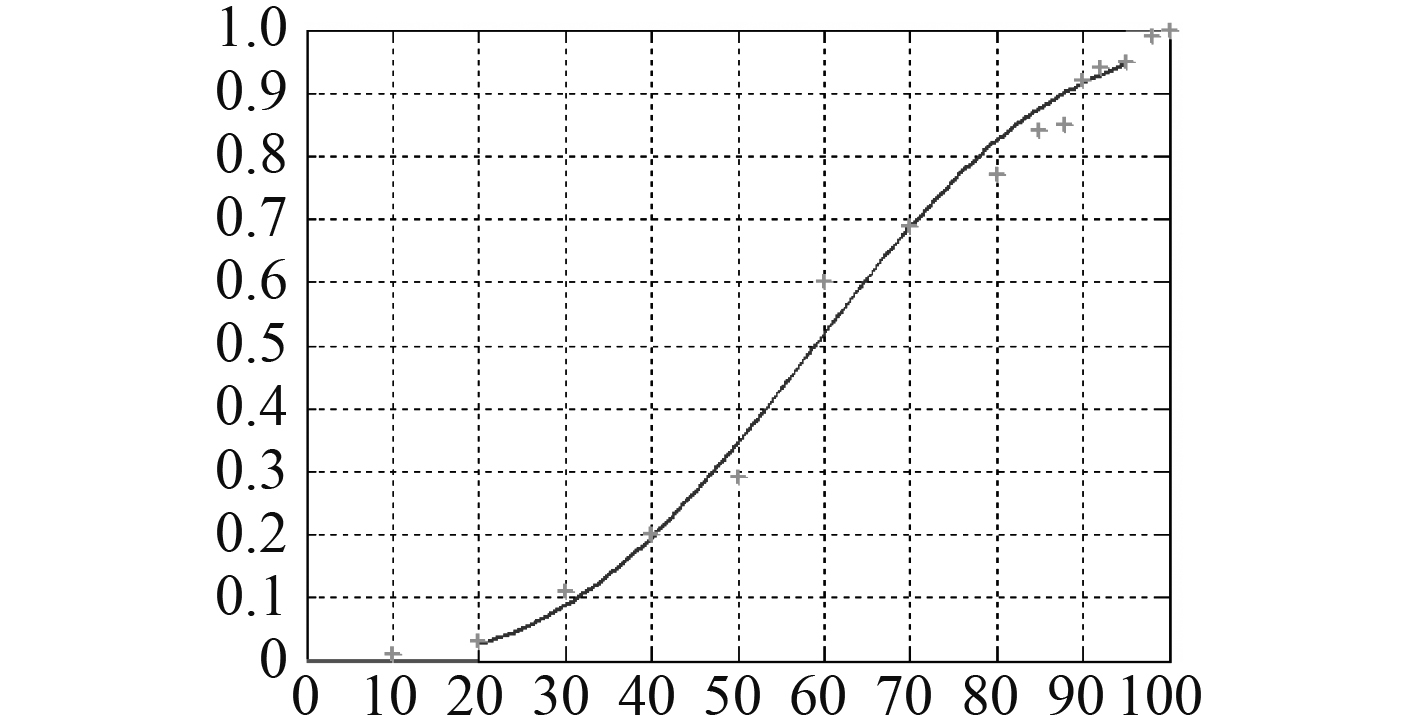
图6为建立的S型函数拟合图,通过对比分析,S型函数弥补了正态分布函数坡度不够的缺点,较好地反映了样本数据的关系,可以作为舰艇作战指挥决策模型中内部组成可信度评估的隶属度函数。
|
图 6 S型函数拟合图 Fig. 6 The fitting graph of S type function |
S型隶属度函数使用范围:
1)评价指标采取百分制的方式,函数自变量为指标分值,且为效益型指标(即随着指标分值的增大,隶属程度也增大);
2)指标与评价等级的隶属关系不成线性比例,且存在指标的某一评分区间其隶属度的增长率明显大于其他部分即S型;
3)指标区间的两端存在一段稳定值。
总而言之,作战态势判断模型的输入信息是敌当前数据和历史数据,具有随机性、模糊性和欺骗性特点;输出信息的关键是判断结论,具有综合性和预测性特点。指挥员和领域专家最初对此类模型往往存在较大分歧,当模型经过不断优化,可信度达到一定预期时,指挥员和领域专家对模型的认可程度会加速达成共识。S型隶属度函数能恰当的反映这一共识过程,适合应用于此类模型的可信度评估。
4 结 语模糊综合评判法以其定性与定量相结合的方式使得评估方法更加合理,隶属度函数是该方法的核心,本文在研究现有的隶属度函数后,通过建立舰艇作战态势判断模型可信度的评估指标体系,分析了指标与评价等级的隶属关系,构建了一种适合舰艇作战态势判断模型可信度评估的S型隶属度函数,并通过数学理论证明了该方法的正确性,运用Matlab对该函数进行了仿真验证,证明了与实际分析的合理性,最后总结了S型隶属度函数的适用范围和条件。
建立符合作战实际的模型是后续工程化的前提。模型的可信度直接体现了一线指挥员与领域专家对模型的认可程度,是主观认可到作战实际的映射。S型隶属度函数能合理地体现作战态势判断模型被认可的过程,具有一定的可信度评估适用性,也可推广应用于评估其他作战决策和预测模型的可信度。
| [1] |
OSMAN B, ROBIN J A, DAVID S M. A collaborative evaluation environment for credibility assessment of modeling and simulation applications[C]//Proceedings of WSC. USA 2002: 322–326.
|
| [2] |
唐见兵, 查亚兵. 作战仿真系统校核、验证与确认及可信度评估[M]. 北京: 国防工业出版社, 2013: 144.
|
| [3] |
谭亚新, 王立国, 杨学会, 等. 作战仿真可信性[M]. 北京: 国防工业出版社, 2014.: 65.
|
| [4] |
王洪利, 冯玉强. 基于灰色的改进白化模型及其在灰色决策中应用[J]. 黑龙江大学自然科学学报, 2006, 23(6): 740-745. DOI:10.3969/j.issn.1001-7011.2006.06.003 |
| [5] |
ROBERT F, HERBERT P. A systems approach to a verification and validation methodology within the FEDEP six-step-process[C]//2001 Europe Computer Simulation Conference, Paper Number: 01E-SIW-085.
|
| [6] |
SIEGFRIED P, DIRK B. Representing results of V&V-activities in fuzzy decision analysis value trees[C]//2005 European Computer Simulation Conference, Paper Number: 05E-SIW-01269.
|
| [7] |
ARAZY O, et al. Recognizing contributions in wikis: authorship categories, algorithms, and visualizations[J]. Journal of the American Society for Information Science and Technology, 2010, 61(6): 1166-1179. |
| [8] |
陈金玉, 徐克虎, 孔德鹏, 等. 混合多属性决策投影算法的装甲分队目标价值评估[J]. 火力与指挥控制, 2015(4): 59-62. DOI:10.3969/j.issn.1002-0640.2015.04.015 |
| [9] |
翟慎涛, 顾健, 占科鹏. 仿真模型可信度评估指标体系研究[J]. 系统仿真学报, 2011(23): 26-29. |
| [10] |
BRADE D M L. Asseeement criteria and VV levels in JP11.20[C]//Spring Simulation Interoperability Workshop, SIOS, Arlington, VA, 2004.
|
| [11] |
BALSOY O, JIN Y, AYDIN G. Automation metadata web service deployment for problem solving environments[J]. Future Generation Comp. Syst, 2005, 21(6): 910-919. DOI:10.1016/j.future.2003.12.018 |
| [12] |
梁保松, 曹殿立. 模糊数学及其应用[M]. 北京: 科学出版社, 2007: 41–45.
|
| [13] |
HERMANN C F. Validation problems in games and simulation with special reference to model of international politics[J]. Behavioral Science, 1967(3): 216-231. |
| [14] |
WIGAN RM. The fitting calibration and validation of simulation models[J]. Simulation, 1972(1): 32-38. |
| [15] |
ERNESTH P, BRADFORDS, CANOVA. A case study of verification, validation, and accreditation for advanced distributed simulation[J]. ACM Transactions on Modeling and Computer Simulation, 1997(11). |
 2019, Vol. 41
2019, Vol. 41
