水下滑翔机是一种新型的水下航行器,其通过改变自身净浮力和质心位置来实现水下滑翔运动。与传统AUV相比,水下滑翔机具有成本低、能耗低、续航力强等优点,更适合大范围、长航程的工作任务,不足之处在于水下滑翔机的航速低、机动性较差[1, 2]。水下滑翔机可通过调节尾舵舵角或改变横滚姿态实现转向,相比于传统的AUV,其在转向调节过程通常需要较大的空间和较长的时间[3, 4]。尤其对于利用横滚姿态进行转向调节的水下滑翔机,所需的时间和空间尺度更大。将滑翔机的转向速度作为摄动参数,Mahmoudian等[5]推导了滑翔机稳态转向时转向速度的近似解析表达式,Yang等[6]推广此方法分析了装有尾舵的滑翔机转向性能。顾建农等[7]基于柯西霍夫方程实现了水下滑翔机的动力学建模和转向运动仿真。朱时雨等[8]分析了水柱测量中的水下滑翔机转向性能。为降低内部机构调节的能耗,在大多数工作时间内,水下滑翔机处于稳态运动。水下滑翔机的稳态螺旋运动,作为一种典型运动形式,常用于水下滑翔机航向的调节。Zhang等[9]建立了一种稳态螺旋运动的快速求解方法,并与Seawing滑翔机的试验结果进行对比验证。赵宝强等[10]采用李雅普诺夫方法进行了螺旋运动稳定性分析。Liu[11]采用理论与试验方法分析了水下滑翔机的反螺旋运动。
当水下滑翔机在近海底或近壁面等限制水域运动时,水域的空间范围会限制其转向运动。水下滑翔机的转弯运动通常可视为稳态螺旋运动的一部分,因此,稳态螺旋运动在时间、空间上的运动尺度特征可以为水下滑翔机在限制水域内的转向运动提供指导。目前,在现有研究中尚未看到螺旋运动时空尺度特征的系统分析,文献[9]也仅是给出了下潜过程中回转半径与滑块转角的变化规律,并未分析其他控制参数和尺度特征。本文从水下滑翔机的运动学和动力学微分方程入手,建立了稳态螺旋运动的时间、空间尺度特征变化规律的研究思路,并以沈阳自动化研究所研制的Seawing水下滑翔机[9, 12](该水下滑翔机通过内部滑块旋转来实现转向)为例开展研究。
1 运动学建模引入惯性坐标系
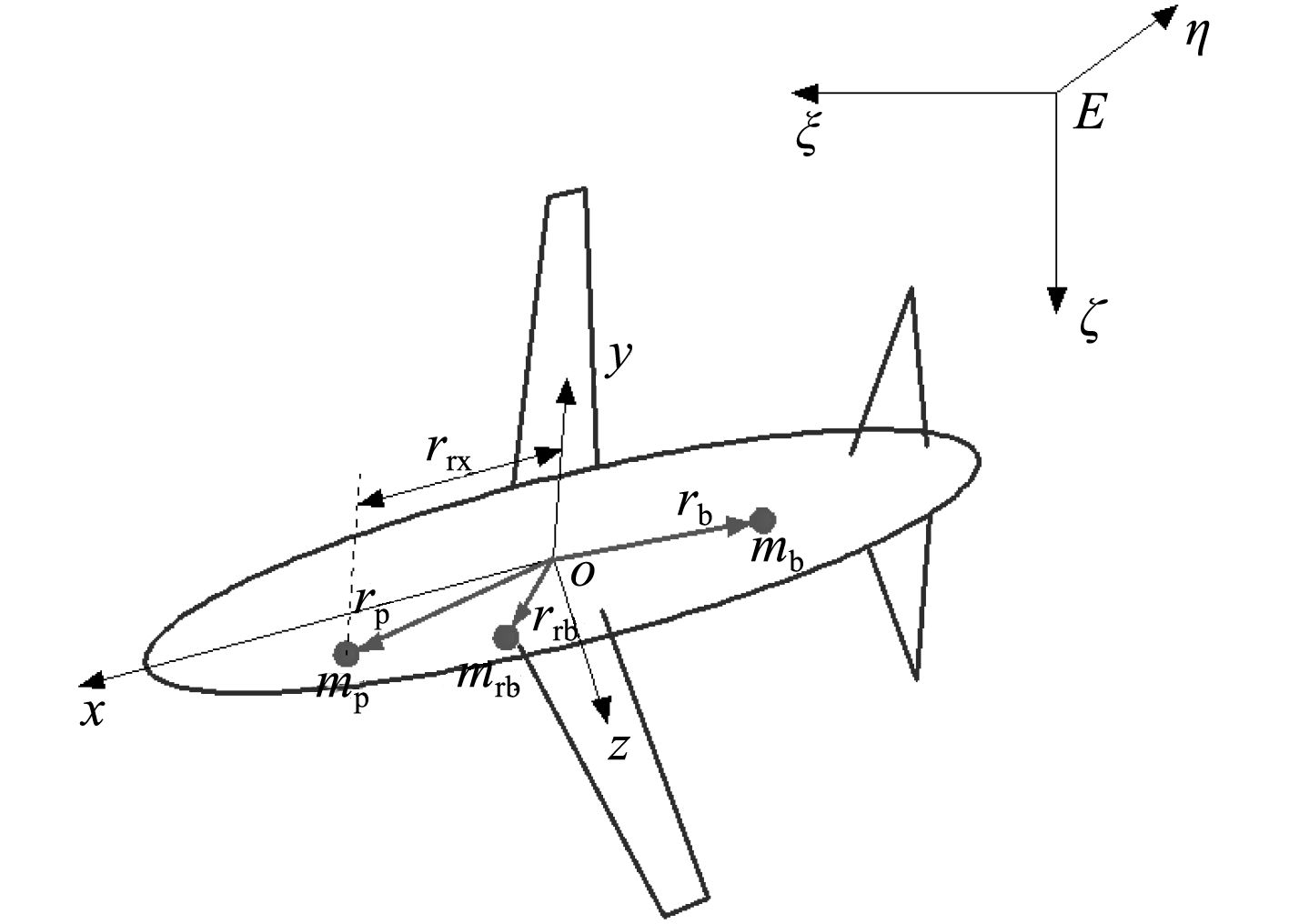
|
图 1 坐标系与质量分布 Fig. 1 Coordinate systems and mass distribution |
| ${{\dot b}} = {{{R}}_{{\rm{EB}}}}{{\upsilon }},{{\dot \varOmega }} = {{{R}}_{\Omega {\rm{B}}}}{{\omega }}\text{。}$ | (1) |
其中,
| $\begin{split} & {{{R}}_{{\rm{EB}}}} \!=\! \left(\!{\begin{array}{*{20}{c}} \!\!\!{{\rm{c}}\theta {\rm{c}}\psi }&{{\rm{s}}\varphi {\rm{s}}\theta {\rm{c}}\psi - {\rm{c}}\varphi {\rm{s}}\psi }&{{\rm{c}}\varphi {\rm{s}}\theta {\rm{c}}\psi + {\rm{s}}\varphi {\rm{s}}\psi }\\ \!\!\!{{\rm{c}}\theta {\rm{s}}\psi }&{{\rm{c}}\varphi {\rm{c}}\psi + {\rm{s}}\varphi {\rm{s}}\theta {\rm{s}}\psi }&{ - {\rm{s}}\varphi {\rm{c}}\psi + {\rm{c}}\varphi {\rm{s}}\theta {\rm{s}}\psi }\\ \!\!\!{ - {\rm{s}}\theta }&{{\rm{s}}\varphi {\rm{c}}\theta }&{{\rm{c}}\varphi {\rm{c}}\theta } \end{array}} \!\!\!\right)\text{,}\\ & {{{R}}_{{\rm{B}}\Omega }} = \left( {\begin{array}{*{20}{c}} 1&0&{ - {\rm{s}}\theta }\\ 0&{{\rm{c}}\varphi }&{{\rm{s}}\varphi {\rm{c}}\theta }\\ 0&{ - {\rm{s}}\varphi }&{{\rm{c}}\varphi {\rm{c}}\theta } \end{array}} \right)\text{。} \end{split}$ | (2) |
水下滑翔机可以视为不同种结构组成的多体系统,包括机身及与机身固结在一起的所有结构mrb,可在机身内部平移和旋转的滑块结构mp,位置不变质量可变的浮力调节机构mb。mrb,mp,mb的质心在体坐标系中的位置分别为向量
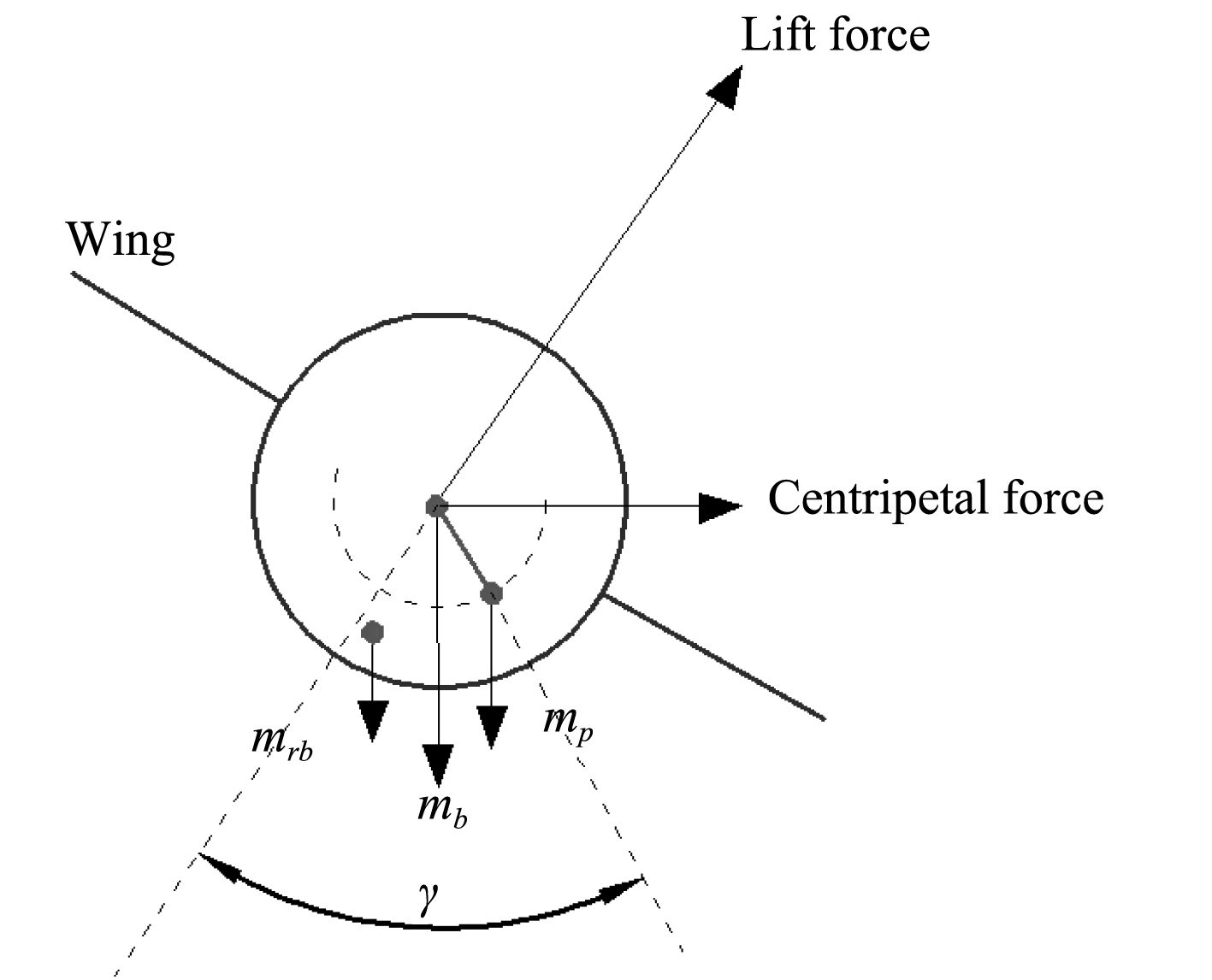
|
图 2 螺旋转向运动的力学机理 Fig. 2 Mechanisms of turning spiraling motion |
水下滑翔机在水下运动时,会带动其周围的附连水共同运动,水下滑翔机及其附连水系统的总体动能可以表达为:
| $T{\rm{ = }}\frac{1}{2}{\left(\!\! {\begin{array}{*{20}{c}} {{\upsilon }} \\ {{\omega }} \end{array}}\!\! \right)^{\rm{T}}}{{M}}\left(\!\! {\begin{array}{*{20}{c}} {{\upsilon }} \\ {{\omega }} \end{array}} \!\!\right){\rm{ = }}\frac{1}{2}{\left(\!\! {\begin{array}{*{20}{c}} {{\upsilon }} \\ {{\omega }} \end{array}} \!\!\right)^{\rm{T}}}\left[ {\begin{array}{*{20}{c}} {{{{M}}_t}}&{{{{C}}_t}} \\ {{{C}}_t^T}&{{{{I}}_t}} \end{array}} \right]\left(\!\! {\begin{array}{*{20}{c}} {{\upsilon }} \\ {{\omega }} \end{array}} \!\!\right)\text{,}$ | (3) |
| $\begin{gathered} {{{M}}_t} = {{{M}}_{{A}}} + ({m_{{\rm{rb}}}} + {m_{\rm{p}}} + {m_{\rm{b}}}){{I}} \text{,} \\ {{{C}}_t} = {{{C}}_{{A}}} - {m_{{\rm{rb}}}}{{{{\hat r}}}_{{\rm{rb}}}} - {m_{\rm{p}}}{{{{\hat r}}}_{\rm{p}}} - {m_{\rm{b}}}{{{{\hat r}}}_{\rm{b}}} \text{,}\\ {{{I}}_t} = {{{J}}_{{A}}} + {{{J}}_{{\rm{rb}}}} - {m_{\rm{p}}}{{{{\hat r}}}_{\rm{p}}}{{{{\hat r}}}_{\rm{p}}} - {m_{\rm{b}}}{{{{\hat r}}}_{\rm{b}}}{{{{\hat r}}}_{\rm{b}}} \text{。}\\ \end{gathered} $ | (4) |
其中:
则系统在体坐标系下的线动量
| ${{P}} = \frac{{\partial T}}{{\partial {{\upsilon }}}},{{\varPi }} = \frac{{\partial T}}{{\partial {{\omega }}}}\text{,}$ | (5) |
进一步表达有
| $\left( {\begin{array}{*{20}{c}} {{P}} \\ {{\varPi }} \end{array}} \right){\rm{ = }}{{M}}\left( {\begin{array}{*{20}{c}} {{\upsilon }} \\ {{\omega }} \end{array}} \right)\text{。}$ | (6) |
在稳态运动时,系统的广义质量矩阵将保持不变,即
| $\left( {\begin{array}{*{20}{c}} {{{\dot P}}} \\ {{{\dot \Pi }}} \end{array}} \right){\rm{ = }}{{M}}\left( {\begin{array}{*{20}{c}} {{{\dot \upsilon }}} \\ {{{\dot \omega }}} \end{array}} \right)\text{。}$ | (7) |
基于动量定理和坐标变换,可得系统的动量变化率
| ${{\dot P}} = {{P}} \times {{\omega }} + {{R}}_{{EB}}^{\rm{T}}({{G}} + {{B}}) + {{{F}}_{\rm{B}}}\text{,}$ | (8) |
| ${{\dot \Pi }} = {{\Pi }} \times {{\omega }} + {{P}} \times {{\upsilon }} + {{{r}}_{{\rm{CG}}}} \times {{R}}_{{EB}}^{\rm{T}}{{G}} + {{{M}}_{\rm{B}}}\text{。}$ | (9) |
其中:
将式(6)、式(7)代入式(8)、式(9),即得到水下滑翔机稳态运动的动力学方程:
| $\left(\!\! {\begin{array}{*{20}{c}} {{{\dot \upsilon }}} \\ {{{\dot \omega }}} \end{array}} \!\!\right){\rm{ = }}{{{M}}^{ - 1}}\left(\!\! {\begin{array}{*{20}{c}} \begin{gathered} ({{{M}}_t}{{\upsilon }} + {{{C}}_t}{{\omega }}) \times {{\omega }}+ \\ {{R}}_{{\rm{EB}}}^{\rm{T}}({{G}} + {{B}}) + {{{F}}_{\rm{B}}} \\ \end{gathered} \\ \begin{gathered} ({{C}}_t^T{{\upsilon }} + {{{I}}_t}{{\omega }}) \times {{\omega }} + ({{{M}}_t}{{\upsilon }} + {{{C}}_t}{{\omega }}) \times {{\upsilon }}+ \\ \begin{array}{*{20}{c}} {}&{}&{} \end{array} {{{r}}_{{\rm{CG}}}} \times {{R}}_{{\rm{EB}}}^{\rm{T}}{{G}} + {{{M}}_{\rm{B}}} \\ \end{gathered} \end{array}} \!\!\right)\text{。}\!\!\!\!\!\!\!\!$ | (10) |
基于水下滑翔机的运动学方程和动力学方程,当给定其控制输入量和
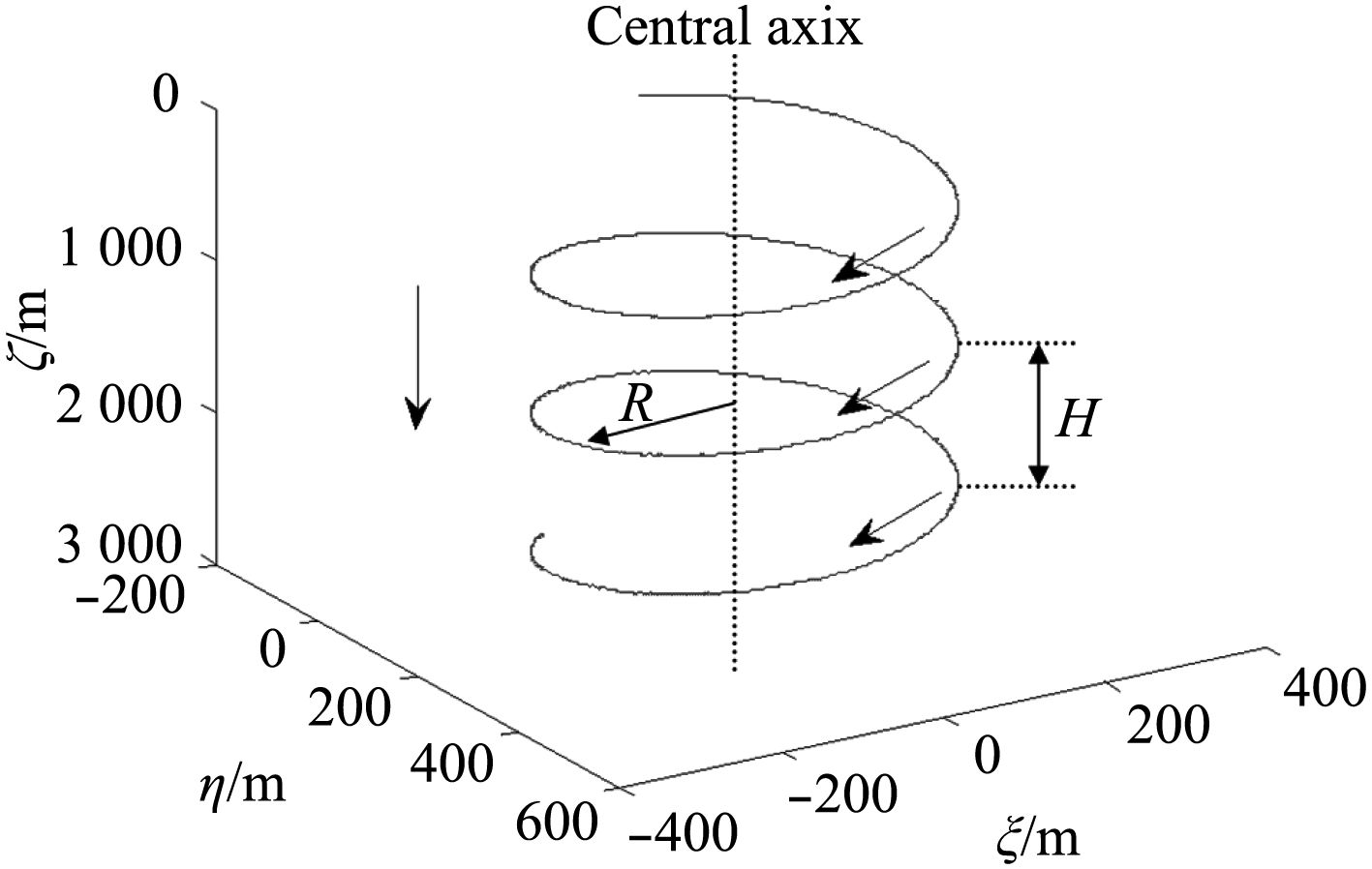
|
图 3 水下滑翔机的螺旋运动轨迹 Fig. 3 The spiral motion trajectory of an underwater glider |
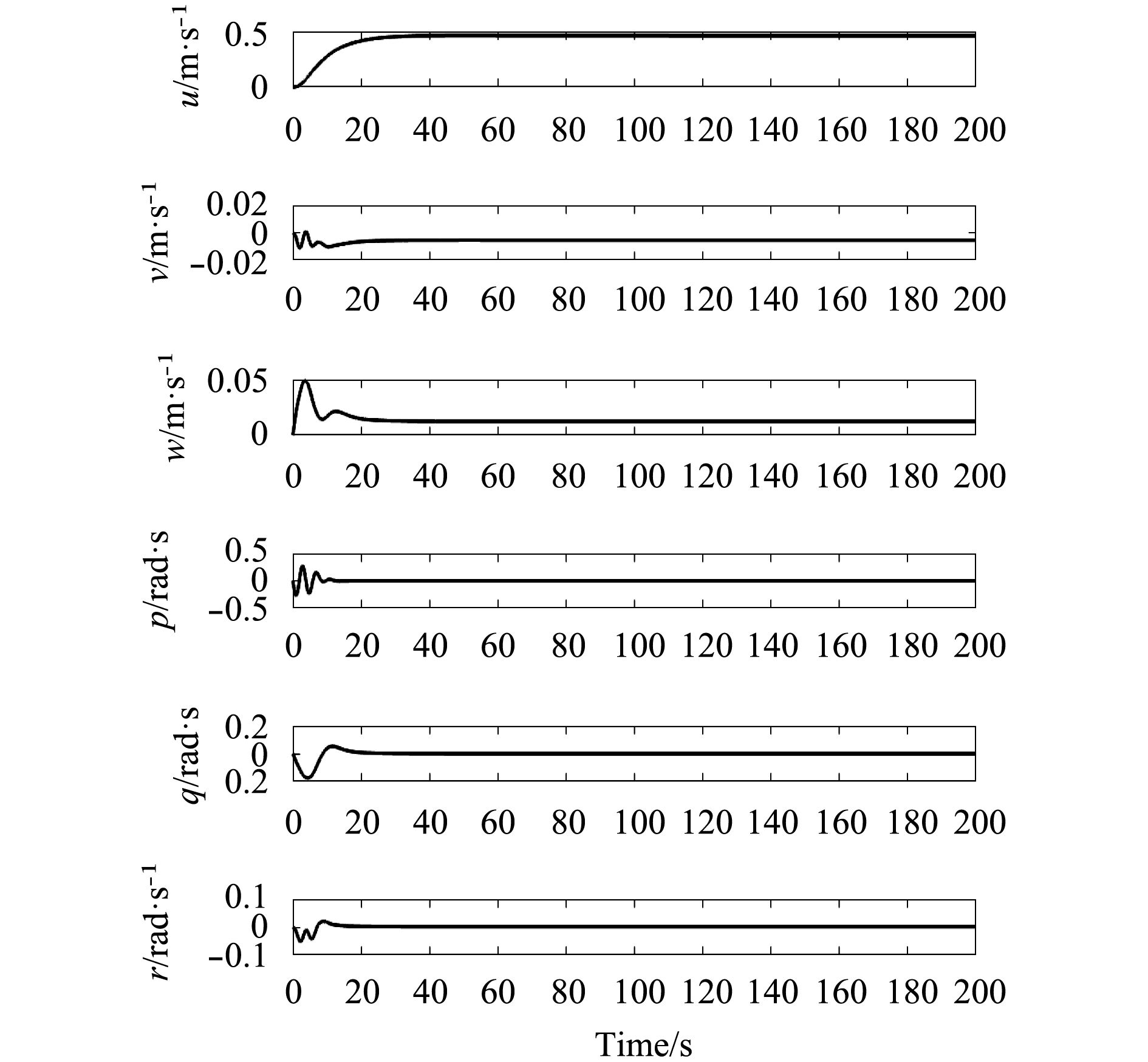
|
图 4 运动速度随时间的变化规律 Fig. 4 Variation of the velocity with the time |
从图4可以看出,随着时间的变化,水下滑翔机的运动速度
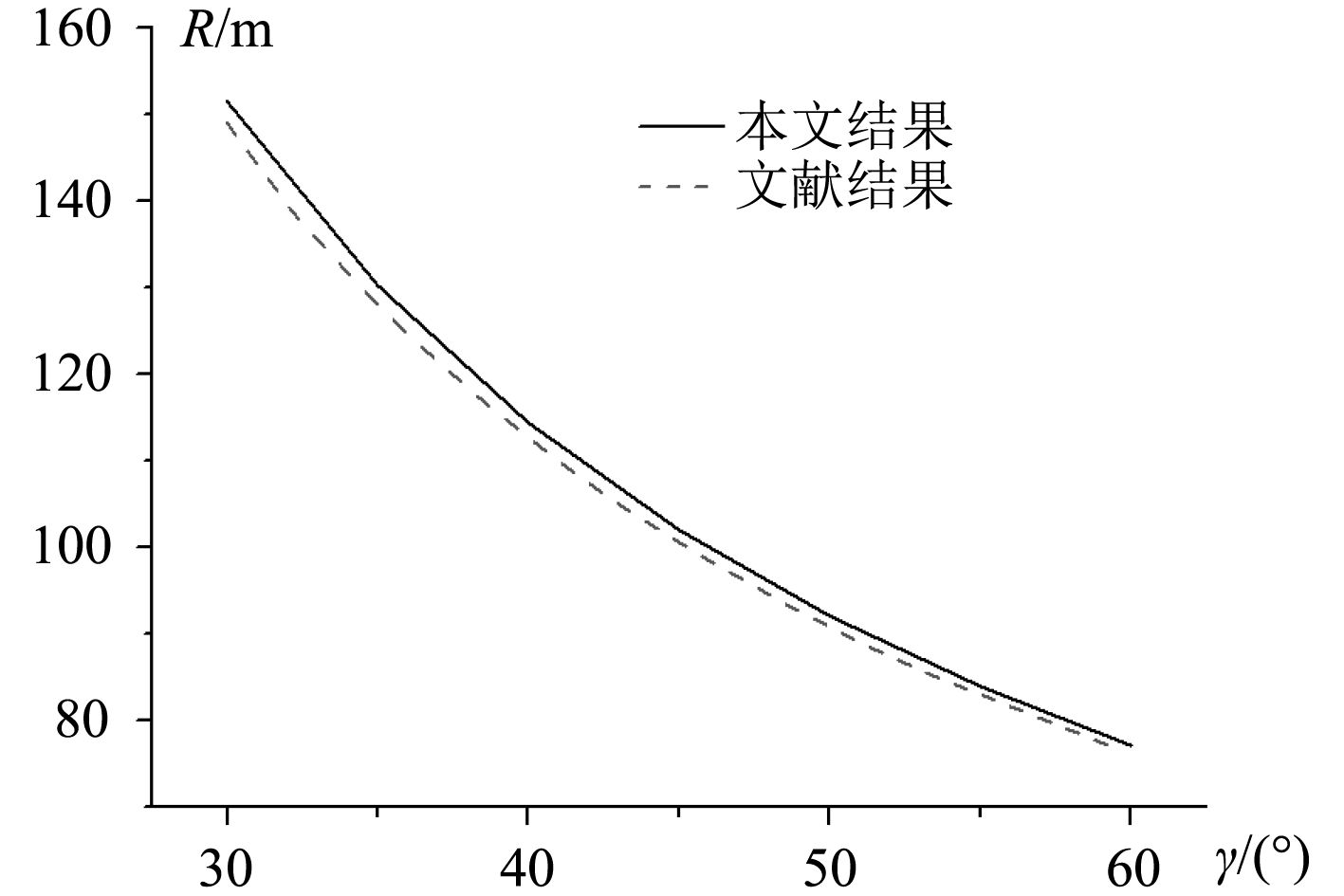
|
图 5 本文方法的验证 Fig. 5 Validation of the method presented in this paper |
根据水下滑翔机沿垂向的运动方向进行分类,水下滑翔机的稳态螺旋运动可分为上浮螺旋运动和下潜螺旋运动。当重力大于浮力,即mb>0时,滑翔机将进行下潜螺旋运动,此时需调节
在下潜和上浮运动中保持
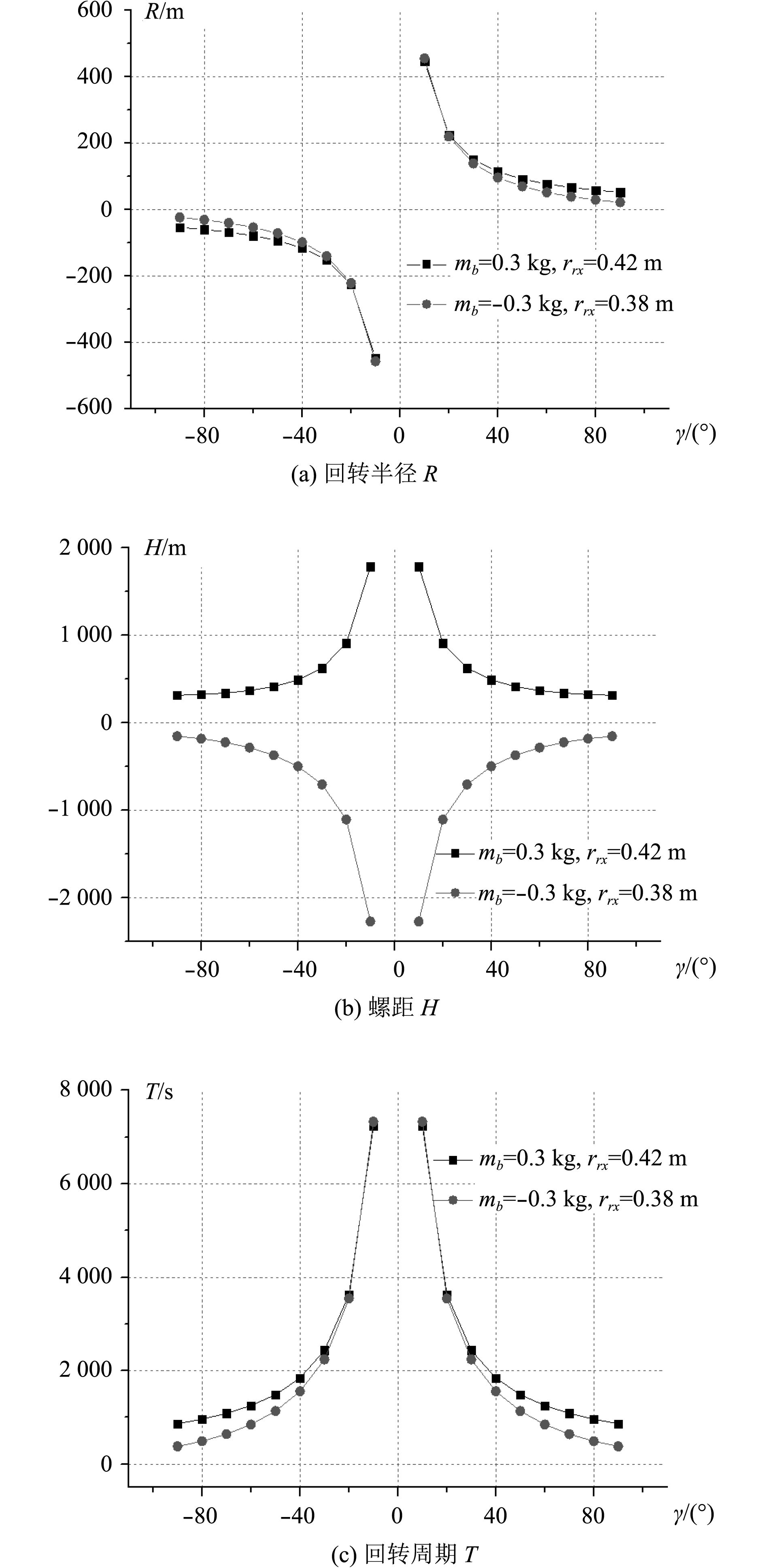
|
图 6 时空尺度随转角的变化规律 Fig. 6 Relationship between the temporal and spatial scales and the rotation angle |
在下潜和上浮运动中保持
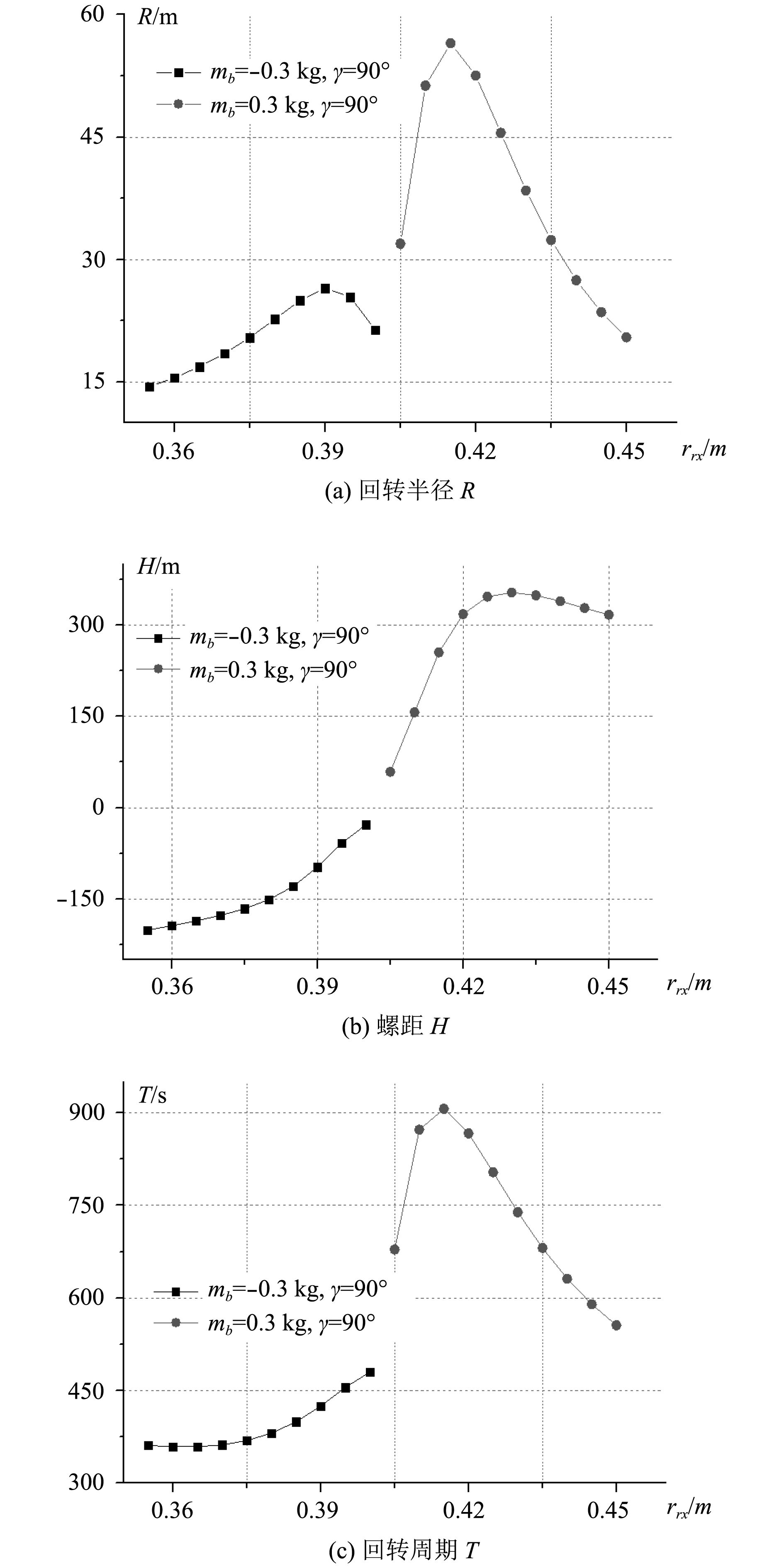
|
图 7 时空尺度随纵向位置的变化规律 Fig. 7 Relationship between the temporal and spatial scales and the longitudinal position of the movable block |
在下潜和上浮运动中保持
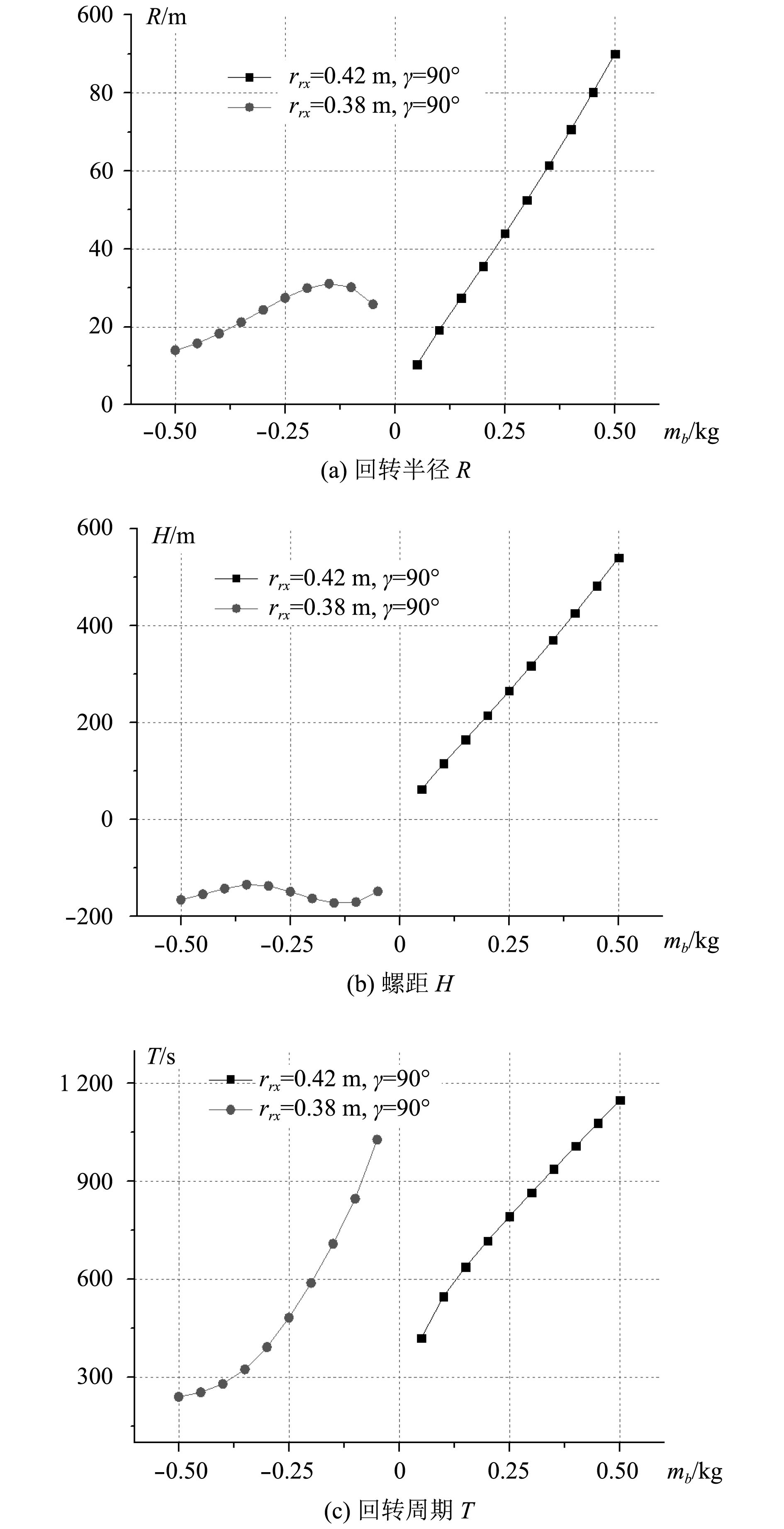
|
图 8 时空尺度随净浮力的变化规律 Fig. 8 Relationship between the temporal and spatial scales and the net buoyancy |
本文通过对水下滑翔机稳态螺旋运动的时间、空间尺度进行分析,得到如下结论:1)建立水下滑翔机的稳态螺旋运动仿真方法,并验证了该方法的正确。2)系统地分析了稳态螺旋运动的时空尺度特征随控制输入参数间的变化规律,发现了上浮和下潜运动中变化规律的不同之处。3)当通过调节移动滑块的转角或纵向位置来降低螺旋运动中的时间、空间尺度时,可考虑增大滑块转角、减小水下滑翔机的重心和浮心的纵向距离来实现。4)当通过调节净浮力来降低螺旋运动中的时间、空间尺度时,在下潜过程中可考虑降低净浮力,在上浮过程中应根据转向时刻mb的具体量值来调节。
| [1] |
MEYER D. Glider technology for ocean observations: a review[J]. Ocean Sci Discuss, 2016, 40: 1-26. |
| [2] |
陈质二, 俞建成, 张艾群. 面向海洋观测的长续航力移动自主观测平台发展现状与展望[J]. 海洋技术学报, 2016, 35(1): 122-130. |
| [3] |
温浩然, 魏纳新, 刘飞. 水下滑翔机的研究现状与面临的挑战[J]. 船舶工程, 2015, 37(1): 1-6. |
| [4] |
杨燕, 孙秀军, 王延辉. 浅海型水下滑翔机技术研究现状分析[J]. 海洋技术学报, 2015, 34(4): 7-14. |
| [5] |
MAHMOUDIAN N, GEISBERT J, WOOLSEY C. Approximate analytical turning conditions for underwater gliders: Implications for motion control and path planning[J]. IEEE Journal of Oceanic Engineering, 2010, 35(1): 131-143. DOI:10.1109/JOE.2009.2039655 |
| [6] |
YANG C, PENG S, FAN S. Performance and stability analysis for ZJU glider[J]. Marine Technology Society Journal, 2014, 48(3): 88-103. |
| [7] |
顾建农, 李启杰, 高磊, 等. 水下滑翔机运动特性建模与仿真[J]. 华中科技大学学报(自然科学版), 2016, 44(1): 76-80. |
| [8] |
朱雨时, 杨灿军, 吴世军, 等. 水柱测量中的水下滑翔机转向性能[J]. 浙江大学学报(工学版), 2016, 50(9): 1637-1645. |
| [9] |
ZHANG S, YU J, ZHANG A, et al. Spiraling motion of underwater gliders: modeling, analysis, and experimental results[J]. Ocean Engineering, 2013, 60: 1-13. DOI:10.1016/j.oceaneng.2012.12.023 |
| [10] |
赵宝强, 王晓浩, 姚宝恒, 等. 水下滑翔机李雅普诺夫稳定性分析[J]. 哈尔滨工程大学学报, 2015, 36(1): 83-87. |
| [11] |
LIU Y, SHEN Q, MA D, et al. Theoretical and experimental study of anti-helical motion for underwater glider[J]. Applied Ocean Research, 2016, 60: 121-140. DOI:10.1016/j.apor.2016.09.001 |
| [12] |
YU J, ZHANG A, JIN W, et al. Development and experiments of the Sea-Wing underwater glider[J]. China Ocean Engineering, 2011, 25(4): 721-736. DOI:10.1007/s13344-011-0058-x |
| [13] |
GRAVER J G. Underwater gliders: dynamics, control and design [D]. USA; Princeton University, 2005: 42–82.
|
 2019, Vol. 41
2019, Vol. 41
