近年来,随着对海洋开发的深入,水下机器人的应用逐渐引起各行业的重视。水下机器人-机械手系统(Underwater Vehicle-Manipulator System,UVMS)是一种可以在水下进行观测和自主作业的自动化装备,在海底科学考察、资源勘探、管道铺设、近海养殖等方面具有很大的潜在应用价值[1]。UVMS系统由水下机器人艇体和水下作业机械手两部分组成,通过水下机器人艇体和水下机械手关节的运动共同完成需要执行的作业任务。UVMS具有非线性、强耦合、时变和高维等动力学特点[2],同时UVMS系统在水下作业时为节省能量,通常采用欠驱动的工作方式[3]。这些情况的存在会使水下机器人-机械手系统的控制变得非常困难。因此,研究水下机器人-机械手系统的控制技术是实现UVMS自主作业的关键之一。UVMS轨迹跟踪控制的目标是选择合适的控制策略,并设计有效的控制律,使其能够跟踪系统的预定轨迹,并保证跟踪误差满足一定要求。目前国内外在水下机器人-机械手系统上采用的控制方法主要有PID控制方法、自适应控制方法、神经网络控制方法以及滑模控制方法等[4]。PID控制方法在实际工程中已经被广泛应用,但由于PID参数需要适应模型参数的变化,而UVMS模型具有很大不确定性,因此PID控制方法不适用于对UVMS的控制。自适应控制通常适用于模型参数不确定性严重、参数变化缓慢和自由度较少的场合,但是稳定性较差[5]。神经网络控制具有很好的学习能力和适应能力,不依赖精确的数学模型,但神经网络控制需要大量的训练样本来提高控制精度[6]。而滑模变结构控制具有响应快、鲁棒性高等优点,被广泛应用于非线性机器人的控制[7]。因此,滑模变结构控制比较适用于海洋工作环境下的UVMS。Bin Xu等[8]提出了一种水下机器人-机械手系统轨迹跟踪滑模控制器,并根据模糊逻辑控制方法实现了增益的协调变化,在携带五自由度机械手的UVMS系统仿真实验中验证了这种控制策略的有效性。Taira等[9]研究了在参数不确定情况下水下机器人-机械手操纵系统的控制方案,开发了自适应控制器和滑模控制器,并将其应用于UVMS的稳定控制。但滑模控制在本质上的不连续开关特性会引起系统的抖振,因此需要削弱系统抖振。目前,国内外在减少滑模控制的抖振方面也有许多研究,主要方法有趋近律方法,观测器方法,智能控制方法,动态滑模方法等[10]。其中趋近律方法可以调整系统滑模点趋近滑模面的速度,从而有效地减小系统惯性引起的抖振[11]。
为了提高系统响应速度和控制精度,同时减少系统抖振,本文基于指数趋近律设计了水下机器人-机械手系统的滑模控制器,用于实现对UVMS系统的轨迹跟踪,并通过仿真验证该控制策略的有效性。
1 水下机器人-机械手系统建模水下机器人-机械手系统的坐标系由固定坐标系

|
图 1 水下机器人-机械手系统坐标系 Fig. 1 Coordinate system of UVMS |
水下机器人-机械手系统由水下机器人艇体和水下机械手两部分组成,其广义坐标和广义控制力分别定义为:
| $ \begin{align} & {{\xi }} = {\left[ {x\;y\;z\;\varphi \;\theta \;\psi \;{q_1}\; \cdot \cdot \cdot \;{q_n}} \right]^{\rm T}}, \\ & {{\tau }} = {\left[ {{F_x}\;{F_y}\;{F_z}\;{W_x}\;{W_y}\;{W_z}\;{\tau _1}\; \cdots \;{\tau _n}} \right]^{\rm T}}{\text{。}} \end{align} $ | (1) |
其中:
根据式(2)第二类拉格朗日方程建立水下机器人-机械手系统的动力学方程,即
| $ \frac{{\rm{d}}}{{{\rm{d}}t}}\left( {\frac{{\partial L}}{{\partial \dot {{\xi }}}}} \right) - \frac{{\partial L}}{{\partial {{\xi }}}} = {{Q}}{\text{。}} $ | (2) |
其中:
| $ {{M}}\left( {{\xi }} \right)\ddot {{\xi }} + {{C}}\left( {{{\xi }}, \dot {{\xi }}} \right)\dot {{\xi }} + {{D}}\left( {\dot {{\xi }}} \right)\dot {{\xi }} + {{G}}\left( {{\xi }} \right) = {{\tau }}{\text{。}} $ | (3) |
其中:
滑模变结构控制的基本原理是控制器将系统当前状态或状态误差限定到滑模面并使之稳定在滑模面上[11]。由于滑模运动特性预先按照要求设计,同时给定的相轨迹与控制对象参数以及外部干扰变化无关,因而滑模控制对参数变化及扰动不灵敏,系统具有极强的鲁棒性。但在实际的控制系统中,由于系统存在质量惯性、时间延迟等因素,滑模变结构控制在滑动模态下会存在抖振。
实现滑模变结构控制的过程主要包括确定系统滑动模态到达条件、选取滑模面以及求取系统滑模控制律,建立滑模控制器。
2.2 水下机器人-机械手系统滑模控制器设计,首先设定UVMS期望轨迹为
| $ {{e}} = {{{\xi }}_d} - {{\xi }}, \\ \dot {{e}} = {\rm{d}}{{e}}/{\rm{d}}t = {\dot {{\xi }}_d} - \dot {{\xi }}\text{,} $ | (4) |
同时选取线性滑模面如下式:
| $ {{s}} = {{ce}} + \dot {{e}}{\text{。}} $ | (5) |
其中:
| $ {{s}} = {\left[ {{s_1}\;{s_2}\; \cdot \cdot \cdot \;{s_N}} \right]^{\rm T}}, \\ {{c}} = {\rm diag}\left\{ {{c_1}\;{c_2}\; \cdot \cdot \cdot \;{c_N}} \right\}\text{。} $ | (6) |
其中
为了改善滑模面动态品质,减少系统抖振,基于式(7)指数趋近律设计水下机器人-机械手系统的滑模控制律。
| $ \dot {{s}} = {\rm{d}}{{s}}/{\rm{d}}t = - \varepsilon {\rm{sgn}} \left( {{s}} \right) - k{{s}}, \varepsilon > 0, k > 0, $ | (7) |
其中:
| $ {\rm{sgn}} \left( {{s}} \right) = \left\{ {\begin{array}{*{20}{c}} {{I}}\text{,}&{{{s}} > {{0}}} \text{,}\\ {{0}}\text{,}&{{{s}} = {{0}}}\text{,} \\ { - {{I}}}\text{,}&{{{s}} < {{0}}} \text{。} \end{array}} \right.。$ | (8) |
综合式(3)~式(7)可得水下机器人-机械手系统滑模控制律为:
| $ \begin{split}{l} & {{u}} = {{\tau }} = {{M}}\left( {{\xi }} \right)\left( {{{c\dot e}} + \varepsilon {{\rm sgn}} \left( {{s}} \right) + k{{s}} + {{{{\ddot \xi }}}_d}} \right)+\\ & {{C}}\left( {{{\xi }}, {{\dot \xi }}} \right)\left( {{{ce}} - {{s}} + {{{{\dot \xi }}}_d}} \right)+\\ & {{D}}\left( {{{\dot \xi }}} \right)\left( {{{ce}} - {{s}} + {{{{\dot \xi }}}_d}} \right)+\\ & {{G}}\left( {{\xi }} \right)\text{。} \end{split} $ | (9) |
为了使系统满足滑动模态到达条件且具有一定稳定性,需要满足Lyapunov稳定性条件。选取系统Lyapunov函数为:
| $ {{V}} = {{{{{s}}^2}}/2}, $ | (10) |
则有
| $ \dot {{V}} = {{s\dot s}}\text{。} $ | (11) |
综合式(7)和式(11)可得
| $ \dot {{V}} = - \varepsilon \left| {{s}} \right| - k{{{s}}^2}\text{。} $ | (12) |
由于
推导得到水下机器人-机械手系统的滑模控制律后,建立UVMS滑模控制系统,控制系统结构如图2所示。以水下机器人-机械手系统的期望轨迹为输入,通过指数趋近滑模控制器解算出广义控制力作为UVMS系统的控制输入,控制UVMS系统的运动。
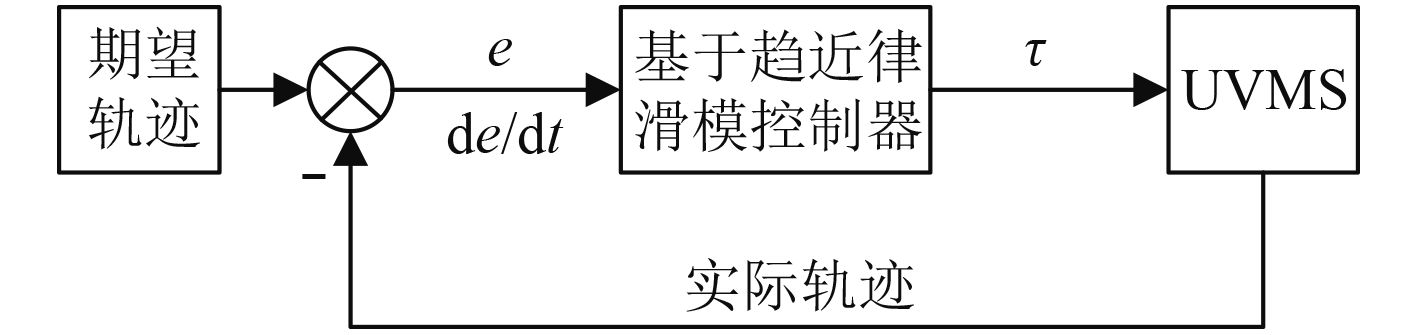
|
图 2 基于指数趋近律的UVMS滑模控制系统 Fig. 2 SMC of UVMS based on exponential reaching law |
为了验证上述滑模变结构控制策略的有效性,在Matlab环境中建立控制仿真系统,对UVMS进行轨迹跟踪控制仿真。仿真对象为携带三自由度机械手的水下机器人-机械手系统,水下机器人艇体具有6个自由度,仿真对象流线型UVMS三维模型如图3所示。

|
图 3 水下机器人-机械手系统三维模型 Fig. 3 Three dimensional model of UVMS |
根据课题组研发的一款UVMS系统,水下机器人-机械手系统质量参数及水下机械手D-H参数分别如表1和表2所示,机械手D-H坐标系如图4所示。
|
|
表 1 水下机器人-机械手系统质量参数 Tab.1 Mass parameters of UVMS |
|
|
表 2 水下机械手D-H参数 Tab.2 D-H parameters of manipulator in UVMS |

|
图 4 本文研究的三自由度水下机械手D-H坐标系 Fig. 4 D-H coordinate system of our 3-DOFs manipulator |
在系统的轨迹跟踪控制仿真中,设定UVMS的期望轨迹为
| $ {{{\xi }}_d} = {[{x_d}\;{y_d}\;{z_d}\;{\varphi _d}\;{\theta _d}\;{\psi _d}\;{q_{1d}}\;{q_{2d}}\;{q_{3d}}]^{\rm T}}{\text{,}} $ |
其中:
| $ {x_d} = 4\cos \left( {0.04{{\text{π}}}t} \right), $ |
| $ {y_d} = 4\sin \left( {0.04{{\text{π}}}t} \right), $ |
| $ {z_d} = 0.5t, $ |
| $ {\varphi _d} = {{0}^ \circ }, $ |
| $ {\theta _d} = {{0}^ \circ }, $ |
| $ {\psi _d} = {{0}^ \circ }, $ |
| $ {q_{1d}} = {10^ \circ }, $ |
| $ {q_{2d}} = {20^ \circ }, $ |
| $ {q_{3d}} = - {3}{{0}^ \circ }{\text{。}} $ |
艇体质心期望轨迹为水下三维螺旋下潜运动,回转周期为50 s,艇体在下潜过程中调整姿态,且水下机械手在下潜过程中展开,UVMS系统初始位置向量为
根据前文所设计的指数趋近滑模控制器以及仿真对象的物理参数,在Matlab环境中进行水下机器人-机械手系统的运动轨迹跟踪控制仿真,其中水下机器人-机械手系统艇体质心的空间运动轨迹跟踪结果如图5所示。

|
图 5 UVMS艇体空间运动轨迹跟踪 Fig. 5 Trajectory tracking of UVMS in 3-dimensional space |
水下机器人-机械手系统艇体质心在
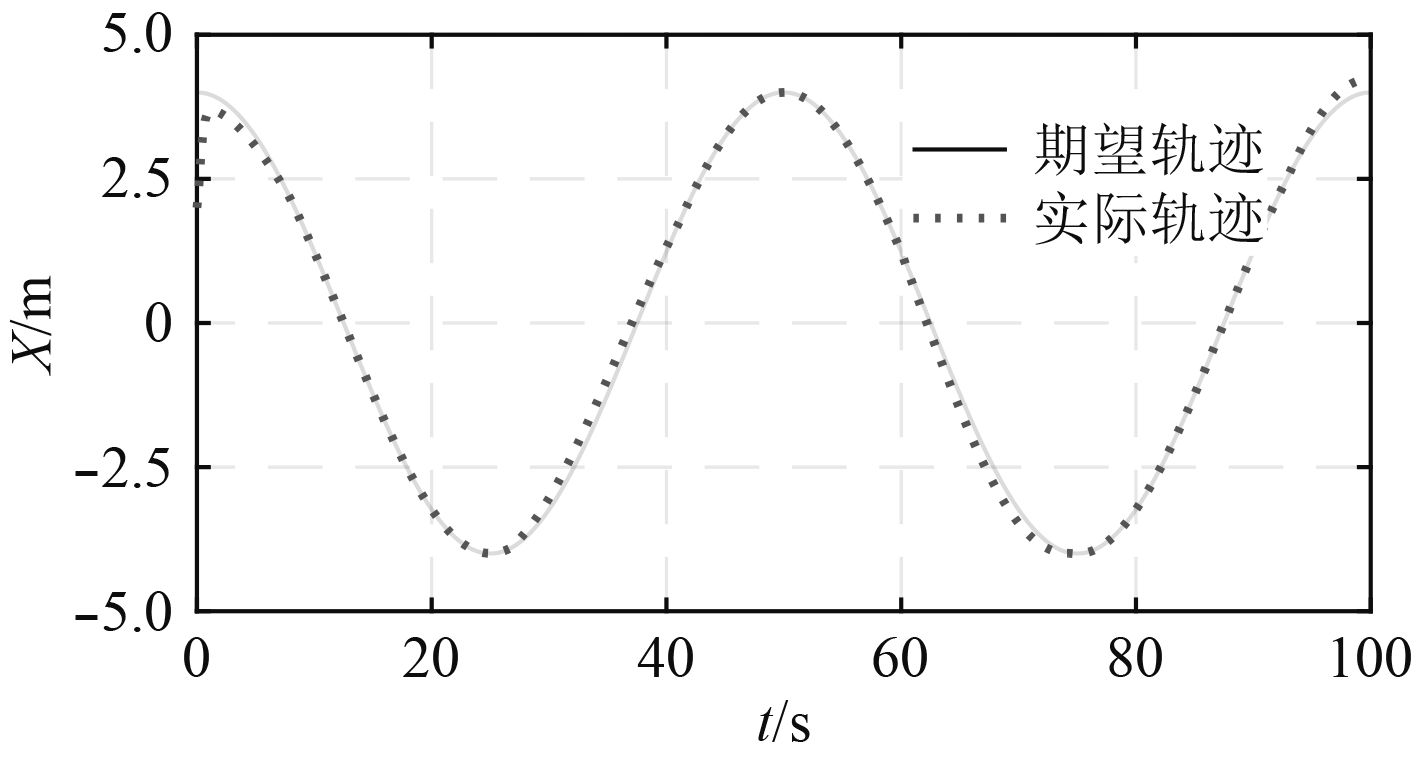
|
图 6 UVMS首向运动轨迹跟踪 Fig. 6 Sway motion tracking of UVMS |
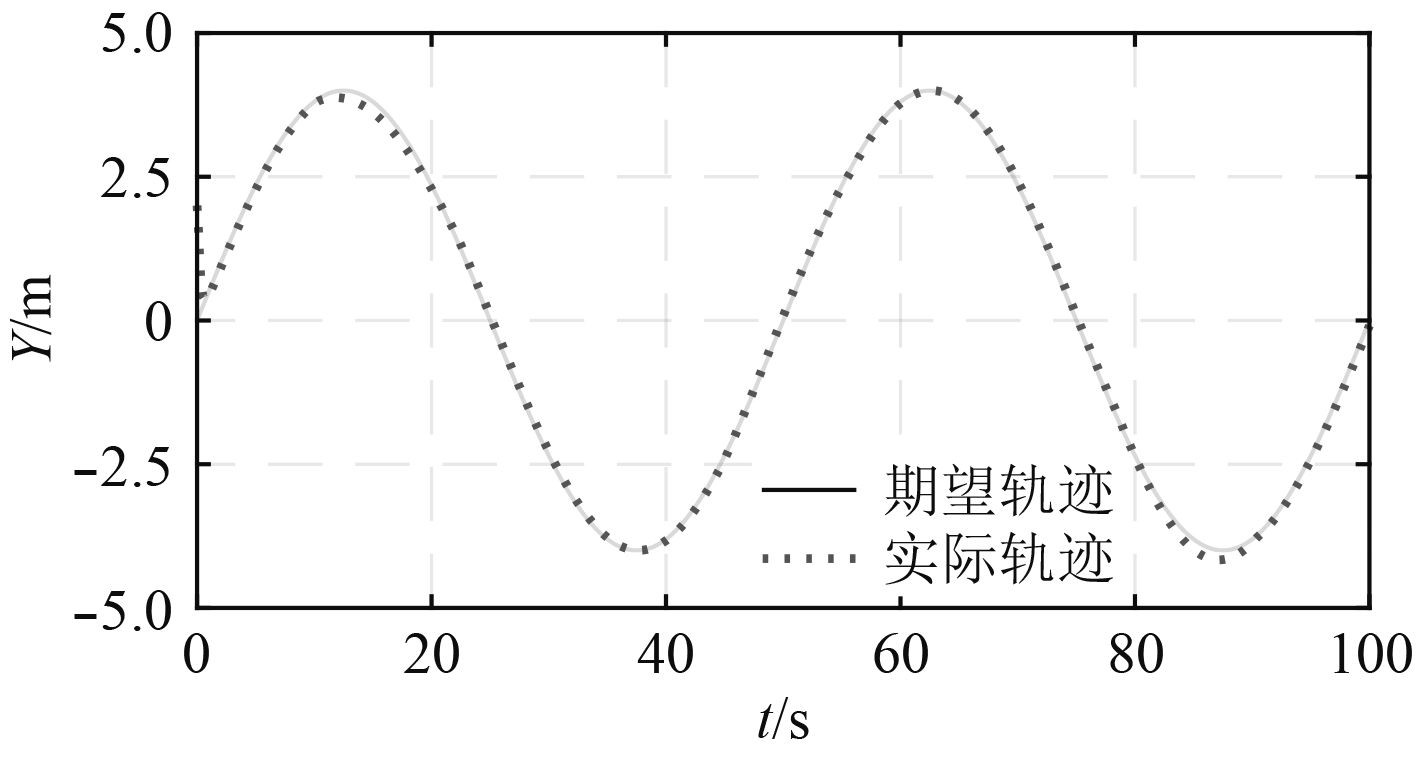
|
图 7 UVMS侧向运动轨迹跟踪 Fig. 7 Surge motion tracking of UVMS |
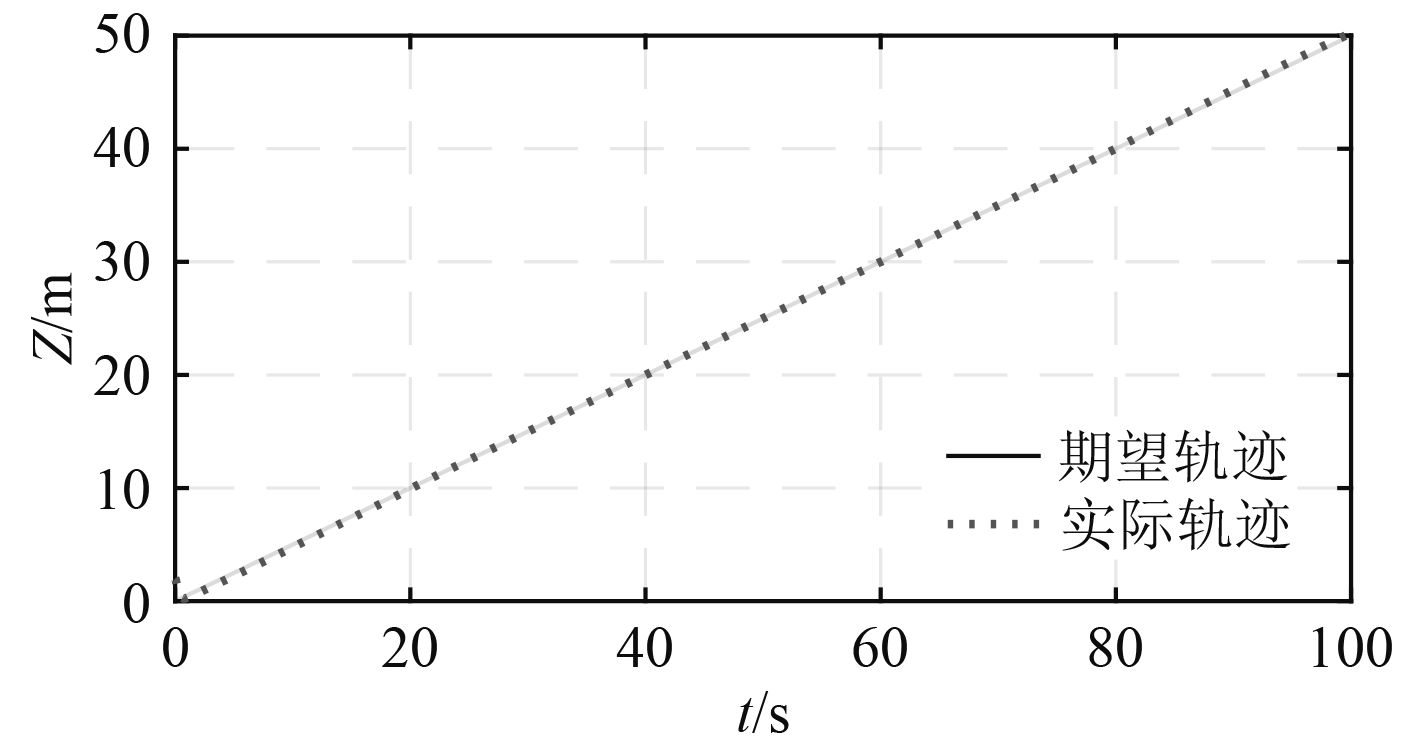
|
图 8 UVMS纵向运动轨迹跟踪 Fig. 8 Heave motion tracking of UVMS |
水下机器人-机械手系统艇体姿态控制仿真结果以及机械手关节控制仿真结果分别如图9和图10所示,其控制要达到的艇体姿态为

|
图 9 UVMS姿态角控制 Fig. 9 Control of attitude angles in UVMS |
|
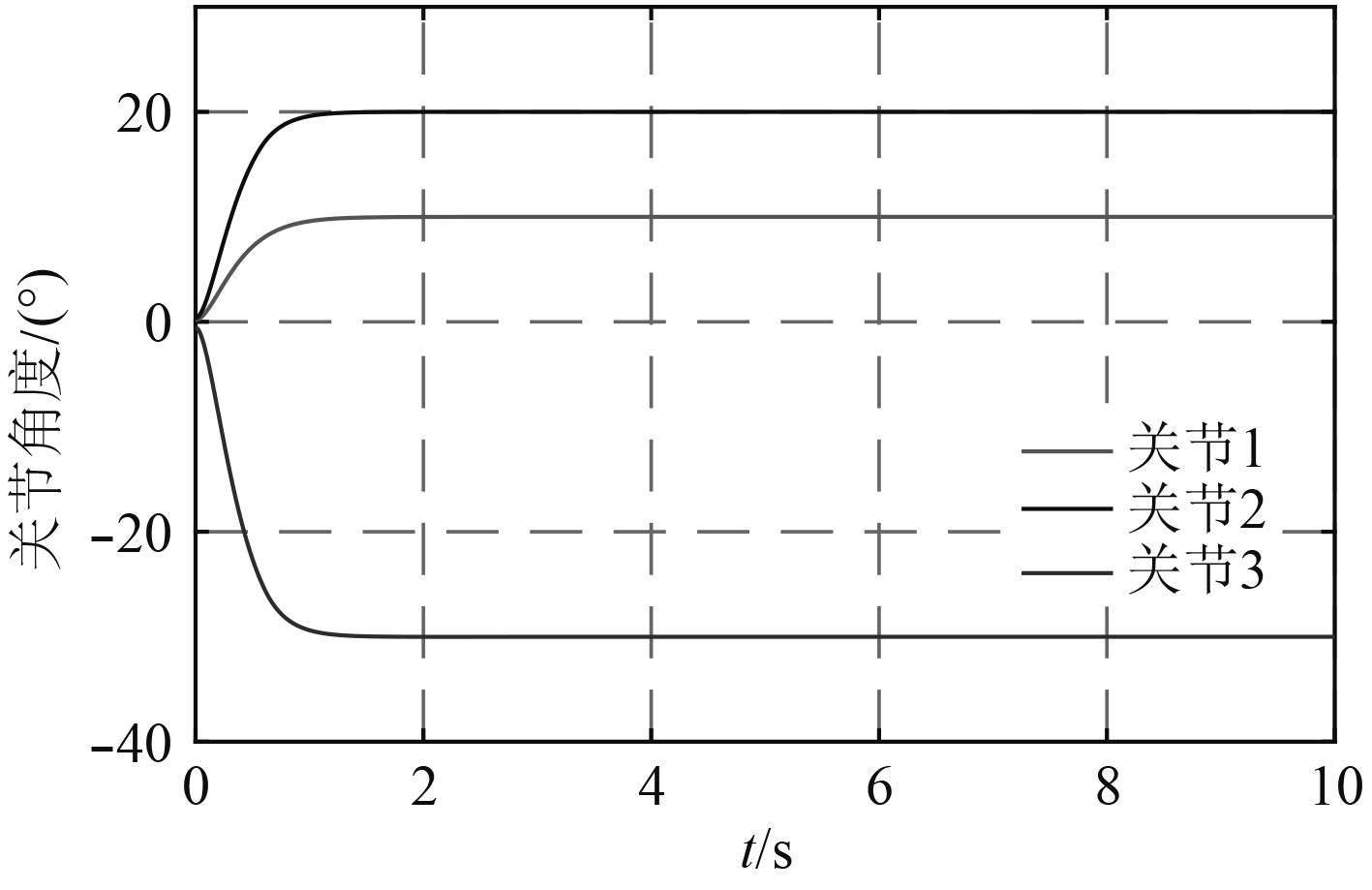
图 10 UVMS机械手关节角度控制 Fig. 10 Control of manipulator joints in UVMS |
从仿真结果看,系统轨迹跟踪效果较好,滑模控制器可以比较精确地实现UVMS的期望轨迹,且对艇体姿态和机械手控制响应速度较快,系统抖振较小。仿真的初始位置不在坐标原点,从仿真开始到定位至预定轨迹需要一定的响应时间,而仿真结果表明滑模控制可以实现UVMS的快速准确定位,有利于提高UVMS的水下作业效率。
4 结 语本文针对水下机器人-机械手系统的轨迹跟踪控制问题,建立了系统整体动力学模型,并基于指数趋近律设计了系统滑模控制器用于UVMS的轨迹跟踪控制。仿真结果表明所设计的滑模控制器总体上可以较精确地实现UVMS水下螺旋下潜运动的轨迹跟踪以及水下机械运动控制,且系统上升时间短,响应速度较快。水下机械手转动时对艇体的耦合作用导致开始阶段误差大于机械手运动完成后的误差。同时由于UVMS运动过程中x方向所受阻力会大于y方向和z方向,因此仿真结果中x方向上轨迹跟踪误差要大于y,z方向跟踪误差。本文研究的UVMS实体系统正在开发中,后续研究将会在实体系统上对所设计的控制器进行实验验证。
| [1] |
余明刚, 张旭, 陈宗恒. 自治水下机器人技术综述[J]. 机电工程技术, 2017, 46(8): 155-157. YU Ming-gang, ZHANG Xu, CHEN Zong-heng. Summary of autonomous underwater vehicle (AUV) technology[J]. Electromechanical Technology, 2017, 46(8): 155-157. DOI:10.3969/j.issn.1009-9492.2017.08.046 |
| [2] |
GIACOMO M, SONG C, JUNKU YUH. Underwater autonomous manipulator for intervention missions AUVs[J]. Ocean Engineering, 2009, 36(8): 15-23. |
| [3] |
MAKOTO I, KAZUO I. Control of an underwater manipulator mounted for an AUV considering dynamic manipulability[J]. International Congress Series, 2006, 46(2): 269-272. |
| [4] |
张奇峰, 张艾群. 自治水下机器人机械手系统协调运动研究[J]. 海洋工程, 2006, 24(3): 79-84. ZHANG Qi-feng, ZHANG Ai-qun. Research on coordinated motion of an autonomous underwater vehicle-manipulator system[J]. The Ocean Engineering, 2006, 24(3): 79-84. DOI:10.3969/j.issn.1005-9865.2006.03.013 |
| [5] |
ZHANG Ming-jun, CHU Zhen-zhong. Adaptive sliding mode control based on local recurrent neural networks for underwater robot[J]. Ocean Engineering, 2012, 45(2): 56-62. |
| [6] |
张文辉, 齐乃明, 尹洪亮. 基于滑模变结构的空间机器人神经网络跟踪控制[J]. 控制理论与应用, 2011, 28(9): 1141-1144. ZHANG Wen-hui, QI Nai-ming, YIN Hong-liang. Neural-network tracking control of space robot based on sliding mode variable structure[J]. Control Theory and Applications, 2011, 28(9): 1141-1144. |
| [7] |
DONGHEE KIM, HYEUNG-S CHOI, KIM J-Y, et al. Trajectorygeneration and sliding-mode controller design of an underwater vehicle-manipulator system with redundancy[J]. International Journal of Plant Engineering and Management, 2015, 16(7): 1561-1570. |
| [8] |
XU Bin, PANDIAN S, PETRY F. A sliding mode fuzzy controller for underwater vehicle-manipulator systems[C]//Annual Meeting of the North American Fuzzy Information Processing Society. Ann Arbor, Michigan, USA, 2005: 181–186.
|
| [9] |
TAIRA Y, OYA M, SAGARA S. Adaptive control of underwater vehicle-manipulator systems using radial basis function networks[C]//The 17th International Symposium on Artificial Life and Robotics, Oita, Japan, 2012: 123–129.
|
| [10] |
陈巍, 魏延辉, 曾建辉, 等. 水下机器人-机械手系统控制方法综述[J]. 重庆理工大学学报(自然科学), 2015, 29(8): 116-123. CHEN Wei, WEI Yan-hui, ZENG Jian-hui, et al. Review of underwater vehicle-manipulator system control method[J]. Journal of Chongqing University of Technology (Natural Science), 2015, 29(8): 116-123. |
| [11] |
孙巧梅, 陈金国, 余万. 基于模糊自适应滑模方法的AUV轨迹跟踪控制[J]. 舰船科学技术, 2017, 39(12): 53-58. SUN Qiao-mei, CHEN Jin-guo, YU Wan. Trajectory tracking control of autonomous underwater vehicles based on fuzzy adaptive sliding mode method[J]. Ship Science and Technology, 2017, 39(12): 53-58. DOI:10.3404/j.issn.1672-7649.2017.12.012 |
 2019, Vol. 41
2019, Vol. 41
