随着造船理论的发展,可靠性设计在造船界越来越被重视,国内外针对船舶结构可靠性开展了大量研究[1 – 3]。舵设备主要由结构、机构件组成,是保证船舶操纵性的重要装置,它在船舶航行中频繁地处于各种工作状态,一旦损坏就很可能发生海损事故[4]。现行规范进行舵设备设计时,所有设计变量都是确定性的,其安全程度用安全系数来描述,而实际上结构尺寸、材料性能和外荷载等,都具有不确定性因素,故上述确定性设计显然不够理想,因此有必要对舵设备进行可靠性设计。
文献[5]对舵设备主要部件建立了安全裕度方程并进行可靠性计算,认为现行规范建议的安全系数取值不合理,舵设备主要部件除舵叶外可靠度都远超设计指标,安全裕度过高,但其没有将结构尺寸作为随机变量;文献[4, 6]分析了舵设备传统设计中的不确定因素,提出了与传统设计相结合的舵设备可靠性设计方法,但没有对所提出的不确定因素在可靠性设计中如何考虑进行逐一分析,也没有将结构尺寸作为随机变量。
本文在考虑计算工况、材料性能、强度裕度、结构尺寸等不确定因素的基础上,对船舶舵设备进行可靠性设计分析,建立舵设备可靠性设计流程与可靠性模型,进行舵设备可靠性指标确定与分配,并以舵杆为例进行了可靠性设计与随机变量分散程度影响分析。同时,对多支撑式舵设备的舵销进行了破损安全可靠性分析。
1 舵设备设计中的不确定因素分析 1.1 舵设备设计中的不确定因素舵设备传统设计方法有2种,一是按照船舶建造规范的有关规定计算式进行计算;二是按照强度理论计算确定。一般来说除了确定舵杆直径可用强度理论计算外,其他零件主要按照规范规定进行计算确定。以上2种传统的舵设备设计方法通常具有以下不确定因素:
1)计算工况的考虑。在传统设计中通常只考虑舵叶上的正常工作载荷,即转舵后舵叶上所受的水动力,并不考虑由于波浪冲击造成的动力载荷以及碰撞或冰块挤压等情况可能造成的非正常载荷。同时正常工作载荷也具有不确定性。
2)应力计算的正确性。转舵后舵叶上所受的水动力是舵设备上的正常工作载荷,除通过模型试验方法直接换算之外,其他计算方法都带有较大近似性,另外计算构件应力时经常采取一些简化的假定,如对载荷的作用方式、支座结构形式的简化,对变断面情况的忽略等,使计算应力具有较大的不确定性。
3)材料的可靠性。所采用材料的化学成份、机械性能及加工精度等都有可能达不到名义上的规定,因而会影响构件的实际强度。
4)结构尺寸公差。舵设备各构件在加工制造过程中不可避免的要产生结构尺寸公差,使构件各尺寸在名义值附近波动,影响构件的真实应力。
5)强度裕度。舵设备中的各部分因强度、液压不足导致破坏或失效后造成的后果严重性不相同。例如,多支撑式不平衡舵,其中一个舵销断裂,对舵叶的转动没有明显的影响;而舵杆却是舵设备中的重要构件,一旦强度不足就会导致整个舵设备失效。可见,不同重要性构件的强度裕度应该不同。
针对上述不确定因素,传统设计中采用的方法为:通过大量统计分析及根据长期积累的使用经验,对以上不确定因素加以恰当的考虑后,为舵设备各构件确定一个强度安全系数。苏联规范中取nS=2.8,挪威规范中nS=4,在我国钢制海船建造规范中,取nb=4~5,在长江钢船建造规范中取nb=3.5。显然这一安全系数的选取具有较大的主观性,受设计思想及设计经验影响较大,这种半经验半理论的确定性设计有时会导致某些构件强度裕度很大,有时又会导致个别构件强度不足。
1.2 不确定因素处理开展舵设备可靠性设计,就是把不确定的设计变量看成是服从某种分布规律的随机变量,用概率统计方法设计出符合可靠性指标的构件参数。这样可以有效避免传统设计方法中安全系数确定时主观性太大的问题。下面用随机变量的思想对上述不确定因素进行处理。
1)计算工况的考虑。船舶在不同航线、同一航线不同航次以及在同一航次的某一次航行过程中,转舵后舵叶上所受的水动力都不是一成不变的,而是在一定范围内波动。将转舵后舵叶上所受的水动力载荷L1(弯矩、扭矩)用均值UL1和变异系数CL1表示。
对于波浪冲击造成的动力载荷L2,可以通过统计分析获得一个动力载荷系数K,与正常工作载荷L1相乘获得,即L2=K×L1。由于舵设备寿命期很长,海况、波浪谱型、浪向具有不确定性,所以动力载荷系数K也应该当成随机变量来处理,通过对海况资料进行统计分析确定UK,CK。若无法获得海况统计资料,也可将动力载荷系数K当作确定性量处理,此时应选用寿命期内可能遇到的较严重海况下的动力载荷系数K。
对于碰撞或冰块挤压等情况可能造成的非正常载荷,可以通过试验或仿真确定其载荷大小,载荷用均值UL3和变异系数CL3表示。需要注意的是,舵设备发生由碰撞或冰块挤压导致失效的概率为碰撞或冰块挤压载荷导致舵设备失效概率与发生碰撞或冰块挤压事件概率的乘积,即

|
(1) |
2)应力计算的正确性。由于正常工作载荷具有随机性,通过模型试验方法直接换算得到的构件也应具有随机性,构件应力σ用应力均值Uσ、变异系数Cσ表示。
除模型试验方法以外,借助有限元工具进行应力分析已经成为各行业进行强度分析的主要手段,有限元工具可以很大程度上模拟真实载荷加载情况,可以实现支座结构、变断面结构建模。进行舵设备有限元分析时可以通过整体建模、关键点处局部细化的方法进行应力计算。计算得到的应力同样具有分散性。
3)材料的可靠性。材料强度的随机性可以按照材料统计特性确定,一般从可靠性手册、材料手册、相关文献及试验值获得,用强度均值US、变异系数CS表示。
4)结构尺寸公差。根据构件加工工艺,由加工厂提供或查询相关公差标准获得构件尺寸公差。结构尺寸值用均值UD、标准差σD或变异系数CD表示。
5)强度裕度。针对舵设备中的各构件破坏后造成的后果严重性不相同的问题,应对不同的构件分配不同的可靠性指标,失效影响越严重的构件,可靠度指标越高(失效概率指标越低),失效影响越小的构件,可靠度指标越低(失效概率指标越高)。同一部件不同故障模式导致的故障影响程度不同时,也应针对故障模式分配不同的可靠性指标。如舵机完全丧失动力比舵机输出动力降低导致的后果更严重,理应分配更高的可靠度指标。
对于多支撑式不平衡舵的舵销结构,应按照破损安全准则进行可靠性计算,即一个舵销破坏不会导致舵叶卡滞,第2个舵销破坏时将会导致舵叶卡滞。应将多个舵销视为一个子系统,对2个舵销接连失效提出可靠性指标。
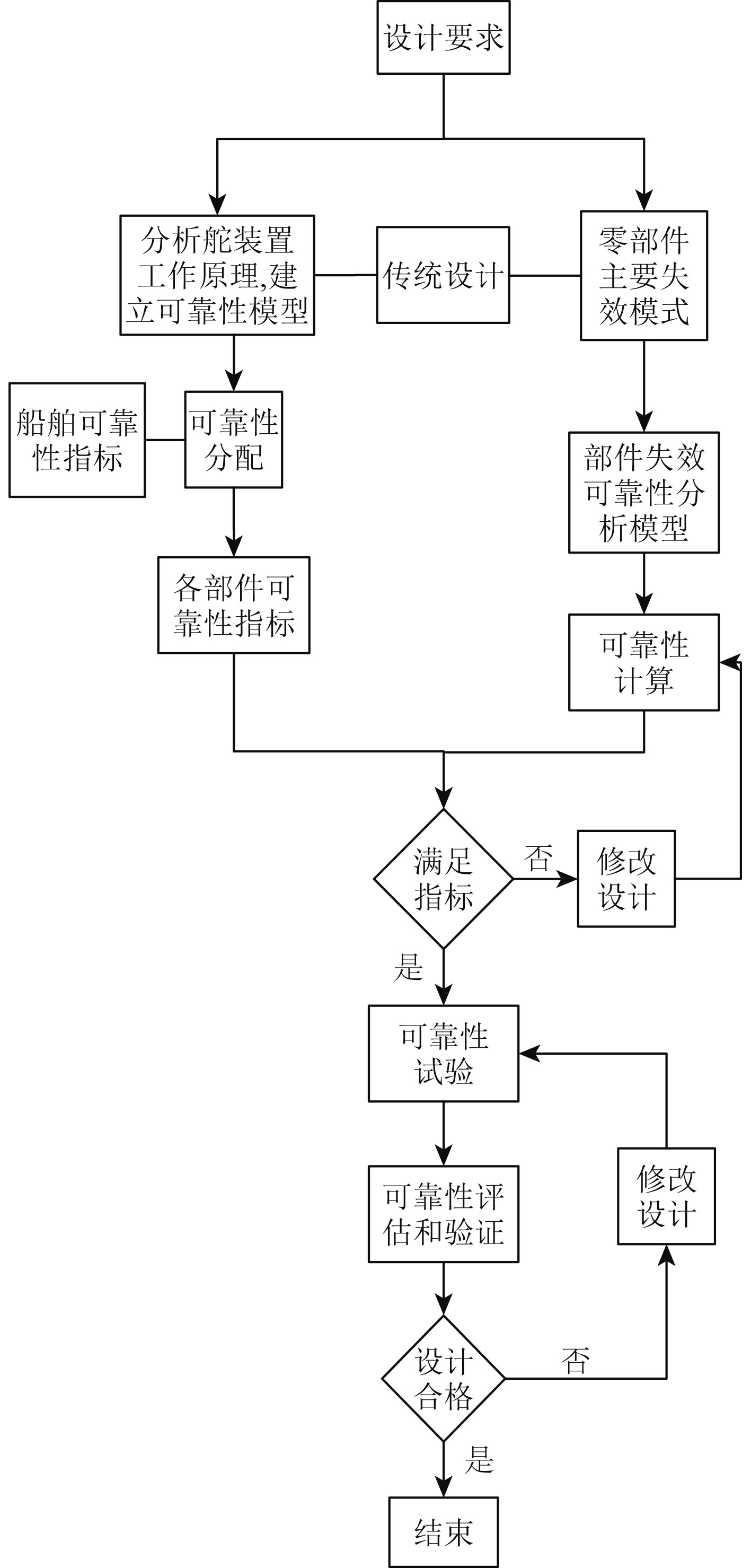
2 舵设备可靠性设计 2.1 舵设备可靠性设计流程开展舵设备的可靠性设计研究,应当在传统舵系设计流程的基础上,引入合理的可靠性设计流程,使两者有机结合,共同为舵设备设计服务。舵设备的可靠性设计流程如图1所示。
|
图 1 舵设备可靠性设计的工作流程 Fig. 1 Working procedure of rudder reliability design |
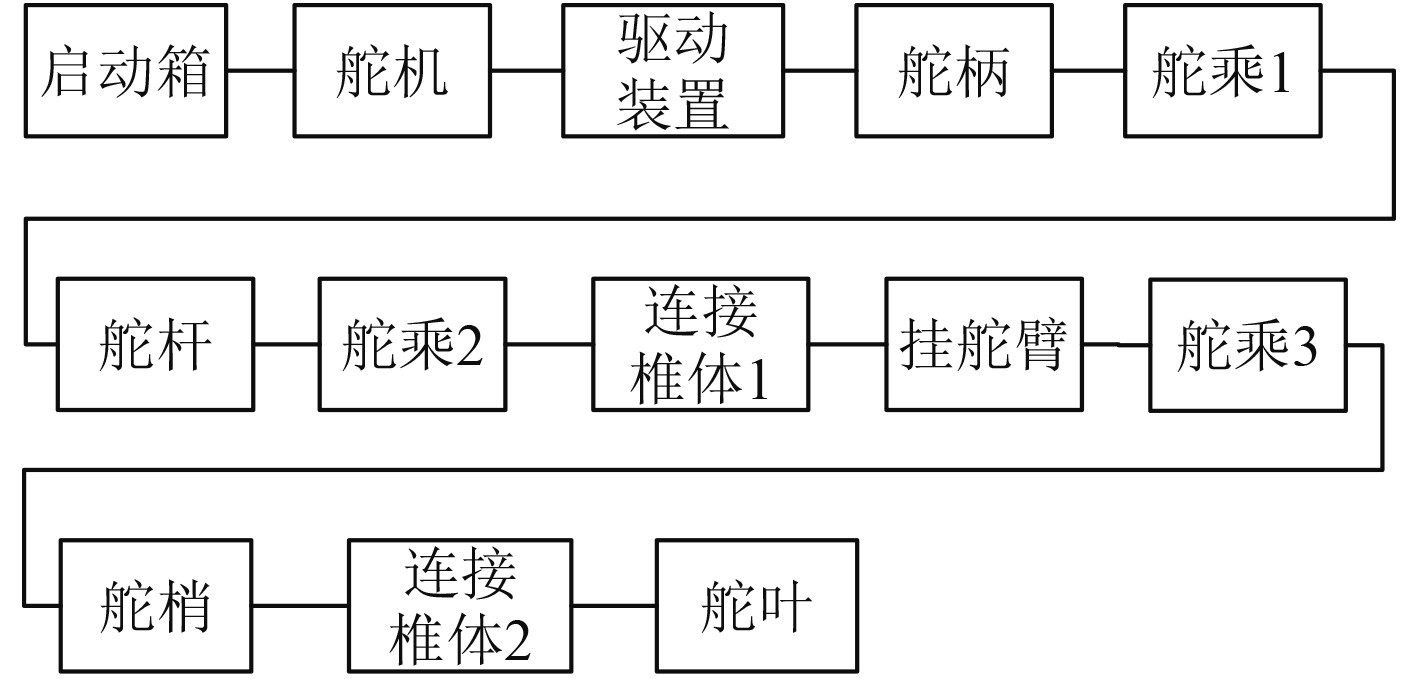
除了按船级社要求配备的辅助操舵设备之外,舵设备任何一个组成构件失效,都将导致整个设备的失效。某船舶舵设备结构组成如图2所示,根据舵设备的工作原理,可将舵设备视为一串联系统,从而画出舵设备的可靠性框图,如图3所示。

|
图 2 舵设备的结构组成 Fig. 2 Structual composition of rudder |
|
图 3 舵设备的可靠性框图 Fig. 3 Reliability configuration or rudder |
对于整个舵设备,其相应的失效概率为:
| $ {P_f} = 1 - \displaystyle\mathop \Pi \limits_{i = 1}^n (1 - {P_{fi}}) \text{。} $ | (2) |
式中:Pf为舵设备失效概率;Pfi为舵设备各组成部分的失效概率。
通过对舵设备各组成部分建立失效模式可靠性分析模型进行求解,可以获得舵设备各部分失效概率,最终代入式(2)得到舵设备失效概率。
2.3 可靠性指标确定与分配进行舵装备可靠性设计时,若已有船舶的总可靠度指标,则由船舶可靠度向舵设备分配指标,然后再向舵设备的各零部件分配,从而得到各组成部分的可靠性指标。
由船舶可靠性指标分配得到的一般为舵设备完全失效的指标要求,没有考虑舵设备具有卡滞、偏转角度不足、转舵时间过长等不同故障模式,有时甚至没有船舶总可靠性指标,此时可以根据舵设备故障的严重程度确定舵设备各故障模式的可靠性指标,指标确定可参考美军标MIL-STD-882D等相关标准。
常用的可靠性分配方法有等分配法、评分分配法、比例组合法和考虑重要度和复杂度分配法[7]。考虑到船舶舵设备设计的产品继承性、可靠性框图结构简单、有老产品的故障统计基础等特点,首先推荐采用比例组合法进行可靠性指标分配。根据老系统中各单元的故障率(故障占比),按新系统可靠性要求给舵设备各单元分配可靠性指标。若所设计舵设备为新研构型或无法获得历史故障数据,则可采用评分分配法分配可靠性指标,评分因素包括各部件复杂程度、故障严酷度、技术水平、工作时间和环境条件等。
舵设备可靠性分配完成之后并不是确定不可变的,可以与可靠性预计结果相比较,确定分配的合理性,根据需要重新进行分配。为尽量避免可靠性分配的次数,在可靠性规定值的基础上,可考虑留出一定的余量。
3 舵设备主要部件可靠性设计对舵设备各部件进行可靠性设计分析,首先应建立安全边界方程:
| $ Z = g\left( {S,R} \right) = R - S \text{。} $ | (3) |
式中:R为结构所能提供的最大抗力,一般为材料屈服强度或极限强度;S为根据舵系设计得到的该构件的最大应力。
当Z>0时,表示结构安全,Z<0时,表示结构失效。
各构件根据具体受力特点,安全边界方程各不相同。对于舵杆、舵柄、舵叶等一旦破坏就会失效的部件,以舵杆为例进行分析。对于多支撑式不平衡舵的舵销结构,则进行破损安全可靠性分析。
3.1 舵杆的可靠性设计1)舵杆可靠性模型
舵杆作为舵设备的重要构件,其一旦失效将导致整个舵设备的失效。造成舵杆失效的主要原因是由于舵杆设计或者制造过程中的失误,导致舵杆整体或局部强度不足,即其工作应力超过许用应力。
舵杆在舵设备工作时主要承受弯矩和扭矩载荷,计算舵杆应力时选取舵杆危险截面计算,舵杆危险截面一般在舵柄处、上舵承处和下舵承处的舵杆位置。
根据第三强度理论,舵杆在危险截面上的应力
| $ \sigma = \frac{{\sqrt {{M^2} + {T^2}} }}{W} = \frac{{32\sqrt {{M^2} + {T^2}} }}{{{\text{π}}{d^3}}} \text{。} $ | (4) |
式中:M为舵杆相应位置处的弯矩;T为舵杆相应位置处的扭矩;W为舵杆相应位置处的抗弯截面系数;d为舵杆相应位置处的舵杆直径。
所以舵杆的安全边界方程为
| $ Z = {\sigma _s} - \frac{{32\sqrt {{M^2} + {T^2}} }}{{{\text{π}} {d^3}}} \text{,} $ | (5) |
式中,σs为舵杆材料屈服极限。
舵杆在该危险截面破坏的概率
| $ {P_f} = P\left\{ {{\sigma _s} - \frac{{32\sqrt {{M^2} + {T^2}} }}{{{\text{π}} {d^3}}} < 0} \right\} \text{。} $ | (6) |
式中:M,T,d,σs均视为随机变量,用均值和变异系数表示。其中载荷M和T服从极值I型分布[8],结构尺寸d和材料性能σs服从正态分布。
可通过J-C法、重要抽样法、蒙特卡罗法等解析和数值计算方法计算出舵杆破坏概率Pf。
2)舵杆失效概率计算
以82KBC为例,对其舵杆进行可靠性设计分析。
舵杆可靠性分析输入参数如表1所示。
|
|
表 1 舵杆可靠性分析参数 Tab.1 Parameters of rudderstock reliability analysis |
对舵杆上、下舵承处危险截面进行失效概率计算,得到结果如表2所示,上舵承处舵杆失效概率为Pf1=8.08×10–7,下舵承处舵杆失效概率为Pf2=9.30×10–17。由于舵杆断裂会导致舵设备完全失效,船舶丧失转向能力,严重威胁船舶安全,考虑工程实际应用并参考美军标MIL-STD-882D中事故可能性等级划分标准,确定舵杆断裂失效可靠性指标为10–6。故上、下舵承处舵杆危险截面失效概率均满足可靠性指标要求。
3)舵杆可靠性设计
由以上分析可知,下舵承处舵杆失效概率远小于10–6,可靠度较高,舵杆尺寸具有优化空间。
通过逐步减小下舵承处舵杆直径,计算得到一系列不同舵杆直径下的失效概率,可以进行给定可靠性指标下的舵杆尺寸设计。从表2可以得到,在给定10–6的可靠性指标下,下舵承处舵杆直径为450 mm。
|
|
表 2 不同舵杆直径下的舵杆失效概率 Tab.2 Failure probability of rudderstock with different diameter |
4)随机变量分散性影响分析
载荷、材料强度和结构尺寸作为随机变量,其变异系数选取是否准确对舵杆失效概率影响非常大。以上舵承舵杆截面失效为例,改变载荷、材料强度和结构尺寸的变异系数,研究变异系数对舵杆失效概率的影响。改变变异系数后的上舵承处舵杆失效概率如表3所示。
|
|
表 3 变异系数变化后的上舵承处舵杆失效概率 Tab.3 Failure probability of rudderstock with different coefficient of variation |
由计算结果可知,舵杆失效概率对载荷、材料强度和结构尺寸的分散性极为敏感,失效概率随着变异系数增大而大幅增长,尤其是舵杆直径和材料屈服强度,舵杆直径变异系数增大0.01,舵杆失效概率增大913%,材料屈服强度变异系数增大0.01,舵杆失效概率增大477.5%。由此可见,材料强度和结构尺寸变异系数的取值是否准确对舵杆可靠性设计分析极为重要,一般按照材料手册、可靠性手册及相关统计资料选取,必要时进行试验测量确定。
当无法获得材料强度和结构尺寸变异系数的准确取值时,变异系数应在取值范围内尽量取得稍大些。同时可以看出,要想获得高可靠性的舵设备,应对加工质量和材料质量进行严格控制。在工程应用中应注意对载荷、材料强度和结构尺寸分散性数据的收集。
3.2 舵销破损安全可靠性分析1)舵销失效可靠性建模
对于含有2个及以上舵销的舵设备,如多支撑式不平衡舵,其中一个舵销破坏一般不会导致舵叶卡滞,认为第2个舵销破坏时将会导致舵叶卡滞。此时应进行舵销破损安全可靠性设计分析,即一个舵销破损后认为是安全的,载荷重新分配后第2个舵销破损则认为舵设备失效。对于只有单个舵销的舵设备,其可靠性分析方法与舵杆相同。
舵销应力计算公式如下[4]:
| $ \sigma = F \times {\left( {\frac{{2.76}}{d}} \right)^2} = \frac{{7.62F}}{{{d^2}}} \text{。} $ | (7) |
式中:F为舵销受到的支反力;d为舵销直径。
所以单个舵销破坏的安全边界方程为
| $ Z = {\sigma _s} - \frac{{7.62F}}{{{d^2}}} \text{,} $ | (8) |
式中,σs为舵销材料屈服极限。
单个舵销破坏的概率
| $ {P_f} = P\left\{ {{\sigma _s} - \frac{{7.62F}}{{{d^2}}} < 0} \right\} \text{。} $ | (9) |
假设舵设备有n个舵销,分别为舵销1、舵销2、…、舵销n,第1个破坏的舵销为舵销i,舵销i破坏概率为Pi,舵销i失效后载荷进行重新分配,剩下舵销的支反力均发生变化,此时舵销j破坏概率最大,记为Pj/i,则舵设备由舵销破坏导致卡滞的失效概率
| $ {P_f} = \sum\limits_{i,j = 1}^n {{P_i}{P_{j/i}}} \text{。} $ | (10) |
一般首个舵销破坏时,各舵销破坏概率相差较大,式(10)取Pi最大项与次大项2项即可。即
| $ {P_f} = {P_i}{P_{j/i}} + {P_l}{P_{m/l}} {\text{,}}$ | (11) |
含义为首个舵销破坏时舵销i破坏概率最大,舵销i破坏后舵销j破坏概率最大;首个舵销破坏时舵销l为破坏概率次大,舵销l破坏后舵销m破坏概率最大。
当n=1时,
2)舵销失效概率计算
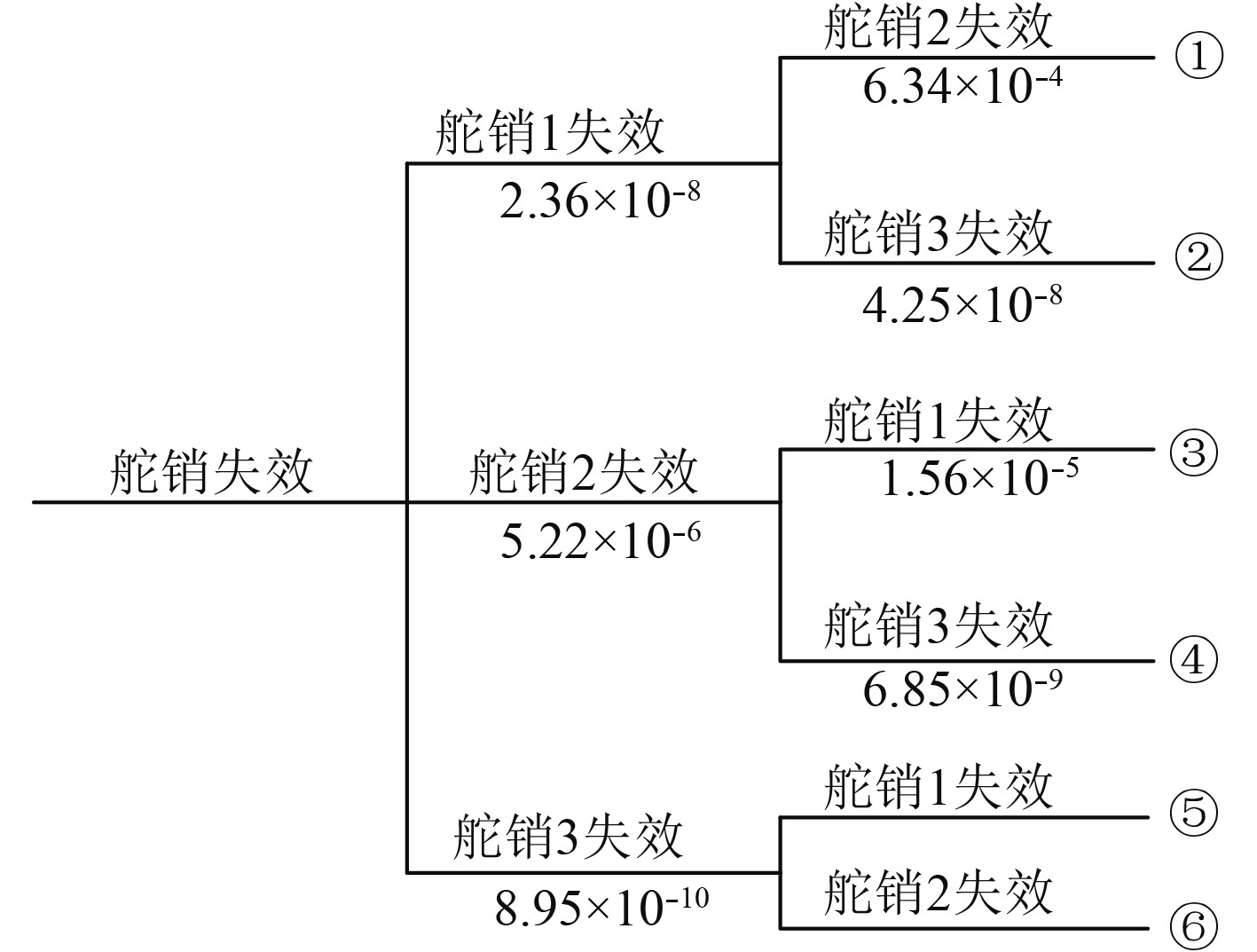
某多支撑式不平衡舵有3个舵销,在正常工作载荷下计算得到舵销的破坏概率及破坏次序如图4所示。
|
图 4 舵销破坏路线及破坏概率 Fig. 4 Failure route and failure probability of rudder pin |
从图3可以看出,在正常工作载荷下,舵销破坏路线为路线①和路线③,路线①为舵销1破坏后,舵销2破坏;路线③为舵销2破坏后,舵销1破坏。所以舵销破损安全失效概率
| $ \begin{split} \;\;\;\,{P_f} = & {P_1}{P_{2/1}} + {P_2}{P_{1/2}} = 1.50 \times {10^{ - 11}} + 8.14 \times {10^{ - 11}}= \\ & 9.64 \times {10^{ - 11}} \text{。} \end{split}(12) $ |
1)分析计算工况、应力计算方法、材料性能、结构尺寸和强度裕度等舵设备设计中的不确定因素,将其作为随机变量开展了舵设备可靠性设计分析,给出舵设备可靠性设计流程,建立舵设备可靠性模型,并提出舵设备可靠性指标确定与分配方法;
2)建立舵设备部件失效安全边界方程,以舵杆为例进行详细可靠性设计,计算得到的上、下舵承处舵杆截面失效概率均满足可靠性指标要求,但下舵承处舵杆可靠度很高,对其进行尺寸优化,得到给定可靠性指标下的舵杆截面尺寸;
3)载荷、材料强度和结构尺寸的分散性对舵杆失效概率影响很大,失效概率随着变异系数增大而大幅增长,对舵杆直径和材料屈服强度分散性尤为敏感。平时要注重对载荷、材料强度和结构尺寸分散性数据的收集,当无法获得变异系数的准确取值时,变异系数应在取值范围内尽量取得稍大些。同时应对加工质量和材料质量进行严格控制。
4)对多舵销舵设备的舵销进行可靠性分析,建立了舵销破损安全可靠性分析模型,获得舵销破损失效路线,对其进行失效概率分析。
| [1] |
BAI Y, JIN W L. Reliability of ship structures[M].Marine Structural Design. 2016.
|
| [2] |
AKPAN U O, AYYUB B M, KOKO T S, et al. Development of reliability-based damage-tolerant optimal design of ship structures[J]. ASCE-ASME Journal of Risk and Uncertainty in Engineering Systems, Part A: Civil Engineering, 2015, 2722: 04015013. |
| [3] |
余建星. 船舶与海洋结构物可靠性原理[M]. 天津: 天津大学出版社, 2001: 165–168.
|
| [4] |
余建星. 船舶与海洋工程设备[M]. 天津: 天津大学出版社, 2011: 16–19.
|
| [5] |
胡云昌, 李晨, 李吉生, 等. 舵设备的可靠性分析[J]. 天津船舶, 1992(1): 39-43. HU Yun-chang, LI Chen, LI Ji-sheng, et al. Reliability analyze of rudder[J]. Tianjin Ship, 1992(1): 39-43. |
| [6] |
周宏. 舵装置的可靠性设计研究[J]. 船舶, 2005, 5: 51-53. ZHOU Hong. Study on reliability design of rudder[J]. Ship and Boat, 2005, 5: 51-53. |
| [7] |
曾声奎. 可靠性设计与分析[M]. 北京: 国防工业出版社, 2011: 37–63.
|
| [8] |
唐松, 张火明, 吴剑国, 等. 船舶波浪弯矩1周短期预报研究[J]. 舰船科学技术, 2014, 36(1): 42-45. TANG Song, ZHANG Huo-ming, WU Jian-guo, et al. Investigation on short-term forecasting of a week for ships’ wave bending moment[J]. Ship Science and Technology, 2014, 36(1): 42-45. DOI:10.3404/j.issn.1672-7649.2014.01.009 |
 2019, Vol. 41
2019, Vol. 41
