船体内部由骨架支撑,外部被钢板包裹,钢板和骨架共同构成了板架结构。船体板架一般分为横骨架式板架结构和纵骨架式板架结构, 但无论其采用横骨架式还是纵骨架式,抑或是混合骨架式,都存在一定结构强度和工艺上的问题,但由于其结构简单,便于加工制造,所以在船舶几百年的发展史上一直处于中坚地位。但是随着造船业的蓬勃发展,各种新式船舶应运而生,它们形态各异,制造难度大,传统的造船方法和船舶结构已经无法满足日新月异的船型发展,可以说传统造船业已经遭遇到发展的瓶颈期,如何寻求新式的制造技术成为解决这一问题的关键。
美国海军马士基公司率先提出了“打印舰艇”的概念[1],卡德洛克海军水面作战中心也成功利用增材制造技术打印出了1艘美军医疗船模型,并对其进行了相应各项测试,结果极具代表性。此外,华中科技大学武汉光电国家实验室(筹)在国内率先完成了“大型金属零件高效激光选区熔化增材制造关键技术与装备”,团队创新性地提出运用4台激光器同时扫描,不仅提高了打印速率,而且大幅度提高了增材制造能打印的高精度金属零件的尺寸,实现了复杂金属的高精度成形,缩短了产品研发周期。无论是在结构上还是技术上,都为增材制造技术应用于船体研究奠定了良好的理论基础。
金属增材制造技术作为增材制造技术的重要分支,经过20多年的发展,已经在材料、成型技术等很多方面取得了不小的突破,被广泛用于航天航空制造业,并逐渐取代传统的制造方法,成为主导[2]。激光选区融化技术(SLM),是金属增材制造技术发展最广泛的一种。SLM技术旨在生产具有良好机械性能的完全致密性零件,利用高亮度激光直接熔化金属粉末材料,它的优势在于能不借助模具直接成形出任意复杂结构零件,且性能与锻件相媲美,后处理步骤的不断精简,大为缩短了生产时间[3]。SLM技术相比于传统的焊接技术,在材料以及结构强度上都有着新的突破,朱海红[4 – 5]通过研究,验证了扫描速度和切片厚度对密度有着显著影响,并且合金金属粉末中加入适量的金属元素,将使结构的致密性有很大的提高,这一研究成果将使得金属增材制造技术逐步领先于传统制造技术,且精简后处理程序,大大节约建造成本。将这一技术运用于船体结构研究,能够突破传统船舶制造业一成不变的结构及外形设计,为新型船舶的研究、设计与发展注入新的活力。不断发展的合金材料研究也将衍生出一批结构性能优越的材料,逐步取代传统造船业钢的地位,推动船体轻量化的发展。
1 模型设计与建模增材制造的优势在于不受形状的限制,能充分发挥结构的最大优势,因此,可将其与仿生学联系起来,仿生学顾名思义,就是根据自然界中生物的结构和相应的功能原理应用到机械产品的设计和开发中来[6]。大自然是最优秀的设计制造者,生物经过几亿年物竞天择的发展,演化出具有各自生存特点的生理结构,这些结构往往具有很强的力学和物理性能,稳定性很高,但是一般都具有极其复杂的结构,也只有利用增材制造技术才能更好地在人类生活中还原其本来的结构特点。
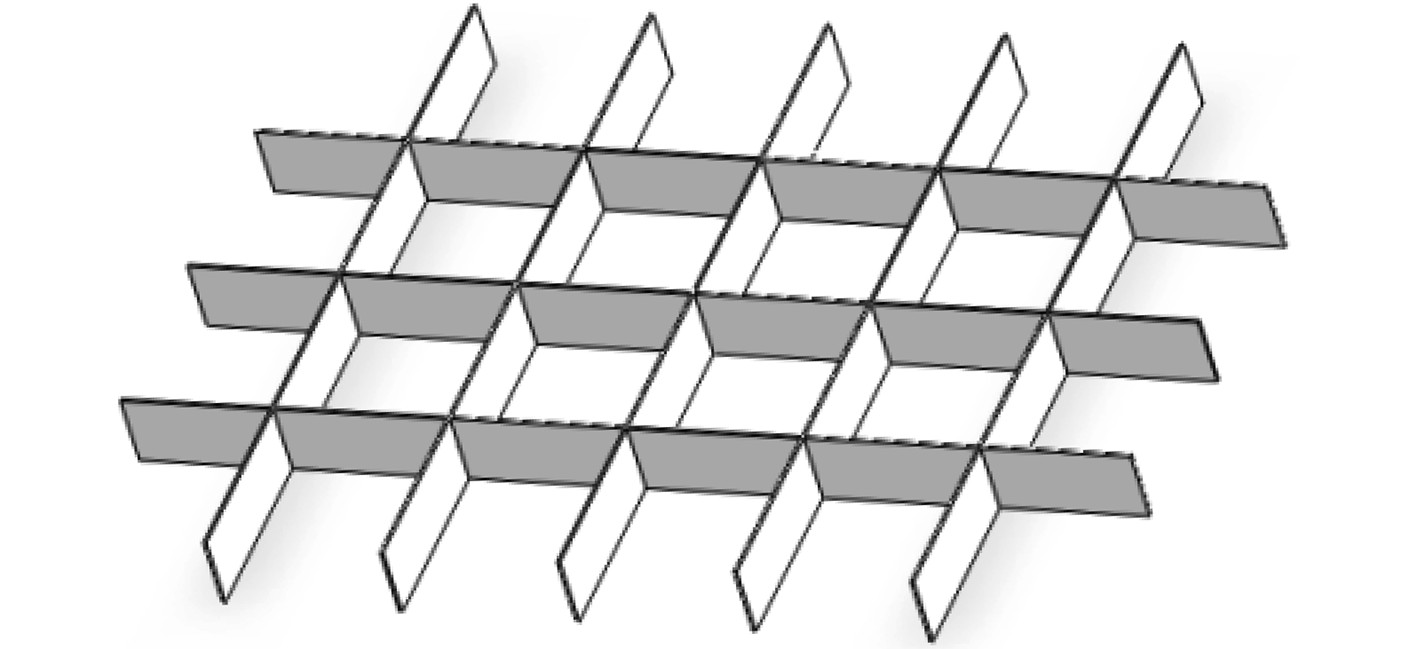
传统的船底板框架为四边形结构,根据规范要求[7],对船底板框架模型型材尺寸按照10:1的比例进行简化设计,取中间一段结构,如图1所示。其各项参数分别为:纵板尺寸0.5×137.12×10 mm,间距25 mm;肋板尺寸0.5×100×10 mm,间距24 mm。
|
图 1 船底板模型 Fig. 1 Model of bottom plate |
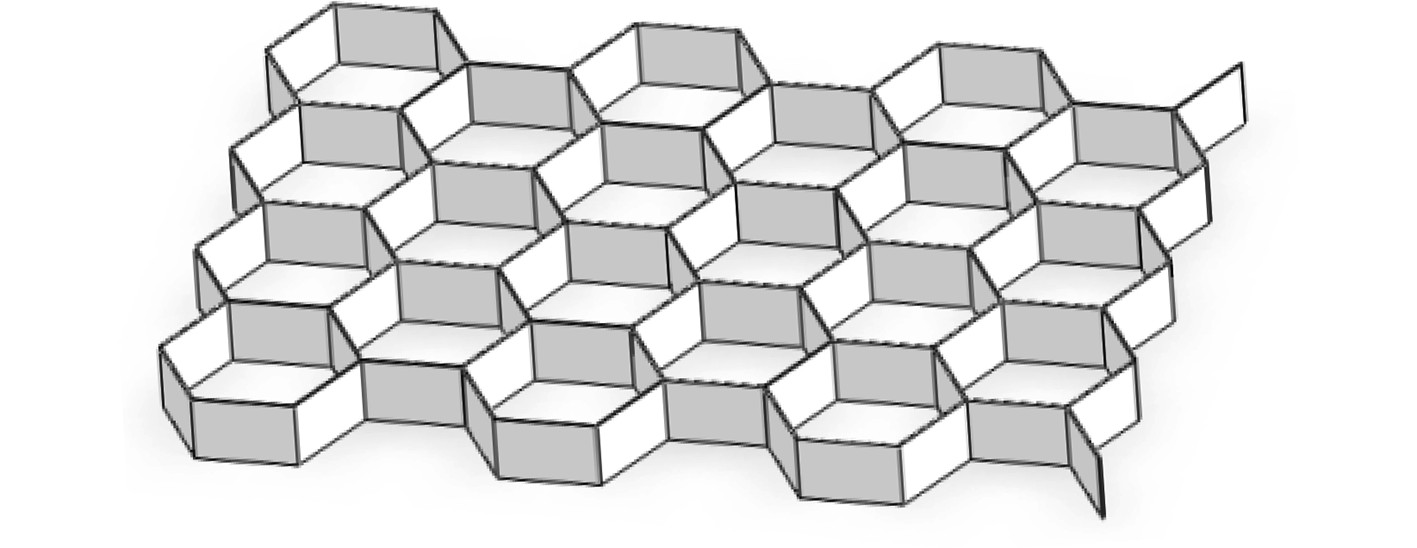
为研究多边形包体结构对框架性能的影响,根据仿生学原理,提出蜂窝状多胞结构模型,如图2所示。蜂窝结构(Cellular Structure)是蜂巢组成的基本结构,由很多个正六边形依次对称组合排列而成,被认为是最佳的覆盖二维平面的拓扑结构[8]。对两者结构强度进行仿真分析,研究蜂窝结构替代矩形结构的可行性。
|
图 2 蜂窝底板框架模型 Fig. 2 Model of cellular bottom plate |
船体结构受力相对而言比较复杂,在静水状态下,船体主要受浮力和自身重力,由于船型的原因,导致船体重力沿船长分布不均,导致船体产生总纵弯曲,而当船在波浪中时,受到水的压力和波浪的冲击力,总纵弯曲也会加剧[9]。
将框架四端固定,在平面中心位置施加垂直向下的集中力,对比分析2种板的受力和变形情况。材料采用结构钢,E=2.06E5 MPa,ε=0.28,屈服应力[σ]=235 MPa,施加竖直向下的面载荷P=103 kg。运用Abaqus软件对其进行受力分析,其结果如图3所示。其中图3(a)和图3(b)为等效应力图,图3(c)和图3(d)为位移图。

|
图 3 模型弯曲应力和位移云图 Fig. 3 Stress and displacement nephogram of bend |
由图3可知,在受相同约束和载荷的情况下,板架结构所受的最大应力σmax=105.4 MPa,最大位移Umax=3.387E–2 mm,蜂窝板结构所受最大应力为σmax=92.54 MPa,最大位移为Umax=4.667E–2 mm。
2.2 扭矩受力分析扭矩(Torque)也称为转矩,是一种特殊的力矩,使物体发生转动[10],通过对模型的扭转分析,能够得出模型的抗扭转能力。模型在扭转过程中产生切应力应变,切应变与相对转角的关系为:
| $\gamma = \frac{{\varphi {{r}}}}{{{l}}}\text{;}$ | (1) |
切应变与切应力满足剪切胡克定律:
| $\tau = {{G}}\gamma \text{;}$ | (2) |
扭转与切应力之间的关系为:
| ${{M}} = \mathop \smallint \nolimits^ \tau {\rm{d}}A \cdot {{r}}\text{。}$ | (3) |
式中:φ为截面间相对转角;γ为切应变;τ为切应力;M为扭矩;r为扭转半径;l为材料长度。
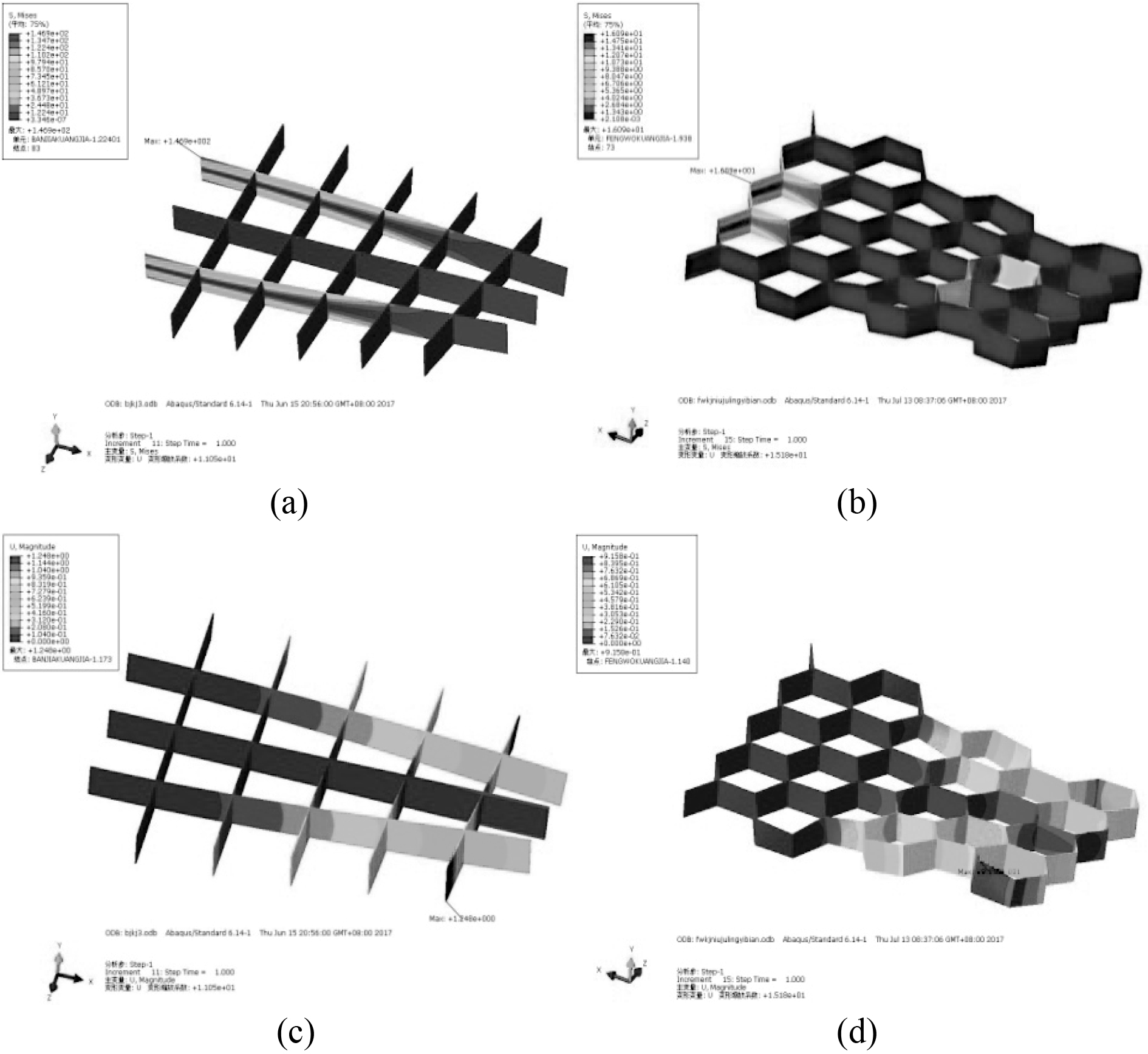
通过有限元软件Abaqus,对2块模型板施加相同扭矩,其结果如图4所示。
|
图 4 扭转应力和位移云图 Fig. 4 Stress and displacement nephogram of torque |
结果显示,在施加M=10 N﹒m扭矩的作用下,板架结构的应力最大值为σmax=146.9 MPa(图4(a)),最大位移为Umax=1.248 mm(图4(b)),蜂窝结构中应力最大值为σmax=87.83 MPa(图4(c)),最大位移为Umax=0.906 1 mm(图4(d))。
3 结构多属性决策分析多属性决策(Multiple Attribute Decision Making,MADM)[11]也叫有限方案多目标决策。通过结构强度分析,直观地了解了模型变形的质量、最大应力和最大位移,由于多个属性之间存在不同的量纲,无法进行直观的比较,因而引入复合比例评估(Complex Proportional assessment ,COPRAS)方法来解决这一问题。通常分为5个阶段,步骤及方法如下:
阶段1 形成初始决策矩阵X,其等式为
| $ \begin{aligned} &{{ X}} = {\left[{{{{x}}_{{{ij}}}}} \right]_{{{mn}}}} = \left[{\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{{{x}}_{11}}}&{{{{x}}_{12}}}\\ {{{{x}}_{21}}}&{{{{x}}_{22}}} \end{array}}&{\begin{array}{*{20}{c}} \cdots \\ \ldots \end{array}}&{\begin{array}{*{20}{c}} {{{{x}}_{1{{n}}}}}\\ {{{{x}}_{2{{n}}}}} \end{array}}\\ {\begin{array}{*{20}{c}} \vdots & \vdots \end{array}}& \vdots & \vdots \\ {\begin{array}{*{20}{c}} {{{{x}}_{{{m}}1}}}&{{{{x}}_{{{m}}2}}} \end{array}}& \cdots &{{{{x}}_{{{mn}}}}} \end{array}} \right]\text{,}\\ &\quad\left( {i = 1, 2 \ldots m} \right), \left( {j = 1, 2 \ldots n} \right)\text{。} \end{aligned}$ | (4) |
其中xij为第i种模型的第j种决策指标。
为了解决大多数决策指标不在同一维度或同一单位内,将矩阵X转换成无量纲化矩阵R,相关系数表示为
| ${{ R}} = {\left[{{{{r}}_{{{ij}}}}} \right]_{{{mn}}}} = \frac{{{{{x}}_{{{ij}}}}}}{{\displaystyle\mathop \sum \nolimits_{{{i}} = 1}^{{m}} {{{x}}_{{{ij}}}}}}\text{。}$ | (5) |
阶段2 确定加权归一化决策矩阵为
| $ {{ D}} = \left[{{{{y}}_{{{ij}}}}} \right] = {{{r}}_{{{ij}}}} \times {{{w}}_{{j}}}{\text{。}} $ | (6) |
其中:rij为第i种模型方案在第j个决策指标上的归一化性能值;wj为第j个决策指标的权重。在此之前,对权重值进行求解,首先对决策指标进行两两对比,共需要比N次,其中N=(n(n-1)/2)。两两比较结果,指标占比重要的记为3,相反记为1,两者相同的同时记为2,最后计算每一个指标得到的总分数:
| $ \sum \nolimits_{{{i}} = 1}^{{m}} {{{N}}_{{{ij}}}} = {{{W}}_{{j}}}\text{。}$ | (7) |
将每个决策指标的总分(Wj)除以全局总分得到每个决策指标的相对占比加权因子wj,则
| ${{{w}}_{{j}}} = \frac{{{{{W}}_{{j}}}}}{{{G}}}\text{,}$ | (8) |
其中全局总分数
阶段3 计算决策指标中正、逆向指标的和。归一化决策矩阵的值包含正向和逆向属性,正向属性表明指标值越大,模型方案越好,反之为逆向属性。其计算公式分别为:
| ${{{S}}_{ + {{i}}}} = \sum \nolimits_{{{j}} = 1}^{{n}} {{{y}}_{ + {{ij}}}}\text{,}$ | (9) |
| ${{{S}}_{ - {{i}}}} = \sum \nolimits_{{{j}} = 1}^{{n}} {{{y}}_{ - {{ij}}}}\text{。}$ | (10) |
阶段4 计算相对重要性(Q)。设计的优先级是基于相对重要性Qi的概念来计算的。Qi的值越大,设计方案的优先级就越高。相对重要性的值表明了这一设计好坏,具有最大相对重要性值Qmax的设计方案是诸多模型方案中的最佳选择。其计算公式为:
| $ \begin{split} &{{{Q}}_{{i}}} = {{{S}}_{ + {{i}}}} + \frac{{{{{S}}_{ - {\min}}}\displaystyle\mathop \sum \nolimits_{{{i}} = 1}^{{m}} {{{S}}_{ - 1}}}}{{{{{S}}_{ - {{i}}}} \displaystyle\sum \nolimits_{{{i}} = 1}^{{m}} \left( {{{{S}}_{ - {\min}}}/{{{S}}_{ - {{i}}}}} \right)}} =\\ &\quad {{{S}}_{ + {{i}}}} + \frac{{ \displaystyle\sum \nolimits_{{{i}} = 1}^{{m}} {{{S}}_{ - 1}}}}{{{{{S}}_{ - {{i}}}} \displaystyle\sum \nolimits_{{{i}} = 1}^{{m}} \left( {1/{{{S}}_{ - {{i}}}}} \right)}}\text{。} \end{split}$ | (11) |
阶段5 确定量化率。其计算公式为
| ${{{U}}_{{i}}} = {{{{{Q}}_{{i}}}}/{{{{Q}}_{\max}}}} \times 100{{\% }}\text{。}$ | (12) |
量化率的值与相对重要性直接相关,量化率的值决定了模型方案优先级的排名。
将之前计算的结果值按照上述步骤进行计算,可以得到决策矩阵,归一化矩阵。评判2种结构采用的指标则是之前计算所得到的质量、弯曲和扭转的应力和位移,应力可以表征结构的强度,而位移则能表征结构的刚度。对于5个指标权重值,因为设计理念中含有轻量化原则,所以与其他指标相比较时,指标权重值为3,扭转最大应力与弯曲最大应力视为相同权重,相互比较时均为2,位移与应力相比值为3,则应力为1。最终得到多准则决策结构如表1所示,可以很直观地得到蜂窝框架结构相比于板架结构具有较好的性能优势。
|
|
表 1 决策矩阵 Tab.1 Decision matrix |
|
|
表 2 无量纲化矩阵 Tab.2 Non-dimensionalized matrix |
|
|
表 3 多准则决策结果 Tab.3 Result of COPRAS |
本文基于金属增材制造技术,提出了蜂窝形多胞结构船底板框架,通过有限元仿真模拟,对矩形多胞结构和正六边形多胞结构进行对比分析,从结果看,正六边形多胞结构抗弯矩和抗扭矩能力要优于矩形结构。通过结构多属性决策理论的引入,也进一步证明蜂窝形多胞结构整体性能要优于矩形多胞结构。这为多胞结构运用于船体创新设计奠定了良好的理论基础。
| [1] |
祁斌. 3D打印技术在船舶领域的应用[J]. 中国船检, 2016(6): 94-100. DOI:10.3969/j.issn.1009-2005.2016.06.022 |
| [2] |
林鑫, 黄卫东. 应用于航空领域的金属高性能增材制造技术[J]. 中国材料进展, 2015, 34(9): 684-688. |
| [3] |
KRUTH J P, MERCELIS P, VAN VAERENBERGH J, et al. Rapid Prot. J.11(2005) 26.
|
| [4] |
HU Z, ZHU H, ZHANG H, et al. Experimental investigation on selective laser melting of 17-4PH stainless steel[J]. Optics & Laser Technology, 2017, 87: 17-25. |
| [5] |
ZHANG Hu, ZHU Hai-hong, NIE Xiao-jia, et al. Effect of zirconium addition on crack, microstructure and mechanical behavior of selective laser melted Al-Cu-Mg alloy[J]. SCRIPTA MATERIALIA, 2017, 134: 6-10. DOI:10.1016/j.scriptamat.2017.02.036 |
| [6] |
李冉冉. 仿生学原理在机械设计中的应用[J]. 华东科技:学术版, 2013(9): 289-289. |
| [7] |
中国船级社. 钢质内河船建造规范[M]. 北京: 人民交通出版社, 2014.
|
| [8] |
陆克中, 江钊, 毛睿, 等. 基于蜂窝结构的传感器网络覆盖问题求解算法[J]. 计算机研究与发展, 2012, 49(8): 1632-1640. |
| [9] |
彭公武. 船体结构与制图[M]. 哈尔滨: 哈尔滨工业大学出版社, 2007.
|
| [10] |
刘鸿文. 材料力学[M]. 北京: 高等教育出版社, 2011.
|
| [11] |
CHATTERJEE P, ATHAWALE V M, CHAKRABORTY S. Materials selection using complex proportional assessment and evaluation of mixed data methods[J]. Materials & Design, 2011, 32(2): 851-860. |
 2019, Vol. 41
2019, Vol. 41
