随现代武器的迅速发展,对舰导弹成为当今武器研究的热点之一。导弹爆炸产生的冲击波和大量高速破片是联合作用在结构上的2种最主要的毁伤元素[1]。战斗部壳体的材料属性、厚度、装药量、装药类型、壳体形状和起爆方式都对冲击波和高速破片的形成存在一定的影响[2 – 5]。早期,国内外学者关于冲击波和高速破片的研究思路大多还是将2种载荷的解耦处理[6 – 7],根据冲击波和高速破片在空气中的衰减特性,求解了冲击波在前、相遇以及冲击波在后的3个阶段传播规律[8]并将二者对结构的毁伤效应解耦成冲击波冲量效应和高速破片穿甲作用2个问题分别研究[9]。但实际在整个传播过程中2种载荷存在着相互影响。在载荷形成阶段,破片的存在会使爆炸产生的一部分能量损耗于高速破片的形成,从而使冲击波的能量减弱[10]。传播阶段,李茂等[11]在研究中指出冲击波遇到破片时存在明显的反射和绕流现象。冲击波传播过程中发生的绕流和反射现象会改变冲击波的超压、比冲量等载荷特性[12 – 13],从而改变实际作用于结构的冲击波强度。
为分析战斗部空中爆炸后冲击波对高速破片的绕流效应,可以更加真实地反映在传播过程中冲击波和高速破片的载荷特性。本文将采用Ansys/LS-DYNA非线性动力有限元分析软件,对端部预制破片工况进行数值模拟。建立多个计算模型对比分析、破片尺寸和破片质量因素对冲击波绕流作用的影响。
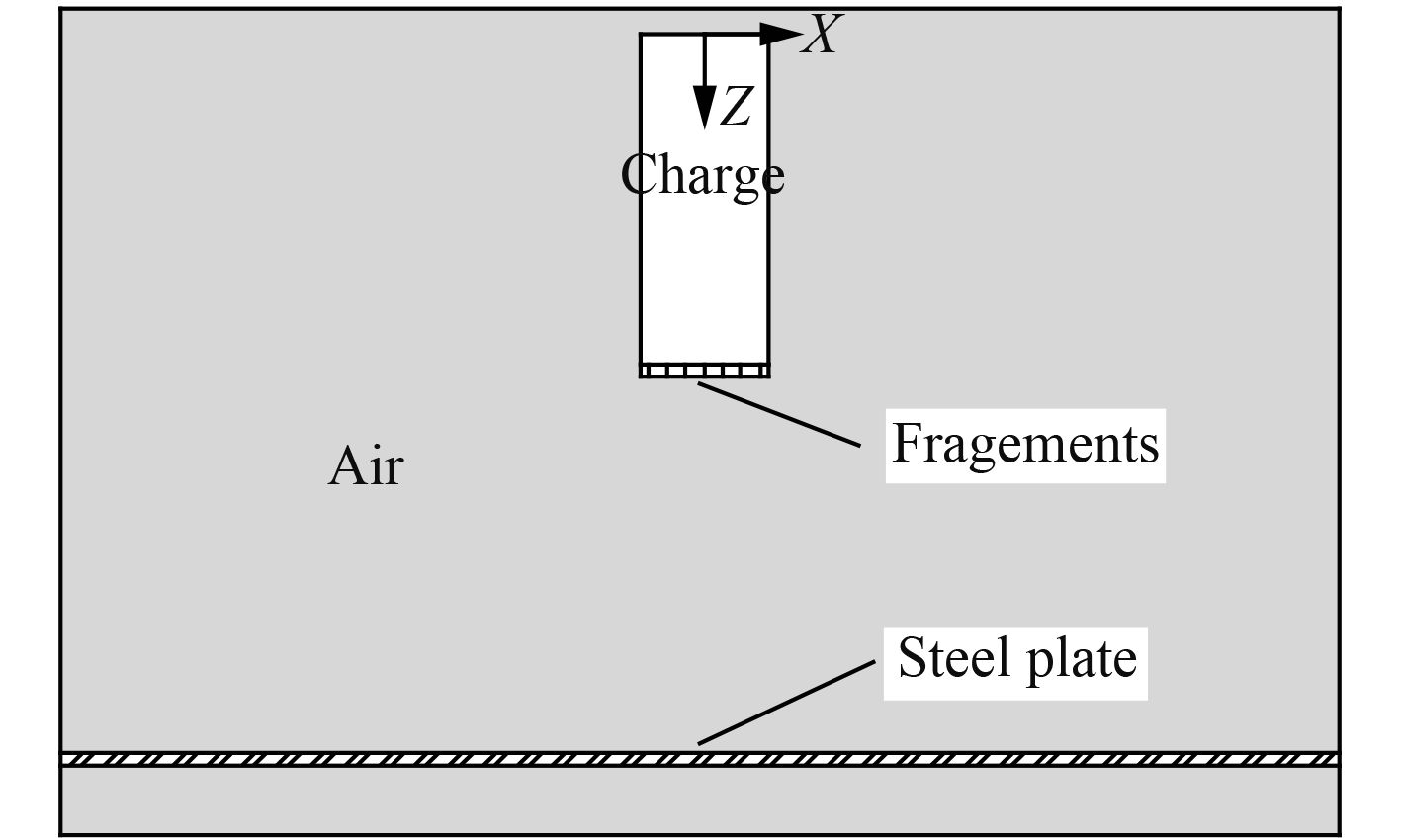
1 模型建立与仿真方法验证 1.1 模型选择及参数设置数值模拟采用g-cm-μs单位制,模型由空气域,破片,炸药,钢板4个部分组成。炸药和空气域均采用Euler单元,使用多物质单元ALE算法,预制破片和钢板采用Lagrange单元。空气域的尺寸取500 mm×500 mm×325 mm,模型布置和模型尺寸剖面示意图如图1所示。通过关键字*CONSTRAINED_LAGRANGE_IN_SOLID定义破片与空气材料间的耦合算法。保证计算精度,模型网格密度应尽可能高,炸药尺寸与炸药网格尺寸比值至少应大于6[14 – 15],但在有限元分析中单元划分越细,节点数目越多,计算步长越短,计算时间越长。为减少计算时间,在保证主要研究区域的网格精度的前提下,空气和钢板模型均采用发散性网格。中心边长140 mm的方形细化区域内,六面体网格边长约为1 mm。最终划分得到空气域单元总数约50万个,炸药单元总数约7万个,钢板单元总数5.6万个。通过试算,确定计算步长因子取0.65。仿真中欧拉域各面均设置无响应边界条件,含钢板模拟工况中钢板四边固支。
|
图 1 模型示意图 Fig. 1 Schematic diagram of the model |
炸药采用*MAT_HIGH_EXPLOSIVE_BURN本构模型,对轰爆产物的膨胀采用*EOS_JWL状态方程来描述:
| $ P = A\left( {1 - \frac{\omega }{{{R_1}V}}} \right){e^{ - {R_1}V}} + B\left( {1 - \frac{\omega }{{{R_2}V}}} \right){e^{ - {R_2}V}} + \frac{{\omega {e_0}}}{V}\text{。} $ | (1) |
式中:P为轰爆压力;e0为初始单位体积炸药内能;V为相对体积。A,B,R1,R2,ω为试验确定的常数,受装药密度、炸药类型等因素的影响。具体参数如表1所示[17]。其中ρ为装药密度;D为爆轰速度;Pcj为压力PCJ;V0为初始相对体积。每个炸药单元的点火时间由该单元距离起爆点的距离和爆速决定。
|
|
表 1 TNT炸药材料参数及状态方程参数 Tab.1 The materials and EOS parameters of TNT |
空气采用*MAT_NULL材料模型及*EOS_LINEAR_POLYNOMIAL状态方程描述。状态方程的线性多项式为:
| $ \begin{split} & P = {C_0} + {C_1}\mu + {C_2}{\mu ^2} + {C_3}{\mu ^3} + \\ & \left( {{C_4} + {C_5}\mu + {C_6}{\mu ^2}} \right){e_0}\text{,} \end{split} $ | (2) |
式中:C0~C6为多项式系数;e0为单位体积内能;μ=1/V–1,其中V为相对体积。当线性多项式状态方程用于理想气体模型时,空气材料参数和状态方程参数如表2所示。
|
|
表 2 空气材料参数及状态方程参数 Tab.2 The materials and EOS parameters of air |
破片采用双线性弹塑性本构模型*MAT_PLASTIC_KINEMATIC,其应变率则由Cowper-Symonds模型描述,应变方程为:
| $ {\sigma _d} = \left( {{\sigma _0} + \frac{{E{E_h}}}{{E - {E_h}}}{\varepsilon _p}} \right)\left[ {1 + {{\left( {\frac{{\dot \varepsilon }}{D}} \right)}^{1/n}}} \right]\text{,} $ | (3) |
式中:σd为动态屈服强度;σ0为静态屈服强度;E为弹性模量;Eh为硬化模量;εp为有效塑性应变;ε为等效塑性应变率;D,n为常数,对于常见低碳钢,通常取D=40.4 s–1,n=5[16]。
钢板采用Johnson-Cook本构模型,该模型考虑了材料在高温高应变率下的软化效应,能够反映高应变率以及高温情况下材料的性质变化,其状态方程为:
| $ {\sigma _d} = \left( {{\sigma _0} + {E_h}{\varepsilon _p}^{{n_0}}} \right)\left[ {1 + c\ln \frac{{{\varepsilon _p}}}{{{\varepsilon _0}}}} \right]\left[ {1 - {{\left( {\frac{{T - {T_0}}}{{{T_m} - {T_0}}}} \right)}^m}} \right]\text{。} $ | (4) |
式中:n0为应变硬化指数;c为应变率系数;m为软化指数;ε0为参考塑性应变率;T,Tm,T0分别为材料温度,材料熔点和参考室温,取Tm=1 793 K,T0=300 K。
材料的失效则由下述方程描述:
| $ \begin{split} & {\varepsilon _f} = \left[ {{D_1} + {D_2}\exp \left( {{D_3}\frac{{{\sigma _h}}}{{{\sigma _{eff}}}}} \right)} \right]\left( {1 + {D_4}\frac{{{\varepsilon _p}}}{{{{\dot \varepsilon }_0}}}} \right) \times\\ & \left[ {1 + {D_5}5{{\left( {\frac{{T - {T_0}}}{{{T_m} - {T_0}}}} \right)}^m}} \right]\text{。} \end{split} $ | (5) |
式中:D1~D5为材料无量纲常数;当破坏参数D =
|
|
表 3 Q235钢力学参数及方程参数 Tab.3 The materials and EOS parameters of Q235 |
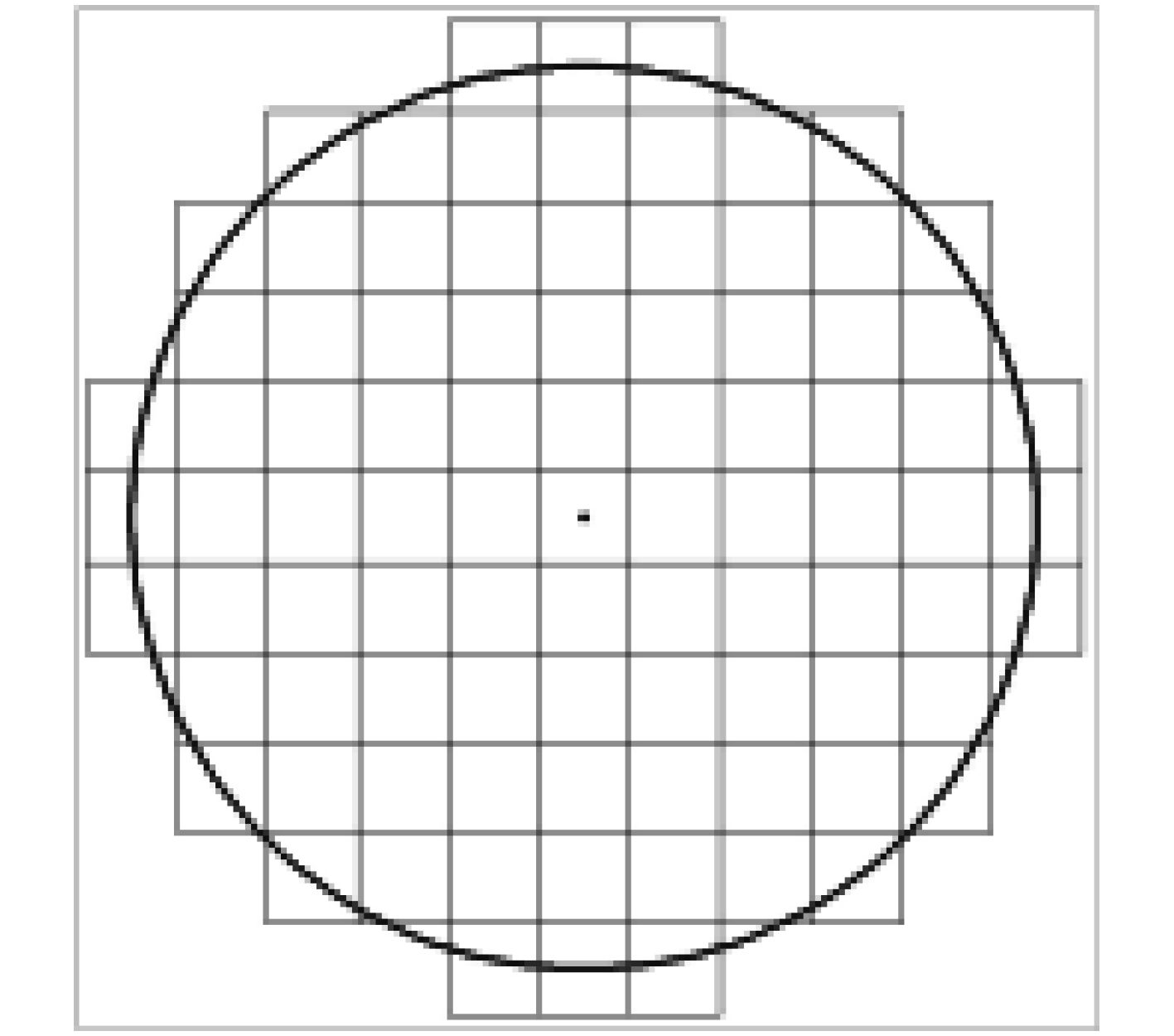
为验证模型建立的合理性,本文首先对空中近爆冲击波载荷作用下钢板的变形试验[17](模型1),近爆载荷联合作用下钢板变形毁伤试验[18](模型2)以及同样装药工况下的2 mm和4 mm的Gurney平板驱动理论模型(模型3、模型4)进行仿真分析。模型中炸药均为两发直径50 mm,高度65 mm的柱形铸装TNT轴向叠加布置,总装药质量400 g。炸药下端面距离平板结构爆距为150 mm,模型1中钢板厚度为4 mm,模型2中钢板和预制破片厚度均为2 mm,破片总数为89枚,总质量为34.9 g,采用对称方式布置(见图2)。
|
图 2 模型2预制破片布置图 Fig. 2 Placed fragments of model 2 |
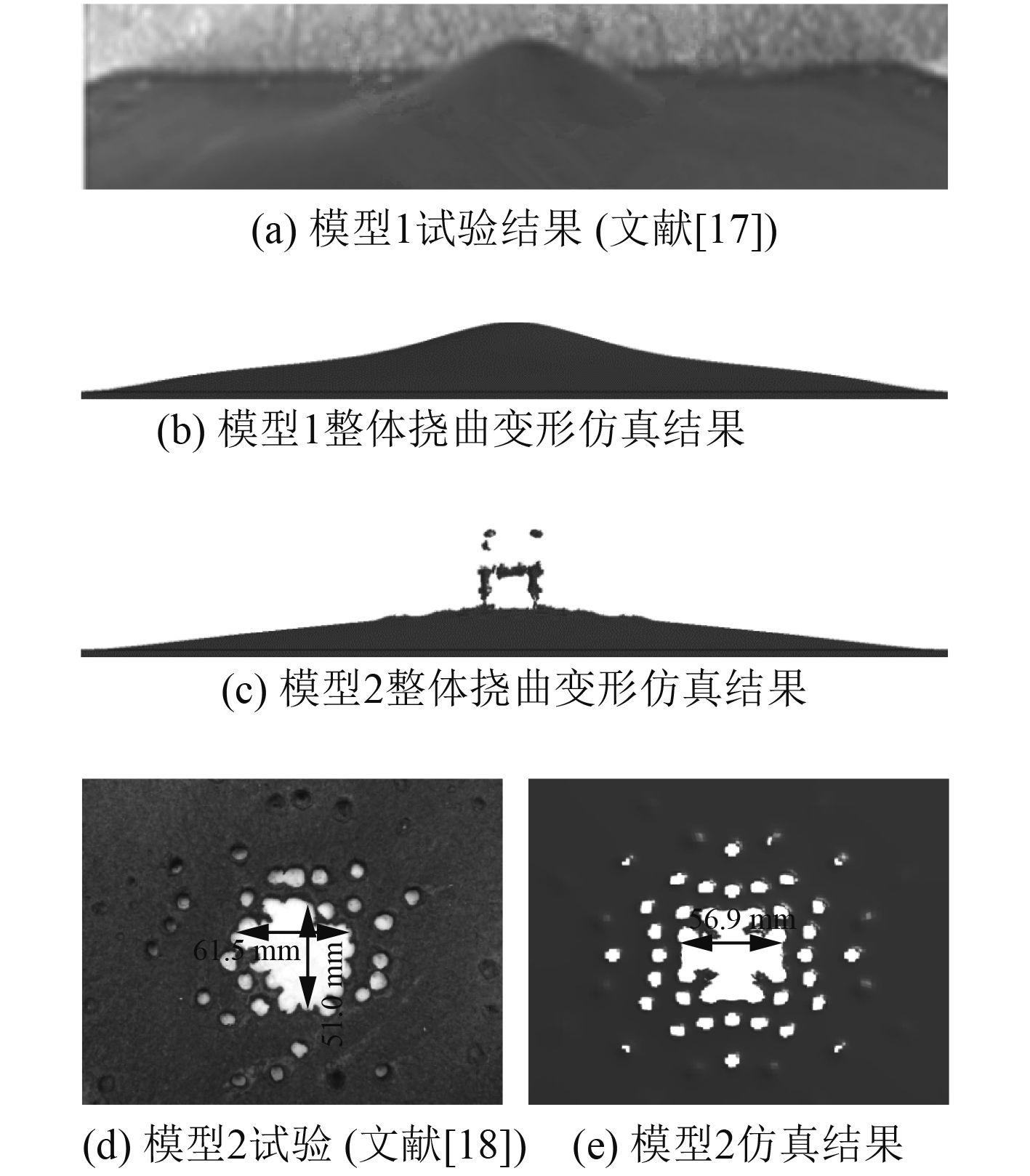
仿真结果如图3所示,模型1中平板的整体挠曲变形在1 140 μs时趋于稳定,中心最大挠曲变形为39.5 mm,与试验值42.3 mm相差约为6.62%;模型2中固支方板模型中心处的冲塞破口直径为56.9 mm,与试验值相当,其最大挠曲变形出现在破口附近,仿真值为24.4 mm,较试验值25 mm小约2.4%;模型3和模型4中平板获得的最终速度仿真结果分别为1 921.6 m/s,1 206.8 m/s,较Gurney平板抛掷公式[19]预测结果1 851.7 m/s,1 246.4 m/s相差分别为3.8%,2.80%。通过以上比较可知,该仿真方法及选取的模型参数较为合理。
|
图 3 试验结果与模型仿真结果 Fig. 3 Experimental and numerical simulation images of damaged steel plate |
图4给出不同时刻下冲击波的传播状态。其中图4(a) ~ 4(c)为模型2的压力云图,从图中可以清楚看出爆炸前,由于破片群无间隙密集布置,爆轰波遇到预制破片后发生反射(t=30 μs),端部爆炸产生的能量初期主要转化为破片的动能。由于受到爆炸作用,高压冲击波持续作用于破片群后,形成与破片群飞散轮廓一致的凸起高压区。由于不同位置破片飞散角不同的飞散特性,随着破片加速运动,破片之间的间隙逐渐增大,在破片群后方冲击波穿过破片间隙(t=50 μs),并绕流至破片之前,在破片前碰撞形成新的冲击波向前继续传播。同时,炸药侧面爆炸产生的高温高压压缩炸药侧面附近区域的空气,使空气的压力密度迅速上升形成弧形冲击波向外传播。近破片端受到破片影响,侧面冲击波向轴向绕流,随传播继续与绕流穿过破片间隙的冲击波碰撞结合,形成凸形冲击波,是作用于轴向平板结构的主要冲击波载荷。
图4(d)和图4(e)为模型3的压力云图,图4(f)为模型4的压力云图。当一端为抛掷平板时,从图中可以看到冲击波对高速破片的绕流主要表现在侧面冲击波绕流至轴向传播。平板正后方冲击波强度较高并持续推动平板向前运动,平板边缘则发生冲击波的局部涡流运动。模型4中平板质量更大,侧面绕流至轴向传播的冲击波传播较平板更加靠前。而且可以看出当炸药一端为覆盖整个炸药端面的平板时且平板在爆炸载荷作用下不发生破碎,冲击波很难从两侧直接绕流至破片正前方。综上现象可以看出冲击波对破片的绕流作用与破片之间间隙、破片尺寸以及破片质量因素存在一定的关系。

|
图 4 模型冲击波压力云图 Fig. 4 Pressure contours of the model 2/3/4 |
为进一步分析比较爆炸产生的冲击波对不同高速破片绕流作用的差异。在同等装药工况下,通过变化预制破片间隙d、单一预制方形破片边长a和破片质量M,进一步研究破片间隙、破片尺寸和破片质量因素对冲击波绕流作用的影响规律。本文建立了如表4所示计算工况模型进行仿真计算,并在距离炸药预制破片端150mm爆距水平位置选取测量点。根据文献[17]可知在150 mm近爆工况钢板的碟形变形区为半径125 mm的圆形区域,所以取预制破片端距离炸药150 mm爆距,半径R=125 mm的圆形区域(见图5)为测量区域。读取轴向测点1的峰值超压ΔPm、比冲量I1及测点1~测点6的比冲量平均值I2,与裸药空爆工况(case-1)比较,对比分析冲击波对高速破片的绕流能力及绕流冲击波的强度。

|
图 5 观测点分布 Fig. 5 View point |
|
|
表 4 计算工况 Tab.4 Computational conditions |
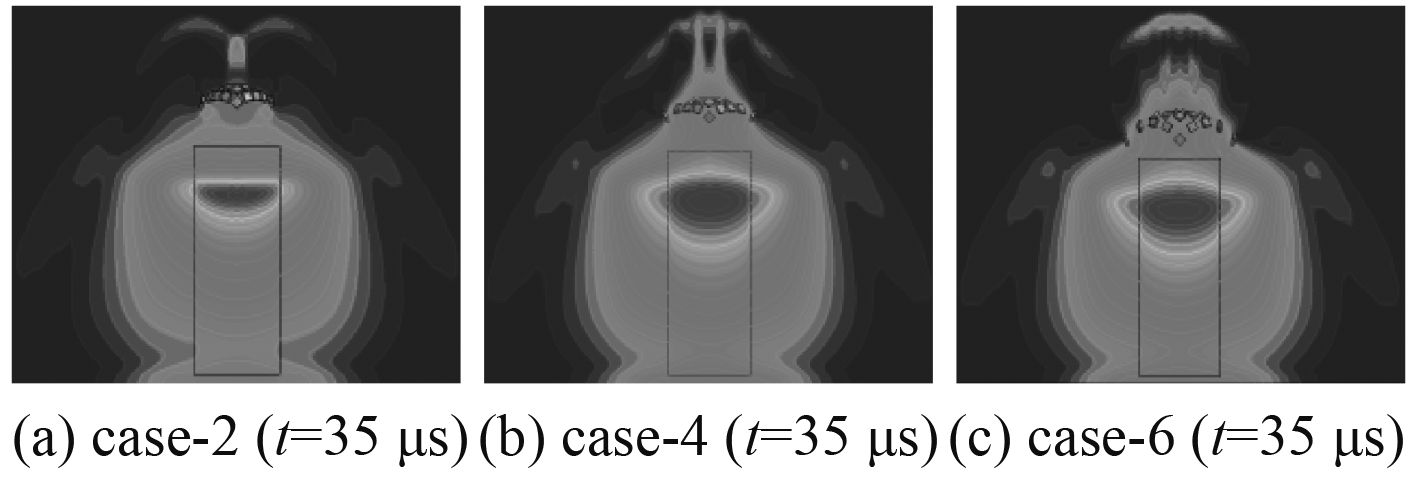
图6是破片间隙与破片边长比值d/a分别为0,0.4,0.8三个工况在35 μs时的冲击波压力云图。从图中可以看出当预制破片在爆炸前不存在间隙时,在破片前传播的冲击波主要还是侧面绕流至破片正前方的冲击波。而当预制破片在爆炸前存在间隙时,冲击波将迅速通过破片间隙绕流至破片之前。由于从破片间隙绕流出去的冲击波传播速度较快,很快与侧壁绕流的冲击波碰撞汇合,形成新的冲击波,在波头和破片之间存在长锥形的正压区域,并且随破片间隙增大,轴向冲击波波形更加接近于裸药空爆的波形。
|
图 6 模型case-2/4/6在35 μs时冲击波压力云图 Fig. 6 Pressure contours of the case-2/4/6 at 35 μs |
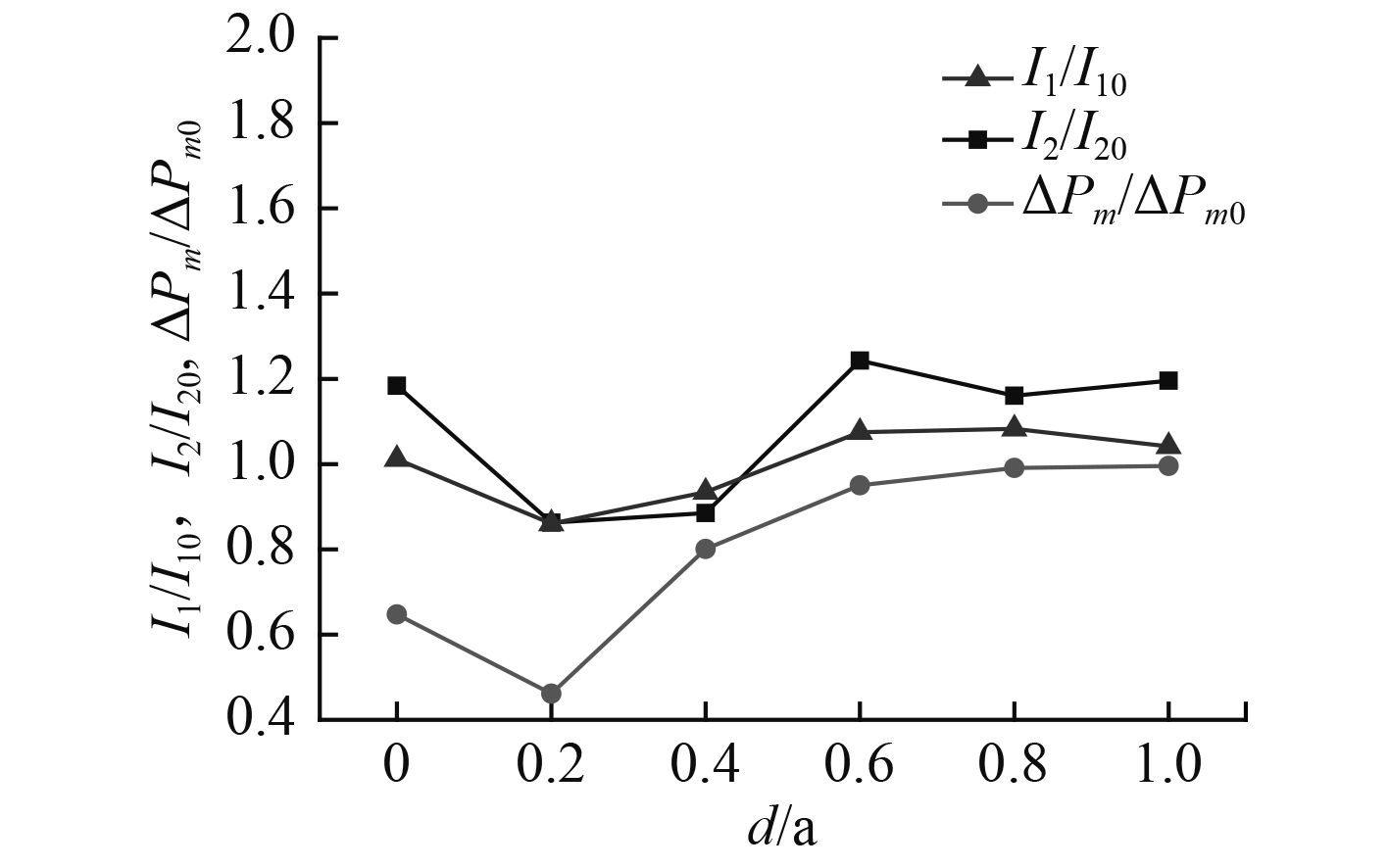
图7为不同间隙工况下测量区域的冲击波超压和比冲量变化折线图。图中ΔPm0,I10,I20分别为裸药空爆仿真模型(case-1)中,测点1的超压值、测点1的比冲量以及测点1 ~ 测点6的平均比冲量,后文与此相同。分析图中折线可以看出,无间隙时,冲击波超压及比冲量比b/a=0.2工况均要大,这主要是因为此时绕流至破片之前的冲击波主要由破片两侧边缘的冲击波绕流至破片之前碰撞生成,而且碰撞后轴线附近冲击波存在叠加增强作用。有间隙时,随着破片间隙的增大,爆距15 cm处的冲击波超压和比冲量均呈增大趋势,但破片间隙达到0.6倍破片边长后,破片间隙对绕流冲击波强度影响减小,而且随破片间隙增大测点处冲击波超压和比冲量数值逐渐逼近裸药空爆冲击波的超压和比冲量。
|
图 7 破片间隙对冲击波绕流影响 Fig. 7 Influence of fragment clearance on wave turbulent flow |
图8是边长分别为5 mm,15 mm,25 mm,厚度为2 mm的单枚预制破片工况在26 μs时的冲击波压力云图。从图中可以看出冲击波对小尺寸破片的绕流能力要比对大尺寸破片的扰流能力强得多,随着破片尺寸增大,破片对TNT炸药端部的覆盖率增大,破片两侧边缘的冲击波绕流速度明显减慢。

|
图 8 模型case-8/13/18在26 μs时冲击波压力云图 Fig. 8 Pressure contours of the case-8/13/18 at 26 μs |
图9为不同破片尺寸工况下测量区域的冲击波超压和比冲量变化折线图,其中R为炸药半径。从图中可以分析得出,随破片尺寸增大则迎爆面面积逐渐增大,绕流形成的冲击波强度逐渐减小;绕流冲击波超压值低于裸药空爆冲击波超压,但测量区域绕流冲击波的比冲量要明显高于裸药空爆冲击波。

|
图 9 破片尺寸对冲击波绕流影响 Fig. 9 Influence of fragment size on wave turbulent flow |
图10为边长25 mm厚度分别为2 mm,4 mm,6 mm的单枚预制破片工况在50 μs时的冲击波压力云图。从图中可以看到此时冲击波主要为两侧绕流冲击波碰撞产生,并在对称轴线上生成碰撞增强的高压点。当破片迎爆面面积不变时,随破片质量增加,绕流形成的冲击波波形差异不大,但破片质量越大,其加速越慢,冲击波绕流过破片并与破片分离速度更快。

|
图 10 模型case-18/21/23在50 μs时冲击波压力云图 Fig. 10 Pressure contours of the case-18/21/23 at 50 μs |
图11为不同破片质量工况下测量区域的冲击波超压和比冲量变化折线图。从图中可以分析得出,随破片质量增大,通过圆形测量区域的冲击波比冲量强度整体变化不大,测点1的超压始终低于ΔPm0,但测量点1的比冲量呈增大趋势。破片质量的增加,主要会增强轴线上冲击波的比冲量。

|
图 11 破片质量对冲击波绕流影响 Fig. 11 Influence of fragment mass on wave turbulent flow |
本文利用有限元分析软件Ansys/LS-DYNA计算了实验模型、Gurney平板抛掷模型,验证了仿真模型的可行性。通过对比分析仿真模型,研究了破片间隙,破片尺寸和破片质量等因素对冲击波绕流的影响规律。得到结论如下:
1)爆炸初期冲击波速度高于破片速度,在对破片加速的过程中,冲击波对高速破片存在绕流作用。
2)当预制破片端为破片群时,冲击波主要透过破片之间间隙,绕流至破片之前碰撞形成新的冲击波向前传播;而对于单一大破片,在破片前传播的冲击波主要是从破片两侧边缘绕流的冲击波在轴线附近碰撞产生,碰撞后对轴线上的冲击波有一定的加强。
3)当预制破片间存在间隙时,随破片间隙的增大,轴线方向的冲击波超压和比冲量增大,其波形和强度都越来越近似于裸药空爆的冲击波。
4)单一预制破片尺寸越大,冲击波对破片的绕流能力越差,绕流产生的冲击波强度随破片尺寸增大而逐渐降低。
5)迎爆面积不变,变化单一预制破片质量对绕流冲击波的波形及强度影响不大,但随破片质量增加,冲击波绕流过破片速度加快。
| [1] |
李伟, 朱锡, 梅志远, 等. 战斗部舱内爆炸对舱室结构毁伤的实验研究[J]. 舰船科学技术, 2009, 31(3): 34-37. DOI:10.3404/j.issn.1672-7649.2009.03.005 |
| [2] |
孔祥韶, 吴卫国, 李晓彬, 等. 圆柱形战斗部破片速度及等效装药特性研究[J]. 振动与冲击, 2013a, 32(9): 146-149. |
| [3] |
HUTCHINSON M D. The escape of blast from fragmenting munition casing[J]. Int J Impact Eng, 2009, 36(2): 185-192. DOI:10.1016/j.ijimpeng.2008.05.002 |
| [4] |
杨亚东, 李向东, 伯雪飞. 起爆方式对可变形定向战斗部威力的影响[J]. 南京理工大学学报, 2012, 36(5): 762-766, 772. DOI:10.3969/j.issn.1005-9830.2012.05.005 |
| [5] |
孔祥韶, 吴卫国, 杜志鹏, 等. 起爆点位置对战斗部爆炸破片特性的影响[J]. 哈尔滨工程大学学报, 2013b, 34(7): 855-861. |
| [6] |
梅志远, 沈全华, 朱锡, 等. 中小型水面舰船抗毁伤结构设计初探[J]. 中国舰船研究, 2007, 2(6): 68-72. DOI:10.3969/j.issn.1673-3185.2007.06.015 |
| [7] |
侯海量, 朱锡, 梅志远. 舱内爆炸载荷及舱室板架结构的失效模式分析[J]. 爆炸与冲击, 2007, 27(2): 151. DOI:10.3321/j.issn:1001-1455.2007.02.010 |
| [8] |
GONG Chao-an, CHEN Zhi-gang, YIN Li-kui. Analysis of movement laws of fragment and shock wave from a blast fragmentation warhead[J]. Journal of Measurement Science and Instrumentation, 2015, 6(3): 218-222. |
| [9] |
KONG X S, WU W G, LI J, et al. Experimental and numerical investigation on a multi-layer protective structure under the synergistic effect of blast and fragment loadings[J]. Int J Impact Eng, 2014, 65(3): 146-162. |
| [10] |
吕晓聪, 许金奈, 白二雷, 等. 弹片与爆炸冲击波耦合作用分析[J]. 解放军理工大学学报, 2007, 8(6): 640-644. |
| [11] |
李茂, 侯海量, 朱锡, 等. 冲击波和高速破片对固支方板的联合作用数值模拟研究[J]. 中国舰船研究, 2015, 10(6): 60-67. DOI:10.3969/j.issn.1673-3185.2015.06.009 |
| [12] |
穆朝民, 王仲琦, 赵衡阳, 等. 爆炸冲击波作用于墙体及对墙体绕射的实验研究[J]. 实验力学, 2008, 23(2): 169-174. |
| [13] |
郝莉, 马天宝, 王成, 等. 爆炸冲击波绕流的三维数值模拟研究[J]. 力学学报, 2010, 42(6): 1042-1049. |
| [14] |
赵蓓蕾, 崔村燕, 陈景鹏, 等. 网格密度对基于LS-DYNA的冲击波数值模拟影响[J]. 自动化与仪器仪表, 2015(9): 227-231. |
| [15] |
Livermore Software Technology Corporation. LS-DYNA Keyword User’s Manual [M]. California : Livermore Software Technology Corporation, 2003.
|
| [16] |
胡昌明, 贺红亮, 胡时胜. 45号钢的动态力学性能研究[J]. 爆炸与冲击, 2003, 23(2): 188-192. DOI:10.3321/j.issn:1001-1455.2003.02.017 |
| [17] |
陈长海, 朱锡, 侯海量, 等. 近距空爆载荷作用下固支方板的变形及破坏模式[J]. 爆炸与冲击, 2012, 32(4): 368-375. DOI:10.3969/j.issn.1001-1455.2012.04.005 |
| [18] |
张成亮, 朱锡, 侯海量, 等. 近距空爆下复合抗爆舱壁变形破坏模式试验研究[J]. 振动与冲击, 2014, 33(11): 33-37. |
| [19] |
孙业斌. 爆炸作用与装药设计[M]. 北京: 国防工业出版社, 1987.
|
 2019, Vol. 41
2019, Vol. 41
