0 引　言

通风孔等功能孔是水下航行器不可少的结构，随着水下航行器速度的提升，由流水孔孔腔振荡产生的流噪声成为不可忽视的因素。

在国内外已经有多位学者对孔腔流噪声展开了研究，首先是在气动声学领域，Lighthill^[1]推导了声类比方程，将流体噪声源等效为紧致极子声源，开创了声类比方法；Powell^[2]提出涡声理论，指出有涡结构的地方才有声音；Howe^[3]指出在极低马赫数下，孔腔气动流噪声的主要声源是由非定常阻力产生的偶极子声源；杨党国^[4]采用CFD计算和气动声学理论在来流马赫数为0.64条件下对长深比为2:1的空腔进行自激振荡发声机理研究，提出了腔内涡脱落-一次声波-新的涡脱落-二次声波的反馈机制发声机理。随着潜艇等水中航行器的发展，水动力声学也逐渐得到了重视和研究，对于水动力声学的研究在数值仿真方面也采用了与气动声学仿真类似的方法。Charib^[5]采用实验手段研究开口腔的水流激发振荡问题，指出了边界层动量损失厚度与流体开口腔振荡模式的关系；张楠^[6]中指出水中孔腔涡旋流场诱导辐射噪声的主要声源是偶极子声源；王玉^[7]提出陷落腔激发的涡流噪声包括低频纯音和宽带连续噪声，其中低频纯音主要由大尺度涡运动引起，声功率较高。高频辐射声呈现宽带特性，是由小尺度涡运动变化的结果；徐俊^[8]通过数值模拟得出空腔噪声的4个声源分别为：腔口剪切层小涡系列、后缘尾涡流系列、腔内大涡以及空腔后缘的涡流撞击与破碎，并且针对其分析结果给出了在孔腔内添加隔板的降噪方案；高岩等^[9]针对全开孔式孔腔模型对其声模态进行研究，对比了刚性壁以及弹性壁条件下的声耦合状况；陈灿^[10]通过大涡模拟-声类比混合方法进行数值模拟，得出来流速度的增大会加剧空腔的振荡，甚至会使孔腔由不振荡变为振荡，但是随着孔腔长深比的减小，振荡会逐渐减弱，说明潜艇流水孔的深腔结构设计在流场方面较为合理，因为深腔的振荡会比浅腔振荡更弱；Yuan Guo-qing^[11]采用大涡模拟-声类比混合方法对局部开孔的腔体模型进行仿真，对浅腔局部开孔腔体的流噪声激励机理进行研究，得到自持振荡反馈环是造成孔腔流噪声的原因。

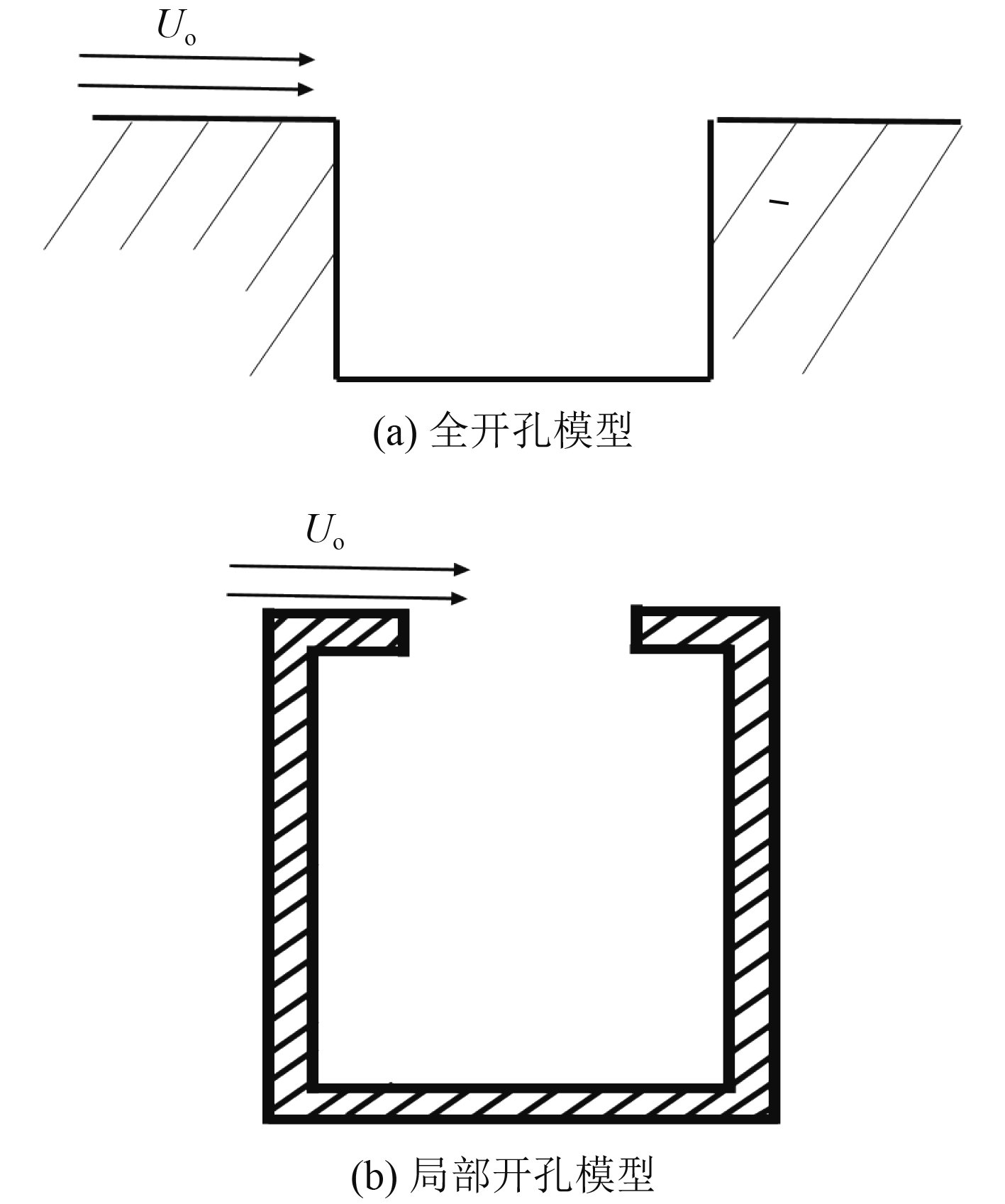
杨党国、王玉、徐俊、陈灿等采用的计算模型均为图1（a）所示的全开孔孔腔模型，Yuan Guo-qing采用的模型则为浅腔局部开孔模型（长深比6:1），与水下航行器潜浮系统的实际模型中采用的局部开孔深腔模型均有较大差异。本文采用大涡模拟-声类比混合方法对图1（b）所示的局部开孔深腔模型的孔腔流噪声发声机理进行研究，根据流场涡量、压强变化以及孔后壁检测点脉动压力的周期、相位异同，结合空腔内声学模态，对局部开孔深腔模型（长深比<1）的孔腔流噪声的发生机理进行研究。

1 数值求解方法 1.1 大涡模拟

湍流N-S方程由于方程的不封闭，因此不能进行解析求解，所以对于N-S方程的求解都采用了数值计算方法。直接数值模拟方法（DNS）、雷诺平均N-S方程方法（RNS）、大涡模拟方法（LES）是目前研究湍流和工程应用的3种方法，其中LES综合考虑了计算机资源和计算精度，对湍流进行过滤，分离湍流中的大涡和小涡，其中大尺度涡在湍流中起主要作用，而小尺度涡则采用特殊方法进行封闭。

大涡模拟采用过滤方法来消除湍流中小尺度脉动，在物理空间中，过滤过程采用积分运算来实现。积分过程可用如下公式表示：

$ \overline {{u_i}} (x,t) = \frac{1}{{{\Delta ^3}}}\int_{ - \frac{\Delta }{2}}^{\frac{\Delta }{2}} {\int_{ - \frac{\Delta }{2}}^{\frac{\Delta }{2}} {\int_{ - \frac{\Delta }{2}}^{\frac{\Delta }{2}} {{u_i}\left( {\xi ,t} \right)G\left( {x - \xi } \right)} } } {\rm d}{\xi _1}{\rm d}{\xi _2}{\rm d}{\xi _3}\text{。}\!\!\!\! $

(1)

其中： $\Delta $ 为积分立方体的边长，其大小称为过滤长度； ${u_i}\left( {\xi ,t} \right)$ 为样本瞬时速度； ${\bar u_i}\left( {x,t} \right)$ 为过滤后的大尺度速度； $G\left( {x - \xi } \right)$ 为过滤函数，其表达式如下：

$G\left( {x - \xi } \right) = \left\{ \begin{array}{l} 1,\left| \eta \right| \leqslant \Delta /2\text{，}\\ 0,\left| \eta \right| > \Delta /2\text{。} \end{array} \right.$

(2)

经过过滤函数之后，湍流速度场或其他湍流流量过滤后仍然为不规则量，只是这些不规则量中小尺度脉动已经过过滤，只剩下尺度大于 $\Delta $ 的脉动。经过滤后的N-S方程（大涡模拟控制方程）如下：

$\frac{{\partial \rho }}{{\partial t}} + \frac{\partial }{{\partial {x_i}}}\left( {\rho \overline {{u_i}} } \right) = 0\text{，}$

(3)

$\frac{\partial }{{\partial t}}\left( {\rho \overline {{u_i}} } \right) + \frac{\partial }{{\partial {x_j}}}\left( {\rho \overline {{u_i}} \overline {{u_j}} } \right) = \frac{\partial }{{\partial {x_j}}}\left( {\nu \frac{{\partial {\sigma _{ij}}}}{{\partial {x_j}}}} \right) - \frac{{\partial \overline p }}{{\partial {x_i}}} - \frac{{\partial {\tau _{ij}}}}{{\partial {x_j}}}\text{。}$

(4)

其中： $i,j = 1,2,3$ ； ${u_i}$ 为与 ${x_i}$ 关联的速度分量； $\overline {{u_i}} $ 为过滤后的平均速度分量； $\rho $ 为流体密度； $\nu $ 为流体运动粘性系数； ${\tau _{ij}}$ 为亚格子应力： ${\tau _{ij}} = \rho \overline {{u_i}} \overline {{u_j}} - \rho \overline {{u_i}{u_j}} $ 。

1.2 FW-H声类比

FW-H方程本质上是非齐次方程，其可以从连续方程以及N-S方程中演化得来，FW-H方程如下：

$ \begin{split} & \frac{1}{{a_0^2}}\frac{{{\partial ^2}p'}}{{\partial {t^2}}} - {\nabla ^2}p' = \frac{{{\partial ^2}}}{{\partial {x_i}\partial {x_j}}}\left\{ {{T_{ij}}H\left( f \right)} \right\} - \\ & \frac{\partial }{{\partial {x_i}}}\left\{ {\left[ {{P_{ij}}{n_j} + \rho {u_i}\left( {{u_n} - {v_n}} \right)} \right]\delta \left( f \right)} \right\} + \\ & \frac{\partial }{{\partial t}}\left\{ {\left[ {{\rho _0}{v_n} + \rho \left( {{u_n} - {v_n}} \right)} \right]\delta \left( f \right)} \right\}\text{。} \end{split} $

(5)

其中： ${u_i}$ 为在 ${x_i}$ 方向上的流体速度分量； ${u_n}$ 为垂直于 $f = 0$ 平面的流体速度分量； ${v_i}$ 为在 ${x_i}$ 方向上的物体速度分量； ${v_n}$ 为垂直于物面方向的物体速度分量； $\delta \left( f \right)$ 为狄拉克函数； $H\left( f \right)$ 为阶跃函数； $p'$ 为远场声压。 $f = 0$ 为物体表面， $f > 0$ 物体外部无界空间； ${a_0}$ 为远场声速， ${\rho _0}$ 为远场密度， ${T_{ij}}$ 为Lighthill应力张量：

$ {T_{ij}} = \rho {u_i}{u_j} + {P_{ij}} - a_0^2\left( {\rho - {\rho _0}} \right){\delta _{ij}}\text{，} $

其中， ${P_{ij}}$ 为压应力张量。对于当前模型而言，来流速度较小，因此可以忽略四极子声源的影响，且物面为静止的无穿透的，有

$ p' = {p'_T}\left( {\vec x,t} \right) + {p'_L}\left( {\vec x,t} \right)\text{。} $

(6)

其中：

$ {p'_L} = \frac{1}{{4{\text{π}} }}\left\{ {\frac{1}{{{a_0}}}\int\limits_{f = 0} {\left[ {\frac{{{{\dot L}_r}}}{r}} \right]} {\rm d}S + \int\limits_{f = 0} {\left[ {\frac{{{L_r} - {L_M}}}{{{r^2}}}} \right]} {\rm d}S} \right\}\text{，} $

$ {p'_T} = \frac{1}{{4{\text{π}}}}\left\{ {\int\limits_{f = 0} {\frac{{{\rho _0}\left( {{{\dot U}_n} + {U_n}} \right)}}{r}} {\rm d}S} \right\}\text{，} $

$ {U_i} = {v_i} + \frac{\rho }{{{\rho _0}}}\left( {{u_i} - {v_i}} \right)\text{，} $

$ {L_i} = {P_{ij}}{\hat n_j} + \rho {u_i}\left( {{u_n} - {v_n}} \right)\text{。} $

对于本文中实例而言，有 ${v_i} = 0$ 。

1.3 计算模型与CFD计算参数设置

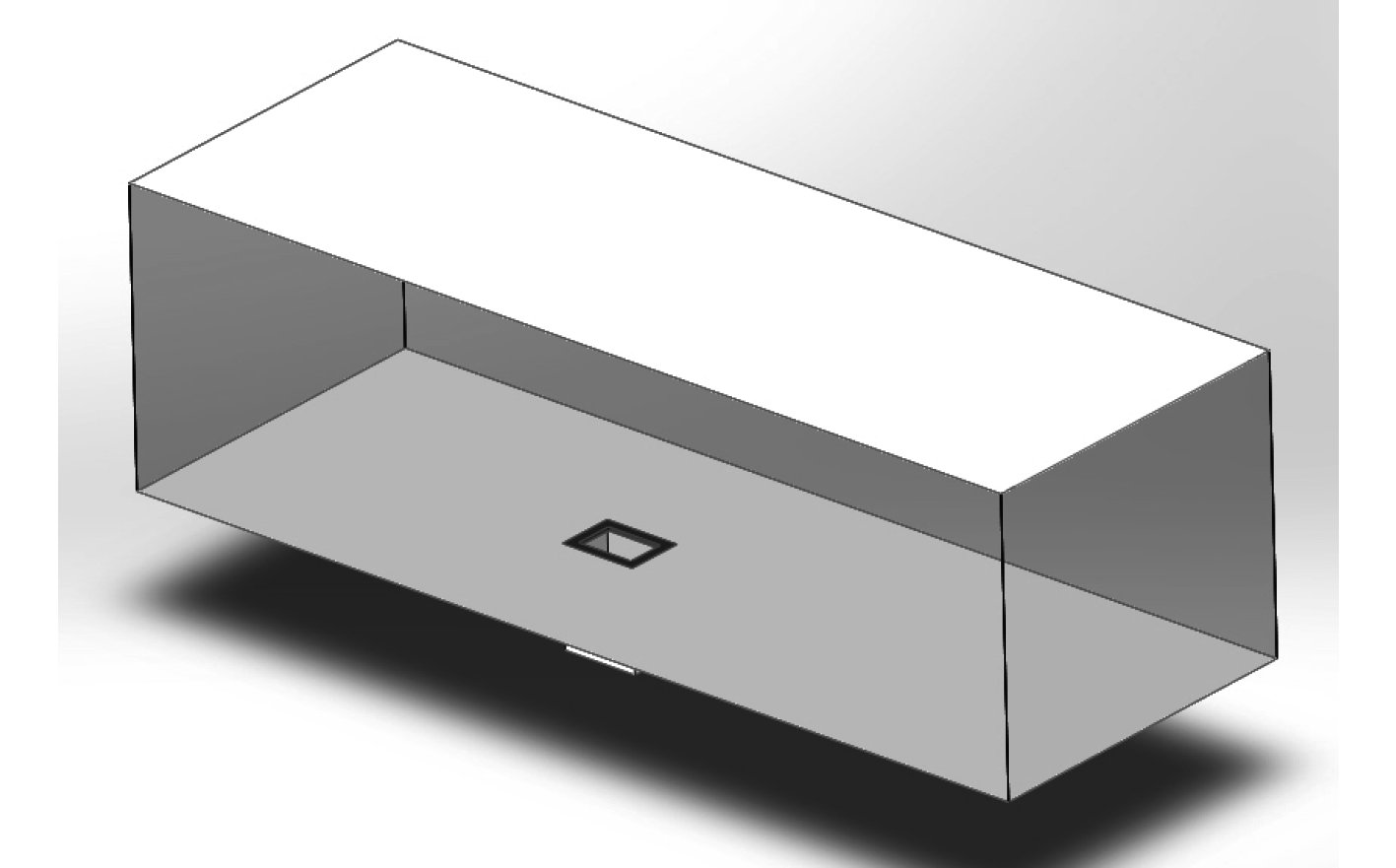
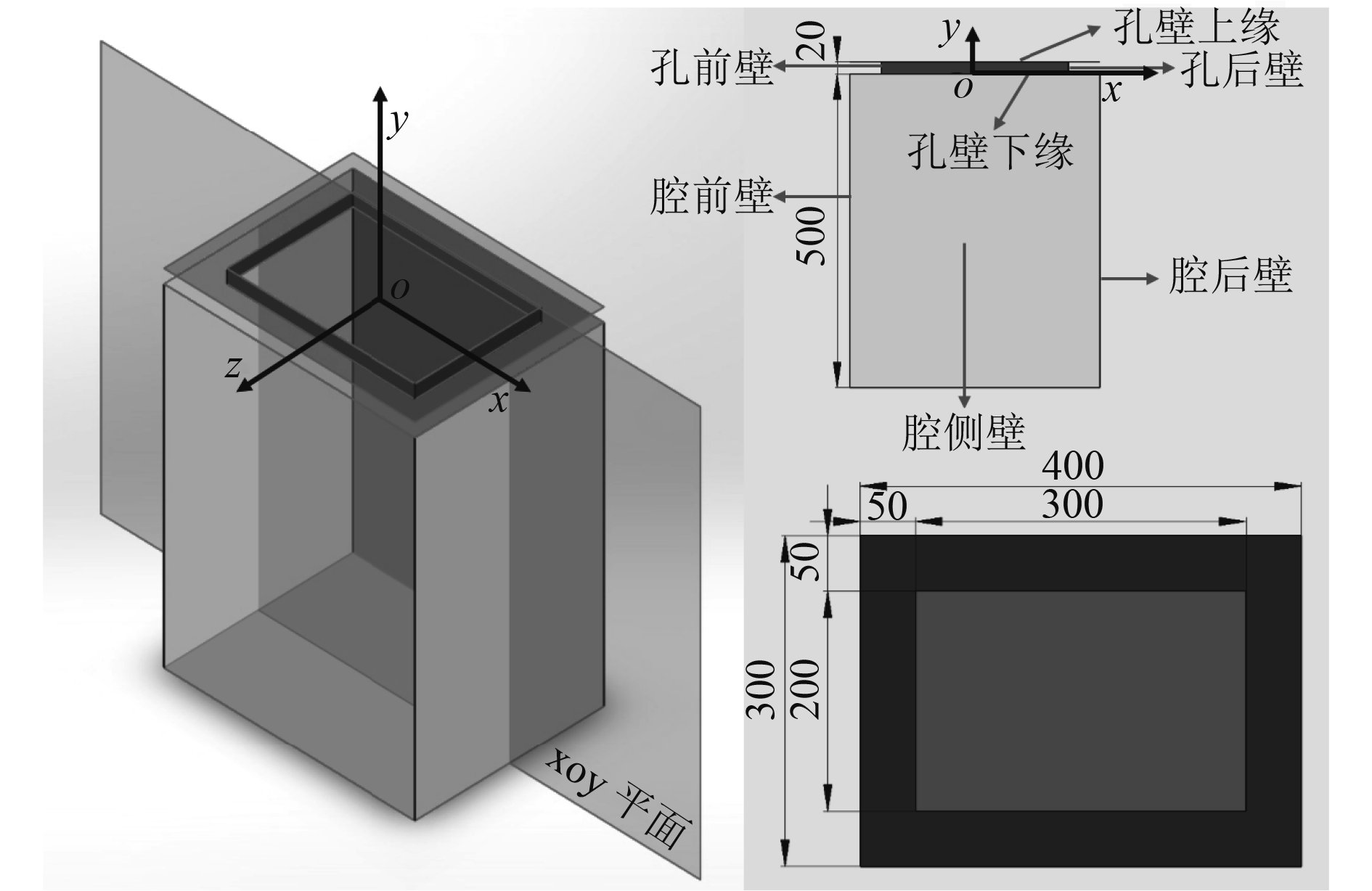
结合水下航行器实际情况，将计算模型等效为带有局部开孔的深腔模型，如图2所示。长宽深分别为L=400 mm，W=300 mm，H=500 mm，其中开孔长宽L_hole=300 mm，W_hole=200 mm，孔颈高度为H_hole=20 mm，按照Sarohia^[12]所提出的划分标准，该模型为深腔模型（长深比<1）。图3所示为深腔模型计算区域，其中计算区域模型尺寸为5 000 mm×1 800 mm×1 500 mm，开口中心距计算域前端及两侧的距离分别为2 000 mm和900 mm。采用SolidWorks进行建模，导入ICEM CFD中进行网格划分。整个计算模型的网格总数为1 676 229，第1层网格距离为0.03，全域采用结构化网格离散，为了在保证仿真准确性同时减少计算量，如图4所示，对边界层网格、腔体开口处进行加密处理。

边界条件设置如图4所示。

速度入口：设定来流的大小为10 m/s，方向与X轴方向平行；

压力出口：设定相对于参考压力为0；

壁面：腔体壁面设置为无滑移光滑壁面；除腔体壁面之外的其余壁面为自由滑移壁面。

2 计算分析

在CFD软件Fluent中，先选用大涡模拟模块进行计算，待计算稳定后，打开FW-H声计算模块，设置局部开口腔体为声源，进行声场计算。

为方便结果分析，在计算过程中布置多个监测点对流场中的孔壁、腔壁压强的变化情况进行监测，在开口中心正上方处布置一个接收点receiver1，坐标为[0，1 020，0]，对声场中声压进行监测，并做图2所示切面xOy，对仿真过程中切面xOy上的流场涡量、压强变化情况进行分析。

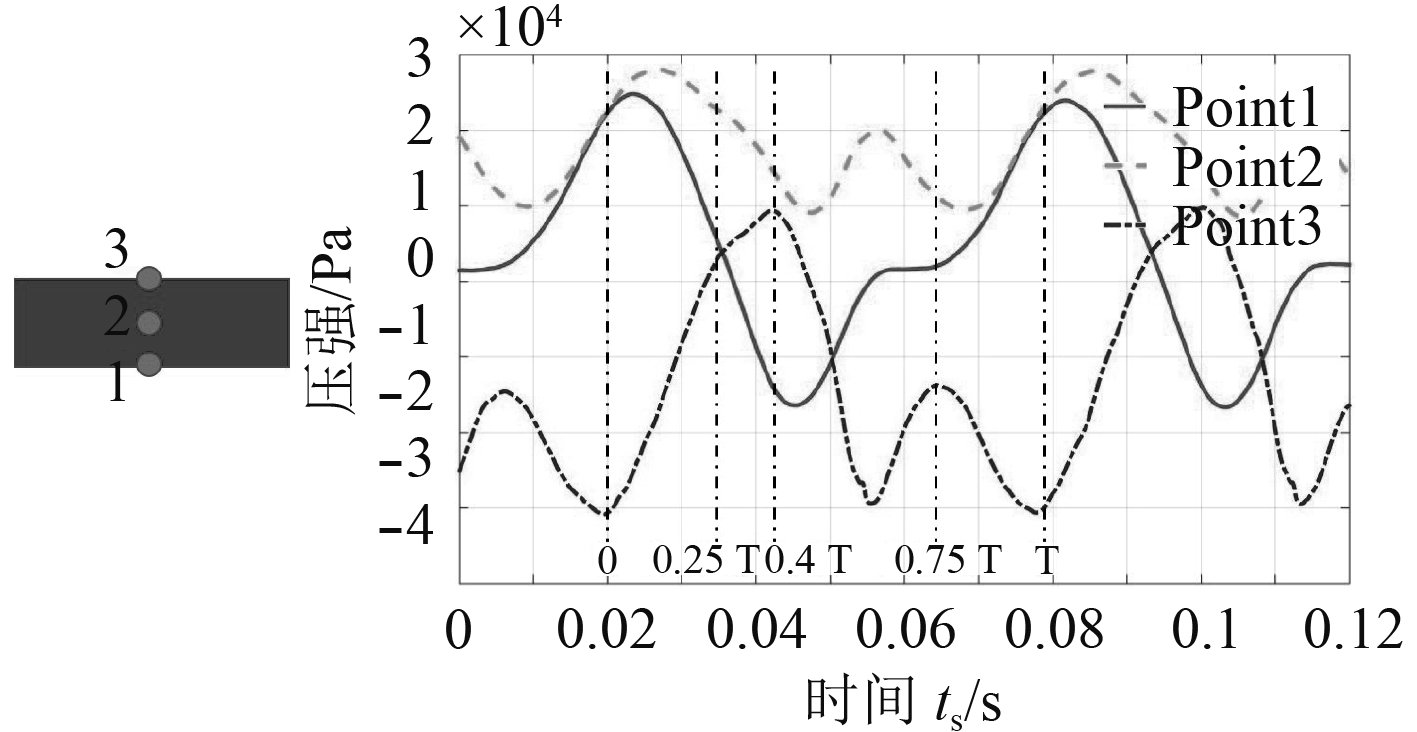
2.1 流场分析

如图5左侧所示，1，2，3点分别为图2中所示孔后壁的垂向中线处的点，监测点1，2，3随时间变化的压强脉动信息变化如图5右侧所示，各监测点压力变化周期相同，但是其相位不同，其中1点和3点相位差值接近π。

当来流流经开口前缘时，由于开口的存在导致来流在开口前缘处发生边界层分离，不断产生一系列分离涡，在来流带动下不断向孔后壁方向运动迁移，来流在运动过程中与壁面发生碰撞，从而引起壁面压强的变化。取点3压力达到最小值的t_S=0.02时刻为周期起点t=0，每个周期时长用T表示，结合时域内流体运动、声场内声波传播、声压变化等因素，对腔体开孔处的涡量、压强周期性变化及不同监测点之间的脉动周期相同、相位不同的原因进行分析。

t=0时刻xOy切面上流场涡量-压强分布云图如图6所示。在t=0时刻，此时孔壁上缘3点附近涡量分布集中，下缘1点处涡量分布较少。由涡运动相关知识可知，在漩涡中，由于离心力被压力所平衡，涡核处离心力最低，压力也最小，所以此时在开口上缘区域压强分布较小，下缘区域压强分布较大。但是由于涡运动对开口上缘附近壁面产生较大冲击，有较大脉动压力，等效为偶极子声源，此时在孔后壁上缘处所产生的声压也较大，随着声波向孔前壁方向传播，对涡结构运动产生排挤，促使后续向孔后壁迁移的涡结构同时向开口下缘移动。

t=0.25 T时刻xOy切面上流场涡量-压强分布云图如图7所示。在上一时刻腔体后壁上缘声源所产生声压的作用下，涡结构向孔后壁移动的同时，逐渐向下缘移动，且随着涡的不断耗散和向后移动，在孔后壁上缘的涡量得不到补充，因此上缘涡量分布减少，而下缘的涡量分布增多。在涡的作用下，下缘1点处附近的压强减小，上缘3点处附近的压强增大，虽然此时3点附近下缘区域的涡量分布增大，对下缘作用产生的脉动压力也增大，但是由此声源产生的声压仍小于由上缘壁面产生的声压，因此在壁面上缘声源产生的大声压作用下，向孔后壁迁移的涡结构继续向开口下缘移动。

t=0.4 T时刻xOy切面上涡量-压强分布云图如图8所示。随着孔壁上缘涡的不断耗散，同时由孔前壁向后壁移动的涡向下缘移动，在孔后壁上缘3点处的涡量持续得不到补充，因此上缘3点处的涡量分布达到周期内的最小值，周边压强较大。而下缘1点处由于涡的持续补充，此时涡量达到较大值，周边压强较小。同理，由于此时在孔后壁下缘处的涡量较大，涡结构运动过程中对开口下缘腔壁造成冲击，产生较大脉动压力，从而作为声源产生较大声压，随着声波向开口前缘传播，对向后运动的涡结构产生排挤，导致向孔后壁迁移的涡结构逐渐向开口上缘移动。

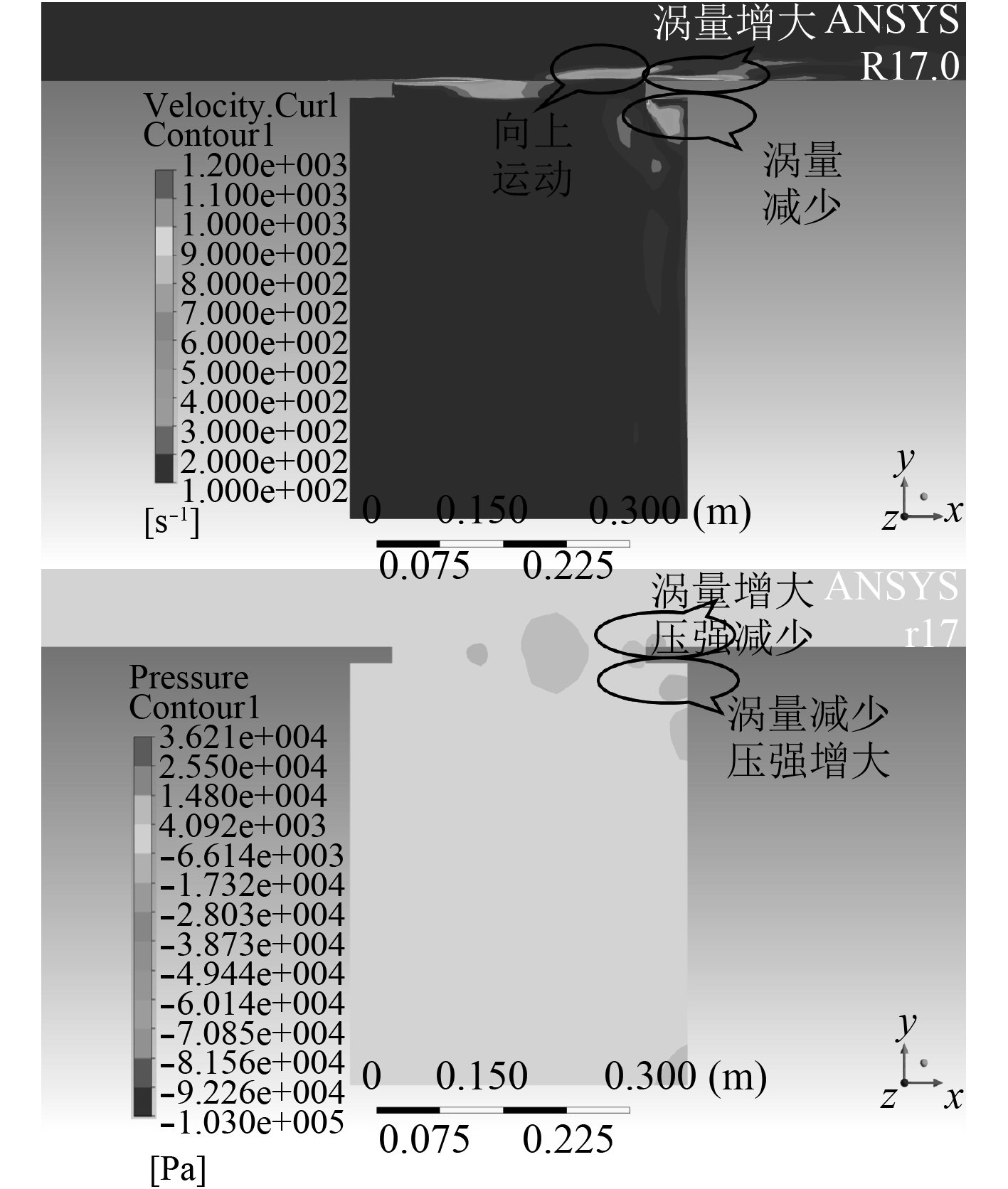
t=0.75 T时刻xOy切面上涡量-压强分布云图如图9所示。由于孔后壁腔体下缘发声产生的声压随着声波向孔前壁方向传播对涡结构产生排挤，因此从孔前壁向后壁迁移的涡逐渐向开口上缘移动，1点处的涡量得不到补充，分布减少，3点处的涡量分布增多，因此1点附近压强增大，3点周边压强减小，此时涡在孔壁下缘声源大声压作用下，继续向开口上缘移动。

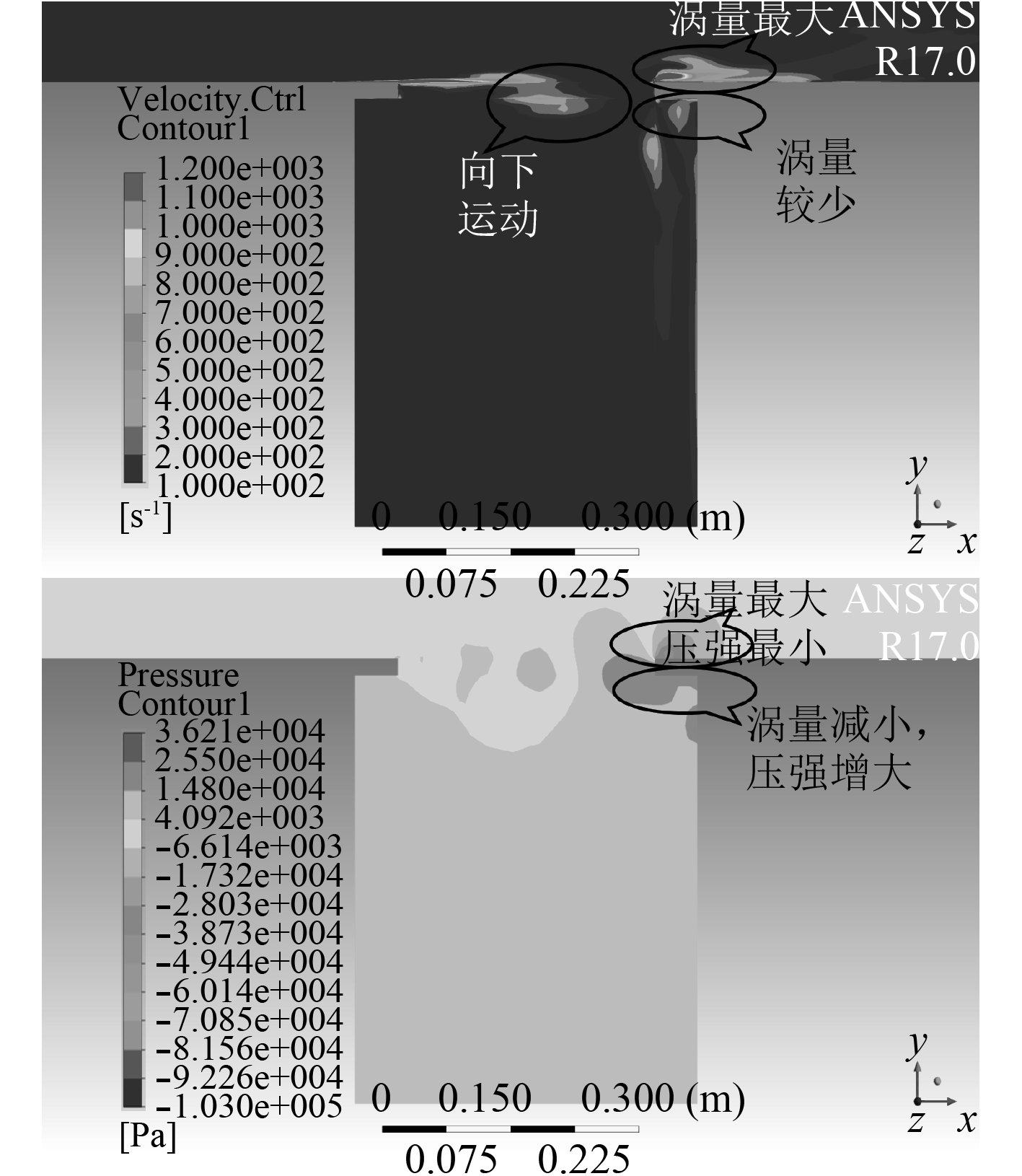
t=T时刻xOy切面上涡量-压强分布云图如图10所示。此时在腔体下缘的涡量分布达到较小值，1点附近压强达到较大值，而在开口上缘3点出的涡量分布达到最大值，附近压强达到最小值，与t=0时刻一致。此时由于上缘涡量分布集中，涡结构运动产生的压力脉动在腔体后缘作为声源产生较大声压，随着声波向前传播，对涡结构移动产生排挤，致使由开口前缘向孔后壁迁移的涡向后迁移的同时向开口下缘移动，从而进入下一个涡结构运动周期。

从以上分析可得，流体在流经开口时，由涡上（下）运动—碰撞发声—涡下（上）运动—碰撞发声—涡上（下）运动整个过程构成的涡-声反馈是造成腔体脉动压力周期性变化及不同相位的主要原因。

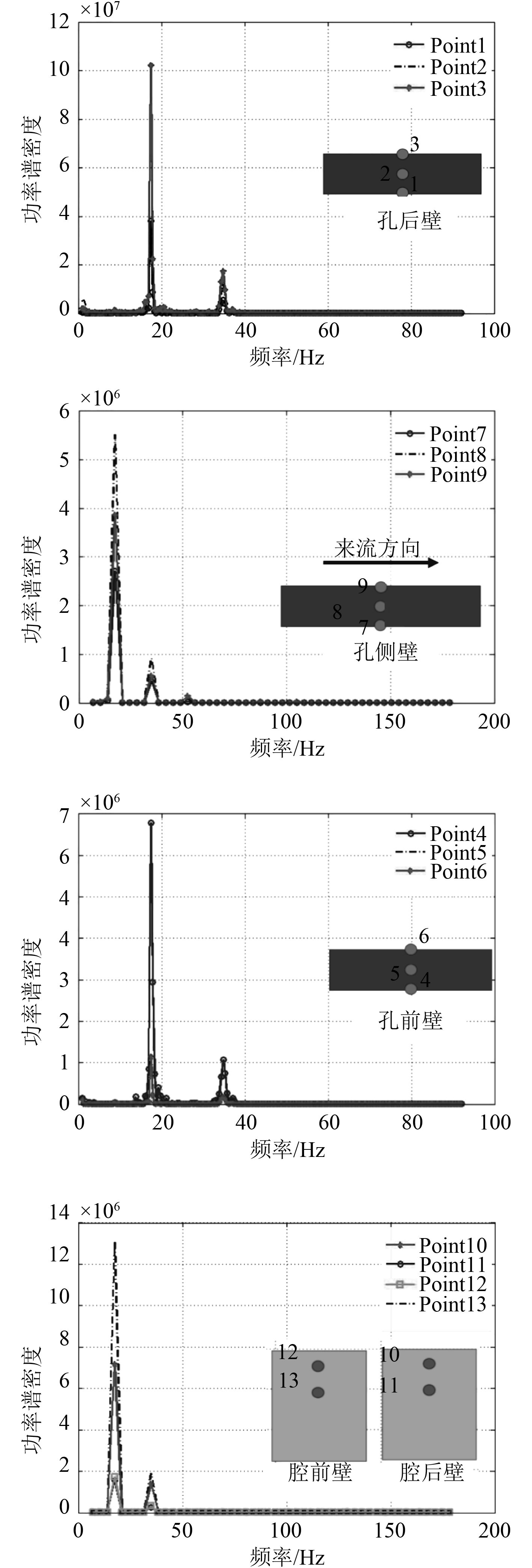
2.2 受力分析

从图5可以看出，各个监测点之间的周期一致均为T=0.057 5 s，即期频率为f_测=1/T=1/0.057 5 s=17.4 Hz。图11为各监测点的压强功率谱曲线，其中点1，2，3位于图2所示孔后壁，点4，5，6位于孔前壁，点7，8，9位于孔侧壁，点10，11和12，13分别位腔后壁和腔前壁。从图中可以得出各个监测点拥有相同频率的特征线谱，1阶特征线谱频率为 ${f_{p1}} = 17.4 $ Hz，2阶特征线谱频率为 ${f_{p2}} = 34.9 $ Hz，说明其所受来自流体的压力频率一致。但是孔后壁的1阶、2阶特征线谱峰值远大于开孔前壁、孔侧壁及开口下方腔体壁的压强功率谱峰值，在孔后壁的上缘点3功率谱密度远高于其他采集点的功率谱密度，表明孔壁后缘压力脉动是声场能量的主要来源，其中以上缘对其影响最大，即孔后壁上缘是开口自持振荡发声的主要声源。

2.3 声场分析

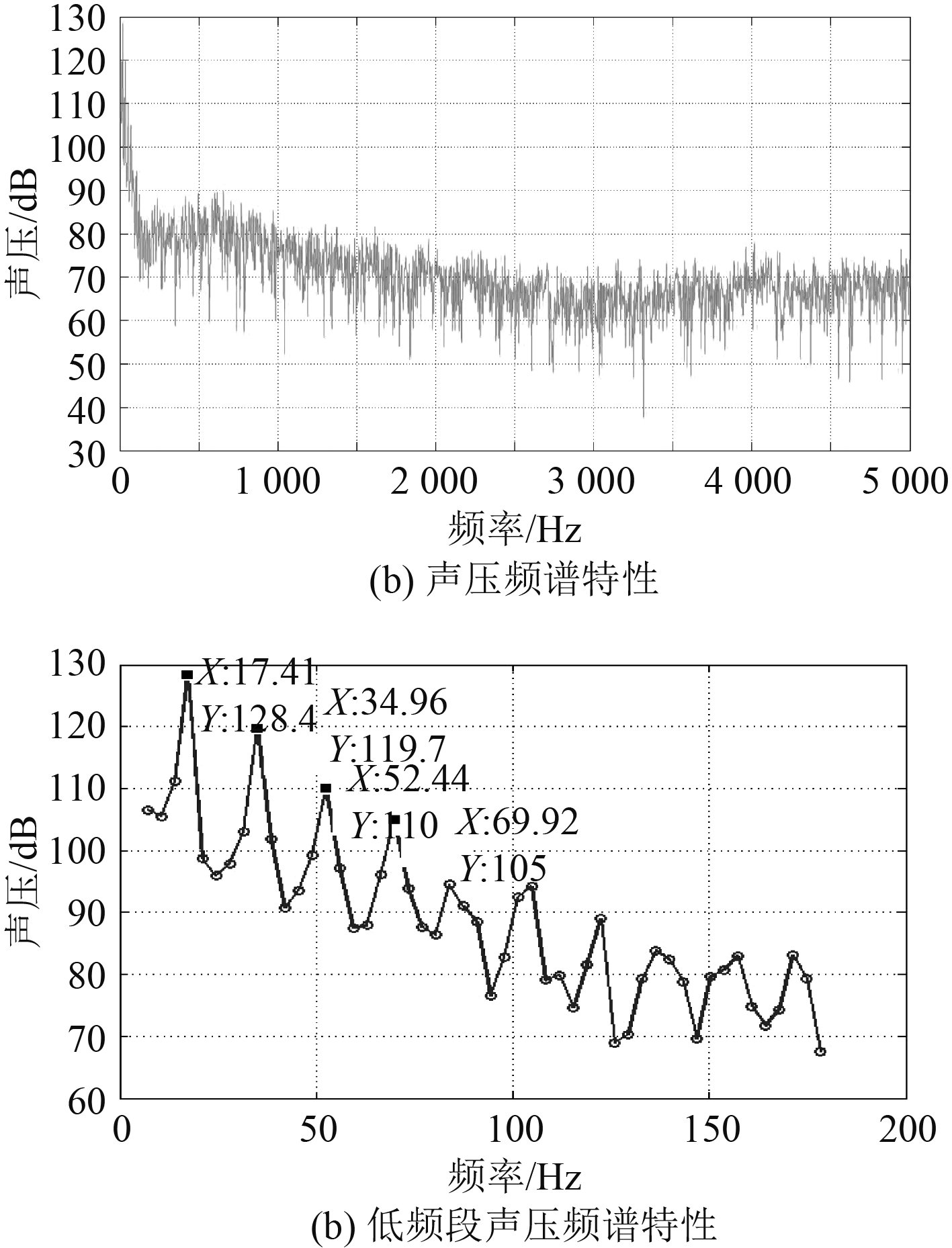
图12（a）为开口正上方1 000 mm（2倍腔体深度）处接收点receiver1的声压频谱特性曲线，截取其中的低频成分进行分析，如图12（b）所示，该声压频谱的前2阶频率分别为 ${f_{s1}} = 17.41 $ Hz， ${f_{s1}} = $ 34.96 Hz，与各采集点压强功率谱的前2阶特征线谱频率一致，说明由流体产生的压力脉动为其主要声源。

由于该腔体为局部开孔腔体，且为深腔，满足声波模态出现的条件^[13]，因此需要考虑某一特定频率下出现孔腔声模态共振现象所导致相应频率上强烈的波动对测量结果的影响。在孔腔内声场模态的简正频率满足：

${f_n} = \frac{{{c_0}}}{2}\sqrt {{{\left( {\frac{{{n_1}}}{L}} \right)}^2} + {{\left( {\frac{{{n_2}}}{B}} \right)}^2} + {{\left( {\frac{{{n_3}}}{H}} \right)}^2}}{\text{。}} $

(7)

式中： ${n_1} = 0,1,2,3 \cdot \cdot \cdot $ ； ${n_2} = 0,1,2,3 \cdot \cdot \cdot $ ; ${n_3} = 0,1,2,3 \cdot \cdot \cdot $ ；对其声波模态进行求解，得到该腔体最低阶声波模态频率为1 500 Hz，远大于接收点所测得的各低阶模态的频率。对比图12（a）可得，在1 500 Hz没有出现特征线谱，因而可以排除腔体声耦合共振对接收点receiver1所测各阶模态的影响。

Rossiter JE^[14]最早对矩形开口腔体绕流振荡机理进行研究，并给出自持振荡频率预测半经验公式：

$ {f_n} = \frac{{{U_\infty }}}{{{L_{hole}}}}\frac{{n - \alpha }}{{{M_a} + 1/{k_c}}}\text{。} $

(8)

其中： $\alpha {\rm{ = }}0.25$ ； ${k_c} = 0.57$ ； ${U_\infty } = 10$ m/s； ${L_{hole}} = 0.3$ m。根据本文实例计算可得 ${f_1}{\rm{ = 14}}{\rm{.29}}$ Hz，仿真计算得到的 ${f_{s1}} = 17.41 $ Hz，与经验公式的预测结果基本吻合，验证了本文仿真结果的准确性。

3 结　语

本文通过大涡模拟-声类比混合方法，进行数值仿真，对局部开孔深腔体的流噪声产生机理进行分析。

1）根据仿真得到一个周期内空腔内部各个时刻的涡量、压强分布云图，首次对孔后壁不同监测点脉动压力变化的周期、相位异同之处进行监测分析，用涡上（下）运动—碰撞发声—涡下（上）运动—碰撞发声—涡上（下）运动的涡-声反馈模型解释孔腔流噪声发声机理。

2）对各个采集点的压强功率谱密度进行对比分析，得出局部开孔深腔的各个部位对声场能量的贡献量不同，其中开孔后壁的贡献量最大。

3）将计算结果与Rossiter经验公式的计算结果进行对比，验证了仿真结果的准确性。