2. 华中科技大学 船舶与海洋工程学院,湖北 武汉 430074
2. School of Naval Architecture and Ocean Engineering, Huazhong University of Science and Technology, Wuhan 430074, China
随着各国海军舰船需求的不断提升以及民用新船型的不断开发,对舰船在极端情况下的强度要求越来越高。舰船总强度是船舶设计人员首要关心的重要问题,现行设计和研究船舶总强度时一般只计及波浪载荷、抨击及上浪载荷等外载荷,而对于军用舰船以及如浮式核电船等特殊船舶,水下爆炸下的舰船总强度问题不容忽略。与一般外载荷下的船体总纵强度问题相比,水下爆炸下的舰船总强度必须要计及冲击振动弯矩的影响,其数量级甚至比波浪载荷诱导下船体总纵弯矩更高。因此本文针对船体水下爆炸冲击振动弯矩进行研究。
水下非接触爆炸载荷通常分为冲击波和气泡脉动载荷,冲击波压力峰值高持续时间短,而气泡脉动压力峰值较低持续时间长,二者先后共同作用于船体造成船体毁伤效应。水下爆炸载荷作用下船体的动态响应问题前人已有了不少研究[1 – 4],主要集中在对于水下爆炸气泡脉动下的船体鞭状振动问题的研究,且并没有经过实船试验验证。结合当前理论与试验研究,本文针对水下爆炸船体冲击振动弯矩问题进行研究,应用泰勒平板流固耦合理论[5]基于模态叠加理论的船体梁模型对船体冲击振动弯矩进行快速化预报,在预报多种船型的基础上探索冲击振动弯矩的规律,并给出冲击振动弯矩的经验公式,为工程设计人员的初步设计校核提供参考。
1 水下爆炸船体冲击动弯矩分析 1.1 简化模型水下爆炸作用下船体主要受重力、浮力、爆炸载荷、船体惯性力等综合作用,静水中重力和浮力是一对平衡力,船体振动引起浮力的变化可简化为浮力弹簧的形式模拟,船体所受爆炸载荷需要考虑船体水下爆炸作用下流固耦合作用,惯性力由达朗贝尔原理得到。采用船体惯性矩等效和质量等效形式把船体等效为变截面等值船体梁,这样等值梁在爆炸载荷、浮力变化力和惯性力的联合作用下产生冲击振动弯矩。其中,垂向附连水质量采用陶德经验公式计算,浮力弹簧根据船体水线面面积近似求得。船体梁模型如图1所示,经模态分析确保船体梁模型的有效性。

|
图 1 水下爆炸船体梁模型示意图 Fig. 1 Schematic diagram of ship hull girder underwater explosion |
舷外水对船体水下爆炸的影响主要体现3个方面:船体振动引起浮力与重力的不平衡,船体附连水质量以及船体所受爆炸载荷需要考虑船体运动的影响。
舰船在遭受水下非接触爆炸载荷作用下产生的船体垂向振动响应会引起浮力变化,这种变化也应计入船体剖面动弯矩计算。采用弹簧等效的方法来模拟此种变化,以弹簧刚度值来代替每站单位吃水引起的浮力变化。船体因冲击载荷在垂向的位移响应导致的吃水变化微小,故采用船体各站水线面在垂向的单位长度的浮力近似代替实际的浮力变化。由此得出水线面各站的弹簧所模拟的刚度计算式:
| $ K = \rho Ag\text{。} $ | (1) |
式中:
舷外水影响的另一个重要方面是附连水质量,采用托德公式通过查表求得,单位长度附连水质量的表达式为:
| $ {m_{av}} = \frac{1}{2}{C_v}{K_i}\rho \pi {b^2}\text{。} $ | (2) |
式中:ρ为水的密度,取1 025 kg/m3;
水下爆炸载荷的确定是舰船冲击动弯矩分析计算的重要方面。前人对爆炸载荷进行了大量的研究,有代表性的是Geers and Hunter模型[7],对水下爆炸冲击波与气泡载荷均有较好的描述,本文中冲击波以经验公式,气泡模型以Geers and Hunter模型公式为基础计算水下爆炸自由场中压力载荷,根据泰勒平板方程来计及船体运动对船体载荷的影响,并且忽略水面截断效应以及冲击波透射作用的影响[8 – 9]。应用Taylor平板理论求解流固耦合界面处的压力方程为:
| ${P_t}(x,y,t) = 2{P_i}(x,y,t) - \frac{{\rho cv(t)}}{{\cos \alpha (x,y)}}\text{。}$ | (3) |
式中:
式(3)为爆炸载荷计算公式为单元载荷,考虑将每站单元力的叠加,计及波传播的延时效果,通过编写程序计算可迭代出船体每站的激励载荷。根据文献[10]中–3.0 MPa的空化临界压力,本文的爆炸载荷不计空化的影响。
1.3 模态叠加法求解冲击动弯矩采用有阻尼多自由度系统受迫振动的运动方程
| $ { M}\ddot u + { C}\dot u + { K}u = F(t)\text{。} $ | (4) |
式中:M为质量矩阵;C为阻尼阵;K为刚度矩阵。
经过模态阵型的坐标变换,即
| ${{ \varPhi} ^{\rm T}}{ M}{ \varPhi} \ddot q + {{ \varPhi} ^{\rm T}}{ C}{ \varPhi} \dot q + {{ \varPhi} ^{\rm T}}{ K}{ \varPhi} q = {{ \varPhi }^{\rm T}}F(t)\text{。}$ | (5) |
式中:
联立式(3)和式(5),即船体外壳某站所受载荷方程与船体振动方程联立求解出船体梁响应和船体所受载荷,同时联立动弯矩的微分方程,得到如下迭代公式:
| $\left\{ \begin{aligned} & {{F_z}({t_i}) = \{ \sum [ 2P(x,y,{t_i}) - \displaystyle\frac{{\rho c\dot u({t_{i - 1}})}}{{\cos \alpha (x,y)}}\delta (x,y,t)] \cdot S{}_z\} }\text{,}\\ & {{ M} = EI\Phi {q^{''}}}\text{,}\\ & {\left[{ M} \right]\left[ {\ddot u({t_i})} \right] + \left[ C \right]\left[ {\dot u({t_i})} \right] + \left[ K \right]\left[ {u({t_i})} \right] = \left[ {{F_z}({t_i})} \right]}\text{。} \end{aligned}\right. $ | (6) |
式中:
采用纽马克平均加速度法迭代求解上述方程式[11],可获得满足工程应用的船体梁响应特性的数值解。
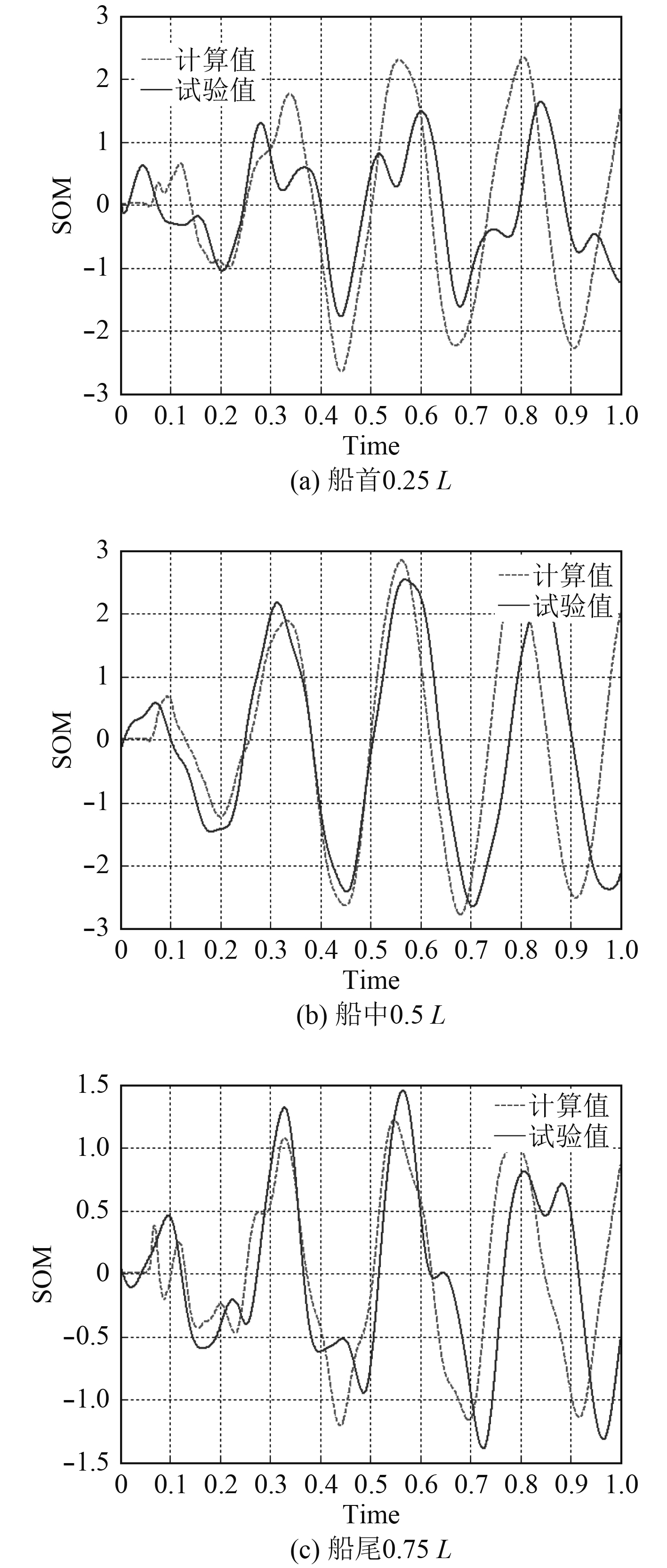
1.4 试验验证以某实船试验为例,选取冲击因子为0.55,工况为船中右舷一侧横向偏离50 m,爆点攻角为30°,其中阻尼采用经典阻尼,取文献[12]中相似船型的阻尼比0.04,经过编程计算出等值梁在爆炸载荷作用下各典型横剖面无量纲化取前3阶总和的动弯矩,并与无量纲化的实船试验值对比分析,如图2和表1所示。
|
图 2 动弯矩对比图 Fig. 2 The contrast diagram of shock vibration bending moment |
|
|
表 1 动弯矩对比表 Tab.1 The comparison chart of shock vibration bending moment |
通过对比可知采用该理论计算值与实验值在船中处吻合较好,误差在10%以内,首部1/4处计算值偏小约30%。船尾1/4处计算值偏大约20%,误差在工程应用可接受的范围之内。由于该方法理论模型简单,计算过程程序化,可在工程精度范围内快速计算船体水下爆炸载荷作用下的动弯矩,并能够应用于初步设计中计及水下爆炸冲击动弯矩的总强度校核。
2 不同船型的冲击动弯矩工程化预报针对不同船型的冲击动弯矩进行快速化工程预报,以6艘不同船型和排水量的舰船作为典型计算模型,设置多种水下爆炸工况,分别计算各型舰船在不同工况下的冲击动弯矩,将结果进行分析对比,探究冲击动弯矩随在不同水下爆炸工况的变化规律,以及动弯矩在相同工况下随舰船标准排水量变化的规律。
2.1 参数设置选择6种不同排水量的舰船分析在相同水下爆炸载荷作用下的冲击动弯矩,表2为各船的基本参数。
|
|
表 2 各舰船的主要参数 Tab.2 Main parameters of typical ships |
各船分别设置4种不同冲击因子的计算工况,药包质量为1 000 kg,药包的位置设置在各船船中剖面处,攻角统一设定为45°,采用龙骨冲击因子,不同工况下的具体参数设定如表3所示,表达式如下式:
|
|
表 3 水下爆炸工况参数设置表 Tab.3 Parameter of conditions underwater explosion |
| $ C = \frac{{\sqrt W }}{{{R_1}}} \times \frac{{1 + \sin \beta }}{2}\text{。} $ | (7) |
式中:
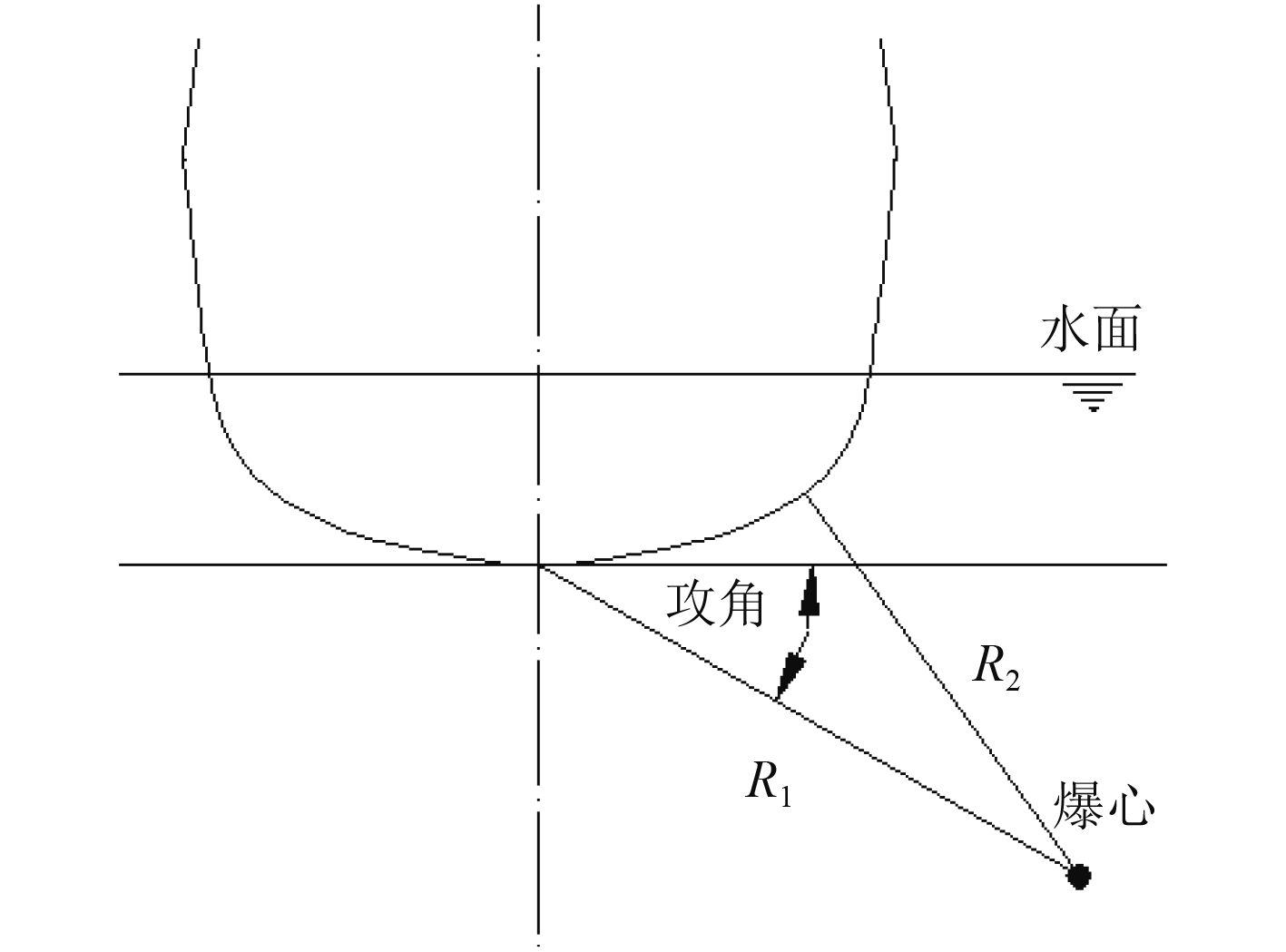
|
图 3 冲击因子工况示意图 Fig. 3 Schematic diagram of keel shock factor (KSF) |
计算得到不同工况下6个船型3个典型剖面的动弯矩,以船A在冲击因子为0.3工况下的动弯矩为例,其各剖面的前3阶总动弯矩如图4所示。

|
图 4 船A冲击动弯矩(KSF=0.3) Fig. 4 Shock vibration bending moment of ship A (KSF=0.3) |
由图4可知,船A在水下爆炸冲击因子为0.3工况下的冲击动弯矩在阻尼的作用下衰减趋势明显;船中剖面的冲击动弯矩为最大,首尾L/4剖面的动弯矩约为船中部位的一半,且船中部位的动弯矩低阶成分更大。
2.3 结果分析取各工况下6个船型典型剖面的总动弯矩最大值,并比较在相同工况下不同船型各剖面的动弯矩随标准排水量的变化。中拱和中垂状态下各剖面动弯矩随舰船标准排水量的变化曲线分别如图5~图8所示。
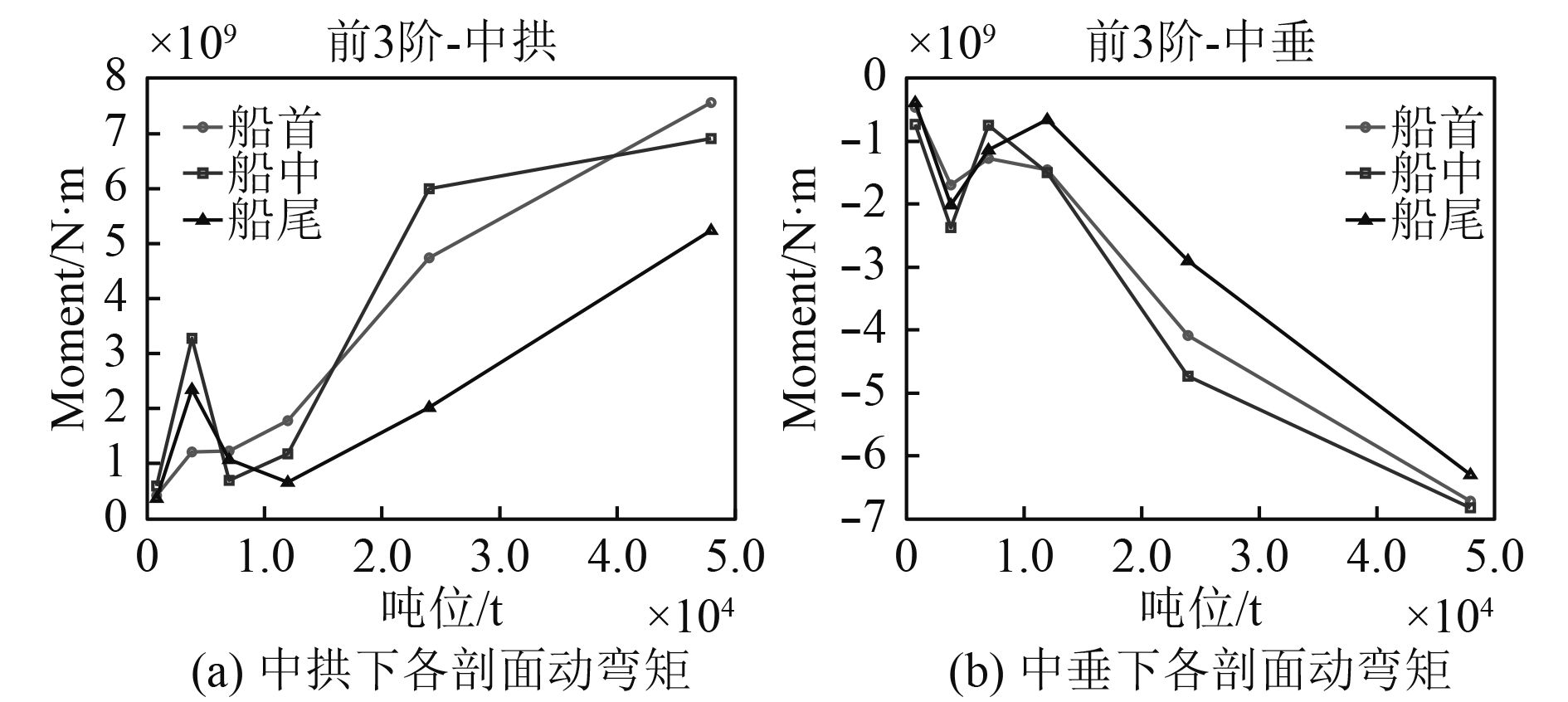
|
图 5 冲击因子0.3时动弯矩随排水量的变化曲线 Fig. 5 SVBM curves varying with displacement (KSF=0.3) |

|
图 6 冲击因子0.5时动弯矩随排水量的变化曲线 Fig. 6 SVBM curves varying with displacement (KSF=0.5) |
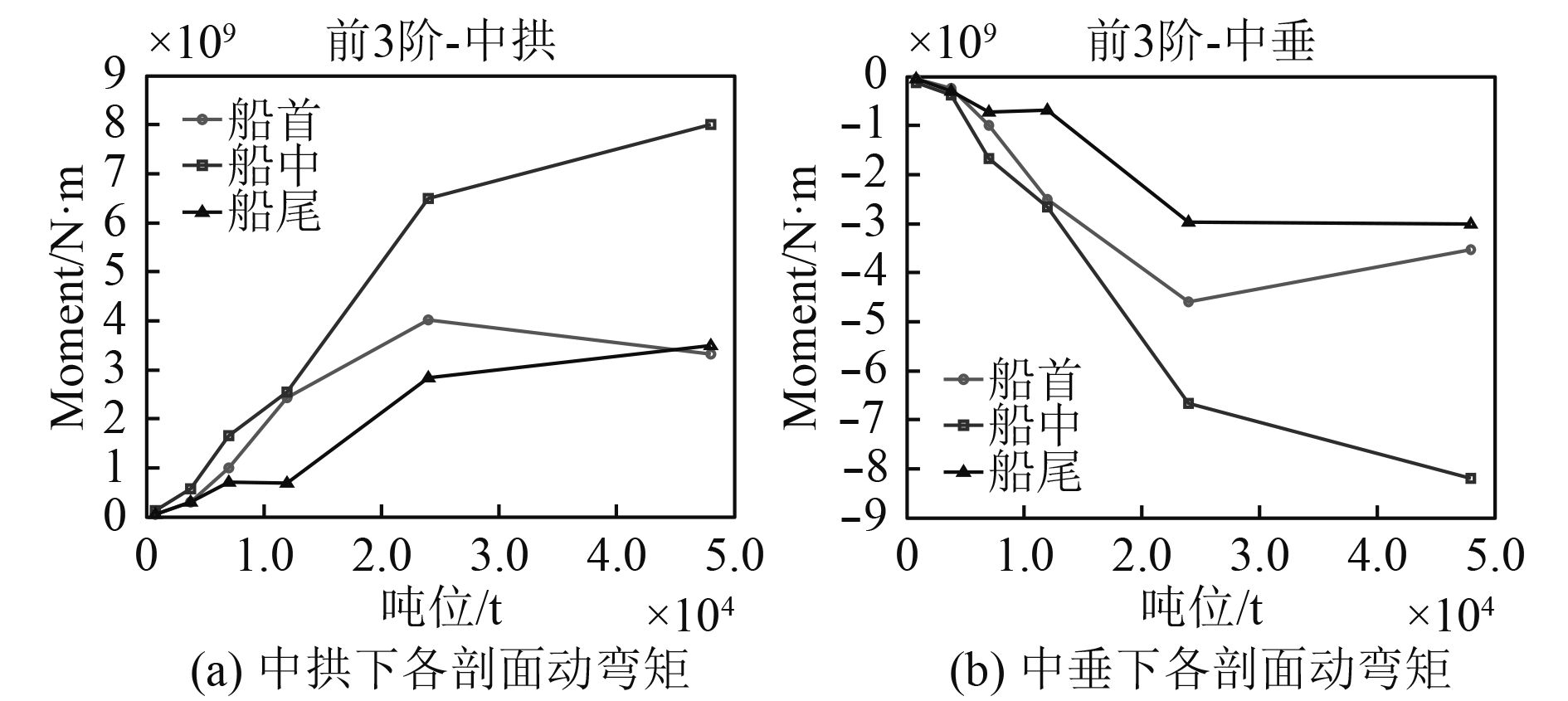
|
图 7 冲击因子0.8时动弯矩随排水量的变化曲线 Fig. 7 SVBM curves varying with displacement (KSF=0.8) |

|
图 8 冲击因子1.2时动弯矩随排水量的变化曲线 Fig. 8 SVBM curves varying with displacement (KSF=1.2) |
从上述4种冲击因子工况下的动弯矩随舰船标准排水量变化曲线图中可以得出,中拱和中垂状态下船首、船中和船尾3个校核剖面的动弯矩变化一致,相同冲击因子工况下的动弯矩均随着标准排水量的增大而呈显著上升趋势,不同标准排水量的舰船在相同工况下产生的动弯矩数量级也不同,而标准排水量接近的舰船动弯矩数量级则较为接近,所以在快速考核分析某标准排水量舰船的动弯矩时,可参考标准排水量相近舰船的动弯矩即可。
3 冲击动弯矩预报的经验公式通过上述6种不同船长及排水量舰船在水下爆炸中远场不同冲击因子下的计算结果,发现总纵动弯矩值大致随排水量或船长呈一定规律。在大量计算工况的基础上,去除明显与相近船型动弯矩值差异较大的值,并借鉴劳氏规范中有关波浪弯矩的经验公式,在对其余结果进行定性分析的基础上得出冲击动弯矩主要与舰船水线长、排水量、中横剖面系数等船型系数以及龙骨冲击因子等因数有关,结合劳氏规范中波浪抨击弯矩经验公式的形式,通过分析得到可以近似估算某船型在某一冲击因子下冲击动弯矩的经验公式,能为舰船初步设计提供参考,估算公式如下:
| $\left\{ {\begin{array}{*{20}{c}} {{M_{hog}} = kL \cdot \Delta /{C_M}^2} \text{,}\\ {{M_{sag}} = - kL \cdot \Delta /{C_M}^2} \text{。} \end{array}} \right.$ | (7) |
式中:
| $ \left\{ \begin{aligned} & {{k_{hog}}{\text{ = }}1.22C - 0.24} \text{,}\\ & {{k_{sag}}{\text{ = }} - 1.08C + 0.15} \text{。} \end{aligned} \right. $ | (8) |
其中,
其中,
|
|
表 4 中拱状态冲击因子C与系数K的关系表(单位N·m) Tab.4 The relationship between coefficient k and KSF C in hogging condition |
|
|
表 5 中垂状态冲击因子C与系数K的关系表(单位N·m) Tab.5 The relationship between coefficient k and KSF C in sagging condition |

|
图 9 系数k与冲击因子C的线性拟合关系图 Fig. 9 Linear fitting relation graph between coefficient k and KSF C |
利用上述拟合出的公式,计算各型船在冲击因子为0.8时的冲击动弯矩,并对比分析,如表6和表7所示。
|
|
表 6 冲击因子0.8时中拱状态船中动弯矩值比较(单位N·m) Tab.6 The contrast diagram of shock vibrationbending moment in hogging condition (KSF=0.8) |
|
|
表 7 冲击因子0.8时中垂状态船中动弯矩值比较(单位N·m) Tab.7 The contrast diagram of shock vibrationbending moment in sagging condition (KSF=0.8) |
可以看出,公式得到的结果与计算值差别波动较大;随着冲击因子的增大,即爆距减小时,公式得到的结果与计算值差别波动较为平缓,因此该经验公式可为舰船初步设计中的冲击动弯矩估算提供一定的参考。
4 结 语通过船体等效为船体梁计算水下爆炸冲击动弯矩,可以得到以下结论:水下中远场爆炸船体等值梁模型动弯矩计算方法的可行性,该工程计算方法的精度从工程角度来看是可以接受的;针对若干不同船长不同排水量的若干艘船舶进行冲击动弯矩的快速化预报,并分析动弯矩随船舶标准排水量的分布规律,相同冲击因子工况下的动弯矩均随着标准排水量的增大而呈显著上升趋势,不同标准排水量的舰船在相同工况下产生的动弯矩数量级也不同,而标准排水量接近的舰船动弯矩数量级则较为接近;给出简化的冲击动弯矩预报经验公式,预报精度在工程应用上处于可接受的范围内,可为舰船初步设计提供参考。
| [1] |
张绮蓉, 马锦华. 水下非接触爆炸对舰船总体强度与局部强度影响的分析028 g实艇水下爆炸试验资料汇编(上册)[M]. 北京: 第六机械工业部船舶系统工程部, 1982: 70–89. ZHANG Qi-rong, MA Jin-hua. Analysis of longitudinal strength and local strength of ship underwater un-contact explosion 028g boat test date[M]. Beijing: Ship System Engineering of Six Machine Industry, 1982: 70–89. |
| [2] |
李玉杰, 张效慈, 吴有生, 等. 水下爆炸气泡激起的船体鞭状运动[J]. 中国造船, 2001, 42(3): 1-7. LI Yu-jie, ZHANG Xiao-ci, WU You-sheng, et al. Whipping response of ship hull induced by underwater explosion bubble[J]. Shipbuilding of China, 2001, 42(3): 1-7. DOI:10.3969/j.issn.1000-4882.2001.03.001 |
| [3] |
朱锡, 方斌. 舰船静置爆炸气泡时总纵强度计算方法研究[J]. 海军工程大学学报, 2007, 19(6): 6-11. ZHU Xi, FANG Bin. Study on longitudinal strength calculation method of hull standing above an explosion bubble[J]. Journal of Naval University Engineering, 2007, 19(6): 6-11. DOI:10.3969/j.issn.1009-3486.2007.06.002 |
| [4] |
李海涛, 朱锡, 张振华. 水下爆炸球面冲击波作用下船体梁的刚塑性动响应特性[J]. 工程力学, 2010, 27(10): 202-207. LI Hai-tao, ZHU Xi, ZHANG Zhen-hua. Dynamic rigid-plastic response of ship-like beam subjected to underwater spherical shock waves[J]. Engineering Mechanics, 2010, 27(10): 202-207. |
| [5] |
汪玉, 华宏星. 舰船现代冲击理论及应用[M]. 北京: 科学出版社, 2005: 220–223.
|
| [6] |
姚熊亮. 舰船振动与噪声[M]. 北京: 国防工业出版社, 2010: 115–121.
|
| [7] |
COLE R H. Underwater explosion[M]. Princeton: Princeton University Press, 1948: 270–352.
|
| [8] |
ZHANG N, ZONG Z. The effect of rigid-body motions on the whipping response of a ship hull subjected to an underwater bubble[J]. Journal of Fluids and Structures, 2011, 27: 1326-1336. DOI:10.1016/j.jfluidstructs.2011.05.004 |
| [9] |
金辉, 周学滨, 周华, 等. 水下爆炸中自由场压力和船体壁压的测量与分析[J]. 海军工程大学学报, 2009, 21(5): 82-87. JIN Hui, ZHOU Xue-bin, ZHOU Hua, et al. Measurement and analysis of free-field pressure and ship hull pressure underwater explosion[J]. Journal of Naval University Engineering, 2009, 21(5): 82-87. |
| [10] |
顾文彬, 苏青笑, 刘建青, 等. 水下平面爆炸冲击波作用卜空化区域形成及其特征[J]. 爆破, 2004, 21(4): 8-11. GU Wen-bin, SU Qing-xiao, LIU Jian-qiang, et al. Formation process of cavitation region affected by underwater plane blast shock wave and its characteristics[J]. Blasting, 2004, 21(4): 8-11. DOI:10.3969/j.issn.1006-7051.2004.04.003 |
| [11] |
刘云龙, 张阿漫, 葛亮, 等. 圆柱壳结构水下爆炸所致鞭状运动特性研究[J]. 振动与冲击, 2013, 32(22): 106-112. LIU Yun-long, ZHANG A-man, GE Liang, et al. Whipping response of a cylindrical shell structure subjected to underwater explosion[J]. Vibration and Shock, 2013, 32(22): 106-112. DOI:10.3969/j.issn.1000-3835.2013.22.020 |
| [12] |
SCHNEIDER N A, SHIN Y S. Ship shock trial modeling and simulation for USS Winston S. Churchill (DDG81). Tech Report NPS-ME-03–004, Naval Postgraduate School, December 2003.
|
 2019, Vol. 41
2019, Vol. 41
