近年来,船舶通常基于极限状态设计方法用于评估船体梁的结构强度,即确定极限强度。加筋结构作为船体结构的主要成分,必须确保它能承受一定的外力载荷而不至于坍塌。为了这个目的,许多研究方法被开发用来预测钢制船舶的纵向极限承载能力,如Caldwell法[1]、Smith法[2]、有限元法[3]以及理想结构单元法[4]。在文献[5-6]中,Paik应用非线性有限元分析方法预测了船舶板架结构在承受纵向载荷以及侧向均布压力共同作用下的极限承载能力,计算结果取得预期要求。
然而,复合材料正在逐渐取代传统钢材,其在船舶领域应用的范围越来越加广泛,部分全复合材料船舶长度已经能达到80~90 m[7]。根据钢制船舶规范,长度超过60 m的船舶必须进行纵向极限强度评估,因此对复合材料船舶的极限强度评估非常迫切,也是复合材料船舶进一步发展的前提。
复合材料的极限强度分析需要研究结构的失效模式、损伤扩展机理以及非线性承载能力,考虑结构的各种影响因素,利用非线性的分析方法得到结构在加载过程的力学响应。
最初预测复合材料强度的方法是通过计算各铺层的即时应力场,根据单层的载荷响应来预测整个复合材料的强度。一种方法认为复合材料层合板的任何一个单层发生失效,则整个复合材料发生失效,被称为首层失效(First Ply Failure)。另一种方法认为,复合材料层合板某一层失效并不代表整个层合板失效。部分单元发生失效后,层合板仍能继续承受载荷,直到各个铺层全部发生失效,才认为整个层合板失效。这个方法被称为最终失效方法(Last Ply Failure),对应的载荷称为极限强度。
对于复合材料而言,由于其具有各项异性且界面复杂,国内外学者对其开展了众多研究工作。Cederbaum等[8]得到了在面内随机静载荷作用下的复合材料层合板的首层失效强度。Engelstad 和Reddy[9]开发了渐进失效有限元方法对复合材料层合板进行最终失效强度预测。Redd和Reddy[10]开发了三维渐进失效算法,并对受单轴拉伸载荷的层合板进行了失效分析。Hwang和Sun[11]利用三维有限单元进行了层合板的失效分析,考虑了纤维断裂、基体开裂和分层3种失效模式,采用改进的Tsai-Wu失效准则来进行判断。Ochoa和Engblom[12]基于高阶板理论建立了有限元模型,并对单轴拉伸载荷作用下的层合板进行了渐进失效分析。Padhi等[13]研究了四边固支的矩形板在横向载荷下的非线性行为,预测了首层失效及最终失效强度。Tan[14]提出了二维逐渐失效模型来分析含开孔层合板在拉伸载荷作用下的失效行为。该模型考虑了纤维破坏和基体破坏2种模式。对复合材料船舶,Chen[15 – 17]基于加筋层合板的复杂强度模型提出一种简化方法为了预测复合材料船舶处于中垂状态下的纵向极限强度。周晓松[18]以某型舰甲板室舷侧复合材料夹层板架结构为对象,重点分析了其静力弯曲问题并对该结构进一步优化设计。为了避免玻璃钢游艇在大开口区域产生疲劳裂痕,对船体结构造成危害,赵文龙[19]对该部位进行了强度校核。
对于舰船上层建筑所使用的板架结构,不仅在船舶航行中受到中拱状态和中垂状态的影响,而且还受到船上各种设备、人员荷重的影响以及甲板上浪抨击作用,因此本文针对某型舰上层建筑夹层板架结构采用渐进失效分析方法研究其在面内载荷和垂向均布力多种组合方式作用下的极限强度。考虑复合材料夹层板架作为船舶上层建筑的受力特性,通过算例对其首层失效强度以及失效位置进行预报。
1 有限元屈曲理论结构的后屈曲理论起始于20世纪30年代,学者发现某些类型的壳体结构屈曲载荷的理论与实验结果极不吻合,其原因在于这些结构的后屈曲状态不稳定,才形成了与过去完全不同的后屈曲性态的研究,这就是弹性稳定的大挠度理论。如四边简支薄板承受面内轴压的能力可以大大超过线性屈曲载荷,而圆柱壳在均匀轴压作用下却在几分之一的线性屈曲载荷下就突然破坏了。
随着有限元程序的不断发展和计算机硬件设备的不断增强,结构的非线性有限元已经成为结构极限强度分析的重要手段。非线性有限元法可以很好地考虑影响结构极限强度的不同因素,如受力形式、结构的几何缺陷以及非线性本构关系等。
按照非线性理论,结构的稳定性问题和强度问题相互联系在一起。非线性平衡路径可以准确地把结构的强度和稳定性,以至于刚度的整个变化历程表示的十分清楚。
非线性屈曲平衡方程的增量形式:
| $\begin{array}{l} {{{ K}_T}} d\left\{ \Delta \right\} = d\left\{ P \right\},\\ {{{{K}}_T}} = \int_\varOmega {{{\mathord{\buildrel{\hbox{$\scriptscriptstyle\frown$}} \over B} }^{\rm T}}{{\mathord{\buildrel{\hbox{$\scriptscriptstyle\frown$}} \over D} }_T}\mathord{\buildrel{\hbox{$\scriptscriptstyle\frown$}} \over B} {\rm {\rm{d}}}V \!+\! } \int_\varOmega {\frac{{\partial {{\mathord{\buildrel{\hbox{$\scriptscriptstyle\frown$}} \over B} }^{\rm T}}}}{{\partial \tilde u}}S{\rm{d}}V - } \frac{{\partial f}}{{\partial \tilde u}} \!=\! {{{{K}}_{{L}}}} \!+\!{{{{K}}_{{\sigma}} }} \!+\! {{{{K}}_{NL}}} \text{。} \end{array}$ | (1) |
其中:KT为切线刚度矩阵;KL为线性应变刚度矩阵;KNL为非线性应变刚度矩阵;
复合材料单层中的纤维单向平行,将单层的材料主方向用1、2和3来表示,纤维方向为1方向,垂直纤维方向为2方向,垂直于单层为3方向。
在材料主方向坐标系下,单层的应力应变关系可表示为:
| $\left\{\! {\begin{array}{*{20}{c}} {{\sigma _1}} \\ {{\sigma _2}} \\ {{\tau _{12}}} \\ {{\tau _{23}}} \\ {{\tau _{13}}} \end{array}}\! \right\} = \left[ \!{\begin{array}{*{20}{c}} {{Q_{11}}}&{{Q_{12}}}&0&0&0 \\ {{Q_{12}}}&{{Q_{22}}}&0&0&0 \\ 0&0&{{Q_{66}}}&0&0 \\ 0&0&0&{{Q_{44}}}&0 \\ 0&0&0&0&{{Q_{55}}} \end{array}}\! \right]\left\{\! {\begin{array}{*{20}{c}} {{\varepsilon _1}} \\ {{\varepsilon _2}} \\ {{\gamma _{12}}} \\ {{\gamma _{23}}} \\ {{\gamma _{13}}} \end{array}}\! \right\}{\text{。}}\!\!\!\!\!\!\!$ | (2) |
式中:Qij为单层材料主方向的折算刚度系数,可以由式(3)得到:
| $\begin{array}{l} {Q_{11}} = \displaystyle\frac{{{E_1}}}{{1 - {\nu _{12}}{\nu _{21}}}},\;\;{Q_{12}} = \displaystyle\frac{{{\nu _{12}}{E_2}}}{{1 - {\nu _{12}}{\nu _{21}}}},\;\;{Q_{22}} = \displaystyle\frac{{{E_2}}}{{1 - {\nu _{12}}{\nu _{21}}}}\\ \;\;\;\;\;{Q_{66}} = {G_{12}},\;\;\;\;\;{Q_{44}} = {G_{23}},\;\;\;\;\;{Q_{55}} = {G_{13}}\;{\text{。}} \end{array}$ | (3) |
式中:E1,E2和G12,G23,G13分别为正交各向异性材料的拉压弹性模量和剪切模量;v12、v21分别正交各向异性材料的主泊松比和副泊松比。
2.2 失效准则Shokrieh等[20]改进了三维的Hashin失效准则,考虑了7种失效模式。
纤维拉伸断裂失效:
| ${\left( {\frac{{{\sigma _{11}}}}{{{X_T}}}} \right)^2} + {\left( {\frac{{{\tau _{12}}}}{{{S_{12}}}}} \right)^2} + {\left( {\frac{{{\tau _{13}}}}{{{S_{13}}}}} \right)^2} \geqslant 1{\text{;}}$ | (4) |
纤维压缩失效:
| ${\left( {\frac{{{\sigma _{11}}}}{{{X_C}}}} \right)^2} \geqslant 1{\text{;}}$ | (5) |
基体拉伸失效:
| ${\left( {\frac{{{\sigma _{22}}}}{{{Y_T}}}} \right)^2} + {\left( {\frac{{{\tau _{12}}}}{{{S_{12}}}}} \right)^2} + {\left( {\frac{{{\tau _{23}}}}{{{S_{23}}}}} \right)^2} \geqslant 1{\text{;}}$ | (6) |
基体压缩失效:
| ${\left( {\frac{{{\sigma _{22}}}}{{{Y_c}}}} \right)^2} + {\left( {\frac{{{\tau _{12}}}}{{{S_{12}}}}} \right)^2} + {\left( {\frac{{{\tau _{23}}}}{{{S_{23}}}}} \right)^2} \geqslant 1{\text{;}}$ | (7) |
纤维基体剪切破坏:
| ${\left( {\frac{{{\sigma _{11}}}}{{{X_c}}}} \right)^2} + {\left( {\frac{{{\tau _{12}}}}{{{S_{12}}}}} \right)^2} + {\left( {\frac{{{\tau _{13}}}}{{{S_{13}}}}} \right)^2} \geqslant 1{\text{,}} {{\sigma _{11}} < 0} {\text{;}}$ | (8) |
拉伸分层:
| ${\left( {\frac{{{\sigma _{22}}}}{{{Z_T}}}} \right)^2} + {\left( {\frac{{{\tau _{13}}}}{{{S_{13}}}}} \right)^2} + {\left( {\frac{{{\tau _{23}}}}{{{S_{23}}}}} \right)^2} \geqslant 1{\text{;}}$ | (9) |
压缩分层:
| ${\left( {\frac{{{\sigma _{33}}}}{{{Z_C}}}} \right)^2} + {\left( {\frac{{{\tau _{13}}}}{{{S_{13}}}}} \right)^2} + {\left( {\frac{{{\tau _{23}}}}{{{S_{23}}}}} \right)^2} \geqslant 1{\text{。}}$ | (10) |
事实上,复合材料结构在加载过程中出现局部破坏失效后,仍能继续承受载荷。为了模拟这种效果,认为损伤单元可以用一个材料参数折减过的单元来代替。
基于该假设,本文采用单层板局部衰减模型,其认为刚度矩阵中仅与失效模式相关的项退化为零或未损伤材料性能参数的一部分。该模式通过刚度退化系数将导致材料失效起主要作用的应力降低,即
| ${p^ * } = k \cdot p{\text{,}}\;\;\;\;\; {k = 0 \sim 1}{\text{。}}$ | (11) |
式中:p*为失效后的刚度参数;p为失效前的刚度参数;k为刚度退化系数。
在有限元渐进失效分析过程中,对破坏单元的刚度折减方法有多种,较容易实现的方法是改变破坏单元的材料属性,通过降低材料的性能以达到降低单元刚度的目的。在有限元分析中常用材料性能退化的方法如表1所示[21]。
|
|
表 1 材料性能退化方法 Tab.1 Material performance degradation methods |
为了本文渐进失效分析方法的精确性和可靠性,将分析复合材料层合板在面内载荷作用下的极限强度,计算结果将与公开文献结果进行对比。
3.1 结构参数以及边界条件层合板长度为508 mm,宽度为178 mm,铺层方式均为[±45°/0°2/±45°/0°2/±45°/0°/90°]2,单层厚度为0.14 mm,均为石墨环氧树脂材料制成,其材料参数如表2所示。边界条件为:x=0边界处Ux=Uy=Uz=Rotx=Roty=Rotz=0;x=a边界处Uz=Rotx=Roty=Rotz=0;y=0,b边界处Uz=Roty=Rotz=0。载荷形式为单轴压缩,即x=a处受压。
|
|
表 2 材料参数 Tab.2 Material properties |
由shell181单元建立有限元模型,该单元是4节点三维单元,每个节点有6个自由度,非常适用于线性分析、大转动变形和非线性的大变形。
为了在极限分析中跃过层合板的屈曲点,有效达到板的极限强度值,本文给模型加上了一定的初始几何缺陷。初始几何缺陷的形状为每块板的第一阶线性屈曲模态,初始几何缺陷幅值为总厚度的5%。图1为层合板的一阶屈曲模态。

|
图 1 一阶弹性屈曲模态 Fig. 1 The first-order elastic buckling mode |
在结构失效前,采用Newton-Raphson法来确定应力应变分布情况。通过激活弧长算法得到结构失效后的临界失效压力曲线。表3展示本文计算结果与相关实验数据以及数值模拟结果的相对误差。由表可知,本文计算结果与文献给出的实验值及有限元计算值误差均在可接受范围内,最大误差为5.13%。造成误差的原因可能有:1)模型是在层合板各单层之间黏合牢固且复合材料为均质连续固体等前提下建立的,是一种比较理想化的模型;2)选取的失效准则以及刚度退化系数的不同。
|
|
表 3 本文计算结果与实验数据[23]和数值结果[22]的比较(kN) Tab.3 Comparison between the estimated results and the experimental data[23] and numerical results[22] |
对于舰船上层建筑所使用的板架结构,不仅在船舶航行中受到中拱状态和中垂状态的影响,而且还受到船上各种设备、人员荷重的影响以及波浪冲击的作用。
4.1 夹层板架结构模型某型舰甲板室舷侧为复合材料夹层板架结构,板架由夹层板、4根横筋和4根纵筋构成。夹层板由上、下玻璃钢表层和PVC泡沫芯材组成,玻璃钢铺层方式为[45°/0°3/45°/90°]s;筋材为帽形筋结构,包括内部芯材和玻璃钢表层。板架尺寸参数如图2所示。
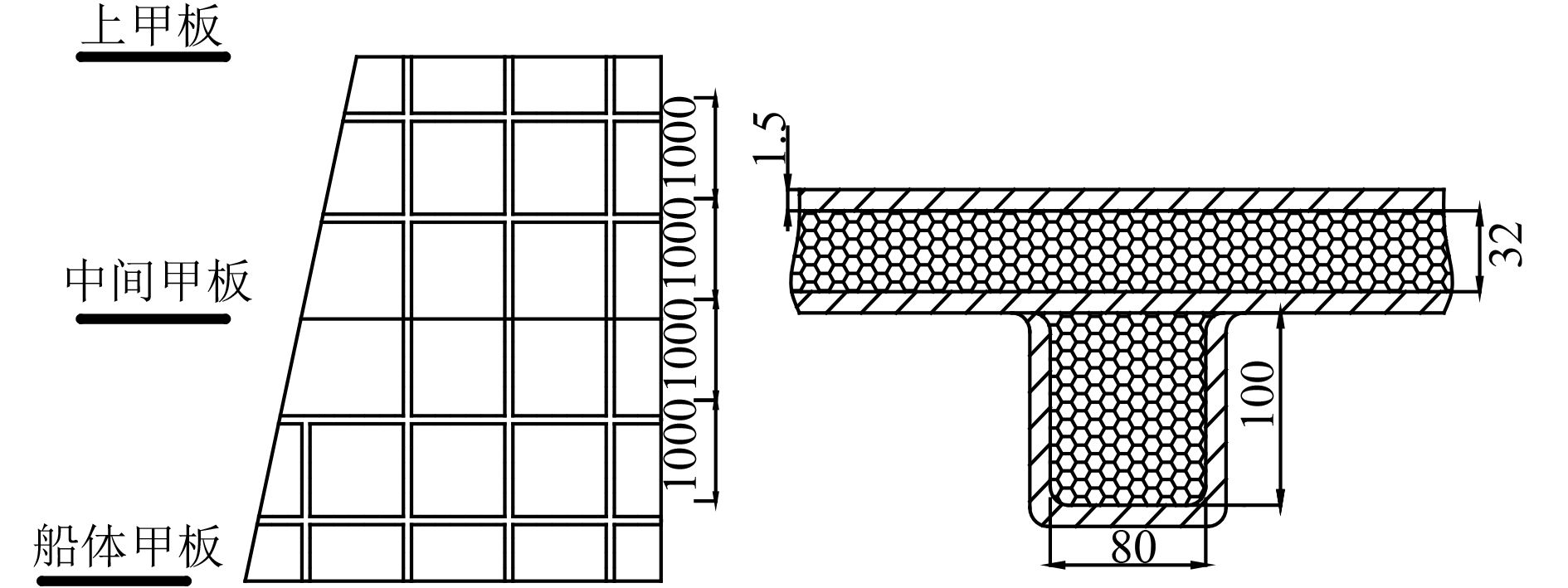
|
图 2 结构布置图及局部示意图 Fig. 2 Structural layout and local schematic diagram |
根据此舷侧结构,本文以长L=4 000 mm,宽b=3 000 mm的夹层板架结构作为研究对象,其夹层板壁板厚度为35 mm,加强筋简化为刀型筋条,厚度为80 mm,高度为100 mm,分析其在多种组合载荷作用下的极限强度。材料参数列于表4。有限元模型中所有构件均采用shell单元建模,该单元使用线性插值法,允许有限薄膜应变和大转角,考虑了剪切变形的影响,适用于几何非线性分析。
|
|
表 4 夹层板材料属性 Tab.4 Material properties of composite sandwich |
船舶甲板结构主要受到纵向(B向)、横向(L向)以及垂向载荷的共同作用。考虑船体板受力特征,面内载荷以沿筋方向的面内压力为主,并且根据国军标(GJB4000)§102.37[24]中对排水型水面舰艇上层建筑强度要求,取设计载荷P=4.91 kPa。因此选取以下2种载荷工况进行研究。
工况1:板架结构仅受面内载荷作用。面内纵向和横向载荷作用分别讨论以下几种情况:Nxx:Nyy=1.0:0.0,Nxx:Nyy=0.7:0.3,Nxx:Nyy=0.5:0.5及Nxx:Nyy=0.0:1.0。
工况2:板架结构受面内载荷和垂向均布压力P同时作用。分析多种面内受压组合载荷和垂向载荷共同作用下的极限强度,受力示意图如图3所示。
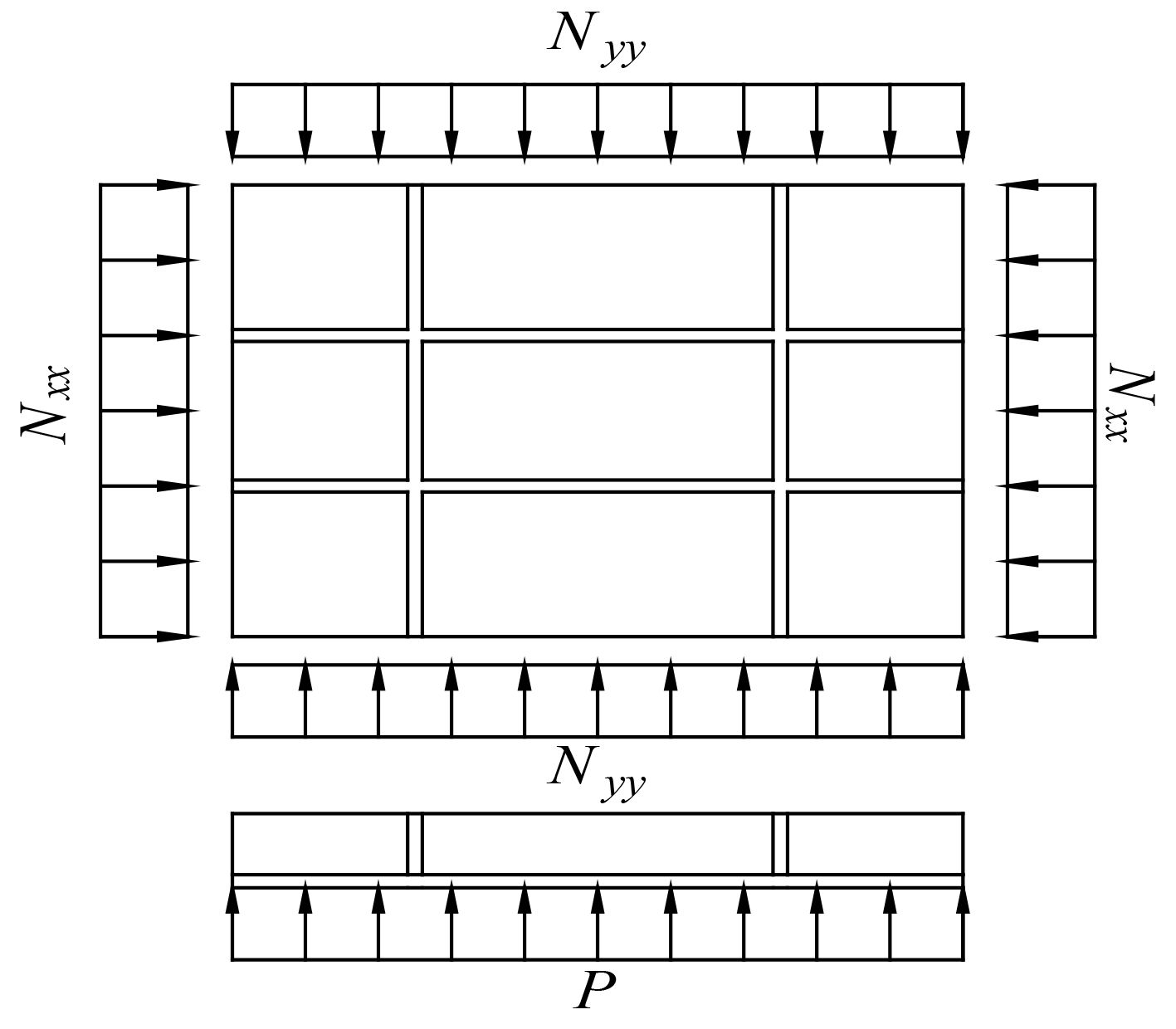
|
图 3 板架结构的组合载荷 Fig. 3 Load modes of frame structure |
在多数研究中,纵骨和横框架之间的板被假定为四周简支,然而船体板是连续的板,每一板格都受到相邻板格的牵制作用,板边不能自由趋近,且当板格受到垂向压力时,相邻的板格因连续而应具有相同的变形。因此本文选取国际船舶结构委员会在2009年总结中提出的约束方式[25],即在A-A1和C-C1处施加沿板长度方向的对称性约束,加筋板的纵向边界及强横梁处Z向简支,在A-C边施加y向约束和在A-A1边施加x向约束以限制刚性位移,并在B-B1,D-D1强横梁处,板上节点UZ=0,筋腹板y向位移相同(又称为直边界),以限制筋在强横梁处的侧向变形;由于所计算的板格取自连续板中的一部分,各边在变形时应施加直边界条件,C-C1处施加x方向直边界条件,该截面所有节点在受力时x向位移相同A1-C1边则y向位移相同,如图4所示。
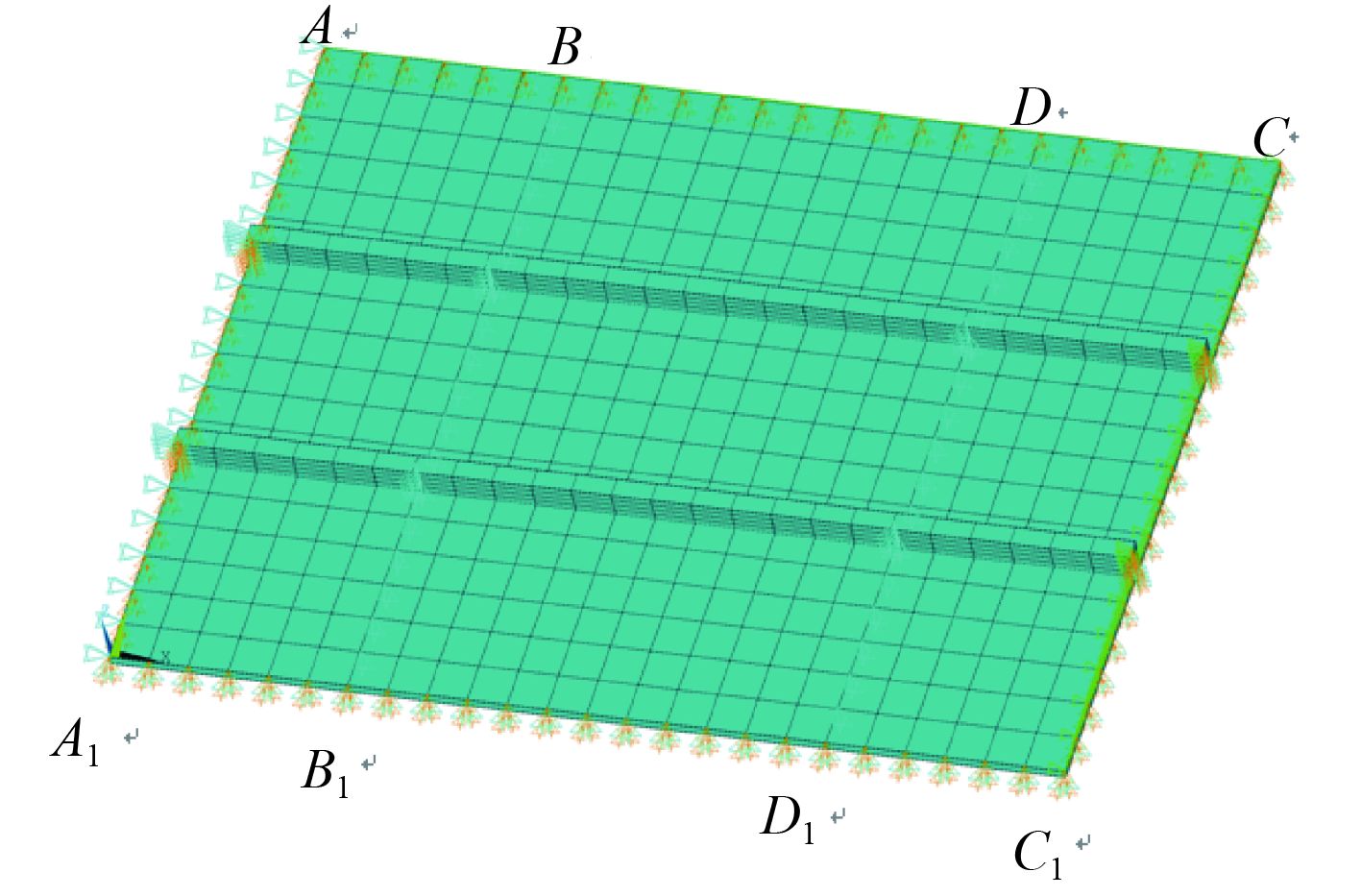
|
图 4 边界条件 Fig. 4 Boundary conditions |
由于复合材料是多种不同性能材料复合而成,从微观上来说,复合材料自身是具有非均匀性和各项异性的力学结构材料,因此分析其在多种组合载荷模式下的极限强度是非常具有意义的,同时对复合材料在船舶行业的推广提供一定的指导价值。图5和图6展示了复合材料夹层板架分别在x,y轴方向的载荷位移曲线。
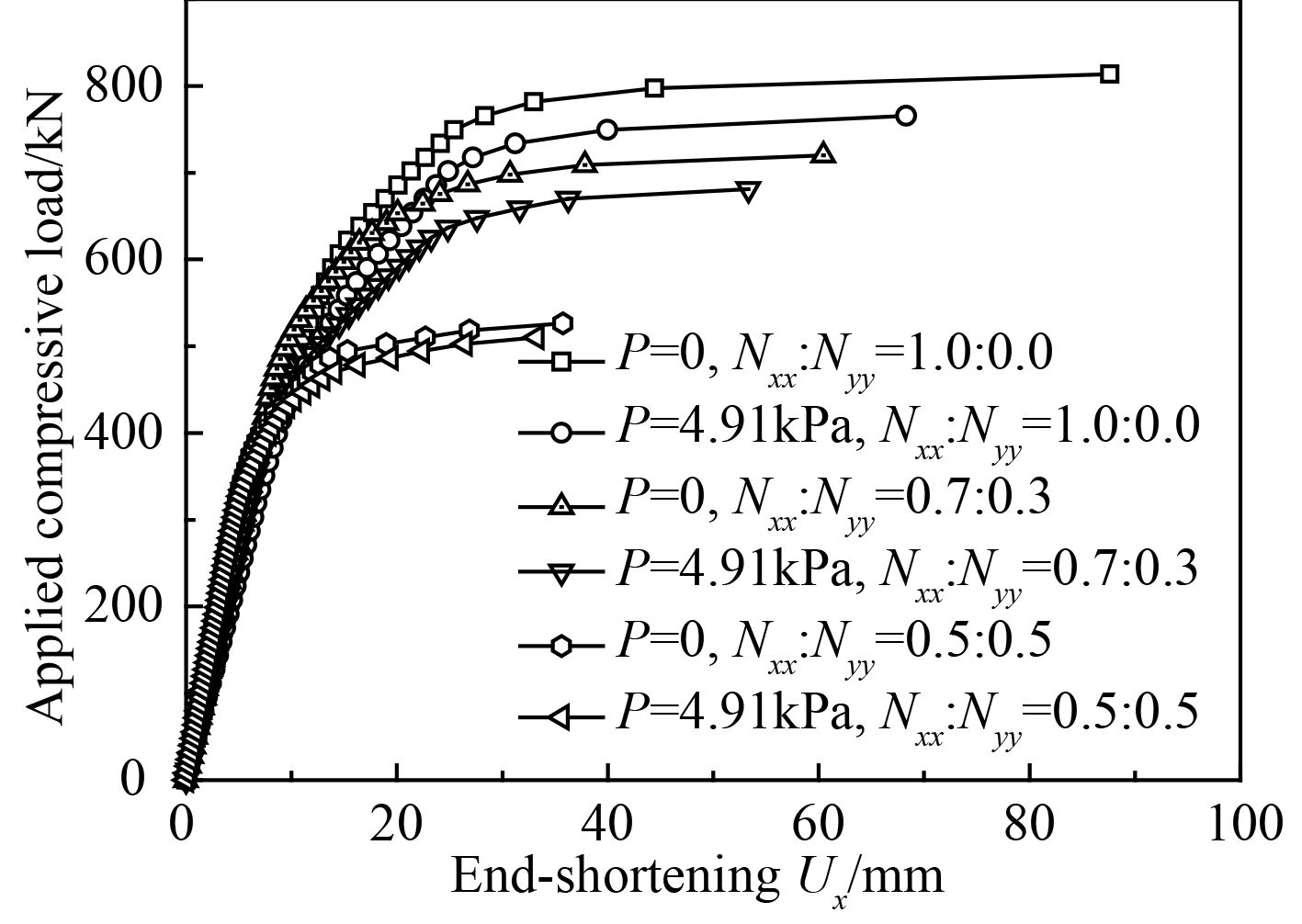
|
图 5 板架结构纵向在组合载荷作用下的载荷位移曲线 Fig. 5 The load-displacement curve along the longtitude direction |
|
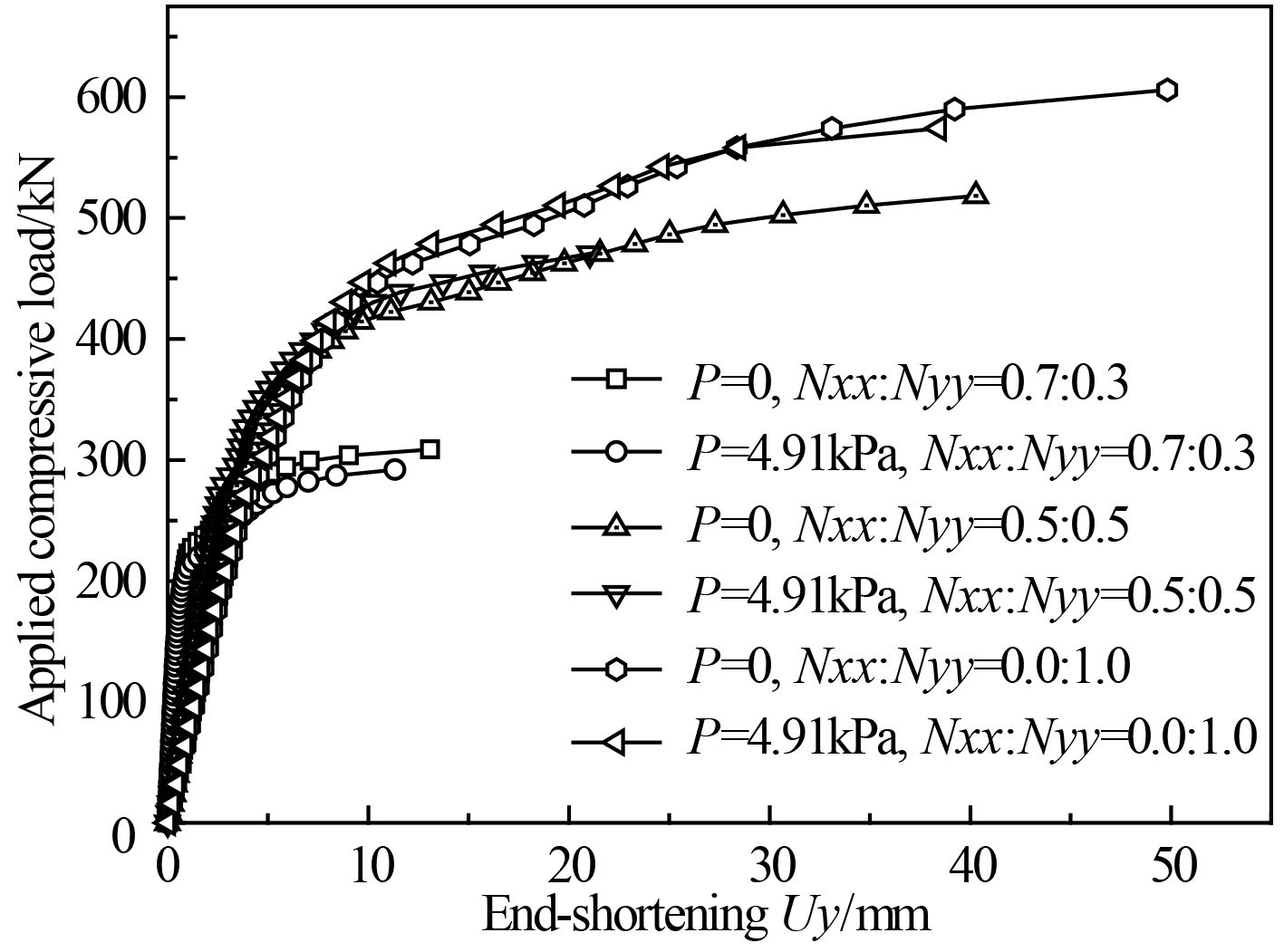
图 6 板架结构横向在组合载荷作用下的载荷位移曲线 Fig. 6 The load-displacement curve along the tranverse direction |
图5为复合材料板架结构纵向在组合载荷作用下的载荷位移曲线,表5为板架结构在组合载荷作用下的首层失效载荷和极限强度载荷以及失效位置预报,由此可以看出:
1)随着纵向载荷的比例减少,纵向首层失效载荷呈现降低趋势,然而对比Nxx:Nyy=1.0:0.0和Nxx:Nyy=0.7:0.3,二者首层失效铺层角度相同,后者首层失效强度大于前者;
2)垂向均布载荷的施加影响了板架结构的纵向极限强度,载荷模式在Nxx:Nyy=1.0:0.0,Nxx:Nyy=0.7:0.3,Nxx:Nyy=0.5:0.5时分别减小了6.00%,5.51%,.56%,随着纵向载荷比例的减少,垂向载荷影响减小;
3)加载方式的不同,复合材料首层失效位置和最终失效位置也发生改变,一般来看往往是垂直于载荷方向的铺层角度最先失效,与载荷方向相同的铺层失效往往是导致结构失去承载能力的主要因素。
图6为复合材料板架结构横向在组合载荷作用下的载荷位移曲线,结合表5可以看出:
|
|
表 5 复合材料板架结构在组合载荷作用下的极限强度值 Tab.5 The ultimate strength value of composite frame structure under combined loadings |
1)P=0时随着横向载荷比例增加,横向失效载荷增大,但是其他因素使Nxx:Nyy=0.0:1.0的首层失效载荷有所降低;
2)垂向载荷的施加减低了加筋板的横向极限强度,载荷模式在Nxx:Nyy=0.7:0.3,Nxx:Nyy=0.5:0.5,Nxx:Nyy=0.0:1.0时分别减小了5.51%,1.56%,5.40%。
5 结 语本文基于渐进失效方法对在组合载荷作用下的复合材料夹层板架结构进行极限强度分析,可以得出如下结论:
1)随着纵向载荷的降低、横向载荷的提高,结构主要承载方向将随提高边转移。侧向均布压力的存在,对结构承载能力影响十分显著,导致结构较快的达到满足失效条件。
2)复合材料首层失效铺层与承载方式相关,一般来看往往是垂直于载荷方向的铺层角度最先失效,与载荷方向相同的铺层失效往往是导致结构失去承载能力的主要因素。
| [1] |
CALDWELL JB. Ultimate longitudinal strength[M]. Trans Roy Inst Naval Architect 1965; 107: 411–30.
|
| [2] |
SMITH CS. Influence of local compressive failure on ultimate longitudinal strength of a ship’s hull[J]. In: Proc. Int. symp. On practical design in shipbuilding. 1977. P. 73–9.
|
| [3] |
CHEN KY, KUTT LM, PIASZCZYK CM, BIENIEK MP. Ultimate strength of shipstructures[J]. SNAME Trans, 1983, 91: 149-68. |
| [4] |
UEDA Y, RASHED SMH. The idealized structural unit method and itsapplication to deep girder structures[J]. Comput Struct, 1984, 18(2): 227-93. |
| [5] |
PAIK J K, KIM B J, SEO J K. Methods for ultimate limit state assessment of ships and ship-shaped offshore structures: Part II stiffened panels[J]. Ocean Engineering, 2008, 35(2): 271-280. DOI:10.1016/j.oceaneng.2007.08.007 |
| [6] |
PAIK J K, SEO J K. Nonlinear finite element method models for ultimate strength analysis of steel stiffened-plate structures under combined biaxial compression and lateral pressure actions—Part II: Stiffened panels[J]. Thin-Walled Structures, 2009, 47(8): 998-1007. |
| [7] |
MOURITZ AP, GELLERT E, BURCHILL P, CHALLIS K. Review of advancedcomposite structures for naval ships and submarines[J]. Compos Struct, 2001, 53: 21-41. DOI:10.1016/S0263-8223(00)00175-6 |
| [8] |
CEDERBAUM G, ELISHAKOFF I, LIBRESCU L. Reliability of laminated plates viathe first-order second-moment method[J]. Compos Struct, 1990, 15: 161-7. DOI:10.1016/0263-8223(90)90005-Y |
| [9] |
ENGELSTAD SP, REDDY JN. Probabilistic nonlinear finite element analysis ofcomposite structures[J]. AIAA J, 1993, 31: 362-9. DOI:10.2514/3.11676 |
| [10] |
REDD Y S, REDDY J N. Three-dimensional finite element progressive failure analysis of composite laminates under axial extension[J]. Journal of Composites Technology & Research, 1993, 15(2): 73-87. |
| [11] |
HWANG W C, SUN C T. Failure analysis of laminated composites by using iterative three-dimensional finite element method[J]. Computers & Structures, 1989, 33(1): 41-47. |
| [12] |
OCHOA O O, ENGBLOM J J. Analysisof failureincomposite[J]. Journal of Heredity, 2012, 103(6): 842-852. DOI:10.1093/jhered/ess070 |
| [13] |
PADHI G S, SHENOI R A, MOY S S J, et al. Progressive failure and ultimate collapse of laminated composite plates in bending[J]. Composite Structures, 1997, 40(3-4): 277-291. DOI:10.1016/S0263-8223(98)00030-0 |
| [14] |
TAN S C. A progressive failure model for composite laminates containing openings[J]. Journal of Composite Materials, 1991, 25(5): 556-577. DOI:10.1177/002199839102500505 |
| [15] |
CHEN N Z, SUN H H, SOARES C G. Reliability analysis of a ship hull in composite material[J]. Composite Structures, 2003, 62(1): 59-66. DOI:10.1016/S0263-8223(03)00084-9 |
| [16] |
CHEN N Z, SOARES C G. Longitudinal strength analysis of ship hulls of composite materials under sagging moments[J]. Composite Structures, 2007, 77(1): 36-44. DOI:10.1016/j.compstruct.2005.06.002 |
| [17] |
CHEN N Z, SOARES C G. Reliability assessment for ultimate longitudinal strength of ship hulls in composite materials[J]. Probabilistic Engineering Mechanics, 2007, 22(4): 330-342. DOI:10.1016/j.probengmech.2007.05.001 |
| [18] |
周晓松, 梅志远. 舰船复合材料夹层板架结构的分级递进优化设计方法[J]. 中国舰船研究, 2014(4): 63-69. DOI:10.3969/j.issn.1673-3185.2014.04.010 |
| [19] |
赵文龙, 刘雪松, 周玉龙. 带有大开口的玻璃钢游艇舷侧夹层板架结构强度分析[J]. 船海工程, 2011, 40(1): 16-18. DOI:10.3963/j.issn.1671-7953.2011.01.005 |
| [20] |
SHOKRIEH M M, LESSARD L B. Effects of material nonlinearity on the three-dimensional stress state of pin-loaded composite laminates[J]. Journal of Composite Materials, 1996, 30(7): 839-861. DOI:10.1177/002199839603000705 |
| [21] |
史文华. 复合材料泡沫夹层板极限承载能力研究[D]. 上海: 上海交通大学, 2011.
|
| [22] |
DAVID W S. Progressive failure analysis methodology for laminated composite structures[J]. 1999.
|
| [23] |
STARNES J H, Jr, ROUSE M. Postbuckling and failure characteristics of selected flat rectangulargraphite-epoxy plates loaded in compression[C]//AIAA, April 1981,4.
|
| [24] |
中国人民解放军总装备部. 舰船通用规范—1组: 船体结构[S]. 上海: 海军论证中心标准规范所.
|
| [25] |
张晓丹. 加筋板极限强度的简化算法[D]. 武汉: 武汉理工大学, 2010.
|
 2019, Vol. 41
2019, Vol. 41
