2. 山东交通学院 威海校区,山东 威海 264200
2. Shandong Jiaotong University Weihai Campus, Weihai 264200, China
海洋资源的深入开发利用以及日益增强的军事和民用需求,使潜艇和潜水器等潜体在科研和军事领域的应用引起广泛重视。良好的操纵性能是潜体安全航行和充分发挥其战技术水平的重要保证[1],也是潜体综合性能的重要组成部分和总体设计的重点。水动力系数是潜艇和潜水器操纵运动方程的系数,因此基于潜体操纵运动方程模拟操纵运动并预报操纵性,必须先确定水动力系数[2]。目前求取水动力系数的方法主要有拘束或自由自航模型试验、计算机数值模拟、半理论半经验的估算方法3种。本文主要针对这3种方法,对近十几年来国内外求取潜水器和潜艇等潜体水动力系数研究进展进行详细概述,总结众多研究者的定性研究结论,对未来的研究方向进行展望。
1 模型试验法水动力模型试验分为拘束模型试验和自由自航船模试验,自由自航船模试验存在“尺度效应”,且目前该问题仍难以解决,所以主要采用的模型试验方法是拘束船模试验。拘束船模试验主要包括:斜航试验(又称直线拖曳试验,ORT)、回转臂试验(RAT)、平面运动机构试验[3]。潜艇体积较为庞大对试验条件要求较高,且如今潜艇Suboff的试验数据已经十分完整,所以本文试验方法部分较少提到潜艇。潜水器体积较小且相比潜艇比较容易进行试验,因此近年来试验方法研究成果较多,本文模型试验方法部分主要对通过拘束模型试验获取潜水器水动力系数的研究成果进行综述。
斜航试验可以确定潜水器在漂角和舵角状态下的位置导数和耦合水动力系数,回转臂试验可以确定与角速度相关的力或力矩导数。目前,很多学者通过斜航试验及回转臂试验求得了相应的水动力系数,并进一步研究获得定性结论。为了研究自由面对潜水器阻力和升力系数的影响,Mansoorzadeh等[4]用1:1的船模在拖曳水池中进行直线拖曳试验,分别求取了潜水器在不同速度及不同深度时的水动力系数,并进一步研究了自由面对阻力和升力系数的影响。为了在初步设计中深入研究小型潜水器的水动力性能,Gala等[5]通过斜航试验和数值模拟方法获得小型潜水器在不同漂角和攻角下的水动力系数,并将2种方法获得的结果进行对比,验证数值方法的可行性。出于相同目的,李刚等[6]以某潜水器为模型进行回转臂试验获得旋转导数,并将所得数据用来验证数值旋转臂水池模型的准确性。
斜航试验只能获取速度系数及舵角系数,回转臂试验只能获取角速度系数,这些实验无法测定与加速度相关的导数即惯性类水动力(附加质量)系数,不能满足操纵性预报所需的水动力系数。美国古德曼和格特勒提出了平面运动机构系统,能方便地求解各项力和力矩的线性加速度导数和线性速度导数。由于PMM还具有一定的综合性、经济性,被世界各国及主要船舶研究机构广泛应用于船舶水动力学研究方面。其中平面运动机构根据运动平面不同可以分为水平面(XOY)和垂直面(XOZ),水平面的平面运动试验包括纯横荡和纯首摇,垂直面的平面运动机构(VPMM)包括纯俯仰和纯升沉。
Avila等[7]用全尺寸的开架式潜水器通过PMM进行纯横荡和纯首摇运动试验,获取线性加速度导数和线性速度导数,从而为操纵性预报提供了较充足的水动力导数,但纯横荡和纯首摇运动模拟只能获得水平面的惯性类水动力系数,无法求取垂直面的惯性类水动力系数。为此,Xu等[8]通过垂直型平面运动机构和循环水槽进行纯升沉和纯俯仰运动试验,获得了潜水器垂直面的惯性类水动力系数。目前,更多的学者利用平面运动机构对潜水器的六自由度耦合运动工况下的水动力进行试验研究,研究成果颇丰。例如,赵金鑫等[9]以某带吊舱小型潜水器为研究对象对其进行直航、斜航、纯升沉、纯俯仰、纯横荡、纯首摇等水动力模型试验,得到潜器操纵性预报所需的水动力系数,并将计算结果与数值计算结果进行对比验证。李刚等[6]利用循环水槽和PMM对穿梭潜器的水动力进行试验测试,得到了相对充足的水动力系数,并对数值模拟和物理模型试验过程进行对比,分析不同数值模拟过程得到的水动力结果变化规律,建立了针对穿梭潜器操纵运动特征的水动力平方项模型。庞永杰等[10]利用循环水槽中的VPMM对无桨和带桨全附体潜艇模型进行拘束模型试验,分析了螺旋桨对潜艇操纵性水动力的影响。
拘束模型试验法是确定水动力系数最成熟的方法,至今仍是工程中解决实用问题的主要手段,测试结果常用来和数值模拟结果作对比验证。但是模型试验通常需要耗费大量的人力和物力,且试验周期长,寻找一种既节约成本又满足精度需求的水动力系数获取方法成为国内外学者研究的重点。
2 半理论半经验的估算方法半理论半经验的估算方法包括近似估算方法和理论计算方法,该方法相对于模型试验法拥有较好的经济性。近似估算方法是建立在“迭加原理”和所谓“相当值”的基础上,即假定潜水器的水动力系数(如速度系数、角速度系数等)于艇体和各附体(舵、翼等)的水动力系数之和,根据等值椭球和等值平板理论,应用近似公式的估算方法求取潜水器的水动力系数。理论计算方法是根据理想流体力学势流理论,根据诱导速度势附加质量,获取与加速度相关的惯性类水动力。由于半经验半理论的估算方法所得水动力系数精度满足不了工程的需求,在实际研究中大多与其他方法结合运用或用于和其他计算方法进行精度对比,所以本文只汇总了相对具有代表性的一些研究。
张赫等[11]以某长航程潜水器作为研究对象,基于近似公式估算粘性类水动力系数,将所得结果与数值计算和模型试验所得数据进行比较分析。张赫、张玲等[11-12]均采用了基于势流理论的 Hess-Smith面元法求解了不同水下航行体的惯性类水动力系数。理论计算方法获取惯性类水动力系数所得结果比较准确,但是忽略了流体的粘性,对于实际粘性流体而言,所得结果偏小。为了考虑流体粘性对计算结果的影响,李刚等[13]采用了基于势流的 Hess-Smith面元法结合数值计算对复杂构型潜器附加质量进行计算。
潜艇用于计算水动力系数的经验公式趋于成熟,本文半经验半理论的估算方法不再提及。潜水器造型各异且附体较多,目前还没有系统的设计资料可用于近似计算,因而多采用水面船舶、潜艇、鱼雷等的经验公式,给潜器的水动力估算带来了很大的误差。总体而言,半经验半理论的估算方法虽然节约了时间和资金成本,但是却达不到工程上要求的精度,仍需要进一步寻求精度更高且节约成本的水动力系数获得方法。
3 数值方法 3.1 数值方法研究现状综述随着流体力学和计算机的迅猛发展,粘性流计算方法被广泛应用于水动力导数模拟计算中,在潜体水动力性能研究中,CFD软件为计算潜体水动力系数提供了一种新的方法,它结合了理论计算与试验的优点,引起国内外学者的关注,常用的CFD软件有Fluent,Star CCM+,CFX等。由于Suboff潜艇试验数据成熟,给数值计算验证提供了有力的证明,所以数值计算方法获取潜体水动力系数进行的研究多针对于Suboff潜艇。
潘子英等[14]基于Fluent软件对标准椭球体和Suboff主艇体进行操纵性水动力数值预报,计算了在无限水域中一系列攻角下受到的水动力,并与试验结果进行对比,验证该方法的准确性,将此数值计算方法运用到系列模型的水动力测定中,辅助建立了潜艇主体操纵性水动力的工程估算公式。詹成胜等[15]采用非结构化网格对潜艇的拖曳及旋臂试验进行数值模拟,得到了潜艇在不同速度、舵角及角速度下的水动力导数。柏铁朝等[16]采用6种不同的湍流模型计算了Suboff 模型在不同漂角和攻角条件下的操纵性水动力,并与试验值进行比较,通过对比发现采用k -ω SST湍流模型所得的数值计算结果与试验值最接近,在进行数值模拟时要根据实际模拟的运动情况对湍流模型进行选择方能保证精度。
近几年的研究成果表明,基于数值计算获得潜体直航和斜航拖曳运动的水动力系数已得到深入研究[17]。为了通过数值计算方法获得角速度导数即旋转导数,需要进一步对回转运动进行数值模拟,并保证所得结果精度达到工程要求。国外对于数值模拟回转运动求取旋转导数的研究已经比较成熟,国内虽然相对起步晚,但是近年来取得了一定成果。卢锦国等[18]基于Fluent软件,采用定常旋转运动坐标系,比较了不同湍流模型及网格分布对水下航行体做单平面回转运动所受力及力矩预报结果的影响,并且证明了预报结果具有较好的精度,表明运用数值预报方法计算旋转导数有效可行。XIAO等[19]采用基于固定坐标系的动网格法对Suboff的角速度导数进行预报,由于没有考虑动量源项的影响,导致结果误差较大。为了解决该问题,曹留帅等[17]以结构网格为计算背景,引入非惯性系(旋转坐标系)使艇体保持不动,由水绕艇体旋转并添加动量源项的方法,实现了全附体潜艇模型回转流场的数值模拟。国内对潜体旋转导数求取尚处于发展阶段,从方法上不能同时保证精度和效率。为了兼顾精度和效率,邓峰等[20]以分区结构化网格为基础,采用基于固定坐标系的滑移网格方法,对Suboff进行旋臂试验数值仿真,结果表明该方法对高效率、高精度求解旋转导数具有一定参考价值。
对直线拖曳试验、回转臂试验的操纵性数值模拟均有较成熟的研究,而对平面运动机构试验等非定常运动的数值计算由于涉及到动网格技术,仍处在探索阶段[21-22]。
庞永杰等[23]利用CFD技术和动网格技术模拟计算了椭球体和潜体小振幅PMM试验中的水动力,动网格处理采用Hrvoje Jasak和Zeljko Tukovic方法,求取了潜体惯性水动力系数和粘性水动力系数,证明了方法的可行性,为潜体PMM的数值模拟作了有益的探讨。ZHANG等[24]基于Fluent软件和动网格技术,通过编写UDF函数控制四面体网格节点位移来实现网格运动,实现了PMM的数值模拟,求得了潜水器相应的惯性类和粘性类水动力系数。动网格技术易发生变形和重生,为了解决网格变形问题,寇冠元等[25]采用一种边界滑移动网格技术,在网格不会发生畸变与重生的前提下,对潜水器的纯首摇运动进行数值模拟。
由于六面体网格(结构化网格)较四面体网格(非结构化网格)在计算收敛性、对数值耗散的抑制以及网格正交性等方面具有优势,基于六面体网格的数值计算结果将更为可信,于是利用六面体网格进行PMM试验的数值模拟势必成为以后主要的研究方向。孙铭泽等[26]基于Ansys CFX软件,以全附体Suboff潜艇为分析对象,利用全局映射式六面体网格进行空间离散,实现了潜艇小振幅PMM试验的数值仿真。将计算结果与试验数据进行对比,证明了该方法在计算水动力系数时的可靠性。针对动网格计算存在的计算资源消耗较大及收敛性不佳等问题[27],胡志强等[28]构建了一种基于随体坐标系采用附加动量源法的水下机器人水动力数值计算方法,该方法对水下机器人各种非定常运动实现了基于静态网格的CFD 计算,并统一了黏性类水动力和惯性类水动力计算框架体系。
3.2 某水下自主航行器数值计算数值计算求取惯性类水动力系数,仍然达不到兼顾计算的精度和效率。CFD技术的迅猛发展为数值计算水动力系数提供了多元化的选择,Star CCM+软件特有的多面体网格可以兼顾计算精度和效率,无需编程直接数值模拟PMM试验的模块更是为数值计算减少了难度。本文以实验室某水下自主航行器为模型运用Star CCM+进对其PMM和VPMM进行模拟计算。
某水下自主航行器的基本尺寸如表1所示。
|
|
表 1 航行器的基本尺寸 Tab.1 Basic parameters of AUV |
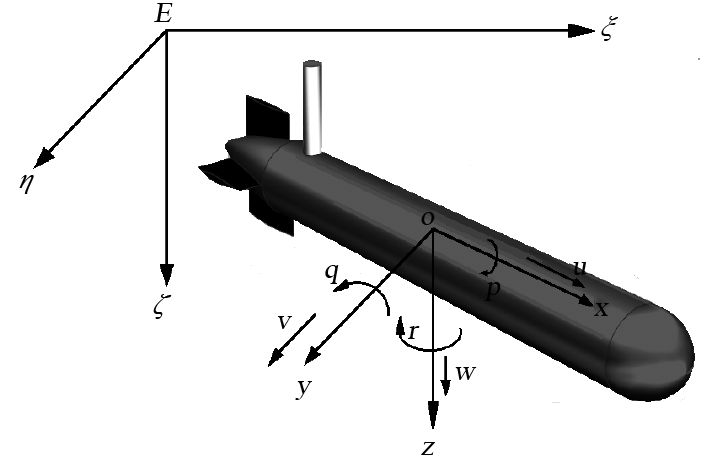
选用UG建模软件对该水下自主航行器进行1:1建模,为建立自主水下航行器空间操纵性运动的数学模型,选择采用ITTC和SNAME等组织公认的坐标系,包括固定坐标系E-ξηζ(简称“定系”)和运动坐标系G-xyz(简称“动系”)。所建模型及关于2种坐标系的具体规定如图1所示。
|
图 1 水下航行器模型 Fig. 1 Underwater vehicles model |
运用Star CCM+的PMM模块设置好运动频率以及航行器的基本参数,进行纯横荡和纯首摇2种运动的计算。将计算结果通过傅里叶积分进行数据处理,获取相应的水动力系数及无因次化后的结果,所得结果如表2所示。
|
|
表 2 平面运动机构水动力系数结果 Tab.2 Hydrodynamic coefficients of PMM |
由于Star CCM+默认的PMM模块只能模拟水平面(XOY)内的纯横荡和纯首摇运动,而对于垂直面(XOZ)内的纯升沉和纯俯仰运动却束手无策。在研究过程中,采用该软件中的Translation模块对VPMM试验进行数值模拟,在此之前通过该模块对纯横荡和纯首摇进行模拟,模拟结果与PMM模块所得结果进行对比验证,验证结果如表3所示。
|
|
表 3 方法验证结果 Tab.3 Method verification results |
所得误差在工程应用中可以接受,对VPMM中纯升沉和纯俯仰2种运动的水动力系数计算结果如表4所示。
|
|
表 4 垂直型平面运动机构水动力系数 Tab.4 Hydrodynamic coefficients of VPMM |
1)通过一定数量的研究,对本文讨论的3种方法的适用范围及存在的问题进行讨论。国内现有的潜体操纵运动水动力估算公式形式简单,不能充分、准确地反映潜水器外型的变化,所以实用性和预报精度达不到工程实用要求,通过近似公式估算的方法适用于设计的最初期,特别适用于主体较规则的椭球体潜水器,能够得到该设计模型水动力性能优劣的基本评价;基于势流理论的面元法能够获得惯性类水动力系数,虽然忽略了流体粘性,但是结果精度相对较高,适用于模型设计完成之后。
2)模型试验法可以较精准测定预报潜体操纵性所需要的水动力系数,但是需要耗费大量的人力、物力和时间,不利于潜水器尤其是小成本潜水器的开发和利用,多用于研究对精度要求较高的功能性潜体和验证数值计算、半经验半理论计算方法的准确性。
3)数值计算方法为获取潜体水动力系数提供了新的方向,几乎涵盖了半经验半理论计算方法和模型试验的全部优点,研究范围也最广。由于Suboff潜艇实验数据完整,所以数值方法目前的研究主要是计算Suboff潜艇的水动力系数,并与试验结果对比验证方法精度,对于潜艇的数值计算方法获取水动力系数已经日趋成熟。然而,对于潜水器水动力系数的数值计算过程主要延用了潜艇的方法,会带来一定的误差。潜水器相比潜艇,灵活性更高,同样的误差等级会给所得结果带来更大的影响,所以与潜艇采用相同的数值计算处理方法存在一定的不合理性。
5 展 望对于潜体水动力系数计算虽然取得了很多成果,但是随着潜体尤其是潜水器的多样化发展,对潜体水动力系数的精度提出了更高的要求。因此,对于潜体水动力系数计算仍有很多方面需要进一步研究:
1)模型试验存在天平量程、流速、循环水槽大小等造成误差的因素,在日后的试验中,试验前应对这3个量的数值进行反复确认,缩小误差。
2)数值模拟应与实际航行情况一致,目前多数研究为了计算简便,忽略了螺旋桨的影响[29 – 31],为了使模拟结果趋于真实情况,对于带桨潜体的数值计算需要进一步深入研究。
3)数值计算过程中忽略了重、浮心相对位置等对潜水器水动力的影响,在以后的研究中应将该因素考虑在内,减小与实际结果的误差。
4)数值计算效率与精度达不到统一,数值模拟时注意选取恰当的网格技术,在保证精度的情况下,提高计算效率,模拟不同的运动选取恰当的湍流模型,保证计算结果与实际相符合。
5)进一步研究潜艇与潜水器数值方法获取水动力系数的不同,实现通过数值方法获得高精度的潜水器水动力系数。
6)对于潜水器的近似公式多采用潜艇、鱼雷等的经验公式,日后应在进行大量试验和精确的数值模拟后获取潜水器的水动力系数估算公式。
| [1] |
徐玉如, 苏玉民, 庞永杰. 海洋空间智能无人运载器技术发展展望[J]. 中国舰船研究, 2006, 1(3): 1-4. XU Yu-ru, SU Yu-min, PANG Yong-jie. Expectation of the development in the technology on ocean space intelligent unmanned vehicles[J]. Naval Science and Technology, 2006, 1(3): 1-4. DOI:10.3969/j.issn.1673-3185.2006.03.001 |
| [2] |
张赫, 庞永杰, 李晔. 潜水器水动力系数计算方法研究[J]. 武汉理工大学学报, 2011, 35(1): 15-18. ZHANG He, PANG Yong-jie, LI Ye. Study of AUV’s hydrodynamic coefficients calculation methods[J]. Journal of Wuhan University of Technology(Transportation Science& Engineering), 2011, 35(1): 15-18. DOI:10.3963/j.issn.1006-2823.2011.01.004 |
| [3] |
张晓频. 多功能潜水器操纵性能与运动仿真研究[D]. 哈尔滨: 哈尔滨工程大学, 2009.
|
| [4] |
MANSOORZADEH S, JAVANMARD E. An investigation of free surface effects on drag and lift coefficients of an autonomous underwater vehicle (AUV) using computational and experimental fluid dynamics methods[J]. Journal of Fluids & Structures, 2014, 51(1): 161-171. |
| [5] |
GALA F L, DUBBIOSO G, ORTOLANI F, et al. Preliminary evaluation of control and manoeuvring qualities for the AUTODROP-UUV vehicle[J]. Ifac Proceedings Volumes, 2012, 45(27): 132-137. DOI:10.3182/20120919-3-IT-2046.00023 |
| [6] |
李刚. 穿梭潜器水动力特性的数值模拟和试验研究[D]. 哈尔滨: 哈尔滨工程大学, 2011.
|
| [7] |
AVILA J P J, ADAMOWSKI J C. Experimental evaluation of the hydrodynamic coefficients of a ROV through Morison’s equation[J]. Ocean Engineering, 2011, 38(17): 2162-2170. |
| [8] |
XU F, ZOU Z J, YIN J C, et al. Identification modeling of underwater vehicles’ nonlinear dynamics based on support vector machines[J]. Ocean Engineering, 2013, 67: 68-76. DOI:10.1016/j.oceaneng.2013.02.006 |
| [9] |
赵金鑫. 某潜器水动力性能计算及运动仿真[D]. 哈尔滨: 哈尔滨工程大学, 2011.
|
| [10] |
庞永杰, 王庆云, 李伟坡. 螺旋桨及其运行对潜艇操纵性水动力影响的模型试验研究[J]. 哈尔滨工程大学学报, 2017, 38(1): 109-114. PANG Yong-jie, WANG Qing-yun, LI Wei-po. Model test study of influence of propeller and its rotation on hydrodynamics of submarine maneuverability[J]. Journal of Harbin Engineering University, 2017, 38(1): 109-114. |
| [11] |
张赫, 庞永杰, 李晔. 基于FLUENT软件模拟平面运动机构试验[J]. 系统仿真学报, 2010, 22(3): 566-569. ZHANG He, PANG Yong-jie, LI Ye. Numeral simulation of hydrodynamic tests using FLUENT[J]. Journal of System Simulation, 2010, 22(3): 566-569. |
| [12] |
张玲, 谢殿伟. 水下机器人惯性类水动力计算研究[J]. 设计与研究, 2004(3): 8-10. ZHANG Ling, XIE Dian-wei. Calculation and study on inertial hydrodynamics force of underwater robot[J]. Ship & Boat, 2004(3): 8-10. |
| [13] |
李刚, 段文洋, 郭志彬. 复杂构型潜器附加质量的研究[J]. 哈尔滨工业大学学报, 2010, 42(7): 1145-1148. LI Gang, DUAN Wen-yang, GUO Zhi-bin. Added mass of submerged vehicles with complex shape[J]. Journal of Harbin Engineering University, 2010, 42(7): 1145-1148. |
| [14] |
潘子英, 吴宝山, 沈泓萃. CFD在潜艇操纵性水动力工程预报中的应用研究[J]. 船舶力学, 2004, 8(5): 42-51. PAN Zi-ying, WU Bao-shan, SHEN Hong-cui. Research of CFD application in engineering estimation of submarine maneuverability hydrodynamic forces[J]. Journal of Ship Mechanics, 2004, 8(5): 42-51. DOI:10.3969/j.issn.1007-7294.2004.05.006 |
| [15] |
詹成胜, 刘祖源, 程细得. 潜艇水动力系数数值计算[J]. 船海工程, 2018, 37(5): 1-44. ZHAN Cheng-sheng, LIU Zu-yuan, CHENG Xi-de. Numerical calculation of the submarine hydrodynamic coefficients[J]. Ship&Ocean Engineering, 2018, 37(5): 1-44. DOI:10.3963/j.issn.1671-7953.2018.05.001 |
| [16] |
柏铁朝, 梁中刚, 周轶美, 等. 潜艇操纵性水动力数值计算中湍流模式的比较与运用[J]. 中国舰船研究, 2010, 5(2): 22-28. BAI Tie-chao, LIANG Zhong-gang, ZHOU Yi-mei, et al. Comparison and application of turbulence modes in submarine maneuvering hydrodynamic forces computation[J]. Chinese Journal of Ship Research, 2010, 5(2): 22-28. DOI:10.3969/j.issn.1673-3185.2010.02.005 |
| [17] |
曹留帅, 朱军, 黄昆仑, 等. 全附体潜艇模型回转运动流场数值模拟[J]. 海军工程大学学报, 2015, 27(4): 17-20. CAO Liu-shuai, ZHU Jun, HUANG Kun-lun, et al. Numerical simulation of fully appended submarine model in steady turn[J]. Jounarnal of Naval University of Engineering, 2015, 27(4): 17-20. |
| [18] |
卢锦国, 梁中刚, 周轶美, 等. 湍流模型及网格分布对水下航行体回转水动力数值计算影响研究[C]// 中国cae工程分析技术年会暨2011全国计算机辅助工程. 2011. LU Jin-guo, LIANG Zhong-gang, ZHOU Yi-mei, et al. Numiereal calculation of forces and moments on submerge body in turning motion[C]// China CAE Engineering Analysis Technology Annual Conference and 2011 National Computer Aided Engineering. 2011. |
| [19] |
XIAO C, LIU R, XU K, et al. Simulation for submarine rotating-arm tests[J]. Journal of Jiangsu University of Science & Technology, 2014. |
| [20] |
邓峰, 戴余良, 陈志法, 等. 基于滑移网格的潜艇旋臂试验数值模拟[J]. 指挥控制与仿真, 2016(1): 122-126. DENG Feng, DAI Yu-liang, CHEN Zhi-fa, et al. Sliding mesh based on numerical simulation of rotating arms tests for submarines[J]. Command Control & Simulation, 2016(1): 122-126. DOI:10.3969/j.issn.1673-3819.2016.01.026 |
| [21] |
林兆伟, 孟生, 殷洪, 等. 潜器操纵性水动力系数的数值预报方法[J]. 中国造船, 2016, 57(1): 59-68. LIN Zhao-wei, MENG Sheng, YIN Hong, et al. Numerical approaches for predicting hydrodynamic coefficients of submersible[J]. Ship Building of China, 2016, 57(1): 59-68. DOI:10.3969/j.issn.1000-4882.2016.01.007 |
| [22] |
黄昆仑, 庞永杰, 苏玉民, 等. 潜器线性水动力系数计算方法研究[J]. 船舶力学, 2008, 12(5): 697-705. HUANG Kun-lun, PANG Yong-jie, SU Yu-min, et al. Research on linearity hydrodynamic coefficients calculation method of submarine vehicle[J]. Journal of Ship Mechanics, 2008, 12(5): 697-705. DOI:10.3969/j.issn.1007-7294.2008.05.004 |
| [23] |
庞永杰, 杨路春, 李宏伟, 等. 潜体水动力导数的CFD计算方法研究[J]. 哈尔滨工程大学学报, 2009, 30(8): 903-908. PANG Yong-jie, YANG Lu-chun, LI Hong-wei, et al. Approaches for predicting hydrodynamic characteristics of submarine objects[J]. Journal of Harbin Engineering University, 2009, 30(8): 903-908. DOI:10.3969/j.issn.1006-7043.2009.08.010 |
| [24] |
ZHANG H, XU Y R, CAI H P. Using CFD software to calculate hydrodynamic coefficients[J]. Journal of Marine Science & Application, 2010, 9(2): 149-155. |
| [25] |
寇冠元, 殷洪, 林兆伟, 等. 基于数值水池的潜艇横摇运动仿真[J]. 舰船科学技术, 2012, 34(3): 26-31. KOU Guan-yuan, YIN Hong, LIN Zhao-wei, et al. Simulation of submarine rolling based on the numerical tank[J]. Ship Science and Technology, 2012, 34(3): 26-31. DOI:10.3404/j.issn.1672-7649.2012.03.005 |
| [26] |
孙铭泽, 王永生, 张志宏, 等. 基于网格变形技术的全附体潜艇操纵性计算[J]. 武汉理工大学学报(交通科学与工程版), 2013, 37(2): 46-56. SUN Ze-ming, WANG Yong-sheng, ZHANG Zhi-hong, et al. Simulation of submarine rolling based on the numerical tank[J]. Ship Science and Technology, 2013, 37(2): 46-56. |
| [27] |
RACINE B, PATERSON E. CFD-Based method for simulation of marine-vehicle maneuvering[C]//Aiaa Fluid Dynamics Conference and Exhibit. 2013: 42–47.
|
| [28] |
胡志强, 衣瑞文, 林扬, 等. 基于随体坐标系的水下机器人水动力数值计算方法[J]. 科学通报, 2013, 58(Suppl. II): 55-66. HU Zhi-qiang, YI Rui-wen, LIN Yang, et al. Numerical calculation methods for hydrodynamics of unmanned underwater vehicles based on body-fixed coordinate frames[J]. China Science Press, 2013, 58(Suppl. II): 55-66. |
| [29] |
CAO Liu-shuai, ZHU Jun, WANG Wen-bin. Numerical Investigation of Submarine Hydrodynamics and Flow Field in Steady Turn[J]. China Ocean Engineering, 2016, 30(1): 57-68. DOI:10.1007/s13344-015-0076-1 |
| [30] |
ZAGHI S, MASCIO A D, BROGLIA R, et al. Application of dynamic overlapping grids to the simulation of the flow around a fully-appended submarine[J]. Mathematics & Computers in Simulation, 2015, 116(C): 75-88. |
| [31] |
WU X, WANG Y, HUANG C, et al. An effective CFD approach for marine-vehicle maneuvering simulation based on the hybrid reference frames method[J]. Ocean Engineering, 2015(109): 83-92. |
 2019, Vol. 41
2019, Vol. 41
