弹射式导弹发射装置采用具有高内能的气体作为工质,通过其膨胀做功来增加导弹的动能和势能,使导弹达到一定的出筒速度,从而完成发射任务。常见的弹射用工质主要包括高压冷空气和固体推进剂燃气。燃气蒸汽式发射装置[1 – 5]则是利用高温燃气和冷却水的掺混物作为工质,通过调节气/水混合比来实现弹射用工质的能量调节,从而满足不同的发射速度需求[4 – 8]。通常情况下工质温度可以达到1 500~2 000 K[5, 7]。在发射过程中,弹射用工质如果直接作用到导弹尾部,导弹发动机的喷管会承受比较严酷的力、力矩和热载荷,这就对发射装置设计提出了较高的要求。特别是工质来流侧向进入发射筒,导弹发动机的喷管承受载荷更加严酷。本文将对发射筒底部的流场和导弹发动机喷管的降载方法进行研究,以改善筒底环境,降低喷管受力。
1 发射筒底部流场数值模拟方法1)问题简化处理方法
对于整个发射过程来说,发射系统启动后弹射工质先在筒底充填建压,随后导弹在发射筒内开始运动,因而筒底流场数值模拟属于典型的非稳态动网格问题。但对于本文的研究来说,试验数据显示导弹运动100 ms之后喷管所受载荷已经恢复正常。根据实测的导弹运动速度可以计算出此时导弹位移量约占筒底自由容积高度的4%~5%,因而将问题简化为固定网格问题在一定程度上是可行的。
尽管燃气—蒸汽式发射装置的弹射用工质是燃气和水的混合物,但从前期大量的研究来看该装置的冷却水在高温燃气中已经形成了过饱和蒸汽。即绝大部分水主要以气态形式存在,对于存在的少量液态水(总质量不超过2%)而言可以将其忽略。因而,发射筒底部流场可以当成纯气相来处理。介质的详细组分则根据发射动力装置的水/气掺混计算结果来确定。
2)流场控制方程及数值解法
流场控制方程采用三维雷诺平均N-S方程,该方程可以采用如下式所示的守恒形式[9]:
| $\frac{\partial }{{\partial t}}\int_\varOmega {W{\rm d}V} + \int_{\partial \varOmega } {(F(W) - G(W)) \cdot n{\rm d}S} = \int_\varOmega {H{\rm d}V}{\text{。}} $ |
其中:W为守恒向量
所采用的湍流模型为RNG k-
| $\rho \frac{{Dk}}{{Dt}} = \frac{\partial }{{\partial {x_i}}}\left[{\alpha _k}{\mu _{eff}}\frac{{\partial k}}{{\partial {x_i}}}\right] + {G_k} + {G_b} - \rho \varepsilon - {Y_M}{\text{,}}$ |
| $\,\rho \frac{{D\varepsilon }}{{Dt}} = \frac{\partial }{{\partial {x_i}}}\left({\alpha _\varepsilon }{\mu _{eff}}\frac{{\partial \varepsilon }}{{\partial {x_i}}}\right) \!+\! {C_{1\varepsilon }}\frac{\varepsilon }{k}\left({G_k} \!+\! {C_{3\varepsilon }}{G_b}\right) \!-\! {C_{2\varepsilon }}\rho \frac{{{\varepsilon ^2}}}{k} \!-\! R{\text{。}}$ |
式中各参数的具体含义参考相关文献[9]。
对于该问题,本文求解的物理时间长度为0.4 s,其中导弹开始运动时间约在200 ms。根据网格划分、流场速度分布及所用的数值求解方法,将非稳态计算的时间步长设为5 μs。在求解过程中,时间方向上采用具有4阶精度的R-K方法。由于筒底入口气流为超声速,在空间方向上采用具有二阶精确度的MUSCL格式进行求解。
根据发射筒底部结构的特点,混合采用了结构化和非结构化网格划分,流场共划分为16个区块,网格总数约290万(原始构型)和320万(改进构型)。为了便于进行结果分析,将筒底流场区域分为了4个象限。
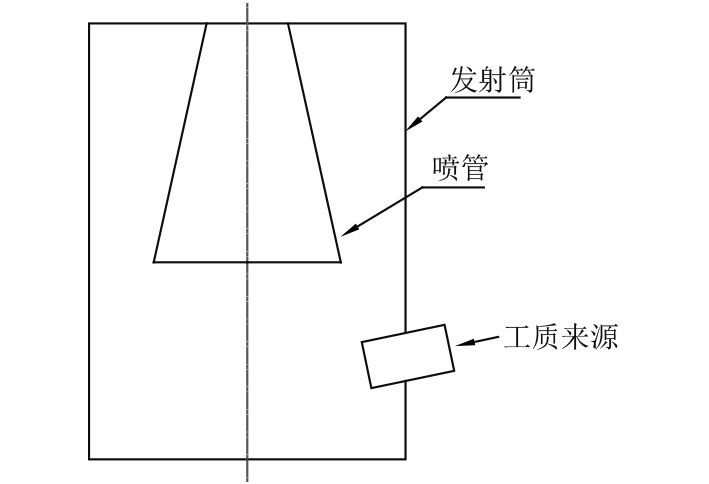
|
图 1 发射筒底部结构示意图 Fig. 1 Sketch of the launch tube bottom |
3)发射筒入口边界条件
发射筒底部入口采用了超声速流量入口条件,给定流量、马赫数和总温,其余边界均为壁面。流量入口参数由燃气发生器产生的高温高压燃气和喷注器产生的冷却水共同决定。在发射筒入口截面上有如下方程组:
连续方程
| ${\dot m_g} + {\dot m_w} = K\frac{p}{{\sqrt {{T_{t, m}}} }}A\frac{{q(M)}}{{{\text{π}} (M)}}{\text{,}}$ |
能量方程
| ${\dot m_g}{h_g}({T_g}) + {\dot m_w}{h_w}({T_0}) = \sum\limits_{i = 1}^n {{w_i}{h_i}({T_{t, m}})}{\text{,}} $ |
动量方程
| $\alpha {\dot m_g}{v_g} + {p_g}{A_g} = ({\dot m_g} + {\dot m_w})v + pA{\text{,}}$ |
状态方程
| $p = \rho R{T_m}{\text{,}}$ |
气体动力学方程
| ${T_m} = {T_{t, m}}\, \tau \left( M \right){\text{。}}$ |
其中:
由于不考虑燃气组分和冷却水之间的化学反应,各组分的质量分数
需要注意的是,尽管在发射过程中燃气的各组分的质量分数是保持不变的,但燃气和冷却水的流量却是不断变化的,这就决定了
为验证所采取的假设处理方法、数值计算模型和计算网格的可信度,利用全尺寸装置的发射试验数据进行校验。图2给出了燃气和冷却水流量的试验数据,利用其对发射筒入口参数进行计算,然后再对发射筒底部流场进行数值模拟。图3给出发射筒内特征位置处的压强数据对比。可以看出,CFD计算结果与试验数据的吻合程度较好。这表明可以利用所建立的数值模拟方法开展研究工作。
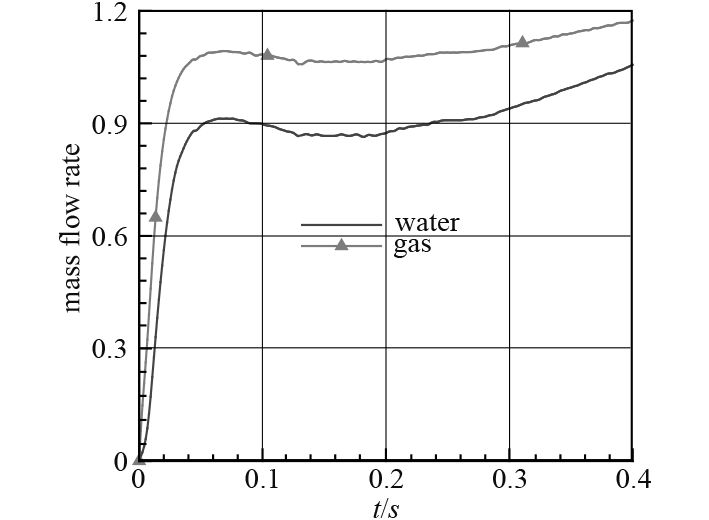
|
图 2 燃气和冷却水流量的试验数据 Fig. 2 Gas and cooling-water mass flow rate from experiment |
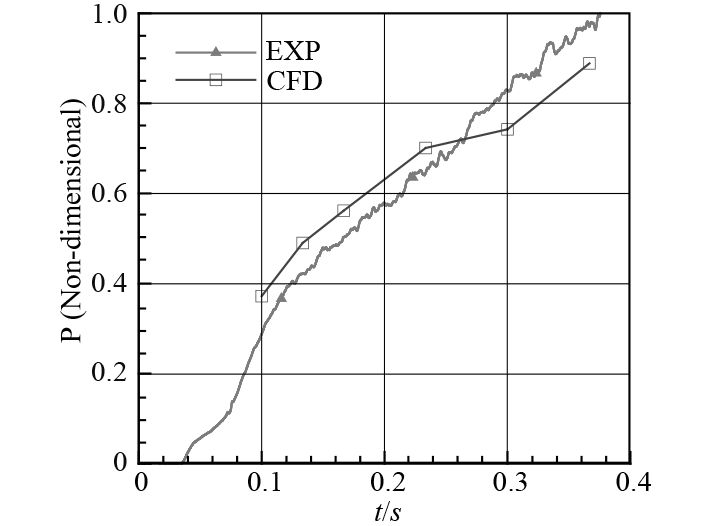
|
图 3 无量纲压强对比 Fig. 3 Non-dimensional pressure |
利用所选的数值模拟方法对该发射装置的筒底流场进行非稳态计算分析。由100 ms和300 ms时刻流线可以看出,流线从入口进入筒底,撞击底部壁面后反射、再进一步撞击侧壁面并改变流向,近乎很集中的作用到发动机喷管上。从图4所示的喷管外表面压强分布云图可以看出,不同位置的压强高低,从而导致喷管受到了很大的Z力矩,其最大值达到了1.15(无量纲处理后)。此外,工质气体对喷管的集中作用也必然会导致喷管局部的热载荷较严重,这与试验中所观测的结果一致。
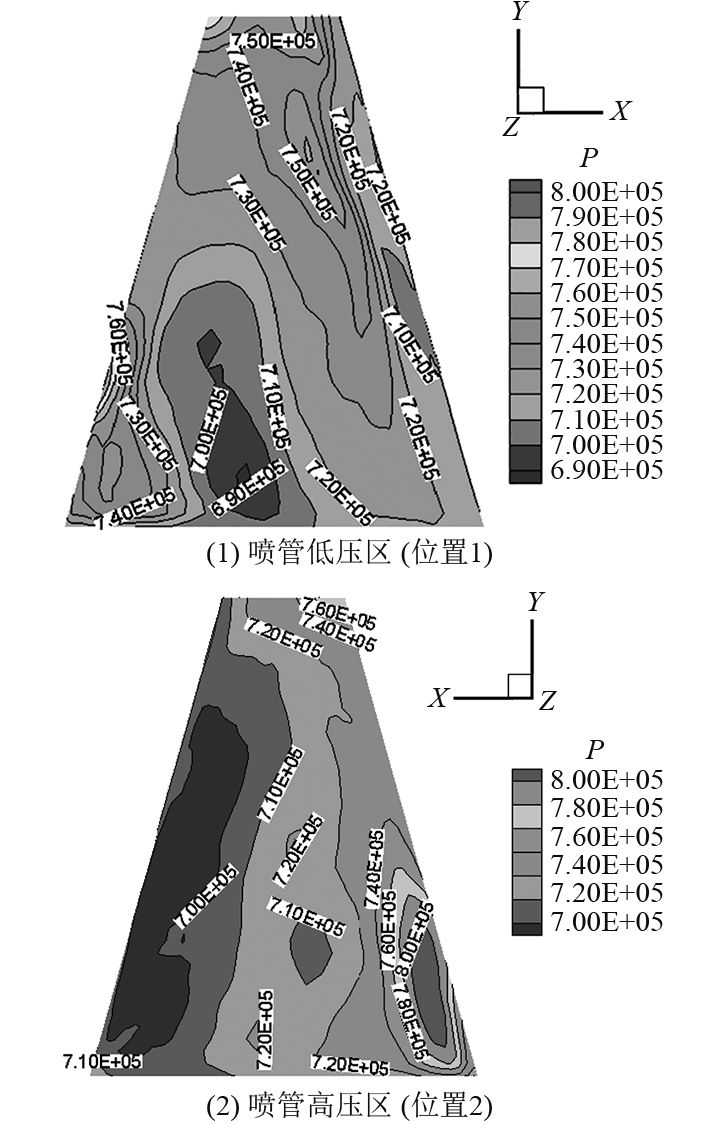
|
图 4 t=100 ms时喷管外表面高、低压强云图(位置对称) Fig. 4 Surface pressure contour at t=100 ms |
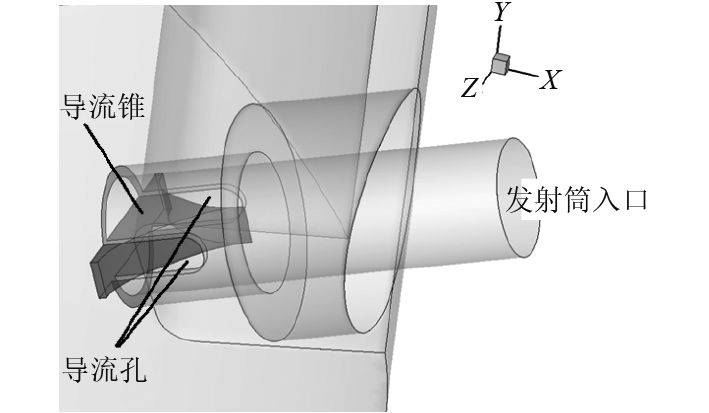
根据上述分析,设计如图5所示的导流装置,将其安装在发射筒入口通道截面上。两侧的导流孔可以对气流进行分流,以避免气流集中作用到发动机喷管上,从而达到降低喷管所受载荷的目的。
|
图 5 导流装置 Fig. 5 Diversion device |
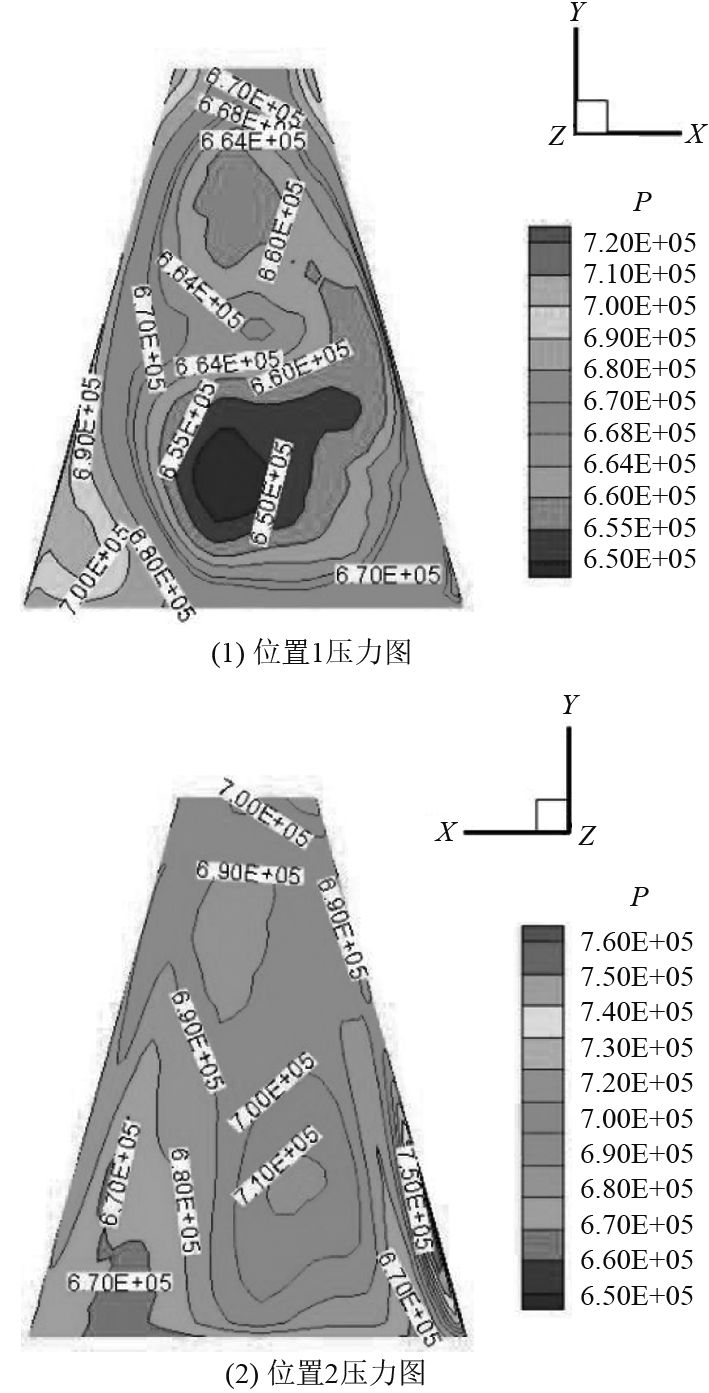
对所设计的改进方案进行数值模拟。图6给出100 ms时喷管外壁面的压强分布,可以看出喷管压强差已经明显缩小,且压强有显著差异的区域面积也在减小。这就意味着喷管所受的X力矩将得到显著改善。
|
图 6 t=100 ms时喷管外表面压强云图 Fig. 6 Nozzle surface pressure contour at t=100 ms |
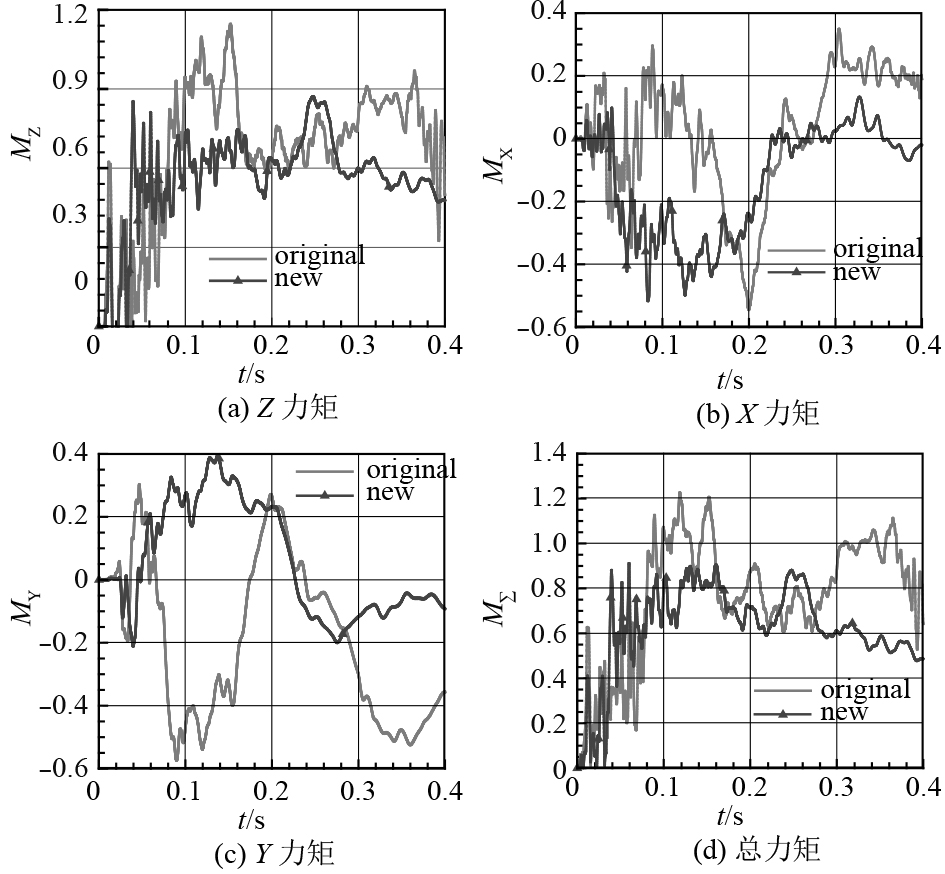
图7给出了经过无量纲处理的力矩对比。由图7(a)可以看出,最为关注的喷管Z力矩下降效果非常明显。在t=0.365 s时刻的降幅最大,达到47%。全程的最大Z力矩降幅为24%(由1.15降为0.87)。由于喷管实际所受的力矩是由X,Y,Z三个矢量所合成,因此研究喷管所受的总力矩更有实际意义。从图7(d)所示的总力矩数据可以看出,个别时刻的最大总力矩下降了53%(t=0.365 s),从整个时间历程来看,最大总力矩的降幅则为26%(由1.23降为0.91)。另外,从计算结果来看X力矩的下降效果并不明显。
|
图 7 喷管所受力矩对比 Fig. 7 Moments on nozzle |
利用该计算结果进行试验,喷管伺服机构所测得的数据均工作正常,从而证明所提出的改进措施很好降低了无尾罩发射时喷管载荷。
4 结 语1)试验数据验证结果表明所建立的三维数值模拟方法适用于燃气—蒸汽式发射装置筒底的非稳态流场研究。
2)对所研究的发射装置筒底流场进行了计算分析,发现工质气体近乎集中的作用在喷管特定区域是导致导弹尾喷管载荷超限的根本原因,在此基础上提出了合适的改进措施。
3)数值模拟和试验结果均表明所设计的导流降载装置能够很好降低喷管所受力矩。数值模拟表明喷管所受的最大Z力矩降幅为24%,最大总力矩的降幅为26%。
| [1] |
EDQUIST C. T. Prediction of the launch pulse for gas generator launched missiles[R]. AIAA-88-3290, 1988.
|
| [2] |
赵险峰, 王俊杰, 编著. 潜地弹道导弹发射系统内弹道学[M]. 哈尔滨: 哈尔滨工程大学出版社, 2001. 4.
|
| [3] |
吕翔, 李江, 陈剑, 等. 变深度水下发射系统内弹道实验研究[J]. 固体火箭技术, 2012, 35(1): 24-28. DOI:10.3969/j.issn.1006-2793.2012.01.005 |
| [4] |
肖虎斌. 潜射导弹燃气蒸汽式发射装置的内弹道建模[J]. 舰船科学技术, 2010, 32(2): 36-39. DOI:10.3404/j.issn.1672-7649.2010.02.008 |
| [5] |
肖虎斌, 赵世平. 燃气蒸汽式发射动力装置复杂内流场数值模拟[J]. 固体火箭技术, 2009, 32(4): 392-395. DOI:10.3969/j.issn.1006-2793.2009.04.009 |
| [6] |
李仁凤, 乐贵高, 马大为, 等. 进气角与注水规律对燃气蒸汽弹射的影响[J]. 航空动力学报, 2017, 32(4): 961-969. |
| [7] |
白俊华, 胡馨博. 进气角度和初始粒径对发射筒内流动特性的影响[J]. 固体火箭技术, 2013, 36(2): 165-169. |
| [8] |
常书丽, 吕翔, 王彦涛, 等. 基于蒙特卡洛方法的燃气蒸汽式发射装置内弹道参数分析方法[J]. 固体火箭技术, 2016, 39(6): 857-86. |
| [9] |
Fluent 6.0. User’s Guide[R]. Fluent Inc., 2006.
|
| [10] |
王保国, 刘淑艳, 黄伟光. 气体动力学[M]. 北京: 北京理工大学出版社, 2005.
|
| [11] |
SANFORD G. Computer program for calculation of complex chemical equilibrium compositions and applications[R]. NASA/RP 1994-1311.
|
 2018, Vol. 40
2018, Vol. 40
