2. 上海船舶设备研究所,上海 200031
2. Shanghai Marine Equipment Research Institute, Shanghai 200031, China
水下机器人在海洋工程和深海探索中运用广泛,但水下机器人转向力不足,抗风浪摆荡能力差,不易保持航行方向和姿态稳定。为水下机器人增加矢量推进装置,并通过算法控制液压驱动矢量推进装置,能按要求调整船体姿态,为了提升整机系统的响应速度、准确度等性能指标,需对液压系统的参数进行优化[1 – 2]。由于液压系统存在效率损失,因此会造成机械系统的运动与预期产生误差,而且这些损失随着液压泵、液压马达、液压缸排量、液压元件参数以及液压系统压力的不同而不同,不同参数组合得到的运动控制效果也不尽相同,而遗传算法在解决这类NP问题、非线性、多目标和多峰值问题方面效果显著[3 – 4]。克里金法在参数联系紧密且数量确定的情况下可以快速模拟响应面,进而得到优化值。因此可采用遗传算法和克里金法进行液压系统的参数优化。
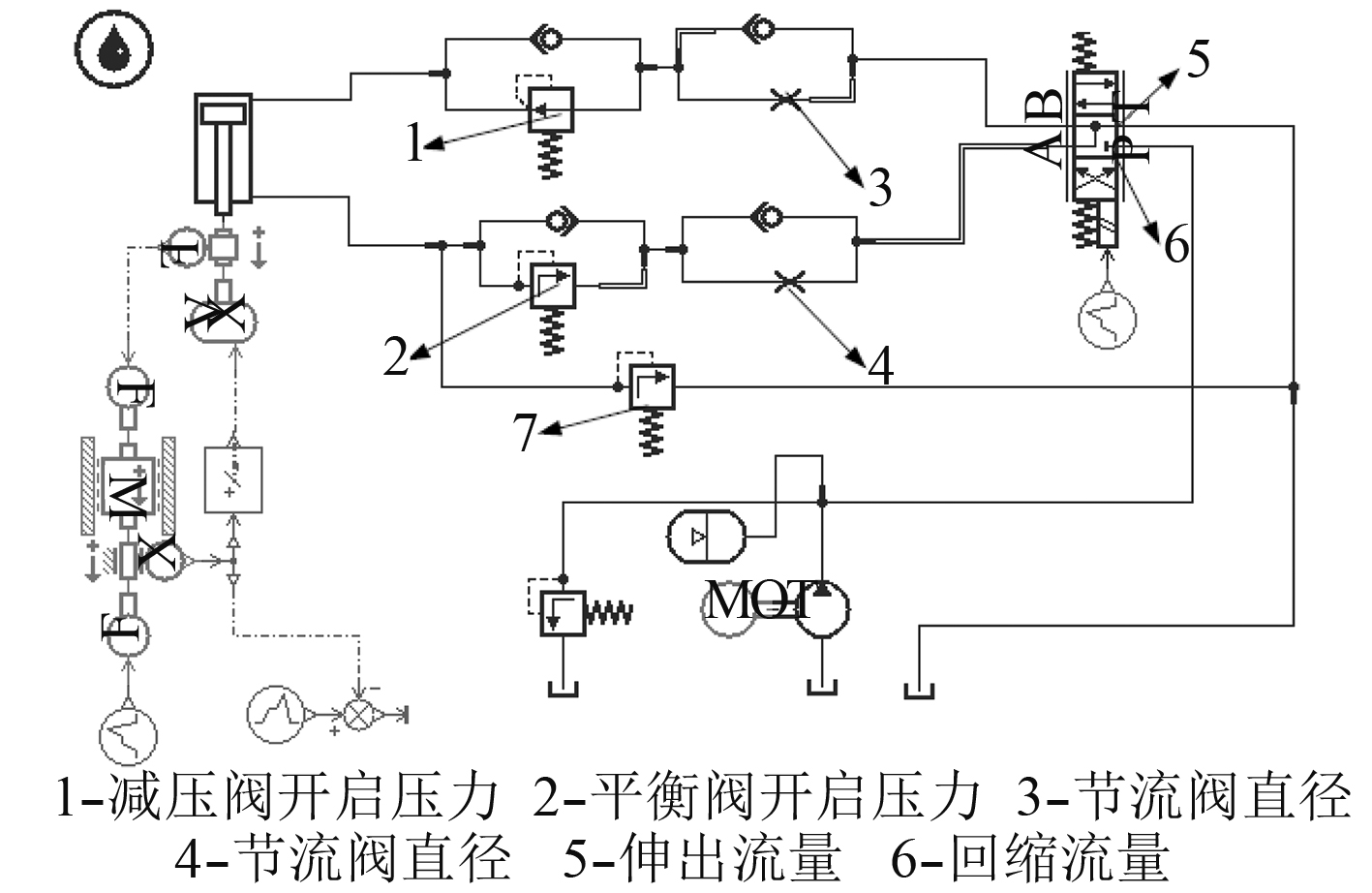
1 水下机器人矢量推进液压液压驱动系统为分析液压参数对矢量推进装置的运动影响,首先要考虑矢量推进装置的运动过程及其液压驱动回路。矢量推进装置要完成升降、回转和锁紧3个动作。3个液压驱动系统并联,故可分3部分分别进行优化设计。若对每个回路的所有液压参数进行优化设计,费时费力,且不易发现关键参数的作用。故可选取液压系统中关键元器件的参数进行优化设计。其关键元器件参数选取如图1~图3所示。
|
图 1 升降运动液压回路 Fig. 1 Lifting hydraulic circuit |
|
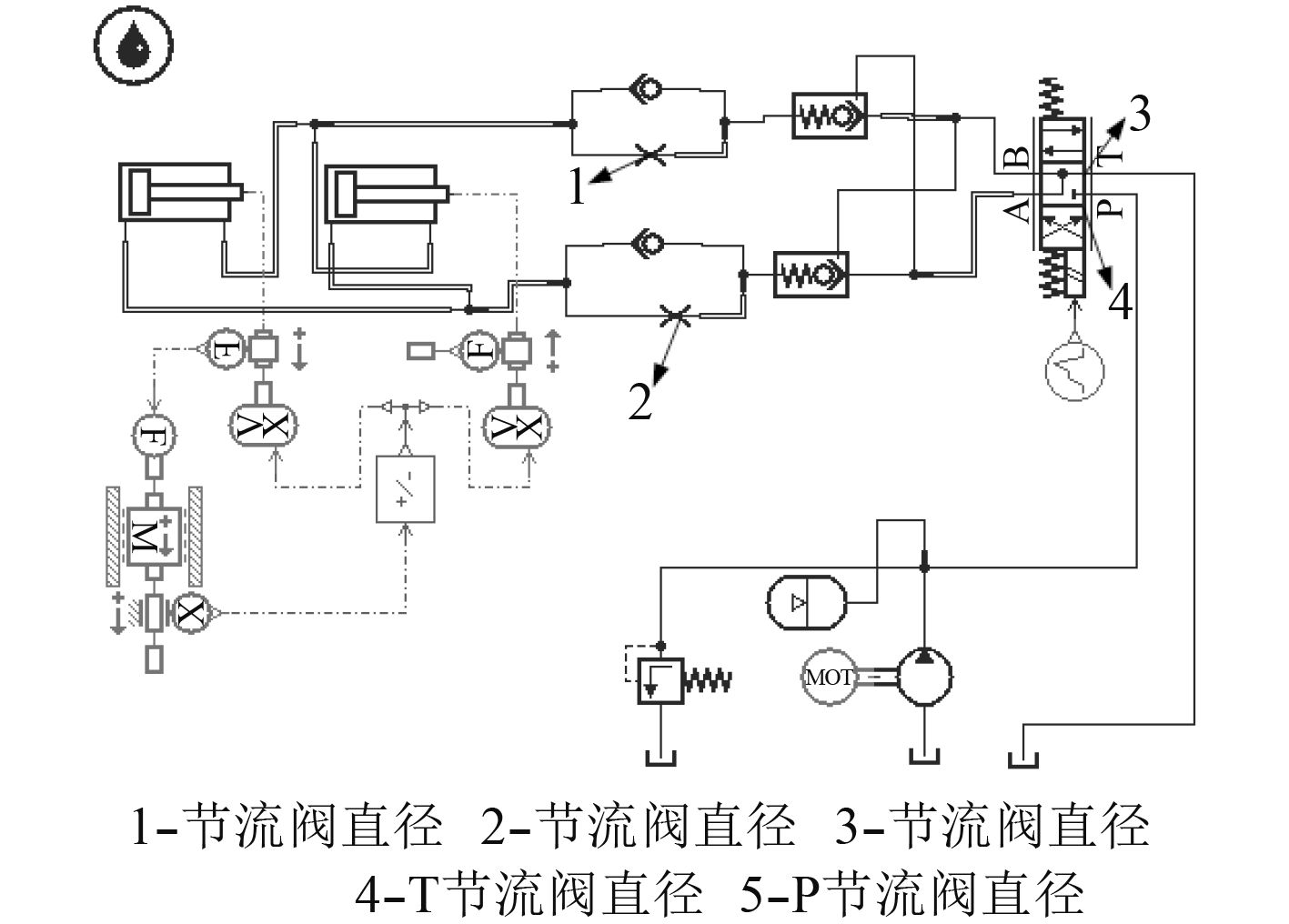
图 3 回转运动液压回路 Fig. 3 Rotary hydraulic circuit |
在保证完成既定动作的前提下需要协调好液压系统中的各主要参数,使得系统具有良好的作业性能、可靠性和高效性。因此需要进行液压系统参数优化。遗传算法相比实验统计方法不用求解系统的近似模型,不必考虑试验点的选取问题,可以给出各因素较大的取值范围。克里金法在参数数量确定情况下可以快速灵活对模型进行预测,因此液压参数部分采用遗传算法进行优化设计,液压控制模块的PID参数采用克里金算法。
2.1 遗传算法遗传算法(Genetic Algorithm,GA)是以自然选择和遗传理论为基础,将生物进化过程中适者生存规则与群体内部染色体的随机信息交换机制相结合的高效全局寻优搜索算法。遗传算法工具箱采用Sheffield遗传算法工具箱[5 – 7]。具体步骤为:
步骤1 编码与解码,确定待优化液压参数范围,将其写成二进制形式所需的位数。通过产生随机数来生成参数对应的二进制编码,并将所有二进制编码首尾连接成一条“染色体”,即为一个个体,多个个体形成种群。二进制解码公式如下:
| $x = L + \left( {\sum\limits_{i = 1}^k {{b_i}{2^{i - 1}}} } \right)\frac{{U - L}}{{{2^{k - 1}}}}{\text{。}}$ | (1) |
其中:
步骤2 适应度计算,将随机数产生的液压参数带入模型并仿真,将实际位移曲线和期望位移曲面的差值的均方根植最小作为控制目标,即适应度函数为:
| ${f_i} = 1 - \frac{{RM{S_i}}}{{\displaystyle\sum\limits_{k = 1}^N {RM{S_k}} }}{\text{。}}$ | (2) |
其中:
步骤3 设定迭代步、种群值、选择算子、交叉和变异算子等初始参数,代入Sheffield工具箱模板进行计算,求得参数优化值。
2.2 克里金法克里金法(Kriging)是一项实用的空间估计技术,其由一个参数模型和一个非参数随机过程联合构成。克里金法比单个的参数化模型具有更强的灵活性和预测能力,同时又克服了非参数化模型处理高维数据的局限性。克里金模型一般包含2部分:多项式和随机分布[8 – 9]。具体模型为:
| $y(x) = F(\beta ,x) + z(x) = {f^{\rm T}}(x)\beta + z(x){\text{。}}$ | (3) |
其中:
| $\operatorname{cov} [z({x_i}),z({x_j})] = {\sigma ^2}R[R({x_i},{x_i})]{\text{。}}$ | (4) |
拉丁超立方抽样,该方法能避免抽样点在小邻域内重合。基本原理如下:如果进行n次抽样,把m个随机变量都分成等概率的n个区间,故整个抽样空间被分成等概率的
步骤1 样本点选取,采用拉丁超立方抽样,设计空间为各液压元件参数取值的范围。
步骤2 系统响应计算,在选取
| $RMS = \sqrt {\frac{{\displaystyle\sum\nolimits_{i = 1}^{{n_s}} {\Delta y_i^2} }}{{{n_s}}}}{\text{。}} $ | (5) |
其中:
步骤3 将样本点和响应值作为已知信息
升降部分的运动为开环控制,抗干扰能力弱,控制精度较低,无自动纠偏能力。升降运动过程固定,各液压元件的压力流量可以根据实际要求计算得出,但元件参数较多,计算复杂,可以通过液压元件参数的匹配使得升降部分的运动符合预期的运动。
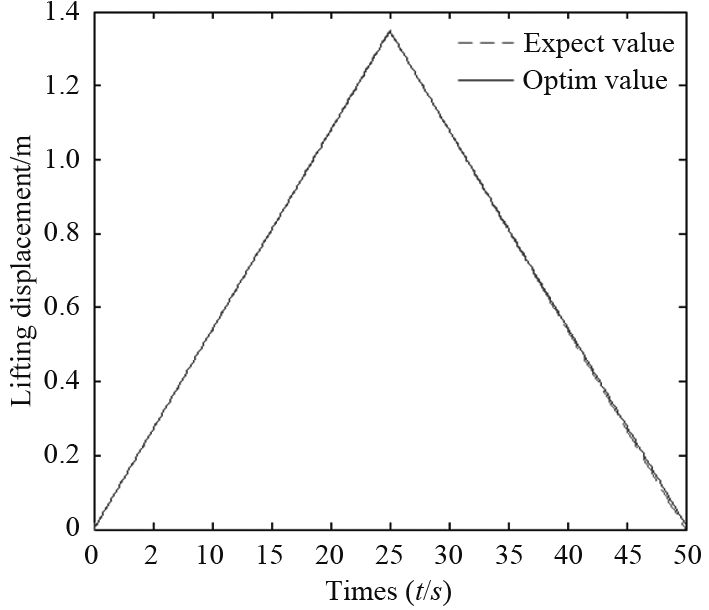
选择图1中4个元器件液压参数进行参数优化优化设计,如表1所示。优化算法采用遗传算法,期望运动曲线和优化曲线如图4所示。从图中可以看到升降部分的实际位移曲线与期望曲线吻合较好,两者的最大误差小于2 mm,控制在运动误差允许范围内。
|
|
表 1 升降运动液压参数优化范围和结果 Tab.1 Optimization range and results of hydraulic parameters for lifting motion |
|
图 4 升降回路优化结果 Fig. 4 Optimization results for lifting circuit |
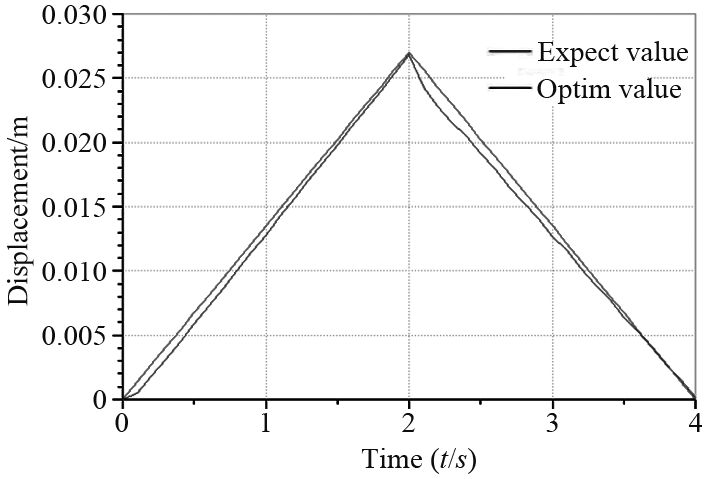
锁紧回路的运动也是开环控制,选择图2中4个液压元件,如表2所示。优化算法采用遗传算法,期望运动曲线和优化运动曲线如图5所示。
|
|
表 2 锁紧运动液压参数优化范围和结果 Tab.2 Optimization range and results of hydraulic parameters for locking motion |
|
图 5 锁紧回路优化结果 Fig. 5 Optimization results for locking circuit |
|
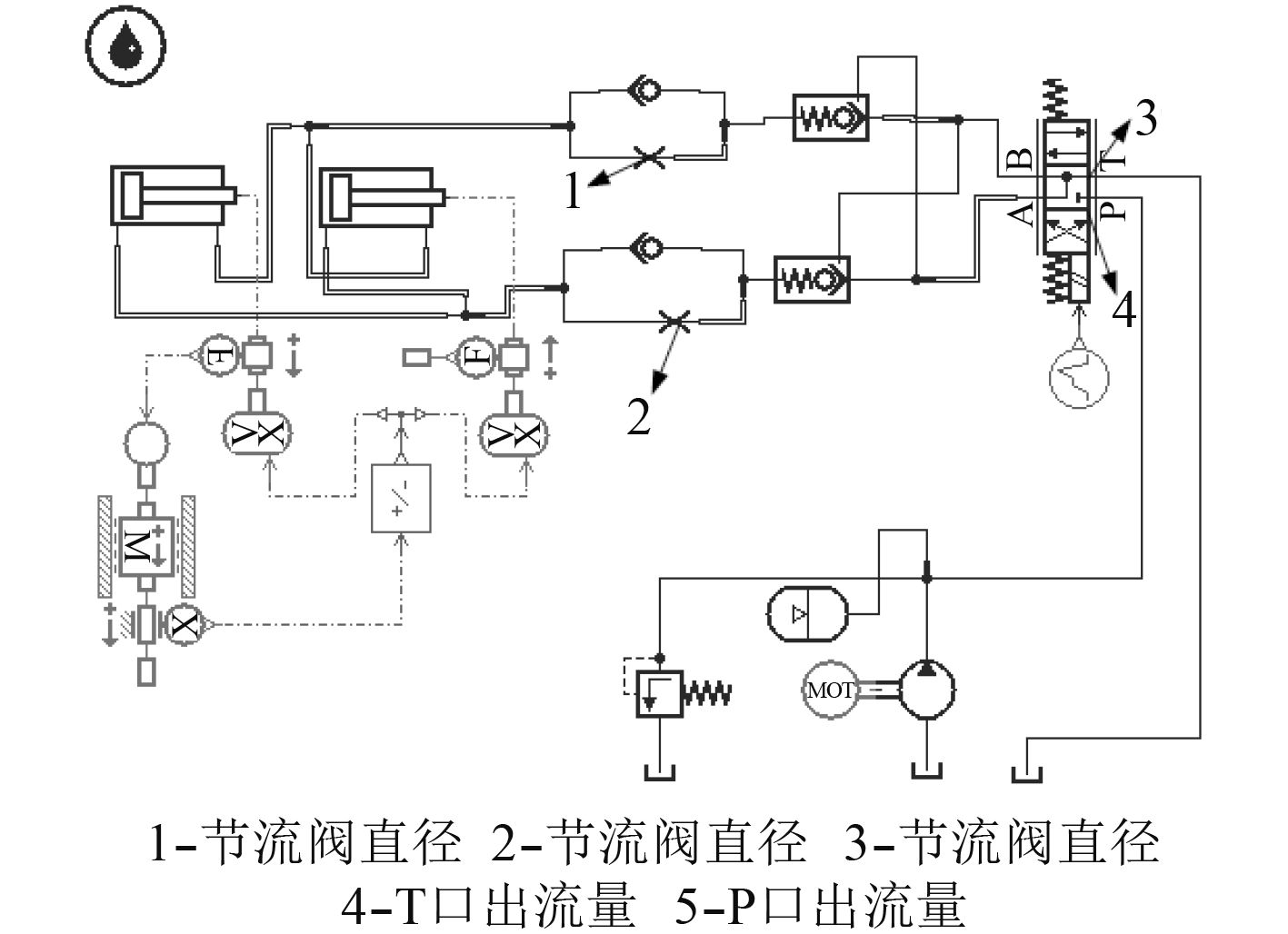
图 2 锁紧运动液压回路 Fig. 2 Locking hydraulic circuit |
从图中可看到实际位移曲线与期望曲线并没有完全重合,这是因为优化参数初始范围给定不合理,最优值在初始边界上获得,可通过调整优化范围来获得更优的优化值。但是在此回路中锁紧销实际能够在响应时间达到相应的位置,符合机构运动的要求。
3.3 回转回路液压参数优化设计回转部分采用PID闭环控制,液压参数选择图3中4个液压元件,如表3所示。优化算法采用遗传算法,期望运动曲线和优化曲线如图6所示。
|
|
表 3 回转运动液压参数优化范围和结果 Tab.3 Optimization range and results of hydraulic parameters for rotary motion |
|
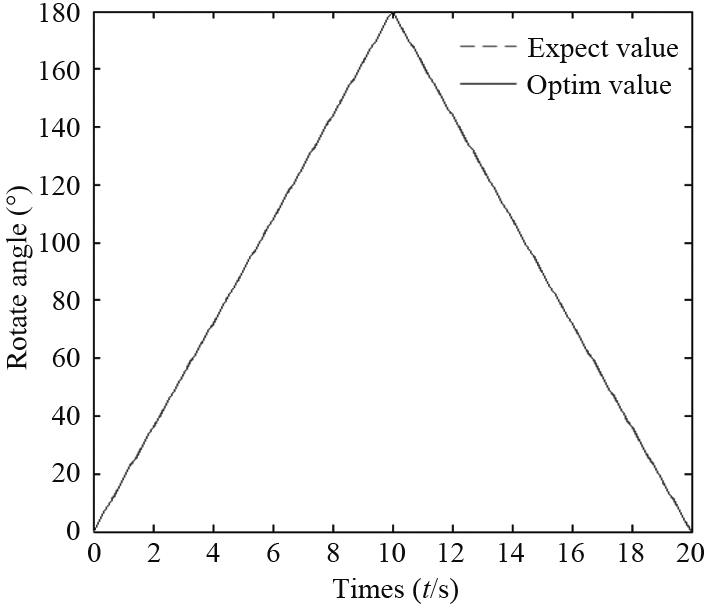
图 6 回转回路优化结果 Fig. 6 Optimization results for rotary circuit |
从图中可以看到回转回路的优化运动曲线与期望曲线重合度高,最大误差角度不超过0.9°。运动控制符合实际要求。
3.4 回转回路PID控制参数优化设计回转回路PID参数数量较少且联系紧密,可采用克里金法进行优化。优化参数范围及结果如表4所示。
|
|
表 4 回转回路PID参数优化范围及结果 Tab.4 Optimization range and results of PID of rotary circuit |
其中可以看出I相比P和D范围变化较小,选择P和D作克里金曲面如图7所示。从图中可看到在D=6.020 4,P=0.142 9处,曲面有一个凹处,即在该处取得最优值。

|
图 7 优化结果 Fig. 7 Optimization result |
矢量推进装置可以增加水下机器人任意工况下的转向力和抗风浪摆荡能力,有利于保持航行方向稳定和姿态稳定。通过对矢量推进装置液压系统的参数进行优化,可以提升整机系统的响应速度、准确度等性能指标,并改善部分元器件的工作状态。
| [1] |
ZHU K, CHEN Y, CAO J, et al. Design and research on high-speed on/off control hydraulic propeller for underwater vehicle propulsion[J]. American Society of Mechanical Engineers, 2009, 597-604. |
| [2] |
BAE J, BAK J, JIN S, et al. Optimal configuration and parametric design of an underwater vehicle manipulator system for a valve task[J]. Mechanism & Machine Theory, 2018, 123: 76-88. |
| [3] |
冯长宝, 韩忠伟, 孙沫莉. 遗传算法和神经网络在船舶柴油机故障诊断中的应用[J]. 舰船科学技术, 2006, 38(6): 40-42. FENG Changbao, HAN Zhongwei, SUN Moli. Genetic algorithm and neural network application in marine diesel engine fault diagnosis[J]. Ship Science and Technology, 2006, 38(6): 40-42. |
| [4] |
刘洋. 基于遗传算法的水下无人潜器结构特性优化分析[J]. 舰船科学技术, 2015, 37(9): 145-148. LIU Yang. Optimization analysis of structure of UUV based on genetic algorithm[J]. Ship Science and Technology, 2015, 37(9): 145-148. DOI:10.3404/j.issn.1672-7649.2015.09.029 |
| [5] |
LIU T, JU X Z. Parameter optimization of hydraulic hybrid vehicle based on genetic algorithm[J]. Applied Mechanics & Materials, 2010, 29–32: 1079-1084. |
| [6] |
HUI S. Multi-objective optimization for hydraulic hybrid vehicle based on adaptive simulated annealing genetic algorithm[J]. Engineering Applications of Artificial Intelligence, 2010, 23(1): 27-33. DOI:10.1016/j.engappai.2009.09.005 |
| [7] |
徐循. 基于遗传算法的船舶推力分配算法研究[J]. 舰船科学技术, 2018, 40(8): 55-57. XU Xun. Research on the method of ship thrust distribution based on genetic algorithm[J]. Ship Science and Technology, 2018, 40(8): 55-57. DOI:10.3404/j.issn.1672-7649.2018.08.011 |
| [8] |
DU J, MENG L, GU H, et al. Optimal design of clamping mechanism for AUV underwater docking device based on Kriging model[C]// Intelligent Robot Systems. IEEE, 2017: 310–314.
|
| [9] |
ZHANG T, XU X, XU S. Method of establishing an underwater digital elevation terrain based on Kriging interpolation[J]. Measurement, 2015, 63: 287-298. DOI:10.1016/j.measurement.2014.12.025 |
 2018, Vol. 40
2018, Vol. 40
