被动目标定位是水声界的一个难题。已有的试验表明,匹配场被动定位方法在条件满足情况下可以获得良好的被动定位结果[1]。Hinich的研究证明,匹配场定位的效果与接收阵观测到模式的数目有关,模式越少,定位效果越差[2]。而简正波各模式是随深度而变化的,为了尽可能提升定位的效果,传统的匹配场被动定位通常采用垂直阵列[3 – 5]。近些年尝试使用水平阵列进行匹配定位的方法,但水平阵在实际定位过程中同样存在缺陷,为满足模式采样的要求,水平阵列的尺寸要求较大[6 – 7],黄勇等[8]利用拖曳短线阵在水平方向的移动合成大的孔径,结合匹配场技术实现了声源定位。矢量水听器的出现为匹配场被动定位拓展出一片新的空间,李楠松等[9]将单矢量水听器与匹配场技术相结合,利用图像处理中的相位相关算法给出目标的距离信息。同时,十字阵等复杂阵列的使用可以有效提高被动声测量的准确度,克服目标空间方位模糊的问题[10]。然而对于运动平台而言,满足定位要求的水听器阵列受制于尺寸等的限制,收放困难,布设复杂,这制约了运动平台匹配场被动定位技术的应用。
本文在稳定噪声信号的假设条件之下,将单阵元依次放置于不同深度等效为一个垂直阵列,从而获得不同观测深度不同时段目标的声场数据,对该数据进行相位补偿,估计等效垂直阵测量场,然后利用该测量场结合匹配场原理,给出目标的位置。最后,通过仿真与实验数据验证方法的有效性。
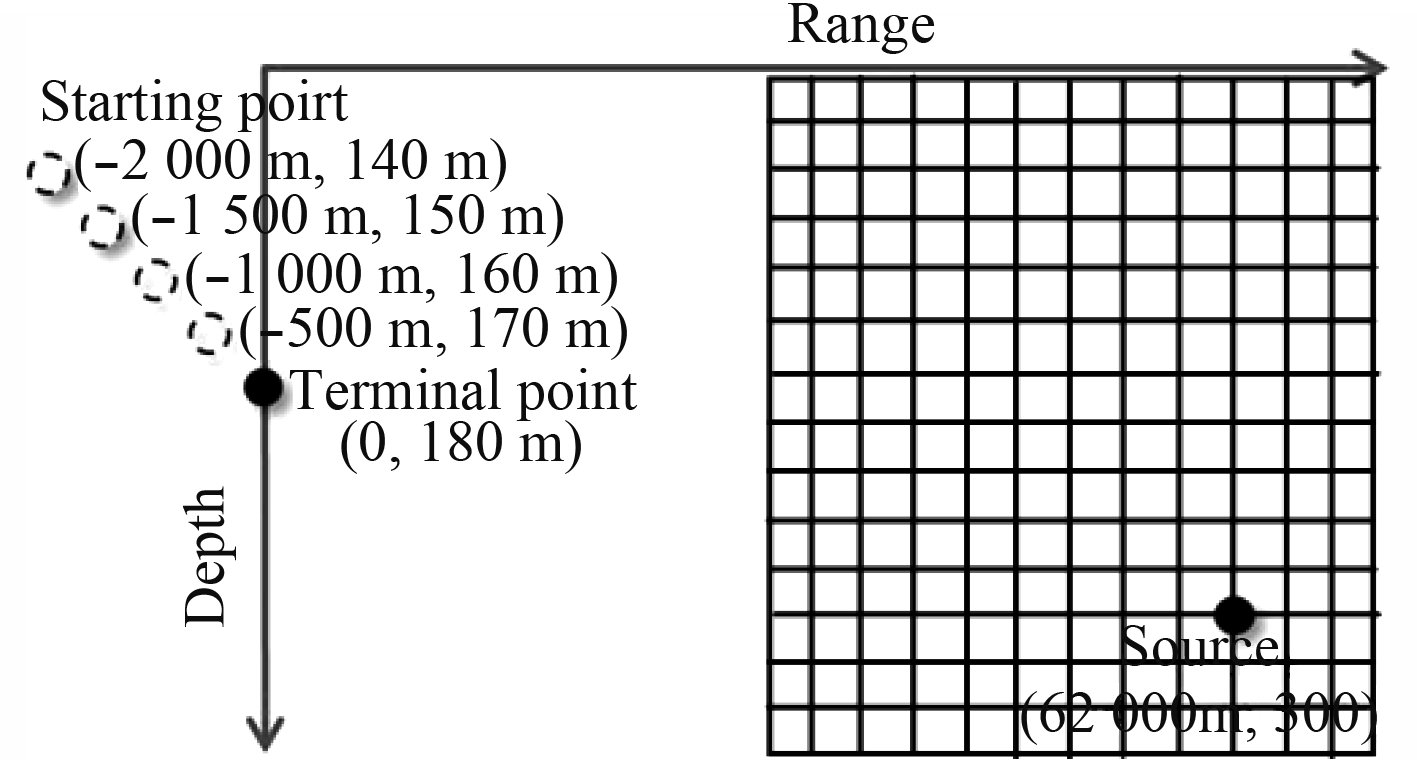
1 原理分析 1.1 单阵元阶梯变深测量场如图1所示,将单阵元按起始点至终点5个深度的顺序依次放置,对目标声场进行采样。假定在单阵元变深采样的过程中接收到的信号连续稳定,海洋声信道缓变,即阵元在某点接收到的不同时间段相同时长的声信号频域特性相同。
|
图 1 单水听器阶梯变深过程 Fig. 1 The changing process of single hydrophone depth |
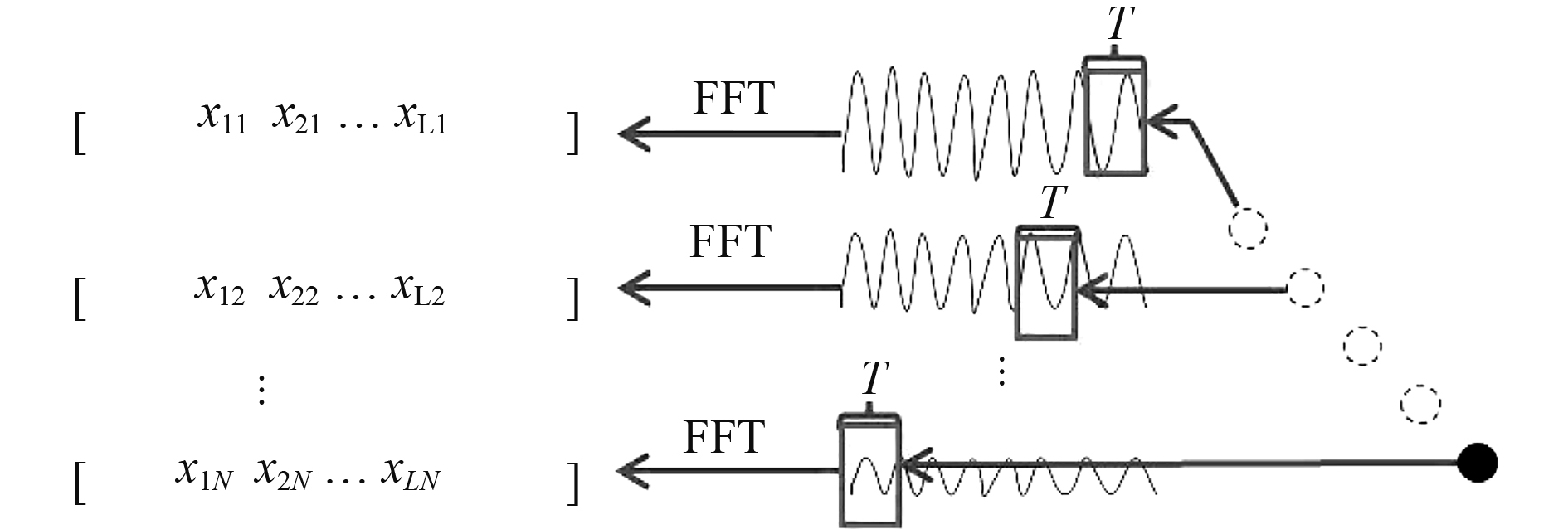
如图2所示,在每一深度上的采样时间为T,若信号的能量集中在L个频率上,将5个深度上的T时段声信号等分为M段后转化到频域,可以得到M组频域快拍数据:
|
图 2 单水听器垂向变深测量场估计 Fig. 2 Single hydrophone measuring field estimation in the process of depth change |
| ${{ Z}_m} = \left[ {\begin{array}{*{20}{c}}{{x_{m11}}} & {{x_{m21}}} & {} & {{x_{mL1}}}\\{{x_{m12}}} & {{x_{m22}}} & {} & {{x_{mL2}}}\\{{x_{m13}}} & {{x_{m23}}} & \ddots & {{x_{mL3}}}\\{{x_{m14}}} & {{x_{m24}}} & {} & {{x_{mL4}}}\\{{x_{m15}}} & {{x_{m25}}} & {} & {{x_{mL5}}}\end{array}} \right],\;\;m = 1:M\text{。}$ | (1) |
为了使非时间同步数据正确估计测量场,需要对各测深的频域快拍进行相位补偿,消除采样时间不同造成的相位差。以频率为fj,第一深度频域快拍
设其中
| ${{ K}_{{f_j}}} = \frac{1}{M}\sum\limits_{m = 1}^M {{x_{{f_j}m}}x_{{f_j}m}^H = {X_{{f_j}}}{X_{{f_j}}}^H} \text{。}$ | (2) |
其中:
| ${{ X}_{{f_j}}} = \frac{1}{{\sqrt M }}{\left[ {\begin{array}{*{20}{c}}{{x_{{f_j}1}}} & {{x_{{f_j}2}}} & \cdots & {{x_{{f_j}M}}}\end{array}} \right]^{\rm T}}\text{。}$ | (3) |
KRAKEN模型[11]声场计算公式为:
| $p(r,z) = \frac{i}{{\rho ({z_s})\sqrt {8\pi r} }}{e^{ - i\pi /4}}\sum\limits_{m = 1}^\infty {{Z_m}({z_s})} {Z_m}(z)\frac{{{e^{i{k_m}(\omega )r}}}}{{\sqrt {{k_m}(\omega )} }}\text{,}$ | (4) |
若声源位于(r,z)点,空间中某一采样点的频率响应用p来表示,单阵元在5个深度上利用KRAKEN模型计算得到频率为fj时的声压值为
| ${{ V}_{{f_j}}} = {\left[ {\begin{array}{*{20}{c}}{{p_{{f_j}1}}} & {{p_{{f_j}2}}} & {{p_{{f_j}3}}} & {{p_{{f_j}4}}} & {{p_{{f_j}5}}}\end{array}} \right]^{\rm T}}\text{,}$ | (5) |
匹配使用的处理器为最小方差无畸变响应匹配场处理器MVDR(Minimum Variance Distortionless Response)[1],则频率为fj时对应的拷贝场为:
| ${w_{{f_j}}}\left( {r,z} \right) = \frac{{K_{{f_j}}^{ - 1}{V_{{f_j}}}\left( {r,z} \right)}}{{{V_{{f_j}}}^H\left( {r,z} \right){K^{ - 1}}{V_{{f_j}}}\left( {r,z} \right)}}\text{。}$ | (6) |
频率为fj时,基于垂向变深的单水听器声源被动定位的模糊度函数可以表示为:
| ${P_{{f_j}}}\left( {r,z} \right) = \frac{1}{{{V_{{f_j}}}^H\left( {r,z} \right)K_{_{{f_j}}}^{ - 1}{V_{{f_j}}}\left( {r,z} \right)}}\text{,}$ | (7) |
对每个频率的定位结果进行加权处理,可以有效利用测量信号中的目标声场信息提高定位精度,联合各频率得到的模糊度函数为[12]:
| $P\left( {r,z} \right) = \sum\limits_{j = 1}^L {{\beta _j}{P_{{f_j}}}\left( {r,z} \right)}\text{,} $ | (8) |
加权原则为频点能量的相对大小:
| ${S_j} - {S_1} = 10\log \left( {\frac{{{\beta _j}}}{{{\beta _1}}}} \right),\;\;\sum\limits_{i = 1}^L {{\beta _L}} = 1\text{。}$ | (9) |
其中Sj为第j个频率对应的能量。
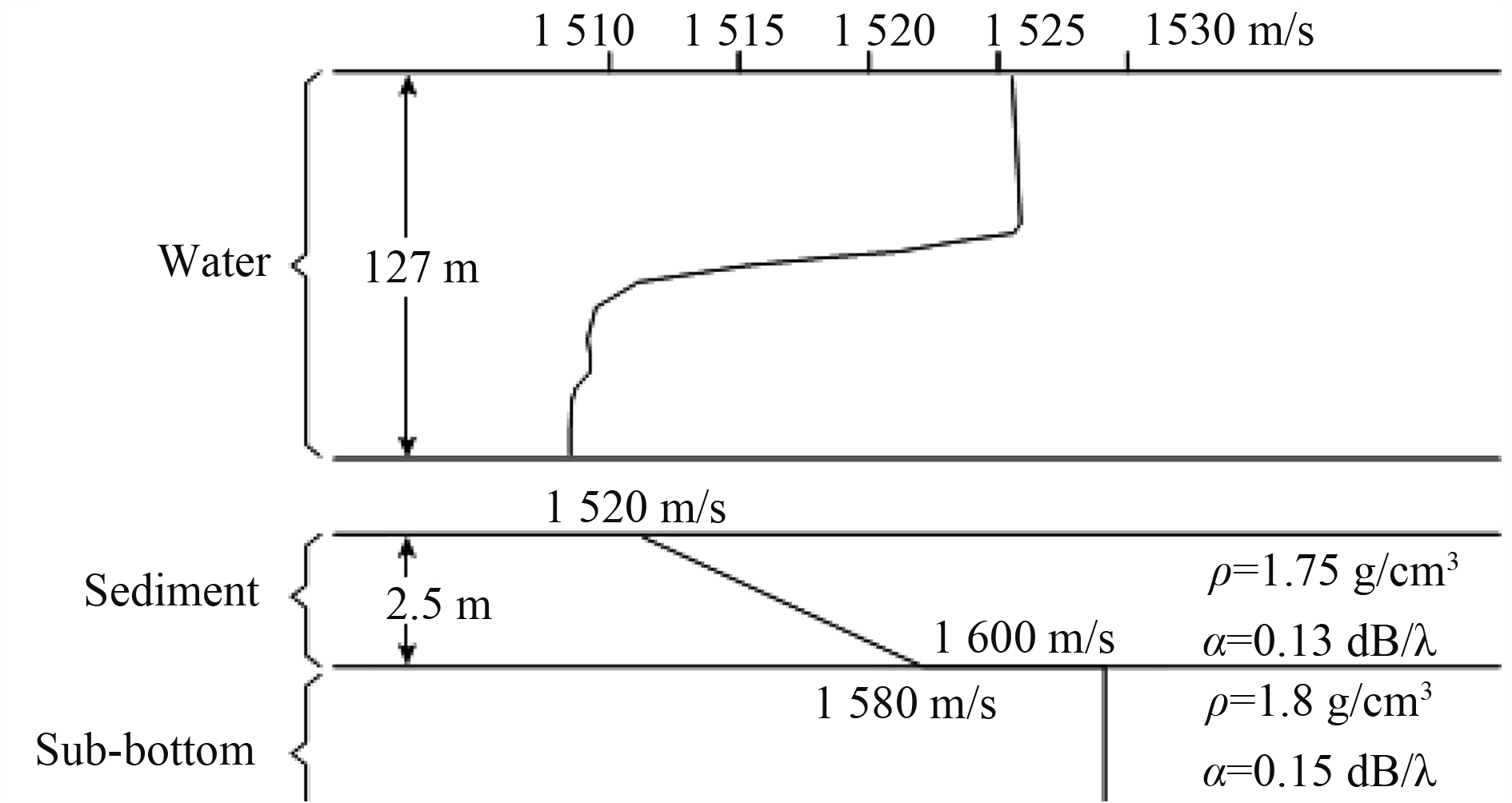
2 试验数据分析采用实测垂直阵非时间同步数据来验证方法。验证采用SACLANT研究中心对外公布的地中海垂直阵数据[13]。试验采用48元垂直线列阵接收信号,第1个阵元的深度为18.7 m,最后1个阵元的深度是112.7 m,阵元间距为2 m,阵孔径为94 m。使用HX-90G声源,声源特性保持不变。此声源发射带宽为12 Hz,中心频率为170 Hz的信号,声源级163 dB,声源被锚定在距接收阵5.8 km远处,深度约为79 m,声源发射连续信号,海底密度为1.8 g/m3,海底声速1 600 m/s,底吸收系数0.15 dB/λ,沉积层2.5 m,具体的声速分布、密度与吸收系数如图4所示,数据采集系统的采样频率为1 kHz,试验采集了10 min内线列阵接收到的信号,每分钟存储为1个数据文件,图5所示为第2分钟接收到的8,15,22,29,36,43号水听器信号经过简单滤波处理后的结果。
|
图 3 试验过程中实测的声场参数 Fig. 3 Sound field parameters measured in the test process |
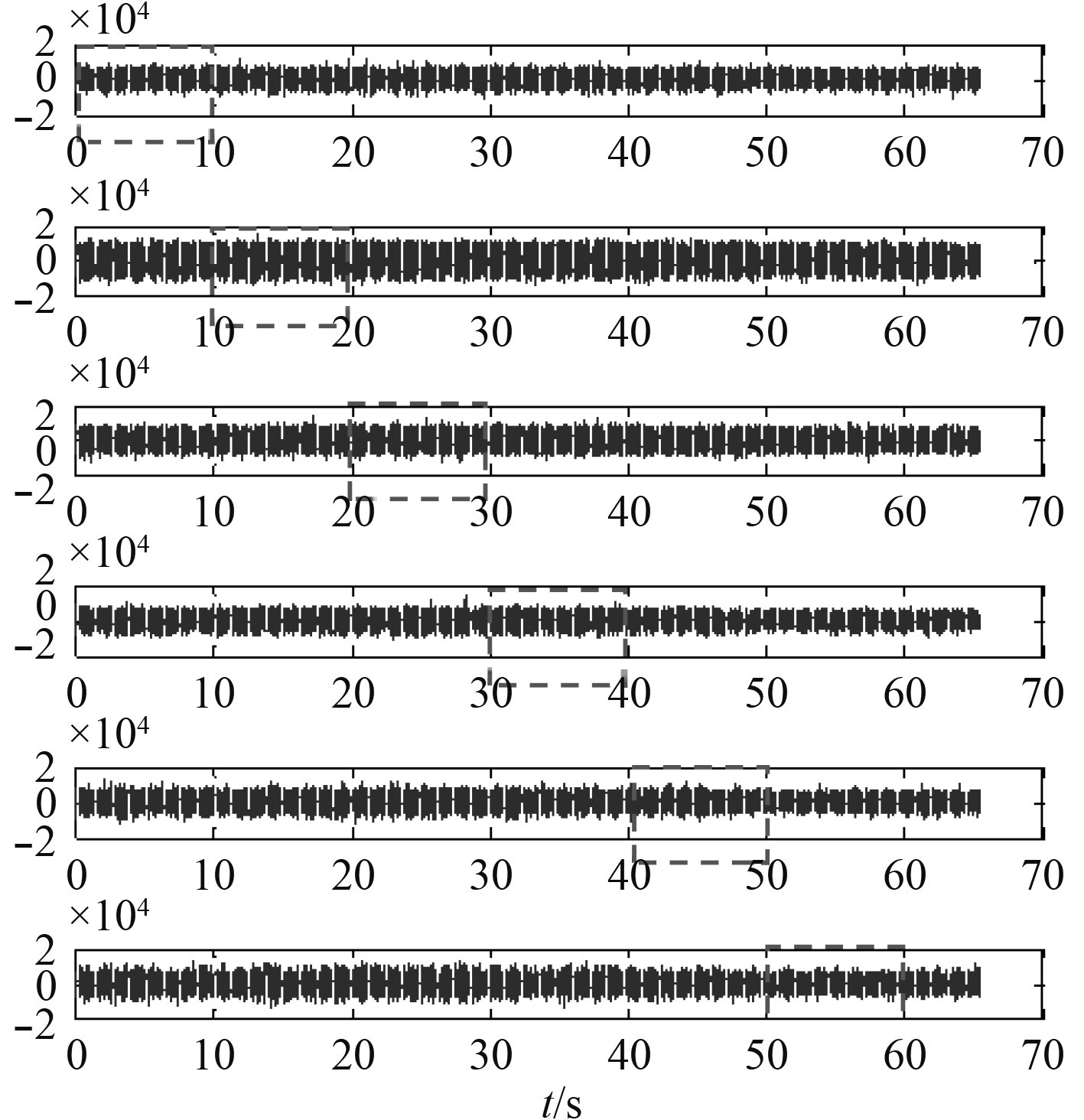
|
图 4 8,15,22,29,36,43号水听器第2 min接收到的信号 Fig. 4 2 min signal received by No.8, 15, 22, 29, 36, 43 hydrophone |
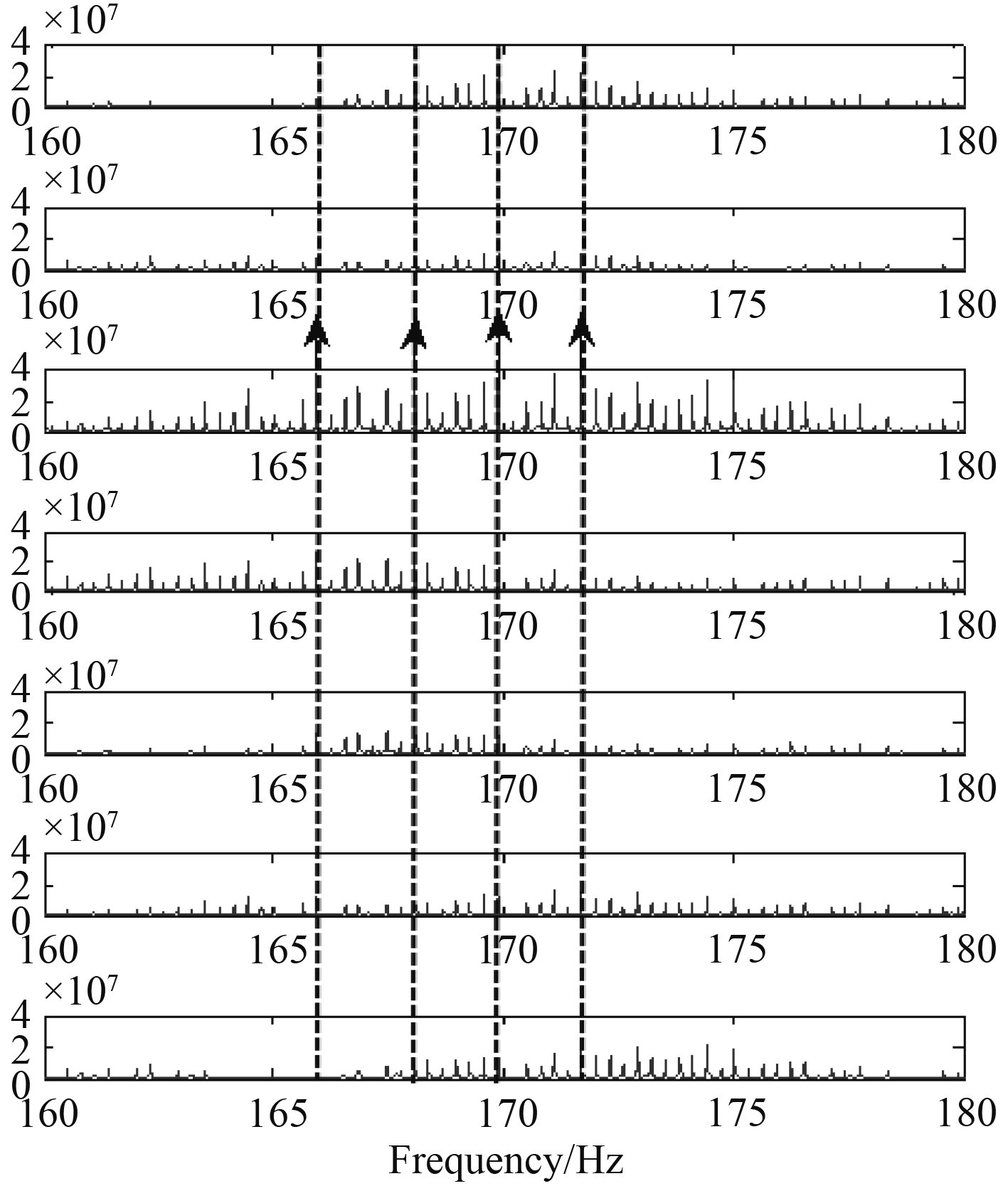
采用图4中圈出的各水听器时长10 s的非时间同步接收信号来等效为单水听器依次放置于8,15,22,29,36,43号水听器位置时接收到的声信号,其相应的频谱如图5所示。为计算简便,选取频谱中能量较大的165.937,168.128,169.921,171.713 Hz四根线谱对应的频域数据进行联合匹配,依次对6个阵元数据的4个谱线频域值进行相位补偿使各线谱频域数据矩阵时间对齐,搜索网格选取10 m×2 m。
|
图 5 截取信号对应频谱 Fig. 5 The frequency spectrum of intercepted signal |
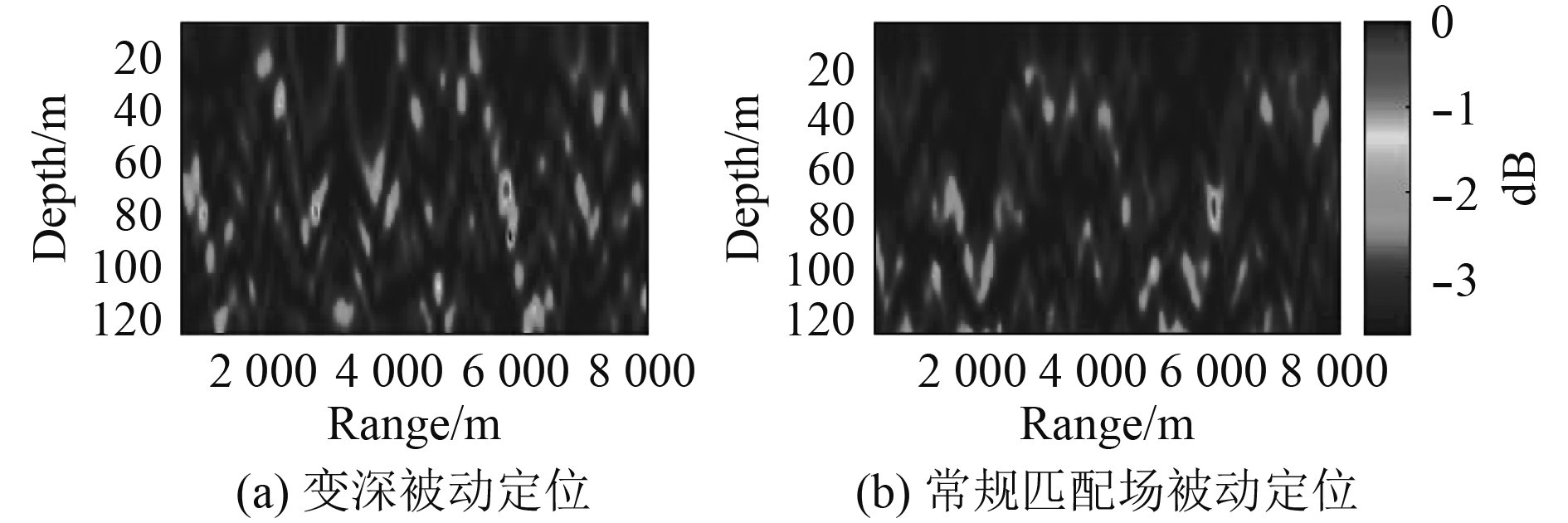
图6为利用上述6阵元数据变深被动定位与常规匹配场定位的结果,匹配计算中两方法采用相同的环境参数和搜索网格设定,引入常用的匹配处理器性能评估量化评估参数:峰值背景比(PBR)[14],结合2种定位结果的峰值点,对比该文方法与常规匹配场被动定位方法,结果如表1所示。
|
图 6 利用6阵元数据变深被动定位与常规匹配场定位模糊面 Fig. 6 Amplitude surface of changing single array element depth and conventional matching field |
图6(a)为利用非时间同步数据,通过补偿相位时间对齐后匹配得到的定位结果,从图中可以看出模糊表面的峰值点为(5 640 m,84.7 m),图6(b)为利用6阵元时间同步数据进行常规匹配场被动定位的结果,模糊表面的峰值点为(5 850 m,76.7 m),图6(a)与图6(b)显示两方法的定位结果与实际声源位置(5 800 m,79 m)相近,均可实现目标的被动定位。
从表1的对比结果来看,采用相同阵元数的情况下,单基阵变深被动定位相较于常规匹配场被动定位的定位偏差稍大,同时峰值背景噪声比(PBR)也较常规匹配场方法要低0.28 dB,2种方法定位结果出现差异的主要原因是单基阵变深被动定位采用非时间同步数据,定位过程中需要对各测深的数据进行相位补偿,补偿后的数据相位与真实时间同步数据的相位存在一定的偏差,故最终的定位结果相较于常规匹配场被动定位偏差稍大,旁瓣能量更高,峰值背景噪声比(PBR)较低。
|
|
表 1 两种方法定位结果对比 Tab.1 Comparison between two methods |
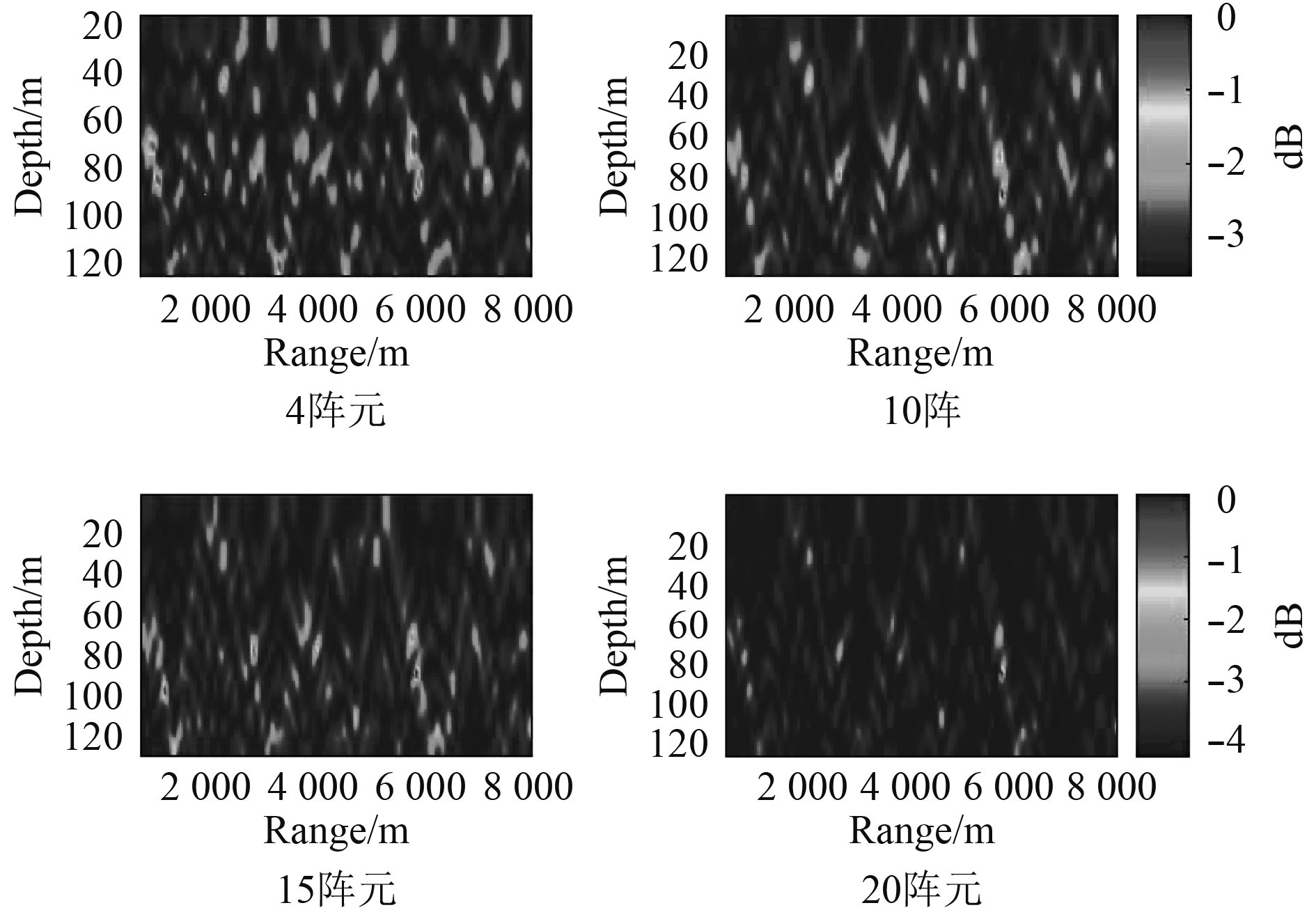
图7为依次使用4,10,15,20个阵元非时间同步数据的定位结果。对各阵元数情况下定位偏差以及PBR进行统计,结果如表2所示。对比可以看出,除了4阵元定位结果偏差较大外,其他阵元数的定位结果偏差都较小,且随着阵元数的增加,PBR增加,主瓣能量增强,旁瓣能量得到抑制,适当增加变深采样点数可以提高定位效果。
|
图 7 使用不同阵元数的数据定位结果 Fig. 7 Data location results using different number of array elements |
|
|
表 2 利用不同阵元数据变深被动定位结果对比 Tab.2 Comparison of passive location results with different array elements |
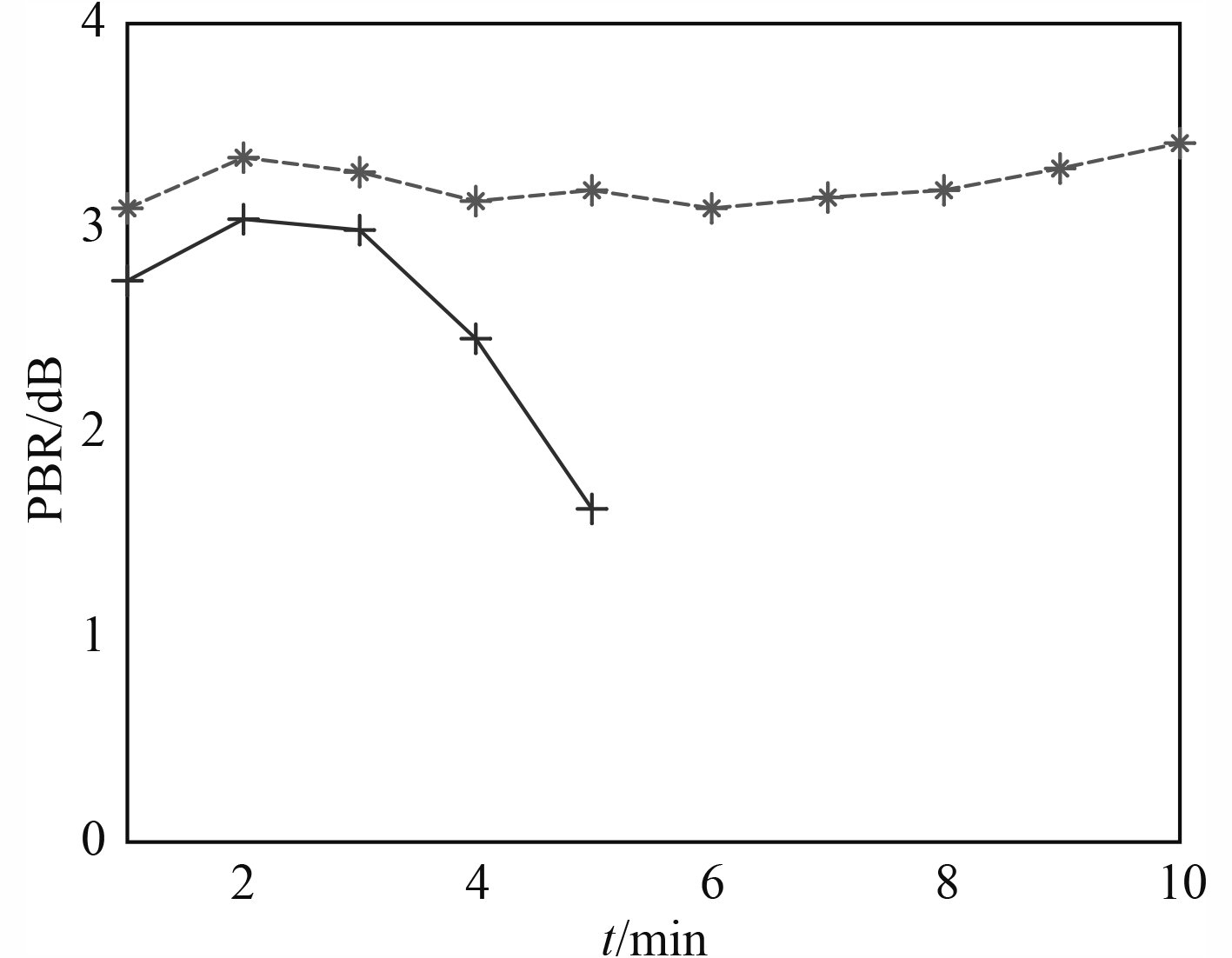
采用6阵元数据,对1–10 min各分钟数据分别采用2种算法进行定位,并计算相应的PBR值,用以相位补偿的四频点对应的频率保持不变,为165.937,168.128,169.921,171.713 Hz,计算对比结果如图8所示。图中虚线表示常规匹配场被动定位结果的PBR值随时间的变化,10 min内常规匹配场方法均实现了目标的准确定位,且PBR值稳定在3.1 dB左右,实线为利用各分钟内非时间同步数据补偿后匹配定位结果,从图中可以看出,前5 min的数据实线了目标的定位,PBR值随时间呈现减小的趋势,5 min后定位失效(有效定位的判别标准为:Δr=±500 m,Δz=±10 m),这可能受接收信号随时间的相关性减弱的影响,总体上前5 min利用相位补偿数据匹配后结果的PBR值要比常规匹配场被动定位结果的PBR值小。
|
图 8 两种方法定位结果的PBR值随时间的变化 Fig. 8 The change of PBR value with time |
本文根据水平合成孔径被动测向的思想,给出一种将垂直合成孔径与广义波束形成相结合的单阵元变深机动的目标被动定位新方法。通过将单阵元先后放置于不同深度,对目标声场进行采样,在连续稳定噪声信号的假设条件下,补偿采样数据的相位并估计测量场,通过求匹配的方法给出目标的位置,方法摆脱了传统水声目标被动定位技术对水听器阵列尺寸的限制,为水声目标被动定位提出了一种新的思路。通过对实测垂直阵数据的分析得到了以下结论:1)本文方法与常规匹配场被动定位效果相近;2)变深采样点的增加有助于提高该方法的定位效果;3)时变的海洋信道会造成接收信号时间相关性减弱,影响数据的相位补偿。
本文使用实测垂直阵的非时间同步数据,等效为单阵元变深采样,而实际中受潜航器的限制,单阵元变深采样往往是一个连续而非阶梯的过程,这会产生2个问题:1)是己方存在一定的速度,这会对接收声场产生多普勒效应,需要通过一定的算法消除多普勒影响;2)是运动中连续采样不同于本文假定的定点采样,采样数据需要经过一定的空间补偿,这也涉及到声场的垂直相关性问题,下一步工作着手进行单水听器连续变深采样的水池试验,进一步验证方法的有效性。
| [1] |
郑胜家, 韩东, 等. 匹配场定位强干扰抑制最小方差无畸变响应处理技术[J]. 仪器仪表学报, 2014, 35(7): 1586-1593. |
| [2] |
HINICH M J. Maximum likelihood signal processing for a vertical array[J]. Acoust. Soc. Am., 1973, 54: 499-503. DOI:10.1121/1.1913606 |
| [3] |
URICK R J. Principles of Underwater Sound [M]. McGraw-Hill, 1983.
|
| [4] |
汪德昭, 尚尔昌. 水声学[M]. 北京: 科学出版社, 2013.
|
| [5] |
BOOTH N O, ABAWI A T. Detectability of low-level broad-bands signals using adaptive matched-field processing with vertical aperture array[R]. IEEE Journal of Oceanic Engineering, 2000, 25(3): 296–312.
|
| [6] |
李风华, 刘建军, 张仁和. 水平阵匹配场定位技术研究[J]. 声学技术, 2004, 23(1): 29-31. DOI:10.3969/j.issn.1000-3630.2004.01.008 |
| [7] |
CHAPMAN N R, YEREMY M L. Matched field source localization with a horizontal line array[J]. Journal of Computational Acoustics, 2011, 02(3): 315-325. |
| [8] |
黄勇, 李宇. 被动合成孔径声呐阵列目标远程定位[J]. 电子与信息学报, 2006, 28(3): 526-531. |
| [9] |
李楠松, 朴胜春. 单矢量水听器被动测距方法研究[J]. 仪器仪表学报, 2015, 36(10): 2273-2282. DOI:10.3969/j.issn.0254-3087.2015.10.015 |
| [10] |
路敬祎, 叶东, 等. 双五元十字阵被动声定位融合算法及性能分析[J]. 仪器仪表学报, 2016, 37(4): 827-833. DOI:10.3969/j.issn.0254-3087.2016.04.015 |
| [11] |
PORTER M B. The KRAKEN normal mode program (draft) [M]. Washington D. C, Navel research Laboratory, 1992.
|
| [12] |
赵德鑫, 李婷, 等. 无人潜航器舷侧阵声呐匹配场被动定位方法研究[J]. 湖南大学学报, 2013, 40(8): 76-77. DOI:10.3969/j.issn.1674-2974.2013.08.014 |
| [13] |
GINGRAS D F, GERSTOFT P. Inversion for geometric and geoacoustic parameters in shallow water: experimental results[J]. Acoust. Soc. Am., 1995, 97(6): 3589-3598. DOI:10.1121/1.412442 |
| [14] |
赵航芳, 李建龙, 宫先仪. 不确实海洋中最小方差匹配场波束形成对环境参量失配的灵敏性分析[J]. 哈尔滨工程大学学报, 2011, 32(2): 200-208. DOI:10.3969/j.issn.1006-7043.2011.02.012 |
 2018, Vol. 40
2018, Vol. 40
