为了克服传统锚泊的应用局限性,目前大多数船舶都装备有动力定位系统,此系统依靠船舶自身推进系统产生推力来抵消外部环境的干扰,使船舶保持在某一位置及首向,以此来保证其正常行驶或作业。推进系统是动力定位系统的执行机构扮演着重要的角色。推力分配问题就是推进系统实时地分配推力及推力角到各个推进器的过程,即船舶推进系统根据控制系统给出的控制指令,通过推力分配单元将控制系统的指令合理、高效的分配到推进系统的各个推进器上,确定各个推进器的推力及方位角,以提供抵消外界环境的干扰且驱动船舶运动的力及力矩[1]。
因此认为推力分配问题就是含有约束的最优化问题,目前主要分为线性二次规划无约束的推力优化分配问题,线性二次规划有约束的推力优化分配问题和非线性约束推力优化分配问题[1 – 4]。常见的求解推力分配问题的方法主要有伪逆法、序列二次规划法、推进器分组法、奇异值分解和滤波法以及阻尼最小方差法等,其中发展最好的就是序列二次规划法,但运用在推力分配问题是显得较为繁琐。由于近年来智能算法的兴起,很多学者都开始使用智能算法对推力分配问题进行求解,如遗传算法[5]等。虽然群智能优化算法在处理推力分配约束条件上具有计算简单、处理速度块等优势,但要在实际工程中应用,必须解决局部最优、搜索效率等问题。
本文提出的遗传混沌粒子群混合算法,其实质是针对粒子群优化算法易依赖初始值、易陷入局部最优、以及后期收敛速度慢、精度较差等缺点,在粒子初始化时加入混沌变量,提高种群多样性和遍历性,并引入遗传算法中的交叉和变异算子,增强了算法的全局收敛性和搜索速度。并将该算法运用到有约束的非线性推力分配问题上,最后通过仿真验证,证实该算法在该问题的可行性。
1 船舶动力定位数学模型为了对船舶推力分配进行更好的研究,首先要建立一个有DP应用特性的船舶非线性数学模型
1.1 船舶运动学对于只研究纵荡、横荡、首摇3个自由度的水平面内的船舶[6],运动学方程可以用下式表示:
| $\dot \eta = {{R}}(\psi ){{v}}, $ | (1) |
式中:
| ${{R}}(\psi ) = \left[ \begin{gathered} \cos \psi \quad - \sin \psi \quad {\rm{ 0}} \\ \sin \psi \quad\ \cos\psi \quad\ {\rm{0}} \\ {{ \ 0 \quad\quad\ \ 0 \quad \quad \ 1}} \\ \end{gathered} \right]{\text{。}}$ | (2) |
动力定位船舶在水平面上低速航行时,变化缓慢,因此忽略了科里奥立向心矩阵
| ${{M}}\dot v + {{Dv}} = {{\tau }} + {{{R}}^{\rm T}}(\psi ){{b}}{\text{。}}$ | (3) |
式中:
船舶推力分配问题通常可以看作是一个多变量有约束的非线性优化问题,通过建立合适的目标函数和约束条件,从而将推进系统的能量消耗、控制系统与推进系统之间的推力误差、推进器磨损等因素降到最低,保证船舶的操纵性,将控制系统的指令分配到各个推进器上,确定各推进器的推力及方位角[7]。
2.1 推力分配数学描述推力分配单元主要的功能是接受来自控制系统发出的力和力矩指令,通过一定的方法确定各个推进器的推力以及推力角大小,其原理如图1所示,数学描述如下:

|
图 1 动力定位系统的推力分配原理图 Fig. 1 Schematic diagram of thrust allocation in power system |
| ${\bf{\tau }} = {{B}}(\alpha )U{\text{。}} $ | (4) |
式中:
| ${{B}}\left( {\bf{\alpha }} \right) \!\!=\!\! \left[\!\!\! {\begin{array}{*{20}{c}} {\cos \,({\alpha _1})\,\;}& \!\!\!\!\!\!\cdots \!\!\!\!\!\!&{\cos ({\alpha _i})\,} \\ {\sin ({\alpha _1})}& \!\!\!\!\!\!\cdots\!\!\!\!\!\! &{\sin ({\alpha _i})} \\ {lx1\sin ({\alpha _1}) - ly1\cos ({\alpha _1})}& \!\!\!\!\!\!\cdots\!\!\!\!\!\! &{lxi\sin ({\alpha _i}) - lyi\cos ({\alpha _i})} \end{array}} \!\!\!\right],$ |
式中,
推力分配问题的约束条件除了需要满足力的平衡方程外,还需要考虑推进器推力、方位角的极值以及推力及方位角变化范围等推进器自身的性能约束,即有如下约束表达式:
| $\left\{ \begin{gathered} U{\rm min} \leqslant U \leqslant U{\rm max}, \hfill \\ \Delta U{\rm min} \leqslant U - U_0 \leqslant \Delta U{\rm max}, \hfill \\ \alpha {\rm min} \leqslant \alpha \leqslant \alpha {\rm max}, \hfill \\ \Delta \alpha {\rm min} \leqslant \alpha - \alpha_0 \leqslant \Delta \alpha {\rm max}{\text{。}} \hfill \\ \end{gathered} \right.$ | (5) |
式中:
一般考虑到能量消耗、推力分配误差、奇异结构以及推进器的磨损,推力分配目标函数可用下式表示:
| $\begin{split} \min J(\alpha ,U,s) = P\mathop \Sigma \limits_{i = 1}^m {\left| U \right|^{\tfrac{3}{2}}} + {s^{\rm T}}{ Q}s + \\ {(\alpha - \alpha 0)^{\rm T}}{\varOmega} (\alpha - \alpha 0) + \frac{\delta }{{\varepsilon + \det [B(\alpha ){B^{\rm T}}(\alpha )]}}{\text{。}}\end{split} $ | (6) |
式中:
粒子群算法是一种群智能算法,粒子作为其基本的组成单位。首先将粒子在可行解空间中进行随机的初始化,在这里,假设D维空间中第i个粒子的位置和速度分别为
| $\begin{gathered} {\upsilon _{id}}(t + 1) = \omega {\upsilon _{id}}(t) + {c_1}{r_1}({p_{id}}(t) - {x_{id}}(t))+ \hfill \\ \;\quad \quad \quad \quad {c_2}{r_2}({p_{gd}}(t) - {x_{id}}(t)) , \hfill \\ \end{gathered} $ | (7) |
| ${x_{id}}(t + 1) = {x_{id}}(t) + {\upsilon _{id}}(t){\text{。}} $ | (8) |
式中:
在分析基本粒子群优化算法后,发现粒子群算法在初始化阶段存在缺陷,即粒子群初始化过程是随机的,随机过程虽然大多可以确保初始解群分布均匀,但对个体的质量却不能保证。如果初始化不好的话,就会出现粒子远离最优解得情况,影响了进化过程的收敛。故采用混沌系列初始化粒子的位置和速度,在不改变粒子群初始化时随机性本质情的况下,利用混沌提高了种群的多样性和粒子搜索的遍历性[10]。
本文采用Logistic混沌映射,其方程如下:
| ${z_{k + 1}} = \mu {z_k}(1 - {z_k}){\text{。}} $ | (9) |
式中:
该混沌映射有以下几个特性[10]:1)该混沌序列不收敛;2)非周期性;3)遍历(0,1)区域;4)混沌序列不可预测。根据以上分析并考虑到混沌特性,本文将混沌变量在粒子群初始化时就加入,使粒子群在初始化时可以更好地靠近最优解,有效地增加粒子群的求解效率和解的质量
3.3 遗传交叉和变异策略遗传算法是通过模拟生物物种繁殖进化过程得出的一种优化搜索算法。通过进行选择、交叉以及变异等遗传算子来交换种群的信息,最终使其产生符合优化目标的参数。正是由于遗传算法中这些算子,使得种群之间可以更好地交流,而粒子群算法的搜索是由靠自身粒子的不断更新速度决定的,缺少整个种群相互交流的信息机制。因此,引入遗传算法中的交叉和变异算子来改进粒子群,使其更好地进行种群间的相互交换以及跳出局部最优[10]。
3.3.1 交叉操作在算法迭代过程中引入个体交叉操作,依据一定的概率
在算法迭代过程中为避免算法在搜索后期陷入局部最优、增加种群多样性,将变异操作引入粒子群算法中,即以一定的变异概率(
| $Pm = \left\{ \begin{gathered} \frac{{k_1({f_{\max }} - f')}}{{{f_{\max }} - {f_{avg}}}},\quad f' \geqslant {f_{avg}}, \hfill \\ k_2, \quad \quad \quad\quad \quad \;f' < favg{\text{。}} \hfill \\ \end{gathered} \right.$ | (10) |
式中:
1)种群初始化:确定种群数N,随机初始化粒子的位置与速度,并限定粒子的位置与速度范围;计算种群适应度值,并初始化种群的全局最优与个体最优。
2)对全局最优粒子的进行混沌化,利用Logistic映射,生成混沌化后的种群,并更新种群的全局最优与个体最优。
3)利用式(7)和式(8)对粒子进行位置和速度更新。
4)更新个体与全局最优:若当前粒子的适应度值优于个体最优,则用当前粒子位置替换个体最优; 若当前种群粒子的适应度值优于全局最优,则用当前粒子位置替换全局最优。
5)交叉操作:随机产生一个数
6)变异操作:随机产生一个数
7)计算适应度值并更新个体与全局最优。
8)判断是否满足停止条件:如最大迭代数或者问题所需精度,如果满足则输出最优搜索结果,否则返回步骤3。
4 船舶动力定位推力分配仿真计算为了验证提出的算法能够解决推力分配优化问题,即对非线性有约束问题能够求解,本文采用第2部分所述的约束条件和目标函数,另外考虑到推进器的角度约束,设置了推力禁区,以某铺管船为对象进行仿真验证,其该船舶的推进器相关参数如表1所示。
|
|
表 1 某船舶推进器相关参数 Tab.1 Parameters of a ship propeller |
船舶初始位置η0=[0, 0, 0],目标位置ηd=[25, 25, 30],船舶运行在海面上,其环境扰动被设置为偏差向量,已经被设置到b=(1×103, 1.1×103, 0.5×103),仿真结果如图2所示,仿真显示,船舶在80 s后达到定位位置点并基本保持稳定。
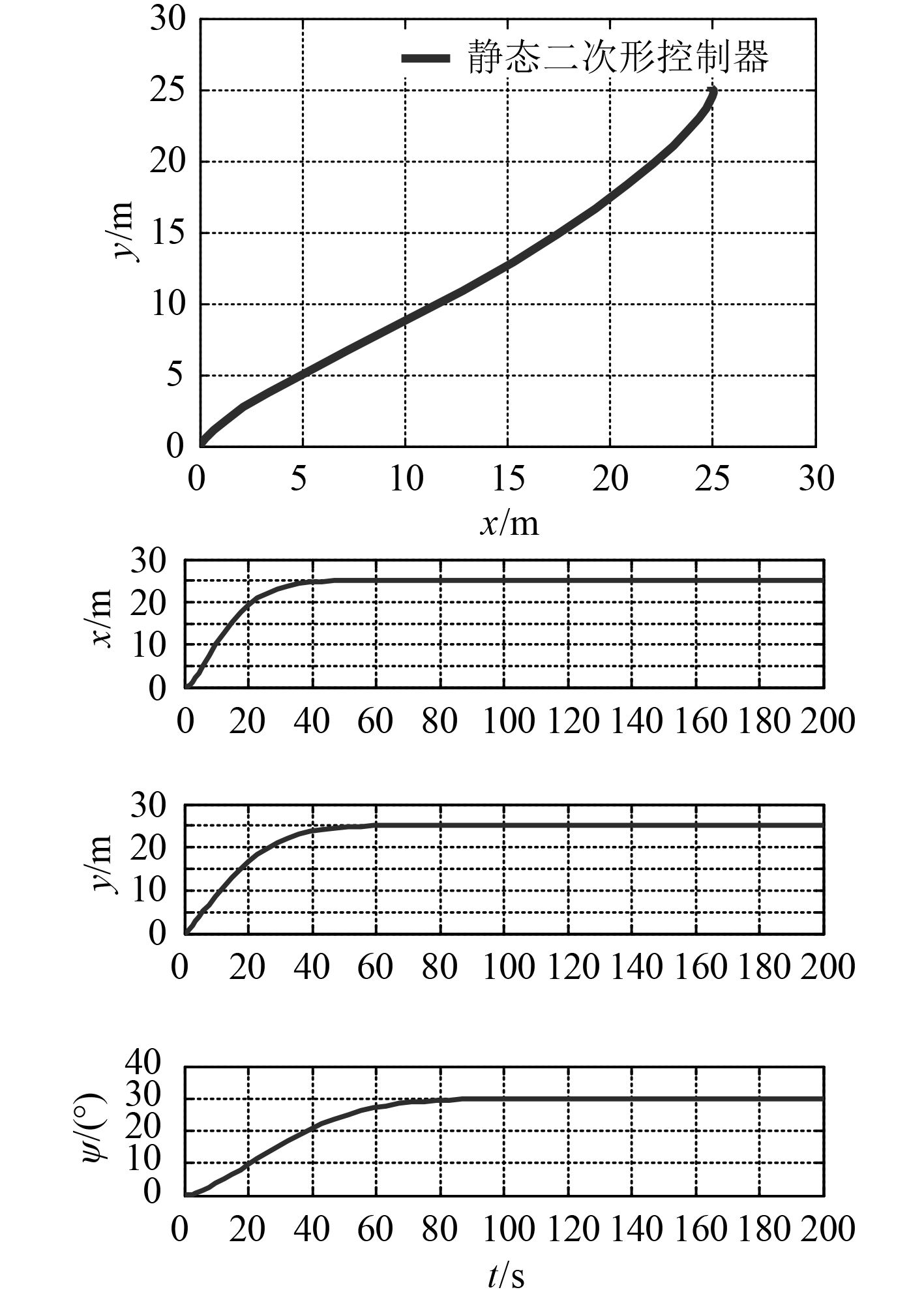
|
图 2 船舶动力定位运动响应 Fig. 2 Ship dynamic positioning motion response |
图3为仿真过程中7个推进器的推力及方位角变化,从图3可以看出,每个推进器的推力和方位角满足推力分配优化模型的约束条件,在每个仿真步长内,推力和方位角变化都趋于平缓,满足推进器推力及方位角变化速率的约束,说明设计的推力分配方法在减少推进器磨损方面效果良好。

|
图 3 推进器推力及方位角变化 Fig. 3 Thrust and azimuth curve of propeller |
从图4可以看出,经该推力分配算法,进行推力分配后,其合力及力矩,能够很好地跟踪控制器推力指令,说明该算法能够合理地分配推力,即该算法能够解决推力分配优化问题。
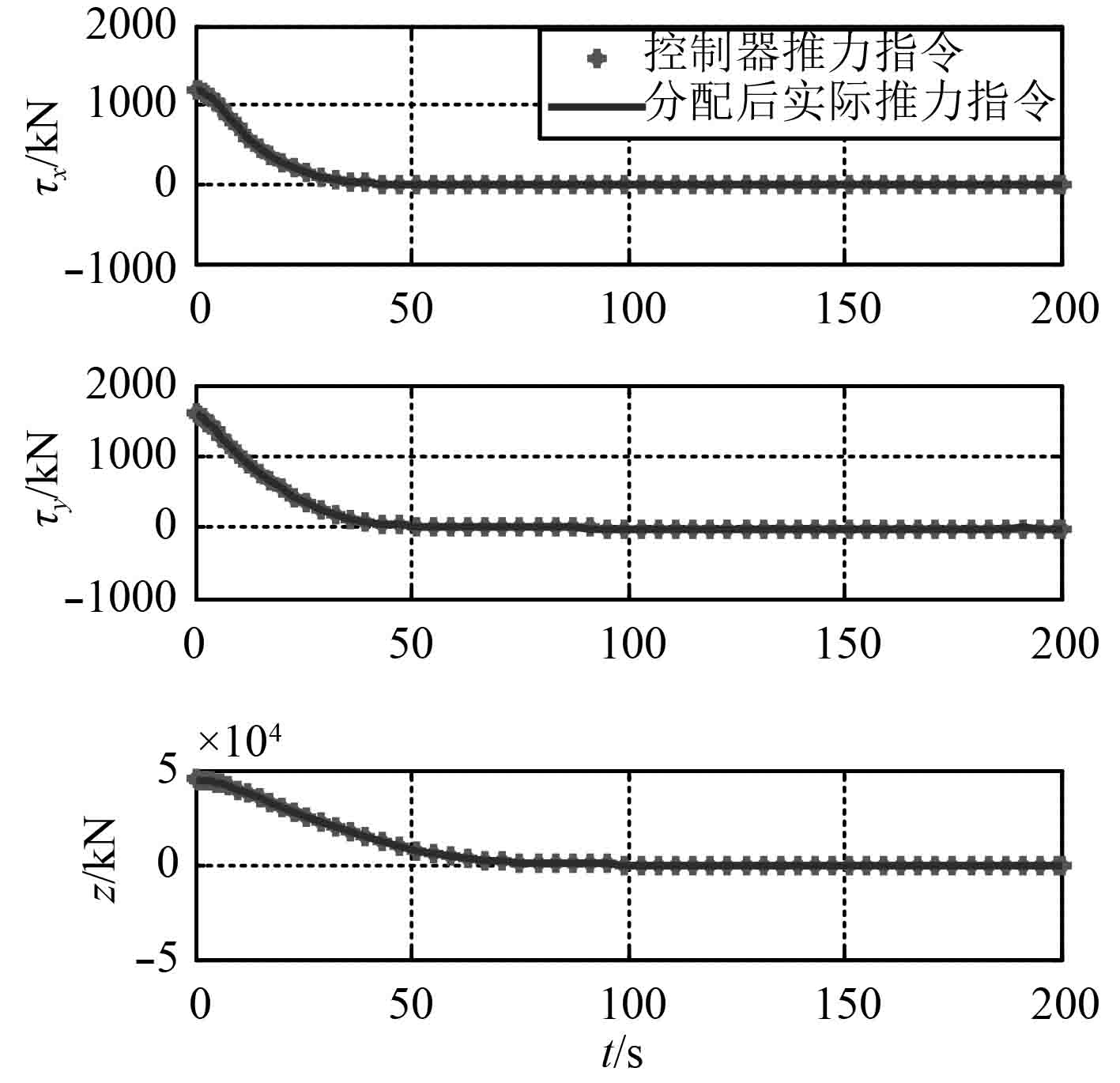
|
图 4 控制器推力指令与分配后实际推力指令 Fig. 4 Comparison of resultant force and moment before and after the allocation |
针对动力定位系统中推力分配优化问题,通过引入遗传算法中的交叉和变异算子及混沌理论对粒子群算法进行改进,设计了基于混合粒子群算法的推力分配策略。通过对某铺管船的仿真,证实了该算法能够解决推力分配优化问题,该算法在兼顾能量消耗的同时,能有效的降低推进器的磨损,由于推进器角度在同一时刻并没有完全一致,故可以有效地解决推进器系统奇异结构的问题,提高了船舶的动态性能。
| [1] |
杨世知, 王磊, 张申. 基于能耗最优化的动力定位推力分配逻辑算法研究[J]. 船舶力学, 2011, 3(15): 217-226. |
| [2] |
JOHANSEN T A, FOSSEN T I, BERGE S P. Constrained Nonlinear Control Allocation with Singularity Avoidance using Sequential Quadratic Programming. IEEE Trans. Control Systems Technology, 2004, 12: 211–216.
|
| [3] |
王彦昊. 耙吸挖泥船动力定位系统推力分配策略研究[J]. 科学技术与工程, 2011, 11(2): 419-422. DOI:10.3969/j.issn.1671-1815.2011.02.047 |
| [4] |
施小成, 魏玉石, 宁继鹏, 等. 基于能量最优的组合偏置推力分配算法研究[J]. 中国造船, 2012, 5(2): 96-104. |
| [5] |
ZHAO Da-wei, DING Fu-guang, TAN Jin-feng, et al. Optimal thrust allocation based GA for dynamic Positioning ship[J]. IEEE International Conference on Mechatronics and Automation, Xi'an, China, 2010, 1254-1258. |
| [6] |
NGONGI W E, DU J, WANG R. Robust fuzzy controller design for dynamic positioning system of ships[J]. International Journal of Control Automation & Systems, 2015, 14(1): 1-12. |
| [7] |
吴显法, 王言英. 动力定位系统的推力分配策略研究[J]. 航海工程, 2008, 3(37): 92-96. |
| [8] |
T I FOSSEN. Marine control systems: guidance, navigation and control of ships, rigs and underwater vehicles. Tapir Trykkeri, 2002.
|
| [9] |
A VEKSLER, T A JOHANSEN, R SKJETNE. Thrust allocation with power management functionality on dynamically positioned vessels, in Proc. Amer. Control Conf., 2012, 6: 1468–1475.
|
| [10] |
黄席樾, 向长城, 殷礼胜. 现代智能算法理论及应用[M]. 北京: 科学出版社, 2009.
|
 2018, Vol. 40
2018, Vol. 40
