2. 华中科技大学,湖北 武汉 430074
2. Huazhong University of Science and Technology, Wuhan 430074, China
随着现代科技和经济的飞速发展,人类对资源的需求量越来越大,而陆地资源开发日趋紧张,海洋开发已经成为了一个具有战略意义的领域。海洋监测技术是开发利用海洋资源的基础,只有拥有强大的海洋监测技术才能更好地完成海洋开发。中国在20世纪60年代开始研究海洋浮标。经过几十年的发展,取得很大的成绩[1 – 3]。Davide Moroni等[4]为溢油早期检测设计了一个灵敏浮标,海洋往往是一个脆弱的环境,通过使用一个装备有先进传感器的新浮标来检测溢油。Mohammad Hossein Jahangir等[5]研究了浮标的运动响应各种参数的内在联系,认为浮标与水之间的阻尼系数是随时间变化的,并将相关结果进行了严格比较。结果表明,浮标的运动并不严格地遵循正弦波的正弦形式。本文设计的浮标体积小、质量轻,具有良好的便携性,方便携带、布放与回收。同时,该浮标具有较好的随浪性。
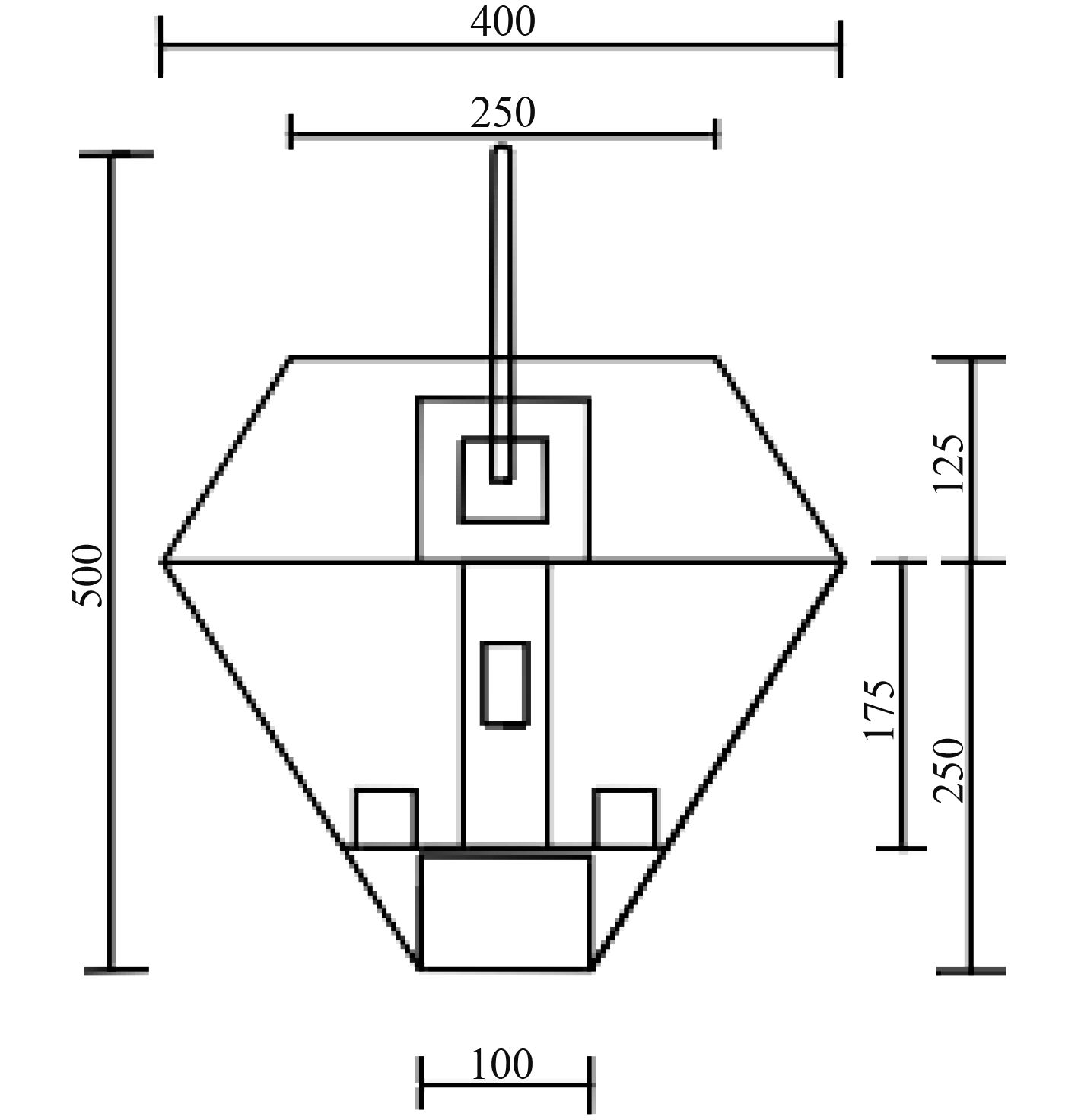
1 浮标总体设计及参数浮标需要具备良好的便携性以及较好的随浪性,设计的外形比较小,外形设计为上下2个共面空心圆台,使波浪急速上涨或者下落时,可以获得更大的加速度或者减速度,使得浮标可以快速响应波浪的运动,提高浮标的随浪性。同时,外扩的形状,对浮标的稳性有所提高,以防止浮标被浪打翻。浮标体采用1 mm厚度的不锈钢制作,这种材料强度与耐腐蚀度都很好,并且容易加工。本浮标的设计如图1和图2所示。
|
图 1 浮标外形(单位:mm) Fig. 1 Buoy shape |
|
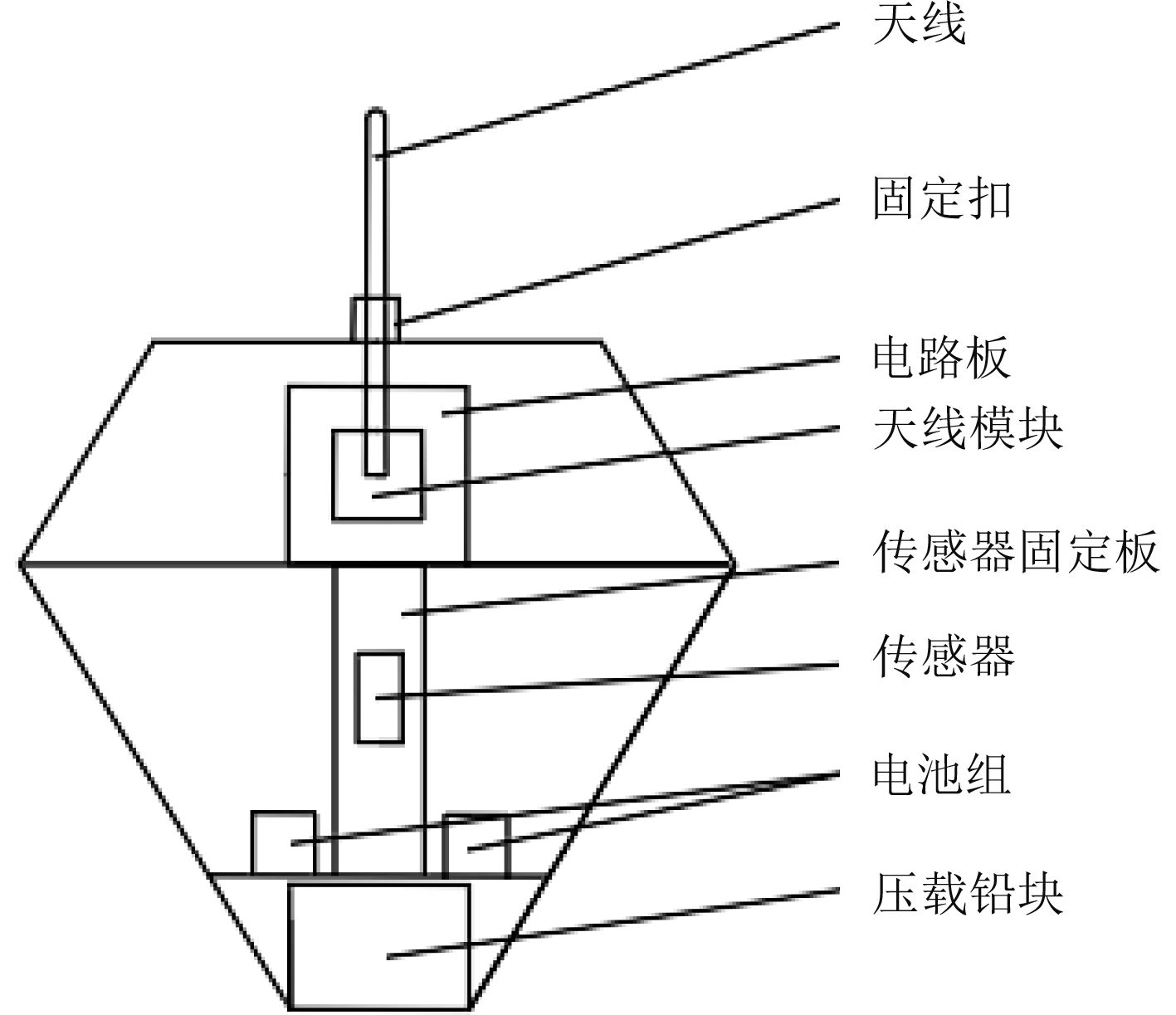
图 2 浮标总布置图 Fig. 2 General layout of buoys |
以浮标底部平面中心为z轴零点,浮标的重心高度为125 mm,浮心高度为150 mm,浮标水线面位于上下圆台共面处,排水体积为0.013 74 m3,排水量为14 kg。
浮标上下部分可以分离,水线面处圆形平台与上半部分相连,下半部分顶部有一个圆筋,使用时上半部分底部平台和下半部分顶部远景用螺钉固定在一起,下半部分内部的平台下方也有一个圆筋,可以使用螺钉将平台固定在圆筋上,浮标顶部的圆形盖子也是与下半部内部圆台的固定方式一样,使用圆筋来固定。固定扣可以用来在浮标布放时就连接一根高强度复合材料缆绳如凯夫拉缆,即可在完成波浪的测量之后通过回收缆绳轻松完成浮标的回收。
2 随浪特性研究 2.1 理论方法 2.1.1 控制方程势流理论假定流体是无旋、无粘的。
速度势能控制方程为:
| ${\nabla ^2}\varphi = 0\left( {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over V} = \nabla \varphi } \right)\text{,}$ | (1) |
体的边界条件为:
| $\left( {\nabla \varphi - \overset{\rightharpoonup}V_S} \right) \cdot {\overset{\rightharpoonup}{n}} = 0\text{,}$ | (2) |
自由表面运动条件为:
| $\frac{{D\left( {z - \zeta } \right)}}{{Dt}} = 0\;i.e.\frac{{\partial \left( {z - \zeta } \right)}}{{\partial t}} + \nabla \varphi \cdot \nabla \left( {z - \zeta } \right) = 0\text{,}$ | (3) |
自由表面动力条件为:
| $\frac{{\partial \varphi }}{{\partial t}} + \frac{p}{\rho } + \frac{1}{2}\nabla \varphi \cdot \nabla \varphi +{\mathcal{g}} \zeta = const\text{,}$ | (4) |
组合自由表面条件为:
| $\frac{{\partial \varphi }}{{\partial z}} - \frac{{{\omega ^2}}}{{\mathcal{g}}}\varphi = 0\text{,}$ | (5) |
海底边界条件为:
| $\nabla \varphi = 0\text{,}({\text{深水}})\text{,}$ | (6) |
| $\frac{{\partial \varphi }}{{\partial z}} = 0\text{,}({\text{浅水}})\text{。}$ | (7) |
压力以及一阶波浪力的求解,对于小尺度单元(D/L<0.2),每个单元上单位长度的波浪力可以由莫里森方程计算得到,莫里森方程为:
| $ {{F}} = \rho {\ddot X\left( {1 + {C_\alpha }} \right)} \varOmega+ 0.5\rho {C_d}V\left| V \right|D \text{。}$ | (8) |
式中:D为单元的直径;Cd为和单元拉力系数;Cα为附加质量;Ω为单位长度单元的体积。
对于非小尺度结构物,结构上的每个面元求解采用线性伯努利方程:
| ${{P}} = - \rho \frac{{\partial \varphi }}{{\partial t}}\text{。}$ | (9) |
要得到一阶波浪力可以对整个结构表面进行积分。
近场求解方法(基于压力积分):
| $\begin{split}F_{strc}^2 = - \mathop \oint \limits_{WL}^{} 0.5\rho g\zeta _r^2\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over n} {\rm d}l + \mathop \int\!\!\!\int \limits_{{S_0}}^{} 0.5\rho {\left| {\nabla \varphi } \right|^2}\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over n} {\rm d}S+\\ \mathop \int\!\!\!\int \nolimits_{{S_0}}^{} \rho \left( {X \cdot \nabla \frac{{\partial \varphi }}{{\partial t}}} \right)\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over n} {\rm d}S + {M_s} \cdot R \cdot {\ddot X _g}\text{,}\end{split}$ | (10) |
式中:S0为平均湿表面积;W为结构表面的平均吃水。
在波浪中的响应X可以通过下面方程得到:
| $\left[ { - {\omega ^2}\left( {{M_s} + {M_a}\left( \omega \right)} \right) - i\omega C\left( \omega \right) + K} \right]X\left( \omega \right) = F\left( \omega \right)\text{。}$ | (11) |
式中:Ma为附加质量;K为流体刚度;C为阻尼;F为波浪力;Ms为结构质量。
计算浮体系统的静态平衡位置时,使用下式:
| ${X_{j + 1}} = {X_j} + {{ K}^{ - 1}}\left( {{X_j}} \right){ F}\left( {{X_j}} \right)\text{。}$ | (12) |
式中:K为系统刚度矩阵;F为力矩阵。
在特定波浪条件下,浮体结构时域运动方程为:
| ${M_\zeta }\ddot X\left( t \right) = F\left( t \right)\text{。}$ | (13) |
式中F(t)为结构总力。
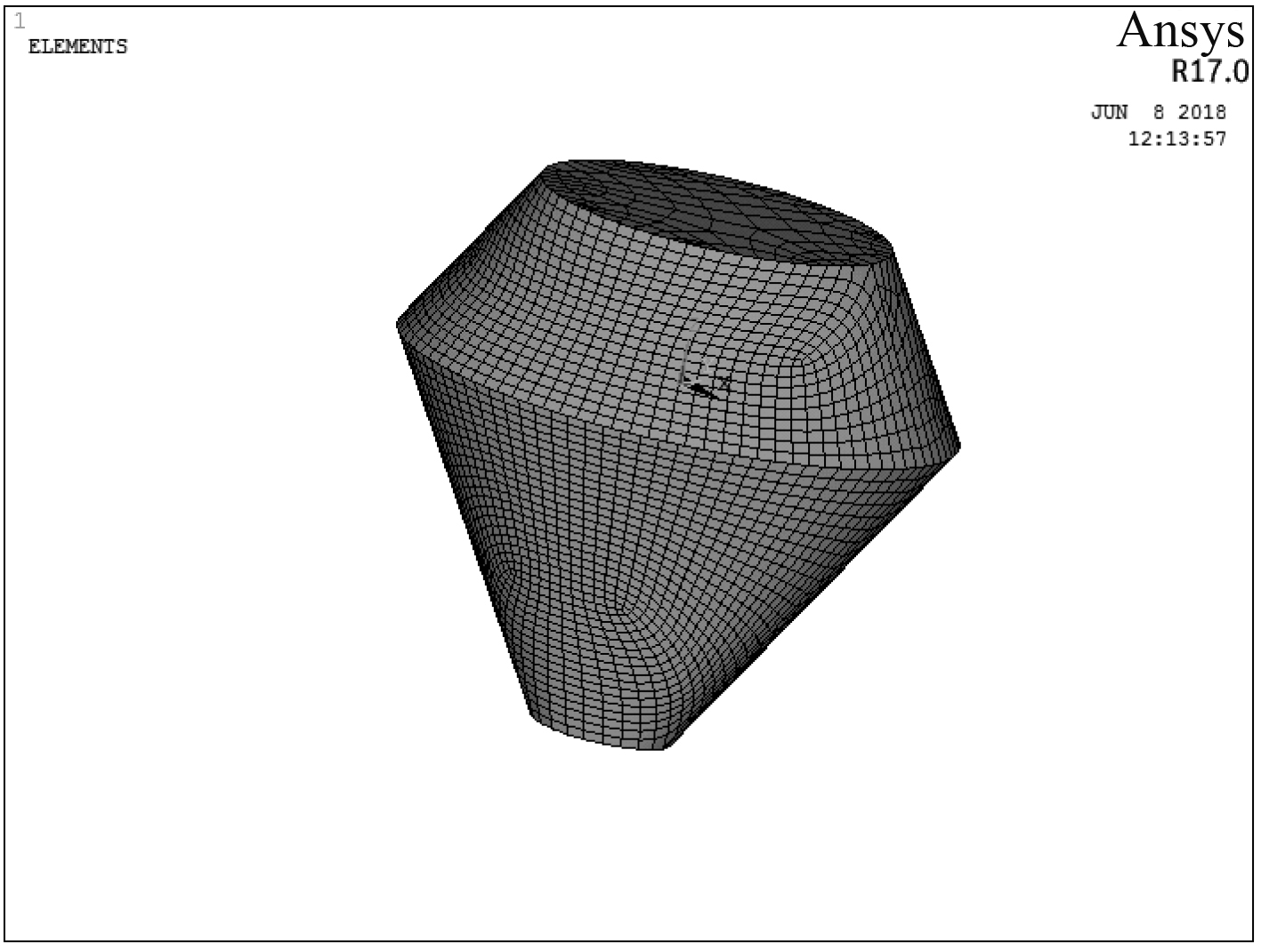
2.1.2 计算网格因为浮标尺寸小、外形结构简单,所以在Ansys中采用Smartsize进行自由网格划分,网格量为3 169,网格划分图如图3所示。
|
图 3 网格分布图 Fig. 3 Grid distribution map |
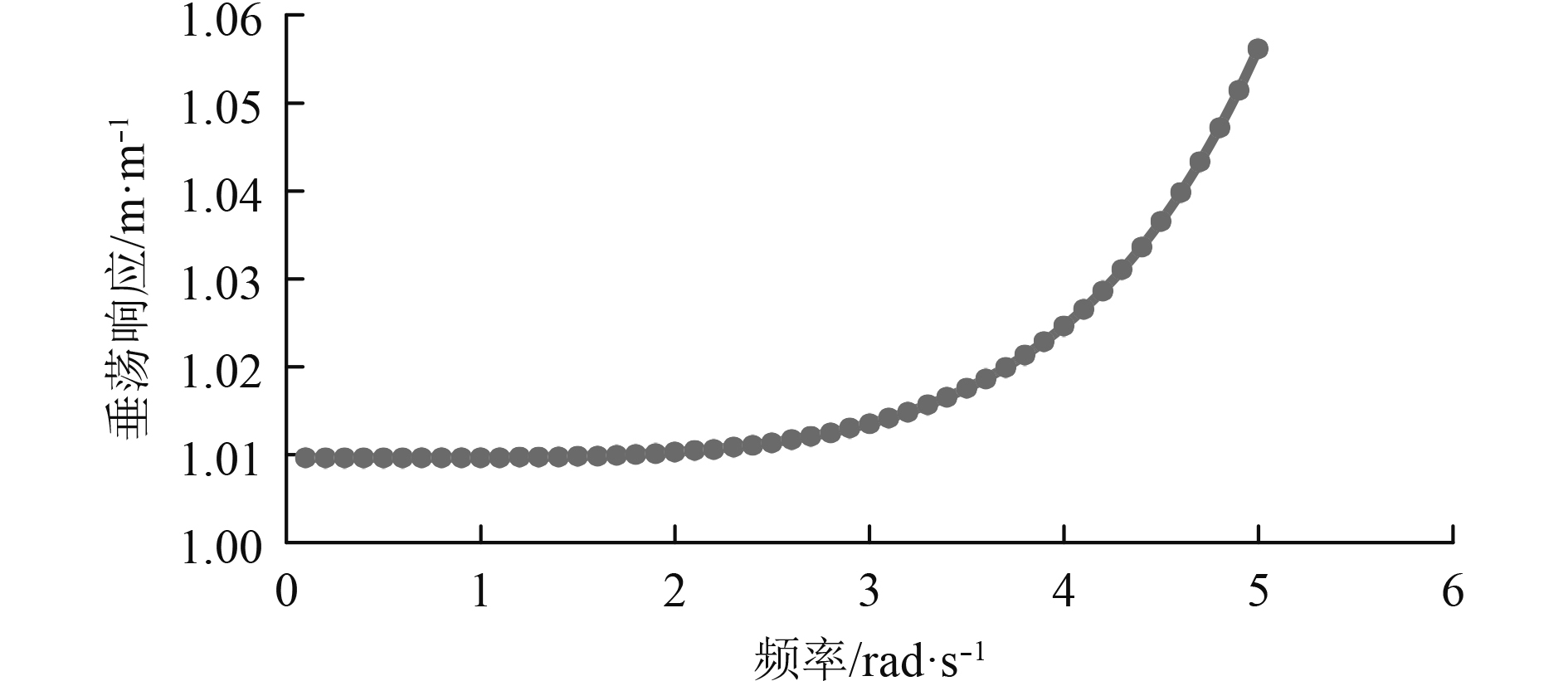
首先计算圆频率在0.1~5.0(间隔为0.1)范围内的50个波浪下垂荡的频域响应,计算结果如图4所示。本文无因次化的各项参数参照下式:
|
图 4 垂荡频响图 Fig. 4 Heave frequency response |
| ${\rm{Z'}} = \frac{Z}{h}\text{。}$ | (14) |
式中:Z为垂荡幅值;h为波高。
由垂荡的频域响应图可得,当波浪频率≤2.8时,频域响应值约等于1.01,将这部分值取出来制表得到表1。
|
|
表 1 垂荡响应结果 Tab.1 Heave response results |
根据表1数据,当波浪频率≤2.8时,响应值在1.010~1.013之间,提出补偿系数为1,其最大偏差为:
| $ \left( {1.013 - 1} \right) \div 1 = 0.013 < 2\% \text{。}$ |
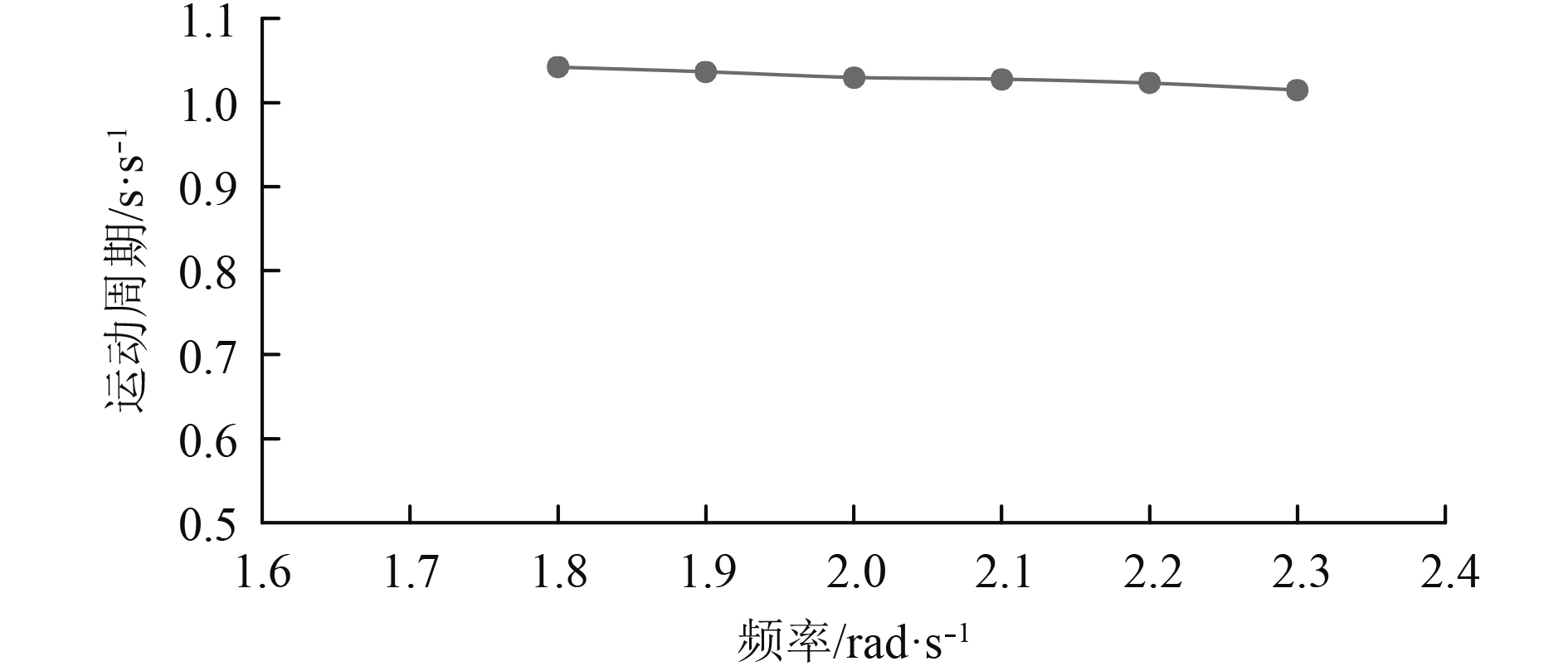
本文计算了频率从1.8~2.3(间隔为0.1)的规则波中浮标的运动响应[6],各波浪参数如表2所示。然后,从垂荡运动的数据中,读出各频率波浪中垂荡运动的周期,将运动周期无因次化之后得到图5,无因次化公式为:
| ${\rm{T'}} = \frac{T}{{{T_B}}}\text{。}$ | (15) |
式中:T为运动周期;TB为波浪周期。
由图5和表2数据可以很直观看出运动周期与波浪周期的比值稳定在1附近,所以波浪周期测试的补偿系数为1。
|
|
表 2 波浪参数及响应 Tab.2 Wave parameters and response |
|
图 5 无因次化运动周期图 Fig. 5 Dimensionless periodic diagram of motion |
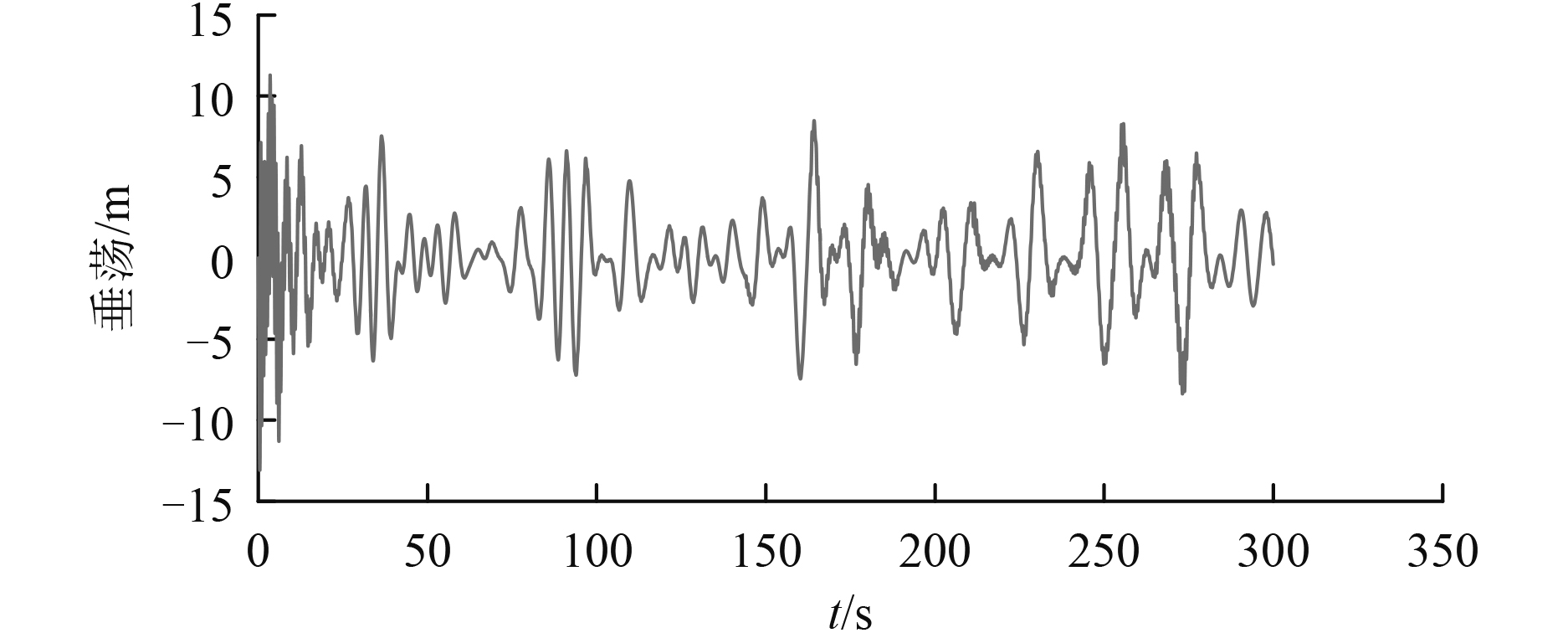
因为浮标的工作环境必然是在不规则波中,为了模拟浮标真实的工作状态,所以选取了4级海况作为浮标的工作环境计算浮标的垂荡运动响应,其计算结果如图6所示。
|
图 6 四级海况中垂荡的时域响应 Fig. 6 Time domain response of heave in four-level sea conditions |
浮标在不规则波中时域下运动响应不便于分析,为了能够分析探索运动响应的规律,将垂荡运动的时域响应转换为频域响应进行分析,运动谱密度函数是表征运动的能量在不同频率运动上的分布情况。
| ${\rm{S}}\left( w \right) = \frac{{\frac{1}{2}\xi _{an}^2}}{{\Delta w}}\left( {{m^2}.s} \right)\text{。}$ | (16) |
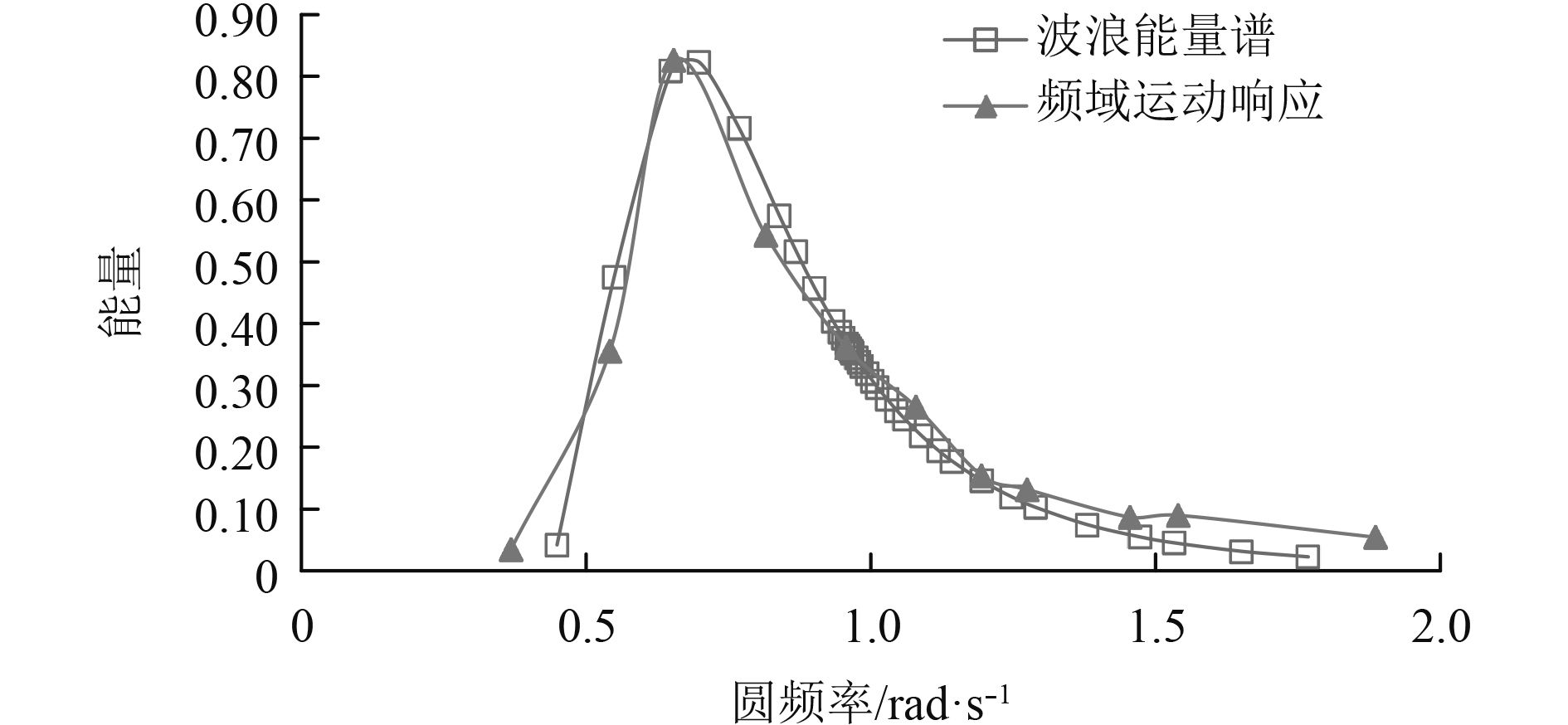
谱密度函数的估算方法有3种,即相关函数法、带通滤波法、直接傅里叶变换。其中相关函数和直接傅里叶变换较为常用[7]。将时域响应通过傅里叶变换后与调整了横纵坐标比例的波浪谱曲线整合到同一张图中之后得到图7。
|
图 7 运动频域响应和波浪谱对比图 Fig. 7 Motion frequency domain response and wave spectrum comparisons |
如图7所示,运动的频谱和波浪的频谱的趋势相似,说明浮标的随浪性比较好。
3 结 语本文的结论如下:
1)浮标的测量范围为波浪的圆频率≤2.8 rad/s;
2)基于势流理论计算了浮标在波浪中的运动响应,计算结果表明浮标的随浪性较好,波高测试补偿系数与周期测试补偿系数均为1。
| [1] |
刘国栋. 波浪浮标系统设计与测波方法研究[J]. 科学技术与工程, 2011, 11(35): 8805-8809. DOI:10.3969/j.issn.1671-1815.2011.35.030 |
| [2] |
唐原广, 康倩. 波浪浮标测波方法比较[J]. 现代电子技术, 2014, 37(422(15)): 121-122. |
| [3] |
唐原广, 王金平. SZF型波浪浮标系统[J]. 海洋技术学报, 2008, 27(2): 31-33. |
| [4] |
MORONI D, PIERI G, SALVETTI O, et al. Sensorized buoy for oil spill early detection[C] Oceans. IEEE, 2015: 1–5.
|
| [5] |
JAHANGIR M H, HOSSEINI S S, MEHRPOOYA M. A detailed theoretical modeling and parametric investigation of potential power in heaving buoys[J]. Energy, 2018. |
| [6] |
王丽元, 唐友刚, 何堃, 等. 球形波浪浮标运动性能分析[J]. 海洋技术, 2012, 31(4): 9-13. |
| [7] |
胡丽莹, 肖蓬. 快速傅里叶变换在频谱分析中的应用[J]. 福建师范大学学报(自然科学版), 2011, 27(4): 27–30.
|
 2018, Vol. 40
2018, Vol. 40
